A Fractional Hybrid Staggered-Grid Grünwald–Letnikov Method for Numerical Simulation of Viscoelastic Seismic Wave Propagation
Abstract
1. Introduction
2. Methodology
2.1. Viscoelastic Equation
2.2. Hybrid Stagged-Grid Grünwald–Letnikov (SGGL) Finite Difference Method
2.3. Stability Analysis
3. Simulations
3.1. Homogeneous Model
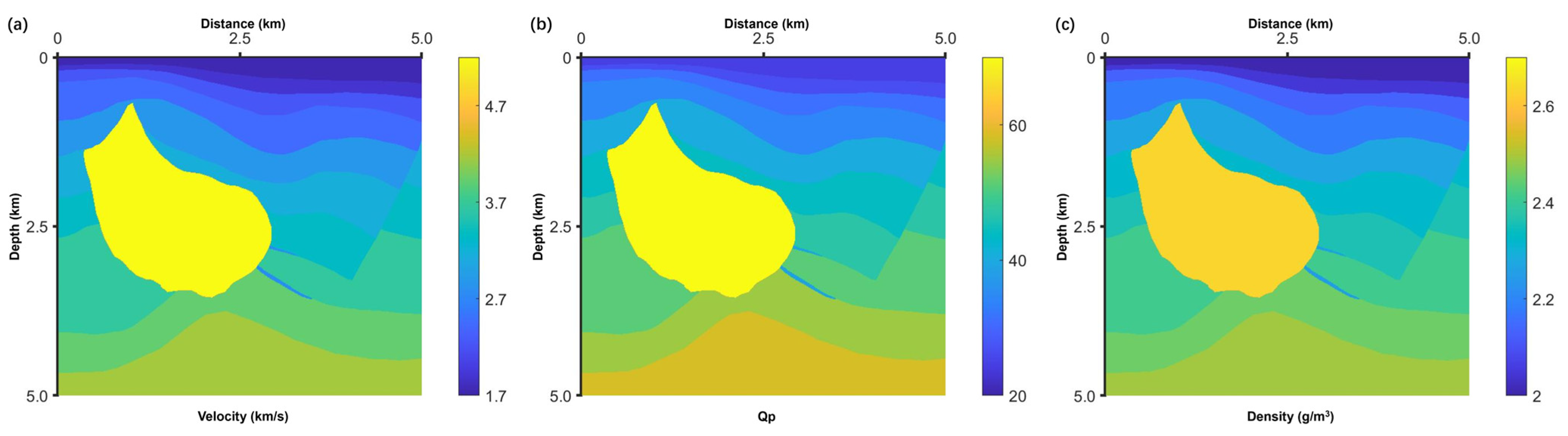
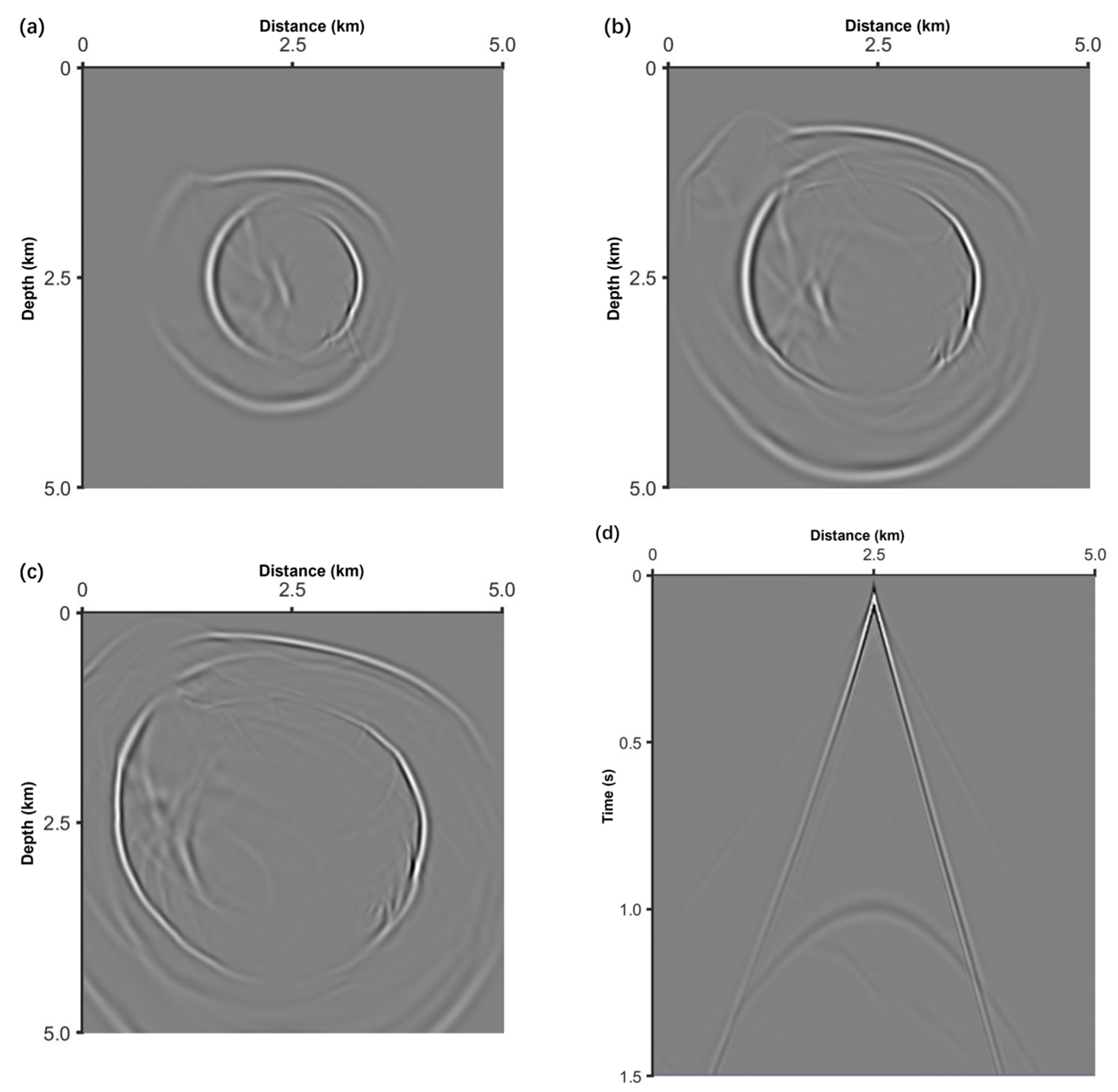
3.2. Fault Model
3.3. Hess Salt Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McDonal, F.; Angona, F.; Mills, R.; Sengbush, R.; Van Nostrand, R.; White, J. Attenuation of shear and compressional waves in Pierre shale. Geophysics 1958, 23, 421–439. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Picotti, S. Fracture-induced anisotropic attenuation. Rock Mech. Rock Eng. 2012, 45, 929–942. [Google Scholar] [CrossRef]
- Wang, Y.; Ning, Y.; Wang, Y. Fractional Time Derivative Seismic Wave Equation Modeling for Natural Gas Hydrate. Energies 2020, 13, 5901. [Google Scholar] [CrossRef]
- Li, Q.; Fu, L.Y.; Zhou, H.; Wei, W.; Hou, W. Effective Q-compensated reverse time migration using new decoupled fractional Laplacian viscoacoustic wave equation. Geophysics 2018, 84, 57–69. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, T. Strategies for stable attenuation compensation in reverse-time migration. Geophys. Prospect. 2018, 66, 498–511. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, H.; Rao, Y. An implicit stabilization strategy for Q-compensated reverse time migration. Geophysics 2020, 85, S169–S183. [Google Scholar] [CrossRef]
- Mu, X.; Huang, J. A simple and high-efficient viscoacoustic reverse time migration calculated by finite difference. Geophysics 2023, 88, S213–S223. [Google Scholar] [CrossRef]
- Li, J.; Yang, D.; Wang, Z.; Liu, L. Attenuation-compensated reverse time migration based on the stereo-modeling operator. Geophysics 2023, 88, S175–S187. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, H.; Rao, Y. Source wavefield reconstruction in fractional Laplacian viscoacoustic wave equation-based full waveform inversion. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6496–6509. [Google Scholar] [CrossRef]
- Xing, G.; Zhu, T. Decoupled Fréchet kernels based on a fractional viscoacoustic wave equation. Geophysics 2022, 87, T61–T70. [Google Scholar] [CrossRef]
- Hu, B.T.; Huang, C.; Dong, L.G.; Zhang, J.M. A constant fractional Laplacian operator based viscoacoustic full waveform inversion for velocity and attenuation estimation. Chin. J. Geophys. 2023, 66, 2123–2137. [Google Scholar]
- Bai, T.; Tsvankin, I. Time-domain finite-difference modeling for attenuative anisotropic media. Geophysics 2016, 81, C69–C77. [Google Scholar] [CrossRef]
- Kjartansson, E. Constant-Q wave propagation and attenuation. J. Geophys. Res. 1979, 84, 4737–4748. [Google Scholar] [CrossRef]
- Carcione, J.M.; Kosloff, D.; Kosloff, R. Wave propagation simulation in a linear viscoacoustic medium. Geophys. J. Int. 1988, 95, 597–611. [Google Scholar] [CrossRef]
- Carcione, J.M. A generalization of the Fourier pseudospectral method. Geophysics 2010, 75, A53–A56. [Google Scholar] [CrossRef]
- Zhu, T.; Carcione, J.M.; Harris, J.M. Approximating constant-Q seismic propagation in the time domain. Geophys. Prospect. 2013, 61, 931–940. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, T.; Zhu, H.; Liu, Y.; Xing, T.; Zhang, X. Approximating constant-Q seismic wave propagations in acoustic and elastic media using a Cole–Cole model. Bull. Seismol. Soc. Am. 2023, 113, 312–332. [Google Scholar] [CrossRef]
- Zhu, T.; Harris, J.M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians. Geophysics 2014, 79, T105–T116. [Google Scholar] [CrossRef]
- Xing, G.; Zhu, T. Modeling frequency-independent Q viscoacoustic wave propagation in heterogeneous media. J. Geophys. Res. Solid Earth 2019, 112, 11568–11584. [Google Scholar] [CrossRef]
- Mu, X.; Huang, J.; Wen, L.; Zhuang, S. Modeling viscoacoustic wave propagation using a new spatial variable-order fractional Laplacian wave equation. Geophysics 2021, 86, T487–T507. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, H.; Liu, Y.; Chen, T. Power-law frequency-dependent Q simulations in viscoacoustic media using decoupled fractional Laplacians. Geophysics 2024, 89, T183–T194. [Google Scholar] [CrossRef]
- Zhu, T.; Carcione, J.M. Theory and modelling of constant-Q P- and S-waves using fractional spatial derivatives. Geophys. J. Int. 2014, 196, 1787–1795. [Google Scholar] [CrossRef]
- Mu, X.; Huang, J.; Yang, J.; Li, Z.; Ivan, M.S. Viscoelastic wave propagation simulation using new spatial variable-order fractional Laplacians. Bull. Seismol. Soc. Am. 2022, 112, 48–77. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Zhu, H.; Chen, T.; Li, J. Modified viscoelastic wavefield simulations in the time domain using the new fractional Laplacians. J. Geophys. Eng. 2022, 19, 346–361. [Google Scholar] [CrossRef]
- Han, G.; He, B.; Zhang, H.; Wang, E. Fractional-order velocity-dilatation-rotation viscoelastic wave equation and numerical solution based on a constant-Q model. Geophysics 2024, 89, T111–T123. [Google Scholar] [CrossRef]
- Carcione, J.; Cavallini, F.; Mainardi, F. Time-domain seismic modeling of constant Q-wave propagation using fractional derivatives. Pure Appl. Geophys. 2002, 159, 1719–1736. [Google Scholar] [CrossRef]
- Carcione, J.M. Theory and modeling of constant-Q P- and S waves using fractional time derivatives. Geophysics 2009, 74, T1–T11. [Google Scholar] [CrossRef]
- Zhu, T. Numerical simulation of seismic wave propagation in viscoelastic-anisotropic media using frequency-independent Q wave equation. Geophysics 2017, 82, WA1–WA10. [Google Scholar] [CrossRef]
- Carcione, J.M.; Picotti, S.; Ba, J. P- and S-wave simulation using a Cole-Cole model to incorporate thermoelastic attenuation and dispersion. J. Acoust. Soc. Am. 2021, 149, 1946–1954. [Google Scholar] [CrossRef]
- Chen, W.; Holm, S. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. J. Acoust. Soc. Am. 2004, 115, 1424–1430. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Cox, B.T. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. J. Acoust. Soc. Am. 2010, 127, 2741–2748. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, T.; Fomel, S. Viscoacoustic modeling and imaging using low-rank approximation. Geophysics 2015, 80, A103–A108. [Google Scholar] [CrossRef]
- Chen, H.; Zhou, H.; Li, Q.; Wang, Y. Two efficient modeling schemes for fractional Laplacian viscoacoustic wave equation. Geophysics 2016, 81, T233–T249. [Google Scholar] [CrossRef]
- Wang, N.; Xing, G.; Zhu, T. Accurately propagating P- and S-waves in attenuation media using spatial-independent-order decoupled fractional Laplacians. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 2019; pp. 3805–3809. [Google Scholar]
- Xue, Z.; Baek, H.; Zhang, H.; Zhao, Y.; Zhu, T.; Fomel, S. Solving fractional Laplacian viscoelastic wave equations using domain decomposition. In Proceedings of the 2018 SEG International Exposition and Annual Meeting, Anaheim, CA, USA, 14–19 October 2018; pp. 3943–3947. [Google Scholar]
- Gu, B.; Zhang, S.; Liu, X.; Han, J. Efficient modeling of fractional Laplacian viscoacoustic wave equation with fractional finite-difference method. Comput. Geosci. 2024, 191, 0098–3004. [Google Scholar] [CrossRef]
- Yao, J.; Zhu, T.; Hussain, F.; Kouri, D.J. Locally solving fractional Laplacian viscoacoustic wave equation using Hermite distributed approximating functional method. Geophysics 2017, 82, T59–T67. [Google Scholar] [CrossRef]
- Ji, M.; Kouri, D.; Zhu, T.; Yao, J. Using PSPI to accelerate seismic Q modeling based on Hermite-distributed approximating functional. In Proceedings of the 2017 SEG International Exposition and Annual Meeting, Houston, TX, USA, 27 September 2017; pp. 4091–4096. [Google Scholar]
- Song, G.; Zhang, X.; Wang, Z.; Chen, Y.; Chen, P. The asymptotic local finite difference method of the fractional wave equation and its viscous seismic wavefield simulation. Geophysics 2020, 85, T179–T189. [Google Scholar] [CrossRef]
- Moczo, P.; Kristek, J.; Halada, L. 3D Fourth-order staggered grid finite-difference schemes: Stability and grid dispersion. Bull. Seismol. Soc. Am. 2000, 90, 587–603. [Google Scholar] [CrossRef]
- Li, Q. High Resolution Seismic Data Processing; Petroleum Industry Press: Beijing, China, 1993. [Google Scholar]
- Yan, H.; Liu, Y. Visco-acoustic prestack reverse-time migration based on the time-space domain adaptive high-order finite-difference method. Geophys. Prospect. 2013, 61, 941–954. [Google Scholar] [CrossRef]
- Komatitsch, D.; Martin, R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics 2007, 72, SM155–SM167. [Google Scholar] [CrossRef]




| Truncated Relative Error | ||||
|---|---|---|---|---|
| QP | 10 × 10−2 | 10 × 10−3 | 10 × 10−4 | 10 × 10−5 |
| ) | 2 | 3 | 8 | 24 |
| ) | 3 | 5 | 13 | 40 |
| ) | 3 | 5 | 15 | 44 |
| ) | 4 | 7 | 18 | 54 |
| ) | 4 | 8 | 22 | 67 |
| ) | 5 | 9 | 24 | 71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Song, G.; Chen, P.; Wang, D. A Fractional Hybrid Staggered-Grid Grünwald–Letnikov Method for Numerical Simulation of Viscoelastic Seismic Wave Propagation. Fractal Fract. 2025, 9, 153. https://doi.org/10.3390/fractalfract9030153
Zhang X, Song G, Chen P, Wang D. A Fractional Hybrid Staggered-Grid Grünwald–Letnikov Method for Numerical Simulation of Viscoelastic Seismic Wave Propagation. Fractal and Fractional. 2025; 9(3):153. https://doi.org/10.3390/fractalfract9030153
Chicago/Turabian StyleZhang, Xinmin, Guojie Song, Puchun Chen, and Dan Wang. 2025. "A Fractional Hybrid Staggered-Grid Grünwald–Letnikov Method for Numerical Simulation of Viscoelastic Seismic Wave Propagation" Fractal and Fractional 9, no. 3: 153. https://doi.org/10.3390/fractalfract9030153
APA StyleZhang, X., Song, G., Chen, P., & Wang, D. (2025). A Fractional Hybrid Staggered-Grid Grünwald–Letnikov Method for Numerical Simulation of Viscoelastic Seismic Wave Propagation. Fractal and Fractional, 9(3), 153. https://doi.org/10.3390/fractalfract9030153








