Certain Analytic Solutions for Time-Fractional Models Arising in Plasma Physics via a New Approach Using the Natural Transform and the Residual Power Series Methods
Abstract
1. Introduction
2. Preliminaries
3. Natural Transformation and Fractional Expansion
4. A Description of the Proposed NRPS Method
5. Applications
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saha, A.; Banerjee, S. Dynamical Systems and Nonlinear Waves in Plasmas; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Varghese, S.S.; Singh, K.; Kourakis, I. Electrostatic Supersolitary Waves: A Challenging Paradigm in Nonlinear Plasma Science and Beyond—State of the Art and Overview of Recent Results. Fundam. Plasma Phys. 2024, 10, 100048. [Google Scholar] [CrossRef]
- Altuijri, R.; Abdel-Aty, A.H.; Nisar, K.S.; Khater, M. Exploring novel wave characteristics in a nonlinear model with complexity arising in plasma physics. Opt. Quantum Electron. 2024, 56, 1128. [Google Scholar] [CrossRef]
- Johnson, R.S. Water waves and Korteweg–de Vries equations. J. Fluid Mech. 1980, 97, 701–719. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Alsaedi, B. Contraction of variational principle and optical soliton solutions for two models of nonlinear Schrodinger equation with polynomial law nonlinearity. AIMS Math. 2024, 9, 6336–6367. [Google Scholar]
- Mubaraki, A.M.; Nuruddeen, R.I.; Ali, K.K.; Gómez-Aguilar, J.F. Additional solitonic and other analytical solutions for the higher-order Boussinesq-Burgers equation. Opt. Quantum Electron. 2024, 56, 165. [Google Scholar] [CrossRef]
- Gulay, T.A.; Zakharov, V.V.; Kron, R.V.; Popova, S.V.; Shibaev, V.P. Algorithmic support of the integrated aircraft control system using the systems embedding technology. AIP Conf. Proc. 2024, 2969, 060009. [Google Scholar]
- Halcrow, C.; John, R.R.; Anusree, N. Modified sine-Gordon theory with static multikinks. Phys. Rev. D 2024, 110, 065010. [Google Scholar] [CrossRef]
- Sagib, M.; Hossain, M.A.; Saha, B.K.; Khan, K. On traveling wave solutions with stability and phase plane analysis for the modified Benjamin-Bona-Mahony equation. PLoS ONE 2024, 19, e0306196. [Google Scholar]
- Hosseini, K.; Hincal, E.; Sadri, K.; Rabiei, F.; Ilie, M.; Akgül, A.; Osman, M.S. The positive multi-complexiton solution to a generalized Kadomtsev–Petviashvili equation. Partial Differ. Equ. Appl. Math. 2024, 9, 100647. [Google Scholar]
- Faridi, W.A.; Iqbal, M.; Riaz, M.B.; AlQahtani, S.A.; Wazwaz, A.M. The fractional soliton solutions of dynamical system arising in plasma physics: The comparative analysis. Alex. Eng. J. 2024, 95, 247–261. [Google Scholar] [CrossRef]
- Alam, M.M.; Alam, M.S. Study of Time-Fractional Dust Ion Acoustic Waves Propagation in Collisionless Unmagnetized Dusty Plasmas. Braz. J. Phys. 2024, 54, 192. [Google Scholar]
- Phoosree, S.; Khongnual, N.; Sanjun, J.; Kammanee, A.; Thadee, W. Riccati sub-equation method for solving fractional flood wave equation and fractional plasma physics equation. Partial Differ. Equ. Appl. Math. 2024, 10, 100672. [Google Scholar] [CrossRef]
- Abdelwahed, H.G.; El-Shewy, E.K.; Alghanim, S.; Abdelrahman, M.A. On the physical fractional modulations on Langmuir plasma structures. Fractal Fract. 2022, 6, 430. [Google Scholar] [CrossRef]
- Poolcharuansin, P.; Bradley, J.W. Short-and long-term plasma phenomena in a HiPIMS discharge. Plasma Sources Sci. Technol. 2010, 19, 025010. [Google Scholar] [CrossRef]
- Alsatami, K.A. Exploring Nonlinear Fractional (2+1)-Dimensional KP–Burgers Model: Derivation and Ion Acoustic Solitary Wave Solution. Int. J. Anal. Appl. 2024, 22, 147. [Google Scholar] [CrossRef]
- Alabedalhadi, M.; Al-Omari, S.; Al-Smadi, M.; Alhazmi, S. Traveling wave solutions for time-fractional mKdV-ZK equation of weakly nonlinear ion-acoustic waves in magnetized electron–positron plasma. Symmetry 2023, 15, 361. [Google Scholar] [CrossRef]
- Lazarus, I.J.; Bharuthram, R.; Hellberg, M.A. Modified Korteweg–de Vries–Zakharov–Kuznetsov solitons in symmetric two-temperature electron–positron plasmas. J. Plasma Phys. 2008, 74, 519–529. [Google Scholar] [CrossRef]
- Verheest, F.; Mace, R.L.; Pillay, S.R.; Hellberg, M.A. Unified derivation of Korteweg-de Vries-Zakharov-Kuznetsov equations in multispecies plasmas. J. Phys. A Math. Gen. 2002, 35, 795. [Google Scholar]
- Zhou, T.Y.; Tian, B.; Zhang, C.R.; Liu, S.H. Auto-Bäcklund transformations, bilinear forms, multiple-soliton, quasi-soliton and hybrid solutions of a (3+1)-dimensional modified Korteweg-de Vries-Zakharov-Kuznetsov equation in an electron-positron plasma. Eur. Phys. J. Plus 2022, 137, 912. [Google Scholar] [CrossRef]
- Rehman, H.U.; Seadawy, A.R.; Younis, M.; Rizvi ST, R.; Anwar, I.; Baber, M.Z.; Althobaiti, A. Weakly nonlinear electron-acoustic waves in the fluid ions propagated via a (3+1)-dimensional generalized Korteweg–de-Vries–Zakharov–Kuznetsov equation in plasma physics. Results Phys. 2022, 33, 105069. [Google Scholar]
- Younas, U.; Ren, J.; Baber, M.Z.; Yasin, M.W.; Shahzad, T. Ion-acoustic wave structures in the fluid ions modeled by higher dimensional generalized Korteweg-de Vries–Zakharov–Kuznetsov equation. J. Ocean Eng. Sci. 2023, 8, 623–635. [Google Scholar] [CrossRef]
- Alhami, R.; Alquran, M. Extracted different types of optical lumps and breathers to the new generalized stochastic potential-KdV equation via using the Cole-Hopf transformation and Hirota bilinear method. Opt. Quantum Electron. 2022, 54, 553. [Google Scholar] [CrossRef]
- Alquran MA RW, A.N. Investigating the revisited generalized stochastic potential-KdV equation: Fractional time-derivative against proportional time-delay. Rom. J. Phys. 2023, 68, 106. [Google Scholar]
- Abbas, N.; Hussain, A.; Riaz, M.B.; Ibrahim, T.F.; Birkea, F.O.; Tahir, R.A. A discussion on the Lie symmetry analysis, travelling wave solutions and conservation laws of new generalized stochastic potential-KdV equation. Results Phys. 2024, 56, 107302. [Google Scholar] [CrossRef]
- Wu TY, T. Generation of upstream advancing solitons by moving disturbances. J. Fluid Mech. 1987, 184, 75–99. [Google Scholar]
- Derakhshan, M.H.; Aminataei, A. A numerical method for finding solution of the distributed-order time-fractional forced Korteweg–de Vries equation including the Caputo fractional derivative. Math. Methods Appl. Sci. 2022, 45, 3144–3165. [Google Scholar] [CrossRef]
- Veeresha, P.; Yavuz, M.; Baishya, C. A computational approach for shallow water forced Korteweg–De Vries equation on critical flow over a hole with three fractional operators. Int. J. Optim. Control Theor. Appl. (IJOCTA) 2021, 11, 52–67. [Google Scholar] [CrossRef]
- Alhejaili, W.; Az-Zo’bi, E.; Shah, R.; El-Tantawy, S.A. On the analytical soliton approximations to fractional forced Korteweg-de Vries equation arising in fluids and Plasmas using two novel techniques. Commun. Theor. Phys. 2024, 76, 085001. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Al-Smadi, M.; Momani, S.; Hayat, T. Numerical solutions of fuzzy differential equations using reproducing kernel Hilbert space method. Soft Comput. 2016, 20, 3283–3302. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Freihat, A.; Khalil, H.; Momani, S.; Ali Khan, R. Numerical multistep approach for solving fractional partial differential equations. Int. J. Comput. Methods 2017, 14, 1750029. [Google Scholar] [CrossRef]
- Hasan, S.; El-Ajou, A.; Hadid, S.; Al-Smadi, M.; Momani, S. Atangana-Baleanu fractional framework of reproducing kernel technique in solving fractional population dynamics system. Chaos Solitons Fractals 2020, 133, 109624. [Google Scholar]
- Momani, S.; Freihat, A.; Al-Smadi, M. Analytical Study of Fractional-Order Multiple Chaotic FitzHugh-Nagumo Neurons Model Using Multistep Generalized Differential Transform Method. Abstr. Appl. Anal. 2014, 2014, 276279. [Google Scholar] [CrossRef]
- Al-Smadi, M.; Gumah, G. On the homotopy analysis method for fractional SEIR epidemic model. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 3809–3820. [Google Scholar]
- Khalil, H.; Khan, R.A.; HAl-Smadi, M.; Freihat, A.A. Approximation of solution of time fractional order three-dimensional heat conduction problems with Jacobi Polynomials. Punjab Univ. J. Math. 2020, 47, 35–56. [Google Scholar]
- Heydari, M.H.; Zhagharian, S.; Razzaghi, M. Discrete Chebyshev polynomials for the numerical solution of stochastic fractional two-dimensional Sobolev equation. Commun. Nonlinear Sci. Numer. Simul. 2024, 130, 107742. [Google Scholar] [CrossRef]
- Sivasankar, K.; Nadhaprasadh, M.; Sathish, K.; Al-Omari, S.; Udhayakuma, R. New study on Cauchy problems of fractional stochastic evolution systems on an infinite interval. Math. Methods Appl. Sci. 2024, 48, 890–904. [Google Scholar]
- Roul, P.; Rohil, V. A high-accuracy computational technique based on L 2-1 σ and B-spline schemes for solving the nonlinear time-fractional Burgers’ equation. Soft Comput. 2024, 28, 6153–6169. [Google Scholar]
- Nawaz, R.; Fewster-Young, N.; Katbar, N.M.; Ali, N.; Zada, L.; Ibrahim, R.W.; Alqahtani, H. Numerical inspection of (3 + 1)-perturbed Zakharov–Kuznetsov equation via fractional variational iteration method with Caputo fractional derivative. Numer. Heat Transf. Part B Fundam. 2024, 85, 1162–1177. [Google Scholar]
- Momani, S.; Odibat, Z.; Alawneh, A. Variational iteration method for solving the space-and time-fractional KdV equation. Numer. Methods Partial Differ. Equ. Int. J. 2008, 24, 262–271. [Google Scholar]
- El-Wakil, S.A.; Abulwafa, E.M.; Zahran, M.A.; Mahmoud, A.A. Time-fractional KdV equation: Formulation and solution using variational methods. Nonlinear Dyn. 2011, 65, 55–63. [Google Scholar]
- Bulut, H.; Pandir, Y.; Demiray, S.T. Exact solutions of time-fractional KdV equations by using generalized Kudryashov method. Int. J. Model. Optim. 2014, 4, 315. [Google Scholar]
- Arqub, O.A.; El-Ajou, A.; Momani, S. Constructing and predicting solitary pattern solutions for nonlinear time-fractional dispersive partial differential equations. J. Comput. Phys. 2015, 293, 385–399. [Google Scholar]
- Abu Arqub, O. Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space. Fundam. Inform. 2019, 166, 87–110. [Google Scholar] [CrossRef]
- Tchier, F.; Inc, M.; Korpinar, Z.S.; Baleanu, D. Solutions of the time fractional reaction–diffusion equations with residual power series method. Adv. Mech. Eng. 2016, 8, 1687814016670867. [Google Scholar]
- El-Ajou, A. Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach. Eur. Phys. J. Plus 2021, 136, 229. [Google Scholar]
- Džrbašjan, M.M. A generalized Riemann-Liouville operator and some of its applications. Math. USSR-Izv. 1968, 2, 1027. [Google Scholar]
- Farman, M.; Alfiniyah, C. A constant proportional caputo operator for modeling childhood disease epidemics. Decis. Anal. J. 2024, 10, 100393. [Google Scholar]
- Trujillo, J.J.; Scalas, E.; Diethelm, K.; Baleanu, D. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016; Volume 5. [Google Scholar]
- Sivasankar, S.; Udhayakumar, R.; Muthukumaran, V.; Gokul, G.; Al-Omari, S. Existence of Hilfer fractional neutral stochastic differential systemswith infinite delay, Bulletin of the Karaganda University. Math. Ser. 2024, 1, 119–174. [Google Scholar]
- Belgacem FB, M.; Silambarasan, R.; Sivasundaram, S. Advances in the natural transform. AIP Conf. Proc.-Am. Inst. Phys. 2012, 1493, 106. [Google Scholar]
- Rawashdeh, M.S.; Al-Jammal, H. New approximate solutions to fractional nonlinear systems of partial differential equations using the FNDM. Adv. Differ. Equ. 2016, 2016, 235. [Google Scholar]
- Maitama, S.; Zhao, W. Beyond Sumudu transform and natural transform: J-transform properties and applications. J. Appl. Anal. Comput. 2020, 10, 1223–1241. [Google Scholar]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
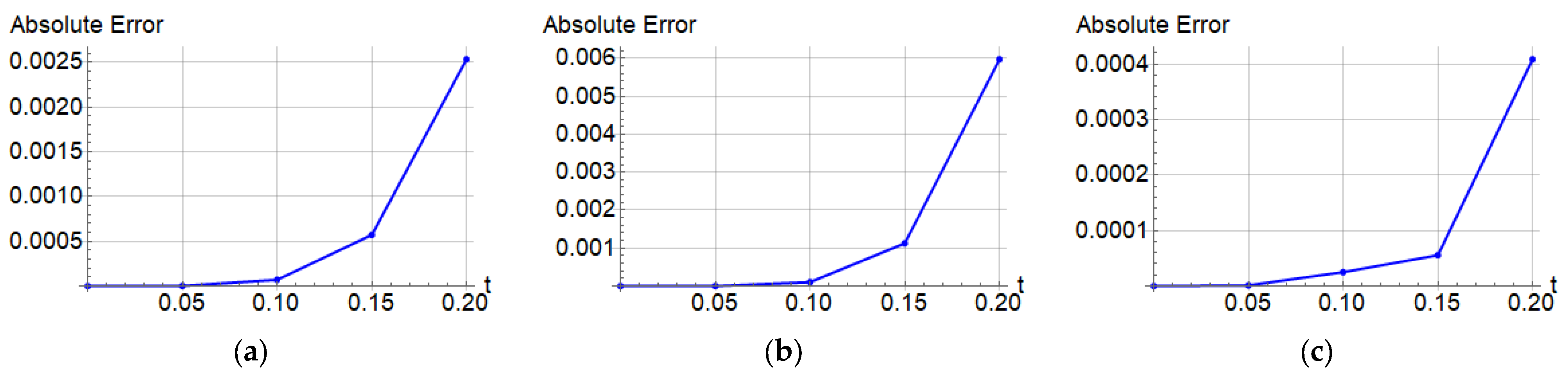

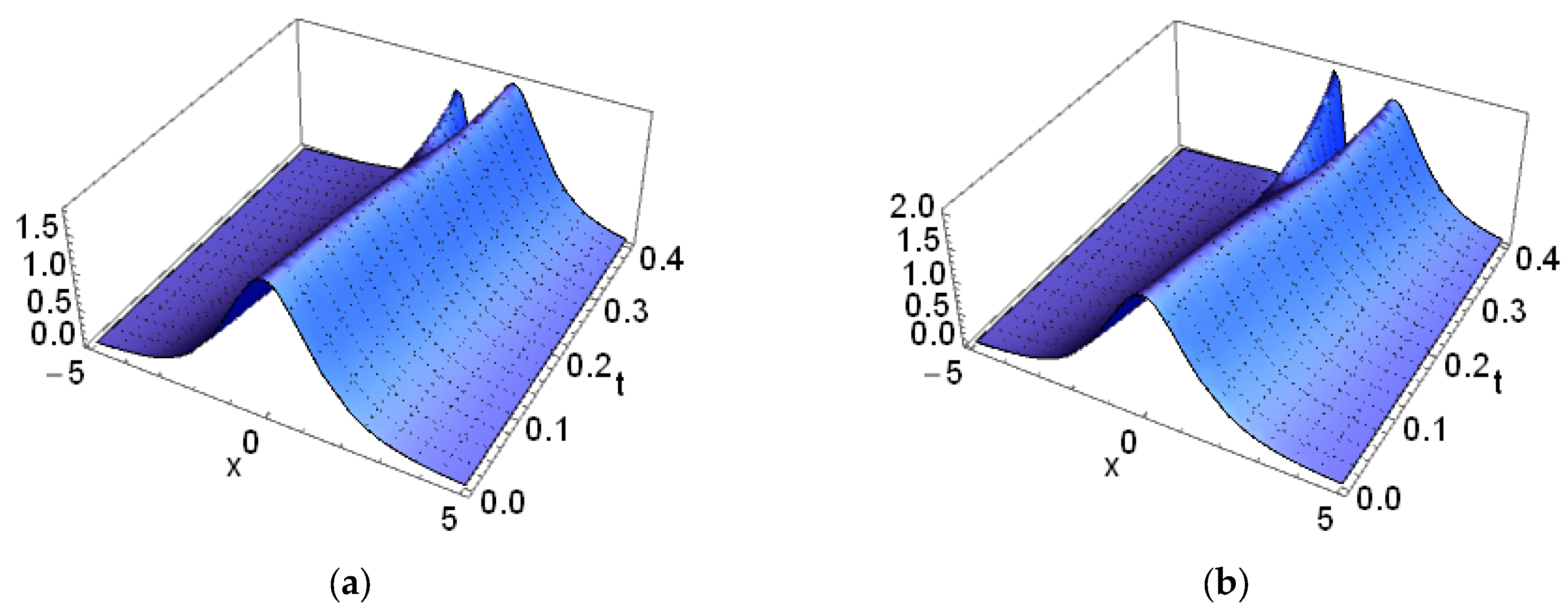

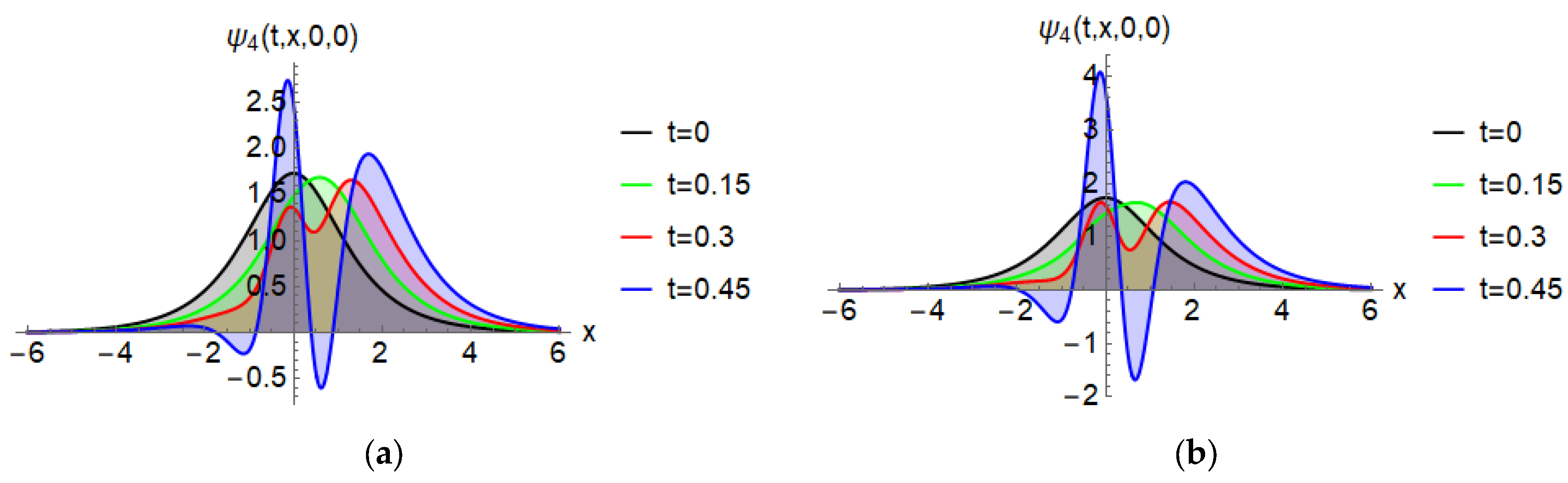
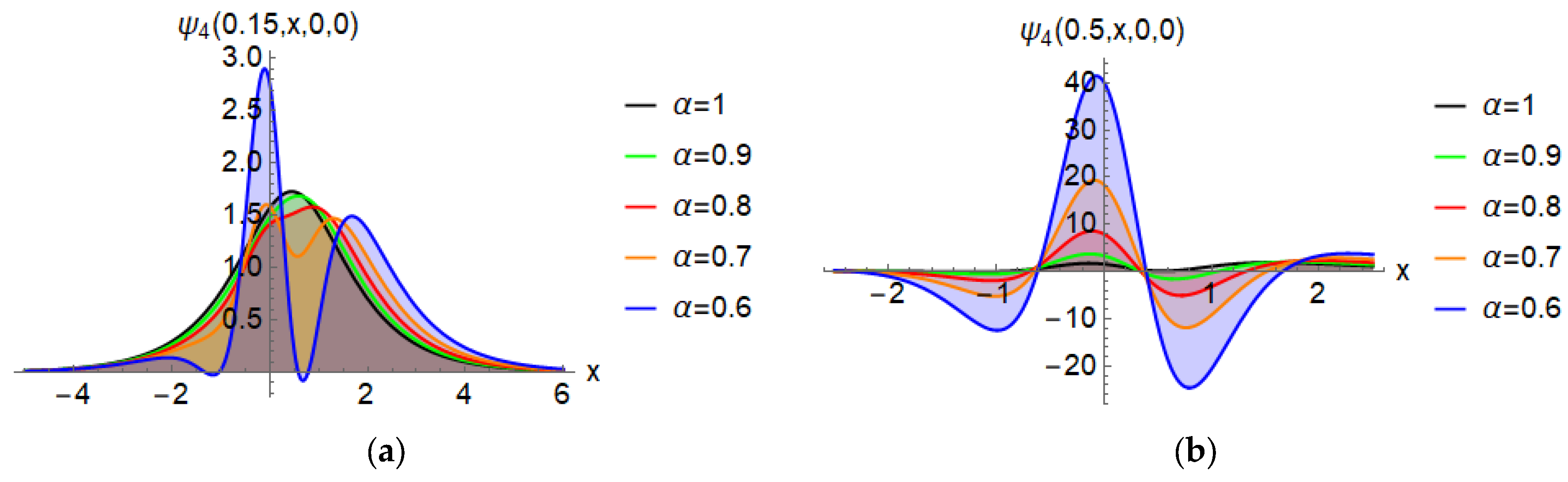
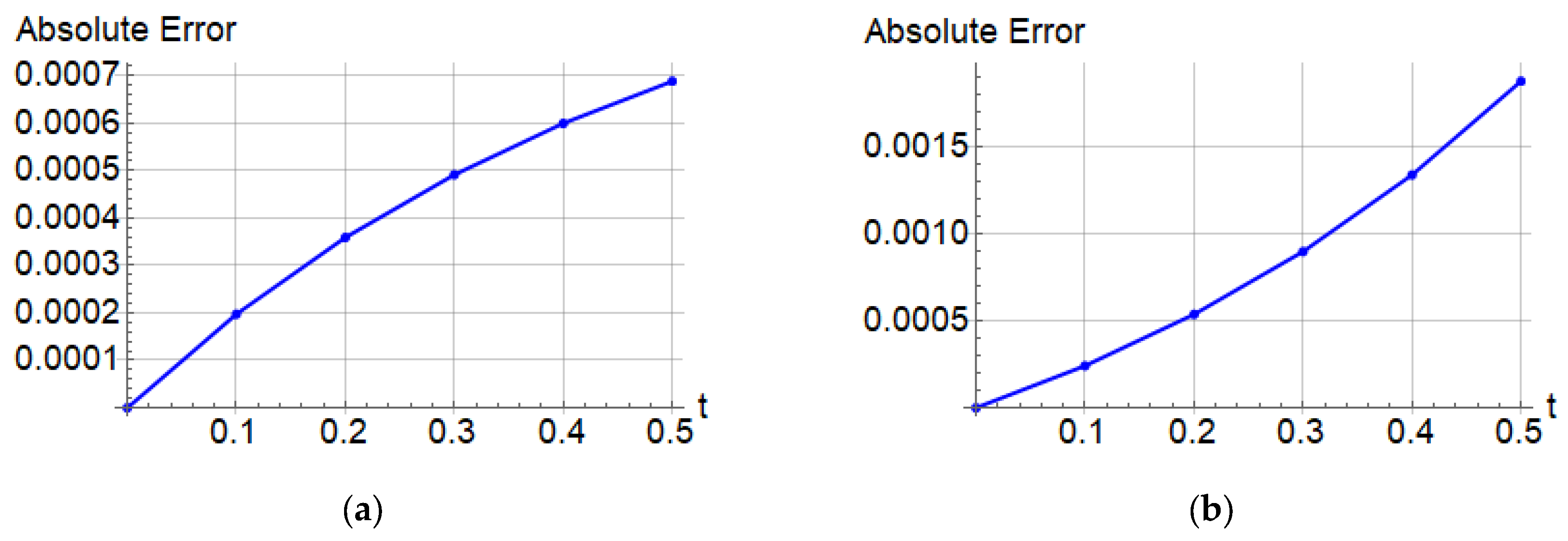
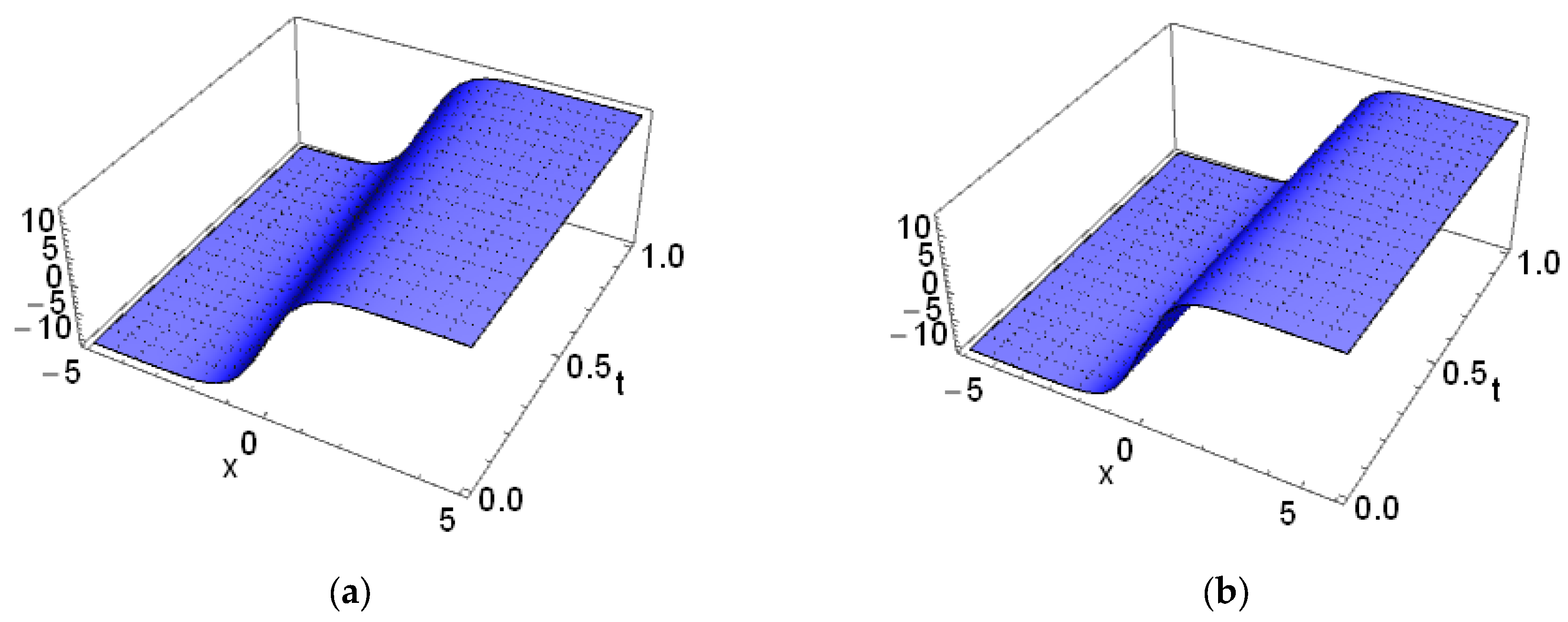




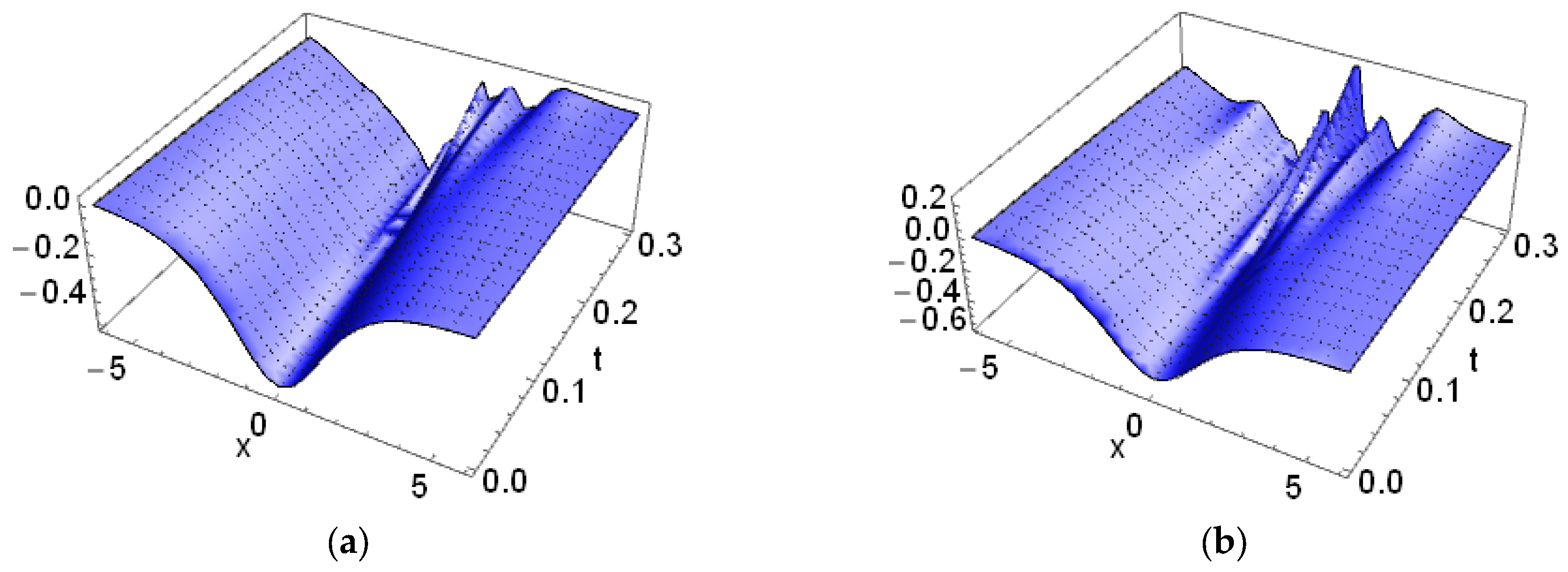
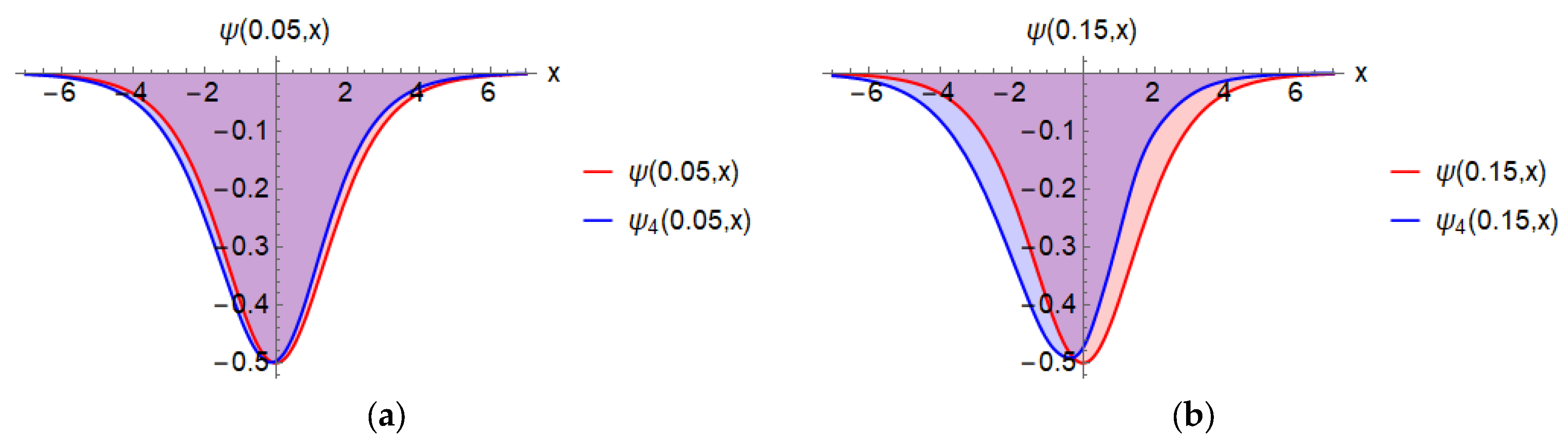
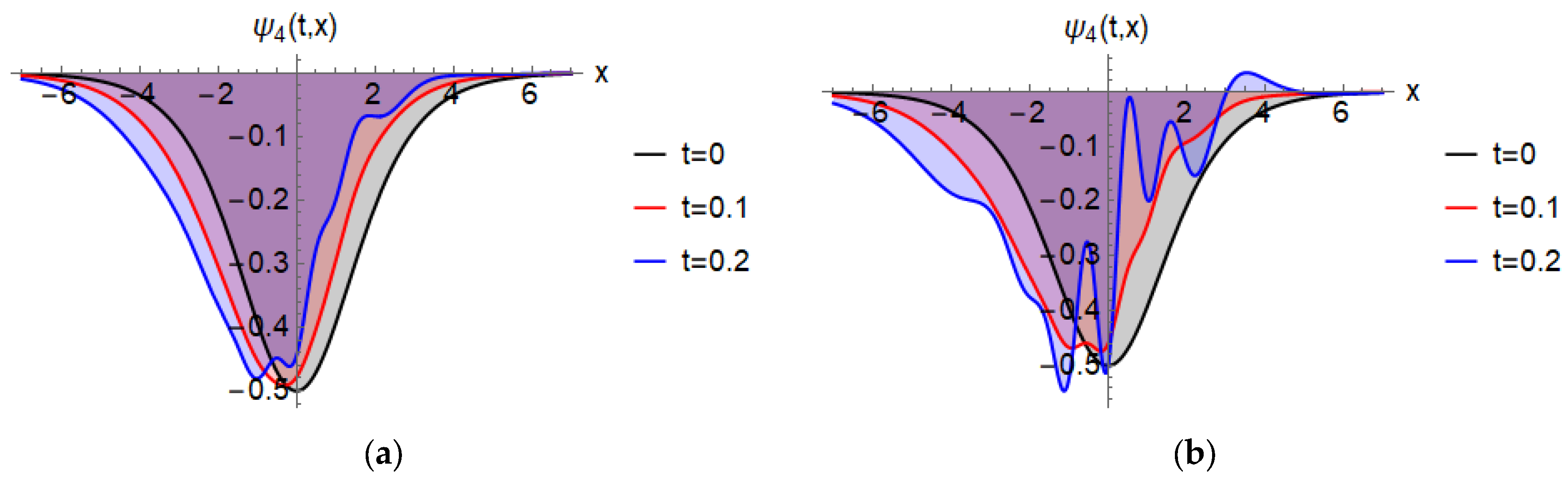
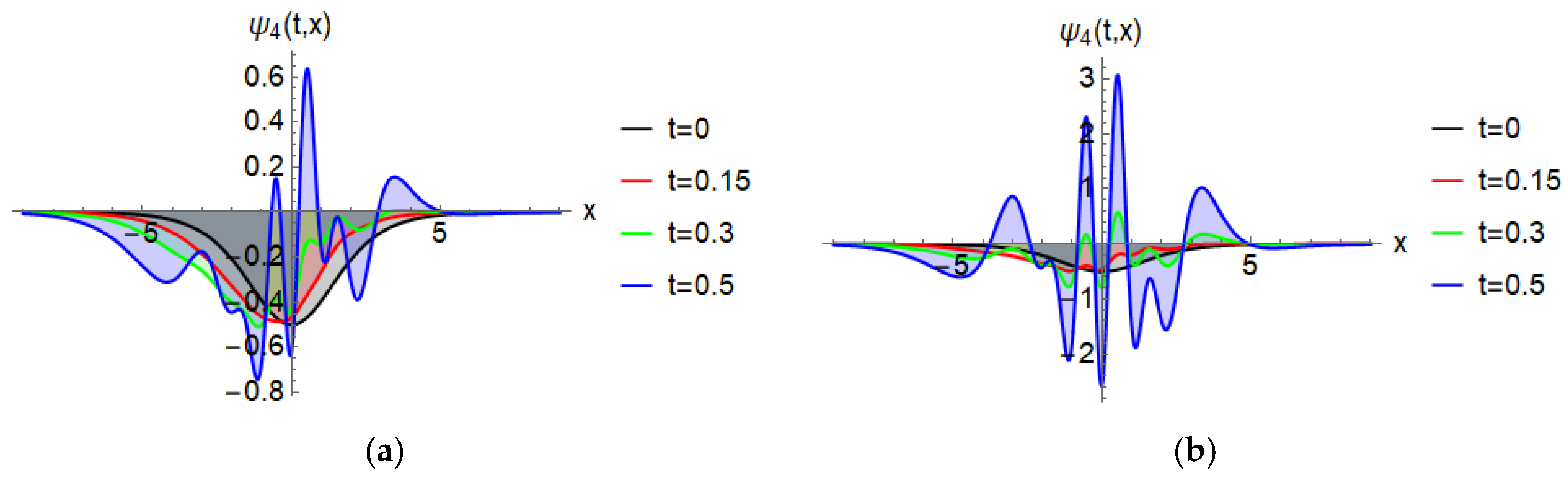
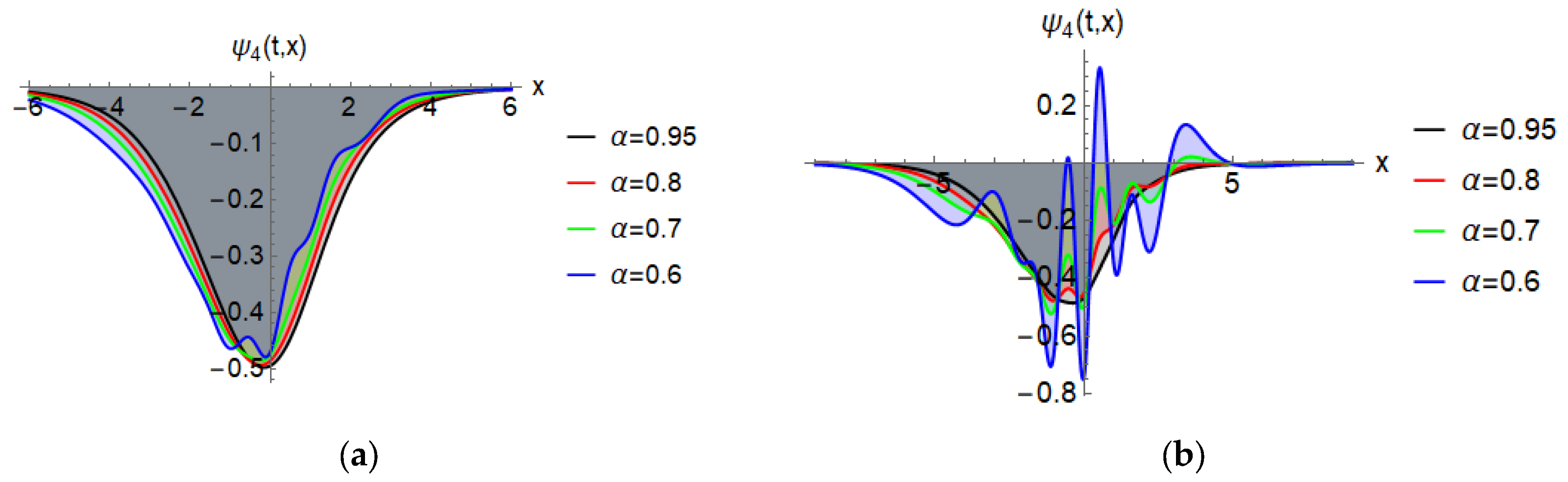

| Exact Solution | NRPS Solution | Absolute Error | Relative Error | CPU Time | ||
|---|---|---|---|---|---|---|
| Exact Solution | NRPS Solution | Absolute Error | Relative Error | CPU Time | ||
|---|---|---|---|---|---|---|
| Exact Solution | NRPS Solution | Absolute Error | Relative Error | CPU Time | ||
|---|---|---|---|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freihat, A.; Alabedalhadi, M.; Al-Omari, S.; Alhazmi, S.E.; Momani, S.; Al-Smadi, M. Certain Analytic Solutions for Time-Fractional Models Arising in Plasma Physics via a New Approach Using the Natural Transform and the Residual Power Series Methods. Fractal Fract. 2025, 9, 152. https://doi.org/10.3390/fractalfract9030152
Freihat A, Alabedalhadi M, Al-Omari S, Alhazmi SE, Momani S, Al-Smadi M. Certain Analytic Solutions for Time-Fractional Models Arising in Plasma Physics via a New Approach Using the Natural Transform and the Residual Power Series Methods. Fractal and Fractional. 2025; 9(3):152. https://doi.org/10.3390/fractalfract9030152
Chicago/Turabian StyleFreihat, Asad, Mohammed Alabedalhadi, Shrideh Al-Omari, Sharifah E. Alhazmi, Shaher Momani, and Mohammed Al-Smadi. 2025. "Certain Analytic Solutions for Time-Fractional Models Arising in Plasma Physics via a New Approach Using the Natural Transform and the Residual Power Series Methods" Fractal and Fractional 9, no. 3: 152. https://doi.org/10.3390/fractalfract9030152
APA StyleFreihat, A., Alabedalhadi, M., Al-Omari, S., Alhazmi, S. E., Momani, S., & Al-Smadi, M. (2025). Certain Analytic Solutions for Time-Fractional Models Arising in Plasma Physics via a New Approach Using the Natural Transform and the Residual Power Series Methods. Fractal and Fractional, 9(3), 152. https://doi.org/10.3390/fractalfract9030152








