Improved Hermite–Hadamard Inequality Bounds for Riemann–Liouville Fractional Integrals via Jensen’s Inequality

Abstract

This paper derives the sharp bounds for Hermite–Hadamard inequalities in the context of Riemann–Liouville fractional integrals. A generalization of Jensen’s inequality called the Jensen–Mercer inequality is used for general points to find the new and refined bounds of fractional Hermite–Hadamard inequalities. The existing Hermite–Hadamard inequalities in classical or fractional calculus have been proved for convex functions, typically involving only two points as in Jensen’s inequality. By applying the general points in Jensen–Mercer inequalities, we extend the scope of the existing results, which were previously proved for two points in the Jensen’s inequality or the Jensen–Mercer inequality. The use of left and right Riemann–Liouville fractional integrals in inequalities is challenging because of the general values involved in the Jensen–Mercer inequality, which we overcame by considering different cases. The use of the Jensen–Mercer inequality for general points to prove the refined bounds is a very interesting finding of this work, because it simultaneously generalizes many existing results in fractional and classical calculus. The application of these new results is demonstrated through error analysis of numerical integration formulas. To show the validity and significance of the findings, various numerical examples are tested. The numerical examples clearly demonstrate the significance of this new approach, as using more points in the Jensen–Mercer inequality leads to sharper bounds.

1. Introduction

Jensen’s Inequality (JI) has a big role in pure and applied mathematics. Particularly in probability theory, JI is useful in establishing bounds for variances and expectations [1]. In optimization theory, JI is useful in algorithms involving the gradient descent method [2], and in information theory it is helpful for establishing inequalities involving mutual information and entropy [3]. The applications of JI can be found in mathematical analysis and economics [4,5,6,7]. JI is defined for a convex function $\stackrel{\sim }{Ƒ}:\left[{\lambda }_1,{\lambda }_2\right]\to \mathbb{R}$ as:

$$\stackrel{\sim }{Ƒ}\left(\sum _{j=1}^n{w}_j{x}_j\right)\le \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(x_j\right),$$

(1)

where $w_j\in \left[0,1\right]$, ${\sum }_{j=1}^n{w}_j=1$, and $x_j\in \left[{\lambda }_1,{\lambda }_2\right]$, $j=1,2,3,\dots ,n.$ Another extension of inequality (1) can be found in [8].

Mercer [9] also provided a new variant of inequality (1) as well as the following inequality for convex function $\stackrel{\sim }{Ƒ}:\left[{\lambda }_1,{\lambda }_2\right]\to \mathbb{R}:$

$$\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\sum _{j=1}^n{w}_j{x}_j\right)\le \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(x_j\right),$$

(2)

where $w_j\in \left[0,1\right]$, ${\sum }_{j=1}^n{w}_j=1$, and $x_j\in \left[{\lambda }_1,{\lambda }_2\right]$, $j=1,2,3,\dots ,n.$ The inequality (2) is known as the Jensen–Mercer inequality and some extensions of this inequality are also provided for convex and general convex functions in [10,11].

In [12], the authors provided a new extension of the single inequality (2) in the form of double inequality for a convex function $\stackrel{\sim }{Ƒ}:\left[{\lambda }_1,{\lambda }_2\right]\to \mathbb{R}$ as follows:

$$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right),\hfill \end{array}$$

(3)

where $a^{*}={\sum }_{j=1}^n{w}_j{a}_j$, $s,w_j\in \left[0,1\right]$, ${\sum }_{j=1}^n{w}_j=1$, and $a_j\in \left[{\lambda }_1,{\lambda }_2\right]$, $j=1,2,3,\dots ,n.$

From inequality (3), one can observe that there is another term that lies between the left and right part of the inequality (2). These findings are very interesting and significant in the field of convex analysis. The inequality (3) may achieve more sharp bounds compared with the inequalities (1) and (2).

In JI (1), if we set $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$, $a_1={\lambda }_1$, and $a_2={\lambda }_2$, then we have the following inequality:

$$\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{{\lambda }_1+{\lambda }_2}{2}}\right)\le {\displaystyle \frac{1}{{\lambda }_2-{\lambda }_1}}{\int }_{{\lambda }_1}^{{\lambda }_2}\stackrel{\sim }{Ƒ}\left(x\right)dx\le {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)}{2}}.$$

(4)

The inequality (4) is known as the Hermite–Hadamard inequality. This inequality has many applications in different areas of mathematics particularly in the field of error analysis of numerical integration formulas [6,7].

The following extension of the inequality (4) was given in [13] by using the Jensen–Mercer inequality (2) with $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$ and $a_1<a_2:$

$$\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a_1+a_2}{2}}\right)\le {\displaystyle \frac{1}{a_2-a_1}}{\int }_{{\lambda }_1+{\lambda }_2-a_2}^{{\lambda }_1+{\lambda }_2-a_1}\stackrel{\sim }{Ƒ}\left(u\right)du\le \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(a_1\right)+\stackrel{\sim }{Ƒ}\left(a_2\right)}{2}}.$$

(5)

The inequality (5) is convertible to (4) if we set $x_1={\lambda }_1$ and $x_2={\lambda }_2.$

In [12], the authors used the double inequality (3) and proved the following more general Hermite–Hadamard inequality:

$$\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\le \sum _{j=1}^n{\displaystyle \frac{w_j}{a^{*}-a_j}}{\int }_{{\lambda }_1+{\lambda }_2-a^{*}}^{{\lambda }_1+{\lambda }_2-a_j}\stackrel{\sim }{Ƒ}\left(u\right)du\le \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).$$

(6)

The inequality (6) provides inequality (5) if we set $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$ and $a_1<a_2.$ One can easily understand that the double inequality (6) is a generalization of both inequalities (4) and (5).

The authors of [12] also proved the following inequalities by using the double inequality (3):

$$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \\ & \le & \sum _{j=1}^n{\displaystyle \frac{w_j}{a^{*}-a_j}}{\int }_{{\lambda }_1+{\lambda }_2-a^{*}}^{{\lambda }_1+{\lambda }_2-a_j}\stackrel{\sim }{Ƒ}\left(u\right)du\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right),\hfill \end{array}$$

(7)

and

$$\stackrel{\sim }{Ƒ}\left(a^{*}\right)\le \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{a^{*}+a_j}{2}}\right)\le \sum _{j=1}^n{\displaystyle \frac{w_j}{a^{*}-a_j}}{\int }_{a_j}^{a^{*}}\stackrel{\sim }{Ƒ}\left(u\right)du\le \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).$$

(8)

The inequalities (7) and (8) are very interesting because they provide sharper left bounds compared to (4)–(6), which serves as the main motivation for establishment (7) and (8).

On the other hand, fractional calculus is a branch of mathematical analysis that extends the concept of ordinary derivatives and integrals. This generalization allows us to model more complex phenomena that cannot be captured by integer-order derivatives and integrals [14,15].

There are many fractional integrals and derivatives, but the Riemann–Liouville fractional integral is widely used and can be defined as follows:

Definition 1 

([14,15]). Let $\stackrel{\sim }{Ƒ}$ be the Lebesgue integrable on $\left[{\lambda }_1,{\lambda }_2\right],$ the left and right Riemann–Liouville fractional integrals of order $\beta >0$ are

$${}^{RL}J_{{\lambda }_1+}^{\beta }\stackrel{\sim }{Ƒ}\left(x\right)={\displaystyle \frac{1}{\Gamma \left(\beta \right)}}{\int }_{{\lambda }_1}^x{\left(x-s\right)}^{\beta -1}\stackrel{\sim }{Ƒ}\left(s\right)ds,x>{\lambda }_1$$

and

$${}^{RL}J_{{\lambda }_2-}^{\beta }\stackrel{\sim }{Ƒ}\left(x\right)={\displaystyle \frac{1}{\Gamma \left(\beta \right)}}{\int }_x^{{\lambda }_2}{\left(s-x\right)}^{\beta -1}\stackrel{\sim }{Ƒ}\left(s\right)ds,x<{\lambda }_2,$$

respectively, where Γ is the well-known Gamma function.

There are many applications of fractional calculus in different areas of mathematics. To find the error bounds for numerical integration formulas in fractional calculus, Sarikaya [16] provided the fractional version of the inequality (4) which was later used to find the error bounds of the trapezoidal formula [16], midpoint formula [17], Simpson’s formula [18], Newton’s formula [19], and many more [20,21,22]. The Hermite–Hadamard inequality for fractional integrals is stated as follows:

$$\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{{\lambda }_1+{\lambda }_2}{2}}\right)\le {\displaystyle \frac{\Gamma \left(\beta +1\right)}{2{\left({\lambda }_2-{\lambda }_1\right)}^{\beta }}}\left[{}^{RL}J_{{\lambda }_1+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)+{}^{RL}J_{{\lambda }_2-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)\right]\le {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)}{2}}.$$

(9)

The fractional version of (5), using the Riemann–Liouville fractional integrals, was established in [23], and is called the fractional Hermite–Hadamard–Mercer inequality. The fractional Hermite–Hadmaard–Mercer inequality is stated as follows:

$$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\hfill \\ & \le & {\displaystyle \frac{\Gamma \left(\beta +1\right)}{2{\left(x_2-x_1\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_2\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_1\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_1\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_2\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_2\right)}{2}}\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(x_1\right)+\stackrel{\sim }{Ƒ}\left(x_2\right)}{2}}.\hfill \end{array}$$

(10)

To the best of our knowledge, the fractional version of Hermite–Hadamard-type inequalities (6), (7), and (8) using the Riemann–Liouville fractional integrals have not been established so far. So, inspired by the above literature and their applications, we establish the fractional variants of Hermite–Hadamard-type inequalities (6), (7) and (8) using the Jensen–Mercer inequality (3) for general values of n in the context of Riemann–Liouville fractional integrals. The newly proposed inequalities are not only the generalization of all the aforementioned inequalities, rather the bounds are also better than all of the aforementioned inequalities. In the newly established inequalities, one can improve the lower and upper bounds for different values of fractional parameters and values of n used in new inequalities because of (3). To show the applications of these new results, we provide some general error bounds for numerical integration formulas that can be useful for approximating the integrals, particularly in the finite volume method. We also show the validity and efficiency of the results through numerical examples for different values of n and the fractional parameter $\beta >0.$

The paper is organized as follows: Section 2 derives three new Hermite–Hadamard-type inequalities for Riemann–Liouville fractional integrals via double inequality (3). In Section 3, we establish an integral identity first and then prove the general error bounds of numerical integration formulas for convex functions. Section 4 is devoted to the numerical examples to prove the validity and efficiency of the newly established inequalities in Section 2 and Section 3. We conclude the work in Section 5 and provide future directions.

2. Main Results

In this section, we prove some new inequalities of Hermite–Hadamard and Mercer-type for the general values of n in the modified form of Jensen–Mercer inequality (3) using Riemann–Liouville fractional integrals. These results are very crucial in fractional calculus because we need to consider the definitions of left and right Riemann–Liouville fractional integrals, which depend on the relationship between $a^{*}$ and $a_j^{\prime }s\in \left[{\lambda }_1,{\lambda }_2\right].$ These concepts will be discussed in detail in this section.

Theorem 1. 

Let $\stackrel{\sim }{Ƒ}$ be a convex function over a real interval $\left[{\lambda }_1,{\lambda }_2\right]$, then the following double inequalities hold:

• If $a^{*}\ne a_i$ for any $i=1,2,3,\dots ,n-1$, there is a possibility $a_i<a^{*}<a_{i+1}.$ Then, we have the following inequality for $a_i<a^{*}<a_{i+1}$

  $$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& \le & \sum _{j=1}^i{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & & +\sum _{j=i+1}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).\hfill \end{array}$$

  (11)
• If $a^{*}=a_j$, which is possible for odd n when $a_j^{\prime }s$ has an equal distance and $w_{j-1}=w_j$ for every j, then

  $$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-w_{{\displaystyle \frac{n+1}{2}}}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\hfill \\ & \le & \sum _{j=1}^{{\displaystyle \frac{n-1}{2}}}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & & +\sum _{j={\displaystyle \frac{n+3}{2}}}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-w_{{\displaystyle \frac{n+1}{2}}}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right),\hfill \end{array}$$

  (12)

where $a^{*}={\displaystyle \sum _{j=1}^n}{w}_j{a}_j,$$a^{*},a_j\in \left[{\lambda }_1,{\lambda }_2\right]$ with $a_j\ge a_{j-1}$, $w_j\in \left[0,1\right]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1.$

Proof. 

As the given $\stackrel{\sim }{Ƒ}$ is a convex function and from inequality (3), we have

$$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& =& \stackrel{\sim }{Ƒ}\left(\sum _{j=1}^n{w}_j\left({\lambda }_1+{\lambda }_2-\left((1-s)a^{*}+s{a}_j\right)\right)\right)\hfill \\ & \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left((1-s)a^{*}+s{a}_j\right)\right)\hfill \\ & =& \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(\left(1-s\right)\left({\lambda }_1+{\lambda }_2-a^{*}\right)+s\left({\lambda }_1+{\lambda }_2-a_j\right)\right)\hfill \\ & \le & \sum _{j=1}^n{w}_j\left[\left(1-s\right)\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+s\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & \le & \sum _{j=1}^n{w}_j[\left(1-s\right)\left\{\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right\}\hfill \\ & +& s\left\{\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\stackrel{\sim }{Ƒ}\left(a_j\right)\right\}].\hfill \end{array}$$

(13)

Now, from definition of $a^{*}$, we have

$$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left((1-s)a^{*}+s{a}_j\right)\right)\hfill \\ & =& \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(\left(1-s\right)\left({\lambda }_1+{\lambda }_2-a^{*}\right)+s\left({\lambda }_1+{\lambda }_2-a_j\right)\right)\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).\hfill \end{array}$$

(14)

Multiplying (14) by $s^{\beta -1}$ and integrating the resultant one over $\left[0,1\right]$, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{\beta }}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& \le & \sum _{j=1}^n{w}_j{\int }_0^1{s}^{\beta -1}\stackrel{\sim }{Ƒ}\left(\left(1-s\right)\left({\lambda }_1+{\lambda }_2-a^{*}\right)+s\left({\lambda }_1+{\lambda }_2-a_j\right)\right)ds\hfill \\ & \le & {\displaystyle \frac{1}{\beta }}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)\right].\hfill \end{array}$$

Here, in the middle part of the inequality, we have the following possible cases because of the relationship between $a^{*}$ and $a_j^{\prime }s$, as follows:

• $a_n$ is always greater than $a^{*}$ and $a_1$ is always less than $a^{*}$, but there is a possibility of $a^{*}\ne a_i$ for any $i=1,2,3\dots n-1$, then for the case $a_i<a^{*}<a_{i+1}$, we have

  $$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& \le & \sum _{j=1}^i{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & & +\sum _{j=i+1}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).\hfill \end{array}$$
• If n is odd, there is a possibility of single value $a^{*}=a_j$ whenever $a_j^{\prime }s$ has uniform mesh with $w_{j-1}=w_j$ for every j and that particular value is $a_{{\displaystyle \frac{n+1}{2}}},$ then

  $$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-w_{{\displaystyle \frac{n+1}{2}}}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\hfill \\ & \le & \sum _{j=1}^{{\displaystyle \frac{n-1}{2}}}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & & +\sum _{j={\displaystyle \frac{n+3}{2}}}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-w_{{\displaystyle \frac{n+1}{2}}}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)\hfill \end{array}$$

Thus, the proof is completed. □

Remark 1. 

For the case $a^{*}=a_j$, there are many more possibilities with any $j=2,3,\dots ,n-1$, but that particular number can appear for a particular case. In general, if

$$\begin{array}{c}\hfill a_j={\displaystyle \frac{w_1{a}_1+w_2{a}_2+\dots +w_{j-1}{a}_{j-1}+w_{j+1}{a}_{j+1}+\dots +w_n{a}_n}{w_1+w_2+\dots +w_{i-1}+w_{i+1}+\dots w_n}},\end{array}$$

then, $a_j={\displaystyle \frac{a^{*}-a_j{w}_j}{1-w_j}}$, which implies that $a^{*}=w_j{a}_j+(1-w_j)a_j=a_j$. Thus, this case can only be addressed with respect to the specific value of j to support Theorem 1 and the forthcoming theorems.

Remark 2. 

If we use $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$ with $a_1=x_1$ and $a_2=x_2$ in Theorem 1, then we have the following inequality

$$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_1-{\displaystyle \frac{x_1+x_2}{2}}\right)\hfill \\ & \le & {\displaystyle \frac{2^{\beta -1}\Gamma \left(\beta +1\right)}{{\left(x_2-x_1\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_1\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_2\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(x\right)+\stackrel{\sim }{Ƒ}\left(y\right)}{2}}.\hfill \end{array}$$

(15)

These inequalities are already proved in Theorem 2 [24].

Remark 3. 

If we set $\beta =1$, in Theorem 1, then we recapture the inequality (6).

Remark 4. 

It is important to mention here that one can establish new inequalities for different values of n and $w_j^{\prime }s$ in Theorem 1.

Theorem 2. 

Let $\stackrel{\sim }{Ƒ}$ be a convex function over a real interval $\left[{\lambda }_1,{\lambda }_2\right]$, then the following double inequalities hold:

• If $a^{*}\ne a_i$ for any $i=1,2,3,\dots ,n-1$, there is a possibility $a_i<a^{*}<a_{i+1}.$ Then, we have the following inequality for $a_i<a^{*}<a_{i+1}$

  $$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\hfill \\ & \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \\ & \le & \sum _{j=1}^i{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & +\sum _{j=i+1}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2}}\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).\hfill \end{array}$$

  (16)
• If $a^{*}=a_j$, which is possible for odd n when $a_j^{\prime }s$ has an equal distance and $w_{j-1}=w_j$ for every j, then

  $$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_{{\displaystyle \frac{n+1}{2}}}\right)\right]\hfill \\ & \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)-w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_{{\displaystyle \frac{n+1}{2}}}\right)\right]\hfill \\ & \le & \sum _{j=1}^{{\displaystyle \frac{n-1}{2}}}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & +\sum _{j={\displaystyle \frac{n+3}{2}}}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2}}\hfill \\ & & -w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_{{\displaystyle \frac{n+1}{2}}}\right)\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)\hfill \\ & -& w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_{{\displaystyle \frac{n+1}{2}}}\right)\right],\hfill \end{array}$$

  (17)

where $a^{*}={\displaystyle \sum _{j=1}^n}{w}_j{a}_j$, $a^{*},a_j\in \left[{\lambda }_1,{\lambda }_2\right]$ with $a_j\ge a_{j-1}$, $w_j\in \left[0,1\right]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1.$

Proof. 

As $\stackrel{\sim }{Ƒ}$ is a convex functions and $a^{*},a_j\in \left[{\lambda }_1,{\lambda }_2\right],$ we have

$$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left(\left(1-s\right)a^{*}+s{a}_j\right)\right)}{2}}\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2}}.\hfill \end{array}$$

(18)

Multiplying (18) by $s^{\beta -1}$ and integrating the result over $\left[0,1\right]$, we have

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{\beta }}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)& \le & {\displaystyle \frac{1}{2}}\left[{\int }_0^1{s}^{\beta -1}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds\right.\hfill \\ & & +\left.{\int }_0^1{s}^{\beta -1}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left(\left(1-s\right)a^{*}+s{a}_j\right)\right)ds\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2\beta }}.\hfill \end{array}$$

Here, in the middle part of the inequality, we have the following possible cases because of the relationship between $a^{*}$ and $a_j^{\prime }s$, as follows:

• $a_n$ is always greater than $a^{*}$ and $a_1$ is always less than $a^{*}$ but there is a possibility of $a^{*}\ne a_i$ for any $i=1,2,3\dots n-1$, then for the case $a_i<a^{*}<a_{i+1}$, we have

  $$\begin{array}{ccc}& & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \\ & \le & \sum _{j=1}^i{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & +\sum _{j=i+1}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2}}\hfill \end{array}$$

  (19)
• For the case $a_i=a^{*},$ we follow the same method used in Theorem 1 and we have

  $$\begin{array}{ccc}& & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \\ & -& w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_{{\displaystyle \frac{n+1}{2}}}\right)\right]\hfill \\ & \le & \sum _{j=1}^{{\displaystyle \frac{n-1}{2}}}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & +\sum _{j={\displaystyle \frac{n+3}{2}}}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right.\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2}}\hfill \\ & & -w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_{{\displaystyle \frac{n+1}{2}}}\right)\right]\hfill \end{array}$$

  (20)

Now, it is easy to understand for a convex function $\stackrel{\sim }{Ƒ}$ and from inequality (3)

$$\begin{array}{ccc}\hfill \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)& =& \stackrel{\sim }{Ƒ}\left(\sum _{j=1}^n{w}_j\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\right)\hfill \\ & \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \end{array}$$

(21)

and the definition of $a^{*},$ we have

$$\begin{array}{ccc}& & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)}{2}}\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)}{2}}\hfill \\ & =& \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).\hfill \end{array}$$

(22)

Thus, we obtain the required results by combining the inequalities (19)–(22). □

Remark 5. 

If we set $\beta =1$, in Theorem 2, then we recapture the inequality (7).

Corollary 1. 

If we set $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$ with $a_1=x_1$ and $a_2=x_2$ in Theorem 2, then we have the following new inequality:

$$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\hfill \\ & \le & {\displaystyle \frac{1}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{3x_1+x_2}{2}}\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+3x_2}{2}}\right)\right]\hfill \\ & \le & {\displaystyle \frac{\Gamma \left(\beta +1\right)}{2^{2-\beta }{\left(x_2-x_1\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_1\right)\right.\hfill \\ & & +{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_2\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_2\right)+}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\hfill \\ & & \left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_1\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\right]\hfill \\ & \le & {\displaystyle \frac{1}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)+{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_2\right)}{2}}\right]\hfill \\ & \le & \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(x_1\right)+\stackrel{\sim }{Ƒ}\left(x_2\right)}{2}}.\hfill \end{array}$$

These inequalities are also new in the literature, the inequalities proved in Theorem 2.3 [23] and Theorem 2 [24] can be obtained as a special case of our inequalities.

Theorem 3. 

Let $\stackrel{\sim }{Ƒ}$ be a convex function over a real interval $\left[{\lambda }_1,{\lambda }_2\right]$, then the following double inequalities hold:

• If $a^{*}\ne a_i$ for any $i=1,2,3,\dots ,n-1$, there is a possibility for particular i, $a_i<a^{*}<a_{i+1}.$ Then, we have the following inequality for $a_i<a^{*}<a_{i+1}$

  $$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left(a^{*}\right)\le \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{a^{*}+a_j}{2}}\right)\hfill \\ & \le & \sum _{j=1}^i{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{a^{*}-}^{\beta }\stackrel{\sim }{Ƒ}\left(a_j\right)+{}^{RL}J_{a_j+}^{\beta }\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & & +\sum _{j=i+1}^n{\displaystyle \frac{w_i\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{a^{*}+}^{\beta }\stackrel{\sim }{Ƒ}\left(a_j\right)+{}^{RL}J_{a_j-}^{\beta }\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)}{2}}\le \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right).\hfill \end{array}$$
• If $a^{*}=a_j$ which is only possible for odd n when $a_j^{\prime }s$ has equal distance and $w_{j-1}=w_j$ for every j, then

  $$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left(a^{*}\right)-w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left(a_{{\displaystyle \frac{n+1}{2}}}\right)+\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{a^{*}+a_j}{2}}\right)-w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left(a_{{\displaystyle \frac{n+1}{2}}}\right)+\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & \le & \sum _{j=1}^{{\displaystyle \frac{n-1}{2}}}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{a^{*}-}^{\beta }\stackrel{\sim }{Ƒ}\left(a_j\right)+{}^{RL}J_{a_j+}^{\beta }\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & & +\sum _{j={\displaystyle \frac{n+3}{2}}}^n{\displaystyle \frac{w_i\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{a^{*}+}^{\beta }\stackrel{\sim }{Ƒ}\left(a_j\right)+{}^{RL}J_{a_j-}^{\beta }\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(a^{*}\right)+{\displaystyle \sum _{j=1}^n}{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)}{2}}-w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left(a_{{\displaystyle \frac{n+1}{2}}}\right)+\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right]\hfill \\ & \le & \sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)-w_{{\displaystyle \frac{n+1}{2}}}\left[\stackrel{\sim }{Ƒ}\left(a_{{\displaystyle \frac{n+1}{2}}}\right)+\stackrel{\sim }{Ƒ}\left(a^{*}\right)\right],\hfill \end{array}$$

where $a^{*}={\displaystyle \sum _{j=1}^n}{w}_j{a}_j$, $a^{*},a_j\in \left[{\lambda }_1,{\lambda }_2\right]$ with $a_j\ge a_{j-1}$, $w_j\in \left[0,1\right]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1.$

Proof. 

The proof of this theorem is the same as the proof of Theorem 2. □

Remark 6. 

If we set $\beta =1$, in Theorem 3, then we recapture the inequality (8).

Corollary 2. 

If we set $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$ with $a_1=x_1$ and $a_2=x_2$ in Theorem 3, then we have the following new inequality:

$$\begin{array}{ccc}& & \stackrel{\sim }{Ƒ}\left({\displaystyle \frac{x_1+x_2}{2}}\right)\le {\displaystyle \frac{1}{2}}\left[\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{3x_1+x_2}{4}}\right)+\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{x_1+3x_2}{4}}\right)\right]\hfill \\ & \le & {\displaystyle \frac{\Gamma \left(\beta +1\right)}{2^{\beta -2}{\left(x_2-x_1\right)}^{\beta }}}\left[{}^{RL}J_{\left({\displaystyle \frac{x_1+x_2}{2}}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left(x_1\right)+{}^{RL}J_{\left({\displaystyle \frac{x_1+x_2}{2}}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left(x_2\right)\right.\hfill \\ & & +\left.{}^{RL}J_{x_2-}^{\beta }\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{x_1+x_2}{2}}\right)+{}^{RL}J_{x_1+}^{\beta }\stackrel{\sim }{Ƒ}\left({\displaystyle \frac{x_1+x_2}{2}}\right)\right]\hfill \\ & \le & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(\frac{x_1+x_2}{2}\right)+\frac{1}{2}\left[\stackrel{\sim }{Ƒ}\left(x_1\right)+\stackrel{\sim }{Ƒ}\left(x_2\right)\right]}{2}}\le {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left(x_1\right)+\stackrel{\sim }{Ƒ}\left(x_2\right)}{2}}.\hfill \end{array}$$

3. Application in Numerical Integration Formulas

This section establishes the error bounds from numerical integration formulas in fractional calculus. The error bounds proved in this section generalize the existing bounds and new bounds are sharper than the existing ones. We will use the results proved in Theorem 2 to establish the bounds, we only will consider one case of Theorem 2 and the rest of the cases are the same.

Let us start with the following lemma.

Lemma 1. 

Let $\stackrel{\sim }{Ƒ}:\left[{\lambda }_1,{\lambda }_2\right]\to \mathbb{R}$ be a differentiable function over $\left(a,b\right)$. If ${\stackrel{\sim }{Ƒ}}^{\prime }$ is a Lebesgue integrable on $\left[{\lambda }_1,{\lambda }_2\right]$, then we have the following fractional integrals equality:

$$\begin{array}{ccc}& & {\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\sum }_{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)}{2}}\hfill \\ & & -\sum _{j=1}^{i-1}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & -\sum _{j=i}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}{\int }_0^1\left(s^{\beta }-{\left(1-s\right)}^{\beta }\right){\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}{\int }_0^1\left(s^{\beta }-{\left(1-s\right)}^{\beta }\right){\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds,\hfill \end{array}$$

(23)

where $a^{*}={\displaystyle \sum _{j=1}^n}{w}_j{a}_j$, $a^{*},a_j\in \left[{\lambda }_1,{\lambda }_2\right]$ with $a_j\ge a_{j-1}$, $w_j\in \left[0,1\right]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1.$

Proof. 

From (23), we have

$$\begin{array}{ccc}& & \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}{\int }_0^1\left(s^{\beta }-{\left(1-s\right)}^{\beta }\right){\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}{\int }_0^1\left(s^{\beta }-{\left(1-s\right)}^{\beta }\right){\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds\hfill \\ & =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}{\int }_0^1{s}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\hfill \\ & & -\sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}{\int }_0^1{\left(1-s\right)}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}{\int }_0^1{s}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds\hfill \\ & & -\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}{\int }_0^1{\left(1-s\right)}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds\hfill \\ & =& I_1+I_2+I_3+I_4.\hfill \end{array}$$

(24)

Througb basic computations and the integration of parts, we have

$$\begin{array}{ccc}\hfill I_1& =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}{\int }_0^1{s}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\hfill \\ & =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)-\beta {\int }_0^1{s}^{\beta -1}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\right]\hfill \\ & =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)-{\displaystyle \frac{\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right].\hfill \end{array}$$

(25)

Similarly, we have

$$\begin{array}{ccc}\hfill I_2& =& -\sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}{\int }_0^1{\left(1-s\right)}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}_j+\left(1-s\right)a^{*}\right)\right)ds\hfill \\ & =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-{\displaystyle \frac{\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right],\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill I_3& =& \sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}{\int }_0^1{s}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds\hfill \\ & =& \sum _{j=i}^n{\displaystyle \frac{w_j}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)-{\displaystyle \frac{\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right],\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill I_4& =& -\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}{\int }_0^1{\left(1-s\right)}^{\beta }{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1+{\lambda }_2-\left(s{a}^{*}+\left(1-s\right)a_j\right)\right)ds\hfill \\ & =& \sum _{j=i}^n{\displaystyle \frac{w_j}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)-{\displaystyle \frac{\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right].\hfill \end{array}$$

(28)

After using (25)–(28) in (24) and the fact that ${\displaystyle \sum _{j=1}^n}{w}_j=1$, we obtain the required equality (23). □

Theorem 4. 

Under the conditions of Lemma 1, if $\left|{\stackrel{\sim }{Ƒ}}^{\prime }\right|$ is a convex function over an interval $\left[{\lambda }_1,{\lambda }_2\right]$, then we have have the following error bound:

$$\begin{array}{ccc}& & \left|{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\sum }_{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)}{2}}\right.\hfill \\ & & -\sum _{j=1}^{i-1}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & \left.-\sum _{j=i}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\right|\hfill \\ & \le & \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{\left(\beta +1\right)}}\left[\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-{\displaystyle \frac{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a_j\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a^{*}\right)\right|}{2}}\right]\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{\left(\beta +1\right)}}\left[\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-{\displaystyle \frac{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a_j\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a^{*}\right)\right|}{2}}\right].\hfill \end{array}$$

Proof. 

Taking modulus in equality (23), using the convexity of $\left|{\stackrel{\sim }{Ƒ}}^{\prime }\right|$ and inequality (3), we have

$$\begin{array}{ccc}& & \left|{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{\sum }_{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)}{2}}\right.\hfill \\ & & -\sum _{j=1}^{i-1}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\hfill \\ & & \left.-\sum _{j=i}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{2{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a^{*}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a_j\right)\right]\right|\hfill \\ & \le & \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{2}}\hfill \\ & \times & \left[{\int }_0^1\left(s^{\beta }+{\left(1-s\right)}^{\beta }\right)\left\{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-\left(s\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a_j\right)\right|+\left(1-s\right)\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a^{*}\right)\right|\right)\right\}ds\right]\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{2}}\hfill \\ & \times & \left[{\int }_0^1\left(s^{\beta }+{\left(1-s\right)}^{\beta }\right)\left\{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-\left(s\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a^{*}\right)\right|+\left(1-s\right)\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a_j\right)\right|\right)\right\}ds\right]\hfill \\ & =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\left(a^{*}-a_j\right)}{\left(\beta +1\right)}}\left[\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-{\displaystyle \frac{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a_j\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a^{*}\right)\right|}{2}}\right]\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\left(a_j-a^{*}\right)}{\left(\beta +1\right)}}\left[\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-{\displaystyle \frac{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a_j\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(a^{*}\right)\right|}{2}}\right].\hfill \end{array}$$

Thus, the proof is completed. □

Corollary 3. 

If we set $n=2$, $w_1=w_2={\displaystyle \frac{1}{2}}$ with $a_1=x_1$ and $a_2=x_2$ in Theorem 3, then we have the following error bounds for the Bullen formula:

$$\begin{array}{ccc}& & \left|{\displaystyle \frac{1}{2}}\left[\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)+{\displaystyle \frac{\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_2\right)}{2}}\right]\right.\hfill \\ & & -{\displaystyle \frac{\Gamma \left(\beta +1\right)}{2^{2-\beta }{\left(x_2-x_1\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_1\right)\right.\hfill \\ & & +{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-x_2\right)+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_2\right)+}\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\hfill \\ & & \left.\left.+{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-x_1\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-{\displaystyle \frac{x_1+x_2}{2}}\right)\right]\right|\hfill \\ & \le & {\displaystyle \frac{\left(x_2-x_1\right)}{4\left(1+\beta \right)}}\left[2\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_1\right)\right|+2\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left({\lambda }_2\right)\right|-{\displaystyle \frac{\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(x_1\right)\right|+\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(x_2\right)\right|+2\left|{\stackrel{\sim }{Ƒ}}^{\prime }\left(\frac{x_1+x_2}{2}\right)\right|}{2}}\right].\hfill \end{array}$$

4. Numerical Examples

In this section, we demonstrate the validity and value of the results. We show the significance of this new approach in proving Hermite–Hadamard inequality in fractional calculus. We also show the value of using fractional integrals, which generalize classical integrals. For the sake of brevity, the following notations are used in the next tables and figures. These notations are used for Theorem 1:

$$\begin{array}{ccc}\hfill E_1& =& \sum _{j=1}^{i-1}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & & +\sum _{j=i}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]-\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right),\hfill \\ \hfill E_2& =& \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)\hfill \\ & & -\sum _{j=1}^{i-1}{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a^{*}-a_j\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)-}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right]\hfill \\ & & \sum _{j=i}^n{\displaystyle \frac{w_j\Gamma \left(\beta +1\right)}{{\left(a_j-a^{*}\right)}^{\beta }}}\left[{}^{RL}J_{\left({\lambda }_1+{\lambda }_2-a_j\right)+}^{\beta }\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\right],\hfill \\ \hfill E_3& =& \stackrel{\sim }{Ƒ}\left({\lambda }_1\right)+\stackrel{\sim }{Ƒ}\left({\lambda }_2\right)-\sum _{j=1}^n{w}_j\stackrel{\sim }{Ƒ}\left(a_j\right)-\stackrel{\sim }{Ƒ}\left({\lambda }_1+{\lambda }_2-a^{*}\right)\hfill \end{array}$$

and the inequalities in Theorems 2 and 3 are denoted in the following way:

$$Left Part\le Right Left Part\le Middle Part\le Right Middle Part\le Right Part$$

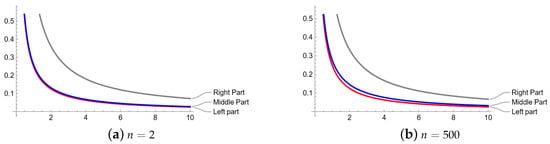
Example 1. 

Let $\stackrel{\sim }{Ƒ}:[0,1]\to \mathbb{R}$ be a convex function that is defined as $\stackrel{\sim }{Ƒ}\left(x\right)=x^2$, then Table 1 and Table 2 show the significance and validity of Theorem 1. We also added figures to show the validity of both n and the fractional parameter β in Theorem 1. In this example $w_j^{\prime }s$ is equal to $1/n$.

Table 1. Significance of n in Theorem 1.

$\mathit{\beta }$	n	${\mathit{E}}_1$	${\mathit{E}}_2$	${\mathit{E}}_3$
	2	0.0111111	0.933333	0.944444
	4	0.02	0.88	0.9
0.5	8	0.0259259	0.844444	0.87037
	16	0.0294118	0.823529	0.852941
	32	0.0313131	0.812121	0.843434
	2	0.00793651	0.306878	0.314815
	4	0.0142857	0.285714	0.3
1.5	8	0.0185185	0.271605	0.290123
	16	0.0210084	0.263305	0.284314
	32	0.0223665	0.258778	0.281145

Table 2. Significance of $\beta$ in Theorem 1.

n	$\mathit{\beta }$	${\mathit{E}}_1$	${\mathit{E}}_2$	${\mathit{E}}_3$
	0.5	0.0272727	0.836364	0.863636
	1.5	0.0194805	0.268398	0.287879
10	2.5	0.0151515	0.157576	0.172727
	3.5	0.0123967	0.11098	0.123377
	4.5	0.0104895	0.0854701	0.0959596
	0.5	0.0301587	0.819048	0.849206
	1.5	0.0215419	0.261527	0.283069
20	2.5	0.0167548	0.153086	0.169841
	3.5	0.0137085	0.107607	0.121315
	4.5	0.0115995	0.0827567	0.0943563

From Table 1 and Table 2, one can easily observe the significance of n and the fractional parameter β. In this example, although the value of $E_1$ increases as n increases, the whole length $E_3$ of the inequality decreases, which is clear, from Table 1. If we discuss the fractional parameter β, then one can easily observe that the bounds becomes sharp for a higher value of the fractional parameter, which is clear from Table 2.

From Figure 1, we can see the validity of the inequalities provided in Theorem 1 for two different values of n with the variation of β in $(0,10]$. From both figures, we can observe that the length of inequalities is short when β is very high, which is an advantage of using the fractional integrals in this work. From the figures, it is clear that the length of the first inequality in Theorem 1 increases when n is increases, but the total length of the double inequality is decreases. So, one can conclude from Table 1 and Table 2 that by choosing higher values for the fractional parameter β and n, we can obtain very sharp bounds.

Figure 1. Comparison of two different values of n in Theorem 1 with $\beta \in (0,10]$ and $w_j^{\prime }s$ are equal to $1/n$.

Example 2. 

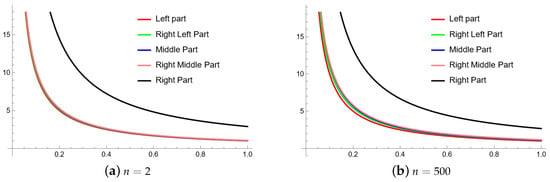
Let $\stackrel{\sim }{Ƒ}:\left[0,2\right]\to \mathbb{R}$ be a convex function, which is defined as $\stackrel{\sim }{Ƒ}\left(x\right)=x^2$, then the validity of Theorem 2 can be observed from Figure 2. It can be observed from the figure that for a small value of n, the length of the inequality was large, but the length decreased for a large value of n. The significance of n in Theorem 2 is also clear from the figure.

Figure 2. Comparison for two different values of n in Theorem 2 with $\beta \in (0,1]$ and $w_j^{\prime }s$ are equal to $1/n$.

Example 3. 

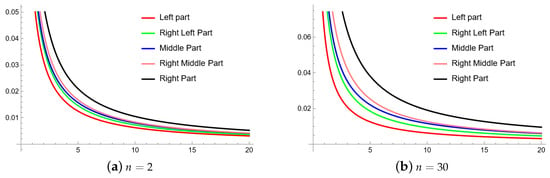
Let $\stackrel{\sim }{Ƒ}:\left[0,1\right]\to \mathbb{R}$ be a convex function, which is defined as $\stackrel{\sim }{Ƒ}\left(x\right)=x^4$, then the validity of Theorem 3 can be observed from the Figure 3.

Figure 3. Comparison of two different values of n in Theorem 3 with $\beta \in (0,20]$ and $w_j^{\prime }s$ are equal to $1/n$.

Example 4. 

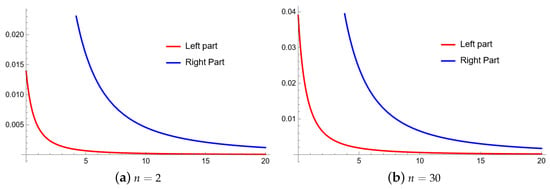
Let $\stackrel{\sim }{Ƒ}:\left[1,2\right]\to \mathbb{R}$ be a function, which is defined as $\stackrel{\sim }{Ƒ}\left(x\right)=x^2$. The derivative of differentiable function $x^2$ on $\left(1,2\right)$ is $2x$, which is a convex on $\left[1,2\right],$ then the validity of Theorem 4 can be observed from Figure 4. We only provide the validity by crossing a higher value of n, the accuracy can be improved by choosing suitable values of n, $w_j^{\prime }s$, and the fractional parameter $\beta >0.$

Figure 4. Comparison of two different values of n in Theorem 4 with $\beta \in (0,20]$ and $w_j^{\prime }s$ are equal to $1/n$.

5. Concluding Remarks and Future Directions

In this work, we established some new bounds for Hermite–Hadamard-type inequalities in the context of fractional integrals using the Jensen–Mercer inequality. Some bounds were already proved for Hermite–Hadamard inequality in classical and fractional calculus, but those bounds were established for only two values in the Jensen–Mercer inequality. Here, we used the general values in the Jensen–Mercer inequality and established some new bounds for Hermite–Hadamard inequality in fractional calculus. It is observed from the numerical examples that the bounds of newly established inequalities can be improved for a suitable value of n, fractional parameter $\beta >0$, and weights used in the Jensen–Mercer inequality. We also found the general error bounds for numerical integration formulas in fractional calculus for differentiable convex functions and these newly established error bounds can be converted to a midpoint formula, trapezoidal formula, and Bullen formula for particular values in the Jensen–Mercer inequality. Moreover, different numerical examples were tested to show the effectiveness and validity of the newly established inequalities. The newly established results can be used in future studies, particularly in the finite volume method for partial differential equations to approximate the integrals because, new results are more effective than the existing ones for different choices. These results can also be extended for functions of two variables and other convexities.