Exploring Fractional Damped Burgers’ Equation: A Comparative Analysis of Analytical Methods
Abstract
1. Introduction
2. Basic Definitions
3. Outline of the Suggested Methodologies
3.1. Introduction of General Implementation of NRPSM
3.2. Problem 1
3.3. Problem 2
3.4. Idea of the Natural Iterative Transform Method
3.4.1. Problem of Fractional PDE with NITM
3.4.2. Problem of Fractional Damped Burger Equation with NITM
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Deniz, S.; Konuralp, A.; De la Sen, M. Optimal perturbation iteration method for solving fractional model of damped Burgers’ equation. Symmetry 2020, 12, 958. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhang, J. A new approximate method to the time fractional damped Burger equation. AIMS Math. 2023, 8, 13317–13324. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. In Mathematics in Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Sene, N. Stokes’ first problem for heated flat plate with Atangana-Baleanu fractional derivative. Chaos Solitons Fractals 2018, 117, 68–75. [Google Scholar] [CrossRef]
- Chu, J.; Liu, Y. Coupling model of a generalized second grade fluid flow and fractional Cattaneo heat transfer with magnetic field and radiation. Results Phys. 2024, 57, 107409. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, S.; Liang, L.; Ding, Q. Multivariate multiscale higuchi fractal dimension and its application to mechanical signals. Fractal Fract. 2024, 8, 56. [Google Scholar] [CrossRef]
- Meng, S.; Meng, F.; Zhang, F.; Li, Q.; Zhang, Y.; Zemouche, A. Observer design method for nonlinear generalized systems with nonlinear algebraic constraints with applications. Automatica 2024, 162, 111512. [Google Scholar] [CrossRef]
- Meng, F.; Pang, A.; Dong, X.; Han, C.; Sha, X. H-∞ optimal performance design of an unstable plant under bode integral constraint. Complexity 2018, 2018, 4942906. [Google Scholar] [CrossRef]
- Meng, F.; Wang, D.; Yang, P.; Xie, G. Application of sum of squares method in nonlinear H-∞ control for satellite attitude maneuvers. Complexity 2019, 2019, 5124108. [Google Scholar] [CrossRef]
- Hu, Y.; Sugiyama, Y. Well-posedness of the initial-boundary value problem for 1D degenerate quasilinear wave equations. Adv. Differ. Equ. 2025, 30, 177–206. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, Y.; Zhou, Y. Meta-transfer learning-based method for multi-fault analysis and assessment in power system. Appl. Intell. 2024, 54, 12112–12127. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Y.; Yan, L.; Li, Z.; Xin, H.; Wei, W. Scaling Graph Neural Networks for Large-Scale Power Systems Analysis: Empirical Laws for Emergent Abilities. IEEE Trans. Power Syst. 2024, 39, 7445–7448. [Google Scholar] [CrossRef]
- Yang, C.; Meng, K.; Yang, L.; Guo, W.; Xu, P.; Zhou, S. Transfer learning-based crashworthiness prediction for the composite structure of a subway vehicle. Int. J. Mech. Sci. 2023, 248, 108244. [Google Scholar] [CrossRef]
- Cheng, Z.; Chen, Y.; Huang, H. Identification and validation of a novel prognostic signature based on ferroptosis-related genes in ovarian cancer. Vaccines 2023, 11, 205. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, L.; Xiao, C.; Huang, Z.; Zhao, F.; Yin, J. Highly efficient upconversion photodynamic performance of rare-earth-coupled dual-photosensitizers: Ultrafast experiments and excited-state calculations. Nanophotonics 2024, 13, 443–455. [Google Scholar] [CrossRef]
- Zhuang, B.; Yang, Y.; Huang, K.; Yin, J. Plasmon-enhanced NIR-II photoluminescence of rare-earth oxide nanoprobes for high-sensitivity optical temperature sensing. Opt. Lett. 2024, 15, 6489–6492. [Google Scholar] [CrossRef] [PubMed]
- Gasimov, Y.S.; Napoles-Vald, J.E. Some refinements of hermite hadamard inequality using K-fractional Caputo derivatives. Fract. Differ. Calc. 2022, 12, 2. [Google Scholar] [CrossRef]
- Salati, S.; Matinfar, M.; Jafari, H. A numerical approach for solving Bagely-Torvik and fractional oscillation equations. Adv. Model. Appl. 2023, 8, 241–252. [Google Scholar]
- Ahmad, S.; Ullah, A.; Shah, K.; Akgul, A. Computational analysis of the third order dispersive fractional PDE under exponential decay and Mittag Leffler type kernels. Numer. Methods Partial. Differ. Equ. 2023, 39, 4533–4548. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Ali Shaikh, A.; Inc, M.; Baleanu, D. Mathematical modeling for adsorption process of dye removal nonlinear equation using power law and exponentially decaying kernels. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 043106. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Ullah, A.; Arfan, M.; Shah, K. On analysis of the fractional mathematical model of rotavirus epidemic with the effects of breastfeeding and vaccination under Atangana-Baleanu (AB) derivative. Chaos Solitons Fractals 2020, 140, 110233. [Google Scholar] [CrossRef]
- Ullah, A.; Abdeljawad, T.; Ahmad, S.; Shah, K. Study of a fractional-order epidemic model of childhood diseases. J. Funct. Spaces 2020, 2020, 5895310. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Dokuyucu, M.A. A fractional order alcoholism model via Caputo-Fabrizio derivative. Aims Math. 2020, 5, 781–797. [Google Scholar] [CrossRef]
- Kai, Y.; Yin, Z. Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation. Phys. Lett. A 2022, 452, 128430. [Google Scholar] [CrossRef]
- He, Y.; Kai, Y. Wave structures, modulation instability analysis and chaotic behaviors to Kudryashov’s equation with third-order dispersion. Nonlinear Dyn. 2024, 112, 10355–10371. [Google Scholar] [CrossRef]
- Xie, J.; Xie, Z.; Xu, H.; Li, Z.; Shi, W.; Ren, J.; Shi, H. Resonance and attraction domain analysis of asymmetric duffing systems with fractional damping in two degrees of freedom. Chaos Solitons Fractals 2024, 187, 115440. [Google Scholar] [CrossRef]
- Yang, Q.; Li, H.; Zhang, L.; Guo, K.; Li, K. Nonlinear flutter in a wind-excited double-deck truss girder bridge: Experimental investigation and modeling approach. Nonlinear Dyn. 2024, 10496. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H. Neural Ordinary Differential Equations for Robust Parameter Estimation in Dynamic Systems with Physical Priors. Appl. Soft Comput. 2024, 169, 112649. [Google Scholar] [CrossRef]
- Shuangjian, G.; Apurba, D. Cohomology and deformations of generalized reynolds operators on Leibniz Algebras. Rocky Mt. J. Math. 2024, 54, 161–178. [Google Scholar]
- Arqub, O.A. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Abo-Hammour, Z.; Al-Badarneh, R.; Momani, S. A reliable analytical method for solving higher-order initial value problems. Discret. Dyn. Nat. Soc. 2013, 2013, 673829. [Google Scholar]
- Arqub, O.A.; El-Ajou, A.; Zhour, Z.A.; Momani, S. Multiple solutions of nonlinear boundary value problems of fractional order: A new analytic iterative technique. Entropy 2014, 16, 471–493. [Google Scholar] [CrossRef]
- El-Ajou, A.; Arqub, O.A.; Momani, S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm. J. Comput. Phys. 2015, 293, 81–95. [Google Scholar] [CrossRef]
- Xu, F.; Gao, Y.; Yang, X.; Zhang, H. Construction of fractional power series solutions to fractional Boussinesq equations using residual power series method. Math. Probl. Eng. 2016, 2016, 5492535. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, Z.; Li, L.; Zhou, C. Least-squares residual power series method for the time-fractional differential equations. Complexity 2019, 2019, 6159024. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Abdel-Muhsen, R. An analytical framework of 2D diffusion, wave-like, telegraph, and Burgers’ models with twofold Caputo derivatives ordering. Nonlinear Dyn. 2018, 93, 1911–1922. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M.; Al-Khaled, K. An analytical study of physical models with inherited temporal and spatial memory. Eur. Phys. J. Plus 2018, 133, 162. [Google Scholar] [CrossRef]
- Alquran, M.; Al-Khaled, K.; Sivasundaram, S.; Jaradat, H.M. Mathematical and numerical study of existence of bifurcations of the generalized fractional Burgers-Huxley equation. Nonlinear Stud. 2017, 24, 235–244. [Google Scholar]
- Zhang, M.F.; Liu, Y.Q.; Zhou, X.S. Efficient homotopy perturbation method for fractional nonlinear equations using Sumudu transform. Therm. Sci. 2015, 19, 1167–1171. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Etemad, S.; Rezapour, S.; Park, C. A novel analytical Aboodh residual power series method for solving linear and nonlinear time-fractional partial differential equations with variable coefficients. AIMS Math. 2022, 7, 16917–16948. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Akgul, A.; Abu-Zinadah, H. Analytical Investigation of Some Time-Fractional Black-Scholes Models by the Aboodh Residual Power Series Method. Mathematics 2023, 11, 276. [Google Scholar] [CrossRef]
- Aboodh, K.S. The New Integral Transform’Aboodh Transform. Glob. J. Pure Appl. Math. 2013, 9, 35–43. [Google Scholar]
- Aggarwal, S.; Chauhan, R. A comparative study of Mohand and Aboodh transforms. Int. J. Res. Advent Technol. 2019, 7, 520–529. [Google Scholar] [CrossRef]
- Benattia, M.E.; Belghaba, K. Application of the Aboodh transform for solving fractional delay differential equations. Univers. J. Math. Appl. 2020, 3, 93–101. [Google Scholar] [CrossRef]
- Delgado, B.B.; Macias-Diaz, J.E. On the general solutions of some non-homogeneous Div-curl systems with Riemann-Liouville and Caputo fractional derivatives. Fractal Fract. 2021, 5, 117. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Smadi, M.; Hashim, I.; Alias, M.A. Residual Power Series Technique for Simulating Fractional Bagley-Torvik Problems Emerging in Applied Physics. Appl. Sci. 2019, 9, 5029. [Google Scholar] [CrossRef]
- Hilfer, R. (Ed.) Application of Fractional Calculus in Physics; World Scientific Publishing Co.: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and applications of fractional differential equations. In North-Holland Mathematics Studies; Elsevier: Amsterdame, The Netherlands, 2006. [Google Scholar]
- Anastassiou, G.A. On right fractional calculus. Chaos Solitons Fractals 2009, 42, 365–376. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Silambarasn, R.; Belgacem, F.B.M. Applications of the natural trans-form to Maxwell’s equations. In Proceedings of the Electromagnet Ics Research Symposium Proceedings, Suzhou, China, 12–16 September 2011; 11p. [Google Scholar]
- Belgacem, F.B.M.; Silambarasan, R. Theory of natural transform, aerospace (MESA). Math. Eng. Sci. 2012, 3, 99–124. [Google Scholar]
- Kumar, S.; Yildirim, A.; Khan, Y.; Wei, L. A fractional model of the diffusion equation and its analytical solution using Laplace transform. Sci. Iran. B 2012, 19, 1117–1123. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. Analytical solutions of fractional order diffusion equations by natural transform method. Iran. J. Sci. Technol. Trans. A Sci. 2018, 42, 1479–1490. [Google Scholar] [CrossRef]
- Acan, O.; Firat, O.; Keskin, Y. Conformable variational iteration method, conformable fractional reduced differential transform method and conformable homotopy analysis method for nonlinear fractional partial differential equations. Waves Random Complex Media 2020, 30, 250–268. [Google Scholar] [CrossRef]
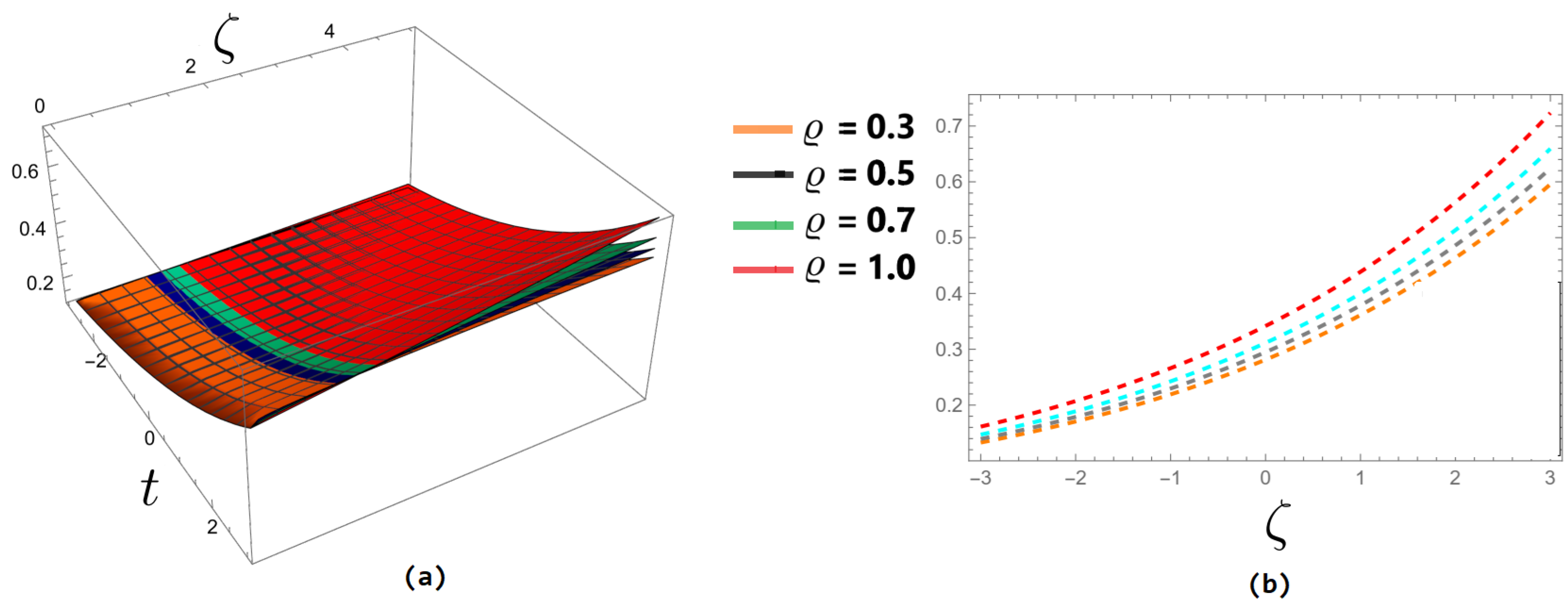

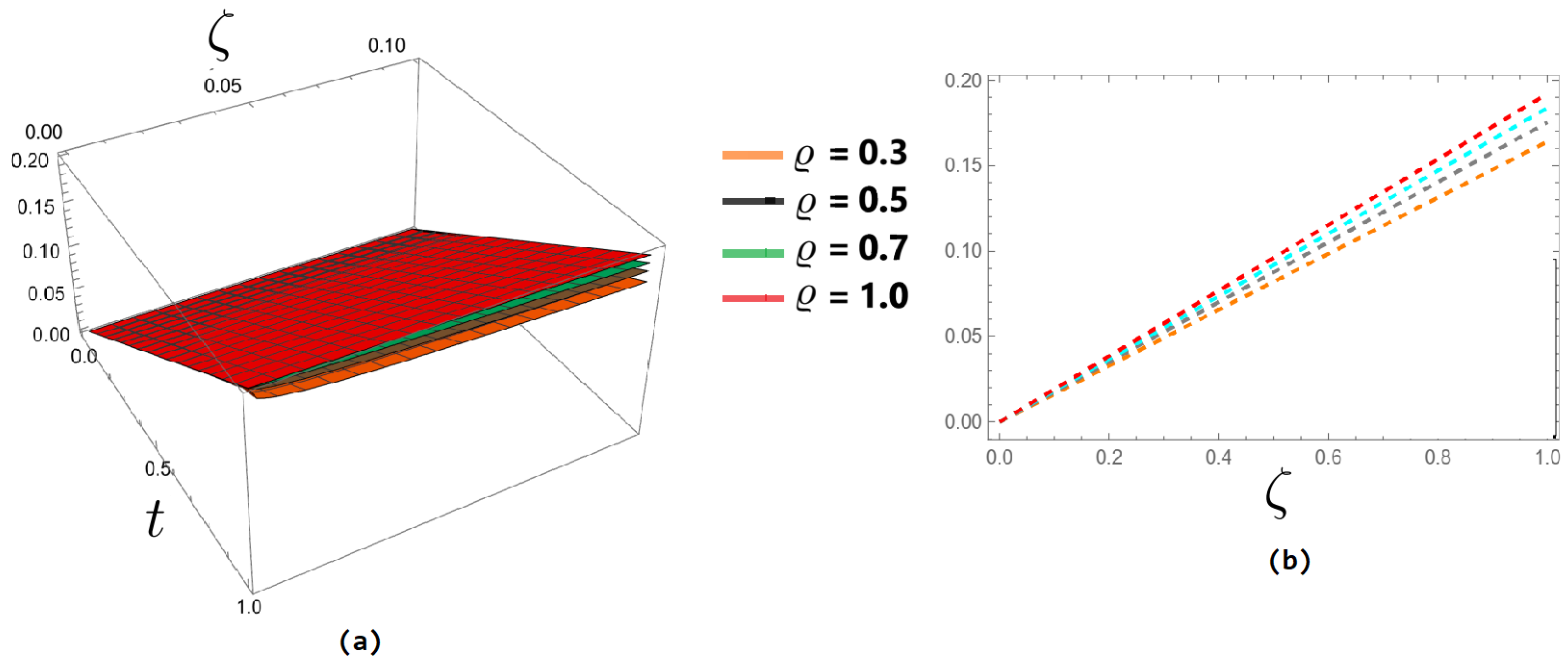
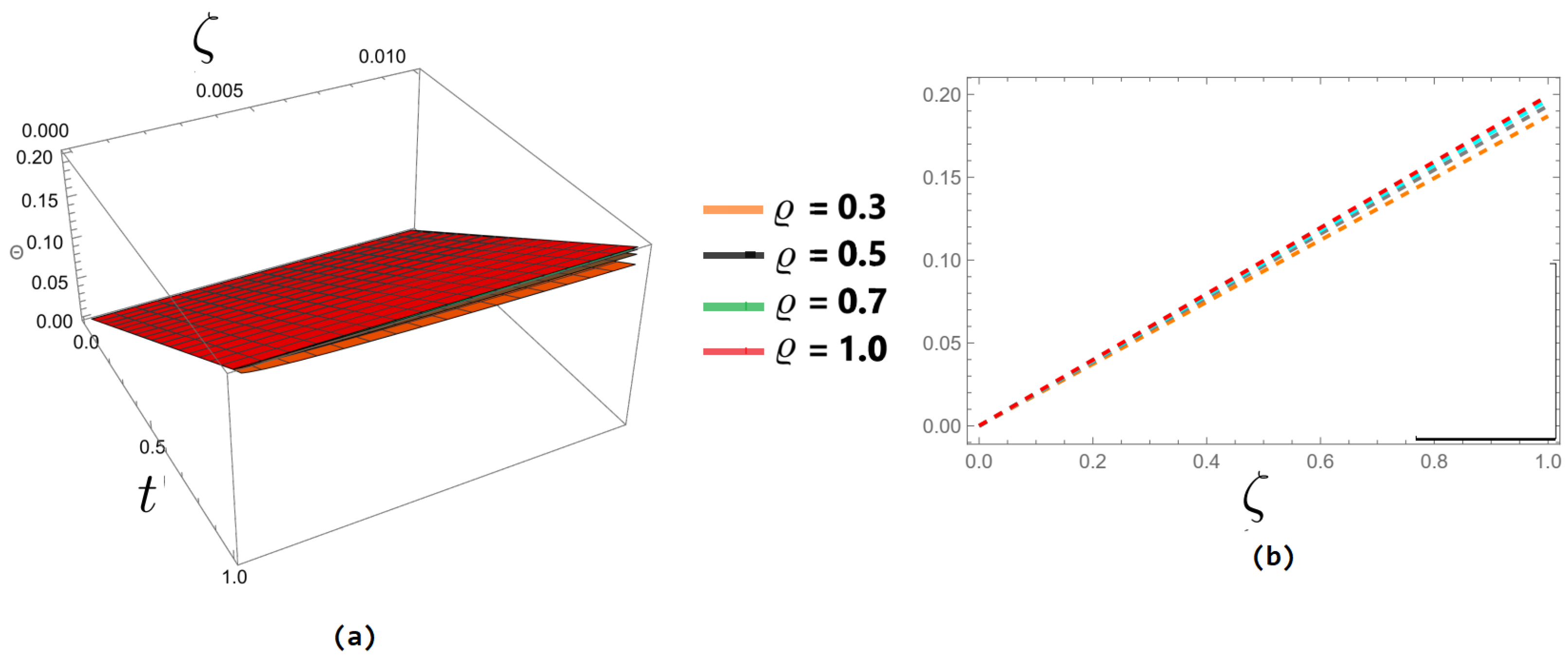

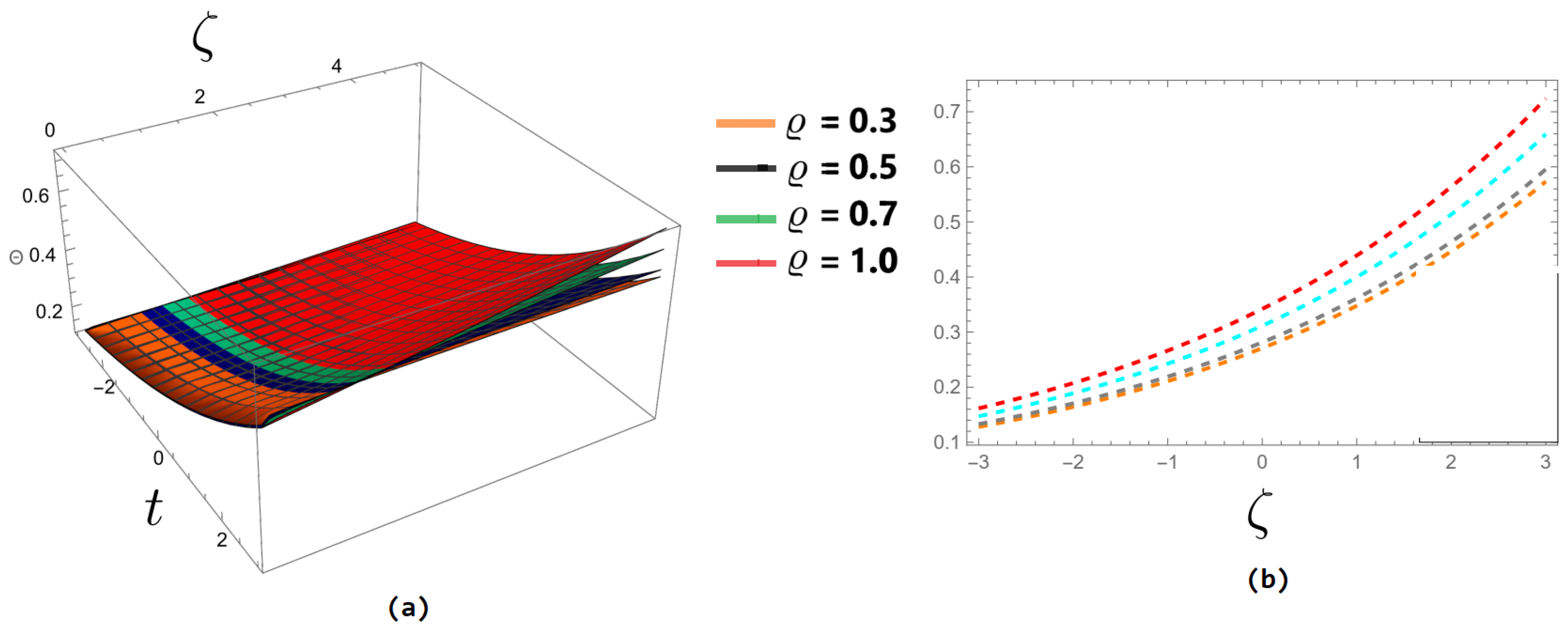


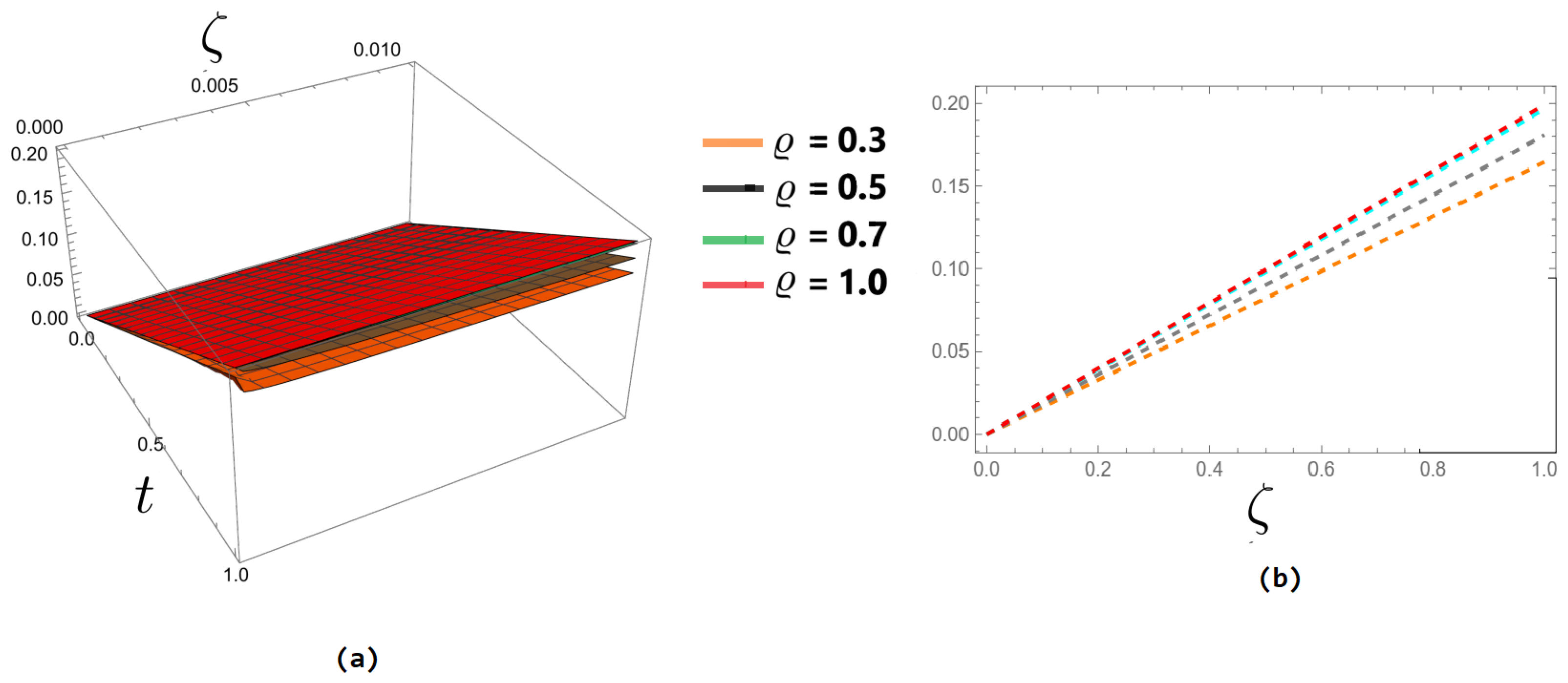
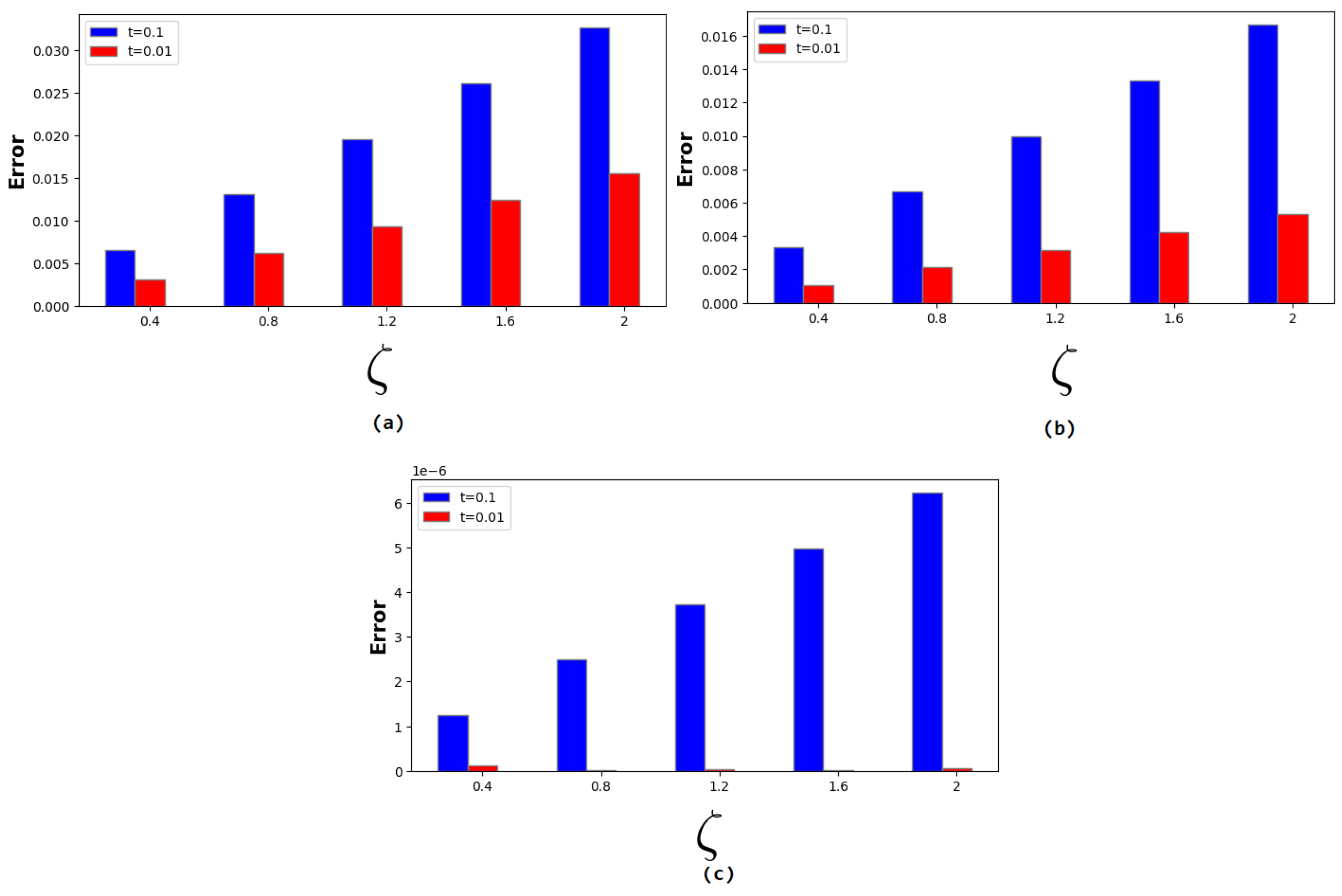
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.268655 | 0.268011 | 0.266124 | 0.266124 | 0.00253169 | 0.0018872 | ||
| 0.4 | 0.29691 | 0.296198 | 0.294112 | 0.294112 | 0.00279795 | 0.00208568 | ||
| 0.6 | 0.328136 | 0.327349 | 0.325044 | 0.325044 | 0.00309222 | 0.00230503 | ||
| 1 | 0.8 | 0.362647 | 0.361777 | 0.359229 | 0.359229 | 0.00341743 | 0.00254745 | |
| 1.0 | 0.400787 | 0.399825 | 0.39701 | 0.39701 | 0.00377684 | 0.00281537 | ||
| 0.2 | 0.262972 | 0.26089 | 0.257936 | 0.257936 | 0.00503609 | 0.00295406 | ||
| 0.4 | 0.290629 | 0.288328 | 0.285063 | 0.285063 | 0.00556574 | 0.00326474 | ||
| 0.6 | 0.321195 | 0.318652 | 0.315044 | 0.315044 | 0.00615109 | 0.0036081 | ||
| 0.5 | 0.8 | 0.354975 | 0.352165 | 0.348177 | 0.348177 | 0.006798 | 0.00398756 | |
| 1.0 | 0.392308 | 0.389202 | 0.384795 | 0.384795 | 0.00751296 | 0.00440694 | ||
| 0.2 | 0.255675 | 0.253463 | 0.251567 | 0.251567 | 0.00410712 | 0.00189519 | ||
| 0.4 | 0.282564 | 0.280119 | 0.278025 | 0.278025 | 0.00453907 | 0.00209451 | ||
| 0.6 | 0.312282 | 0.30958 | 0.307265 | 0.307265 | 0.00501645 | 0.00231479 | ||
| 0.1 | 0.8 | 0.345124 | 0.342139 | 0.33958 | 0.33958 | 0.00554403 | 0.00255824 | |
| 1.0 | 0.381422 | 0.378122 | 0.375294 | 0.375294 | 0.00612711 | 0.00282729 |
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.07015 | 0.073533 | 0.0768932 | 0.0768933 | 0.00674328 | 0.00336034 | ||
| 0.4 | 0.1403 | 0.147066 | 0.153786 | 0.153787 | 0.0134866 | 0.00672067 | ||
| 0.1 | 0.6 | 0.21045 | 0.220599 | 0.23068 | 0.23068 | 0.0202298 | 0.010081 | |
| 0.8 | 0.2806 | 0.294132 | 0.307573 | 0.307573 | 0.0269731 | 0.0134413 | ||
| 1.0 | 0.35075 | 0.367665 | 0.384466 | 0.384467 | 0.0337164 | 0.0168017 | ||
| 0.2 | 0.0765701 | 0.078622 | 0.079681 | 0.079681 | 0.00311089 | 0.00105894 | ||
| 0.4 | 0.15314 | 0.157244 | 0.159362 | 0.159362 | 0.00622178 | 0.00211787 | ||
| 0.01 | 0.6 | 0.22971 | 0.235866 | 0.239043 | 0.239043 | 0.00933267 | 0.00317681 | |
| 0.8 | 0.30628 | 0.314488 | 0.318724 | 0.318724 | 0.0124436 | 0.00423574 | ||
| 1.0 | 0.38285 | 0.39311 | 0.398405 | 0.398405 | 0.0155544 | 0.00529468 |
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.268012 | 0.268012 | 0.266124 | 0.266124 | 0.0018883 | 0.0018883 | ||
| 0.4 | 0.296199 | 0.296199 | 0.294113 | 0.294112 | 0.00208689 | 0.00208689 | ||
| 0.6 | 0.32735 | 0.32735 | 0.325045 | 0.325044 | 0.00230637 | 0.00230637 | ||
| 1 | 0.8 | 0.361778 | 0.361778 | 0.35923 | 0.359229 | 0.00254893 | 0.00254893 | |
| 1.0 | 0.399827 | 0.399827 | 0.39701 | 0.39701 | 0.00281701 | 0.00281701 | ||
| 0.2 | 0.26089 | 0.26089 | 0.257936 | 0.257936 | 0.00295422 | 0.00295422 | ||
| 0.4 | 0.288328 | 0.288328 | 0.285063 | 0.285063 | 0.00326492 | 0.00326492 | ||
| 0.6 | 0.318652 | 0.318652 | 0.315044 | 0.315044 | 0.00360829 | 0.00360829 | ||
| 0.5 | 0.8 | 0.352165 | 0.352165 | 0.348177 | 0.348177 | 0.00398778 | 0.00398778 | |
| 1.0 | 0.389202 | 0.389202 | 0.384795 | 0.384795 | 0.00440718 | 0.00440718 | ||
| 0.2 | 0.253463 | 0.253463 | 0.251567 | 0.251567 | 0.00189519 | 0.00189519 | ||
| 0.4 | 0.280119 | 0.280119 | 0.278025 | 0.278025 | 0.00209451 | 0.00209451 | ||
| 0.6 | 0.30958 | 0.30958 | 0.307265 | 0.307265 | 0.00231479 | 0.00231479 | ||
| 0.1 | 0.8 | 0.342139 | 0.342139 | 0.33958 | 0.33958 | 0.00255824 | 0.00255824 | |
| 1.0 | 0.378122 | 0.378122 | 0.375294 | 0.375294 | 0.0028273 | 0.0028273 |
| t | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.0703566 | 0.0735629 | 0.0768945 | 0.0768933 | 0.00653675 | 0.00333041 | ||
| 0.4 | 0.140713 | 0.147126 | 0.153789 | 0.153787 | 0.0130735 | 0.00666082 | ||
| 0.1 | 0.6 | 0.21107 | 0.220689 | 0.230684 | 0.23068 | 0.0196103 | 0.00999123 | |
| 0.8 | 0.281426 | 0.294252 | 0.307578 | 0.307573 | 0.026147 | 0.0133216 | ||
| 1.0 | 0.351783 | 0.367814 | 0.384473 | 0.384467 | 0.0326838 | 0.016652 | ||
| 0.2 | 0.0765761 | 0.0786222 | 0.079681 | 0.079681 | 0.00310486 | 0.00105871 | ||
| 0.4 | 0.153152 | 0.157244 | 0.159362 | 0.159362 | 0.00620971 | 0.00211742 | ||
| 0.01 | 0.6 | 0.229728 | 0.235867 | 0.239043 | 0.239043 | 0.00931457 | 0.00317614 | |
| 0.8 | 0.306304 | 0.314489 | 0.318724 | 0.318724 | 0.0124194 | 0.00423485 | ||
| 1.0 | 0.382881 | 0.393111 | 0.398405 | 0.398405 | 0.0155243 | 0.00529356 |
| t | ||||||
|---|---|---|---|---|---|---|
| 0.2 | 0.266124 | 0.266124 | 0.266124 | |||
| 0.4 | 0.294112 | 0.294113 | 0.294112 | |||
| 0.6 | 0.325044 | 0.325045 | 0.325044 | |||
| 1 | 0.8 | 0.359229 | 0.35923 | 0.359229 | ||
| 1.0 | 0.39701 | 0.39701 | 0.39701 | |||
| 0.2 | 0.257936 | 0.257936 | 0.257936 | |||
| 0.4 | 0.285063 | 0.285063 | 0.285063 | |||
| 0.6 | 0.315044 | 0.315044 | 0.315044 | |||
| 0.5 | 0.8 | 0.348177 | 0.348177 | 0.348177 | ||
| 1.0 | 0.384795 | 0.384795 | 0.384795 | |||
| 0.2 | 0.251567 | 0.251567 | 0.251567 | |||
| 0.4 | 0.278025 | 0.278025 | 0.278025 | |||
| 0.6 | 0.307265 | 0.307265 | 0.307265 | |||
| 0.1 | 0.8 | 0.33958 | 0.33958 | 0.33958 | ||
| 1.0 | 0.375294 | 0.375294 | 0.375294 |
| t | ||||||
|---|---|---|---|---|---|---|
| 0.2 | 0.0768933 | 0.0768945 | 0.0768932 | |||
| 0.2 | 0.153787 | 0.153789 | 0.153786 | |||
| 0.1 | 0.6 | 0.23068 | 0.230684 | 0.23068 | ||
| 0.8 | 0.307573 | 0.307578 | 0.307573 | |||
| 1.0 | 0.384467 | 0.384473 | 0.384466 | |||
| 0.2 | 0.079681 | 0.079681 | 0.079681 | |||
| 0.4 | 0.159362 | 0.159362 | 0.159362 | |||
| 0.01 | 0.6 | 0.239043 | 0.239043 | 0.239043 | ||
| 0.8 | 0.318724 | 0.318724 | 0.318724 | |||
| 1.0 | 0.398405 | 0.398405 | 0.398405 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehry, A.S.; Shah, R. Exploring Fractional Damped Burgers’ Equation: A Comparative Analysis of Analytical Methods. Fractal Fract. 2025, 9, 107. https://doi.org/10.3390/fractalfract9020107
Alshehry AS, Shah R. Exploring Fractional Damped Burgers’ Equation: A Comparative Analysis of Analytical Methods. Fractal and Fractional. 2025; 9(2):107. https://doi.org/10.3390/fractalfract9020107
Chicago/Turabian StyleAlshehry, Azzh Saad, and Rasool Shah. 2025. "Exploring Fractional Damped Burgers’ Equation: A Comparative Analysis of Analytical Methods" Fractal and Fractional 9, no. 2: 107. https://doi.org/10.3390/fractalfract9020107
APA StyleAlshehry, A. S., & Shah, R. (2025). Exploring Fractional Damped Burgers’ Equation: A Comparative Analysis of Analytical Methods. Fractal and Fractional, 9(2), 107. https://doi.org/10.3390/fractalfract9020107








