Analytical Techniques for Studying Fractional-Order Jaulent–Miodek System Within Algebraic Context
Abstract
1. Introduction
2. Fractional Calculus Fundamental Concepts
- ,
- ,
- ,
- .
3. Methodologies
3.1. ARPSM Technique
3.2. ATIM Technique
4. Application of the Proposed Methods
4.1. Solution of the Problem Using ARPSM
4.2. Solution of the Problem Using ATIM
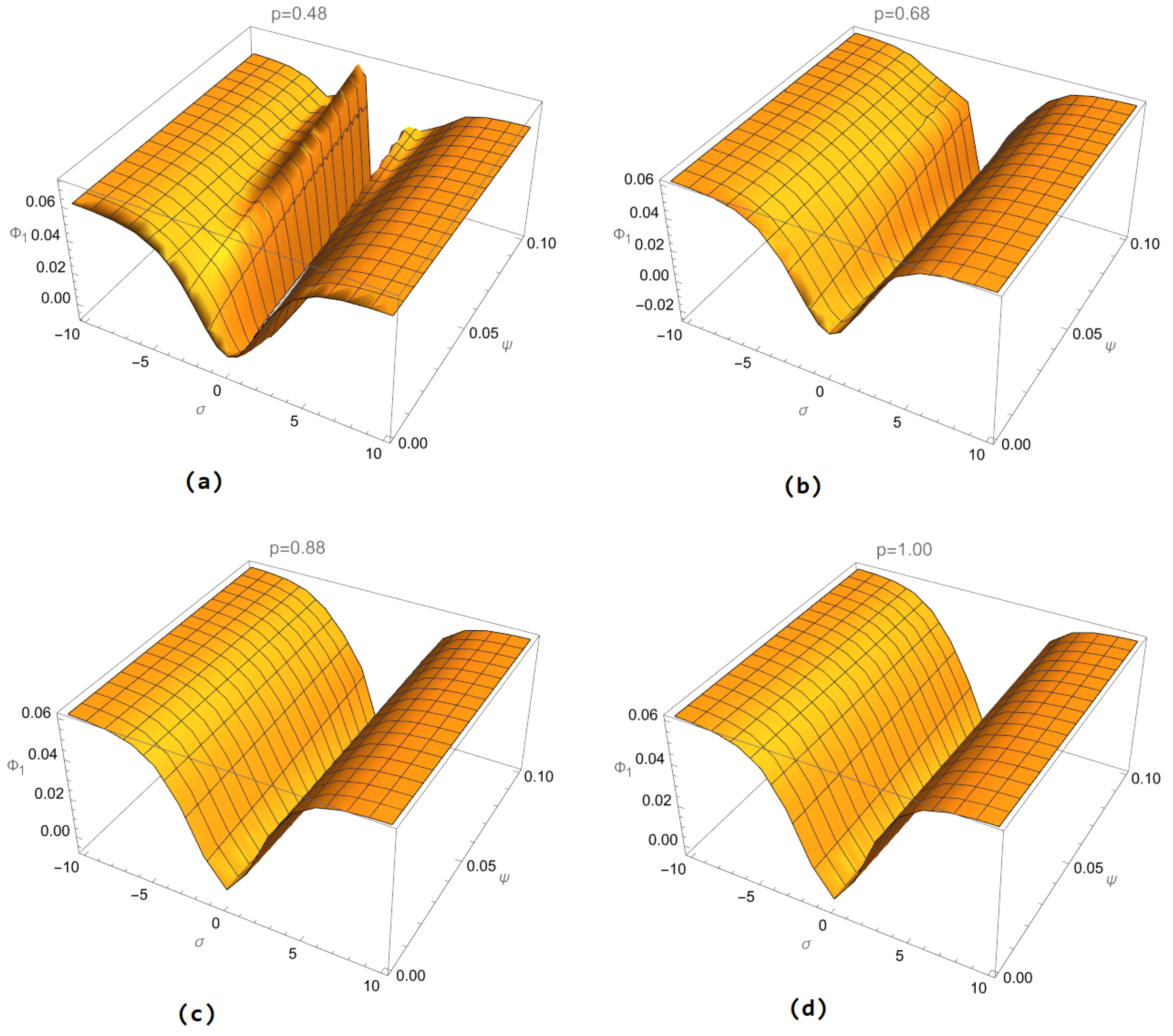
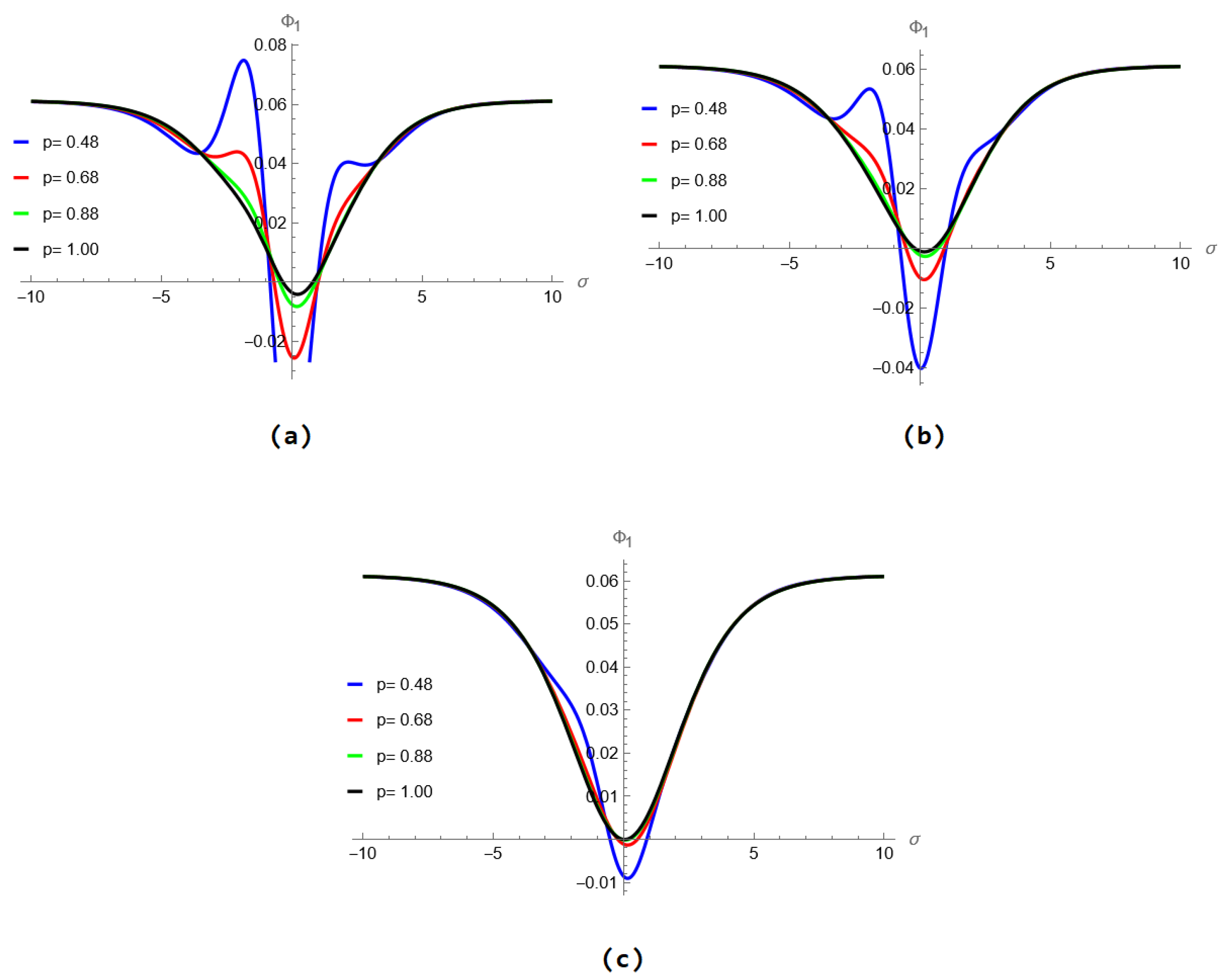
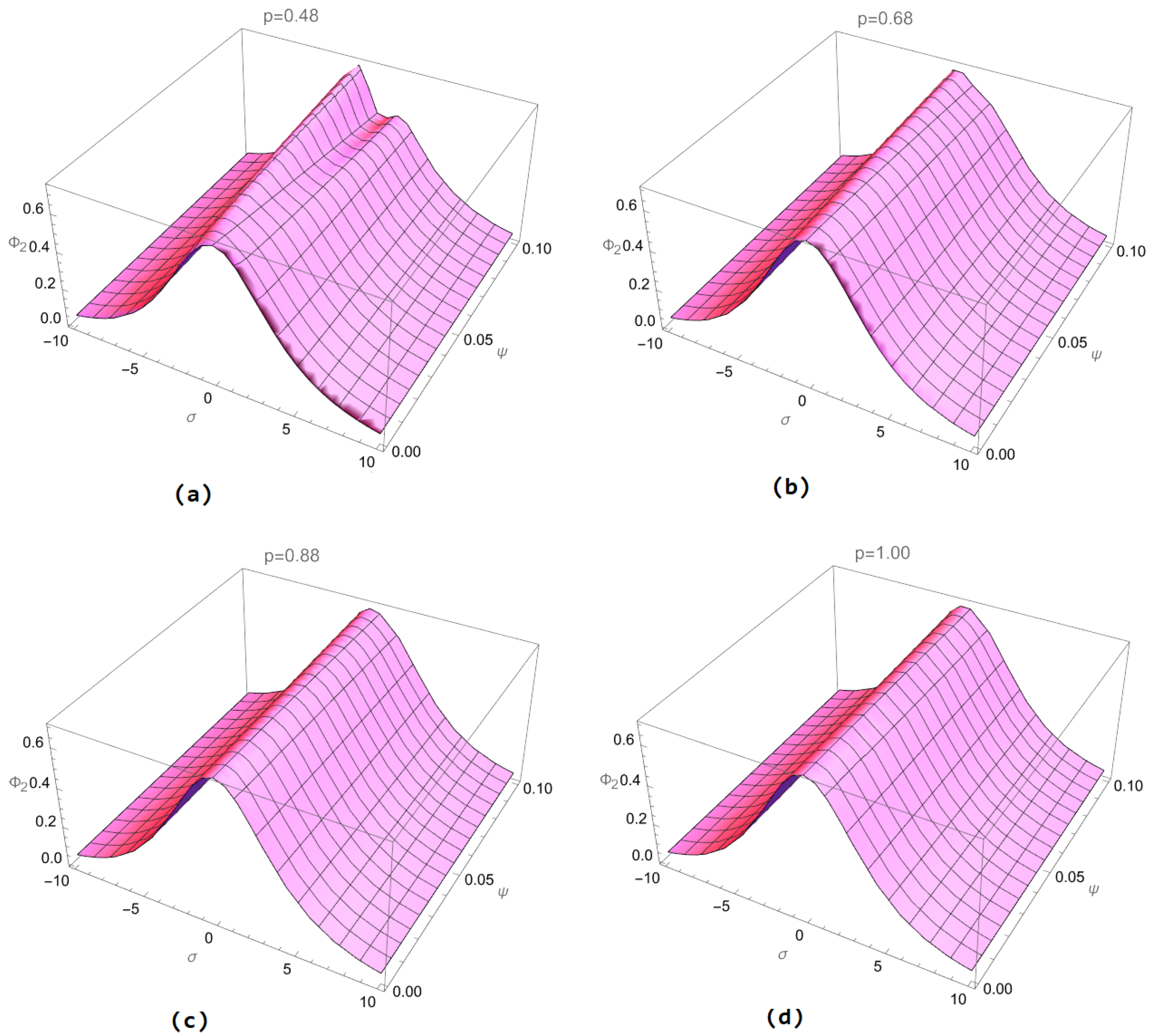
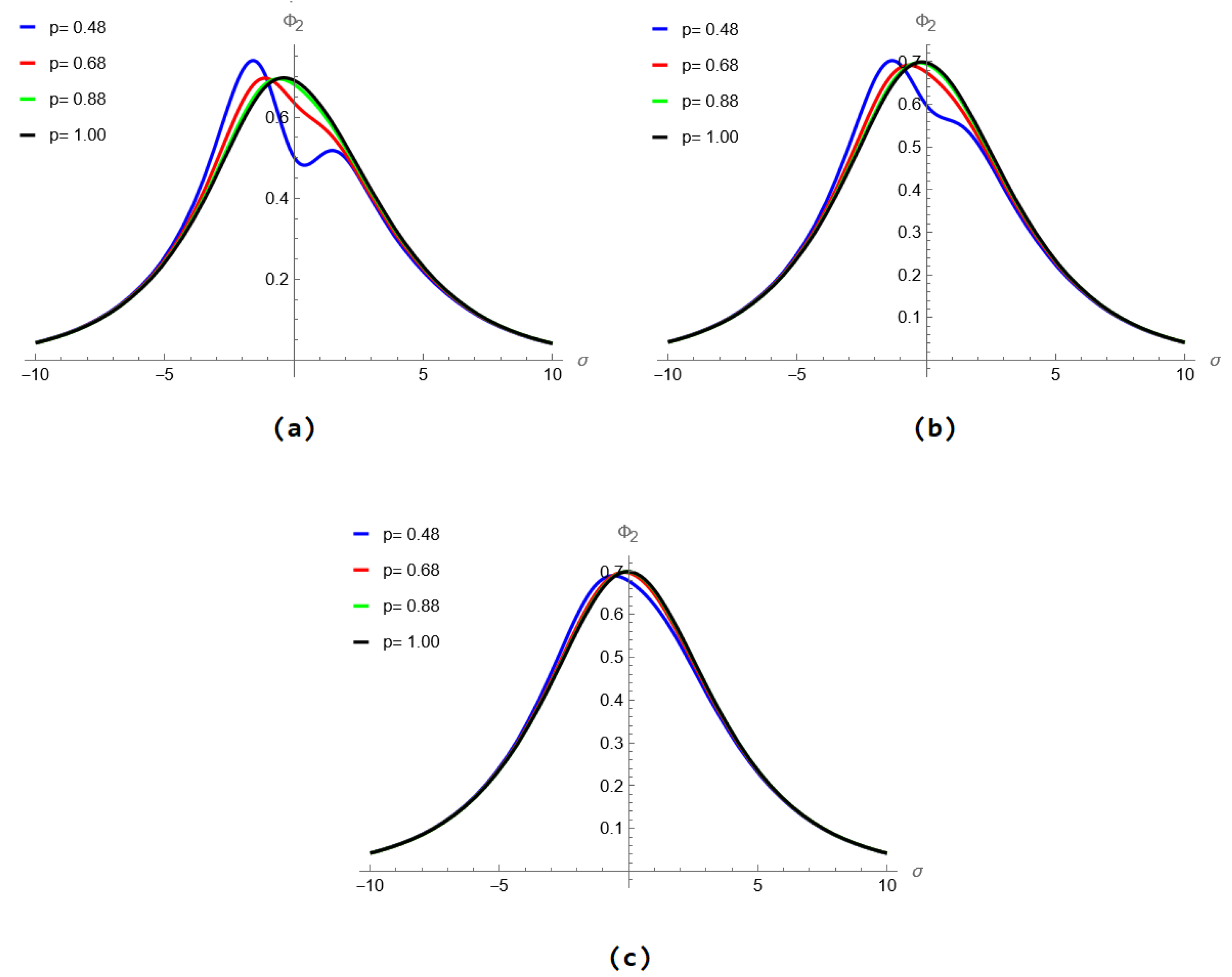
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Lizzy, R.M.; Balachandran, K.; Trujillo, J.J. Controllability of nonlinear stochastic fractional neutral systems with multiple time varying delays in control. Chaos Solitons Fractals 2017, 102, 162–167. [Google Scholar] [CrossRef]
- Cai, W.; Wang, Z.; Wang, F. Temperature and strain-rate dependent fractional constitutive model for glassy polymers. Chaos Solitons Fractals 2024, 185, 115116. [Google Scholar] [CrossRef]
- Ray, S.S.; Atangana, A.; Noutchie, S.C.; Kurulay, M.; Bildik, N.; Kilicman, A. Fractional calculus and its applications in applied mathematics and other sciences. Math. Probl. Eng. 2014, 2014, 849395. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Diethelm, K.; Ford, N.J. The analysis of fractional differential equations. Lect. Notes Math. 2010, 2004, 3–12. [Google Scholar]
- Kuroda, L.K.B.; Gomes, A.V.; Tavoni, R.; de Arruda Mancera, P.F.; Varalta, N.; de Figueiredo Camargo, R. Unexpected behavior of Caputo fractional derivative. Comput. Appl. Math. 2017, 36, 1173–1183. [Google Scholar] [CrossRef]
- Almeida, R.; Bastos, N.; Teresa, M.; Monteiro, T. A prelude to the fractional calculus applied to tumor dynamic. Math. Methods Appl. Sci. 2016, 39, 4846–4855. [Google Scholar] [CrossRef]
- Podlubny, I.; Chechkin, A.; Skovranek, T.; Chen, Y.; Jara, B.M.V. Matrix approach to discrete fractional calculus II: Partial fractional differential equations. J. Comput. Phys. 2009, 228, 3137–3153. [Google Scholar] [CrossRef]
- Losada, J.; Nieto, J.J. Properties of a new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Forte, F.; Mudambi, R.; Navarra, P.M. (Eds.) A Handbook of Alternative Theories of Public Economics; Edward Elgar Publishing: Cheitenham, UK, 2014. [Google Scholar]
- Sulaiman, T.A.; Yavuz, M.; Bulut, H.; Baskonus, H.M. Investigation of the fractional coupled viscous Burgers’ equation involving Mittag-Leffler kernel. Phys. A Stat. Mech. Its Appl. 2019, 527, 121126. [Google Scholar] [CrossRef]
- Atangana, A.; Gomez-Aguilar, J.F. A new derivative with normal distribution kernel: Theory, methods and applications. Phys. A Stat. Mech. Its Appl. 2017, 476, 1–14. [Google Scholar] [CrossRef]
- Ali, A.; Gul, Z.; Khan, W.A.; Ahmad, S.; Zeb, S. Investigation of fractional order sine-Gordon equation using Laplace Adomian decomposition method. Fractals 2021, 29, 2150121. [Google Scholar] [CrossRef]
- Khan, K.; Khan, Z.; Ali, A.; Irfan, M. Investigation of Hirota equation: Modified double Laplace decomposition method. Phys. Scr. 2021, 96, 104006. [Google Scholar] [CrossRef]
- Meng, S.; Meng, F.; Zhang, F.; Li, Q.; Zhang, Y.; Zemouche, A. Observer design method for nonlinear generalized systems with nonlinear algebraic constraints with applications. Automatica 2024, 162, 111512. [Google Scholar] [CrossRef]
- Meng, F.; Pang, A.; Dong, X.; Han, C.; Sha, X. H-∞ optimal performance design of an unstable plant under bode integral constraint. Complexity 2018, 2018, 4942906. [Google Scholar] [CrossRef]
- Meng, F.; Wang, D.; Yang, P.; Xie, G. Application of sum of squares method in nonlinear H-∞ control for satellite attitude maneuvers. Complexity 2019, 2019, 5124108. [Google Scholar] [CrossRef]
- Hu, Y.; Sugiyama, Y. Well-posedness of the initial-boundary value problem for 1D degenerate quasilinear wave equations. Adv. Differ. Equ. 2025, 30, 177–206. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, Y.; Zhou, Y. Meta-transfer learning-based method for multi-fault analysis and assessment in power system. Appl. Intell. 2024, 54, 12112–12127. [Google Scholar] [CrossRef]
- Kai, Y.; Yin, Z. On the Gaussian traveling wave solution to a special kind of Schrodinger equation with logarithmic nonlinearity. Mod. Phys. Lett. B 2021, 36, 2150543. [Google Scholar] [CrossRef]
- Xie, J.; Xie, Z.; Xu, H.; Li, Z.; Shi, W.; Ren, J.; Shi, H. Resonance and attraction domain analysis of asymmetric duffing systems with fractional damping in two degrees of freedom. Chaos Solitons Fractals 2024, 187, 115440. [Google Scholar] [CrossRef]
- Yang, Q.; Li, H.; Zhang, L.; Guo, K.; Li, K. Nonlinear flutter in a wind-excited double-deck truss girder bridge: Experimental investigation and modeling approach. Nonlinear Dyn. 2024, 1–19. [Google Scholar] [CrossRef]
- An, X.; Du, L.; Jiang, F.; Zhang, Y.; Deng, Z.; Kurths, J. A few-shot identification method for stochastic dynamical systems based on residual multipeaks adaptive sampling. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 073118. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H. Neural Ordinary Differential Equations for Robust Parameter Estimation in Dynamic Systems with Physical Priors. Appl. Soft Comput. 2024, 169, 112649. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Taghavifar, H.; Zhang, C.; Alattas, K.A.; Liu, J.; Vu, M.T. A non-linear fractional-order type-3 fuzzy control for enhanced path-tracking performance of autonomous cars. IET Control Theory Appl. 2024, 18, 40–54. [Google Scholar] [CrossRef]
- Guo, S.; Wang, S. Twisted relative Rota-Baxter operators on Leibniz conformal algebras. Commun. Algebra 2024, 52, 3946–3959. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhou, Y.; Yan, L.; Li, Z.; Xin, H.; Wei, W. Scaling Graph Neural Networks for Large-Scale Power Systems Analysis: Empirical Laws for Emergent Abilities. IEEE Trans. Power Syst. 2024. [Google Scholar] [CrossRef]
- Yang, C.; Meng, K.; Yang, L.; Guo, W.; Xu, P.; Zhou, S. Transfer learning-based crashworthiness prediction for the composite structure of a subway vehicle. Int. J. Mech. Sci. 2023, 248, 108244. [Google Scholar] [CrossRef]
- Cheng, Z.; Chen, Y.; Huang, H. Identification and validation of a novel prognostic signature based on ferroptosis-related genes in ovarian cancer. Vaccines 2023, 11, 205. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, L.; Xiao, C.; Huang, Z.; Zhao, F.; Yin, J. Highly efficient upconversion photodynamic performance of rare-earth-coupled dual-photosensitizers: Ultrafast experiments and excited-state calculations. Nanophotonics 2024, 13, 443–455. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, B.; Yang, Y.; Huang, K.; Yin, J. Plasmon-enhanced NIR-II photoluminescence of rare-earth oxide nanoprobes for. PAT 2004, 2. [Google Scholar]
- Xiong, W.; Liu, Y. Physical significance and periodic solutions of the high-order good Jaulent-Miodek model in fluid dynamics. AIMS Math. 2024, 9, 31848–31867. [Google Scholar] [CrossRef]
- Jaulent, M.; Miodek, I. Nonlinear evolution equations associated with ‘enegry-dependent Schrodinger potentials’. Lett. Math. Phys. 1976, 1, 243–250. [Google Scholar] [CrossRef]
- Atangana, A.; Alabaraoye, E. Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv. Differ. Equ. 2013, 2013, 94. [Google Scholar] [CrossRef]
- Atangana, A.; Kilicman, A. Analytical solutions of the space-time fractional derivative of advection dispersion equation. Math. Probl. Eng. 2013, 2013, 853127. [Google Scholar] [CrossRef]
- Atangana, A.; Botha, J.F. Analytical solution of the groundwater flow equation obtained via homotopy decomposition method. J. Earth Sci. Clim. Chang. 2012, 3, 115. [Google Scholar] [CrossRef]
- Das, G.C.; Sarma, J.; Uberoi, C. Explosion of soliton in a multicomponent plasma. Phys. Plasmas 1997, 4, 2095–2100. [Google Scholar] [CrossRef]
- Hong, T.; Wang, Y.; Huo, Y. Bogoliubov quasiparticles carried by dark solitonic excitations in nonuniform Bose-Einstein condensates. Chin. Phys. Lett. 1998, 15, 550. [Google Scholar]
- Ma, W.X.; Li, C.X.; He, J. A second Wronskian formulation of the Boussinesq equation. Nonlinear Anal. Theory Methods Appl. 2009, 70, 4245–4258. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Numerical approach to differential equations of fractional order. J. Comput. Appl. Math. 2007, 207, 96–110. [Google Scholar] [CrossRef]
- Ray, S.S.; Bera, R.K. Analytical solution of a fractional diffusion equation by Adomian decomposition method. Appl. Math. Comput. 2006, 174, 329–336. [Google Scholar]
- Abdulaziz, O.; Hashim, I.; Momani, S. Application of homotopy-perturbation method to fractional IVPs. J. Comput. Appl. Math. 2008, 216, 574–584. [Google Scholar] [CrossRef]
- Abdulaziz, O.; Hashim, I.; Momani, S. Solving systems of fractional differential equations by homotopy-perturbation method. Phys. Lett. A 2008, 372, 451–459. [Google Scholar] [CrossRef]
- Ganji, Z.Z.; Ganji, D.D.; Jafari, H.; Rostamian, M. Application of the homotopy perturbation method to coupled system of partial differential equations with time fractional derivatives. Topol. Methods Nonlinear Anal. 2008, 31, 341–348. [Google Scholar]
- HosseinNia, S.H.; Ranjbar, A.; Momani, S. Using an enhanced homotopy perturbation method in fractional differential equations via deforming the linear part. Comput. Math. Appl. 2008, 56, 3138–3149. [Google Scholar] [CrossRef]
- Yildirim, A.; Gulkanat, Y. Analytical approach to fractional Zakharov-Kuznetsov equations by He’s homotopy perturbation method. Commun. Theor. Phys. 2010, 53, 1005. [Google Scholar] [CrossRef]
- Neamaty, A.; Agheli, B.; Darzi, R. Variational iteration method and He’s polynomials for time-fractional partial differential equations. Prog. Fract. Differ. Appl. 2015, 1, 47–55. [Google Scholar]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Solving smoking epidemic model of fractional order using a modified homotopy analysis transform method. Math. Sci. 2019, 13, 115–128. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G. Solution for fractional Zakharov-Kuznetsov equations by using two reliable techniques. Chin. J. Phys. 2019, 60, 313–330. [Google Scholar] [CrossRef]
- Prakasha, D.G.; Veeresha, P.; Rawashdeh, M.S. Numerical solution for (2+1)-dimensional time-fractional coupled Burger equations using fractional natural decomposition method. Math. Methods Appl. Sci. 2019, 42, 3409–3427. [Google Scholar] [CrossRef]
- Momani, S.; Arqub, O.A.; Freihat, A.; Al-Smadi, M. Analytical approximations for Fokker-Planck equations of fractional order in multistep schemes. Appl. Comput. Math. 2016, 15, 319–330. [Google Scholar]
- Bhalekar, S.; Daftardar-Gejji, V. New iterative method: Application to partial differential equations. Appl. Math. Comput. 2008, 203, 778–783. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V.; Bhalekar, S. Solving fractional boundary value problems with Dirichlet boundary conditions using a new iterative method. Comput. Math. Appl. 2010, 59, 1801–1809. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S.; Akpan, U. Iterative methods for solving fourth-and sixth-order time-fractional Cahn-Hillard equation. Math. Methods Appl. Sci. 2020, 43, 4050–4074. [Google Scholar] [CrossRef]
- Abu Arqub, O.; Abo-Hammour, Z.; Al-Badarneh, R.; Momani, S. A reliable analytical method for solving higher-order initial value problems. Discret. Dyn. Nat. Soc. 2013, 2013, 673829. [Google Scholar] [CrossRef]
- Abdulaziz, O.; Hashim, I.; Saif, A. Series solutions of time-fractional PDEs by homotopy analysis method. Int. J. Differ. Equ. 2009, 2008, 1–16. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Domairry, G.; Dinarvand, S. The homotopy analysis method for explicit analytical solutions of Jaulent-Miodek equations. Numer. Methods Partial. Differ. Equ. Int. J. 2009, 25, 430–439. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Shirzadi, A. Homotopy analysis method for multiple solutions of the fractional Sturm-Liouville problems. Numer. Algorithms 2010, 54, 521–532. [Google Scholar] [CrossRef]
- Arqub, O.A. Series solution of fuzzy differential equations under strongly generalized differentiability. J. Adv. Res. Appl. Math. 2013, 5, 31–52. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Khan, A.; Alam, M.A.; Pandit, M.K.; Etemad, S.; Rezapour, S. Approximate and closed-form solutions of Newell-Whitehead-Segel equations via modified conformable Shehu transform decomposition method. Math. Probl. Eng. 2022, 2022, 6752455. [Google Scholar] [CrossRef]
- Alquran, M.; Ali, M.; Alsukhour, M.; Jaradat, I. Promoted residual power series technique with Laplace transform to solve some time-fractional problems arising in physics. Results Phys. 2020, 19, 103667. [Google Scholar] [CrossRef]
- Eriqat, T.; El-Ajou, A.; Moa’ath, N.O.; Al-Zhour, Z.; Momani, S. A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations. Chaos Solitons Fractals 2020, 138, 109957. [Google Scholar] [CrossRef]
- Alquran, M.; Alsukhour, M.; Ali, M.; Jaradat, I. Combination of Laplace transform and residual power series techniques to solve autonomous n-dimensional fractional nonlinear systems. Nonlinear Eng. 2021, 10, 282–292. [Google Scholar] [CrossRef]
- Khan, A.; Junaid, M.; Khan, I.; Ali, F.; Shah, K.; Khan, D. Application of homotopy analysis natural transform method to the solution of nonlinear partial differential equations. Sci. Int. 2017, 29, 297–303. [Google Scholar]
- Zhang, M.F.; Liu, Y.Q.; Zhou, X.S. Efficient homotopy perturbation method for fractional non-linear equations using Sumudu transform. Therm. Sci. 2015, 19, 1167–1171. [Google Scholar] [CrossRef]
- Al-Deiakeh, R.; Ali, M.; Alquran, M.; Sulaiman, T.A.; Momani, S.; Al-Smadi, M. On finding closed-form solutions to some nonlinear fractional systems via the combination of multi-Laplace transform and the Adomian decomposition method. Rom. Rep. Phys. 2022. [Google Scholar]
- Eltayeb, H.; Kilicman, A. A note on double Laplace transform and telegraphic equations. In Abstract and Applied Analysis; Hindawi: London, UK, 2013; Volume 2013. [Google Scholar]
- Alquran, M.; Al-Khaled, K.; Ali, M.; Ta’any, A. The combined Laplace transform-differential transform method for solving linear non-homogeneous PDEs. J. Math. Comput. Sci. 2012, 2, 690–701. [Google Scholar]
- Liaqat, M.I.; Etemad, S.; Rezapour, S.; Park, C. A novel analytical Aboodh residual power series method for solving linear and nonlinear time-fractional partial differential equations with variable coefficients. AIMS Math. 2022, 7, 16917–16948. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Akgul, A.; Abu-Zinadah, H. Analytical Investigation of Some Time-Fractional Black-Scholes Models by the Aboodh Residual Power Series Method. Mathematics 2023, 11, 276. [Google Scholar] [CrossRef]
- Ojo, G.O.; Mahmudov, N.I. Aboodh transform iterative method for spatial diffusion of a biological population with fractional-order. Mathematics 2021, 9, 155. [Google Scholar] [CrossRef]
- Awuya, M.A.; Ojo, G.O.; Mahmudov, N.I. Solution of Space-Time Fractional Differential Equations Using Aboodh Transform Iterative Method. J. Math. 2022, 2022, 4861588. [Google Scholar] [CrossRef]
- Awuya, M.A.; Subasi, D. Aboodh transform iterative method for solving fractional partial differential equation with Mittag-Leffler Kernel. Symmetry 2021, 13, 2055. [Google Scholar] [CrossRef]
- Aboodh, K.S. The New Integral Transform’Aboodh Transform. Glob. J. Pure Appl. Math. 2013, 9, 35–43. [Google Scholar]
- Aggarwal, S.; Chauhan, R. A comparative study of Mohand and Aboodh transforms. Int. J. Res. Advent Technol. 2019, 7, 520–529. [Google Scholar] [CrossRef]
- Benattia, M.E.; Belghaba, K. Application of the Aboodh transform for solving fractional delay differential equations. Univers. J. Math. Appl. 2020, 3, 93–101. [Google Scholar] [CrossRef]
- Delgado, B.B.; Macias-Diaz, J.E. On the general solutions of some non-homogeneous Div-curl systems with Riemann-Liouville and Caputo fractional derivatives. Fractal Fract. 2021, 5, 117. [Google Scholar] [CrossRef]
- Alshammari, S.; Al-Smadi, M.; Hashim, I.; Alias, M.A. Residual Power Series Technique for Simulating Fractional Bagley-Torvik Problems Emerging in Applied Physics. Appl. Sci. 2019, 9, 5029. [Google Scholar] [CrossRef]




| 0.01 | 02 | 0.0221098 | 0.0211957 | 0.0220352 | 0.0223319 | 2.967220 × |
| 04 | 0.0478296 | 0.0480287 | 0.0480221 | 0.0479905 | 3.152320 × | |
| 06 | 0.0579054 | 0.0577927 | 0.0577084 | 0.0576779 | 3.045560 × | |
| 08 | 0.0604411 | 0.0603879 | 0.0603586 | 0.0603492 | 9.415964 × | |
| 10 | 0.0610519 | 0.0610369 | 0.0610291 | 0.0610266 | 2.447684 × | |
| 0.05 | 02 | 0.0321943 | 0.0220065 | 0.0210241 | 0.0221707 | 1.146590 × |
| 04 | 0.0467622 | 0.0478049 | 0.0480399 | 0.0479098 | 1.301040 × | |
| 06 | 0.0579458 | 0.0579430 | 0.0577994 | 0.0576540 | 1.453130 × | |
| 08 | 0.0605275 | 0.0604561 | 0.0603895 | 0.0603430 | 4.649000 × | |
| 10 | 0.0610793 | 0.0610560 | 0.0610373 | 0.0610251 | 1.218940 × | |
| 0.10 | 02 | 0.0467014 | 0.0263525 | 0.0205183 | 0.0219690 | 1.450630 × |
| 04 | 0.0453932 | 0.0473046 | 0.0479997 | 0.0478083 | 1.914300 × | |
| 06 | 0.0578265 | 0.0580034 | 0.0578972 | 0.0576240 | 2.732150 × | |
| 08 | 0.0605779 | 0.0605112 | 0.0604268 | 0.0603352 | 9.150590 × | |
| 10 | 0.0610981 | 0.0610727 | 0.0610474 | 0.0610231 | 2.425630 × |
| 0.01 | 02 | 0.532107 | 0.545468 | 0.554964 | 0.557983 | 3.019230 × |
| 04 | 0.314878 | 0.320959 | 0.324483 | 0.325693 | 1.209400 × | |
| 06 | 0.165805 | 0.167696 | 0.168655 | 0.169047 | 3.916230 × | |
| 08 | 0.083746 | 0.084402 | 0.084733 | 0.084892 | 1.587480 × | |
| 10 | 0.041770 | 0.042055 | 0.042199 | 0.042274 | 7.408930 × | |
| 0.05 | 02 | 0.524115 | 0.527784 | 0.544750 | 0.559138 | 1.438730 × |
| 04 | 0.306140 | 0.313125 | 0.320750 | 0.326682 | 5.932430 × | |
| 06 | 0.162208 | 0.165296 | 0.167652 | 0.169610 | 1.958690 × | |
| 08 | 0.082488 | 0.083570 | 0.084387 | 0.085182 | 7.945760 × | |
| 10 | 0.041231 | 0.041693 | 0.042048 | 0.042419 | 3.705760 × | |
| 0.10 | 02 | 0.533186 | 0.519364 | 0.533576 | 0.560578 | 2.700240 × |
| 04 | 0.302176 | 0.307277 | 0.316344 | 0.327923 | 1.157840 × | |
| 06 | 0.159580 | 0.163130 | 0.166398 | 0.170317 | 3.918810 × | |
| 08 | 0.081560 | 0.082815 | 0.083954 | 0.085545 | 1.591250 × | |
| 10 | 0.040839 | 0.041368 | 0.041859 | 0.042600 | 7.414770 × |
| 0.01 | 02 | 0.0220278 | 0.0211997 | 0.0220355 | 0.0223319 | 2.963860 × |
| 04 | 0.0478545 | 0.0480306 | 0.0480221 | 0.0479905 | 3.156600 × | |
| 06 | 0.0579072 | 0.0577928 | 0.0577084 | 0.0576779 | 3.045750 × | |
| 08 | 0.0604412 | 0.0603879 | 0.0603586 | 0.0603492 | 9.416050 × | |
| 10 | 0.0610519 | 0.0610369 | 0.0610291 | 0.0610266 | 2.447689 × | |
| 0.05 | 02 | 0.0308651 | 0.0219002 | 0.0210279 | 0.0221707 | 1.142720 × |
| 04 | 0.0469628 | 0.0478345 | 0.0480414 | 0.0479098 | 1.315680 × | |
| 06 | 0.0579619 | 0.0579451 | 0.0577994 | 0.0576540 | 1.453970 × | |
| 08 | 0.0605283 | 0.0604562 | 0.0603895 | 0.0603430 | 4.649390 × | |
| 10 | 0.0610793 | 0.0610560 | 0.0610373 | 0.0610251 | 1.218970 × | |
| 0.10 | 02 | 0.0427823 | 0.0257535 | 0.0205113 | 0.0219690 | 1.457670 × |
| 04 | 0.0459034 | 0.0474097 | 0.0480076 | 0.0478083 | 1.992630 × | |
| 06 | 0.0578686 | 0.0580115 | 0.0578977 | 0.0576240 | 2.737310 × | |
| 08 | 0.0605800 | 0.0605116 | 0.0604268 | 0.0603352 | 9.153030 × | |
| 10 | 0.0610983 | 0.0610728 | 0.0610474 | 0.0610231 | 2.425800 × |
| 0.01 | 02 | 0.528615 | 0.545031 | 0.554950 | 0.557983 | 3.032920 × |
| 04 | 0.314284 | 0.320883 | 0.324481 | 0.325693 | 1.211790 × | |
| 06 | 0.165761 | 0.167690 | 0.168655 | 0.169047 | 3.918050 × | |
| 08 | 0.083742 | 0.084402 | 0.084733 | 0.084892 | 1.587640 × | |
| 10 | 0.041770 | 0.042055 | 0.042199 | 0.042274 | 7.409110 × | |
| 0.05 | 02 | 0.506951 | 0.523760 | 0.544404 | 0.559138 | 1.473360 × |
| 04 | 0.303296 | 0.312441 | 0.320690 | 0.326682 | 5.992400 × | |
| 06 | 0.162000 | 0.165245 | 0.167647 | 0.169610 | 1.963240 × | |
| 08 | 0.082470 | 0.083566 | 0.084387 | 0.085182 | 7.949810 × | |
| 10 | 0.041229 | 0.041693 | 0.042048 | 0.042419 | 3.706200 × | |
| 0.10 | 02 | 0.498744 | 0.508760 | 0.532171 | 0.560578 | 2.840760 × |
| 04 | 0.296573 | 0.305501 | 0.316103 | 0.327923 | 1.181980 × | |
| 06 | 0.159179 | 0.162999 | 0.166380 | 0.170317 | 3.937010 × | |
| 08 | 0.081525 | 0.082803 | 0.083952 | 0.085545 | 1.592860 × | |
| 10 | 0.040836 | 0.041367 | 0.041859 | 0.042600 | 7.416530 × |
| 0.01 | 02 | 0.0223319 | 0.0220352 | 0.0220355 | 2.967220 × | 2.963860 × |
| 04 | 0.0479905 | 0.0480221 | 0.0480221 | 3.152320 × | 3.156600 × | |
| 06 | 0.0576779 | 0.0577084 | 0.0577084 | 3.045560 × | 3.045750 × | |
| 08 | 0.0603492 | 0.0603586 | 0.0603586 | 9.415964 × | 9.416050 × | |
| 10 | 0.0610266 | 0.0610291 | 0.0610291 | 2.447684 × | 2.447689 × | |
| 0.05 | 02 | 0.0221707 | 0.0210241 | 0.0210279 | 1.146590 × | 1.142720 × |
| 04 | 0.0479098 | 0.0480399 | 0.0480414 | 1.301040 × | 1.315680 × | |
| 06 | 0.0576540 | 0.0577994 | 0.0577994 | 1.453130 × | 1.453970 × | |
| 08 | 0.0603430 | 0.0603895 | 0.0603895 | 4.649000 × | 4.649390 × | |
| 10 | 0.0610251 | 0.0610373 | 0.0610373 | 1.218940 × | 1.218970 × | |
| 0.10 | 02 | 0.0219690 | 0.0205183 | 0.0205113 | 1.450630 × | 1.457670 × |
| 04 | 0.0478083 | 0.0479997 | 0.0480076 | 1.914300 × | 1.992630 × | |
| 06 | 0.0576240 | 0.0578972 | 0.0578977 | 2.732150 × | 2.737310 × | |
| 08 | 0.0603352 | 0.0604268 | 0.0604268 | 9.150590 × | 9.153030 × | |
| 10 | 0.0610231 | 0.0610474 | 0.0610474 | 2.425630 × | 2.425800 × |
| 0.01 | 02 | 0.557983 | 0.554964 | 0.554950 | 3.019230 × | 3.032920 × |
| 04 | 0.325693 | 0.324483 | 0.324481 | 1.209400 × | 1.211790 × | |
| 06 | 0.169047 | 0.168655 | 0.168655 | 3.916230 × | 3.918050 × | |
| 08 | 0.084892 | 0.084733 | 0.084733 | 1.587480 × | 1.587640 × | |
| 10 | 0.042274 | 0.042199 | 0.042199 | 7.408930 × | 7.409110 × | |
| 0.05 | 02 | 0.559138 | 0.544750 | 0.544404 | 1.438730 × | 1.473360 × |
| 04 | 0.326682 | 0.320750 | 0.320690 | 5.932430 × | 5.992400 × | |
| 06 | 0.169610 | 0.167652 | 0.167647 | 1.958690 × | 1.963240 × | |
| 08 | 0.085182 | 0.084387 | 0.084387 | 7.945760 × | 7.949810 × | |
| 10 | 0.042419 | 0.042048 | 0.042048 | 3.705760 × | 3.706200 × | |
| 0.10 | 02 | 0.560578 | 0.533576 | 0.532171 | 2.700240 × | 2.840760 × |
| 04 | 0.327923 | 0.316344 | 0.316103 | 1.157840 × | 1.181980 × | |
| 06 | 0.170317 | 0.166398 | 0.166380 | 3.918810 × | 3.937010 × | |
| 08 | 0.085545 | 0.083954 | 0.083952 | 1.591250 × | 1.592860 × | |
| 10 | 0.042600 | 0.041859 | 0.041859 | 7.414770 × | 7.416530 × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkhezi, Y.; Shafee, A. Analytical Techniques for Studying Fractional-Order Jaulent–Miodek System Within Algebraic Context. Fractal Fract. 2025, 9, 50. https://doi.org/10.3390/fractalfract9010050
Alkhezi Y, Shafee A. Analytical Techniques for Studying Fractional-Order Jaulent–Miodek System Within Algebraic Context. Fractal and Fractional. 2025; 9(1):50. https://doi.org/10.3390/fractalfract9010050
Chicago/Turabian StyleAlkhezi, Yousuf, and Ahmad Shafee. 2025. "Analytical Techniques for Studying Fractional-Order Jaulent–Miodek System Within Algebraic Context" Fractal and Fractional 9, no. 1: 50. https://doi.org/10.3390/fractalfract9010050
APA StyleAlkhezi, Y., & Shafee, A. (2025). Analytical Techniques for Studying Fractional-Order Jaulent–Miodek System Within Algebraic Context. Fractal and Fractional, 9(1), 50. https://doi.org/10.3390/fractalfract9010050








