Fixed-Time Synchronization of Fractional-Order Hopfield Neural Networks with Unbounded Proportional Delay and Bounded Parameter Uncertainties

Abstract

This paper investigates the fixed-time synchronization of fractional-order proportional delay Hopfield neural networks (PDHNNs) with bounded parameter uncertainties. Unlike constant delay and bounded variable delay, proportional delay has time-varying and unbounded characteristics, which pose challenges for the synchronization control of primary–secondary fractional neural networks. To achieve fixed-time synchronization, we propose a new nonlinear multi-module feedback controller. It consists of three key functional modules: eliminating the impact of proportional delay on system stability; ensuring convergence within a fixed time frame without being limited by initial conditions; and expanding the selectable range of parameters. Combining the stability lemma and inequality techniques, synchronization criteria of PDHNNs are derived based on the construction of a Lyapunov function with a negative fractional derivative. The settling time can be effectively estimated, which depends on the control parameters and is independent of initial values. Two numerical experiments verify the effectiveness of the theorem and corollary in this study.

1. Introduction

With the gradual improvement of computers’ ability to process big data, neural networks (NNs) are becoming increasingly widely used in various fields, such as data visualization [1], intelligent computation [2,3,4], automation [5,6], and system stability [7,8,9]. Synchronization, as one of the most typical collective dynamic behaviors in NNs, refers to the phenomenon where the discharge activities or state evolutions of multiple or even all neurons in the network tend to be consistent over time [10]. In biological brains, synchronization is believed to be closely related to various cognitive functions, such as attention, perceptual binding, memory formation, and information transmission. Understanding and controlling synchronization behaviors are crucial for designing intelligent information processing systems in artificial NNs and neuromorphic computing [11]. The common synchronization types of NNs include bipartite synchronization [12], projective synchronization [13], finite-time synchronization [14], fixed-time synchronization [15,16], etc.

To characterize the change rate of network dynamic behavior over time, traditional integer calculus operators are commonly used for network modeling [17]. The information propagation efficiency between network nodes is influenced by factors such as network topology, node degree, and inter-node distance [18]. For many NNs, relying solely on the evolution of the network itself is not enough, and external control inputs need to be applied to achieve the synchronization objective [19]. The commonly used control methods include feedback control [20], adaptive control [21], hybrid control [22], and event-triggered control [23]. In reality, finite-time and fixed-time synchronization control technologies offer disturbance rejection capabilities and enhanced robustness, making them applicable across a wide range of fields. Therefore, researchers have paid attention to finite-time and fixed-time synchronization for various NNs and have obtained many important results. For instance, Abdurahman et al. [24] focused on the fixed-time synchronization patterns of nonlinear coupled NNs under the stability theory and inequality techniques. Qiao et al. [25] investigated the fixed-time synchronization of coupled delayed networks by intermittent feedback control schemes. The authors in [26] discussed the fixed-time synchronization of coupled NNs by adaptive feedback control schemes. More fixed-time synchronization results of NNs by means of different control schemes can be found in [27,28].

Fractional calculus, as an extension of traditional calculus, includes an integral term from the initial moment to the current moment [29]. This means that when calculating the fractional derivative at the current time, all information from the entire historical process needs to be considered [30,31,32,33]. Hence, fractional-order NNs can describe complex processes with memory and historical dependencies, which is difficult to achieve by traditional integer-order NNs [34]. In reality, the charging and discharging behavior of batteries, as well as the penetration of drugs into tissues, naturally exhibit fractional-order kinetic characteristics. Recently, scholars have extensively investigated various dynamic behaviors of fractional-order delayed NNs, such as synchronization [35,36], dissipativity [37,38], and stability [39,40]. For integer-order systems, the Lyapunov direct method is a powerful tool for proving synchronization stability and designing controllers. But its direct generalization in fractional-order systems faces enormous mathematical challenges. Up to now, many studies on fractional-order NNs have mainly focused on specific kinds of time delays, such as fixed delay [35,37], bounded variable delay [36], and bounded mixed delay [40].

Proportional delay differs from the fixed delay and the bounded delay mentioned earlier, as it is an unbounded time-varying delay proportional to the current time u [41]. This type of time delay is generally defined as $\vartheta \left(u\right)=(1-\lambda )u$, where $0<\lambda <1$, and has been widely studied in the context of various physical phenomena, biological systems, and synchronization control [42]. For instance, Xu et al. [43] investigated the feedback control synchronization of fractional-order proportional delay neural networks (PDNNs) by constructing a graph-theoretical Lyapunov function that includes three-term functions. In [44], the authors discussed the bipartite synchronization of fractional-order coupled PDNNs based on graph theory and the Razumikhin method. In [45], He et al. deliberated on the event-triggered synchronization of fractional-order PDNNs with quaternion values utilizing the Razumikhin theorem and stability theory, thereby facilitating the application of the results to image encryption and decryption. Additionally, Duan et al. [46] solved the finite-time synchronization of complex-valued PDNNs by combining non-smooth theory and complex domain inequalities.

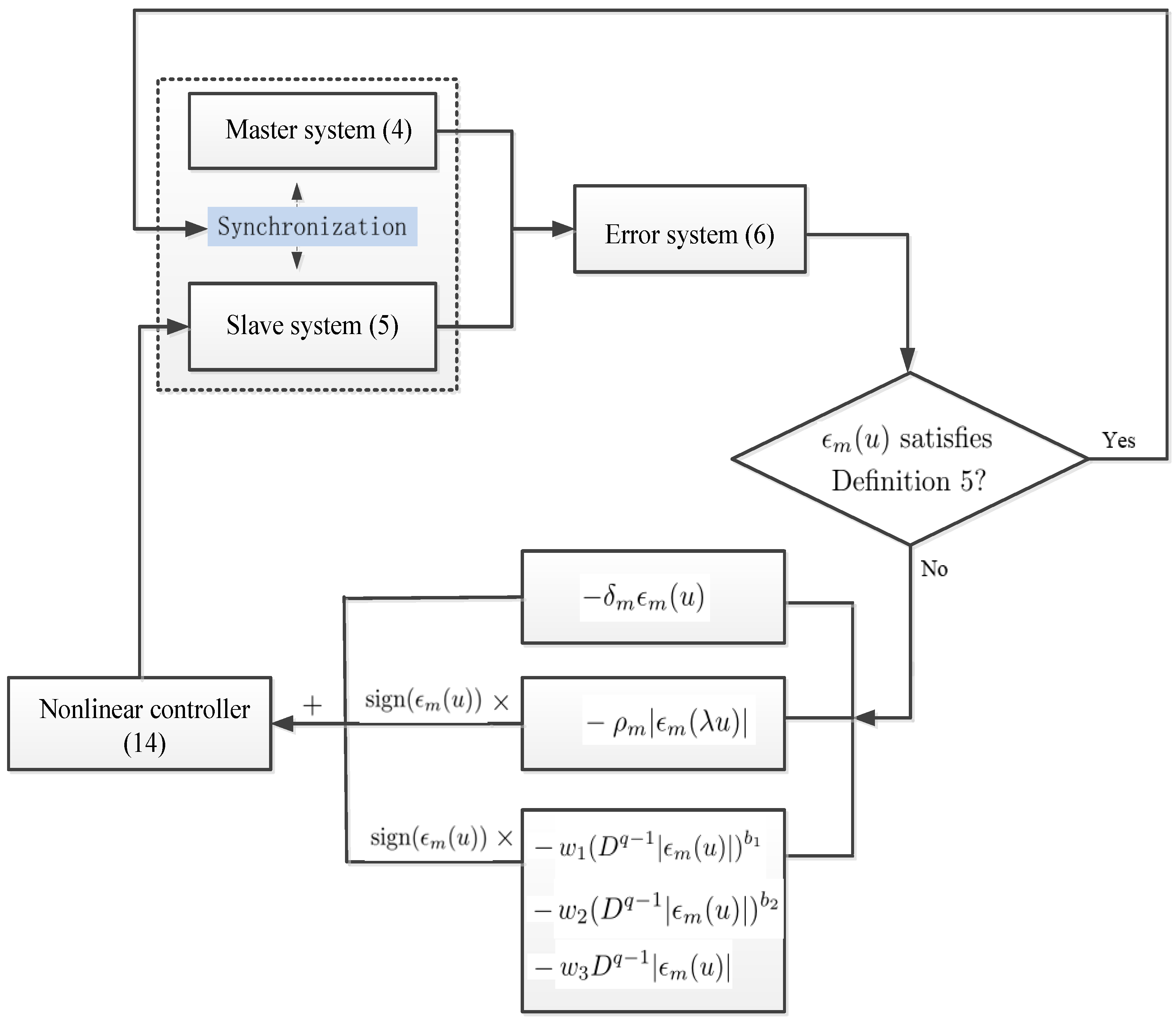
In addition, the limited performance of observers and the sensitivity of systems to external environments may lead to uncertainties in NNs. Deterministic parameters will produce ordered behavior, while uncertainties in the parameters may cause the network to be in an unstable state, thereby increasing control difficulty [47]. Kong et al. [48] were devoted to the fixed-time synchronization of Cohen–Grossberg NNs with uncertainties by adaptive control methods. Scholars have studied various synchronization frameworks for NNs with parameter uncertainties and obtained many important synchronization results [49,50]. However, both unbounded proportional delay and bounded parameter uncertainty can lead to long-term instability of the system state. To our knowledge, very few works focus on the fixed-time synchronization of fractional-order Hopfield NNs with unbounded proportional delay and bounded uncertainties, using state feedback with negative fractional derivatives. Therefore, a key objective of this work is to design a multi-module feedback controller to mitigate the combined impacts of uncertainties and proportional delay on system stability, which constitutes the primary challenge addressed in this paper.

Inspired by the preceding analysis, this paper deliberates on the fixed-time synchronization for fractional-order PDHNNs with parameter uncertainties. The key contributions are summarized as three aspects. First, we consider a fractional-order nonlinear model that accounts for both unbounded delays and bounded uncertainties, which is different from the bounded delayed NNs in [36,39]. Second, we design a robust feedback controller that includes three important function modules: a module designed to eliminate the impact of proportional delay on system stability; a module that ensures fixed-time convergence independent of the initial conditions; and a module that expands the selectable range of controller parameters. In existing works [33,34,35,44], the submodule function in multi-module controllers tends to infinity over time evolution, which affects their generalization and application. Unlike these control strategies, both our controller and Lyapunov function contain negative fractional derivatives of the error function, and each submodule function is bounded. Lastly, by applying the fixed-time stability lemma and fractional Lyapunov function and inequality techniques, the synchronization criteria for PDHNNs are derived under the proposed control schemes, and the calculation formula of the settling time is independent of the initial values of the system.

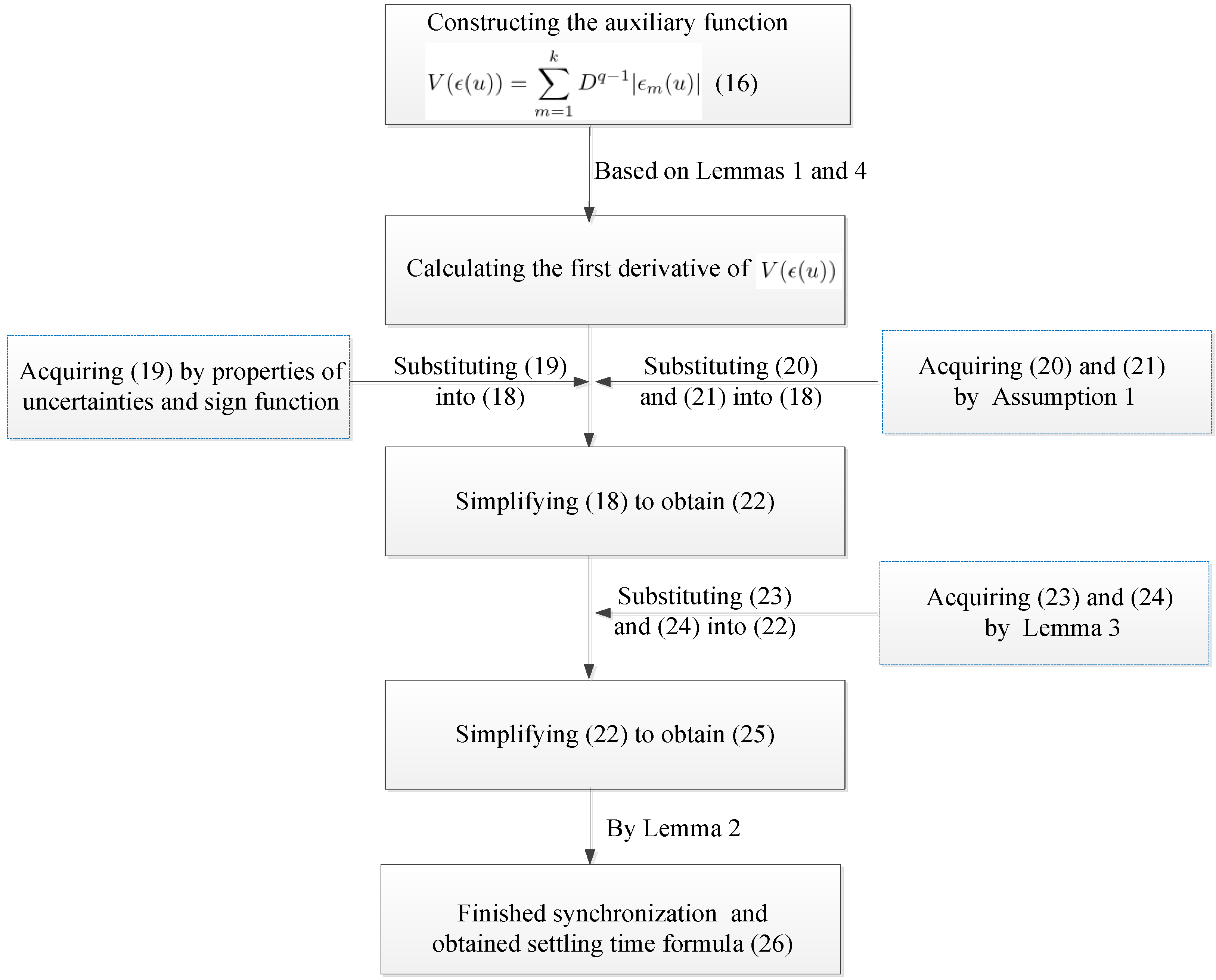
2. Preliminaries and Fractional-Order PDHNNs

This section provides some fundamental background knowledge about fractional-order integrals and derivatives. Then, fractional-order primary–secondary PDHNNs with parameter uncertainties are given.

Definition 1

([29]). For $u>0$, the Gamma function is defined as

$$\begin{array}{c}\hfill \mathsf{\Gamma }\left(u\right)={\int }_0^{+\infty }{t}^{u-1}{e}^{-t}dt.\end{array}$$

(1)

Definition 2

([29]). For a continuous integrable function $\mathcal{F}\left(u\right)$, the q-order Caputo integral is

$$\begin{array}{c}\hfill {}_{u_0}^c{D}_u^{-q}\mathcal{F}\left(u\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(q\right)}}{\int }_{u_0}^u{(u-\varsigma )}^{q-1}\mathcal{F}\left(\varsigma \right)d\varsigma ,\end{array}$$

(2)

where $u\ge u_0$ and $q>0$.

Definition 3

([29]). The q-order Caputo derivative of a function $\mathcal{F}\left(u\right)$ is

$$\begin{array}{c}\hfill {}_{u_0}^c{D}_u^q\mathcal{F}\left(u\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(n-q)}}{\int }_{u_0}^u{(u-\varsigma )}^{n-q-1}{\mathcal{F}}^{\left(n\right)}\left(\varsigma \right)d\varsigma ,\end{array}$$

(3)

where $u\ge u_0$, and $0\le n-1<q<n,n\in {\mathbb{Z}}^{+}$. Especially, when $0<q<1$, ${}_{u_0}^c{D}_u^q\mathcal{F}\left(u\right)={\displaystyle \frac{1}{\mathsf{\Gamma }(1-q)}}{\int }_{u_0}^u{(u-\varsigma )}^{-q}{\mathcal{F}}^{\prime }\left(\varsigma \right)d\varsigma$.

Lemma 1

([34]). For the function $\mathcal{F}\left(u\right)\in {\mathbb{C}}^n([u_0,+\infty ],\mathbb{R})$, $0\le \kappa \le d$, one can obtain

$$\begin{array}{cc}\hfill & {}_{u_0}^c{D}_u^{\kappa }{}_{u_0}^c{D}_u^{-d}\mathcal{F}\left(u\right)={}_{u_0}^c{D}_u^{\kappa -d}\mathcal{F}\left(u\right).\hfill \\ \hfill & {}_{u_0}^c{D}_u^{\kappa }{}_{u_0}^c{D}_u^{-\kappa }\mathcal{F}\left(u\right)=\mathcal{F}\left(u\right).\hfill \\ \hfill & {}_{u_0}^c{D}_u^{-\kappa }{}_{u_0}^c{D}_u^{\kappa }\mathcal{F}\left(u\right)=\mathcal{F}\left(u\right)-\mathcal{F}\left(u_0\right),\kappa \in (0,1).\hfill \end{array}$$

Remark 1.

Caputo fractional derivatives can be used to model network systems with non-local features. Unlike Riemann-Liouville fractional derivatives, it takes into account the initial conditions of the function, giving them clear physical meaning and making them more practical in engineering applications. To simplify the expression, we denote ${}_{u_0}^c{D}_u^q\mathcal{F}\left(u\right)=D^q\mathcal{F}\left(u\right)$ in the remainder of this article.

Consider fractional-order PDHNNs with unbounded proportional delay and bounded parameter uncertainties as follows:

$$\left\{\begin{array}{c}{D}^q{\varphi }_m\left(u\right)=-({\alpha }_m+\Delta {\alpha }_m\left(u\right)){\varphi }_m\left(u\right)+{\displaystyle \sum _{n=1}^k}({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))g_n\left({\varphi }_n\left(u\right)\right)\hfill \\ +{\displaystyle \sum _{n=1}^k}{\gamma }_{mn}{g}_n\left({\varphi }_n\left(\lambda u\right)\right)+I_m,\hfill \\ {\varphi }_m\left(u\right)={\omega }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.$$

(4)

where $0<q<1$, $m=1,2,\cdots ,k$. ${\alpha }_m>0$ is the self-regulating coefficient. ${\varphi }_m\left(u\right)$ is the mth state variable at instant u. $g_n(·)$ represents the nonlinear activation of the nth neuron. ${\beta }_{mn}$ and ${\gamma }_{mn}$ represent the connection weights of the unit n to the unit m at instants u and $\lambda u$, respectively. $\lambda$ denotes the proportional delay factor satisfying $0<\lambda <1$. $\lambda u=u-(1-\lambda )u$ describes the transmission delay $(1-\lambda )u$, which represents the unbounded time-varying delay. $\Delta {\alpha }_m\left(u\right)$ and $\Delta {\beta }_{mn}\left(u\right)$ characterize the parameter uncertainties, which satisfy bounded conditions $|\Delta {\alpha }_m\left(u\right)|\le {\daleth }_m$ and $|\Delta {\beta }_{mn}\left(u\right)|\le {\gimel }_{mn}$. $I_m$ stands for the mth external constant input.

Taking q-order PDHNNs (4) as the primary system, then the q-order secondary system is given by

$$\left\{\begin{array}{c}{D}^q{\phi }_m\left(u\right)=-({\alpha }_m+\Delta {\alpha }_m\left(u\right)){\phi }_m\left(u\right)+{\displaystyle \sum _{n=1}^k}({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))g_n\left({\phi }_n\left(u\right)\right)\hfill \\ +{\displaystyle \sum _{n=1}^k}{\gamma }_{mn}{g}_n\left({\phi }_n\left(\lambda u\right)\right)+I_m+W_m\left(u\right),\hfill \\ {\phi }_m\left(u\right)={\varpi }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.$$

(5)

where $0<q<1$, $m=1,2,\cdots ,k$, and ${\phi }_m\left(u\right)$ is the mth state variable in the secondary system. ${\varpi }_m\left(u\right)$ denotes the initial condition and $W_m\left(u\right)$ represents the control input at instant u.

To derive the error expression between systems (4) and (5), we define the synchronization error as ${ϵ}_m\left(u\right)={\phi }_m\left(u\right)-{\varphi }_m\left(u\right),m=1,2,\cdots ,k$. Then one can get

$$\left\{\begin{array}{c}{D}^q{ϵ}_m\left(u\right)=-({\alpha }_m+\Delta {\alpha }_m\left(u\right)){ϵ}_m\left(u\right)+{\displaystyle \sum _{n=1}^k}({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))\left[g_n\left({\phi }_n\left(u\right)\right)-g_n\left({\varphi }_n\left(u\right)\right)\right]\hfill \\ +{\displaystyle \sum _{n=1}^k}{\gamma }_{mn}\left[g_n\left({\phi }_n\left(\lambda u\right)\right)-g_n\left({\varphi }_n\left(\lambda u\right)\right)\right]+W_m\left(u\right),\hfill \\ {ϵ}_m\left(u\right)={\psi }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.$$

(6)

where $0<q<1$, $m=1,2,\cdots ,k$.

For convenience, we define $ϵ\left(u\right)={({ϵ}_1\left(u\right),{ϵ}_2\left(u\right),\cdots ,{ϵ}_k\left(u\right))}^T$ and $\psi \left(u\right)=({\psi }_1\left(u\right),$ ${\psi }_2\left(u\right),\cdots ,{\psi }_k{\left(u\right))}^T$.

Assumption 1.

For the activation function $g_n(·)$, there exist a constant $F_n>0$ satisfying

$$\begin{array}{c}\hfill |g_n\left(v_1\right)-g_n\left(v_2\right)|\le F_n|v_1-v_2|, n=1,2,\cdots ,k,\end{array}$$

(7)

for $\forall v_1,v_2\in \mathbb{R}$.

Definition 4

([38]). The origin of network system (6) is finite-time stable if there exists $T\left(\psi \right)>0$ satisfying

$$\underset{u\to T\left(\psi \right)}{lim}\parallel ϵ\left(u\right)\parallel =0 \mathit{and} \parallel ϵ\left(u\right)\parallel =0, \forall u>T\left(\psi \right),$$

(8)

where $T\left(\psi \right)$ denotes the settling time.

Definition 5

([38]). The origin of network system (6) is fixed-time stable if the origin of (6) is finite-time stable and there is a fixed scalar $T^{\ast }>0$ such that $T\left(\psi \right)\le T^{\ast }$ for ∀$\psi \in {\mathbb{R}}^n$.

Remark 2.

From the above two definitions, finite-time synchronization achieves the convergence of the error state of a dynamical system within a time dependent on the initial state, whereas fixed-time synchronization guarantees convergence within a bounded, pre-computable time independent of the initial states.

Remark 3.

Finite-time synchronization tasks of fractional-order NNs have been studied in [33,34,35]. In contrast, fixed-time synchronization is a significant development of finite-time synchronization, ensuring that the primary and secondary systems synchronize within a unified time range, and the synchronization results are independent of initial states. The fixed-time synchronization results are particularly suitable for scenarios with strict convergence-time requirements, such as multi-agent systems, drone formations, and robot collaboration. For example, in a drone swarm performing collaborative reconnaissance or material transport, all units must achieve highly consistent posture, position, and velocity information. By treating each drone as a dynamical subsystem, a multi-mode controller can be designed to synchronize the entire swarm within a fixed time, ensuring timely and coordinated task execution.

Remark 4.

In [30,31], various dynamic behaviors of fractional-order Hopfield NNs have been studied using methods such as bifurcation diagrams and Lyapunov exponent analysis. In [32], fractional-order Hopfield NNs have been applied to achieve medical image encryption. In contrast, this work investigates a more general model that incorporates both unbounded proportional delay and bounded uncertainties, thereby addressing a broader and more practical class of systems.

Lemma 2

([51]). Assume $V(·):{\mathbb{R}}^n\to {\mathbb{R}}_{+}\cup \left\{0\right\}$ is a continuous and unbounded function meeting

(I) 

$V\left(ϵ\right(u\left)\right)=0$ if $ϵ\left(u\right)=0$.

(II) 

Each solution of system (6) satisfies

$$\dot{V}\left(ϵ\left(u\right)\right)\le -c_1{V}^{b_1}\left(ϵ\left(u\right)\right)-c_2{V}^{b_2}\left(ϵ\left(u\right)\right)-c_{3}V\left(ϵ\left(u\right)\right),$$

(9)

where $c_1,c_2,c_3>0$, $0<b_1<1$, and $b_2>1$. Then the origin of system (6) is fixed-time stable. The settling time can be estimated by

$$T^{\ast }={\displaystyle \frac{b_2-b_1}{c_3(b_2-1)(1-b_1)}}\ln \left[1+{\displaystyle \frac{c_3}{c_1}}{({\displaystyle \frac{c_1}{c_2}})}^{{\displaystyle \frac{1-b_1}{b_2-b_1}}}\right].$$

(10)

Lemma 3

([11]). Let ${\eta }_m\ge 0(m=1,2,\cdots ,k)$, $0<\lambda <1$, and $\mu >1$. Then one can obtain

$${\eta }_1^{\lambda }+{\eta }_2^{\lambda }+\cdots +{\eta }_k^{\lambda }\ge {({\eta }_1+{\eta }_2+\cdots +{\eta }_k)}^{\lambda },$$

(11)

and

$${\eta }_1^{\mu }+{\eta }_2^{\mu }+\cdots +{\eta }_k^{\mu }\ge k^{1-\mu }{({\eta }_1+{\eta }_2+\cdots +{\eta }_k)}^{\mu }.$$

(12)

Lemma 4

([52]). For a continuously differentiable function $\mathcal{F}\left(u\right)$, one can get

$$D^q\left|\mathcal{F}\left(u\right)\right|\le \mathit{sign}\left(\mathcal{F}\left(u\right)\right)D^q\mathcal{F}\left(u\right), 0<q<1,$$

(13)

where sign(·) denotes the signum function.

Remark 5.

Lemma 4 has an extensive application in the synchronization control of fractional-order networks, providing excellent estimation for the fractional derivatives of the absolute value parts, such as [45,53]. In this paper, the lemma plays a crucial role in the stability analysis of error systems based on Lyapunov functions, particularly when dealing with the absolute value function of ${ϵ}_m\left(u\right)$.

3. New Synchronization Criteria of Fractional PDHNNs

Based on the fixed-time stable definition and the distinguishing features of the fractional primary–secondary PDHNNs, we consider the nonlinear controller with negative fractional derivatives as follows:

$$\begin{array}{cc}\hfill W_m\left(u\right)=& -{\delta }_m{ϵ}_m\left(u\right)-\mathrm{sign}\left({ϵ}_m\left(u\right)\right)[{\rho }_m|{ϵ}_m\left(\lambda u\right)|+w_1(D^{q-1}|{ϵ}_m\left(u\right){\left|\right)}^{b_1}\hfill \\ \hfill & +w_2(D^{q-1}|{ϵ}_m{\left(u\right)\left|\right)}^{b_2}+w_3{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|],\hfill \end{array}$$

(14)

where $m=1,2,\cdots ,k$, $w_1,w_2,w_3>0$, $0<b_1<1$, $b_2>1$, and ${\delta }_m,{\rho }_m$ represent positive feedback constants.

Remark 6.

Figure 1 gives the nonlinear control block diagram between primary–secondary systems (4) and (5). Our goal is to apply external nonlinear control to the secondary system so that the error between the primary–secondary systems satisfies Definition 5. The nonlinear controller (14) consists of three key functional modules, which have different functions and roles. The first part $-{\delta }_m{ϵ}_m\left(u\right)$ expands the selectable range of system parameters. The second part $-{\rho }_m\left|{ϵ}_m\left(\lambda u\right)\right|$ eliminates the impact of proportional delay on system stability. The last part $-w_1(D^{q-1}|{ϵ}_m\left(u\right){\left|\right)}^{b_1}$, $-w_2(D^{q-1}|{ϵ}_m\left(u\right){\left|\right)}^{b_2}$, and $-w_3{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|$ ensures that systems converge within a fixed time frame regardless of initial conditions, as can be clearly seen from the settling time estimation formula.

Remark 7.

In existing works [33,34,35], nonlinear feedback controllers with multiple functional modules have been applied to the synchronization issues of various coupled and non-coupled NNs. These feedback control strategies have similar characteristics, namely considering ${\displaystyle \frac{{ϵ}_m\left(u\right)}{|{ϵ}_m\left(u\right)|}}$ and ${\displaystyle \frac{{ϵ}_m(u-\tau )}{|{ϵ}_m\left(u\right)|}}$ as one of the submodules. Under the action of such controllers, if the error ${ϵ}_m\left(u\right)$ approaches zero, the boundary of the feedback controller may approach infinity, which will affect its generalization and application. Unlike these control schemes, we circumvent this problem by considering negative fractional derivatives of the error ${ϵ}_m\left(u\right)$. We construct a fractional Lyapunov function and then combine the properties of integer-order and fractional-order calculus for system stability analysis.

Theorem 1.

Under Assumption 1, if the two conditions listed below are satisfied,

$$\begin{array}{cc}\hfill & \left(\mathrm{i}\right) \sum _{n=1}^k\left(\right|{\beta }_{nm}|+{\gimel }_{nm})F_m-({\alpha }_m+{\delta }_m-{\daleth }_m)\le 0,\hfill \\ \hfill & \left(\mathrm{ii}\right)\sum _{n=1}^k\left|{\gamma }_{nm}\right|F_m-{\rho }_m\le 0,\hfill \end{array}$$

where $m=1,2,\cdots ,k$, then the fixed-time synchronization between fractional PDHNNs (4) and (5) is achieved via nonlinear controller (14). Furthermore, the settling time is estimated by

$$\begin{array}{c}\hfill T^{\ast }={\displaystyle \frac{b_2-b_1}{w_3(b_2-1)(1-b_1)}}\ln \left[1+{\displaystyle \frac{w_3}{w_1}}{({\displaystyle \frac{w_1}{w_2{k}^{1-b_2}}})}^{{\displaystyle \frac{1-b_1}{b_2-b_1}}}\right].\end{array}$$

(15)

Proof. 

Select the positive auxiliary function as

$$\begin{array}{c}\hfill V\left(ϵ\left(u\right)\right)=\sum _{m=1}^k{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|.\end{array}$$

(16)

Based on Lemmas 1 and 4, calculating the first derivative of $V\left(ϵ\right(u\left)\right)$ gives

$$\begin{array}{cc}\hfill \dot{V}\left(ϵ\left(u\right)\right)=& D^q\left(D^{1-q}V\left(ϵ\left(u\right)\right)\right)\hfill \\ \hfill =& D^q\left(D^{1-q}{D}^{q-1}\sum _{m=1}^k\left|{ϵ}_m\left(u\right)\right|\right)\hfill \\ \hfill =& \sum _{m=1}^k{D}^q\left|{ϵ}_m\left(u\right)\right|\hfill \\ \hfill \le & \sum _{m=1}^k\mathrm{sign}\left({ϵ}_m\left(u\right)\right)D^q{ϵ}_m\left(u\right).\hfill \end{array}$$

(17)

Substituting error system (6) into (17), one can get

$$\begin{array}{cc}\hfill \dot{V}\left(ϵ\left(u\right)\right)\le & \sum _{m=1}^k\mathrm{sign}\left({ϵ}_m\left(u\right)\right)\{-({\alpha }_m+\Delta {\alpha }_m\left(u\right)){ϵ}_m\left(u\right)+\sum _{n=1}^k({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))[g_n\left({\phi }_n\left(u\right)\right)\hfill \\ \hfill & -g_n\left({\varphi }_n\left(u\right)\right)]+\sum _{n=1}^k{\gamma }_{mn}\left[g_n\left({\phi }_n\left(\lambda u\right)\right)-g_n\left({\varphi }_n\left(\lambda u\right)\right)\right]-{\delta }_m{ϵ}_m\left(u\right)\hfill \\ \hfill & -\mathrm{sign}\left({ϵ}_m\left(u\right)\right)[{\rho }_m|{ϵ}_m\left(\lambda u\right)|+w_1(D^{q-1}|{ϵ}_m{\left(u\right)\left|\right)}^{b_1}+w_2(D^{q-1}|{ϵ}_m\left(u\right){\left|\right)}^{b_2}\hfill \\ \hfill & +w_3{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|\left]\right\}.\hfill \end{array}$$

(18)

Based on the boundedness of uncertainties and the properties of the sign function, one can derive

$$\begin{array}{c}\hfill \sum _{m=1}^k\mathrm{sign}\left({ϵ}_m\left(u\right)\right)\left[-({\alpha }_m+\Delta {\alpha }_m\left(u\right))\right]{ϵ}_m\left(u\right)\le \sum _{m=1}^k(-{\alpha }_m+{\daleth }_m)\left|{ϵ}_m\left(u\right)\right|.\end{array}$$

(19)

Based on Assumption 1, one can obtain

$$\begin{array}{cc}\hfill \sum _{m=1}^k& \mathrm{sign}\left({ϵ}_m\left(u\right)\right)\sum _{n=1}^k({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))\left[g_n\left({\phi }_n\left(u\right)\right)-g_n\left({\varphi }_n\left(u\right)\right)\right]\hfill \\ \hfill \le & \sum _{m=1}^k\sum _{n=1}^k|{\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right)\left|\right|g_n\left({\phi }_n\left(u\right)\right)-g_n\left({\varphi }_n\left(u\right)\right)|\hfill \\ \hfill \le & \sum _{m=1}^k\sum _{n=1}^k\left(\right|{\beta }_{mn}|+{\gimel }_{mn})F_n\left|{ϵ}_n\left(u\right)\right|,\hfill \end{array}$$

(20)

and

$$\begin{array}{cc}\hfill \sum _{m=1}^k& \mathrm{sign}\left({ϵ}_m\left(u\right)\right)\sum _{n=1}^k{\gamma }_{mn}\left[g_n\left({\phi }_n\left(\lambda u\right)\right)-g_n\left({\varphi }_n\left(\lambda u\right)\right)\right]\hfill \\ \hfill \le & \sum _{m=1}^k\sum _{n=1}^k|{\gamma }_{mn}\left|\right|g_n\left({\phi }_n\left(\lambda u\right)\right)-g_n\left({\varphi }_n\left(\lambda u\right)\right)|\hfill \\ \hfill \le & \sum _{m=1}^k\sum _{n=1}^k|{\gamma }_{mn}|F_n\left|{ϵ}_n\left(\lambda u\right)\right|.\hfill \end{array}$$

(21)

Based on conditions (i)–(ii), substituting inequalities (19)–(21) into (18), we have

$$\begin{array}{cc}\hfill \dot{V}& \left(ϵ\right(u\left)\right)\hfill \\ \hfill \le & \sum _{m=1}^k(-{\alpha }_m+{\daleth }_m)|{ϵ}_m\left(u\right)|+\sum _{m=1}^k\sum _{n=1}^k(|{\beta }_{mn}|+{\gimel }_{mn})F_n|{ϵ}_n\left(u\right)|\hfill \\ \hfill & +\sum _{m=1}^k\sum _{n=1}^k|{\gamma }_{mn}|F_n|{ϵ}_n\left(\lambda u\right)|-\sum _{m=1}^k{\delta }_m|{ϵ}_m\left(u\right)|\hfill \\ \hfill & -\sum _{m=1}^k\left[{\rho }_m|{ϵ}_m\left(\lambda u\right)|+w_1(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_1}+w_2(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_2}+w_3{D}^{q-1}|{ϵ}_m\left(u\right)|\right]\hfill \\ \hfill \le & \sum _{m=1}^k(-{\alpha }_m+{\daleth }_m)|{ϵ}_m\left(u\right)|+\sum _{m=1}^k\sum _{n=1}^k(|{\beta }_{nm}|+{\gimel }_{nm})F_m|{ϵ}_m\left(u\right)|\hfill \\ \hfill & +\sum _{m=1}^k\sum _{n=1}^k|{\gamma }_{nm}|F_m|{ϵ}_m\left(\lambda u\right)|-\sum _{m=1}^k{\delta }_m|{ϵ}_m\left(u\right)|\hfill \\ \hfill & -\sum _{m=1}^k\left[{\rho }_m|{ϵ}_m\left(\lambda u\right)|+w_1(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_1}+w_2(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_2}+w_3{D}^{q-1}|{ϵ}_m\left(u\right)|\right]\hfill \\ \hfill =& \sum _{m=1}^k\{\left[\sum _{n=1}^k(|{\beta }_{nm}|+{\gimel }_{nm})F_m-({\alpha }_m+{\delta }_m-{\daleth }_m)\right]|{ϵ}_m\left(u\right)|\hfill \\ \hfill & +(\sum _{n=1}^k|{\gamma }_{nm}|F_m-{\rho }_m)|{ϵ}_m\left(\lambda u\right)|\hfill \\ \hfill & -\left[w_1(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_1}+w_2(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_2}+w_3{D}^{q-1}|{ϵ}_m\left(u\right)|\right]\}\hfill \\ \hfill \le & -\sum _{m=1}^k\left[w_1(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_1}+w_2(D^{q-1}|{ϵ}_m{\left(u\right)|)}^{b_2}+w_3{D}^{q-1}|{ϵ}_m\left(u\right)|\right].\hfill \end{array}$$

(22)

For $0<b_1<1$ and $b_2>1$, using Lemma 3 gives that

$$\begin{array}{c}\hfill \sum _{m=1}^k{\left(D^{q-1}\left|{ϵ}_m\left(u\right)\right|\right)}^{b_1}\ge {\left(\sum _{m=1}^k{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|\right)}^{b_1},\end{array}$$

(23)

and

$$\begin{array}{c}\hfill \sum _{m=1}^k{\left(D^{q-1}\left|{ϵ}_m\left(u\right)\right|\right)}^{b_2}\ge k^{1-b_2}{\left(\sum _{m=1}^k{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|\right)}^{b_2}.\end{array}$$

(24)

Then substituting inequalities (23) and (24) into (22) gives

$$\begin{array}{cc}\hfill \dot{V}\left(ϵ\left(u\right)\right)\le & -w_1{\left(\sum _{m=1}^k{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|\right)}^{b_1}-w_2{k}^{1-b_2}{\left(\sum _{m=1}^k{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|\right)}^{b_2}\hfill \\ \hfill & -w_3\sum _{m=1}^k{D}^{q-1}\left|{ϵ}_m\left(u\right)\right|\hfill \\ \hfill =& -w_1{V}^{b_1}\left(ϵ\left(u\right)\right)-w_2{k}^{1-b_2}{V}^{b_2}\left(ϵ\left(u\right)\right)-w_{3}V\left(ϵ\left(u\right)\right).\hfill \end{array}$$

(25)

Hence, inequality (25) satisfies the framework requirement for nonnegative functions in Lemma 2. According to Lemma 2, the fixed-time synchronization between primary system (4) and secondary system (5) can be achieved, and the settling time is estimated by

$$T^{\ast }={\displaystyle \frac{b_2-b_1}{w_3(b_2-1)(1-b_1)}}\ln \left[1+{\displaystyle \frac{w_3}{w_1}}{({\displaystyle \frac{w_1}{w_2{k}^{1-b_2}}})}^{{\displaystyle \frac{1-b_1}{b_2-b_1}}}\right].$$

(26)

□

Remark 8.

This article proves the fixed-time synchronization of PDHNNs by the comparison theorem and Lyapunov function method. As shown in Figure 2, we give a proof schematic diagram of Theorem 1, which demonstrates the logical deduction between mathematical relationships (16)–(26). First, select the auxiliary function with $(q-1)$-order derivative ($-1<q-1<0$) and calculate the first derivative of $V\left(ϵ\right(u\left)\right)$. Second, acquire (19) by properties of uncertainties and the sign function, and acquire (20) and (21) by Assumption 1. Based on (19)–(21), simplify (18) to obtain (22). Third, by Lemmas 2 and 3, one can get (25) and (26) and finish the proof.

Especially, when modeling PDHNNs without considering uncertainties, the primary system can be described as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}^q{\varphi }_m\left(u\right)=-{\alpha }_m{\varphi }_m\left(u\right)+{\displaystyle \sum _{n=1}^k}{\beta }_{mn}{g}_n\left({\varphi }_n\left(u\right)\right)+{\displaystyle \sum _{n=1}^k}{\gamma }_{mn}{g}_n\left({\varphi }_n\left(\lambda u\right)\right)+I_m,\hfill \\ {\varphi }_m\left(u\right)={\omega }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.\end{array}$$

(27)

where $0<q<1$, $m=1,2,\cdots ,k$. Then, the fractional-order secondary system can be given by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}^q{\phi }_m\left(u\right)=-{\alpha }_m{\phi }_m\left(u\right)+{\displaystyle \sum _{n=1}^k}{\beta }_{mn}{g}_n\left({\phi }_n\left(u\right)\right)+{\displaystyle \sum _{n=1}^k}{\gamma }_{mn}{g}_n\left({\phi }_n\left(\lambda u\right)\right)+I_m+W_m\left(u\right),\hfill \\ {\phi }_m\left(u\right)={\varpi }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.\end{array}$$

(28)

where $0<q<1$, $m=1,2,\cdots ,k$. Utilizing a similar derivation process as in Theorem 1, we can acquire the following corollary under nonlinear controller (14).

Corollary 1.

Under Assumption 1, if the two conditions listed below are satisfied,

$$\begin{array}{cc}\hfill & \left(\mathrm{iii}\right) \sum _{n=1}^k\left|{\beta }_{nm}\right|F_m-({\alpha }_m+{\delta }_m)\le 0,\hfill \\ \hfill & \left(\mathrm{iv}\right)\sum _{n=1}^k\left|{\gamma }_{nm}\right|F_m-{\rho }_m\le 0,\hfill \end{array}$$

where $m=1,2,\cdots ,k$, then the fixed-time synchronization between fractional PDHNNs (27) and (28) is achieved via nonlinear controller (14). In addition, the settling time is evaluated by

$$\begin{array}{c}\hfill T^{\ast }={\displaystyle \frac{b_2-b_1}{w_3(b_2-1)(1-b_1)}}\ln \left[1+{\displaystyle \frac{w_3}{w_1}}{({\displaystyle \frac{w_1}{w_2{k}^{1-b_2}}})}^{{\displaystyle \frac{1-b_1}{b_2-b_1}}}\right].\end{array}$$

(29)

Remark 9.

In [25,26], fixed-time synchronization issues of NNs with bounded delays have been investigated. Different from the two works, the synchronization results obtained in Corollary 1 are based on the fractional NNs with unbounded proportional delay instead of integer-order NNs. Hence, the result of Corollary 1 can be seen as a generalized version of these works.

4. Simulation Examples

Two simulation experiments are given to confirm the applicability of synchronization results in Theorem 1 and Corollary 1.

Example 1.

Consider 2-dimensional fractional PDHNNs with bounded uncertainties as the primary system, which is described by

$$\left\{\begin{array}{c}{D}^{0.96}{\varphi }_m\left(u\right)=-({\alpha }_m+\Delta {\alpha }_m\left(u\right)){\varphi }_m\left(u\right)+{\displaystyle \sum _{n=1}^2}({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))g_n\left({\varphi }_n\left(u\right)\right)\hfill \\ +{\displaystyle \sum _{n=1}^2}{\gamma }_{mn}{g}_n\left({\varphi }_n\left(\lambda u\right)\right)+I_m,\hfill \\ {\varphi }_m\left(u\right)={\omega }_m\left(u\right), u\in [\lambda ,1].\hfill \end{array}\right.$$

(30)

Then, the consequential secondary system can be defined by

$$\left\{\begin{array}{c}{D}^{0.96}{\phi }_m\left(u\right)=-({\alpha }_m+\Delta {\alpha }_m\left(u\right)){\phi }_m\left(u\right)+{\displaystyle \sum _{n=1}^2}({\beta }_{mn}+\Delta {\beta }_{mn}\left(u\right))g_n\left({\phi }_n\left(u\right)\right)\hfill \\ +{\displaystyle \sum _{n=1}^2}{\gamma }_{mn}{g}_n\left({\phi }_n\left(\lambda u\right)\right)+I_m+W_m\left(u\right),\hfill \\ {\phi }_m\left(u\right)={\varpi }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.$$

(31)

where ${\alpha }_1=3,{\alpha }_2=4,{\beta }_{11}=1,{\beta }_{12}=-1.2,{\beta }_{21}=-0.4,{\beta }_{22}=0.8$, ${\gamma }_{11}=0.1,{\gamma }_{12}=-0.5,{\gamma }_{21}=0.3,{\gamma }_{22}=0.1$, $\Delta {\alpha }_1\left(u\right)=\Delta {\beta }_{1n}\left(u\right)=0.1\sin u,\Delta {\alpha }_2\left(u\right)=\Delta {\beta }_{2n}\left(u\right)=0.1\cos u$, $\lambda =0.5$. Giving the activation functions $g_1\left(u\right)=g_2\left(u\right)=\tanh \left(u\right)$, we can check that Assumption 1 holds for $F_1=F_2=1$.

Let parameters $w_1=2,w_2=1.5,w_3=2,b_1=0.5,b_2=1.5,{\delta }_1=0.5,{\delta }_2=1,{\rho }_1=0.6,{\rho }_2=0.8$, and ${\daleth }_m={\gimel }_{mn}=0.1$. Through simple calculations, one can obtain ${\displaystyle \sum _{n=1}^2}\left(\right|{\beta }_{n1}|+{\gimel }_{n1})F_1-({\alpha }_1+{\delta }_1-{\daleth }_1)=-1.8\le 0$, ${\displaystyle \sum _{n=1}^2}\left(\right|{\beta }_{n2}|+{\gimel }_{n2})F_2-({\alpha }_2+{\delta }_2-{\daleth }_2)=-2.7\le 0$, ${\displaystyle \sum _{n=1}^2}\left|{\gamma }_{n1}\right|F_1-{\rho }_1=-0.2\le 0$, ${\displaystyle \sum _{n=1}^2}\left|{\gamma }_{n2}\right|F_2-{\rho }_2=-0.2\le 0$.

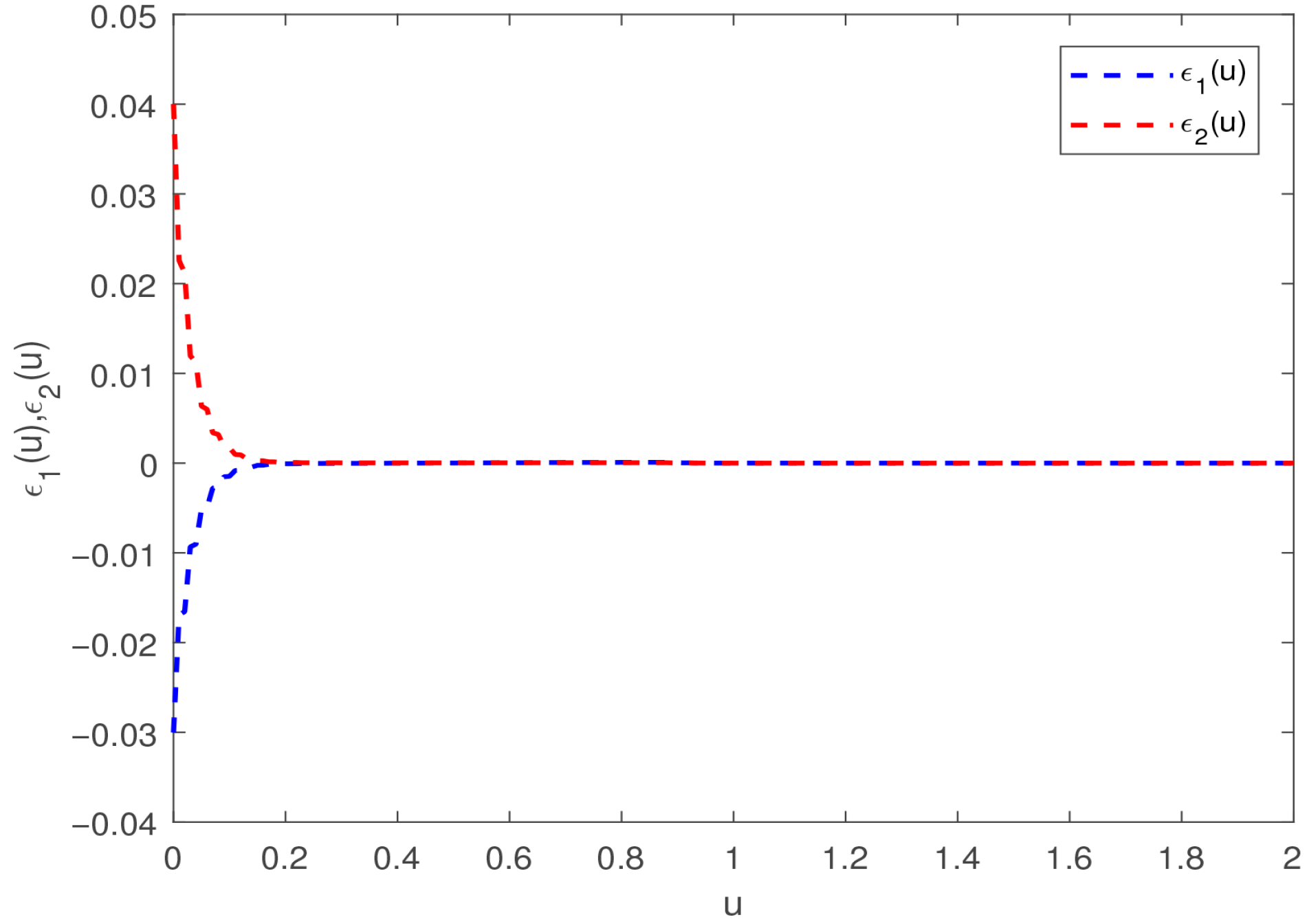
It is clear that the above parameter values satisfy the conditions in Theorem 1. According to calculation Formula (15), the settling time can be estimated as 1.7285 s. The initial conditions are chosen as ${\varphi }_1\left(u\right)=0.15,{\varphi }_2\left(u\right)=-0.14,{\phi }_1\left(u\right)=0.1,{\phi }_2\left(u\right)=-0.1$. 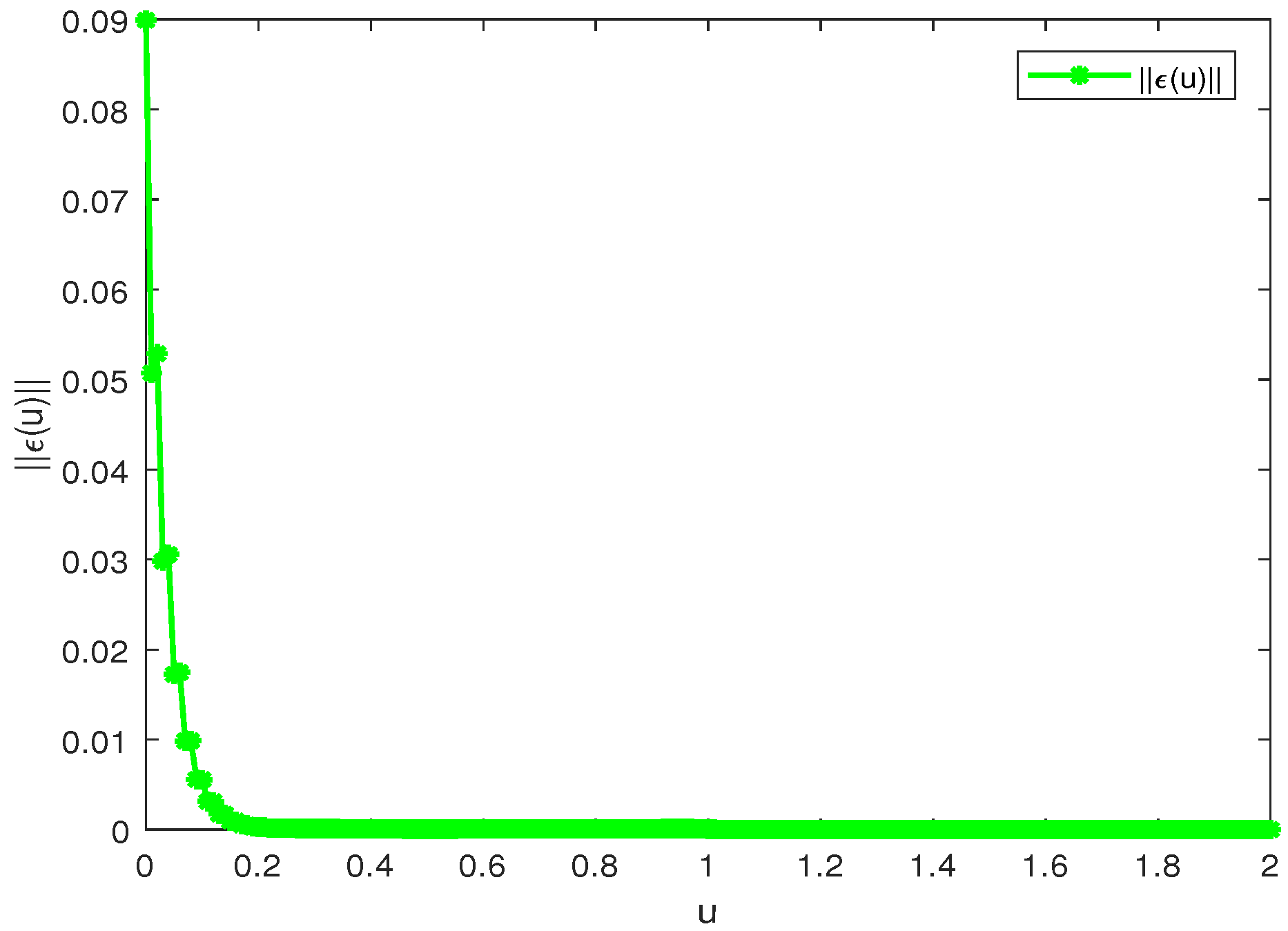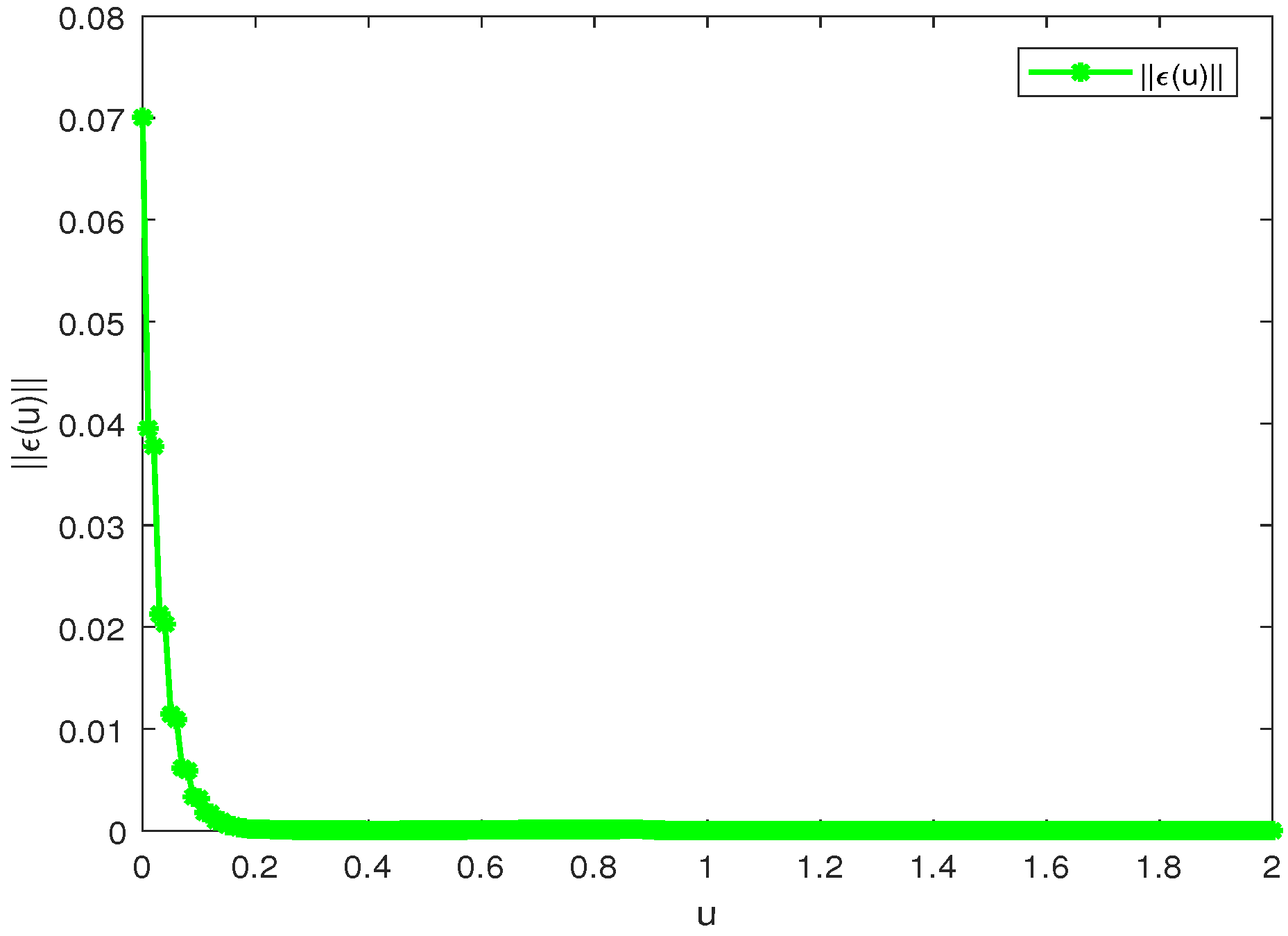Under the above control parameters, the error evolution of each neuron over time is shown in Figure 3. The blue and red dashed lines represent the error states of the first and second neurons, respectively. The evolution of the error norm over time can be seen in Figure 4. From Figure 3 and Figure 4, it is evident that the errors of primary–secondary systems (30) and (31) converge to zero within the specified time, indicating that the network achieves synchronization within a fixed time.

To assess the impact of parameter changes on synchronization capability, we focus on studying the uncertainties and the strength of feedback control. To simultaneously evaluate the robustness of our controller, initial values were randomly selected from the range of $[-0.3,0.3]$. Two types of experiments use different initial values, and experiments of the same type use the same initial values to ensure experimental fairness. The coefficients of parameter uncertainties are selected as 0.1, 0.2, and 0.3, respectively. As shown in Figure 5, the larger the coefficient, the longer the time spent for the system to achieve synchronization. In addition, we adjust the control strength ${\rho }_1$ under the same initial conditions and observe its impact on system synchronization. Figure 6 shows that as the control strength increases, the time for the primary–secondary networks to achieve synchronization gradually decreases. The above experiments indicate that our control method is not limited by the changes of initial conditions and parameters. As long as the parameters satisfy the conditions of Theorem 1, the fixed-time synchronization task of fractional PDHNNs can be completed.

To observe the influence of control parameters on the settling time, we first adjust $w_1$ with a step size of 0.2 and keep the other parameters unchanged. The results in

Table 1. The impact of the adjustable parameter $w_1$ on the settling time.

Parameter $w_1$	2.2	2.4	2.6	2.8	3.0	3.2	3.4
Settling time	1.6739	1.6250	1.5809	1.5407	1.5040	1.4701	1.4388

indicate that as $w_1$ increases, the settling time actually decreases. Similarly, using step sizes of 0.2 and 0.5 to change the parameters $w_2$ and $w_3$, one can see that the larger $w_2$ and $w_3$ are, the shorter the settling time, as shown in

Table 2. The impact of the adjustable parameter $w_2$ on the settling time.

Parameter $w_2$	1.7	1.9	2.1	2.3	2.5	2.7	2.9
Settling time	1.6570	1.5951	1.5407	1.4924	1.4490	1.4097	1.3738

and

Table 3. The impact of the adjustable parameter $w_3$ on the settling time.

Parameter $w_3$	2.5	3.0	3.5	4.0	4.5	5.0	5.5
Settling time	1.5989	1.4911	1.3996	1.3208	1.2520	1.1913	1.1372

. Furthermore, adjusting the parameter $b_1$ from 0.65 to 0.95 with a step size of 0.05, it is not difficult to find that the settling time is proportional to the parameter $b_1$, as shown in

Table 4. The impact of the adjustable parameter $b_1$ on the settling time.

Parameter $b_1$	0.65	0.70	0.75	0.80	0.85	0.90	0.95
Settling time	2.0211	2.1843	2.4133	2.7575	3.3324	4.4844	7.9463

. Eventually,

Table 5. The impact of the adjustable parameter $b_2$ on the settling time.

Parameter $b_2$	1.6	1.7	1.8	1.9	2.0	2.1	2.2
Settling time	1.5873	1.4864	1.4108	1.3519	1.3049	1.2664	1.2343

shows that selecting a larger parameter $b_2$ is beneficial to shorten the settling time. The above discussion provides a guide on how to select control parameters to derive small settling time. In practical applications, it is necessary to select control parameters in conjunction with control cost.

Example 2.

Consider 2-dimensional fractional PDHNNs without uncertainties as the primary system, described as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}^{0.90}{\varphi }_m\left(u\right)=-{\alpha }_m{\varphi }_m\left(u\right)+{\displaystyle \sum _{n=1}^2}{\beta }_{mn}{g}_n\left({\varphi }_n\left(u\right)\right)+{\displaystyle \sum _{n=1}^2}{\gamma }_{mn}{g}_n\left({\varphi }_n\left(\lambda u\right)\right)+I_m,\hfill \\ {\varphi }_m\left(u\right)={\omega }_m\left(u\right), u\in [\lambda ,1].\hfill \end{array}\right.\end{array}$$

(32)

Then, the consequential secondary system can be given by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{D}^{0.90}{\phi }_m\left(u\right)=-{\alpha }_m{\phi }_m\left(u\right)+{\displaystyle \sum _{n=1}^2}{\beta }_{mn}{g}_n\left({\phi }_n\left(u\right)\right)+{\displaystyle \sum _{n=1}^2}{\gamma }_{mn}{g}_n\left({\phi }_n\left(\lambda u\right)\right)+I_m+W_m\left(u\right),\hfill \\ {\phi }_m\left(u\right)={\varpi }_m\left(u\right), u\in [\lambda ,1],\hfill \end{array}\right.\end{array}$$

(33)

where ${\alpha }_1=2,{\alpha }_2=1,{\beta }_{11}=0.5,{\beta }_{12}=0.3,{\beta }_{21}=0.6,{\beta }_{22}=0.4$, ${\gamma }_{11}=-0.2,{\gamma }_{12}=0.1,{\gamma }_{21}=0.1,{\gamma }_{22}=-0.3$, $\lambda =0.4$. The activation functions are $g_1\left(u\right)=g_2\left(u\right)=\tanh \left(u\right)$, which satisfy Assumption 1 for $F_1=F_2=1$.

Let parameters $w_1=2,w_2=2,w_3=2,b_1=0.5,b_2=1.5,{\delta }_1=0.5,{\delta }_2=0.8,{\rho }_1=0.4$, and ${\rho }_2=0.5$. Through simple calculations, one can get ${\displaystyle \sum _{n=1}^2}\left|{\beta }_{n1}\right|F_1-({\alpha }_1+{\delta }_1)=-1.4\le 0$, ${\displaystyle \sum _{n=1}^2}\left|{\beta }_{n2}\right|F_2-({\alpha }_2+{\delta }_2)=-1.1\le 0$, ${\displaystyle \sum _{n=1}^2}\left|{\gamma }_{n1}\right|F_1-{\rho }_1=-0.1\le 0$, and ${\displaystyle \sum _{n=1}^2}\left|{\gamma }_{n2}\right|F_2-{\rho }_2=-0.1\le 0$.

The above inequalities demonstrate that the selected parameters satisfy the conditions in Corollary 1. By calculation Formula (15), the settling time can be estimated as 1.5671 s. The initial conditions are chosen as ${\varphi }_1\left(u\right)=0.2,{\varphi }_2\left(u\right)=-0.18,{\phi }_1\left(u\right)=0.17$ and ${\phi }_2\left(u\right)=-0.14$. Under the nonlinear controller with the above parameters, Figure 7 gives the time evolution of neuron errors ${ϵ}_1\left(u\right)$ and ${ϵ}_2\left(u\right)$ between systems (32) and (33). Figure 8 depicts the corresponding time evolution of error norm $\parallel ϵ\left(u\right)\parallel$. As shown in Figure 7 and Figure 8, the fixed-time synchronization of controlled systems can be achieved within the settling time. For convenience in observing the variation of the error,

Table 6. Discrete time evolution of error norm $\parallel ϵ\left(u\right)\parallel$ between controlled systems (32) and (33).

Time u	0.03	0.06	0.09	0.12	0.15	0.18	0.21
Error norm	0.026	0.013	0.008	0.005	0.003	0.001	0

presents the state of the changes in the error norm. As can be seen, the error norm $\parallel ϵ\left(u\right)\parallel$ gradually converges to zero within 0.21 s.

To compare the performance of different feedback controllers, we take into account the average convergence time and variance. Considering that some control strategies cannot address the synchronization problem in unbounded-delay networks, the system and controllers do not account for proportional delay. Randomly select initial values from [−0.3, 0.3], and execute six times for each controller under the same conditions. From

Table 7. Comparisons of average convergence time and variance under different controllers.

Control Schemes	Average Convergence Time	Variance
Communication feedback controller in [33]	0.221	0.021
Information feedback controller in [49]	0.228	0.019
Nonlinear feedback controller in [34]	0.212	0.018
Our multi-module controller	0.196	0.016

, the multi-mode controller proposed in this paper has advantages in average convergence time and variance. The convergence time of our controller is $7.55\%$ lower than the second-place controller, and the variance is $11.11\%$ smaller than the nonlinear feedback controller in [34].

Remark 10.

For the numerical simulation of fractional-order delayed systems, we employ the Adams–Bashforth–Moulton method [54] to solve the differential equations within the MATLAB R2020b environment. The implementation involves two key steps. First, the time domain is uniformly discretized, and the product rectangle formula is applied to estimate the fractional-order integral, yielding an initial approximate solution (the predictor). Subsequently, a corrected solution is computed using the product trapezoidal formula, which refines the initial estimate for higher accuracy (the corrector). The predictor-corrector steps ensure the robustness and accuracy of the simulation results.

5. Conclusions

This article is devoted to the fixed-time synchronization of fractional PDHNNs with bounded parameter uncertainties. To address the impact of unbounded time delay and uncertainties on synchronization, we design a nonlinear feedback controller composed of three modules with different functions. Unlike existing methods for constructing auxiliary functions, the Lyapunov function considered in this paper contains a $(q-1)$-order derivative ($-1<q-1<0$). By utilizing first-order derivative and inequality techniques, synchronization conditions for fractional PDHNNs are derived based on the proposed controller. Synchronization experiments and parameter analysis demonstrate the effectiveness and robustness of the method proposed in this paper.

The control scheme in this article belongs to continuous feedback control, which requires uninterrupted communication between nodes or with the central controller, occupying a large amount of communication bandwidth in application scenarios. Continuous operation of the actuator results in high control costs. Dynamic event-triggered control introduces internal dynamic variables, allowing triggering conditions to dynamically change over time. It can achieve a more intelligent balance between synchronization accuracy and communication costs. For tasks that require high transient performance, such as fixed-time synchronization, dynamic event-triggered control can ensure dense triggering during critical stages and reduce triggering during steady stages. In the future, combining multi-module feedback control and dynamic event-triggered control can be utilized to achieve fixed-time synchronization in fractional PDHNNs, thereby reducing communication costs and saving control time.