Fractal and CT Analysis of Water-Bearing Coal–Rock Composites Under True Triaxial Loading–Unloading

Abstract

To reveal the deformation and failure mechanisms as well as the fracture evolution patterns of water-bearing coal–rock composites under complex stress conditions, this study established a true triaxial stress model for the key load-bearing structure of mined coal pillar dams and developed a true triaxial loading apparatus capable of implementing localized unloading paths. True triaxial loading–unloading tests were conducted on coal–rock composites under different water content conditions, and the internal fracture structures were quantitatively characterized using CT scanning combined with fractal analysis. The results indicate that: (1) under a constant axial stress-unloading confining stress path, failure primarily occurs in the coal component, and the extent of failure significantly increases with the water content of the roof rock. For instance, the total fracture volume in the coal body increased by approximately 66% from the dry to the saturated state, while the lateral strain at peak stress decreased by about 65% over the same range, indicating a transition towards more brittle behavior. (2) CT scanning and three-dimensional reconstruction results reveal that the fracture system exhibits pronounced multi-scale polarization, with significant differences in volume, surface area, and morphological parameters between the main fractures and micropores, reflecting strong heterogeneity and anisotropy; (3) fractal dimension analysis of two-dimensional slices indicates that the fracture structures exhibit fractal characteristics in all directions, with the spatial distribution of fractal dimensions closely related to the loading direction. Overall, the XY-direction fractures exhibit the highest complexity, whereas the XZ and YZ directions show pronounced directional anisotropy. As water content increases, the amplitude of fractal dimension fluctuations rises, reflecting an enhancement in the geometric complexity of the fracture system.

1. Introduction

Underground coal mine reservoirs utilize goaf areas as water storage spaces, and effective storage and utilization of mine water are achieved through the construction of coal pillar dams and artificial dams. This approach represents one of the efficient methods for developing and utilizing water resources in mined-out areas [1,2,3]. To date, 35 underground coal mine reservoirs have been constructed in western China, with a total storage capacity of approximately 25 million m³, supplying over 95% of the production and domestic water demands in the mining regions [4,5]. The dam body constitutes the main engineering rock mass in the construction of underground coal mine reservoirs, including artificial dams [6,7,8] and coal pillar dams [9,10,11]. Coal pillar dams are formed by modifying low-strength, structurally developed coal–rock masses underground, which are difficult to maintain in long-term stability under complex geomechanical conditions, making them the weak link in ensuring the safe operation of underground coal mine reservoirs [12,13]. As a crucial component of underground coal mine reservoirs, coal pillar dams consist of mined-out coal pillar dams and boundary coal pillar dams. Among them, mined-out coal pillar dams are reconstructed from coal pillars that have undergone multiple mining influences, characterized by long construction spans, complex stress environments, high stability requirements, and extended service life [14,15,16].

Studies have shown that the instability of coal pillars is progressive and time-dependent [17]. Under long-term effects of overlying rock stress and hydrostatic and hydrodynamic pressures, gradual spalling occurs on both sides of the coal pillar, with the plastic failure zone extending toward the elastic core, leading to a reduction in the effective size of the coal pillar and a decrease in stability, eventually resulting in failure. For coal pillar dams, the influence of water accumulation in goaf areas further accelerates the progressive failure of the coal pillar dam [18,19,20,21]. The fundamental condition for maintaining the stability of a coal pillar dam is that the width of the elastic core in the central region of the coal pillar dam should exceed twice the coal pillar height [22,23,24,25] and meet impermeability requirements. Additionally, the time-dependent effects of progressive failure must be considered. The coal–rock mass adjacent to the roadway is a key load-bearing structure affecting the long-term stability of coal pillar dams and is the primary target for safety monitoring and control measures. By integrating the coal pillar dam with the overlying roof strata to form a coal–rock composite structure, investigating the mechanical behavior and instability mechanisms of the “coal pillar dam-roof” load-bearing system is of significant importance for engineering issues such as coal pillar dam width design, stability assessment, and monitoring and early warning [26,27].

During roadway excavation and its service period, the stress state of the surrounding rock dynamically changes, with the coal in the roadway ribs generally exhibiting vertical loading, radial unloading, and longitudinal constant load characteristics [28]. To reveal the deformation and failure mechanisms of coal under more realistic surrounding rock stress conditions, researchers have conducted true triaxial loading–unloading tests on coal–rock specimens [29,30], focusing on the mechanical behavior of coal–rock specimens under true triaxial loading and single-face unloading conditions. These studies have examined the effects of confining stress magnitude, unloading rate, and unloading mode on mechanical behavior, damage and deformation, and acoustic-thermal responses of coal–rock specimens, as well as the instability mechanisms of roadway rib coal under unloading conditions. Substantial findings have been obtained, providing a theoretical basis for stability control of coal–rock masses and prevention of dynamic disasters [31,32,33].

The stress adjustment process of key load-bearing structures in coal pillar dams can be conceptualized as a local unloading–loading–constant load process of coal within a coal–rock composite under triaxial stress states. Taking the coal–rock composite as the research object and considering rock properties and water content, conducting true triaxial loading–unloading tests on water-bearing coal–rock composites to investigate their deformation and failure characteristics is essential for analyzing the stability of coal pillar dams under different surrounding rock stress conditions during their service life.

In coal pillar dams, stress redistribution during roadway excavation is inherently localized, causing asymmetric deformation and directional fracture propagation. Therefore, the local unloading path adopted here more realistically reflects the in situ stress evolution. Based on a conceptual stress model of the key load-bearing structure of mined-out coal pillar dams, this study employed a self-developed true triaxial local unloading testing apparatus to analyze the mechanical behavior of water-bearing coal–rock composites under true triaxial loading–unloading conditions. The deformation and failure patterns of coal under local unloading within coal–rock composites with different water contents were investigated. Furthermore, CT scanning and three-dimensional fracture reconstruction methods, combined with fractal theory, were used to quantitatively characterize the internal fracture complexity and evolution of coal within the coal–rock composites. These analyses provide a foundation for revealing the failure mechanisms of key load-bearing structures in coal pillar dams.

2. Experimental Apparatus and Scheme

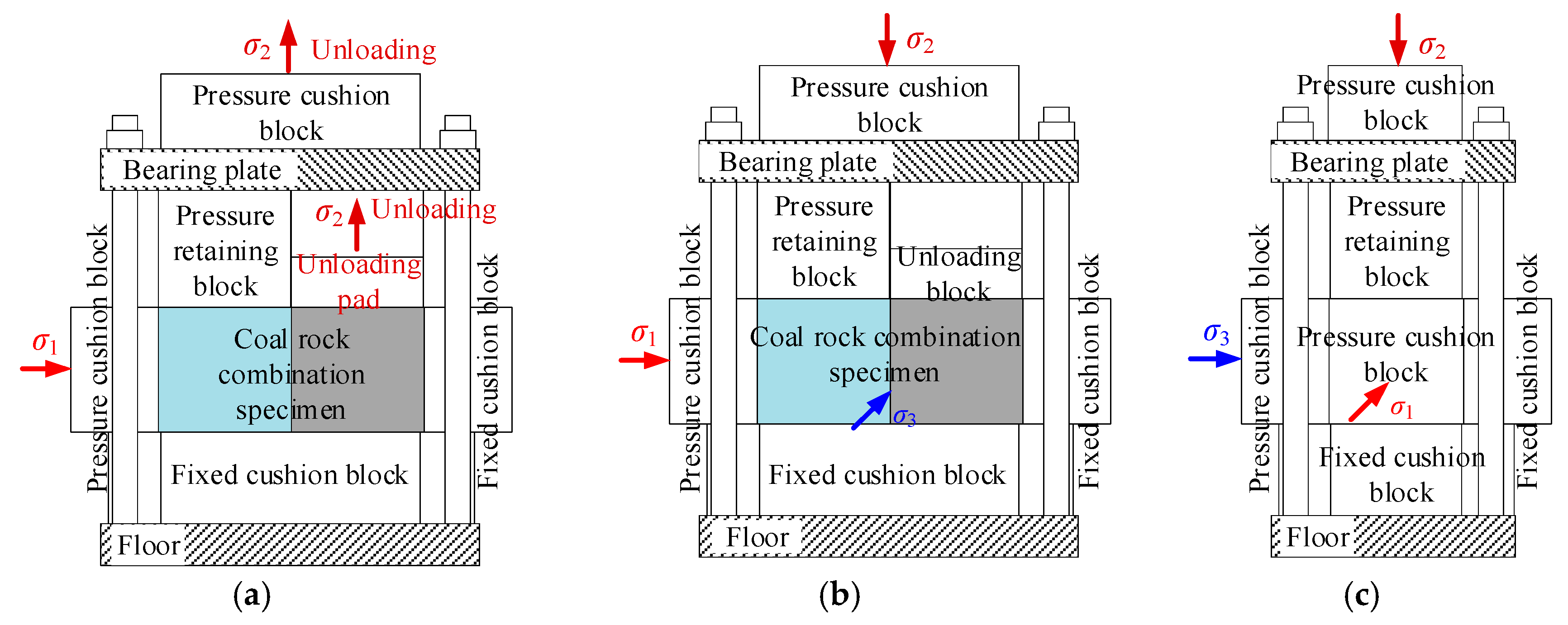
2.1. True Triaxial Local Unloading Test System for Coal–Rock Composite Specimens

2.1.1. Construction of the True Triaxial Stress Model for Coal–Rock Composites

During the service period of coal pillar dams, both sides are exposed, with one side facing the goaf area and the other side adjacent to the mined-out roadway [34,35]. Prior to mining, the coal–rock mass is in a triaxial stress equilibrium state (with the first principal stress σ₁, the second principal stress σ₂, and the third principal stress σ₃). Following roadway excavation, the lateral confining stress on the coal pillar dam is reduced (potentially to zero), transforming the stress state from triaxial to biaxial. Under the action of unbalanced forces, the shallow coal undergoes failure and moves into the roadway space until the coal–rock mass within this region re-establishes stress equilibrium. Based on this, the stress model of the coal–rock composite can be simplified, as illustrated in Figure 1.

2.1.2. True Triaxial Loading Test System

The tests were conducted using the true triaxial electro-hydraulic servo loading system at the State Key Laboratory of Intelligent Construction and Healthy Operation and Maintenance of Deep Underground Engineering, China University of Mining and Technology, as shown in Figure 2a. The testing apparatus primarily consists of a true triaxial electro-hydraulic servo loading control system and a true triaxial loading test platform, capable of accommodating cubic specimens with edge lengths up to 300 mm. The electro-hydraulic servo loading control system enables independent rigid loading control of σ₁, σ₂, and σ₃ directions on coal–rock specimens. As illustrated in Figure 2b, the maximum loads that can be applied are 2000 kN in the σ₁ direction, 500 kN in the σ₂ direction, and 300 kN in the σ₃ direction. The system achieves a stress loading accuracy of 0.01 kN and a displacement measurement accuracy of 0.002 mm.

The true triaxial loading test platform mainly comprises the test frame, loading mechanisms, and the triaxial pressure chamber. To ensure accurate stress application for composite specimens measured 50 mm × 50 mm × 100 mm, with coal and rock each occupying 50 mm in height, spatially interlaced loading platen arrangements were employed inside the triaxial pressure chamber, as shown in Figure 2c, to prevent mutual extrusion between platens and improve measurement precision. Under the control of the electro-hydraulic servo loading system, the loading mechanisms can perform loading and unloading in all three directions of the pressure chamber.

2.1.3. True Triaxial Local Unloading Test Device

After roadway excavation, the stress rebalancing process in the surrounding rock is manifested in both coal ribs as mining-induced unloading. This unloading causes coal fragmentation, and the unloading mode also determines the form and extent of deformation and failure in the coal ribs. Accordingly, most researchers have focused on experimental studies of coal–rock mechanical behavior under unloading and single-face unloading stress paths, yielding substantial research outcomes. However, for the key load-bearing structures of coal pillar dams, the unloading induced by roadway excavation primarily occurs in the coal seam. Therefore, a triaxial loading with local unloading stress path in a coal–rock composite is closer to the actual engineering conditions. Currently, true triaxial testing equipment can independently control loading and unloading in the σ₁, σ₂, and σ₃ directions, but single-face local unloading cannot be achieved. In this study, a true triaxial loading apparatus with local unloading capability was developed, enabling coal–rock specimens to undergo local unloading stress paths under true triaxial conditions. The working principle of the apparatus is illustrated in Figure 3.

In this true triaxial local unloading testing apparatus, pressure-retaining blocks and unloading blocks are arranged on the unloading surfaces of the specimen. By restricting the movement of the pressure-retaining blocks, local pressure is maintained on the coal–rock specimen, while the upward movement of the unloading blocks achieves local unloading of the specimen. Furthermore, by varying the areas of the pressure-retaining and unloading blocks on the specimen’s unloading surface, local unloading can be applied to different extents on a single face of the specimen.

The procedure for conducting true triaxial loading–unloading tests on coal–rock specimens using this apparatus is as follows:

(1)

Place the true triaxial local unloading testing apparatus, containing the specimen, at the center of the loading mechanism. Ensure that the fixed blocks and pressure-applying blocks are in contact with the passive and active end platens of the triaxial testing machine, respectively. Apply the initial stress in all three directions of the coal–rock specimen at a predetermined loading rate.

(2)

Tighten the pressure-retaining nuts and unload along the σ₂ direction at the designed rate. The pressure-retaining blocks are constrained by the bearing plates and cannot move, thus maintaining constant pressure on the specimen, while the unloading blocks are flexibly connected to the bearing plates to achieve synchronous unloading.

(3)

Upon completion of the test, release the stress in all three directions, loosen the pressure-retaining nuts, and remove the specimen.

2.2. Specimen Preparation and Experimental Scheme

2.2.1. Specimen Preparation

In the 3-1 coal seam, 33,301 return air entry of Guodian Construction & Investment Inner Mongolia Energy Co., Ltd., Ordos, China, large coal blocks (300 × 300 × 200 mm) were selected, and core specimens of the roof strata (75 mm) were drilled from the same region, obtaining coarse sandstone directly above the roadway. The coal–rock specimens were cut and drilled along vertical bedding planes in the laboratory and processed into cubic specimens measuring 50 × 50 × 50 mm. Coal–rock composite specimens were bonded using epoxy resin, with end faces perpendicular to the specimen axis (angular deviation within 0.001 radians) and non-parallelism not exceeding 0.02 mm, as shown in Figure 4. It should be noted that epoxy resin is stronger than natural coal–rock interfaces, which may reduce interface slip and slightly enhance composite stiffness. This limitation will be addressed in future studies.

According to the experimental objectives, a total of nine coarse sandstone–coal composite specimens were prepared. The coal within the composites retained its natural water content, while the coarse sandstone was prepared in three different water content conditions: dry, natural, and saturated. The classification and numbering of the specimens are listed in

Table 1. Classification and Identification of Triaxial Specimens.

Specimen Type	Specimen ID	Confining Pressure Level/MPa		Water Content State (Rock–Coal)
		σ2	σ3
Sandstone–Coal Composite	CM1	15	10	Dry-Natural
	CM2	15	10	Natural-Natural
	CM3	15	10	Saturated-Natural

. The selected confining stresses (σ₂ = 15 MPa and σ₃ = 10 MPa) correspond to the measured horizontal stresses at a depth of 430 m in the Guodian Mine.

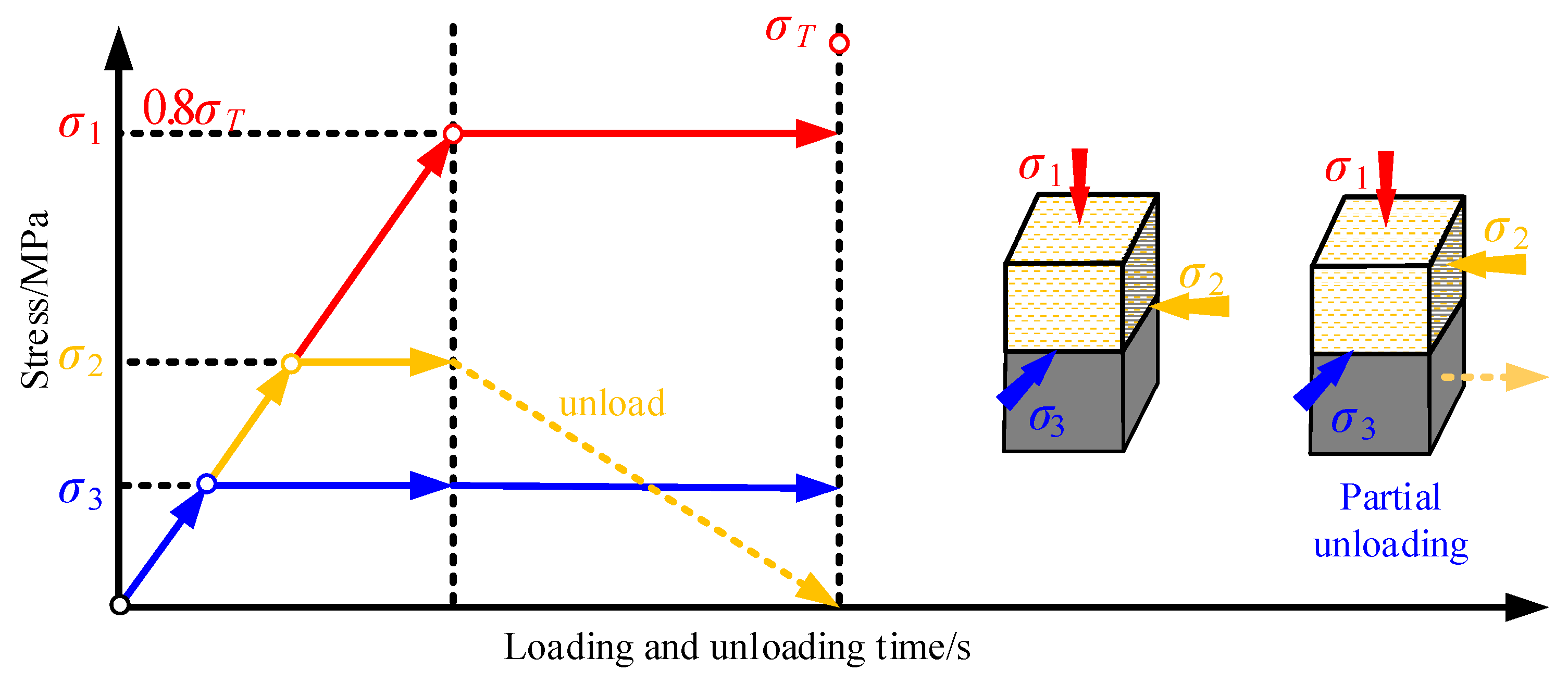
2.2.2. Experimental Scheme

Based on the stress model of the coal–rock composite, a confining pressure level was applied to investigate the mechanical behavior of the composite specimens under true triaxial compression. The effects of different water content conditions on the unloading and failure characteristics of coal within the composite were comparatively analyzed. Combined with the in situ stress measurement results from the study area, the true triaxial loading–unloading path used in this experiment is shown in Figure 5.

The loading path and procedure followed a constant axial stress with decreasing confining pressure path, simulating the stress adjustment process associated with lateral stress reduction in coal pillar dams during roadway excavation. The specific steps were as follows:

• Apply axial stress σ₁ and horizontal stresses σ₂ and σ₃ simultaneously to the target values (σ₁ > σ₂ > σ₃), and reset displacements in all directions to zero.
• Increase axial stress σ₁ to 0.8σ_T and maintain it constant (σ_T is the triaxial compressive strength of the coal specimen).
• Keep stresses in the σ₁ and σ₃ directions constant, and unload the σ₂ stress to zero using the local unloading testing apparatus at a loading–unloading rate of 0.1 MPa/s. The rate of 0.1 MPa/s was chosen to simulate quasi-static excavation processes, consistent with typical mining-induced stress adjustments.
• Since coal is the primary material undergoing failure within the coal–rock composite specimens, only the coal portion of the composite was subjected to CT scanning and analysis to investigate the development of internal microfractures.

2.3. CT Scanning

CT scanning is an X-ray computed tomography (CT) technique, widely used for physical structure analysis. An X-ray source emits radiation, which scans the material placed on a mechanically controlled stage [36,37,38]. After penetrating the material, the X-rays are attenuated and detected by a detector, and the signals are fed back to a computer for analysis [39]. The X-ray intensity is fixed, and the feedback signals are converted into digital signals. The computer calculates the value of each pixel based on the measured attenuation coefficients and determines the grayscale for each point in the image. These values are then reconstructed into an image, revealing the internal structure of the material. Through computer signal processing and differences in X-ray attenuation of various materials, the scanned images can be automatically obtained. In this experiment, the Zeiss Xradia 510 Versa system was used. The scanning pixel size was 52.7666 μm, and the image dimensions were 1004 × 1024 pixels.

3. Experimental Results and Discussion

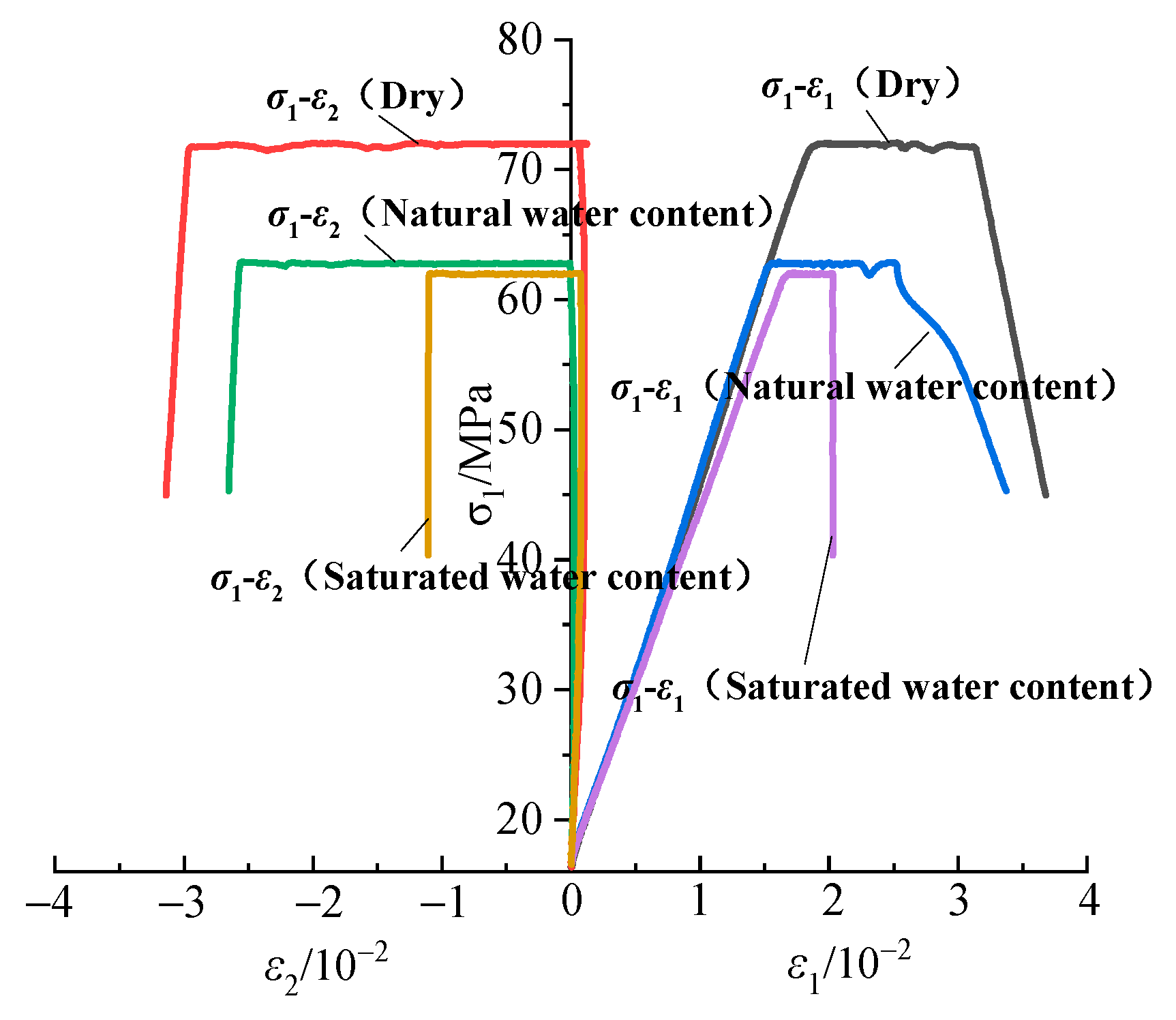
3.1. Mechanical Behavior of Coal–Rock Composite Specimens Under True Triaxial Loading

Figure 6 shows the axial (σ₁) and lateral (σ₂) stress–strain curves of the coal–rock composite specimens under the constant axial stress with decreasing confining pressure path. As shown, after the confining pressures σ₂ and σ₃ reached the set values of 15 MPa and 10 MPa, respectively, both axial compression and circumferential compression increased linearly with the increment of axial stress. The lateral (σ₂) compressive deformation during this stage is mainly due to lateral expansion of the composite specimen along the minimum principal stress direction (σ₃) under axial loading, which further compresses the specimen in the σ₂ direction to maintain constant stress in that direction.

Once the axial stress reached the target value (0.8σ_T) and was held constant, the σ₂ stress was unloaded to zero at a constant rate of 0.1 MPa/s. During unloading, the coal within the composite specimen dilated along the unloading direction, and internal damage fractures gradually developed. The axial stress further compressed the specimen to maintain constant stress in the axial direction. As unloading progressed, internal fractures rapidly propagated and interconnected, ultimately leading to specimen failure, accompanied by a sharp drop in axial stress. Compared with conventional true triaxial compression tests, where specimens typically exhibit pronounced plastic failure, the constant axial stress with decreasing confining pressure test demonstrated a more brittle failure behavior in the composite specimens.

Composite specimens consisting of coal and high-water-content rock are more prone to unloading-induced failure. For coarse sandstone with dry, natural, and saturated water content conditions, the lateral (σ₂) strains at failure due to unloading were 0.0314, 0.02655, and 0.01107, respectively, while the corresponding axial (σ₁) strains were 0.03678, 0.03371, and 0.02028. This behavior is primarily attributed to the relatively lower elastic modulus of high-water-content coarse sandstone under the same initial confining pressure, which allows it to store more elastic energy. Although the modulus is lower, the stored elastic energy is higher under the same stress due to greater deformation in high water content rock. During unloading of the coal portion, the energy stored in the rock is released and transmitted to the coal, promoting the propagation of internal fractures and triggering instability and failure within the coal.

Figure 7 presents the failure photographs and sketch diagrams of crack propagation in coal–rock composite specimens under the constant axial stress with decreasing confining pressure path for different water content conditions. As shown, failure in all specimens occurred primarily within the coal portion, with no obvious crack propagation or macroscopic failure observed in the rock portion. The failure mode of coal within the composite mainly involved shear failure or tensile-shear combined failure along the constant confining stress plane (σ₃ plane). Shear cracks propagated through the region near the unloading surface, forming macroscopic failure surfaces that expanded toward the unloading direction.

The water content of the rock significantly influenced the failure mode of coal within the composite. In addition to mechanical weakening, water-induced clay swelling softens cleat surfaces and promotes microcrack initiation, contributing to accelerated fracture development under local unloading. For example, in coarse sandstone–coal composite specimens:

When the coarse sandstone was dry, conjugate shear cracks appeared on both sides of the constant confining stress plane near the unloading surface, resulting in failure characterized by the detachment and fragmentation of the upper coal portion.

When the coarse sandstone had natural water content, a shear crack developed from the lower left to the upper right of the constant confining stress plane, accompanied by multiple tensile and tensile-shear cracks in the upper right part of the coal, leading to detachment and fragmentation of the upper-right coal region.

When the coarse sandstone was saturated, prominent tensile cracks formed on both sides of the constant confining stress plane near the unloading surface, mainly distributed in the lower part of the coal, resulting in detachment and fragmentation of the lower coal region. The dominant shear angles for all water-content conditions fall within approximately 55–90°, suggesting that water content does not significantly alter the primary shear orientation. However, the saturated specimen shows more secondary cracks and local tensile branches, indicating that increased water promotes a transition toward mixed tensile-shear failure rather than modifying the main shear angle.

These observations indicate that under the constant axial stress with decreasing confining pressure path, the severity of coal failure in the composite specimens increased with the water content of the rock. This is primarily because, under the same axial stress, rocks with lower elastic modulus store more energy. The reduction in lateral stress in the coal facilitates the release of stored energy in the rock, promoting the unstable propagation of internal coal fractures. These findings suggest that saturated pillars require enhanced tensile reinforcement, such as stronger roof–coal bonding, high-strength bolts, and measures to limit water infiltration.

From the above analysis, it is evident that the properties and water content of the roof rock significantly influence the mechanical behavior of coal pillar dams under different stress paths, including excavation-induced unloading, long-term constant loading, and mining-induced loading. These factors must be taken into account when formulating stability control measures for coal pillar dams under varying geological and engineering conditions. Due to the high strength of epoxy, no interface failure was observed. In field conditions, coal–rock interfaces often contain weak layers where slip may occur, and this limitation should be considered when extrapolating the results.

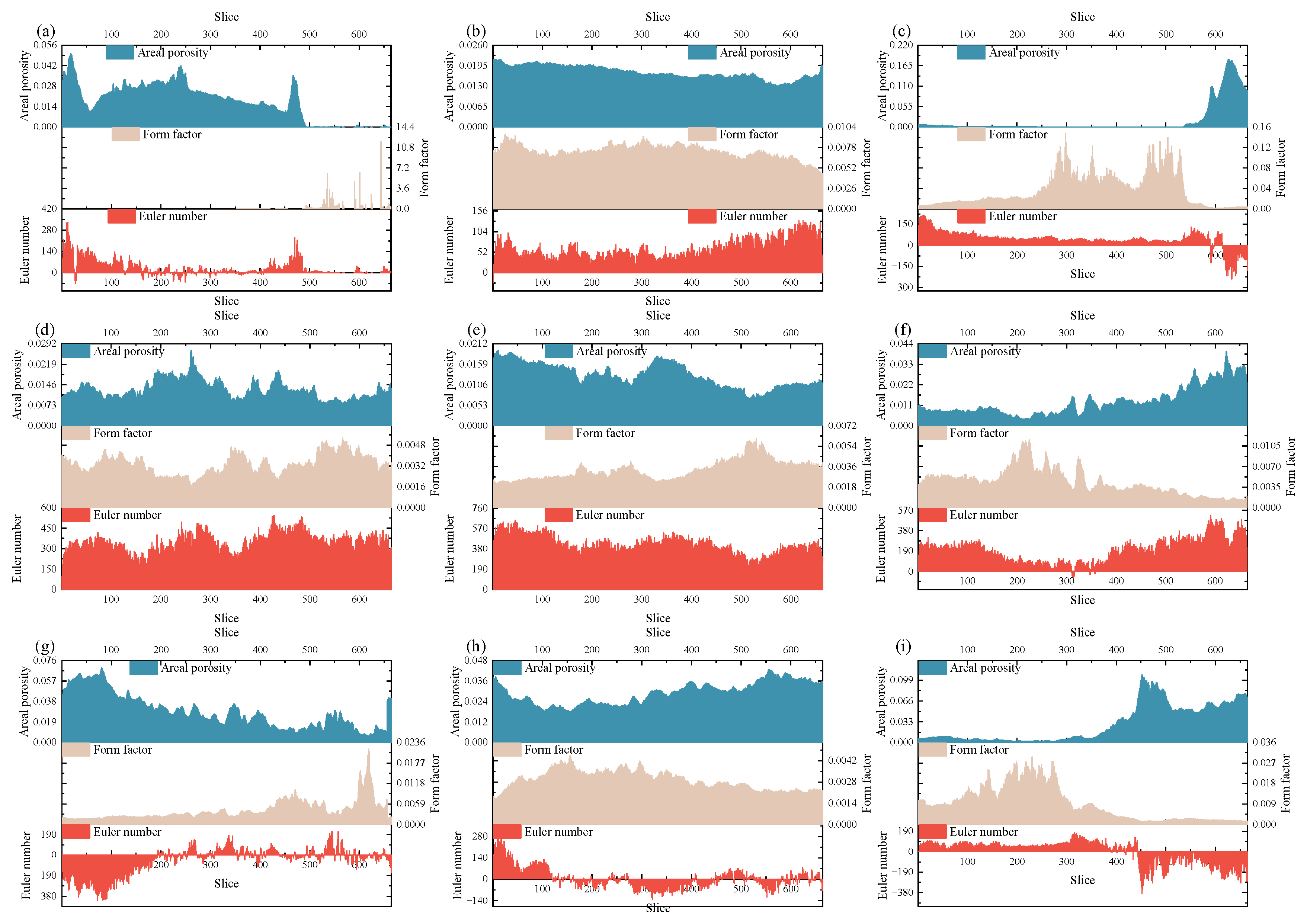
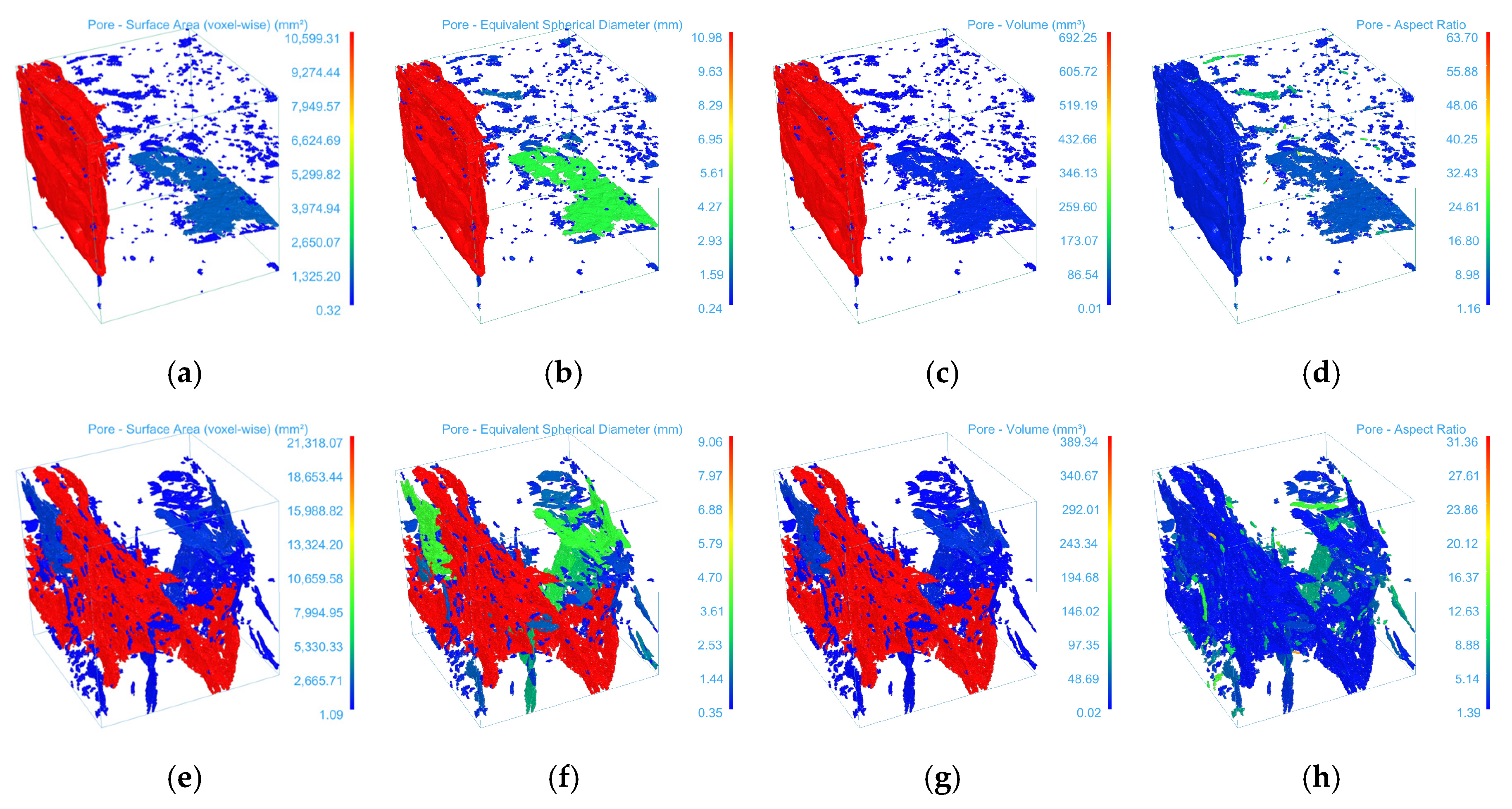
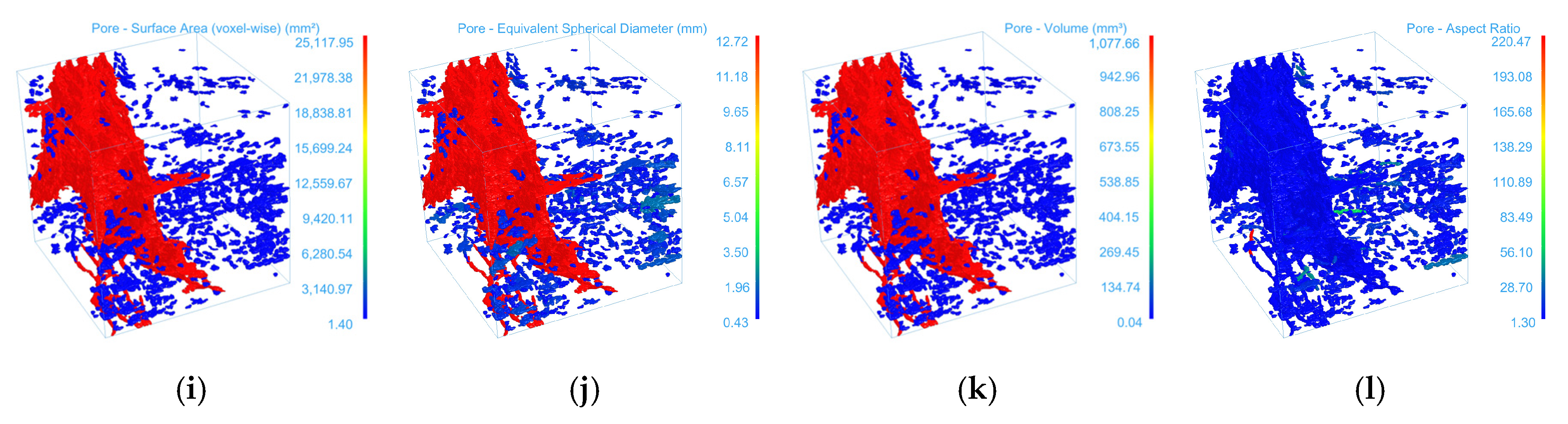
3.2. 3D Reconstruction and Parameter Characterization of CT Images

To investigate the evolution of internal fractures in coal within the coal–rock composite under the true triaxial constant axial stress with decreasing confining pressure path, Dragonfly 2024.1 software was used for three-dimensional visualization reconstruction and parameter characterization of the CT scan slices. A hybrid thresholding method (Otsu-based initialization + histogram adjustment + visual refinement) was used to accurately segment pores in heterogeneous coal for two-dimensional slice analysis. The areal porosity, Euler number, and shape factor were calculated for the XY, XZ, and YZ planes, and the results are shown in Figure 8.

Areal porosity is defined as the ratio of the pore area to the total area in a slice, reflecting the degree of local pore development. The Euler number is a topological parameter that characterizes the connectivity of the pore structure: a positive value indicates that pore-like structures dominate with poor connectivity, while a negative value indicates that network-like structures dominate with good connectivity. The form factor describes the complexity of the pore shapes, with values close to 1 indicating regular (approximately circular) shapes, and values close to 0 indicating highly irregular and complex shapes.

CM1 specimen:

XY plane: The areal porosity ranged from 1.59 × 10⁻⁵ to 4.14 × 10⁻², showing pronounced periodic fluctuations, with multiple peaks occurring within slices 1–300, followed by gradual attenuation. The maximum porosity appeared near slice 591 (13.07%), indicating a prominent pore development zone in this region. The Euler number varied dramatically between −241 and 331, suggesting significant spatial differences in pore connectivity. The form factor ranged from 0.00219 to 11.86, with most values concentrated between 0.003 and 0.01, indicating highly complex pore shapes; the extreme value occurred at slice 644 (11.86).

XZ plane: The areal porosity remained relatively stable, ranging from 2.04 × 10⁻² to 2.16 × 10⁻², with uniform distribution and minor fluctuations, indicating good structural homogeneity in this direction. The Euler number was generally positive (3–133), suggesting that isolated pores dominated, and connectivity was poor. The form factor ranged from 0.00612 to 0.00993, with a relatively concentrated distribution, indicating fairly uniform pore shapes.

YZ plane: The areal porosity ranged from 4.11 × 10⁻⁴ to 18.3 × 10⁻², with low and stable values in the early slices, followed by a sharp increase after slice 530, showing a pronounced stratified structural feature. The Euler number varied widely (−217 to 211), indicating complex connectivity changes and evident anisotropy. The form factor ranged from 0.00196 to 0.02702, with generally low values, indicating highly irregular pore boundaries.

CM2 specimen:

XY plane: Areal porosity ranged from 8.73 × 10⁻³ to 2.70 × 10⁻² (0.873% to 2.70%). Throughout the entire slice sequence (1–664), the porosity exhibited fluctuations without clear periodicity. A peak appeared near slice 260 (~2.70%), indicating a local pore development zone in this region. Thereafter, the porosity gradually decreased, reaching the minimum (~0.873%) near slice 500. The Euler number ranged from 98 to 496, with all values positive, indicating that isolated pores dominated and connectivity was poor. The form factor ranged from 0.00232 to 0.00535, with most values concentrated between 0.002 and 0.005, indicating complex and irregular pore shapes.

XZ plane: Areal porosity ranged from 7.36 × 10⁻³ to 1.94 × 10⁻² (0.736% to 1.94%). Porosity distribution was relatively uniform, with minor fluctuations, suggesting good structural homogeneity and stable pore development in this direction. The Euler number ranged from 423 to 646, all positive and relatively high, further confirming the dominance of isolated pores and poor connectivity. The form factor ranged from 0.00216 to 0.00543, with a relatively concentrated distribution (mostly 0.002–0.005), indicating relatively uniform pore shapes.

YZ plane: Areal porosity ranged from 4.15 × 10⁻³ to 3.99 × 10⁻² (0.415% to 3.99%). In slices 1–200, the values were low and stable (~0.5–1%), then decreased to a minimum (~0.415% at slice 192). From slice 300 onwards, porosity sharply increased, reaching a peak (~3.99%) near slice 622. This variation indicates a pronounced stratified structural feature. The Euler number ranged from −56 to 519, spanning a wide range and including negative values (e.g., −56 at slice 313), suggesting complex spatial variations in pore connectivity. Positive values represent isolated pores, while negative values indicate connected pore networks, reflecting the anisotropic heterogeneity of the YZ plane pore structure. The form factor ranged from 0.00113 to 0.00942, with generally low values; the minimum occurred at slice 622 (0.00113) and the maximum at slice 192 (0.00942). Low form factor values indicate highly irregular pore boundaries and highly complex pore shapes.

CM3 specimen:

XY plane: Areal porosity ranged from 8.63 × 10⁻⁶ to 6.91 × 10⁻² (0.000863% to 6.91%), showing an overall trend of initial decrease followed by fluctuations. Within slices 1–100, porosity was relatively high, peaking near slice 80 at 6.91%, then gradually decreasing to the minimum (~8.63 × 10⁻⁶) near slice 600, indicating the presence of a significant pore development zone and a dense zone. The Euler number varied dramatically from −419 to 219, with negative values predominating, suggesting pronounced spatial differences in pore connectivity and high connectivity in most regions. The form factor ranged from 0.00155 to 0.00835, generally low and concentrated, indicating complex and irregular pore shapes with highly tortuous boundaries.

XZ plane: Areal porosity was relatively stable, ranging from 1.91 × 10⁻² to 4.23 × 10⁻² (1.91% to 4.23%), uniformly distributed with minor fluctuations, indicating good structural homogeneity and consistent pore distribution in this direction. The Euler number ranged from −95 to 265, with positive values predominating, indicating dominance of isolated pores and poor connectivity; the pore network was relatively dispersed. The form factor ranged from 0.00166 to 0.00451, relatively concentrated, indicating relatively uniform pore shapes with more regular boundaries.

YZ plane: Areal porosity ranged from 2.65 × 10⁻³ to 1.09 × 10⁻¹ (0.265% to 10.9%). In slices 1–400, porosity was low and stable, then sharply increased after slice 400, peaking near slice 452 (10.9%), indicating a pronounced stratified structural feature and significant late-stage pore development. The Euler number varied widely from −331 to 182, alternating between negative and positive values, suggesting complex changes in connectivity with clear anisotropy and heterogeneity. The form factor ranged from 0.00136 to 0.02405, generally low, indicating highly irregular pore boundaries and complex shapes; in regions with lower values, the pore structures were even more distorted.

Figure 9 shows the three-dimensional reconstruction of the specimen. Based on connectivity, multiple regions of interest (Multi-ROIs) were generated to calculate the volume, surface area, equivalent spherical diameter, and aspect ratio of fractures and pores. Using these calculated parameters, a hierarchical visualization of fractures and pores was produced, as shown in Figure 10.

The analysis results indicate a pronounced parameter polarization within the fracture system, where primary fractures and micropores exhibit significant differentiation in geometric scale and morphological characteristics. Primary fractures typically display high volume, large surface area, greater equivalent spherical diameter, and high aspect ratio, forming the main flow channels and structural control units within the coal matrix. In contrast, micropores are widely distributed but small in scale, possess limited surface area, and tend to exhibit isotropic morphology. This polarization is visually manifested in the three-dimensional reconstructions as spatially separated regions of high values (red) and low values (blue), reflecting the multi-scale complexity and heterogeneity of the fracture system.

Figure 11 presents the histograms of volume, surface area, equivalent spherical diameter, and aspect ratio for different specimens. Considering that the polarization phenomenon is not well represented in linear scale, a logarithmic transformation was applied to the X-axis, and the frequency intervals were reduced. The Y-axis represents the frequency.

For the CM1 specimen, the mean volume of fractures was 0.94 mm³, but the standard deviation reached 24.49 mm³, and the maximum value was as high as 692.25 mm³, indicating a highly dispersed distribution of fracture volumes, likely dominated by a few very large fractures. The minimum volume was 0.01 mm³, with both the 25th and 50th percentiles at 0.01 mm³, suggesting that most fractures are small. The mean equivalent spherical diameter was 0.37 mm, with a standard deviation of 0.42 mm; the maximum (10.98 mm) and minimum (0.24 mm) values also show pronounced dispersion, although slightly less than that of volume. The mean surface area was 16.61 mm², with a standard deviation of 376.85 mm² and a maximum of 10,599.31 mm², far exceeding the mean, reflecting extreme fluctuations and the presence of a few fractures with exceptionally large surface areas. The mean aspect ratio was 4.20, with a standard deviation of 4.12, and values ranged from 1.16 to 63.70, indicating a wide variation in fracture shapes. Overall, the fracture characteristics of the CM1 specimen exhibit strong dispersion across all metrics, reflecting a highly complex and heterogeneous internal fracture structure.

For the CM2 specimen, the mean fracture volume was 0.70 mm³, smaller than that of CM1, and the standard deviation was 13.83 mm³, also relatively lower; however, the maximum value of 389.34 mm³ indicates the presence of some large fractures. Percentile analysis shows that most fractures are slightly larger in volume than those in CM1. The mean equivalent spherical diameter was 0.54 mm, greater than CM1, with a standard deviation of 0.42 mm, similar to CM1, indicating a larger average diameter but comparable dispersion. The mean surface area was 38.94 mm², higher than CM1, with a standard deviation of 757.43 mm² and a maximum of 21,318.07 mm², far exceeding CM1, reflecting that the fracture surface areas in CM2 are generally larger and exhibit more pronounced fluctuations. The mean aspect ratio was 4.84, greater than CM1, while the standard deviation was 3.21, smaller than CM1, suggesting that aspect ratios are generally higher and relatively more concentrated. Overall, the fractures in the CM2 specimen tend to be larger in volume, diameter, and surface area, with higher aspect ratios, indicating a different internal fracture structure compared to CM1.

For the CM3 specimen, the mean fracture volume was 1.56 mm³, the largest among the three specimens, with a standard deviation of 38.10 mm³, also the highest. The maximum volume reached 1077.66 mm³, far exceeding those of the other specimens, indicating a highly dispersed distribution and the presence of exceptionally large fractures. The mean equivalent spherical diameter was 0.66 mm, the largest value, with a standard deviation of 0.49 mm, reflecting both a larger average diameter and high dispersion. The mean surface area was 39.04 mm², similar to CM2, while the standard deviation of 887.85 mm² was the largest, and the maximum surface area reached 25,117.95 mm², the highest among the three specimens, indicating the most pronounced fluctuations in fracture surface area. The mean aspect ratio was 5.25, the largest, with a standard deviation of 9.14, also the highest; the maximum value of 220.47 and minimum of 1.30 reveal a wide variation, indicating the most complex and diverse fracture shapes. Overall, the fracture characteristics of CM3 exhibit higher values and greater dispersion than CM1 and CM2, reflecting the most complex and heterogeneous internal fracture structure.

The mean equivalent spherical diameter of the fractures increased from 0.37 mm (CM1, dry rock) to 0.54 mm (CM2, natural rock) and further to 0.66 mm (CM3, saturated rock), indicating a clear trend of pore structure coarsening with increasing water content in the overlying rock.

3.3. Fracture Characteristics Based on Fractal Theory

In two-dimensional CT images (e.g., coal fracture slices), the fractal dimension D describes the complexity of fracture contours or the area occupied by fractures across different scales [40,41,42]. The most commonly used measurement method is the box-counting method [43,44], which involves the following steps:

(1)

Cover the target image with a grid of squares with side length r;

(2)

Count the number of squares N(r) that contain fracture pixels;

(3)

Vary the square size r and record the corresponding N(r);

(4)

If the fracture structure exhibits fractal characteristics, then:

$$N(r)\propto r^{-D}$$

(1)

where r is the measurement scale (box size), and N(r) is the number of pore/fracture elements counted within boxes of size r. Taking the logarithm yields:

$$\log N\left(r\right)=-D\log r+C$$

(2)

Here, D represents the fractal dimension, which can be obtained through linear regression (with the slope taken as the negative value). D ≈ 1 indicates that the fractures are nearly linear; D ≈ 2 indicates dense fractures with high area coverage; a larger D value corresponds to a more complex fracture structure.

2D fractal dimensions were calculated from CT slices along the XY, XZ, and YZ planes to capture the directional evolution of fracture complexity. The fractal dimension was calculated using ImageJ 1.54r software, with the fractal dimension of individual slices shown in Figure 12. To quantitatively characterize the geometric complexity of coal fracture structures, representative slices from different directions were selected, and the FracLac plugin was employed to compute the fractal dimensions of multiple slices. The coal CT slice images were converted to binary images, with fracture or pore pixels represented in white and the matrix in black. Square boxes of varying sizes were used to cover the target area, with box scales r set to 1, 2, 4, 8, 16, 32, and 64 pixels. The computation results are presented in Figure 13.

The directional anisotropy in fractal dimension is primarily induced by the true triaxial stress path, while being modulated by the coal’s inherent structural anisotropy. Anisotropic analysis of multi-directional fractal dimensions in single coal specimens:

(1)

CM1 Coal Specimen (XY, XZ, YZ Directions)

XY Direction: The fractal dimension remains relatively high, ranging from 1.83 to 1.86, and exhibits a trend of “slight increase—stabilization—gradual decrease” with increasing slice number. This indicates that the fractures in the XY plane were initially well-developed, continued to evolve during loading, but did not undergo severe damage. The fracture network maintained a high level of complexity throughout.

XZ Direction: The fractal dimension fluctuates between 0.98 and 1.10, significantly lower than that in the XY direction. Its evolution follows a “sharp rise—oscillation—recovery” pattern, suggesting that fracture development in the XZ plane is staged: rapid nucleation occurs initially, followed by multiple phases of expansion and adjustment, and finally a partial recovery of fracture complexity, although overall it remains lower than in the XY plane.

YZ Direction: The fractal dimension exhibits large fluctuations between 0.40 and 1.40, showing a pattern of “sharp decrease—stabilization—continuous recovery.” The initial sharp drop reflects local fracture connectivity or directional propagation, while the subsequent continuous recovery indicates the nucleation of new fractures and reconstruction of the fracture network.

In summary, the fracture complexity of the CM1 coal specimen is highest in the XY direction, while significant directional anisotropy exists in the XZ and YZ directions. This anisotropy is closely related to the initial defect distribution and mineralogical anisotropy within the coal specimen across different planes.

(2)

CM2 Coal Specimen (XY, XZ, YZ Directions)

XY Direction: The fractal dimension fluctuates between 1.83 and 1.855, showing a trend of “oscillatory increase—peak—gradual decrease—recovery.” The appearance of peaks corresponds to active stages of fracture propagation, while subsequent decreases and recoveries reflect local fracture connectivity and secondary development. Overall, the fractures in the XY plane remain in a highly complex evolutionary state throughout.

XZ Direction: The fractal dimension ranges from 1.68 to 1.84, exhibiting multi-stage behavior of “gradual decline—oscillatory increase—sharp drop—recovery.” These dramatic fluctuations indicate that fractures in the XZ plane undergo a process of “expansion—local instability—re-expansion,” highlighting the nonlinear evolution of fractures under loading.

YZ Direction: The fractal dimension varies between 1.74 and 1.82, following the trend of “continuous decline—stabilization—rapid recovery.” The initial decline may be caused by directional propagation of primary fractures, reducing the local fractal dimension, while the later rapid recovery reflects the extensive nucleation of secondary fractures.

The directional anisotropy of the CM2 coal specimen is also pronounced. Fracture complexity is highest in the XY direction, whereas fracture evolution in the XZ and YZ directions is characterized by multi-stage instability and reconstruction, reflecting fundamentally different mechanical responses of the specimen to applied loads across planes.

(3)

CM3 Coal Specimen (XY, XZ, YZ Directions)

XY Direction: The fractal dimension fluctuates dramatically between 1.72 and 1.86, showing extreme variations of “decline—recovery—oscillation—sharp drop—sudden rise.” This intense fluctuation indicates that fractures in the XY plane undergo multiple cycles of “nucleation—connectivity—re-nucleation,” reflecting poor mechanical stability of the specimen in this direction and highly nonlinear fracture evolution.

XZ Direction: The fractal dimension gradually increases from 1.795 to 1.825, then oscillates slightly and stabilizes within 1.80–1.82. The overall trend of “continuous increase—oscillatory stabilization” reflects a process in which fractures in the XZ plane develop slowly at first and then expand steadily, with a gradual enhancement of fracture network complexity.

YZ Direction: The fractal dimension rises continuously between 1.78 and 1.85, with only minor oscillations in the mid-phase. This indicates that fractures in the YZ plane continuously nucleate and propagate during loading without obvious connectivity failure, showing a monotonic increase in fracture complexity. Among the three directions, the YZ plane exhibits the most sustained fracture evolution.

The directional anisotropy of the CM3 coal specimen is pronounced: the YZ direction shows continuously increasing fracture complexity, the XY direction exhibits extreme instability in evolution, and the XZ direction demonstrates phase-wise stability. This highlights the dominant influence of the specimen’s internal structural anisotropy on fracture evolution.

Comparison of fractal dimension among multiple coal specimens in the XY direction (CM1, CM2, CM3):

The mean fractal dimension in the XY direction is highest and exhibits the smallest fluctuation for CM1, indicating that the initial fracture network in the XY plane is well-developed and evolves relatively stably during loading. CM2 shows multi-stage fluctuations in the XY direction, reflecting the staged instability in fracture evolution. CM3 exhibits extreme oscillations in the XY direction, demonstrating nonlinear fracture evolution caused by internal structural heterogeneity. These differences are primarily attributed to variations in the initial porosity and fracture distribution among specimens, as well as the anisotropic arrangement of mineral grains.

Comparison of fractal dimension among multiple coal specimens in the XZ direction (CM1, CM2, CM3):

The fractal dimension in the XZ direction for CM1 is significantly lower than that of CM2 and CM3, indicating that fracture development in the XZ plane is generally weak. CM2 exhibits the largest fluctuations in the XZ direction, highlighting the most pronounced staged evolution of fractures. CM3 shows a gradually increasing and then stabilizing trend in the XZ direction, reflecting more continuous fracture evolution compared with CM2. These differences are closely related to stress concentration effects and the sensitivity of initial defects within the XZ plane of the coal specimens.

Comparison of Fractal Dimension Among Multiple Coal Specimens in the YZ Direction (CM1, CM2, CM3):

In the YZ direction, CM1 exhibits the lowest initial fractal dimension, followed by a pronounced increase in the later stages, reflecting early-stage local fracture connectivity and subsequent extensive secondary fracture initiation. CM2 shows a two-stage “decline-rebound” pattern, indicating strong reversibility in fracture evolution. CM3 displays a continuously increasing fractal dimension, representing the most sustained fracture development among the three specimens in this direction. These differences reflect individual variations in load transfer efficiency and fracture propagation resistance within the YZ plane of the coal specimens.

Published CT studies report D values between 1.60 and 1.85 for fractured coal, which aligns with the present results (1.71–1.82). The results are subject to scale effects, as the 50 mm specimens do not capture the full heterogeneity of field-scale coal pillars. Thus, the fractal parameters mainly represent small-scale fracture behavior.

4. Conclusions

This study employed a self-developed true triaxial local unloading apparatus to simulate the stress path under constant axial stress and unloading of confining stress. Combined with CT-based three-dimensional reconstruction, statistical analysis of fracture geometric parameters, and two-dimensional fractal dimension analysis, the multi-scale complexity and fractal characteristics of fractures within coal specimens in water-containing coal–rock composite specimens were quantitatively revealed. The main conclusions are as follows:

(1)

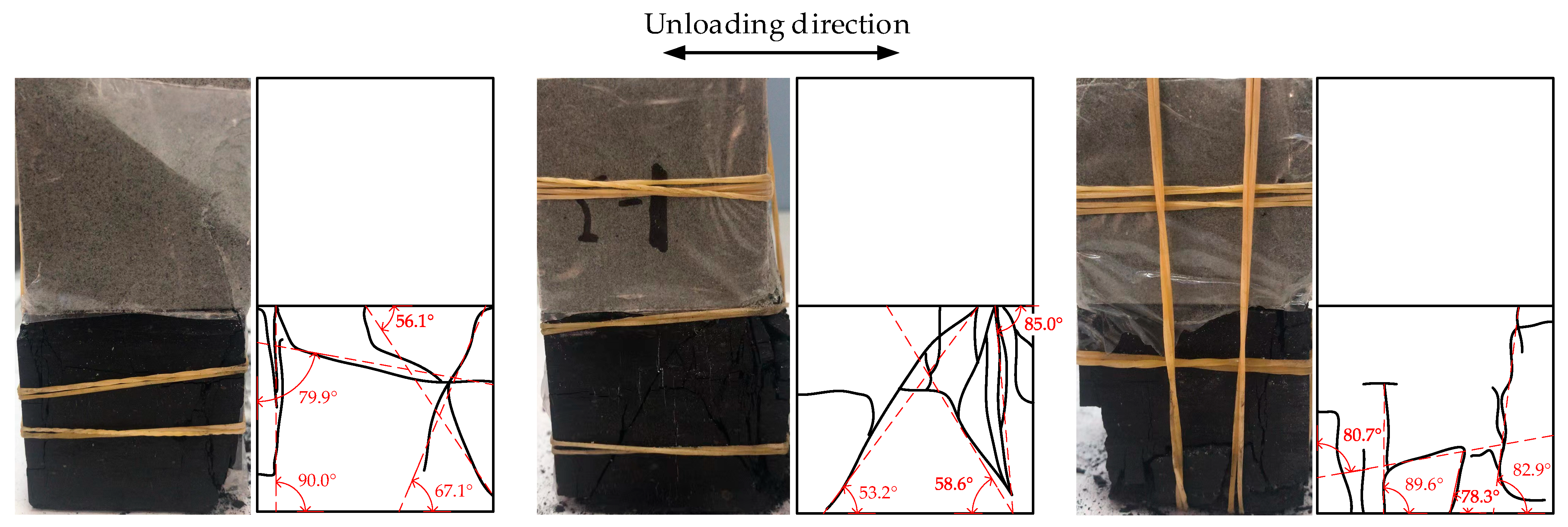
Under the stress path of constant axial stress and unloading of confining stress, the axial strains of the three specimens (CM1, CM2, and CM3) were 0.03678, 0.03371, and 0.02028, respectively, while the lateral strains were 0.0314, 0.02655, and 0.01107, respectively. This indicates that as the rock’s water content increases from dry, natural to saturated states, the deformability of the specimens at failure progressively decreases. The failure mode evolves from shear failure to tensile-shear composite failure and ultimately to tensile failure, reflecting that rocks with higher water content possess lower elastic moduli. Consequently, at the same pre-unloading load level, they accumulate greater elastic strain energy. The release of this larger amount of stored energy to the coal component during unloading makes the coal more susceptible to brittle failure.

(2)

The three-dimensional reconstruction results indicate that the mean volumes of fractures were 0.94 mm3, 0.70 mm3, and 1.56 mm3, with standard deviations reaching as high as 24.49, 13.83, and 38.10 mm3, respectively. The surface area could reach up to 25,117.95 mm2, and the maximum aspect ratio was 220.47. These findings demonstrate that the fracture system exhibits significant scale differentiation: a few dominant fractures control the overall flow and mechanical behavior, while a large number of micropores form a dispersed structural background. Fractures of different scales spatially assemble into a stratified, heterogeneous network, reflecting a pronounced parameter polarization phenomenon.

(3)

Analysis of two-dimensional slices indicates that the areal porosity, Euler number, and fractal dimension in the XY direction are all higher than those in the XZ and YZ directions. Taking specimen CM1 as an example, the fractal dimension in the XY direction remains stable between 1.83 and 1.86, while it is only 0.98–1.10 in the XZ direction and fluctuates between 0.40 and 1.40 in the YZ direction, demonstrating a strong directional dependence. For specimen CM3, the fractal dimension in the YZ direction gradually increases from 1.78 to 1.85, exhibiting a continuous evolutionary trend, indicating that fracture propagation and connectivity are highly anisotropic.

(4)

The fractal dimensions under different water content conditions exhibit pronounced stage-wise fluctuations: as the water content increases, the complexity of the fracture network significantly intensifies. The rising stages of fractal dimension correspond to periods of fracture connectivity and energy release, whereas the declining stages correspond to fracture closure and local reconstruction. The magnitude and frequency of fractal dimension variations can serve as quantitative indicators of the evolution and damage state of the internal fracture network within the coal matrix.

Although the present study focuses on the short-term mechanical response of water-bearing coal–rock composites using deionized water saturation, it should be noted that, in underground reservoir environments, water-rock chemical reactions (e.g., dissolution of cementing minerals, leaching, and pyrite oxidation) may further influence long-term strength degradation. These geochemical effects were beyond the scope of this mechanical study but represent an important direction for future research.