Fractional Mean-Square Inequalities for (P, m)-Superquadratic Stochastic Processes and Their Applications to Stochastic Divergence Measures

Abstract

In this study, we introduce and rigorously formalize the notion of (P, m)-superquadratic stochastic processes, representing a novel and far-reaching generalization of classical convex stochastic processes. By exploring their intrinsic structural characteristics, we establish advanced Jensen and Hermite–Hadamard ($\mathbb{H}.\mathbb{H}$)-type inequalities within the mean-square stochastic calculus framework. Furthermore, we extend these inequalities to their fractional counterparts via stochastic Riemann–Liouville ($\mathbb{RL}$) fractional integrals, thereby enriching the analytical machinery available for fractional stochastic analysis. The theoretical findings are comprehensively validated through graphical visualizations and detailed tabular illustrations, constructed from diverse numerical examples to highlight the behavior and accuracy of the proposed results. Beyond their theoretical depth, the developed framework is applied to information theory, where we introduce new classes of stochastic divergence measures. The proposed results significantly refine the approximation of stochastic and fractional stochastic differential equations governed by convex stochastic processes, thereby enhancing the precision, stability, and applicability of existing stochastic models. To ensure reproducibility and computational transparency, all graph-generation commands, numerical procedures, and execution times are provided, offering a complete and verifiable reference for future research in stochastic and fractional inequality theory.

1. Introduction

The mathematical notion of convexity occupies a pivotal role in engineering and mathematics, as it supports a wide range of theoretical and applied phenomena. The core of convex analysis are convex sets and convex functions that are essential tools in simplifying very complicated systems and optimizing complex mathematical models. By virtue of their well-behaved nature, especially the fact that there is a global minimum problems in convex functions become much easier to handle, and hence are central in optimization. Besides its interest for its own sake as pure mathematics, convexity has deep implications in most fields like control theory, economics, and systems engineering. In control theory, for instance, convexity guarantees that the designs for systems are stable and robust over a wide range of operating conditions. In economics, convexity also plays a role in the description of consumer preferences and analysis of market behavior, hence enabling efficient decision-making and resource allocation. It is interesting to note that convexity has practical applications in addition to being a theoretical or academic idea. Convex structures are frequently encountered by engineers and practitioners who are attempting to maximise system performance in order to increase operational efficiency and dependability. Convex functions are essential to integral inequalities, which may be the most aesthetically beautiful use of convexity. In mathematical analysis, integral inequalities are essential, particularly when it comes to bounding or approximating integral values. The $\mathbb{H}.\mathbb{H}$ inequality, which gives estimates of the average value of a convex function over a specified interval, is one of the most significant of these [1,2,3]. The topic is a rich and potent area of current mathematics research because of the relationship between convexity and integral-type inequalities.

Fractional calculus that generalizes classical calculus to non-integer order derivatives and integrals has emerged as a hot topic in recent years due to its ability to model systems with memory and with hereditary characteristics. It emerges as a valuable tool in physics, engineering, and even perhaps surprisingly in computer science [4]. Its increasing relevance is not only restricted to practical sciences; fractional calculus has also been instrumental in the building of inequality theory. Fractional integral inequality is now a favorite and rapidly developing field of research in recent years. Sarikaya et al. [5] added an important contribution by using the $\mathbb{RL}$ fractional integrals framework to establish the generalized $\mathbb{H}.\mathbb{H}$ inequality. Their research enhanced the mathematical techniques employed in dynamic systems analysis and the theory of inequality analysis by creating tighter bounds in analytical terms and greater understanding of the behavior of convex functions. Recent studies also broadened this field with new methods for fractional integral operators and inequalities. Nápoles-Valdés and Bayraktar in 2025 [6], explored Caputo-weighted integrals and their uses, citing the potential to generalize traditional results and refine analytical procedures in fractional frameworks. Similarly, Guzmán and Nápoles-Valdés in 2025 [7], explored $\mathbb{H}.\mathbb{H}$-type fractional integral inequalities, formulating new bounds and extensions that close the gap between classic analysis and modern fractional theory. These advances in their entirety enrich the knowledge of the structural features and uses of fractional integral inequalities in mathematics analysis and applied sciences.

After the landmark discovery of the $\mathbb{H}.\mathbb{H}$ inequalities for the $\mathbb{RL}$ fractional integrals, important advances have been made in extending $\mathbb{H}.\mathbb{H}$-type inequalities to several fractional integral definitions. Researchers have explored these inequalities in the context of numerous fractional operators, including the generalized proportional fractional integrals [8], Sarikaya fractional integrals [9], Katugampola fractional integrals [10], k-fractional integrals [11], $\psi$-$\mathbb{RL}$-fractional integrals [12], $(k-p)$-fractional integrals [13], generalized $\mathbb{RL}$-fractional integrals [14] and conformable fractional integrals [15]. Alongside these developments, a wide array of inequalities of fractional order has also been established, reflecting the growing depth and diversity of the field. These include fractal Hadamard-Mercer-type inequalities [16], Simpson-type inequalities [17], Euler-Maclaurin-type inequalities [18], Bullen-type inequalities [19], and Ostrowski-type inequalities [20], among others. For readers seeking a comprehensive overview of recent advancements in fractional integral inequalities, several up-to-date contributions are recommended, such as those found in [21,22,23] and the references therein.

A collection of random variables parameterized by time or space describing the change of a system under uncertainty is referred to as a stochastic process in statistics and probability theory. They characterize the apparently random change of a system, often over different time or space separations. The term “stochastic” qualifies processes that occur at unpredictable or irregular rates. Stochastic processes can be used to simulate random change over time in systems. For instance, there are many random parameters that may result in fluctuations of bacterial growth, but long-term forecasting is not impossible. Just as thermal noise within electrical systems produces random changes in voltage or current, such apparently random behavior can be represented by simple stochastic processes, and these can offer insight into the behavior of the system.

Physicists and mathematicians have traditionally used stochastic processes as mathematical models to describe a wide range of phenomena, including changes in population in ecosystems, randomly diffusing gas molecules, and stock price fluctuation. Stochastic models, which have many uses in research and engineering, can often be used to model these processes and other elements like molecular interactions whenever there is unpredictability. They mimic population dynamics or the emergence of diseases in biology, and they depict systems based on the mobility of various molecules in physics. The importance of stochastic processes lies in their ability to systematically explain systems that behave randomly. They are vital in domains where randomness or particular results at every stage are critical, such as computer science, data transfer, cryptography, and signal processing. They are therefore essential for conducting research and resolving practical issues. Scientists and engineers are able to forecast future trends, optimize systems, and design solutions that consider environmental uncertainties by numerically simulating these processes. System state prediction, data compression algorithms, and secure communication through cryptography are other significant applications. Recent developments in fractional stochastic processes provide a strong foundation for our study. Jiang and Miao [24] examined anomalous stochastic processes via generalized fractional calculus, offering models for non-classical diffusion behavior. Sahebi Fard et al. [25] introduced a financial market model using the $\psi$-Caputo fractional derivative, effectively capturing memory and hereditary effects in market dynamics. Guidoum et al. [26] analyzed fractional and higher-order moments of stochastic differential equations, highlighting the behavior of moments under fractional dynamics. These works collectively illustrate the breadth and applicability of fractional stochastic modeling.

Convex stochastic processes, which generalize the concept of classical convex functions to stochastic processes systems including randomness were initially introduced by Nikodem [27] in 1980. Further, he found that such stochastic processes exhibit a number of properties similar to classical convex functions. The Jensen convex mapping, central to the theory of inequalities, is one such useful tool in this respect. A number of crucial inequalities can be obtained from this mapping, and their applicability to stochastic processes was demonstrated by Skowronski [28] in 1992. Expanding on these concepts, Kotrys [29] showed that, in particular, for convex stochastic processes, the upper and lower bounds of the $\mathbb{H}.\mathbb{H}$ inequality may be found using integral operators. Kotrys’s work showed how the $\mathbb{H}.\mathbb{H}$ inequality, an important result in convex analysis, could be adapted for stochastic processes. There have been a great many papers in the literature over the last few years on all sorts of convexity for stochastic processes. Okur et al. [30] used the idea of p-convexity, which is a particular kind of convexity, to construct the $\mathbb{H}.\mathbb{H}$ inequality for stochastic processes. Erhan [31] made a further contribution by building these inequalities with the use of another version of convexity called s-convexity. Budak et al. [32] generalised the work of other academics by presenting these inequalities using the concept of h-convexity. As mentioned in the sources [33,34,35], there have been many research investigating different kinds of convexity for individuals who are interested in the most recent developments in stochastic processes. Further broadening the applicability of these mathematical ideas, Tunç in [36] made a substantial contribution by developing the Ostrowski-type inequality particularly for h-convex functions. Zhao et al. [37] have connected inequality to interval mathematics, putting these inequality within the context of interval analysis. Using interval analysis as a foundation, Afzal et al. [38] presented the notion of stochastic processes before the end of 2022. They also created new versions of the Jensen and $\mathbb{H}.\mathbb{H}$ inequalities that are particularly designed for stochastic processes, fusing these two mathematical ideas in an innovative way. A novel mathematical framework called the $(\mathrm{m},h_1,h_2)$-G-convex stochastic process was presented by Eliecer et al. [39]. It incorporates functions $h_1$ and $h_2$ together with a parameter $\mathrm{m}$ to extend classical convexity to stochastic processes. By this approach, they were able to establish some inequalities associated with stochastic analysis. By utilizing fractional operators in order to use fractional calculus on the $(\mathrm{m},h_1,h_2)$-convex stochastic process, Cortez [40] generalized this work and obtained more inequalities. These developments strengthen mathematical models in many disciplines through the power of estimating systems subject to fractional dynamics and uncertainty. Hafiz [41] discussed the applications of fractional calculus to stochastic processes, paving the way for modeling stochastic processes reliant on memory. Kotrys [42] extended classical inequalities such as Jensen, $\mathbb{H}.\mathbb{H}$, and Fejér inequalities to strongly convex stochastic processes, providing vital information regarding probabilistic convexity theory. Further advances were made by Agahi and Babakhani [43], who introduced fractional-order forms of Jensen and $\mathbb{H}.\mathbb{H}$ inequalities for convex stochastic processes to make them more effective in stochastic modeling fields. Fu et al. [44] subsequently investigated n-polynomial convex stochastic processes and presented $\mathbb{H}.\mathbb{H}$-type inequalities for such functions, which determined the domain of stochastic optimization and uncertainty modeling. The work in general stresses the importance of convexity in stochastic situations and its use in mathematical inequalities, probability theory, and optimization in practice.

Superquadraticity gives tighter and more reliable bounds than ordinary convexity, considerably enhancing integral inequality theory. This is extremely welcomed in applications of applied mathematics, where a better approximation means increased model accuracy, and for optimisation tasks, where boundary estimate quality decides the optimum solution. Thus, superquadraticity broadens the theory basis of inequality structures and enhances their applicability. It effectively presents a robust analytical foundation for the development and use of integral inequalities in a wide range of mathematical and applied problems.

The concept of superquadraticity extending the traditional convexity was first introduced by Abramovich et al. [45]. This initial work prepared the ground for a wider analytical framework that could provide tighter inequalities compared to those obtained from regular convex functions. Abramovich and co-authors [46] later introduced a formal definition for superquadratic functions together with essential theoretical observations that further enhanced the understanding of this function class. Working from this basis, Li and Chen [47] took the theory further by applying the fractional view of $\mathbb{H}.\mathbb{H}$-type inequalities through $\mathbb{RL}$ fractional integrals, representing a huge step beyond superquadraticity to the world of fractional calculus. More was done by Alomari et al. [48], who brought about the concept of h-superquadraticity, studied their structural properties and defined a new subclass within the larger family. In a valuable work in interval analysis and generalized function theory, Khan and Butt [49] introduced cr-order interval-valued superquadratic functions and their fractional counterparts, emphasizing their applicability through multiple illustrations. Following this endeavor, Khan et al. [50] introduced the $(P,m)$-superquadratic function, an even broader concept that includes examples, fundamental characteristics, integral inequalities, and real-world applications, thus enriching superquadraticity’s functional atmosphere. Continuing their exploration of information-theoretic applications, Butt and Khan [51] developed information inequalities for superquadratic functions using the tools of interval calculus, connecting functional inequalities with measures of information. A foundational theoretical advance was made by Banić et al. [52], who refined classical inequalities and solidified the theoretical underpinnings of superquadratic functions, paving the way for future researchs in the study of superquadratic stochastic processes.

In the aforementioned, we have discussed several well-known stochastic extensions of convexity, such as convex stochastic processes, p-convex, s-convex, h-convex, $(\mathrm{m},h_1,h_2)$-G-convex, and n-polynomial convex stochastic processes, each providing generalizations within the convexity framework. However, the recently developed concept of (P, m)-superquadraticity serves as a refinement of convexity, offering significantly sharper bounds than those obtained from the classical and modern variants of convexity. Despite its strong potential, neither a stochastic formulation of (P, m)-superquadraticity nor its fractional counterpart has appeared in the literature. To fill this gap, the present work introduces the new class of (P, m)-superquadratic stochastic processes, establishes their key properties, develops Jensen-type and $\mathbb{H}.\mathbb{H}$-type inequalities of integer order, and further generalizes them to fractional $\mathbb{H}.\mathbb{H}$-type inequalities via stochastic $\mathbb{RL}$ fractional integrals. Moreover, we provide the first applications of this new class in information theory, demonstrating its analytical strength and broad applicability beyond the traditional convexity-based stochastic models.

The paragraph that follows provides an explanation of the paper’s structure:

Following the review of the required background knowledge and pertinent data regarding convexity, superquadraticity, convex stochastic processes and their inequalities in Section 1 and Section 2, we use 2D and 3D graphical representations to analyze the stochastic version of superquadraticity and their features. More importantly, in Section 3, we develop new Jensen’s and $\mathbb{H}.\mathbb{H}$-type inequalities. Then, in Section 4, Inequalities of $\mathbb{H}.\mathbb{H}$-type are obtained in fractional form. To evaluate the effectiveness of the results, examples and graphic descriptions of the findings are also taken into account. How the findings may be used to information theory is covered in Section 5. In the final section, Section 6, a clear and concise conclusion is drawn, accompanied by an overview of potential future developments inspired by the current work.

2. Preliminaries

The terms of significance for fractional integrals, convexity, and superquadraticity are defined in this section along with the associated inequalities.

Definition 1

([3]). Let the function $\mathsf{\Psi }:[{\mathcal{U}}_o,{\mathcal{V}}_o]\subset \Re ⟶\Re$ be a convex then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathrm{y}}_1+(1-\beta ){\mathrm{y}}_2)\le \beta \mathsf{\Psi }\left({\mathrm{y}}_1\right)+(1-\beta )\mathsf{\Psi }\left({\mathrm{y}}_2\right),\hfill \end{array}$$

(1)

is valid for every ${\mathrm{y}}_1$, ${\mathrm{y}}_2\in [{\mathcal{U}}_o,{\mathcal{V}}_o]$, and $\beta \in [0,1].$

The $\mathbb{H}.\mathbb{H}$’s inequality is a fundamental mathematical result that establishes both lower and upper bounds for mean values. In inequality theory, it is among the first types of inequality to use convex functions. For error calculations that use numerical integration, such as the trapezoidal and midpoint formulae, this inequality is an essential tool. This well-known finding is defined as follows.

Theorem 1

([3]). $\mathbb{H}.\mathbb{H}$’s inequality states that if the function $\mathsf{\Psi }:\mathrm{I}\subseteq \Re ⟶\Re$, is convex in $\mathfrak{I}\subseteq \Re$, where ${\mathcal{V}}_o>{\mathcal{U}}_o$. The following statement satisfies:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}\right)\le {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(\mathrm{y}\right)d\mathrm{y}\le {\displaystyle \frac{\mathsf{\Psi }\left({\mathcal{U}}_o\right)+\mathsf{\Psi }\left({\mathcal{V}}_o\right)}{2}},\hfill \end{array}$$

(2)

∀ ${\mathcal{U}}_o,{\mathcal{V}}_o\in \mathfrak{I}$.

Definition 2.

$\mathbb{RL}$-fractional integrals with order $\beta \ge 0$ with ${\mathcal{U}}_o\ge 0$ are defined as

$$\begin{array}{cc}\hfill & {\mathfrak{I}}_{{\mathcal{U}}_{\mathfrak{o}}}^{\beta }+\mathsf{\Psi }\left(\mathrm{y}\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_{{\mathcal{U}}_o}^{\mathrm{y}}{(\mathrm{y}-{\mathrm{y}}_o)}^{\beta -1}\mathsf{\Psi }\left({\mathrm{y}}_o\right)d{\mathrm{y}}_o,(\mathrm{y}>{\mathcal{U}}_o),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\mathfrak{I}}_{{\mathcal{V}}_{\mathfrak{o}}}^{\beta }-\mathsf{\Psi }\left(\mathrm{y}\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\beta \right)}}{\int }_{\mathrm{y}}^{{\mathcal{V}}_o}{({\mathrm{y}}_o-\mathrm{y})}^{\beta -1}\mathsf{\Psi }\left({\mathrm{y}}_o\right)d{\mathrm{y}}_o,(\mathrm{y}<{\mathcal{V}}_o).\hfill \end{array}$$

The notations ${\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\beta }\mathsf{\Psi }\left(\mathrm{y}\right)$ and ${\mathfrak{I}}_{{\mathcal{V}}_{\mathfrak{o}}}^{\beta }-\mathsf{\Psi }\left(\mathrm{y}\right)$ are the left and right sided operators. Where Γ is a stated as gamma function and given by $\mathsf{\Gamma }\left(\beta \right)={\int }_0^{\infty }{{\mathrm{y}}_o}^{\beta -1}{e}^{-{\mathrm{y}}_o}d{\mathrm{y}}_o$.

Definition 3.

A function $\mathsf{\Psi }:[0,\infty )⟶\Re$ is superquadratic, if

$$\begin{array}{c}\hfill \mathsf{\Psi }\left({\mathrm{y}}_o\right)\ge \mathsf{\Psi }\left(\mathrm{y}\right)+{\mathfrak{C}}_{\mathrm{y}}({\mathrm{y}}_o-\mathrm{y})+\mathsf{\Psi }\left(\right|{\mathrm{y}}_o-\mathrm{y}\left|\right),\end{array}$$

(3)

holds for every ${\mathrm{y}}_o\ge 0$, ${\mathfrak{C}}_{\mathrm{y}}\in \Re$, where $\mathrm{y}\ge 0$ and ${\mathfrak{C}}_{\mathrm{y}}$ is a constant.

Remark 1.

If the inequality (3) is reversed then Ψ is called subquadratic.

As an example, we may use $\mathsf{\Psi }\left(\mathrm{y}\right)={\mathrm{y}}^{\mathrm{k}}$. The function $\mathsf{\Psi }$ is superquadratic for $\mathrm{y}\ge 0$ and $\mathrm{k}\ge 2$, but subquadratic for $0\le \mathrm{k}<2$. Let ${\mathfrak{C}}_{\mathrm{y}}=\mathrm{k}{\mathrm{y}}^{{\mathfrak{q}}_o-1}$ in this instance. At $\mathrm{k}=2$, equality is also preserved in (3).

More precisely, any randomly chosen superquadratic function meets the three supplementary conditions outlined in Lemma 1:

Lemma 1.

Let $\mathsf{\Psi }:[0,\infty )\to \Re$ be a superquadratic function, then

• $\mathsf{\Psi }\left(0\right)\le 0$.
• Provided that Ψ is differentiable at $\mathrm{y}>0$ and satisfies $\mathsf{\Psi }\left(0\right)={\mathsf{\Psi }}^{\prime }\left(0\right)=0$, it follows that ${\mathsf{\Psi }}^{\prime }\left(\mathrm{y}\right)={\mathfrak{C}}_{\mathrm{y}}$.
• If Ψ is positive and $\mathsf{\Psi }\left(0\right)={\mathsf{\Psi }}^{\prime }\left(0\right)=0$ on $(0,\infty )$, then Ψ is convex.

Two major inequalities that contribute to the growth and development of superquadraticity are inequalities of Jensen’s and $\mathbb{H}.\mathbb{H}$’s types, which are the most significant and frequently applied results.

Theorem 2

([46]). Let $\mathsf{\Psi }:J\subset [0,\infty [⟶\Re$ be a superquadratic then

$$\begin{array}{cc}\hfill & \sum _{i=1}^{\mathfrak{n}}{\beta }_i\mathsf{\Psi }\left({\mathrm{y}}_i\right)\ge \mathsf{\Psi }\left(\overline{\mathrm{y}}\right)+\sum _{i=1}^{\mathfrak{n}}{\beta }_i\mathsf{\Psi }\left(\right|{\mathrm{y}}_i-\overline{\mathrm{y}}\left|\right),\hfill \end{array}$$

(4)

holds for all ${\beta }_i\in (0,1)$ and ${\mathrm{y}}_i\ge 0$, where $\overline{\mathrm{y}}$ = ${\sum }_{i=1}^{\mathfrak{n}}{\beta }_i{\mathrm{y}}_i$, and ${\sum }_{i=1}^{\mathfrak{n}}$ ${\beta }_i=1$.

Banić et al. [52] contributed to the field of superquadraticity by formulating the following $\mathbb{H}.\mathbb{H}$-type inequalities.

Theorem 3.

Let $\mathsf{\Psi }:J\subset [0,\infty [⟶\Re$ be a superquadratic on J = $[{\mathcal{U}}_o,{\mathcal{V}}_o]$ then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}\right)+{\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(|\mathrm{y}-{\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}|\right)d\mathrm{y}\le {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(\mathrm{y}\right)d\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{\Psi }\left({\mathcal{U}}_o\right)+\mathsf{\Psi }\left({\mathcal{V}}_o\right)}{2}}-{\displaystyle \frac{1}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^2}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}[({\mathcal{V}}_o-\mathrm{y})\mathsf{\Psi }(\mathrm{y}-{\mathcal{U}}_o)+(\mathrm{y}-{\mathcal{U}}_o)\mathsf{\Psi }({\mathcal{V}}_o-\mathrm{y})]d\mathrm{y}.\hfill \end{array}$$

(5)

The line of support concept of superquadraticity is defined in Definition 3. In the following, we offer an additional definition.

Definition 4

([45]). Let $\mathsf{\Psi }:J\subset [0,\infty [⟶\Re$ be a superquadratic function then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }((1-\beta ){\mathrm{y}}_1+\beta {\mathrm{y}}_2)\le (1-\beta )\mathsf{\Psi }\left({\mathrm{y}}_1\right)+\beta \mathsf{\Psi }\left({\mathrm{y}}_2\right)-\beta \mathsf{\Psi }((1-\beta )|{\mathrm{y}}_1-{\mathrm{y}}_2\left|\right)\hfill \\ \hfill & -(1-\beta )\mathsf{\Psi }\left(\beta \right|{\mathrm{y}}_1-{\mathrm{y}}_2\left|\right),\hfill \end{array}$$

(6)

holds for every $\beta \in (0,1)$ and ${\mathrm{y}}_1,{\mathrm{y}}_2\ge 0$.

Remark 2.

Subquadraticity of the function Ψ corresponds to the reversal of the inequality sign in (6).

Theorem 4

([47]). Let $\mathsf{\Psi }:J\subset [0,\infty [⟶\Re$ be a superquadratic function on J = $[{\mathcal{U}}_o,{\mathcal{V}}_o]$ then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}\right)+{\displaystyle \frac{\beta }{2{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\beta }}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}-x|\right)({({\mathcal{V}}_o-\mathrm{y})}^{\beta -1}+{(\mathrm{y}-{\mathcal{U}}_o)}^{\beta -1})d\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{\Gamma }(1+\beta )}{2{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\beta }}}\left({\mathrm{I}}_{{{\mathcal{U}}_o}^{+}}^{\beta }\mathsf{\Psi }\left({\mathcal{V}}_o\right)+{\mathrm{I}}_{{{\mathcal{V}}_o}^{-}}^{\beta }\mathsf{\Psi }\left({\mathcal{U}}_o\right)\right)\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{\Psi }\left({\mathcal{U}}_o\right)+\mathsf{\Psi }\left({\mathcal{V}}_o\right)}{2}}-{\displaystyle \frac{\beta }{2{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\beta }}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\left(\left({\displaystyle \frac{\mathrm{y}-{\mathcal{U}}_o}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\right)\mathsf{\Psi }({\mathcal{V}}_o-\mathrm{y})+\left({\displaystyle \frac{{\mathcal{V}}_o-\mathrm{y}}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\right)\mathsf{\Psi }(\mathrm{y}-{\mathcal{U}}_o)\right)\hfill \\ \hfill & \times ({({\mathcal{V}}_o-\mathrm{y})}^{\beta -1}+{(\mathrm{y}-{\mathcal{U}}_o)}^{\beta -1})d\mathrm{y},\hfill \end{array}$$

(7)

where ${\mathrm{I}}_{{{\mathcal{U}}_o}^{+}}^{\beta }$ and ${\mathrm{I}}_{{{\mathcal{V}}_o}^{-}}^{\beta }$ are given in Definition 2.

Definition 5

([50]). A function $\mathsf{\Psi }:J\subseteq \Re \to \Re$ is called (P, m)-superquadratic on $J=[0,\mathrm{k}]$ for $\mathrm{k}>0$ and $\mathrm{m}\in [0,1]$; if

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o\right)\le \beta [\mathsf{\Psi }\left({\mathcal{U}}_o\right)-\mathsf{\Psi }\left((1-\beta )|{\mathcal{U}}_o-{\mathcal{V}}_o|\right)]\hfill \\ & +\mathrm{m}(1-\beta )[\mathsf{\Psi }\left({\mathcal{V}}_o\right)-\mathsf{\Psi }\left(\beta |{\mathcal{U}}_o-{\mathcal{V}}_o|\right)],\hfill \end{array}$$

holds for any ${\mathcal{U}}_o,{\mathcal{V}}_o\in J$ and $\beta \in [0,1]$. Ψ is defined as a (P, m)-subquadratic function whenever its negation $-\mathsf{\Psi }$ satisfies the (P, m)-superquadratic condition.

Definition 6

([27]). A mapping $\mathsf{\Psi }:\prod \to \Re$ is considered a random variable if it is $\mathfrak{A}$-measurable. It is defined on the probability space $(\prod ,\mathfrak{A},\mathrm{P})$, where ∏ denotes the set of all possible outcomes, $\mathfrak{A}$ is a σ-algebra representing the collection of measurable events (subsets of ∏), and $\mathrm{P}$ is a probability measure that assigns probabilities to these events.

Example 1.

Imagine a coin toss in which $\prod =\{H=Head,T=Tail\}$, $\mathfrak{A}$ includes complete subsets of ∏, and $\mathrm{P}$ assigns a probability of ${\displaystyle \frac{1}{2}}$ to each conceivable circumstance. So, $\mathsf{\Psi }\left(T\right)=1$ and $\mathsf{\Psi }\left(H\right)=0$ would be the definitions of a random variable Ψ.

Definition 7

([27]). If for all $\mathrm{y}\in J$, $\mathsf{\Psi }(\mathrm{y},·)$ is a random variable, then a map $\mathsf{\Psi }:J\times \prod \to \Re$ is called a stochastic process.

Example 2.

Think about taking daily readings of the temperature at noon for a week. ∏ can represent all possible weather conditions in this instance, $J=\{1,2,\dots ,7\}$ represents each day of the week, and $\mathsf{\Psi }(\mathrm{y},\omega )$ gives the temperature on day $\mathrm{y}$, provided that ω is met. As a random variable, $\mathsf{\Psi }(\mathrm{y},·)$ for each fixed day $\mathrm{y}$ shows how the temperature varies under different meteorological conditions. Temperature variation over time, as influenced by changes in $\mathrm{y}$, is modeled by the stochastic process $\mathsf{\Psi }(\mathrm{y},·)$.

Definition 8

([27]). A stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$, is called to be continuous on $J\subset \Re$, if for every $\mathrm{k}\in J$, we have

$$\begin{array}{c}\hfill \mathrm{P}-\underset{\mathrm{y}\to \mathrm{k}}{lim}\mathsf{\Psi }(\mathrm{y},·)=\mathsf{\Psi }(\mathrm{k},·).\end{array}$$

The notation $\mathrm{P}\text{-}lim$ is used to represent convergence in probability within a probability space.

Definition 9

([27]). A stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$, is called to be mean-square continuous on $J\subset \Re$, if for every $\mathrm{k}\in J$, we have

$$\begin{array}{c}\hfill \underset{\mathrm{y}\to \mathrm{k}}{lim}E\left[{(\mathsf{\Psi }(\mathrm{y},·)-\mathsf{\Psi }(\mathrm{k},·))}^2\right]=0.\end{array}$$

Where the random variable’s expectation is represented by $E\left[\mathsf{\Psi }(\mathrm{y},·)\right]$.

Remark 3.

Probability continuity is obviously shown by mean-square continuity, while the contrary is not true.

Definition 10

([27]). A stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$ is called to be mean-square differentiable on $J\subset \Re$ at $\mathrm{k}$, if a random variable ${\mathsf{\Psi }}^{\prime }:J\times \prod \to \Re$ is given. This means that:

$$\begin{array}{c}\hfill {\mathsf{\Psi }}^{\prime }(\mathrm{k},·)=\mathrm{P}-\underset{\mathrm{y}\to \mathrm{k}}{lim}{\displaystyle \frac{\mathsf{\Psi }(\mathrm{y},·)-\mathsf{\Psi }(\mathrm{k},·)}{\mathrm{y}-\mathrm{k}}},\end{array}$$

Definition 11

([27]). A stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$, is called to be mean-square integrable on $J\subset \Re$, if for every $\mathrm{y}\in J$, with $E\left[\mathsf{\Psi }{(\mathrm{y},·)}^2\right]<\infty$, $\left[{\mathrm{y}}_1,{\mathrm{y}}_2\right]\subseteq J$, ${\mathrm{y}}_1={\mathrm{k}}_0<{\mathrm{k}}_1<{\mathrm{k}}_2\dots <{\mathrm{k}}_n={\mathrm{y}}_2$, partitions $\left[{\mathrm{y}}_1,{\mathrm{y}}_2\right]$, and ${\mathrm{y}}_i\in \left[{\mathrm{k}}_{i-1},{\mathrm{k}}_i\right],\forall i=1,\dots ,n$ then

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}E\left[{\left(\sum _{i=1}^n\mathsf{\Psi }({\mathrm{y}}_i,·)({\mathrm{k}}_i-{\mathrm{k}}_{i-1})-S(·)\right)}^2\right]=0.\end{array}$$

It indicates that the stochastic process’s mean-square integral is $S:J\times \prod \to \Re$, and it may be expressed as

$$\begin{array}{c}\hfill S(·)={\int }_{{\mathrm{y}}_1}^{{\mathrm{y}}_2}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}.\end{array}$$

(8)

Remark 4.

The mean-square continuity of the stochastic process Ψ is sufficient to ensure the existence of the mean-square integral.

Remark 5.

It asserts that if $\mathsf{\Psi }(\mathrm{y},·)\le S(\mathrm{y},·)$ for all $\mathrm{y}\in [{\mathrm{y}}_1,{\mathrm{y}}_2]$, then the following holds:

$$\begin{array}{c}\hfill {\int }_{{\mathrm{y}}_1}^{{\mathrm{y}}_2}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\le {\int }_{{\mathrm{y}}_1}^{{\mathrm{y}}_2}S(\mathrm{y},·)d\mathrm{y}.\end{array}$$

(9)

Lemma 2

([29]). Let a stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$ be defined by $\mathsf{\Psi }(\mathrm{y},·)=\mathrm{A}(·)\mathrm{y}+\mathrm{B}(·)$, where $\mathrm{A},\mathrm{B}:\prod \to \Re$ are such that $E\left({\mathrm{A}}^2\right)<\infty$ and $E\left({\mathrm{B}}^2\right)<\infty$. If $[{\mathrm{y}}_1,{\mathrm{y}}_2]\subset J$, then the following holds:

$$\begin{array}{c}\hfill {\int }_{{\mathrm{y}}_1}^{{\mathrm{y}}_2}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}=\mathrm{A}(·){\displaystyle \frac{{{\mathrm{y}}_2}^2-{{\mathrm{y}}_1}^2}{2}}+\mathrm{B}(·)({\mathrm{y}}_2-{\mathrm{y}}_1),\end{array}$$

(10)

where $\mathrm{A}$ and $\mathrm{B}$ denote random variables.

Definition 12

([29]). We define a process $\mathsf{\Psi }:J\times \prod \to \Re$ to be convex stochastic on $J\subset \Re$ if, for every $\beta \in [0,1]$, the following condition is satisfied:

$$\begin{array}{c}\hfill \mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)\le \beta \mathsf{\Psi }({\mathcal{U}}_o,·)+(1-\beta )\mathsf{\Psi }({\mathcal{V}}_o,·),\end{array}$$

(11)

for any ${\mathcal{U}}_o,{\mathcal{V}}_o\in J$.

If $\beta ={\displaystyle \frac{1}{2}}$ is chosen in (11), the process Ψ is referred to as Jensen convex. Furthermore, if Ψ exhibits convexity, then its negation $-\mathsf{\Psi }$ is regarded as a concave stochastic process. For more interesting characteristics, the reader is referred to [28].

Lemma 3

([28]). If ${\mathrm{y}}_1,{\mathrm{y}}_2\in J_o$ and ${\mathrm{y}}_1<{\mathrm{y}}_2$, then the following inequalities hold.

$$\begin{array}{c}\hfill {\mathsf{\Psi }}_{-}^{\prime }({\mathrm{y}}_1,·)\le {\mathsf{\Psi }}_{+}^{\prime }({\mathrm{y}}_1,·)\le {\mathsf{\Psi }}_{-}^{\prime }({\mathrm{y}}_2,·)\le {\mathsf{\Psi }}_{+}^{\prime }({\mathrm{y}}_2,·).\end{array}$$

(12)

where ${\mathsf{\Psi }}_{+}^{\prime }$, and ${\mathsf{\Psi }}_{-}^{\prime }$, are the right and left derivatives of Ψ.

Theorem 5

([28]). It states that if a convex stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$ is mean-square continuous and satisfies Jensen’s convexity on J, then the following inequalities holds

$$\begin{array}{c}\hfill \mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_1+{\mathrm{y}}_2}{2}},·\right)\le {\displaystyle \frac{1}{{\mathrm{y}}_2-{\mathrm{y}}_1}}{\int }_{{\mathrm{y}}_1}^{{\mathrm{y}}_2}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\le {\displaystyle \frac{\mathsf{\Psi }({\mathrm{y}}_1,·)+\mathsf{\Psi }({\mathrm{y}}_2,·)}{2}},\end{array}$$

(13)

for every ${\mathrm{y}}_1,{\mathrm{y}}_2\in J$

Definition 13

([41]). Let $\mathsf{\Psi }:J\times \prod \to \Re$ be a stochastic process satisfying the conditions stated in Definition 11. Then, the mean-square stochastic $\mathbb{RL}$ fractional integrals of order $\alpha >0$, denoted by $I_{{{\mathcal{U}}_o}^{+}}^{\alpha }$ and $I_{{{\mathcal{V}}_o}^{-}}^{\alpha }$, are defined for Ψ as follows.

$$\begin{array}{c}\hfill I_{{{\mathcal{U}}_o}^{+}}^{\alpha }\left[\mathsf{\Psi }\right]\left(\mathrm{y}\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_{{\mathcal{U}}_o}^{\mathrm{y}}{(\mathrm{y}-\mathfrak{s})}^{\alpha -1}\mathsf{\Psi }(\mathfrak{s},·)d\mathfrak{s},\mathrm{y}>{\mathcal{U}}_o,\end{array}$$

and

$$\begin{array}{c}\hfill I_{{{\mathcal{V}}_o}^{-}}^{\alpha }\left[\mathsf{\Psi }\right]\left(\mathrm{y}\right)={\displaystyle \frac{1}{\mathsf{\Gamma }\left(\alpha \right)}}{\int }_{\mathrm{y}}^{{\mathcal{V}}_o}{(\mathfrak{s}-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }(\mathfrak{s},·)d\mathfrak{s},\mathrm{y}<{\mathcal{V}}_o.\end{array}$$

3. Analysis of Integral Inequalities Involving (P, m)-Superquadratic Stochastic Processes

In this section, we begin by introducing the definition of an (P, m)-superquadratic stochastic process, which generalizes the concept of an (P, m)-convex stochastic process. This generalization allows for the development of more refined results. Based on this definition, we investigate its properties and establish associated integral inequalities.

Definition 14.

Let $\mathsf{\Psi }:J\times \prod \to \Re$ be a (P, m)-superquadratic stochastic process over $J=[0,\mathrm{k}]$, Where $\mathrm{k}>0$ for $m\in [0,1]$ then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{U}}_o+m(1-\beta ){\mathcal{V}}_o,·)\le \left[\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right]\hfill \\ & +m\left[\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,.)\right],\hfill \end{array}$$

(14)

holds for every $\beta \in [0,1]$ and ${\mathcal{U}}_o,{\mathcal{V}}_o\in J$.

If $\beta ={\displaystyle \frac{1}{2}}$ is chosen in (14), then the process $\mathsf{\Psi }$ is termed as Jensen-(P, m)-superquadratic. If the process $\mathsf{\Psi }$ is classified as (P, m)-superquadratic, then $-\mathsf{\Psi }$ is then termed as (P, m)-subquadratic stochastic process.

Example 3.

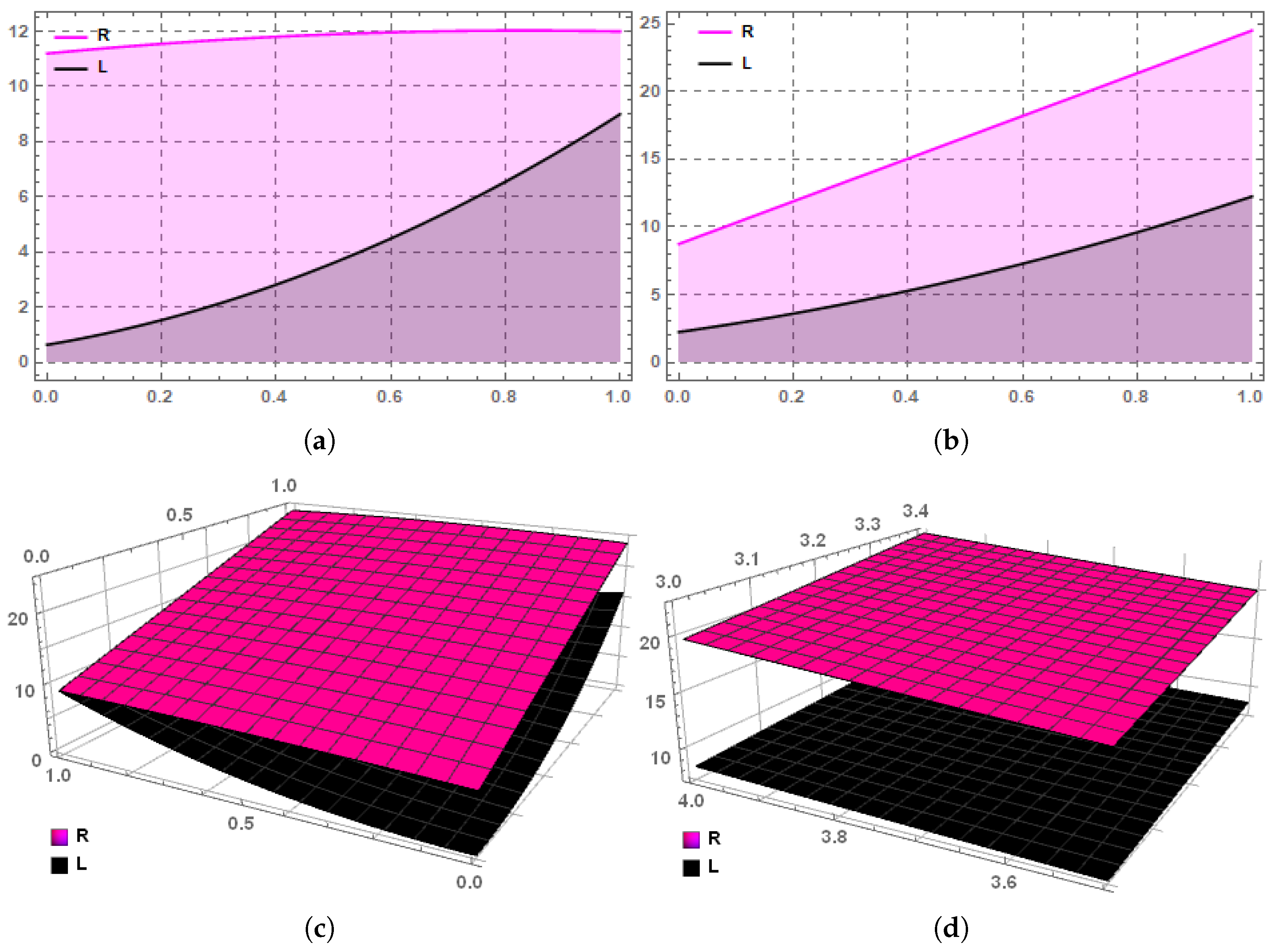
A process Ψ: $[2,\infty ]\times \prod \to \Re$ defined by $\mathsf{\Psi }(\mathrm{y},·)={\mathrm{y}}^{\mathrm{k}}$ for $\mathrm{k}\ge 2$ is a (P, m)-superquadratic stochastic process for every $m\in [0,1]$. The graphs in Figure 1 illustrate the validity of Definition 14 via the process Ψ considering different values of the parameters that go into it. Let R and L denote the right and left sides of the expression (14) respectively. It has been shown in the in Figure 1 that pink color represents the right term of the Definition 14 while black color represents the left term of the Definition 14. We noticed that for various values of the parameters m, ${\mathcal{U}}_o$ and ${\mathcal{V}}_o$ and β, the pink color always occurs above the black color. It implies that the Definition 14 holds true.

Next, we investigate the core properties that define and characterize (P, m)-superquadratic stochastic processes.

Proposition 1.

If ${\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2:[0,\mathrm{k}]\times \prod \to \Re$ are (P, m)-superquadratic stochastic processes, then ${\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2$ and $\mathrm{r}\mathsf{\Psi }$, where $\mathrm{r}>0$ are (P, m)-superquadratic stochastic processes.

Proof. 

Let ${\mathsf{\Psi }}_1$ and ${\mathsf{\Psi }}_2$ be (P, m)-superquadratic stochastic processes, we have

$$\begin{array}{cc}\hfill & {\mathsf{\Psi }}_1\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\le \left({\mathsf{\Psi }}_1({\mathcal{U}}_o,·)-{\mathsf{\Psi }}_1((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathrm{m}({\mathsf{\Psi }}_1({\mathcal{V}}_o,·)\hfill \\ & -{\mathsf{\Psi }}_1(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\mathsf{\Psi }}_2\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\le \left({\mathsf{\Psi }}_2({\mathcal{U}}_o,·)-{\mathsf{\Psi }}_2((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathrm{m}({\mathsf{\Psi }}_2({\mathcal{V}}_o,·)\hfill \\ & -{\mathsf{\Psi }}_2(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)),\hfill \end{array}$$

now

$$\begin{array}{cc}\hfill & ({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)={\mathsf{\Psi }}_1\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)+{\mathsf{\Psi }}_2\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\hfill \\ \hfill & \le \left({\mathsf{\Psi }}_1({\mathcal{U}}_o,·)-{\mathsf{\Psi }}_1((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathrm{m}\left({\mathsf{\Psi }}_1({\mathcal{V}}_o,·)-{\mathsf{\Psi }}_1(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ \hfill & +\left({\mathsf{\Psi }}_2({\mathcal{U}}_o,·)-{\mathsf{\Psi }}_2((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathrm{m}\left({\mathsf{\Psi }}_2({\mathcal{V}}_o,·)-{\mathsf{\Psi }}_2(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ \hfill & =\left(({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)({\mathcal{U}}_o,·)-({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ & +\mathrm{m}\left(({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)({\mathcal{V}}_o,·)-({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right).\hfill \end{array}$$

Thus we have

$$\begin{array}{cc}\hfill & ({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\le \left(({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)({\mathcal{U}}_o,·)-({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ \hfill & +\mathrm{m}\left(({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)({\mathcal{V}}_o,·)-({\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2)(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right).\hfill \end{array}$$

(15)

Similarly

$$\begin{array}{cc}\hfill & \mathrm{r}\mathsf{\Psi }\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\hfill \\ & \le \mathrm{r}\left(\left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathrm{m}\left(\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\right)\hfill \\ \hfill & =\left(\mathrm{r}\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathrm{r}\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathrm{m}\left(\mathrm{r}\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathrm{r}\mathsf{\Psi }(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right).\hfill \end{array}$$

Thus we have

$$\begin{array}{cc}\hfill & \mathrm{r}\mathsf{\Psi }\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\le (\left(\mathrm{r}\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathrm{r}\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ & +\mathrm{m}\left(\mathrm{r}\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathrm{r}\mathsf{\Psi }(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right).\hfill \end{array}$$

(16)

Therefore, (15) and (16) jointly imply that both ${\mathsf{\Psi }}_1+{\mathsf{\Psi }}_2$ and $\mathrm{r}\mathsf{\Psi }$ satisfy the definition of m-superquadratic stochastic processes.  □

Proposition 2.

Let ${\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2:[0,\mathrm{k}]\times \prod \to \Re$ be the (P, m)-superquadratic stochastic processes, then $\mathsf{\Psi }(\mathrm{y},·)=max\{{\mathsf{\Psi }}_1(\mathrm{y},·),{\mathsf{\Psi }}_2(\mathrm{y},·)\}$ is a (P, m)-superquadratic stochastic process.

Proof. 

Since one derives that

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\hfill \\ \hfill & =max\{{\mathsf{\Psi }}_1\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right),{\mathsf{\Psi }}_2\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·\right)\}\hfill \\ \hfill & \le max\{[{\mathsf{\Psi }}_1({\mathcal{U}}_o,·)-{\mathsf{\Psi }}_1((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)]+\mathrm{m}[{\mathsf{\Psi }}_1({\mathcal{V}}_o,·)-{\mathsf{\Psi }}_1(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)],\hfill \\ \hfill & [{\mathsf{\Psi }}_2({\mathcal{U}}_o,·)-{\mathsf{\Psi }}_2((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)]+\mathrm{m}[{\mathsf{\Psi }}_2({\mathcal{V}}_o,·)-{\mathsf{\Psi }}_2(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)]\}\hfill \\ \hfill & \le \left[max\{{\mathsf{\Psi }}_1({\mathcal{U}}_o,·),{\mathsf{\Psi }}_2({\mathcal{U}}_o,·)\}-max\{{\mathsf{\Psi }}_1((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·),{\mathsf{\Psi }}_2((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\}\right]\hfill \\ \hfill & +\mathrm{m}\left[max\{{\mathsf{\Psi }}_1({\mathcal{V}}_o,·),{\mathsf{\Psi }}_2({\mathcal{V}}_o,·)\}-max\{{\mathsf{\Psi }}_1(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·),{\mathsf{\Psi }}_2(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\}\right]\hfill \\ \hfill & =[\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)]+\mathrm{m}[\mathsf{\Psi }({\mathcal{V}}_o.·)-\mathsf{\Psi }(\beta |{\mathcal{V}}_o-{\mathcal{U}}_o|,·)].\hfill \end{array}$$

(17)

Consequently, $\mathsf{\Psi }(\mathrm{y},·)$ is a (P, m)-superquadratic stochastic process.  □

Theorem 6.

Let $\mathsf{\Psi }:[0,\mathrm{k}]\times \prod \to \Re$ be a (P, m)-superquadratic stochastic process and ${\mathrm{y}}_1<{\mathrm{y}}_2<{\mathrm{y}}_3$ for all ${\mathrm{y}}_1,{\mathrm{y}}_2,{\mathrm{y}}_3\in [0,\mathrm{k}]$, then

$$\begin{array}{cc}\hfill \left|\begin{array}{cc}\mathsf{\Psi }({\mathrm{y}}_2,·)& 0\\ 0& 1\end{array}\right|& \le \left|\begin{array}{cc}\mathsf{\Psi }({\mathrm{y}}_1,·)& 1\\ \mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathrm{y}}_2-{\mathrm{y}}_1)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)& 1\end{array}\right|+\mathrm{m}\left|\begin{array}{cc}\mathsf{\Psi }({\mathrm{y}}_3,·)& 1\\ \mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_2)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)& 1\end{array}\right|\hfill \end{array}$$

(18)

holds, for every $\mathrm{m}\in [0,1]$.

Proof. 

Let the stochastic process $\mathsf{\Psi }$ is a (P, m)-superquadratic, then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\beta \mathrm{y}+\mathrm{m}(1-\beta ){\mathrm{y}}_o,·\right)\le \left(\mathsf{\Psi }(\mathrm{y},·)-\mathsf{\Psi }((1-\beta )|\mathrm{y}-{\mathrm{y}}_o|,·)\right)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }({\mathrm{y}}_o,·)-\mathsf{\Psi }(\beta |\mathrm{y}-{\mathrm{y}}_o|,·)\right).\hfill \end{array}$$

(19)

Setting

$$\begin{array}{c}\hfill {\mathrm{y}}_2=\beta \mathrm{y}+\mathrm{m}(1-\beta ){\mathrm{y}}_o.\end{array}$$

(20)

Next putting $\mathrm{y}={\mathrm{y}}_1$ and ${\mathrm{y}}_o={\mathrm{y}}_3$ in (20), we get

$$\begin{array}{cc}\hfill & {\mathrm{y}}_2=\beta {\mathrm{y}}_1+\mathrm{m}(1-\beta ){\mathrm{y}}_3.\hfill \\ \hfill & \Rightarrow \beta ={\displaystyle \frac{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_2}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}.\hfill \end{array}$$

Substituting $\mathrm{y}={\mathrm{y}}_1$, ${\mathrm{y}}_o={\mathrm{y}}_3$ and $\beta ={\displaystyle \frac{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_2}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}$ in (19), we get

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\mathrm{y}}_2,·\right)\le \left[\mathsf{\Psi }({\mathrm{y}}_1,·)-\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathrm{y}}_2-{\mathrm{y}}_1)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)\right]\hfill \\ & +m\left[\mathsf{\Psi }({\mathrm{y}}_3,·)-\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_2)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)\right].\hfill \end{array}$$

It implies that

$$\begin{array}{cc}\hfill & \left[\mathsf{\Psi }({\mathrm{y}}_1,·)-\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathrm{y}}_2-{\mathrm{y}}_1)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)\right]\hfill \\ & +m\left[\mathsf{\Psi }({\mathrm{y}}_3,,·)-\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_2)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)\right]-\mathsf{\Psi }\left({\mathrm{y}}_2,·\right)\ge 0.\hfill \end{array}$$

(21)

Inequality (21) can be written as follows

$$\begin{array}{ccc}\hfill \left|\begin{array}{cc}\mathsf{\Psi }({\mathrm{y}}_1,·)& 1\\ \mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathrm{y}}_2-{\mathrm{y}}_1)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)& 1\end{array}\right|& +m\left|\begin{array}{cc}\mathsf{\Psi }({\mathrm{y}}_3,·)& 1\\ \mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_2)({\mathrm{y}}_3-{\mathrm{y}}_1)}{\mathrm{m}{\mathrm{y}}_3-{\mathrm{y}}_1}}\right|,·\right)& 1\end{array}\right|\hfill & \hfill \ge \left|\begin{array}{cc}\mathsf{\Psi }({\mathrm{y}}_2,·)& 0\\ 0& 1\end{array}\right|.\end{array}$$

(22)

Hence this concludes the proof.  □

Next we provide the proof of an inequality of Jensen’s type for (P, m)-superquadratic stochastic processes.

Theorem 7.

Let $\mathsf{\Psi }:[0,\mathrm{k}]\times \prod \to \Re$ be a (P, m)-superquadratic stochastic process then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\sum _{i=1}^{\mathfrak{n}}{\beta }_i{\mathrm{y}}_i,·\right)\le \sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right),\hfill \end{array}$$

(23)

holds $\forall {\mathrm{y}}_1,\dots ,{\mathrm{y}}_n\in [0,\mathrm{k}],{\beta }_1,\dots ,{\beta }_{\mathfrak{n}}>0$, such that ${\sum }_{i=1}^{\mathfrak{n}}{\beta }_i=1$, where $\mathrm{m}\in [0,1]$.

Proof. 

We prove this result by using the principle of mathematical induction, therefore by taking $\mathfrak{n}=2$ in (23), we have

$$\begin{array}{c}\hfill \mathsf{\Psi }\left({\beta }_1{\mathrm{y}}_1+{\beta }_2{\mathrm{y}}_2,·\right)\le \mathsf{\Psi }({\mathrm{y}}_2,·)-\mathsf{\Psi }\left({\beta }_1|{\mathrm{y}}_2-{\displaystyle \frac{{\mathrm{y}}_1}{\mathrm{m}}}|,·\right)+\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_1}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\beta }_2|{\mathrm{y}}_2-{\displaystyle \frac{{\mathrm{y}}_1}{\mathrm{m}}}|,·\right)\right).\end{array}$$

Which reflects the Definition 14. Thus the statement (23) is true for $\mathfrak{n}$ = 2.

Next we assuming the validity of (23) for $\mathfrak{n}-1$, it follows that:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\sum _{i=1}^{\mathfrak{n}-1}{\beta }_i{\mathrm{y}}_i,·\right)\le \sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-1-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-1-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-1-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-1-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-1-i}}}|,·\right),\hfill \end{array}$$

(24)

now let us prove that (23) is valid for $\mathfrak{n}.$

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\sum _{i=1}^{\mathfrak{n}}{\beta }_i{\mathrm{y}}_i,·\right)=\mathsf{\Psi }\left({\beta }_n{\mathrm{y}}_n+\mathrm{m}\beta \sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }},·\right),\hfill \end{array}$$

where $\beta ={\sum }_{i=1}^{\mathfrak{n}-1}{\beta }_i$, then it implies that

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\sum _{i=1}^{\mathfrak{n}}{\beta }_i{\mathrm{y}}_i,·\right)\le \mathsf{\Psi }({\mathrm{y}}_n,·)+\mathrm{m}\mathsf{\Psi }\left(\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right),·\right)\hfill \\ \hfill & -\mathsf{\Psi }\left(\beta |{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right)|,·\right)-\mathrm{m}\mathsf{\Psi }\left({\beta }_n|{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right)|,·\right),\hfill \end{array}$$

(25)

using (24) in (25), then we obtain

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left(\sum _{i=1}^{\mathfrak{n}}{\beta }_i{\mathrm{y}}_i,·\right)\le \mathsf{\Psi }({\mathrm{y}}_n,·)+\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right)\hfill \\ \hfill & -\mathsf{\Psi }\left(\beta |{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right)|,·\right)-\mathrm{m}\mathsf{\Psi }\left({\beta }_n|{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right)|,·\right)\hfill \\ \hfill & ={\mathrm{m}}^{n-n}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_n}{{\mathrm{m}}^{n-n}}},·\right)+\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right)\hfill \\ \hfill & -\mathsf{\Psi }\left(\beta |{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right)|,·\right)-\mathrm{m}\mathsf{\Psi }\left({\beta }_n|{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{\mathrm{m}\beta }}\right)|,·\right)\hfill \\ \hfill & \le \sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right)-\mathsf{\Psi }\left(\beta |{\mathrm{y}}_n-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{n-i}\beta }}\right)|,·\right)\hfill \\ \hfill & =\sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right)\hfill \\ \hfill & -{\mathrm{m}}^{n-n}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_n}{{\mathrm{m}}^{n-n}}}-{\displaystyle \frac{{\beta }_n{\mathrm{y}}_n}{{\mathrm{m}}^{n-n}}}-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{n-i}}}\right)|,·\right)\hfill \\ \hfill & =\sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right)\hfill \\ \hfill & -{\mathrm{m}}^{n-n}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_n}{{\mathrm{m}}^{n-n}}}-{\displaystyle \frac{{\beta }_n{\mathrm{y}}_n}{{\mathrm{m}}^{n-n}}}-\sum _{i=1}^{\mathfrak{n}-1}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{n-i}}}\right)|,·\right)\hfill \\ \hfill & =\sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}-1}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}-1}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right)\hfill \\ \hfill & -{\mathrm{m}}^{n-n}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_n}{{\mathrm{m}}^{n-n}}}-\sum _{i=1}^{\mathfrak{n}}\left({\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{n-i}}}\right)|,·\right)\hfill \\ & =\sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}},·\right)-\sum _{i=1}^{\mathfrak{n}}{\mathrm{m}}^{\mathfrak{n}-i}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}-\sum _{i=1}^{\mathfrak{n}}{\displaystyle \frac{{\beta }_i{\mathrm{y}}_i}{{\mathrm{m}}^{\mathfrak{n}-i}}}|,·\right).\hfill \end{array}$$

Hence the proof.  □

Theorem 8.

The following statements are true for $\mathrm{m}\in [0,1]$ and ∀ ${\mathcal{U}}_o$, ${\mathcal{V}}_o$, ${\mathfrak{c}}_o\in [0,\mathrm{k}]$ and $\beta \in [0,1]$

1. 

$\mathsf{\Psi }\in S_{\mathrm{m}}[0,\mathrm{k}]$, where $S_{\mathrm{m}}[0,\mathrm{k}]$=Set of (P, m)-superquadratic stochastic processes.

2. 

The process Ψ holds the result given below:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\beta }_1{\mathcal{U}}_o+(1-{\beta }_1){\mathcal{V}}_o,·\right)\le \mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-{\beta }_1)|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right).\hfill \end{array}$$

3. 

For ${\beta }_1+{\beta }_2=1$, the process Ψ holds the inequality given below:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\beta }_1{\mathcal{U}}_o+{\beta }_2{\mathcal{V}}_o,·\right)\le \mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left({\beta }_2|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right).\hfill \end{array}$$

4. 

For ${\mathcal{U}}_o\le {\mathfrak{c}}_o\le {\mathcal{V}}_o$ the inequality given below holds:

$$\begin{array}{cccc}|& \begin{array}{c}1\\ -1\\ 0\end{array}& \begin{array}{c}\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-\beta )|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\\ \mathrm{m}\left[\left(\mathsf{\Psi }({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·)-\mathsf{\Psi }\left(\beta |{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right)\right]\\ \mathsf{\Psi }({\mathfrak{c}}_o,·)\end{array}& |\end{array}\ge 0.$$

Proof. 

It is straightforward that (1) ⇔ (2) ⇔ (3) and (3) ⇔ (4). Since ${\mathcal{U}}_o\le {\mathfrak{c}}_o\le {\mathcal{V}}_o$ there exists a scalar ${\beta }_1\in [0,1]$ such that ${\mathfrak{c}}_o={\beta }_1{\mathcal{U}}_o+{\beta }_2{\mathcal{V}}_o={\beta }_1{\mathcal{U}}_o+(1-{\beta }_1){\mathcal{V}}_o$. Consequently, the following results can be established.

$$\begin{array}{cc}\hfill & \mathsf{\Psi }({\mathfrak{c}}_o,·)=\mathsf{\Psi }({\beta }_1{\mathcal{U}}_o+{\beta }_2{\mathcal{V}}_o,·)=\mathsf{\Psi }({\beta }_1{\mathcal{U}}_o+(1-{\beta }_1){\mathcal{V}}_o,·)=\mathsf{\Psi }\left({\beta }_1{\mathcal{U}}_o+\mathrm{m}(1-{\beta }_1){\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)\hfill \\ \hfill & \le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-{\beta }_1)|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right)+\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right).\hfill \end{array}$$

Since it follows that

$$\begin{array}{cc}& \begin{array}{ccccc}|& \begin{array}{c}1\\ -1\\ 0\end{array}& \begin{array}{c}\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-{\beta }_1)|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\\ \mathrm{m}\left(\mathsf{\Psi }({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·)-\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right)\\ \mathsf{\Psi }({\mathfrak{c}}_o,·)\end{array}& \begin{array}{c}1\\ 0\\ 1\end{array}& |\end{array}\hfill \\ & =\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-{\beta }_1)|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right)-\mathsf{\Psi }({\mathfrak{c}}_o,·)\ge 0.\hfill \end{array}$$

Hence, (4) is satisfied (4) ⇒ (1). In view of the assumption

$$\begin{array}{cc}\hfill & \mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-{\beta }_1)|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)+\mathrm{m}(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)\hfill \\ & -\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right))-\mathsf{\Psi }({\mathfrak{c}}_o,·)\le 0,\hfill \end{array}$$

it can be applied to

$$\begin{array}{cc}\hfill & \mathsf{\Psi }({\mathfrak{c}}_o,·)=\mathsf{\Psi }\left({\beta }_1{\mathcal{U}}_o+(1-{\beta }_1){\mathcal{V}}_o,·\right)\hfill \\ & \le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-{\beta }_1)|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|\right),·\right)+\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\beta }_1|{\mathcal{U}}_o-{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}|,·\right)\right).\hfill \end{array}$$

Hence the proof.  □

Next we offer the $\mathbb{H}.\mathbb{H}$’s inequality for (P, m)-superquadratic stochastic processes.

Theorem 9.

Let Ψ: $[{\mathcal{U}}_o,{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}]\times \prod \to \Re$ be a mean-square integrable (P, m)-superquadratic stochastic process, then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)+{\displaystyle \frac{1+\mathrm{m}}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ \hfill & \le \mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\},\hfill \end{array}$$

(26)

holds $\forall {\mathcal{U}}_o,{\mathcal{V}}_o>0$ and $m\in (0,1)$.

Proof. 

Since $\mathsf{\Psi }$ is a (P, m)-superquadratic stochastic process therefore we have

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{\mathrm{y}+{\mathrm{y}}_o}{2}},·\right)=\mathsf{\Psi }\left({\displaystyle \frac{\mathrm{y}}{2}}+\left({\displaystyle \frac{\mathrm{m}}{2}}\right)\left({\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}}\right),·\right)\le \left(\mathsf{\Psi }(\mathrm{y},·)-\mathsf{\Psi }\left({\displaystyle \frac{1}{2}}|\mathrm{y}-{\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}}|,·\right)\right)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\displaystyle \frac{1}{2}}|\mathrm{y}-{\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}}|,·\right)\right).\hfill \end{array}$$

(27)

Replacing $\mathrm{y}$ by $\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o$ and ${\mathrm{y}}_o$ by $\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o$ in (27), we get.

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)\le \mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)+\mathrm{m}\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}},·\right)\hfill \\ \hfill & -(1+\mathrm{m})\mathsf{\Psi }\left(\left|{\displaystyle \frac{(1+\mathrm{m})({\mathcal{U}}_o\beta +{\mathcal{V}}_o(1-\beta ))-({\mathcal{U}}_o+{\mathcal{V}}_o)}{2\mathrm{m}}}\right|,·\right).\hfill \end{array}$$

(28)

After mean-square integration of (28) w.r.t $\beta$ over $[0,1]$, we have

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)\le {\int }_0^1\mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)d\beta +\mathrm{m}{\int }_0^1\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}}\right)d\beta \hfill \\ \hfill & -(1+\mathrm{m}){\int }_0^1\mathsf{\Psi }\left(\left|{\displaystyle \frac{(1+\mathrm{m})({\mathcal{U}}_o\beta +{\mathcal{V}}_o(1-\beta ))-({\mathcal{U}}_o+{\mathcal{V}}_o)}{2\mathrm{m}}}\right|,·\right)d\beta .\hfill \end{array}$$

It implies after change of variables and simple calculations that

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)\le {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ \hfill & -{\displaystyle \frac{1+\mathrm{m}}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}.\hfill \end{array}$$

Thus

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)+{\displaystyle \frac{1+\mathrm{m}}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}.\hfill \end{array}$$

(29)

Since $\mathsf{\Psi }$ is an (P, m)-superquadratic stochastic process, it follows that

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)+\mathrm{m}\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}},·\right)\hfill \\ \hfill & =\mathsf{\Psi }\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta )({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}\right),·)+\mathrm{m}\mathsf{\Psi }\left((1-\beta ){\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}+\mathrm{m}\beta \left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right),·\right)\hfill \\ \hfill & \le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-\beta )\left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{\mathrm{m}}}\right|,·\right)\right)+\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left(\beta \left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{\mathrm{m}}}\right|,·\right)\right)\hfill \\ \hfill & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left(\beta \left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right|,·\right)\right)+{\mathrm{m}}^2\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)-\mathsf{\Psi }\left((1-\beta )\left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right|,·\right)\right),\hfill \end{array}$$

(30)

integrating (30) w.r.t $\beta$ over $[0,1]$ and after simple calculation and change of variables we get

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ \hfill & \le \mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(31)

Combining (29) and (31), we get what we want.  □

Corollary 1.

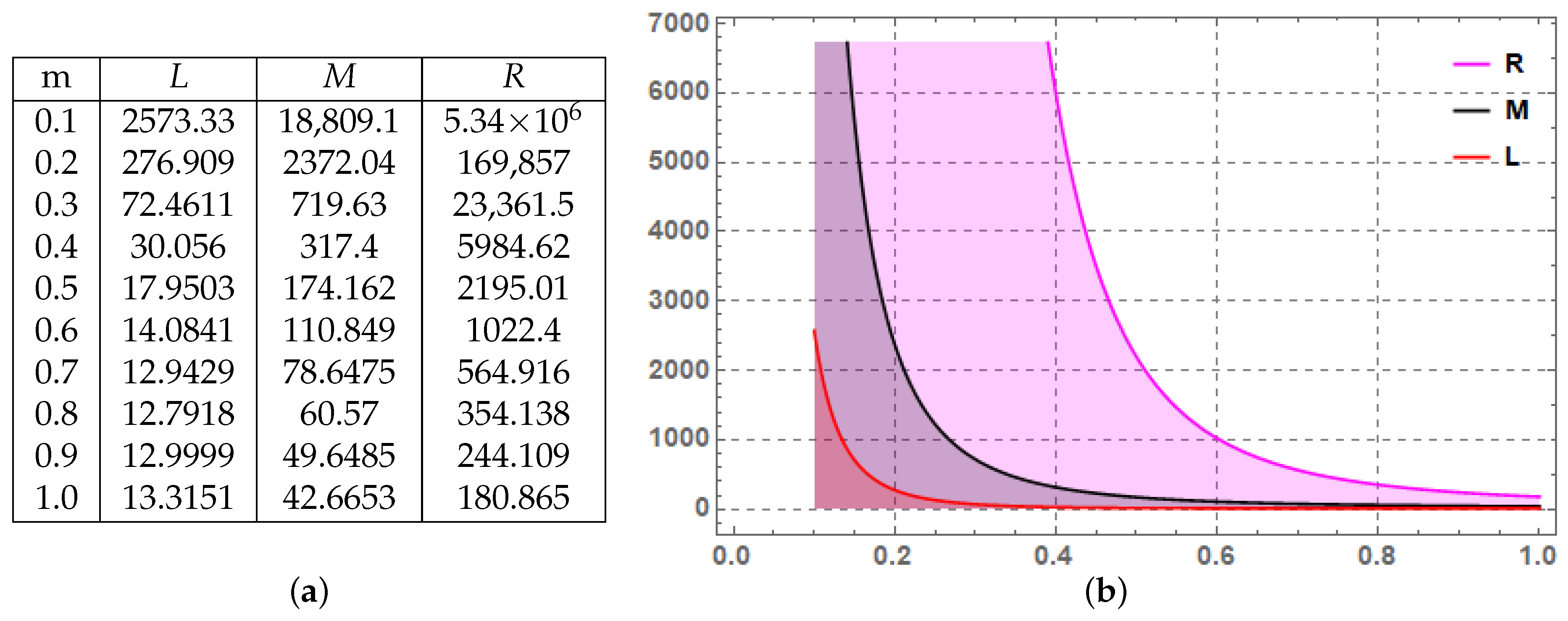
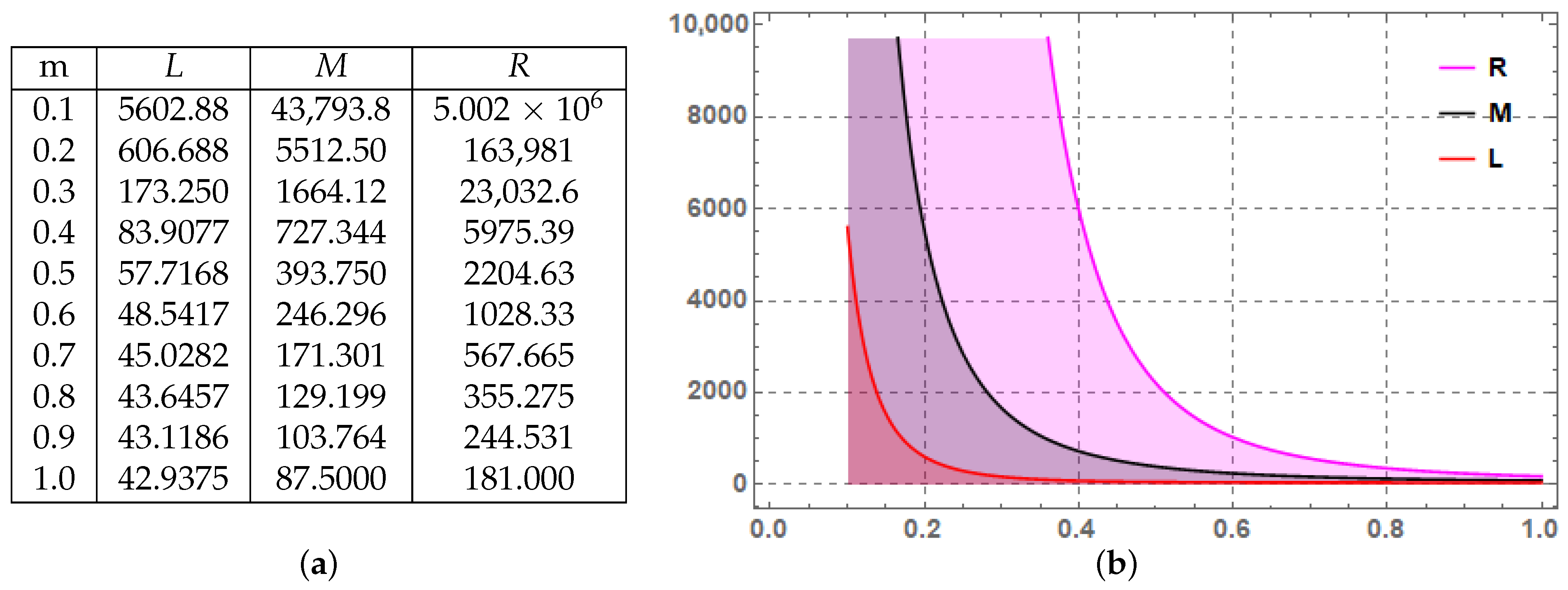
When the inequality in (26) is reversed, it gives rise to an inequality of $\mathbb{H}.\mathbb{H}$-type characterizing (P,m)-subquadratic stochastic processes.

To verify Theorem 9, we present the following example involving (P,m)-superquadratic stochastic process.

Example 4.

Consider the same process as given in Example 3, then we have the Figure 2a,b given by Figure 2, depict the right, middle and left terms, which are denoted by R, M and L respectively for Theorem 9.

In the aforementioned Example 4, the graph consists of three colors: pink, black and red. Pink, black and red stands for the right, middle and right terms of Theorem 9, respectively. It is obvious from Theorem 9 that right term is always greater than the middle and middle term is greater than the left term, therefore the graph’s pink color always occur above the black, and black always occur above the red color for various values of the parameters involved in it. This graphically confirms that the established result is true.

4. $\mathbb{H}\mathbf{.}\mathbb{H}$ Type Inequalities for (P, m)-Superquadratic Stochastic Processes: A Fractional Calculus Approach

This section is devoted to deriving fractional analogues of the $\mathbb{H}.\mathbb{H}$ inequalities via $\mathbb{RL}$ fractional operators.

Theorem 10.

Let Ψ: $[{\mathcal{U}}_o,{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}]\times \prod \to \Re$ be a mean-square integrable (P, m)-superquadratic stochastic process, then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{u}}_o+{\mathcal{V}}_o}{2}},·\right)+{\displaystyle \frac{2(1+\mathrm{m})\alpha }{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}{\int }_{{\mathcal{U}}_o}^{{\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left[{\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }({\mathcal{V}}_o,·)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)\right]\hfill \\ \hfill & \le \mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{\alpha }{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\},\hfill \end{array}$$

(32)

holds for all ${\mathcal{U}}_o,{\mathcal{V}}_o\ge 0$ and $m\in (0,1)$.

Proof. 

Let the process $\mathsf{\Psi }$, satisfying the conditions of (P, m)-superquadratic stochastic process, suggest that

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{\mathrm{y}+{\mathrm{y}}_o}{2}},·\right)=\mathsf{\Psi }\left({\displaystyle \frac{\mathrm{y}}{2}}+\left({\displaystyle \frac{\mathrm{m}}{2}}\right)\left({\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}}\right),·\right)\le \left(\mathsf{\Psi }(\mathrm{y},·)-\mathsf{\Psi }\left({\displaystyle \frac{1}{2}}|\mathrm{y}-{\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}}|,·\right)\right)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left({\displaystyle \frac{1}{2}}|\mathrm{y}-{\displaystyle \frac{{\mathrm{y}}_o}{\mathrm{m}}}|,·\right)\right),\hfill \end{array}$$

(33)

Replacing $\mathrm{y}$ with $\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o$ and ${\mathrm{y}}_o$ with $\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o$ in (33), we obtain the following

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)\le \mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)+\mathrm{m}\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}},·\right)\hfill \\ \hfill & -(1+\mathrm{m})\mathsf{\Psi }\left(\left|{\displaystyle \frac{(1+\mathrm{m})({\mathcal{U}}_o\beta +{\mathcal{V}}_o(1-\beta ))-({\mathcal{U}}_o+{\mathcal{V}}_o)}{2\mathrm{m}}}\right|,·\right),\hfill \end{array}$$

(34)

Multiplying (34) by ${\beta }^{\alpha -1}$ and then integrating it via $\beta$ over $[0,1]$, we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\alpha }}\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)\le {\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)d\beta +\mathrm{m}{\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}},·\right)d\beta \hfill \\ \hfill & -(1+\mathrm{m}){\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(1+\mathrm{m})({\mathcal{U}}_o\beta +{\mathcal{V}}_o(1-\beta ))-({\mathcal{U}}_o+{\mathcal{V}}_o)}{2\mathrm{m}}}\right|,·\right)d\beta ,\hfill \end{array}$$

it implies that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\alpha }}\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)\le {\displaystyle \frac{1}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+{\mathrm{m}}^{\alpha }{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}{\left(\mathrm{y}-{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}\right)}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ \hfill & -{\displaystyle \frac{1+\mathrm{m}}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y},\hfill \end{array}$$

thus

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\alpha }}\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)+{\displaystyle \frac{1+\mathrm{m}}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{\mathsf{\Gamma }\left(\alpha \right)}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left[{\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }({\mathcal{V}}_o,·)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)\right],\hfill \end{array}$$

(35)

again as $\mathsf{\Psi }$ is a (P, m)-superquadratic stochastic process, then we have

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)+\mathrm{m}\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}},·\right)\hfill \\ \hfill & =\mathsf{\Psi }\left(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta )({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}\right),·)+\mathrm{m}\mathsf{\Psi }\left((1-\beta ){\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}+\mathrm{m}\beta \left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right),·\right)\hfill \\ \hfill & \le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-\beta )\left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{\mathrm{m}}}\right|,·\right)\right)+\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left(\beta \left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{\mathrm{m}}}\right|,·\right)\right)\hfill \\ \hfill & +\mathrm{m}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left(\beta \left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right|,·\right)\right)\hfill \\ & +{\mathrm{m}}^2\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)-\mathsf{\Psi }\left((1-\beta )\left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right|,·\right)\right),\hfill \end{array}$$

(36)

Multiplying (36) by ${\beta }^{\alpha -1}$ and then integrating it via $\beta$ over $[0,1]$, we have

$$\begin{array}{cc}\hfill & {\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }(\beta {\mathcal{U}}_o+(1-\beta ){\mathcal{V}}_o,·)d\beta +\mathrm{m}{\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left({\displaystyle \frac{\beta {\mathcal{V}}_o+(1-\beta ){\mathcal{U}}_o}{\mathrm{m}}},·\right)d\beta \hfill \\ \hfill & \le {\int }_0^1{\beta }^{\alpha -1}\left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left((1-\beta )\left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{\mathrm{m}}}\right|,·\right)\right)d\beta \hfill \\ & +\mathrm{m}{\int }_0^1{\beta }^{\alpha -1}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left(\beta \left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{\mathrm{m}}}\right|,·\right)\right)d\beta \hfill \\ \hfill & +\mathrm{m}{\int }_0^1{\beta }^{\alpha -1}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)-\mathsf{\Psi }\left(\beta \left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right|,·\right)\right)d\beta \hfill \\ & +{\mathrm{m}}^2{\int }_0^1{\beta }^{\alpha -1}\left(\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)-\mathsf{\Psi }\left((1-\beta )\left|{\displaystyle \frac{\mathrm{m}{\mathcal{U}}_o-{\mathcal{V}}_o}{{\mathrm{m}}^2}}\right|,·\right)\right)d\beta .\hfill \end{array}$$

(37)

It implies that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+{\mathrm{m}}^{\alpha }{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}{\left(\mathrm{y}-{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}\right)}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ \hfill & \le {\displaystyle \frac{1}{\alpha }}\mathsf{\Psi }({\mathcal{U}}_o,·)+{\displaystyle \frac{1}{\alpha }}\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\},\hfill \end{array}$$

(38)

thus

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Gamma }\left(\alpha \right)}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left[{\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }({\mathcal{V}}_o,·)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)\right]\hfill \\ \hfill & \le {\displaystyle \frac{1}{\alpha }}\mathsf{\Psi }({\mathcal{U}}_o,·)+{\displaystyle \frac{1}{\alpha }}\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(39)

The proof is completed by merging inequalities (35) and (39). □

Corollary 2.

The fractional inequalities of $\mathbb{H}.\mathbb{H}$-type for (P, m)-subquadratic stochastic processes are obtained by applying $\mathbb{RL}$ fractional integral operators, provided that the inequalities in (32) are reversed.

Corollary 3.

The $\mathbb{H}.\mathbb{H}$ type inequalities for $(P,\mathrm{m})$-superquadratic stochastic process are obtained by taking $\alpha =1$ in (32).

Theorem 11.

Let Ψ: $[{\mathcal{U}}_o,{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}]\times \prod \to \Re$ be a mean-square integrable (P, m)-superquadratic stochastic process, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{2(\mathrm{m}+1)}}\{{\displaystyle \frac{1}{{(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left({\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }(\mathrm{m}{\mathcal{V}}_o,·)+{\mathfrak{I}}_{\mathrm{m}{{\mathcal{V}}_o}^{-}}^{\alpha }\mathsf{\Psi }({\mathcal{U}}_o,·)\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{{({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}^{\alpha }}}\left({\mathfrak{I}}_{{{\mathcal{V}}_o}^{-}}^{\alpha }\mathsf{\Psi }(\mathrm{m}{\mathcal{U}}_o,·)+{\mathfrak{I}}_{\mathrm{m}{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }({\mathcal{V}}_o,·)\right)\}\hfill \\ & \le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)+\mathsf{\Psi }({\mathcal{V}}_o,·)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{2{(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left({\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\hfill \\ \hfill & +\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\left)d\beta \right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha }{2{({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}^{\alpha }}}\left({\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\hfill \\ \hfill & +\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\left)d\beta \right).\hfill \end{array}$$

(40)

holds for all ${\mathcal{U}}_o,{\mathcal{V}}_o\ge 0$ and $m\in (0,1)$.

Proof. 

Suppose that the process $\mathsf{\Psi }$ exhibits $(P,\mathrm{m})$-superquadraticity, then

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·)\le \mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right),\hfill \end{array}$$

(41)

and

$$\begin{array}{cc}\hfill & \mathsf{\Psi }((1-\beta ){\mathcal{U}}_o+\mathrm{m}\beta {\mathcal{V}}_o,·)\le \mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right).\hfill \end{array}$$

(42)

Adding inequalities (41) and (42), we arrive at the following result:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·)+\mathsf{\Psi }((1-\beta ){\mathcal{U}}_o+\mathrm{m}\beta {\mathcal{V}}_o,·)\hfill \\ & \le \mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)+\mathrm{m}\left(\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ & +\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)+\mathrm{m}\left(\mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)\hfill \\ \hfill & =2\mathsf{\Psi }({\mathcal{U}}_o,·)+2\mathrm{m}\mathsf{\Psi }({\mathcal{V}}_o,·)-(1+\mathrm{m})\left(\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)+\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\left)\right).\hfill \end{array}$$

(43)

The inequality (43) is multiplied by ${\beta }^{\alpha -1}$ and integrating via $\beta$ over [0, 1], so we then attain that

$$\begin{array}{cc}\hfill & {\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }(\beta {\mathcal{U}}_o+\mathrm{m}(1-\beta ){\mathcal{V}}_o,·)d\beta +{\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }((1-\beta ){\mathcal{U}}_o+\mathrm{m}\beta {\mathcal{V}}_o,·)d\beta \hfill \\ & \le 2{\int }_0^1{\beta }^{\alpha -1}\left(\mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\mathsf{\Psi }({\mathcal{V}}_o,·)\right)d\beta \hfill \\ \hfill & -(1+\mathrm{m})\left({\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)d\beta +{\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left((1-\beta )\right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)d\beta \right),\hfill \end{array}$$

(44)

it implies that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\alpha }{{(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }\left(\mathrm{y}\right)d\mathrm{y}+{\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}{(\mathrm{y}-{\mathcal{U}}_o)}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ & \le \left(2\mathsf{\Psi }({\mathcal{U}}_o,·)+2\mathrm{m}\mathsf{\Psi }({\mathcal{V}}_o,·)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha (1+\mathrm{m})}{{(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left({\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\hfill \\ \hfill & +\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\left)d\beta \right),\hfill \end{array}$$

(45)

thus

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{2{(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }(\mathrm{m}{\mathcal{V}}_o,·)+{\mathfrak{I}}_{\mathrm{m}{{\mathcal{V}}_o}^{-}}^{\alpha }\mathsf{\Psi }({\mathcal{U}}_o,·)\right\}\le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\mathsf{\Psi }({\mathcal{V}}_o,·)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha (1+\mathrm{m})}{2{(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left({\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\hfill \\ \hfill & +\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\left)d\beta \right),\hfill \end{array}$$

(46)

Likewise, there are

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{V}}_o+\mathrm{m}(1-\beta ){\mathcal{U}}_o,·)\le \mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right),\hfill \end{array}$$

(47)

and

$$\begin{array}{cc}\hfill & \mathsf{\Psi }((1-\beta ){\mathcal{V}}_o+\mathrm{m}\beta {\mathcal{U}}_o,·)\le \mathsf{\Psi }({\mathcal{V}}_o,·)-\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\hfill \\ & +\mathrm{m}\left(\mathsf{\Psi }({\mathcal{U}}_o,·)-\mathsf{\Psi }((1-\beta )|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right).\hfill \end{array}$$

(48)

Adding inequalities (47) and (48), we derive:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }(\beta {\mathcal{V}}_o+\mathrm{m}(1-\beta ){\mathcal{U}}_o,·)+\mathsf{\Psi }((1-\beta ){\mathcal{V}}_o+\mathrm{m}\beta {\mathcal{U}}_o,·)\hfill \\ \hfill & \le 2\mathsf{\Psi }({\mathcal{V}}_o,·)+2\mathrm{m}\mathsf{\Psi }({\mathcal{U}}_o,·)-(1+\mathrm{m})\left(\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)+\mathsf{\Psi }\left((1-\beta )\right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)\right)),\hfill \end{array}$$

(49)

the inequality (49) is multiplied by ${\beta }^{\alpha -1}$ and integrating via $\beta$ over [0, 1], we then attain that

$$\begin{array}{cc}\hfill & {\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }(\beta {\mathcal{V}}_o+\mathrm{m}(1-\beta ){\mathcal{U}}_o,·)d\beta +{\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }((1-\beta ){\mathcal{V}}_o+\mathrm{m}\beta {\mathcal{U}}_o,·)d\beta \hfill \\ & \le 2{\int }_0^1{\beta }^{\alpha -1}\left(\mathsf{\Psi }({\mathcal{V}}_o,·)+\mathrm{m}\mathsf{\Psi }({\mathcal{U}}_o,·)\right)d\beta \hfill \\ \hfill & -(1+\mathrm{m})\left({\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left(\beta \right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)d\beta +{\int }_0^1{\beta }^{\alpha -1}\mathsf{\Psi }\left((1-\beta )\right|{\mathcal{V}}_o-{\mathcal{U}}_o|,·)d\beta \right),\hfill \end{array}$$

(50)

it implies that

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\alpha }{{({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+{\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ & \le \left(2\mathsf{\Psi }({\mathcal{V}}_o,·)+2\mathrm{m}\mathsf{\Psi }({\mathcal{U}}_o,·)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha (1+\mathrm{m})}{{({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}^{\alpha }}}\left({\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\hfill \\ \hfill & +\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\left)d\beta \right),\hfill \end{array}$$

(51)

thus

$$\begin{array}{cc}\hfill & {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{2{({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}^{\alpha }}}\left\{{\mathfrak{I}}_{{{\mathcal{V}}_o}^{-}}^{\alpha }\mathsf{\Psi }(\mathrm{m}{\mathcal{U}}_o,·)+{\mathfrak{I}}_{\mathrm{m}{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }({\mathcal{V}}_o,·)\right\}\le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\mathsf{\Psi }({\mathcal{V}}_o,·)\right)\hfill \\ \hfill & -{\displaystyle \frac{\alpha (1+\mathrm{m})}{2{({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}^{\alpha }}}\left({\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\hfill \\ \hfill & +\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\left)d\beta \right).\hfill \end{array}$$

(52)

The required result is obtained by summing (46) and (52).  □

Corollary 4.

Under the assumptions of Theorem 11, and by taking $\alpha =1$, one arrives at the following inequality for $(P,\mathrm{m})$-superquadratic functions.

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{(\mathrm{m}+1)}}\left\{{\displaystyle \frac{1}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+{\displaystyle \frac{1}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}{\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\le \left(\mathsf{\Psi }({\mathcal{U}}_o,·)+\mathsf{\Psi }({\mathcal{V}}_o,·)\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{2(\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o)}}\left({\int }_{{\mathcal{U}}_o}^{\mathrm{m}{\mathcal{V}}_o}\left(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{m}{\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)+\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{\mathrm{m}{\mathcal{V}}_o-{\mathcal{U}}_o}}\right|,·\right)\right)d\beta \right)\hfill \\ \hfill & -{\displaystyle \frac{1}{2({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}}\left({\int }_{\mathrm{m}{\mathcal{U}}_o}^{{\mathcal{V}}_o}\left(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-\mathrm{m}{\mathcal{U}}_o)({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)+\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-{\mathcal{U}}_o)}{{\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o}}\right|,·\right)\right)d\beta \right),\hfill \end{array}$$

(53)

Example 5.

Consider the same process as given in Example 3, then we have the Figure 3a,b given by Figure 3, shows the right, middle and left terms, which are denoted by R, M and L respectively for Theorem 10.

In the aforementioned Example 5, the graph consists of three colors: pink, black and red. Pink, black and red stand for the right, middle and right terms of Theorem 10, respectively. It is obvious from Theorem 10 that right term is always greater than the middle and middle term is greater than the left term, therefore the graph’s pink color always occur above the black, and black always occur above the red color for various values of the parameters involved in it. This graphically confirms that the established result is true.

5. Implications for Information Theory

Distinguishing between two probability distributions is a fundamental task across various disciplines, including statistics, information theory and machine. Divergence measures serve as quantitative tools for assessing the dissimilarity between probability distributions. Lin [53], in 1991, proposed a novel class of divergence measures derived from Shannon entropy, a core principle in information theory used to quantify uncertainty and the informational content within a probability distribution. Lin’s departure provided a principled, information-theoretic way of measuring distributional discrepancy. Shioya and Da-te [54] later built on Lin’s contribution by bringing out the $\mathbb{H}.\mathbb{H}$ $\mathsf{\Psi }$-divergence in 1995. Their development utilized the $\mathbb{H}.\mathbb{H}$ inequality, a standard mathematical finding connected with convex functions, to create an extended and more versatile basis. This breakthrough greatly extended the range of application of divergence measures, allowing deeper understanding and new applications in the comparative examination of probability distributions.

For clarity and focus, we restrict ourselves to the definitions that are directly relevant to the results that follow.

Definition 15

([55]). Csiszár Ψ-divergence is defined as follows:

$$\begin{array}{c}\hfill D_{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}\right)d\mathcal{U}\left(\mathrm{y}\right),{\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}.\end{array}$$

In this context, $\mathbf{P}$ represents the collection of all probability densities with respect to a σ-finite measure $\mathcal{U}$, ℧ is assumed to be a nonempty set, and Ψ is a convex function defined over $(0,+\infty )$.

$$\begin{array}{c}\hfill \mathbf{P}=\left\{{\mathfrak{p}}_o|{\mathfrak{p}}_o:\mho \to \Re ,{\mathfrak{p}}_o\left(\mathrm{y}\right)\ge 0,{\int }_{\mho }{\mathfrak{p}}_o\left(\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)=1\right\}.\end{array}$$

Remark 6.

Taking the function Ψ as an (P, m)-superquadratic function yields the Csiszár Ψ-divergence for (P, m)-superquadratic function.

Definition 16

([56]). $\mathbb{H}.\mathbb{H}$ Ψ-divergence is denoted and defined as follows:

$$\begin{array}{c}\hfill D_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right){\displaystyle \frac{{\int }_1^{\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}\mathsf{\Psi }\left(\mathrm{y}\right)d\mathrm{y}}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}d\mathcal{U}\left(\mathrm{y}\right),{\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}.\end{array}$$

(54)

Definition 17

([57]). $\mathbb{RL}$ fractional $\mathbb{H}.\mathbb{H}$ Ψ-divergence is denoted and defined as follows:

$$\begin{array}{c}\hfill {}^{\alpha }SD_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right){\displaystyle \frac{\left[\left({\mathfrak{I}}_{1^{+}}^{\alpha }\mathsf{\Psi }\right)\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}\right)+\left({\mathfrak{I}}_{\left({\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}^{-}\right)}^{\alpha }\mathsf{\Psi }\left(1\right)\right)\right]}{2{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}d\mathcal{U}\left(\mathrm{y}\right),{\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}.\end{array}$$

(55)

Where the Definition 2 provides the fractional operators used in (55).

Remark 7.

We obtain (54), if $\alpha =1$ is set in (55).

Definition 18

([58]). Let $\mathsf{\Psi }:J\times \prod \to \Re$ be a convex stochastic process defined on $\mathrm{J}\subseteq (0,\infty )$, satisfying the condition $\mathsf{\Psi }(1,·)=0$. Then, the stochastic divergence associated with ${\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}$ is defined as follows:

$$\begin{array}{c}\hfill {SD}_{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}},.\right)d\mathcal{U}\left(\mathrm{y}\right),{\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}.\end{array}$$

(56)

Remark 8.

When the convex stochastic process in (56) is substituted with an (P, m)-superquadratic stochastic process, the resulting expression defines the stochastic divergence for (P, m)-superquadratic stochastic processes.

Definition 19

([58]). The stochastic $\mathbb{H}.\mathbb{H}$-divergence for ${\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}$ for a convex stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$ on $\mathrm{J}\subseteq (0,\infty )$ is stated as

$$\begin{array}{c}\hfill {SD}_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right){\displaystyle \frac{{\int }_1^{\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}\mathsf{\Psi }(\mathrm{y},.)d\mathrm{y}}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}d\mathcal{U}\left(\mathrm{y}\right),{\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}.\end{array}$$

(57)

Remark 9.

We find stochastic $\mathbb{H}.\mathbb{H}$-divergence for P-superquadratic stochastic process when P-superquadratic stochastic process is substituted for convex stochastic process in (57).

Definition 20

([58]). A convex stochastic process $\mathsf{\Psi }:J\times \prod \to \Re$, defined on $\mathrm{J}\subseteq (0,\infty )$ and satisfies $\mathsf{\Psi }(1,·)=0$, provides the following definition for the stochastic divergence corresponding to ${\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}$ and is called $\mathbb{RL}$ fractional stochastic $\mathbb{H}.\mathbb{H}$-divergence.

$$\begin{array}{c}\hfill {}^{\alpha }SD_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)=\mathsf{\Gamma }(\alpha +1){\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right){\displaystyle \frac{\left[{\mathrm{I}}_{1^{+}}^{\alpha }\left[\mathsf{\Psi }\right]\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}\right)+{\mathrm{I}}_{{\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}^{-}}^{\alpha }\left[\mathsf{\Psi }\right]\left(1\right)\right]}{2{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}d\mathcal{U}\left(\mathrm{y}\right),{\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}.\end{array}$$

(58)

The fractional integral operators appearing in (58) are those provided in Definition 13.

Remark 10.

By replacing the convex stochastic process in (58) with an P-superquadratic stochastic process, we derive the $\mathbb{RL}$ fractional stochastic $\mathbb{H}.\mathbb{H}$ divergence corresponding to the P-superquadratic case.

Here, we present the proofs of the results pertaining to fractional stochastic $\mathbb{H}.\mathbb{H}$-divergence and stochastic $\mathbb{H}.\mathbb{H}$-divergence for P-superquadratic stochastic processes.

Theorem 12.

Let Ψ: $[{\mathcal{U}}_o,{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}]\times \prod \to \Re$ be a mean-square integrable (P, m)-superquadratic stochastic process, and $\mathsf{\Psi }(1,.)=0$, then

$$\begin{array}{cc}\hfill & {SD}_{\mathsf{\Psi }}\left({\displaystyle \frac{1}{2}}{\mathfrak{q}}_o+{\displaystyle \frac{1}{2}}{\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o\right)+{\eta }_1\le 2{SD}_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)\le 2{SD}_{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)-{\eta }_2.\hfill \end{array}$$

(59)

∀ ${\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}$, where

$$\begin{array}{cc}\hfill & {SD}_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(\mathrm{y},·\right)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right),\hfill \\ \hfill & {\eta }_1={\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)\left(2\right)}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}|,·\right)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right),\hfill \\ & \mathrm{and}\hfill \\ & {\eta }_2=\left\{{\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\right({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)\}.\hfill \end{array}$$

holds for all ${\mathcal{U}}_o,{\mathcal{V}}_o\ge 0$ and $m\in (0,1)$.

Proof. 

Consider the $\mathbb{H}.\mathbb{H}$’s inequalities for (P, m)-superquadratic stochastic processes, from Theorem 9:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}},·\right)+{\displaystyle \frac{1+\mathrm{m}}{{\mathcal{V}}_o-{\mathcal{U}}_o}}{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right\}\hfill \\ \hfill & \le \mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{{\mathcal{V}}_o-{\mathcal{U}}_o}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(60)

Now setting ${\mathcal{U}}_o=1$, and ${\mathcal{V}}_o={\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}$, in (60), we obtain

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+{\displaystyle \frac{1+\mathrm{m}}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-{\displaystyle \frac{(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{1}{\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1}}\left\{{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{1}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(\mathrm{y},·\right)d\mathrm{y}\right\}\hfill \\ \hfill & \le \mathsf{\Psi }(1,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathrm{m}}^2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left\{{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m}\right)}{\mathrm{m}\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\right|\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(61)

Since $\mathsf{\Psi }(1,·)=0$, it follows that:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+{\displaystyle \frac{1+\mathrm{m}}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-{\displaystyle \frac{(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{1}{\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1}}\left\{{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}+\mathrm{m}{\int }_{{\displaystyle \frac{1}{\mathrm{m}}}}^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(\mathrm{y},·\right)d\mathrm{y}\right\}\hfill \\ \hfill & \le \mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathrm{m}}^2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{1}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left\{{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m}\right)}{\mathrm{m}\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\right|\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(62)

Multiplying both sides of (62) by ${\mathfrak{q}}_o\left(\mathrm{y}\right)\ge 0$, for all $\mathrm{y}\in \mho$, and integrating the resulting expression over ℧, yields:

$$\begin{array}{cc}\hfill & {\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ & +{\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)(1+\mathrm{m})}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(|{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-{\displaystyle \frac{(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}|,·\right)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ & \le {\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left({\int }_{{\displaystyle \frac{1}{m}}}^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }(\mathrm{y},·)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)+\mathrm{m}{\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left({\int }_{{\displaystyle \frac{1}{m}}}^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{m{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\mathsf{\Psi }\left(\mathrm{y},·\right)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ \hfill & \le \mathrm{m}\{{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)d\mathcal{U}\left(\mathrm{y}\right)+{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ & +{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathrm{m}}^2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)d\mathcal{U}\left(\mathrm{y}\right)\}-\{{\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}}\left({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)\}.\hfill \end{array}$$

(63)

By applying the definitions of stochastic divergence and stochastic $\mathbb{H}.\mathbb{H}$-divergence, we arrive at the desired result.  □

Theorem 13.

Let Ψ: $[{\mathcal{U}}_o,{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}]\times \prod \to \Re$ be a mean-square integrable (P, m)-superquadratic stochastic process, and $\mathsf{\Psi }(1,.)=0$, then

$$\begin{array}{cc}\hfill & {\displaystyle \frac{{SD}_{\mathsf{\Psi }}\left(\frac{1}{2}{\mathfrak{q}}_o+\frac{1}{2}{\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o\right)}{\mathsf{\Gamma }(1+\alpha )}}+{\displaystyle \frac{2\alpha (1+m){\tau }_1}{\mathsf{\Gamma }(1+\alpha )}}\le 2{}^{\alpha }{SD}_m_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)\hfill \\ \hfill & \le {\displaystyle \frac{\mathrm{m}}{\mathsf{\Gamma }(1+\alpha )}}\left\{{SD}_{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|m{\mathfrak{q}}_o)+{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)d\mathcal{U}\left(\mathrm{y}\right)+\mathrm{m}\alpha {SD}_{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|m^2{\mathfrak{q}}_o)\right\}\hfill \\ & -{\displaystyle \frac{\alpha {\tau }_2}{\mathsf{\Gamma }(1+\alpha )}}.\hfill \end{array}$$

∀ ${\mathfrak{p}}_o,{\mathfrak{q}}_o\in \mathbf{P}$, and $\alpha >0$, where

$$\begin{array}{c}\hfill {}^{\alpha }{SD}_m_{HH}^{\mathsf{\Psi }}({\mathfrak{p}}_o\left|\right|{\mathfrak{q}}_o)={\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{2{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}\left[{\mathfrak{I}}_{1^{+}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)\right]d\mathcal{U}\left(\mathrm{y}\right),\end{array}$$

$$\begin{array}{cc}\hfill & {\tau }_1={\int }_{\mho }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}{\int }_1^{{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left(1+\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\tau }_2={\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}\left({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right).\hfill \end{array}$$

holds for all ${\mathcal{U}}_o,{\mathcal{V}}_o\ge 0$ and $m\in (0,1)$.

Proof. 

Consider the fractional $\mathbb{H}.\mathbb{H}$-type inequalities for (P, m)-superquadratic stochastic processes, established via $\mathbb{RL}$ integral operators of order $\alpha >0$, as presented in Theorem 10:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathrm{u}}_o+{\mathcal{V}}_o}{2}},·\right)+{\displaystyle \frac{2(1+\mathrm{m})\alpha }{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}{\int }_{{\mathcal{U}}_o}^{{\displaystyle \frac{{\mathcal{U}}_o+{\mathcal{V}}_o}{2}}}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\mathsf{\Psi }\left(\left|{\displaystyle \frac{\left({\mathcal{U}}_o+{\mathcal{V}}_o\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ & \le {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left[{\mathfrak{I}}_{{{\mathcal{U}}_o}^{+}}^{\alpha }\mathsf{\Psi }({\mathcal{V}}_o,·)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)\right]\hfill \\ \hfill & \le \mathsf{\Psi }({\mathcal{U}}_o,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{U}}_o}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathcal{V}}_o}{{\mathrm{m}}^2}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{\alpha }{{({\mathcal{V}}_o-{\mathcal{U}}_o)}^{\alpha }}}\left\{{\int }_{{\mathcal{U}}_o}^{{\mathcal{V}}_o}{({\mathcal{V}}_o-\mathrm{y})}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{\mathrm{m}({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{({\mathcal{V}}_o-\mathrm{y})({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-{\mathcal{U}}_o)({\mathcal{V}}_o-\mathrm{m}{\mathcal{U}}_o)}{{\mathrm{m}}^2({\mathcal{V}}_o-{\mathcal{U}}_o)}}\right|,·\right)\left)d\mathrm{y}\right\},\hfill \end{array}$$

(64)

Now setting ${\mathcal{U}}_o=1$, and ${\mathcal{V}}_o={\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}$, in (64), we obtain

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},.\right)+{\displaystyle \frac{2\alpha (1+\mathrm{m})}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}{\int }_1^{{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\hfill \\ & \times \mathsf{\Psi }\left(\left|{\displaystyle \frac{\left(1+\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}^{\alpha }}}\left[{\mathfrak{I}}_{1^{+}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)\right]\hfill \\ \hfill & \le \mathsf{\Psi }(1,·)+\mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathrm{m}}^2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{\alpha }{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}\left\{{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(65)

Given that $\mathsf{\Psi }(1,·)=0$, it follows that:

$$\begin{array}{cc}\hfill & \mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},.\right)+{\displaystyle \frac{2\alpha (1+\mathrm{m})}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}{\int }_1^{{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\hfill \\ & \times \mathsf{\Psi }\left(\left|{\displaystyle \frac{\left(1+\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y}\hfill \\ \hfill & \le {\displaystyle \frac{\mathsf{\Gamma }(1+\alpha )}{{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}^{\alpha }}}\left[{\mathfrak{I}}_{1^{+}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)\right]\hfill \\ \hfill & \le \mathrm{m}\left\{\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)+\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathrm{m}}^2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)\right\}\hfill \\ & -{\displaystyle \frac{\alpha }{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}\left\{{\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\right(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right\}.\hfill \end{array}$$

(66)

By multiplying both sides of (66) by ${\mathfrak{q}}_o\left(\mathrm{y}\right)\ge 0$, where $\mathrm{y}\in \mho$, and integrating the resulting expression over ℧, we derive the following:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{\mathsf{\Gamma }(1+\alpha )}}{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},.\right)d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ & +{\displaystyle \frac{2\alpha (1+\mathrm{m})}{\mathsf{\Gamma }(1+\alpha )}}{\int }_{\mho }({\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}{\int }_1^{{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)+{\mathfrak{p}}_o\left(\mathrm{y}\right)}{2{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}\hfill \\ & \times \mathsf{\Psi }\left(\left|{\displaystyle \frac{\left(1+\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}\right)-(\mathrm{m}+1)\mathrm{y}}{2\mathrm{m}}}\right|,·\right)d\mathrm{y})d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ \hfill & \le {\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}\left[{\mathfrak{I}}_{1^{+}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)+{\mathrm{m}}^{\alpha }{\mathfrak{I}}_{{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}^{-}}^{\alpha }\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)\right]d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ \hfill & \le {\displaystyle \frac{\mathrm{m}}{\mathsf{\Gamma }(1+\alpha )}}\{{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{\mathrm{m}{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)d\mathcal{U}\left(\mathrm{y}\right)\hfill \\ & +{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{1}{\mathrm{m}}},·\right)d\mathcal{U}\left(\mathrm{y}\right)+{\int }_{\mho }{\mathfrak{q}}_o\left(\mathrm{y}\right)\mathsf{\Psi }\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathrm{m}}^2{\mathfrak{q}}_o\left(\mathrm{y}\right)}},·\right)d\mathcal{U}\left(\mathrm{y}\right)\}\hfill \\ & -{\displaystyle \frac{\alpha }{\mathsf{\Gamma }(1+\alpha )}}\left\{{\int }_{\mho }{\displaystyle \frac{{\mathfrak{q}}_o\left(\mathrm{y}\right)}{{\left(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1\right)}^{\alpha }}}\right({\int }_1^{{\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}}{\left({\displaystyle \frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}}-\mathrm{y}\right)}^{\alpha -1}(\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{\mathrm{m}(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)+\mathrm{m}\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{y})(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\hfill \\ \hfill & +{\mathrm{m}}^2\mathsf{\Psi }\left(\left|{\displaystyle \frac{(\mathrm{y}-1)(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-\mathrm{m})}{{\mathrm{m}}^2(\frac{{\mathfrak{p}}_o\left(\mathrm{y}\right)}{{\mathfrak{q}}_o\left(\mathrm{y}\right)}-1)}}\right|,·\right)\left)d\mathrm{y}\right)d\mathcal{U}\left(\mathrm{y}\right)\}.\hfill \end{array}$$

(67)

Employing the definitions of stochastic divergence, stochastic $\mathbb{H}.\mathbb{H}$-divergence and $\mathbb{RL}$ fractional stochastic $\mathbb{H}.\mathbb{H}$-divergence, we obtain the required result.  □

Remark 11.

By setting $\alpha =1$ in Theorem 13, we recover the result stated in Theorem 12.

5.1. Assumptions Underlying the Study and Their Limitations

This study is built upon a carefully designed set of assumptions that ensure both mathematical rigor and practical relevance. The new class of (P,m)-superquadratic stochastic processes is treated within the context of mean-square continuity, a general but natural assumption which ensures integrability of the stochastic $\mathbb{RL}$ fractional integrals used in our construction. The random variables and the stochastic processes are assumed to be square-integrable, thus enhancing the stability and robustness of the theoretical results. The derivation of more intricate $\mathbb{H}.\mathbb{H}$-type inequalities finds its basis in the generalized convexity through the m-superquadratic requirement, significantly broadening the range of investigation beyond the conventional techniques based on convexity. Through the use of $\mathbb{RL}$ operators within fractional extensions, the article opens new doors in stochastic fractional calculus and provides a sound basis for future investigation with other fractional operators like Caputo or Hadamard. The methodology through demonstrating its application within information theory, namely through the presentation of innovative stochastic measures of divergence, and thereby highlighting its interdisciplinary importance. To ensure the theoretical contributions are credible, the paper has informative numerical examples and accurate visualizations with the computation times specifically noted. Together, these contributions provide a solid foundation for future work and application, positioning this paper as an important contribution to the new field of stochastic analysis and applications.

5.2. Complexity and Implementation

In order to justify the theoretical results and verify the applicability of our suggested framework to (P, m)-superquadratic stochastic processes, we supply numerical benchmarks for all symbolic calculations and plot outputs. The symbolic procedures employed to create figures and numerical results for the Jensen-type and $\mathbb{H}.\mathbb{H}$ inequalities and their fractional $\mathbb{RL}$ counterparts were run using Mathematica 11.3 on a typical computing platform (Intel Core i7 processor with 16 GB RAM). For illustrative tasks, the measured wall-clock times varied between about 0.142565 and 5.36818 s, depending on the levels of symbolic integration and plotting required. In spite of the symbolic character of the procedures, these findings establish that the calculations remain within efficient and comfortably within practical limits. To allow complete reproducibility and transparency of computations, we share a publicly available GitHub repository with the entire Mathematica notebook: https://github.com/dawoodpk1947/-P-m–superquadratic-stochastic-processes.git. Further, precise timing results can be viewed through: https://github.com/dawoodpk1947/time-for-P-m–superquadratic-stochastic-processes.git (visited on 10 July 2025), enabling the users to navigate and replicate the computational steps stepwise.

6. Conclusions

In this work, we first proposed the notion of (P, m)-superquadratic stochastic processes, which provided a new and mathematically rigorous extension of traditional superquadratic theories in the context of mean-square stochastic calculus. Through rigorous analysis of their structural characteristics, we established extended forms of Jensen’s inequality and $\mathbb{H}.\mathbb{H}$ inequalities, and then further extended these findings to their fractional analogues by stochastic $\mathbb{RL}$ fractional integrals. These results greatly expand the analytical arsenal available for fractional stochastic analysis.

The theoretical results were supplemented by well-conceived graphical representations and tabulated illustrations, confirming both the applicability and the generality of the inequalities suggested. The legitimacy of the framework was also demonstrated further through novel applications in information theory, specifically in constructing new classes of stochastic divergence measures.

In order to facilitate reproducibility and computational transparency, all symbolic procedures, graphical plots, and running times have been well documented and made publicly available. This work not only contributes to the theoretical development of stochastic inequalities but also opens the door for further investigation in fractional stochastic processes and their inter-disciplinary applications.