Local Fractional Perspective on Weddle’s Inequality in Fractal Space
Abstract
1. Introduction
Yang Local Fractional Calculus
- ,
- ,
- ,
- .
- How can the error terms of Weddle’s rule be established for local fractional differentiable mappings? Mathematically,
- How different generalized classes of mappings can be used to evaluate the bounds of the above inequality?
- What are the applications of the proposed bounds?
- How can the bounds of several local fractional integrals be found incorporated with the proposed inequalities?
2. Fractal Estimates of Weddle’s Inequality
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- .
3. Applications
3.1. Applications to Means
- 1.
- The generalized arithmetic mean:
- 2.
- The generalized weighted arithmetic mean:
- 3.
- The generalized log--mean:
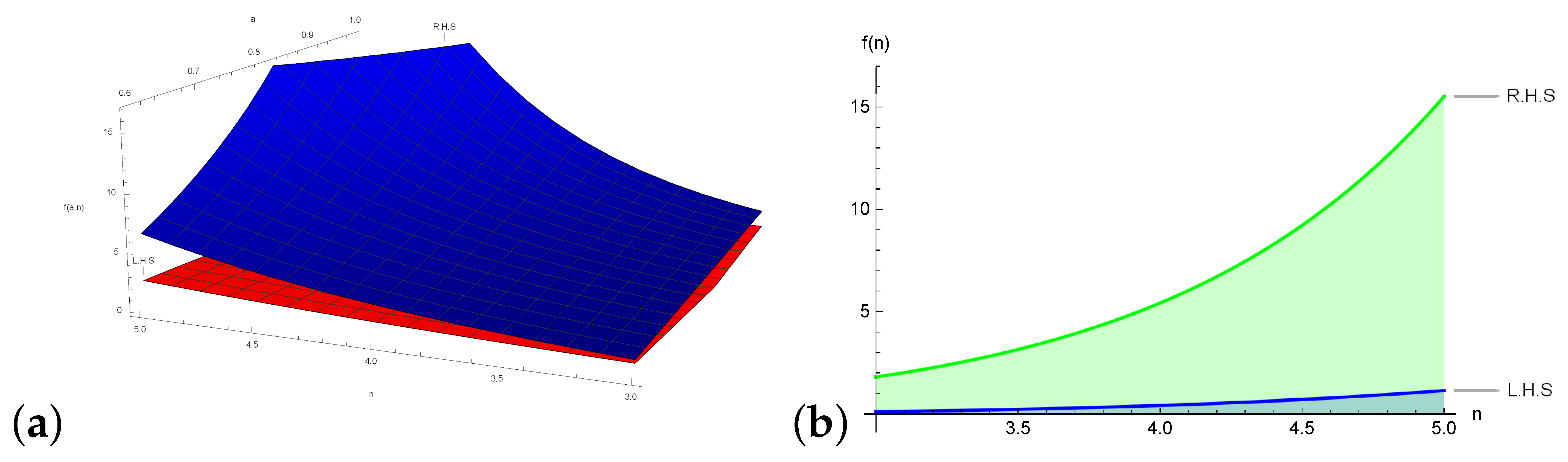
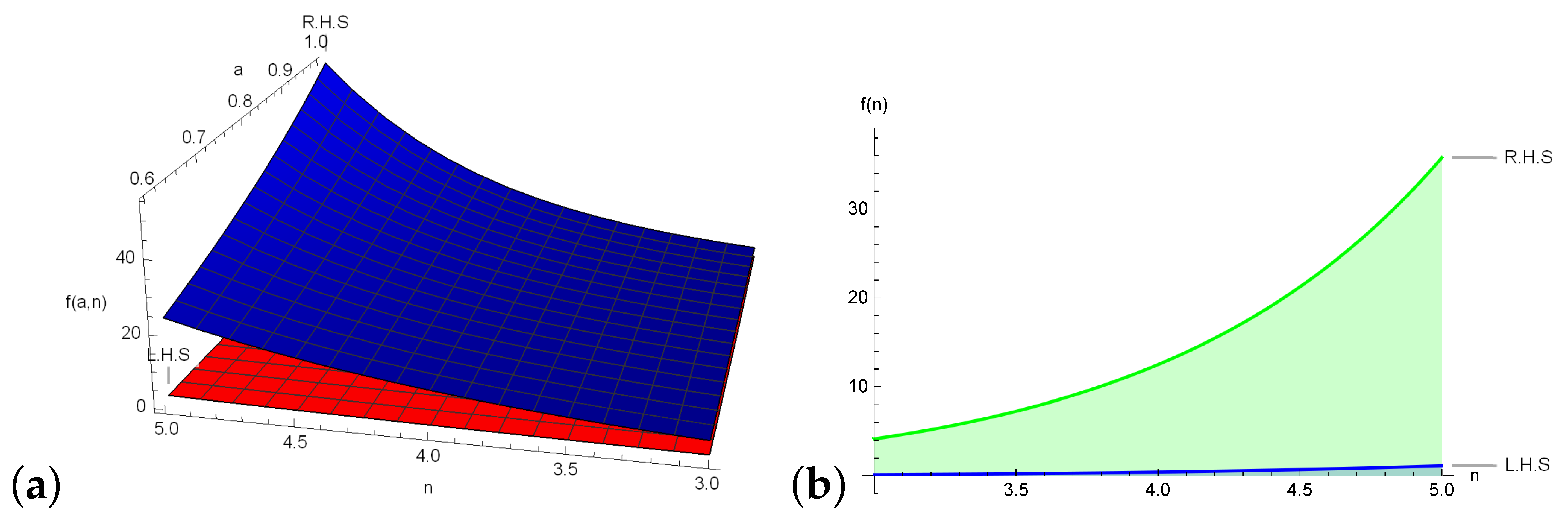
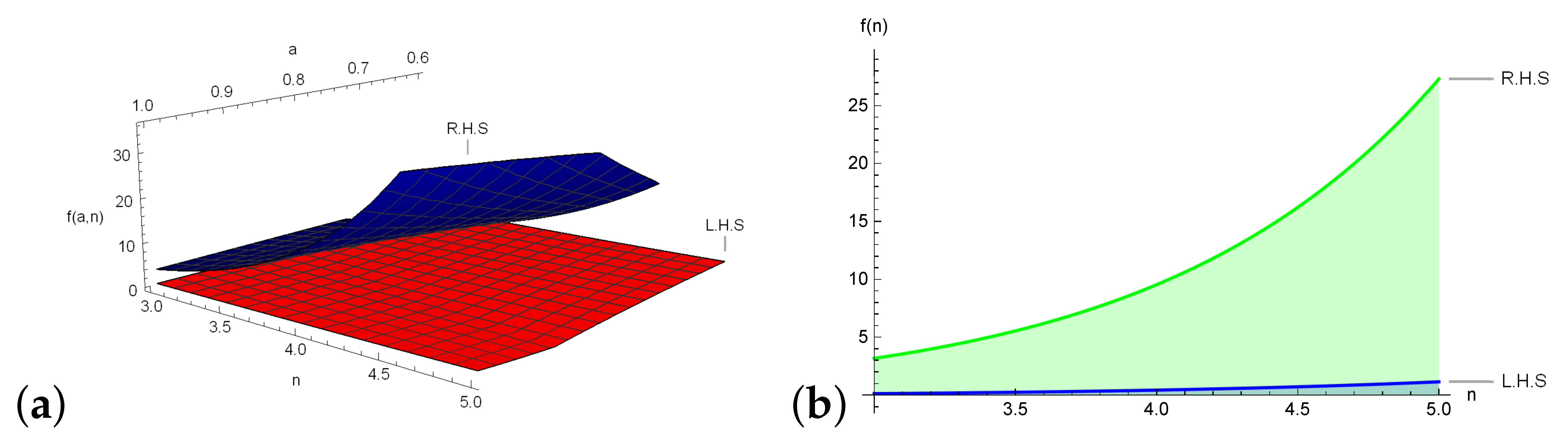
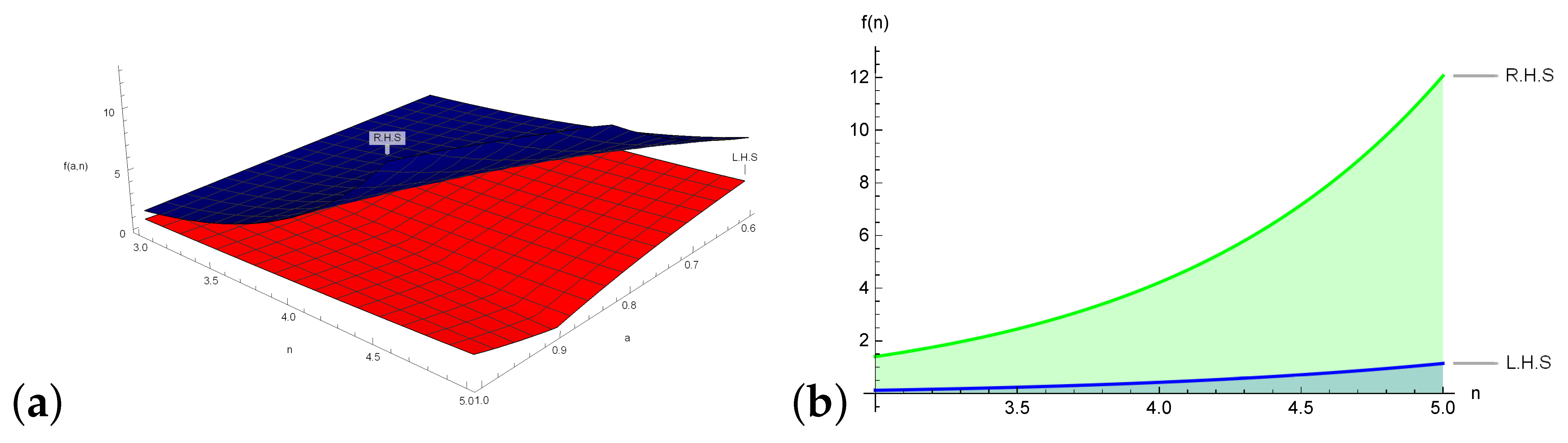
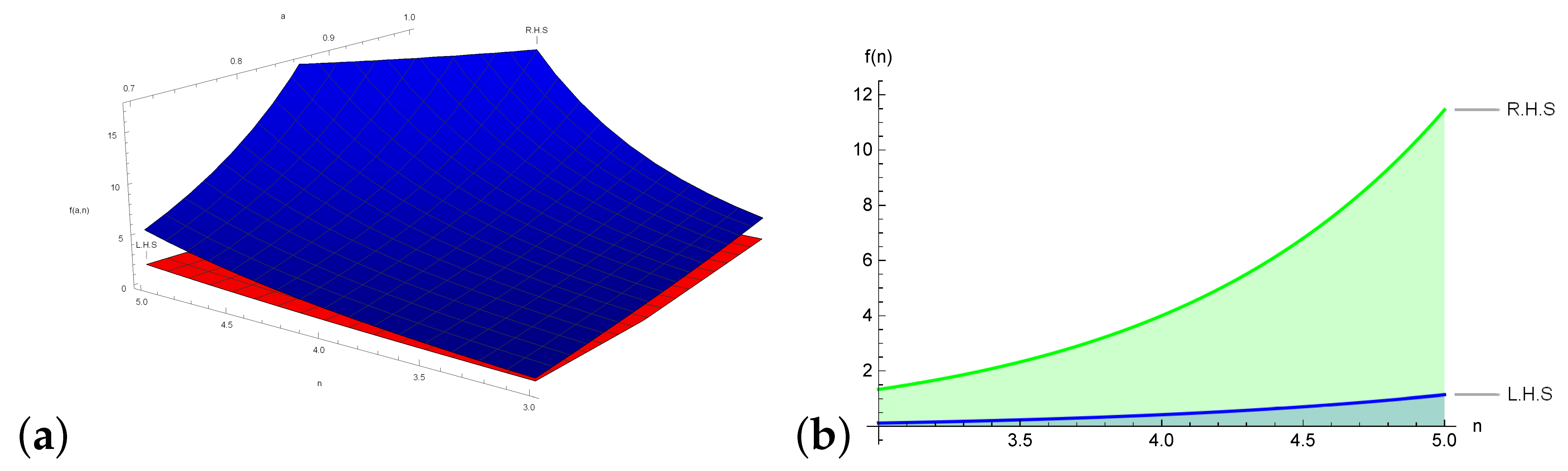
3.2. Error Bounds
3.3. Applications to Probability
- It is a known fact that various definite integrals cannot be evaluated through analytical techniques neither in classical nor in Yang local fractional calculus. They are approximated through Newton–Cotes schemes. In the aforementioned sections, we have provided the error bounds of definite integrals approximated through generalized Weddle’s incorporated with various classes of mappings. Our results provide the upper bounds of error terms for first-order local differentiable mapping. Additionally, from these bounds one can compute the upper bounds of definite integrals. For this, we apply Theorem 7 for over with . Then we get . Note that this bound can be refined by increasing the order of differentiability. Through the application of our proposed inequalities, one can establish the bounds and relation between special functions like q-digamma function, modified Bessel functions and Beta functions. For further detail, consult [29,30,31].
- Adopting the technique of [32], several new iterative methods to solve non-linear equations can be obtained. To discuss the convergence and dynamic analysis of proposed methods will be a new challenge for researchers.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dwilewicz, R.J. A short history of convexity. Differ. Geom.-Dyn. Syst. 2009, 112. [Google Scholar]
- Dragomir, S.S.; Agarwal, R. Two inequalities for differentiable mappings and applications to special means of real numbers and to trapezoidal formula. Appl. Math. Lett. 1998, 11, 91–95. [Google Scholar] [CrossRef]
- Alomari, M.; Darus, M.; Dragomir, S.S. New inequalities of Simpson’s type for s–convex functions with applications. Res. Rep. Collect. 2009, 12. [Google Scholar]
- Awan, M.U.; Noor, M.A.; Noor, K.I. Hermite-Hadamard inequalities for exponentially convex functions. Appl. Math. Inf. Sci. 2018, 12, 405–409. [Google Scholar] [CrossRef]
- Iscan, I. Hermite-Hadamard type inequalities for r1–convex functions. Int. J. Anal. Appl. 2016, 11, 137–145. [Google Scholar]
- Mitrinovic, D.S.; Lackovic, I.B. Hermite and convexity. Aequationes Math. 1985, 28, 229–232. [Google Scholar] [CrossRef]
- Beckenbach, E.F. Convex functions. Bull. Am. Math. Soc. 1948, 54, 439–460. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Agarwal, R.P.; Cerone, P. On Simpson’s inequality and applications. RGMIA Res. Rep. Collect. 1999, 2. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Courier Corporation: New York, NY, USA, 2007. [Google Scholar]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science Publisher: New York, NY, USA, 2012. [Google Scholar]
- Mo, H.; Sui, X. Generalized s–convex functions on fractal sets. Abstr. Appl. Anal. 2014, 2014, 254737. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Budak, H. On Fejér type inequalities via local fractional integrals. J. Fract. Calc. Appl. 2017, 8, 59–77. [Google Scholar]
- Sarikaya, M.Z.; Erden, S.; Budak, H. Some generalized Ostrowski type inequalities involving local fractional integrals and applications. Adv. Inequal. Appl. 2016. [Google Scholar]
- Sarikaya, M.Z.; Tunc, T.; Budak, H. On generalized some integral inequalities for local fractional integrals. Appl. Math. Comput. 2016, 276, 316–323. [Google Scholar] [CrossRef]
- Erden, S.; Sarikaya, M.Z. Generalized Pompeiu type inequalities for local fractional integrals and its applications. Appl. Math. Comput. 2016, 274, 282–291. [Google Scholar] [CrossRef]
- Almutairi, O.; Kilicman, A. Generalized integral inequalities for Hermite-Hadamard-type inequalities via s–convexity on fractal sets. Mathematics 2019, 7, 1065. [Google Scholar] [CrossRef]
- Luo, C.; Wang, H.; Du, T. Fejér-Hermite-Hadamard type inequalities involving generalized h–convexity on fractal sets and their applications. Chaos Solitons Fractals 2020, 131, 109547. [Google Scholar] [CrossRef]
- Sun, W.; He, X. Hermite–Hadamard type inequalities and convex functions in signal processing. IEEE Access 2024, 12, 92906–92918. [Google Scholar] [CrossRef]
- Butt, S.I.; Yousaf, S.; Younas, M.; Ahmad, H.; Yao, S.W. Fractal Hadamard-Mercer-type inequalities with applications. Fractals 2022, 30, 2240055. [Google Scholar] [CrossRef]
- Luo, C.; Yu, Y.; Du, T. An improvement of Hölder integral inequality on fractal sets and some related Simpson-like inequalities. Fractals 2021, 29, 2150126. [Google Scholar] [CrossRef]
- Alsharari, F.; Fakhfakh, R.; Lakhdari, A. On fractal-fractional Simpson-type inequalities: New insights and refinements of classical results. Mathematics 2024, 12, 3886. [Google Scholar] [CrossRef]
- Meftah, B.; Lakhdari, A.; Saleh, W.; Kiliçman, A. Some new fractal Milne-type integral inequalities via generalized convexity with applications. Fractal Fract. 2023, 7, 166. [Google Scholar] [CrossRef]
- Liu, Q.; Rukhsar; Awan, M.U.; Bin-Mohsin, B.; Javed, M.Z.; Ciurdariu, L.; Meftah, B. Bridging pre-invex mappings and fractional integrals: A pathway to iterative schemes via error boundaries of Maclaurin’s rule. Fractal Fract. 2024, 8, 734. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Awan, M.U.; Asif, U.; Javed, M.Z.; Budak, H. Advances in Ostrowski–Mercer like inequalities within fractal space. Fractal Fract. 2023, 7, 689. [Google Scholar] [CrossRef]
- Javed, M.Z.; Awan, M.U.; Bin-Mohsin, B.; Budak, H.; Dragomir, S.S. Some classical inequalities associated with generic identity and applications. Axioms 2024, 13, 533. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Asif, U.; Javed, M.Z.; Awan, M.U.; Almalki, Y.; Alsalami, O.M. A new approach to error inequalities: From Euler–Maclaurin bounds to cubically convergent algorithm. AIMS Math. 2024, 9, 35885–35909. [Google Scholar] [CrossRef]
- Wang, Y.; Asif, U.; Javed, M.Z.; Awan, M.U.; Meftah, B.; Kashuri, A.; Noor, M.A. Numerical and visual analysis of Maclaurin type inequalities in the setting of generalized fractional calculus and applications. J. Math. Comput. Sci. 2025, 38, 281–297. [Google Scholar] [CrossRef]
- Budak, H.; Sarikaya, M.Z.; Yildirim, H. New inequalities for local fractional integrals. Iran. J. Sci. Technol. Trans. A Sci. 2017, 41, 1039–1046. [Google Scholar] [CrossRef]
- Tariq, M.; Ahmad, H.; Shaikh, A.A.; Ntouyas, S.K.; Hınçal, E.; Qureshi, S. Fractional Hermite–Hadamard-type inequalities for differentiable preinvex mappings and applications to modified Bessel and q-digamma functions. Math. Comput. Appl. 2023, 28, 108. [Google Scholar] [CrossRef]
- Mohammed, P.O.; Sarikaya, M.Z.; Baleanu, D. On the generalized Hermite–Hadamard inequalities via the tempered fractional integrals. Symmetry 2020, 12, 595. [Google Scholar] [CrossRef]
- Hwang, S.R.; Yeh, S.Y.; Tseng, K.L. On some Hermite–Hadamard inequalities for fractional integrals and their applications. Ukr. Math. J. 2020, 72, 407–424. [Google Scholar] [CrossRef]
- Javed, M.Z.; Awan, M.U.; Bin-Mohsin, B.; Treanţă, S. Upper bounds for the remainder term in Boole’s quadrature rule and applications to numerical analysis. Mathematics 2024, 12, 2920. [Google Scholar] [CrossRef]
- Dragomir, S.S. Approximating the finite Hilbert transform via Ostrowski type inequalities for absolutely continuous functions. Bull. Korean Math. Soc. 2002, 39, 543–559. [Google Scholar] [CrossRef][Green Version]
- Liu, W.; Gao, X.; Wen, Y. Approximating the finite Hilbert transform via some companions of Ostrowski’s inequalities. Bull. Malays. Math. Sci. Soc. 2016, 39, 1499–1513. [Google Scholar] [CrossRef]
- Chen, G.S. The local fractional Hilbert transform in fractal space. J. Appl. Eng. Sci. 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Asif, U.; Awan, M.U.; Javed, M.Z.; Khan, A.G.; Bin-Asfour, M.; Albalawi, K.S. Local Fractional Perspective on Weddle’s Inequality in Fractal Space. Fractal Fract. 2025, 9, 662. https://doi.org/10.3390/fractalfract9100662
Wang Y, Asif U, Awan MU, Javed MZ, Khan AG, Bin-Asfour M, Albalawi KS. Local Fractional Perspective on Weddle’s Inequality in Fractal Space. Fractal and Fractional. 2025; 9(10):662. https://doi.org/10.3390/fractalfract9100662
Chicago/Turabian StyleWang, Yuanheng, Usama Asif, Muhammad Uzair Awan, Muhammad Zakria Javed, Awais Gul Khan, Mona Bin-Asfour, and Kholoud Saad Albalawi. 2025. "Local Fractional Perspective on Weddle’s Inequality in Fractal Space" Fractal and Fractional 9, no. 10: 662. https://doi.org/10.3390/fractalfract9100662
APA StyleWang, Y., Asif, U., Awan, M. U., Javed, M. Z., Khan, A. G., Bin-Asfour, M., & Albalawi, K. S. (2025). Local Fractional Perspective on Weddle’s Inequality in Fractal Space. Fractal and Fractional, 9(10), 662. https://doi.org/10.3390/fractalfract9100662





