1. Introduction
With the continuous development of marine resource exploitation and deep-sea exploration, autonomous underwater vehicles (AUVs) have become indispensable unmanned platforms in modern ocean engineering. Owing to their autonomous control and long-endurance capabilities, AUVs have been widely deployed in tasks such as seabed mapping, pipeline inspection, resource exploration, and ocean environmental monitoring [
1,
2,
3]. In recent years, multi-AUV cooperative formation control has attracted increasing attention. By enabling cooperative operations among multiple agents, multi-AUV systems can significantly enhance mission efficiency, spatial coverage, and system robustness in uncertain and dynamic marine environments. However, due to strong nonlinearities, environmental uncertainties, dynamic communication topologies, and limitations of underwater acoustic bandwidth [
4,
5,
6], achieving accurate formation tracking and coordination remains a challenging problem.
The primary objectives of AUV formation control are precise trajectory tracking and stable formation maintenance. However, the intrinsic characteristics of AUVs—including nonlinear dynamics, strong coupling effects, and underactuation—introduce significant modeling uncertainties such as parameter disturbances, unmodeled dynamics, and external ocean disturbances. These uncertainties severely compromise both control accuracy and system stability. To mitigate these effects, a variety of robust control and disturbance observation strategies have been developed, including PID control [
7,
8,
9], fuzzy control [
10,
11], sliding mode control (SMC) [
12,
13,
14], neural network compensation [
15,
16,
17], sliding mode observer [
18,
19,
20], extended state observers (ESO) [
9,
21,
22], and nonlinear disturbance observers [
12,
13], while [
14] employed Linear Active Disturbance Rejection Control (LADRC) to observe and provide feedforward compensation for lumped disturbances. Among them, sliding mode control has been extensively applied to underwater systems due to its strong robustness and low dependency on model accuracy; however, the well-known chattering phenomenon limits its control precision. To alleviate this problem, terminal sliding mode control [
23,
24,
25] and high-order sliding mode control [
26,
27] have been introduced to improve convergence speed while suppressing chattering. Meanwhile, disturbance estimation approaches based on neural networks and observers have demonstrated superior robustness. For instance, adaptive radial basis function neural networks (RBFNNs) have been utilized for real-time disturbance estimation [
15,
16]; extended state observers have been applied to estimate and compensate for lumped disturbances to enhance tracking accuracy [
9,
28]; and nonlinear disturbance observers combined with SMC have achieved stronger robustness [
12,
13]. Furthermore, finite-time and fixed-time disturbance observers [
29,
30] have improved estimation rapidity and accuracy. Recently, fractional calculus has been introduced into sliding mode control to enrich the controller design space. The fractional operator provides a memory effect that allows smoother transition in both time and frequency domains, effectively suppressing chattering and enhancing disturbance attenuation. Therefore, fractional-order SMC offers potential advantages in terms of robustness, smoothness, and dynamic response [
19,
20], while fractional-order sliding mode or fuzzy-neural composite controllers [
31] enhance system dynamic response and disturbance rejection. Motivated by these findings, this study proposes an integrated fractional-order sliding mode observation–control framework (FOSMO–FOTSMC), which leverages the memory–attenuation characteristics of fractional calculus to smooth high-frequency switching in the frequency domain and accelerate error convergence in the time domain. This framework achieves zero residual disturbance estimation within a prescribed time while effectively mitigating chattering.
In terms of formation control structures, the leader–follower method has been widely adopted due to its simplicity and ease of implementation, where the leader provides global trajectory information and followers adjust their states accordingly [
15]. However, single-leader failures may cause formation collapse. To address this, multi-leader, virtual leader, and redundant chain strategies [
32,
33] have been introduced, improving robustness at the cost of increased communication complexity. The Virtual Structure method treats the formation as a rigid body to achieve high precision [
34], but its rigid assumption limits shape flexibility. To improve adaptability, a “virtual path + parameter consensus” mechanism was proposed [
19,
35], allowing each AUV to follow an individual trajectory while coordinating parameters, though it remains dependent on pre-defined global paths, compromising full decentralization. Alternatively, consensus-based approaches, founded on graph theory, achieve distributed coordination through local information exchange [
22,
36,
37,
38], offering good scalability but potentially suffering from oscillations under time delays, packet loss, or topology variations. The behavior-based method [
39,
40] employs rule-based individual behaviors (e.g., target seeking, collision avoidance) to achieve group coordination but lacks global stability guarantees. On the other hand, considering the limited bandwidth and energy-sensitive engineering constraints of underwater acoustic communication, traditional periodic communication strategies often result in redundant communication and energy waste. Consequently, event-triggered communication (ETC) has gradually emerged as a frontier in distributed control research [
16,
29,
41]. This mechanism significantly reduces communication load by exchanging information only when trigger conditions are met. Related research includes intelligent control based on the dynamic event-triggered mechanism (DETM) [
17], which utilizes the DETM to optimize communication resource allocation. Combined with finite-time sliding mode Zeno-resistant communication strategies [
25] and energy-optimization methods based on fixed-time convergence [
29,
41], these approaches achieve a favorable balance between performance and communication efficiency.
Inspired by these works, this paper proposes a hierarchical consensus-based formation control framework integrating dynamic event-triggered communication. The framework adopts a “upper-layer consensus-lower-layer tracking” decoupled design: the upper layer employs a distributed consensus protocol to generate reference trajectories under local communication topology, while the lower layer utilizes the FOSMO-FOTSMC structure for precise tracking and robust disturbance rejection. Furthermore, an adaptive dynamic-threshold event-triggered strategy is introduced to regulate communication frequency according to real-time state errors, achieving a “dense-near, sparse-far” communication policy that optimizes both energy consumption and stability.
The main contributions of this paper are given by the following:
(1) Fractional-order sliding mode observation–control integrated design: An integrated fractional-order sliding mode control method (FOSMO-FOTSMC) is proposed, which utilizes the memory properties of fractional-order calculus to achieve precise estimation and compensation of lumped disturbances. This approach enhances the trajectory tracking accuracy and disturbance rejection capability of AUVs in uncertain environments, providing a solid foundation for reliable formation control.
(2) Hierarchical consensus-based coordination architecture: A distributed control structure with “upper-layer coordination and lower-layer tracking” is designed. The upper layer generates reference trajectories based on consensus protocols, while the lower layer performs precise tracking and compensation. This decouples cooperative control tasks from tracking, enhancing the system’s fault tolerance against individual failures and improving the formation system’s scalability and flexibility in reconfiguring formations.
(3) Dynamic event-triggered communication mechanism: An adaptive dynamic threshold triggering strategy is proposed, adjusting trigger conditions based on real-time errors. This approach effectively reduces communication load and energy consumption while ensuring formation stability.
(4) Stability and performance validation: The stability and convergence of the proposed control strategy are rigorously proven using the Lyapunov stability theory. Simulations validate its superior performance in robustness, formation maintenance, and communication energy efficiency.
It is worth emphasizing the key distinctions between this work and our prior research [
19]. Reference [
19] focused on a path-following formation problem, where the coordination was achieved through consensus on a single path parameter. In contrast, this paper addresses a more general trajectory-tracking formation problem. We develop a novel distributed virtual trajectory generator, which, combined with a dynamic event-triggered communication mechanism, forms a hierarchical control architecture. This new architecture not only enhances system robustness against dynamic topology changes but also significantly improves communication efficiency. The remainder of this paper is organized as follows:
Section 2 introduces the necessary preliminaries and problem formulation.
Section 3 presents the design of the proposed AUV observer–controller framework and provides stability analysis.
Section 4 details the hierarchical formation control architecture, including the consensus-based trajectory generation method, dynamic event-triggered communication strategy, and theoretical proofs.
Section 5 presents numerical simulations and discusses the results. Finally,
Section 6 concludes the paper and outlines future research directions.
4. Formation Controller Design
4.1. Controller Principle
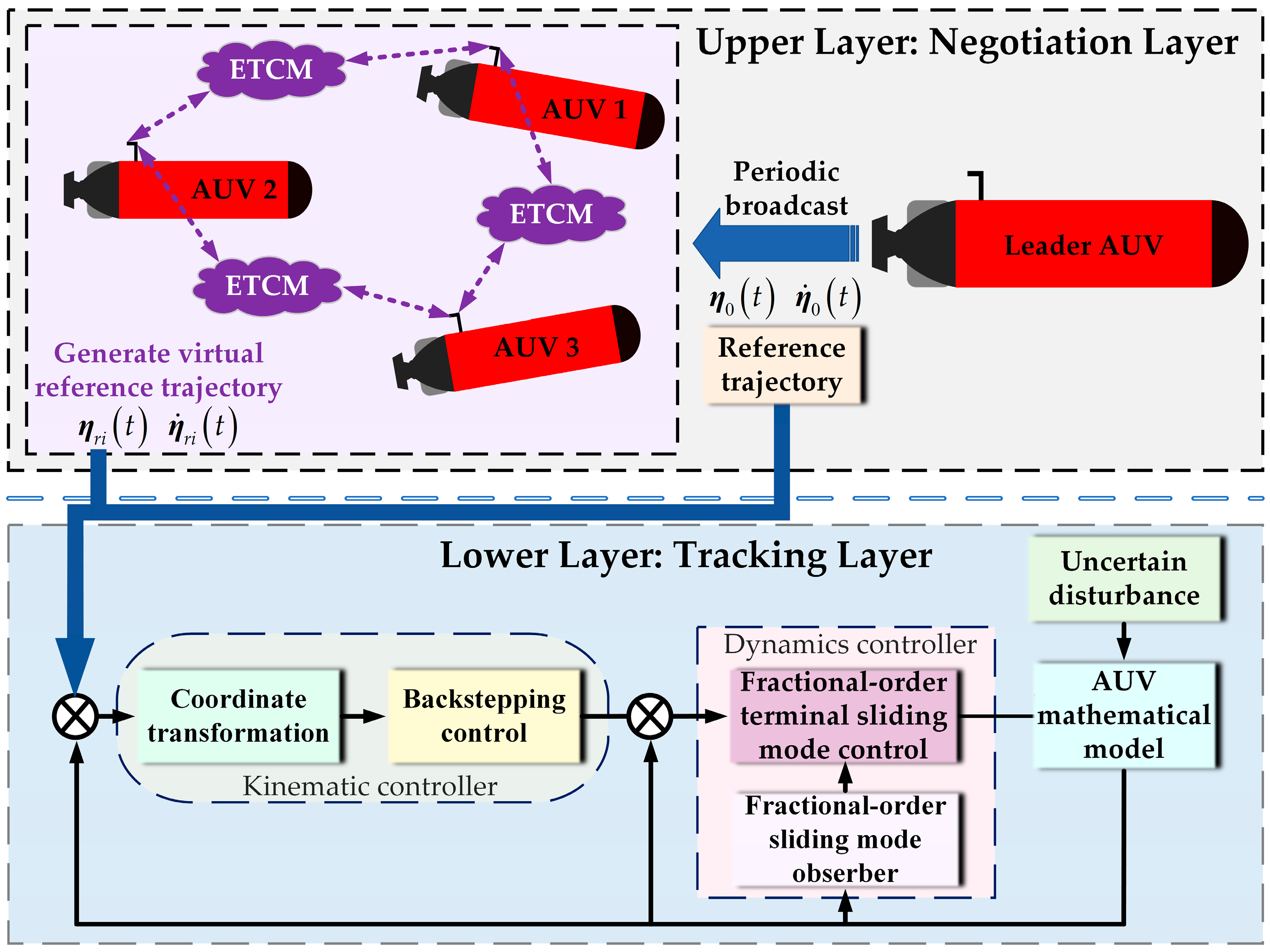
The proposed formation controller adopts a hierarchical “upper-layer consensus—lower-layer tracking” architecture, as illustrated in
Figure 3. The core idea is to decouple the leader’s global guidance information from the followers’ local cooperative information. Key data are exchanged on demand via a dynamic event-triggered communication mechanism, effectively reducing redundant communication compared with conventional periodic broadcasting, while the consensus protocol ensures formation accuracy and synchronization.
At the upper consensus layer, the leader AUV periodically broadcasts its state information to all followers. Each follower communicates only with its predefined neighbors when the event-triggering condition is satisfied. Using the locally received neighbor information, each follower generates its virtual reference trajectory through a distributed dynamic consensus algorithm, achieving cooperative trajectory coordination and global synchronization within the formation. This design exhibits strong fault tolerance: if a single AUV fails, its tracking error affects only its own local performance and does not propagate to adjacent agents through the control law. Other AUVs can still negotiate their desired trajectories through local communication, maintaining overall formation integrity. Moreover, formation reconfiguration can be achieved simply by adjusting relative offsets in the upper-layer consensus process without modifying the lower-layer tracking controller, enhancing flexibility and robustness. At the lower tracking layer, each AUV uses its locally generated virtual trajectory as a reference and executes a fractional-order sliding mode observer (FOSMO) combined with a fractional-order terminal sliding mode controller (FOTSMC). This robust control law guarantees finite-time convergence of the AUV’s actual motion to the reference trajectory, thereby achieving high-precision formation control in three-dimensional space.
4.2. Consensus-Based Trajectory Generation
The consensus-based trajectory generation follows a distributed update law that enables coordinated motion among AUVs. Each follower iteratively adjusts its virtual reference trajectory based on relative state discrepancies with its neighbors within the dynamically changing communication topology. The update law is designed as
where
denotes each follower AUV’s reference trajectory, and serves as a virtual reference state used to construct the upper-layer consensus model.
represents the leader’s desired reference trajectory.
denotes the communication neighbor set of AUV
i.
is the element of the adjacency matrix.
represents the leader’s connectivity weight.
denotes the desired relative offset between follower
i and follower
j as determined by the formation geometry, and
represents the desired relative offset between follower
i and the leader.
and
are tuning coefficients.
This consensus protocol ensures that all followers asymptotically synchronize their virtual trajectories with the leader’s reference, thereby maintaining both geometric formation integrity and motion coordination—even in the presence of switching communication topologies or localized link failures.
Assumption 7. The communication topology graph G among followers is undirected and connected.
4.3. Dynamic Event-Triggered Communication Mechanism
In multi-AUV formation systems, the event-triggered mechanism (ETM) aims to balance formation consistency and communication efficiency. It minimizes unnecessary underwater acoustic transmissions—thereby reducing energy consumption and channel congestion—while ensuring that state synchronization occurs in time to maintain formation stability. For each follower, define its state error as
where the variable
is introduced to measure the deviation between the current state of an AUV and its last broadcasted state, serving as the core basis for triggering communication.
denotes the most recent triggering instant determined by the triggering law,
represents the broadcasted value of AUV i at the last triggering instant
, and
is its current actual value
Remark 7. A larger value of indicates that the AUV’s current state has significantly deviated from its previously broadcasted state. If neighboring AUVs continue to update based on outdated information, their trajectories will diverge.
The threshold setting adopts an adaptive strategy: during the initial stage of system operation, since tracking errors are relatively large, the threshold is relaxed to reduce redundant communications. As the system converges and the tracking error decreases, the threshold is gradually tightened to improve control precision. The dynamic event-triggering law is designed as
where
is the designed dynamic threshold that varies according to changes in state deviation. The terms
and
represent the lower and upper bounds of the threshold, respectively.
is confined to the interval
through saturation to ensure smooth variation, balancing both stability and feasibility.
,
, and
are tuning coefficients. A small constant
is introduced and maintained after convergence to prevent
from becoming exactly zero.
Remark 8. To prevent abrupt jumps in variable , it is smoothed using the formula , where is the threshold value at the previous instant and is a tuning coefficient.
The above design exhibits the following characteristics: during the initial phase with large errors, a wider threshold effectively reduces unnecessary event triggers; as the error gradually converges, the threshold automatically shrinks to ensure final control precision and stability. By setting upper and lower bounds on the threshold, the system avoids performance degradation due to overly large or small thresholds. Smooth and continuous variation in the threshold prevents controller oscillations caused by abrupt changes. Furthermore, an exponential decay term is introduced to further enhance the system’s convergence speed.
4.4. Stability of ETM and Lower Bound on Triggering Intervals Analysis
To ensure the practical applicability of the proposed distributed formation control strategy, this section rigorously analyzes the stability of the closed-loop system and the feasibility of the communication mechanism.
Let the consensus deviation variable of follower AUV
i (
i = 1,2,…,
N) be denoted as
, and the control objective is defined as
According to the triggering instants determined by the dynamic event-triggered mechanism, the consensus trajectory update rule in Equation (34) can be rewritten as
where
denotes the broadcast deviation at triggering instant
.
Theorem 4. Consider the multi-AUV formation system. If the consensus trajectory update rule satisfies Equation (39), then the consensus deviation variable will converge to zero, indicating that the system is asymptotically stable.
Proof of Theorem 4. Taking the derivative with respect to
and substituting Equation (39) yields
A Lyapunov function is designed as
Taking the derivative of Equation (41), bringing Equation (40) into it yields
From Equations (37) and (38), it is known that the error between the broadcast deviation
and the current value
at the triggering instant satisfies
, where
is the lower bound of the triggering threshold. Thus, using the approximation
, substituting into Equation (42) gives
Define the extended Laplacian matrix
, where
is composed of
and
is the leader connectivity matrix. Since
and
B are symmetric matrices,
is also symmetric and has a minimum eigenvalue
such that
□
Zeno behavior, characterized by excessively frequent event triggers in a short time leading to system failure, must be avoided by proving the existence of a strictly positive lower bound for the triggering interval [
41,
46].
Theorem 5. Under the dynamic event-triggered law (36) proposed in this paper, for any AUV i, the time interval between two consecutive triggering instants has a strictly positive lower bound, i.e., no Zeno behavior occurs in the system.
Proof of Theorem 5. Let
be the
triggering instant of AUV
i, and the subsequent triggering instant be
. The triggering interval is defined as
. The state error is defined as
Taking the derivative of Equation (45) yields
. Since
converges,
has an upper bound. Let
and
, then we obtain
.
At the triggering instant
, the error is reset, i.e.,
. According to the mean value theorem for integrals, for any
, we obtain
When
, the triggering condition is satisfied with
. Combining this with
as defined in Equation (37), we obtain
Since and , it follows that , implying the existence of a strictly positive lower bound for the triggering interval. Therefore, no Zeno behavior occurs in the system. □
4.5. Overall Closed-Loop System Stability
The proposed control framework constitutes a hierarchical closed-loop system. While the preceding theorems have established the stability of individual components, this subsection provides a synthesized stability analysis for the overall integrated system, explicitly considering the interplay between the sliding mode observer, controller, and the time-varying network.
The overall formation error for follower AUV i can be decomposed into two distinct components:
- 1.
The consensus error is , which is governed by the upper-layer dynamics.
- 2.
The tracking error is , which is governed by the lower-layer dynamics.
The stability of the overall system is analyzed as follows:
1. Upper-layer stability with event-triggered communication: As proven in Theorem 4 and Theorem 5, the distributed consensus protocol under the dynamic event-triggered mechanism guarantees that the consensus error is asymptotically stable, and the system does not exhibit Zeno behavior. Considering bounded perturbations present in practical systems, the consensus error is uniformly ultimately bounded (UUB). A key feature of this mechanism is that the broadcasted reference trajectory is held constant between triggering instants. This introduces a piecewise-constant nature to the input of the lower-level tracker. However, the triggering law (Equation (36)) is specifically designed to ensure that the resulting error . Consequently, the actual input to the lower-level controller is a bounded signal with bounded discontinuities.
2. Lower-layer stability with sliding mode observer: The lower-level tracking loop for each AUV is a closed-loop system comprising the plant dynamics, the FOSMO (Theorem 2), and the FOTSMC (Theorem 3). Theorem 2 establishes that the disturbance estimation error of the FOSMO converges to a small region around zero in fixed time. Building upon this accurate estimation, Theorem 3 proves that the velocity tracking error also converges in finite time. This finite-time convergence property is strong and implies that the lower-level tracking loop is input-to-state stable and possesses inherent robustness to bounded input variations. Therefore, even when the reference input is piecewise-constant due to the event-triggered mechanism, the resulting tracking error remains UUB. The robust sliding mode controller and the disturbance-estimating observer effectively treat the jumps in the reference signal as a form of bounded, additive disturbance.
3. Integrated system performance: The overall formation error is a superposition of the UUB tracking error and the UUB consensus error. Therefore, the total formation error is also UUB. This proves the practical stability of the entire multi-AUV formation control system. The event-triggered communication successfully reduces network usage at the cost of introducing bounded, non-smooth variations in the reference trajectories, but it does not compromise the ultimate boundedness of the overall system.
4. Robustness to time-varying dynamics: The stability of the overall closed-loop system holds in the presence of the time-varying factors considered in this work:
Time-varying disturbances: The FOSMO (Theorem 2) is specifically designed to estimate and compensate for time-varying lumped disturbances in finite time, ensuring the robustness of the lower-level loop.
Time-varying communication topology: The stability of the upper-layer consensus (Theorem 4) is analyzed under a Laplacian matrix, provided the graph remains jointly connected.
In conclusion, the decoupled hierarchical design, combined with the finite-time and UUB stability properties of its components, guarantees that the overall closed-loop system, integrating the sliding mode observer, controller, and event-triggered communication, is uniformly ultimately bounded stable under realistic time-varying conditions.
5. Numerical Simulation and Result Analysis
To verify the proposed control framework in terms of trajectory-tracking accuracy, disturbance estimation capability, and system robustness, two simulation cases are conducted. The simulations utilized the team’s nonlinear underactuated AUV model [
9,
12,
13,
19], with the complete set of parameters provided in
Appendix A. All simulations were executed within the MWORKS 2024a (Suzhou Tongyuan Software, Suzhou, China).
5.1. Case 1: Single AUV Tracking Performance Verification
This case validates the tracking and disturbance estimation performance of the proposed FOSMO–FOTSMC control structure. The AUV follows a three-dimensional figure-eight helical trajectory, and four control methods are compared as follows:
Method 1: Integer-order SMO + conventional sliding mode control (baseline).
Method 2: FOSMO + terminal sliding mode control (controller improvement only).
Method 3: ESO + FOTSMC (observer improvement only).
Method 4: FOSMO + FOTSMC (proposed method).
The parameterized equation of the trajectory is given by the following:
The initial position is
, and the initial velocity is
. The applied environmental disturbance is given by
The controller parameters are as follows:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
. The detailed controller structures and parameters of the three methods used for comparison are provided in
Appendix B.
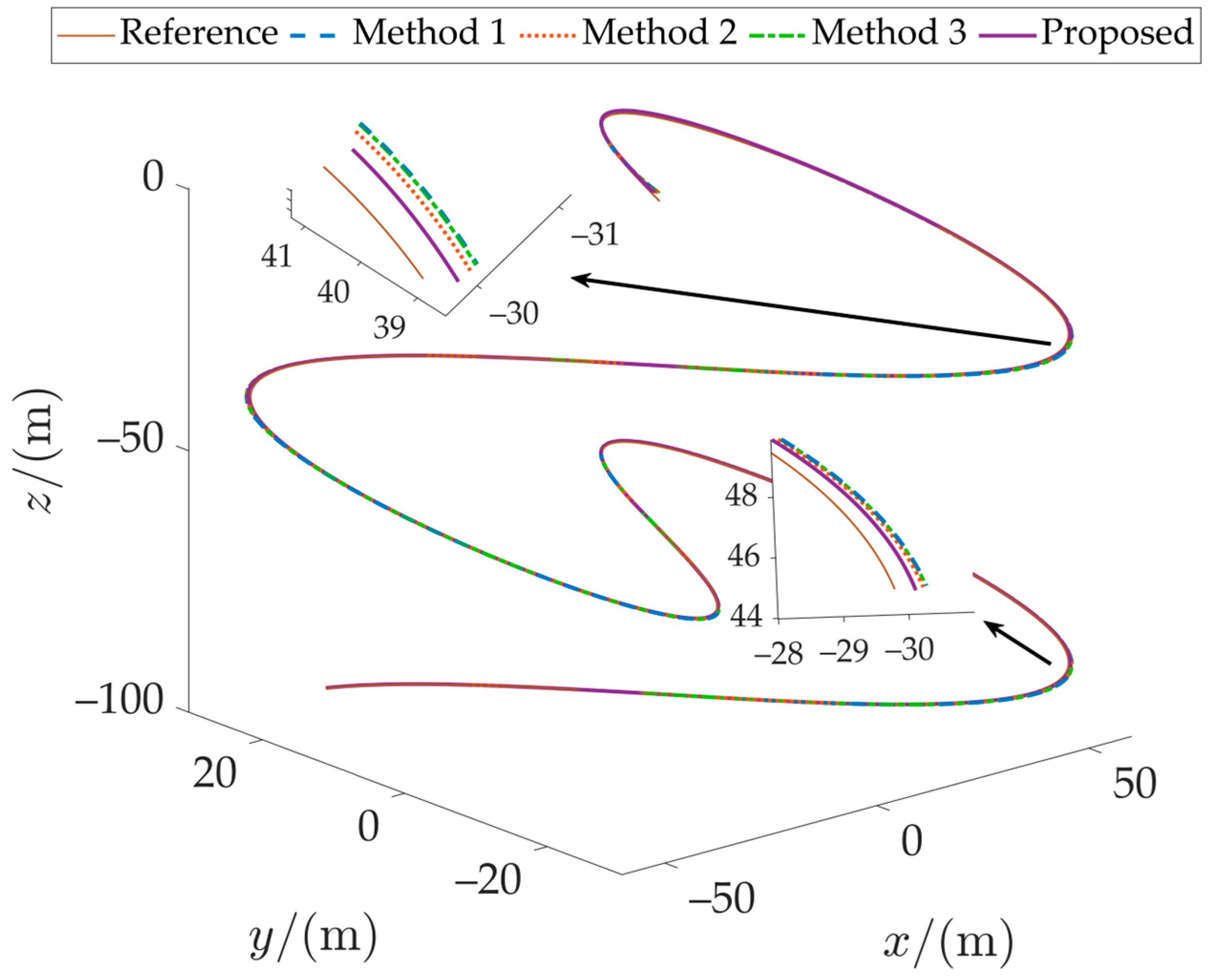
Figure 4 presents the trajectory tracking results of the underactuated AUV in three-dimensional space. It can be observed that all four control strategies achieve effective tracking of the desired trajectory, though differences exist in tracking accuracy.
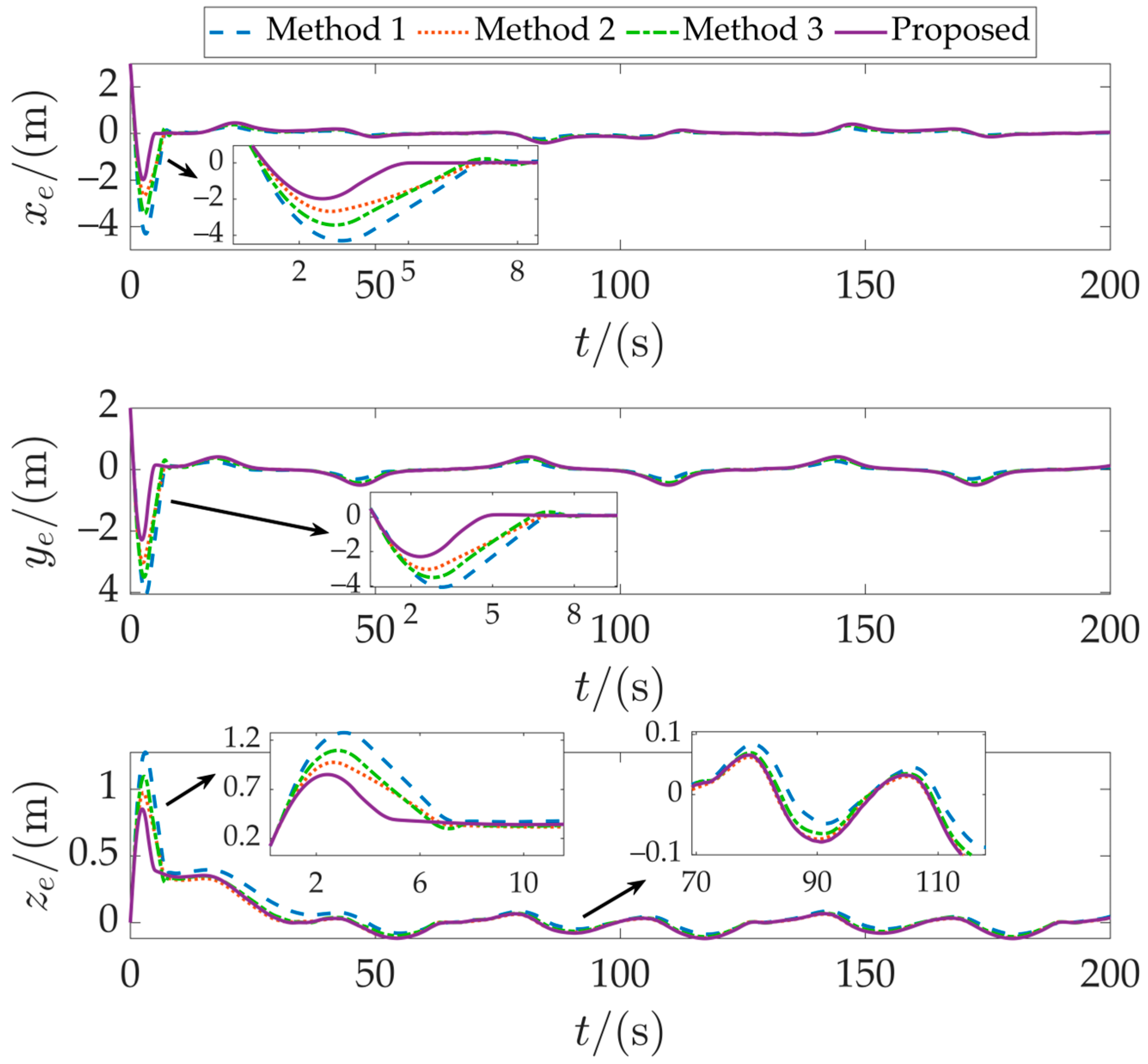
Figure 5 illustrates the positional error comparison among the methods. Method 1 exhibits the largest error amplitude, followed by Method 3. While Method 2 shows improvement over the baseline method, its overall error remains higher than that of the proposed method.
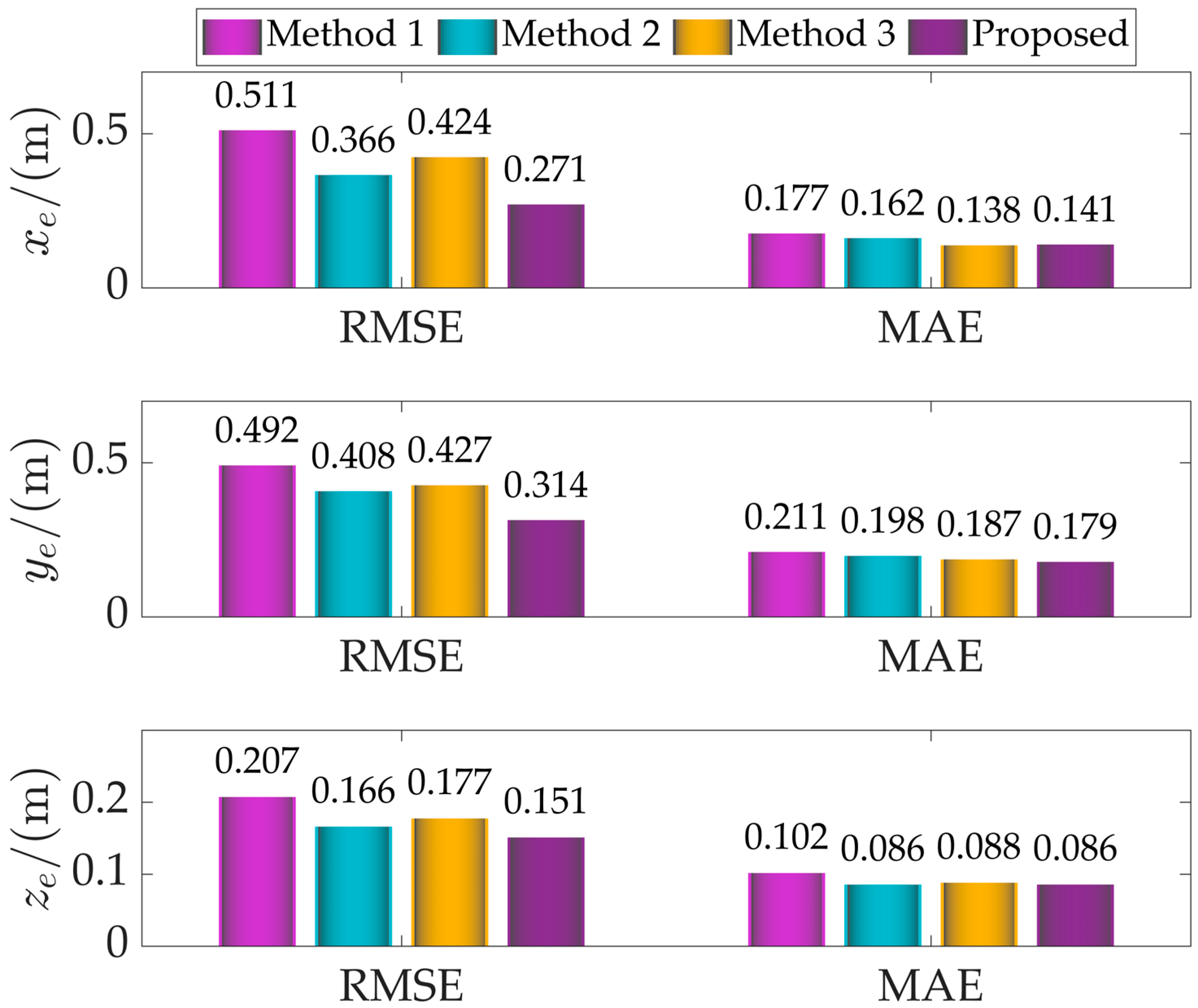
For quantitative evaluation, root mean square error (RMSE) and mean absolute error (MAE) were employed as performance metrics, with results shown in
Figure 6. The proposed method achieves optimal values for both metrics, while Method 1 performs the worst. Notably, Method 2 exhibits significant fluctuations during both initial and later stages.
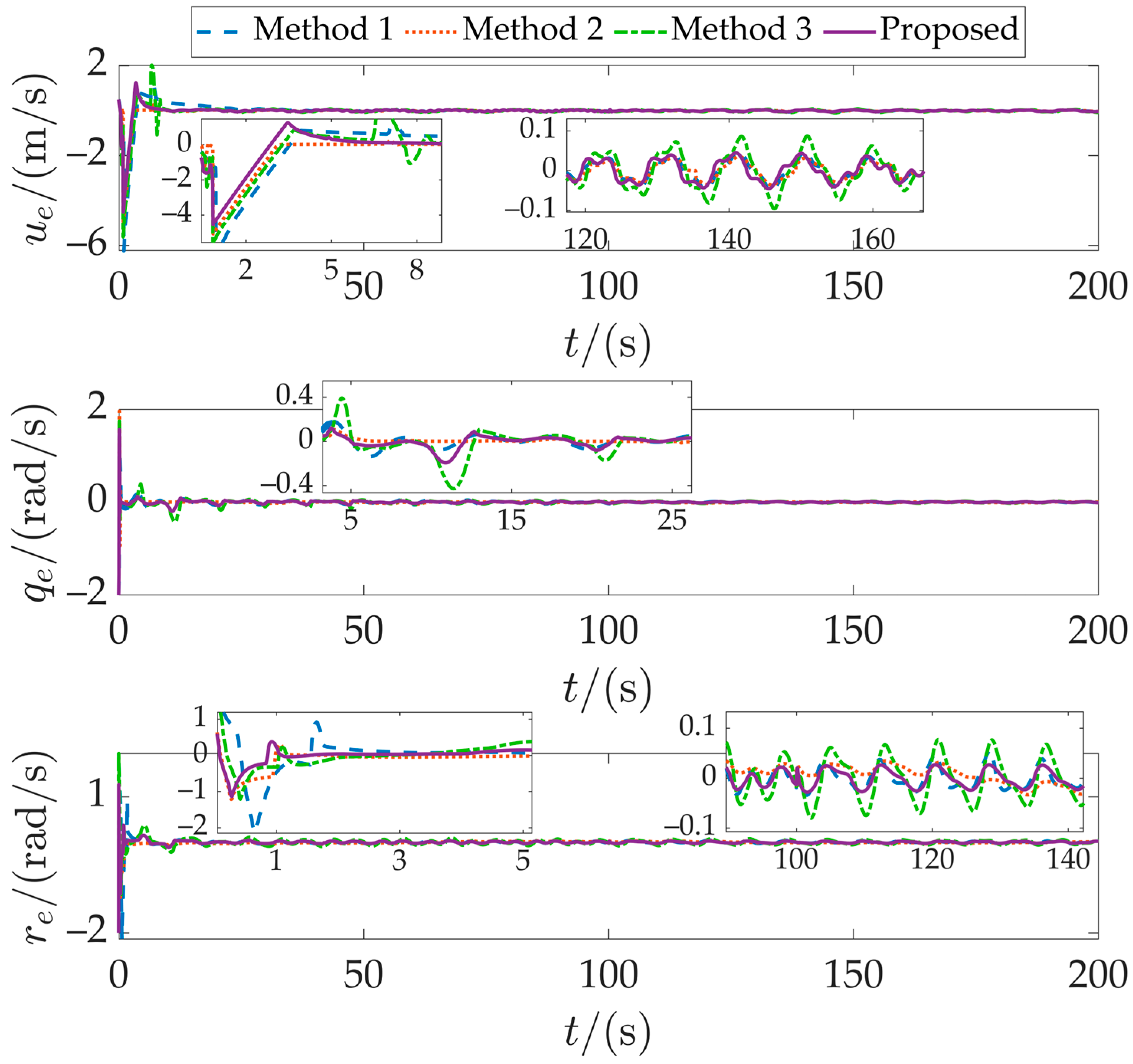
Figure 7 presents the velocity tracking error results. The proposed method responds rapidly and stabilizes near the desired velocity, demonstrating superior dynamic tracking capability and steady-state performance. In contrast, Methods 1 and 3 show substantial velocity fluctuations, with Method 3 exhibiting more pronounced oscillations under disturbances.
To further evaluate observer performance,
Figure 8 displays the disturbance estimation results for the three observers: (a) fractional-order sliding mode observer (FOSMO), (b) integer-order sliding mode observer, and (c) extended state observer (ESO). Overall, all three methods capture the general disturbance trends, but with notable differences in detail. The integer-order sliding mode observer shows significant estimation bias with substantial fluctuations and drift. ESO exhibits phase lag in estimation, particularly failing to accurately track rapidly varying disturbances (e.g., in the x-direction). In contrast, the proposed FOSMO achieves stable and precise estimation of external disturbances across all directions, rapidly converging to true values even during abrupt disturbance changes. The FOSMO introduces a memory-weighted estimation that achieves a balance between fast transient response and smooth steady-state behavior, enabling accurate and low-noise disturbance reconstruction even under abrupt changes. The FOTSMC, on the other hand, modulates the switching dynamics through fractional-order surfaces, suppressing high-frequency chattering. When combined, the two modules yield more precise disturbance compensation and smoother control actions, which explains the reduced tracking error observed in
Figure 5 and
Figure 7.
Overall, the fractional-order design enhances disturbance estimation accuracy and robustness. Compared with ESO-based methods, the proposed FOSMO-FOTSMC maintains high tracking precision and stability even under strong, time-varying disturbances.
5.2. Case 2: Formation Tracking Performance Verification
This case comprehensively evaluates formation control and communication efficiency under dynamic formation transitions and event-triggered communication. The formation consists of one leader and three followers, where the leader tracks the figure-eight helical path from case 1 and periodically broadcasts reference positions. Followers exchange local information and generate their own desired trajectories using the distributed consensus mechanism.
The simulation consists of two phases:
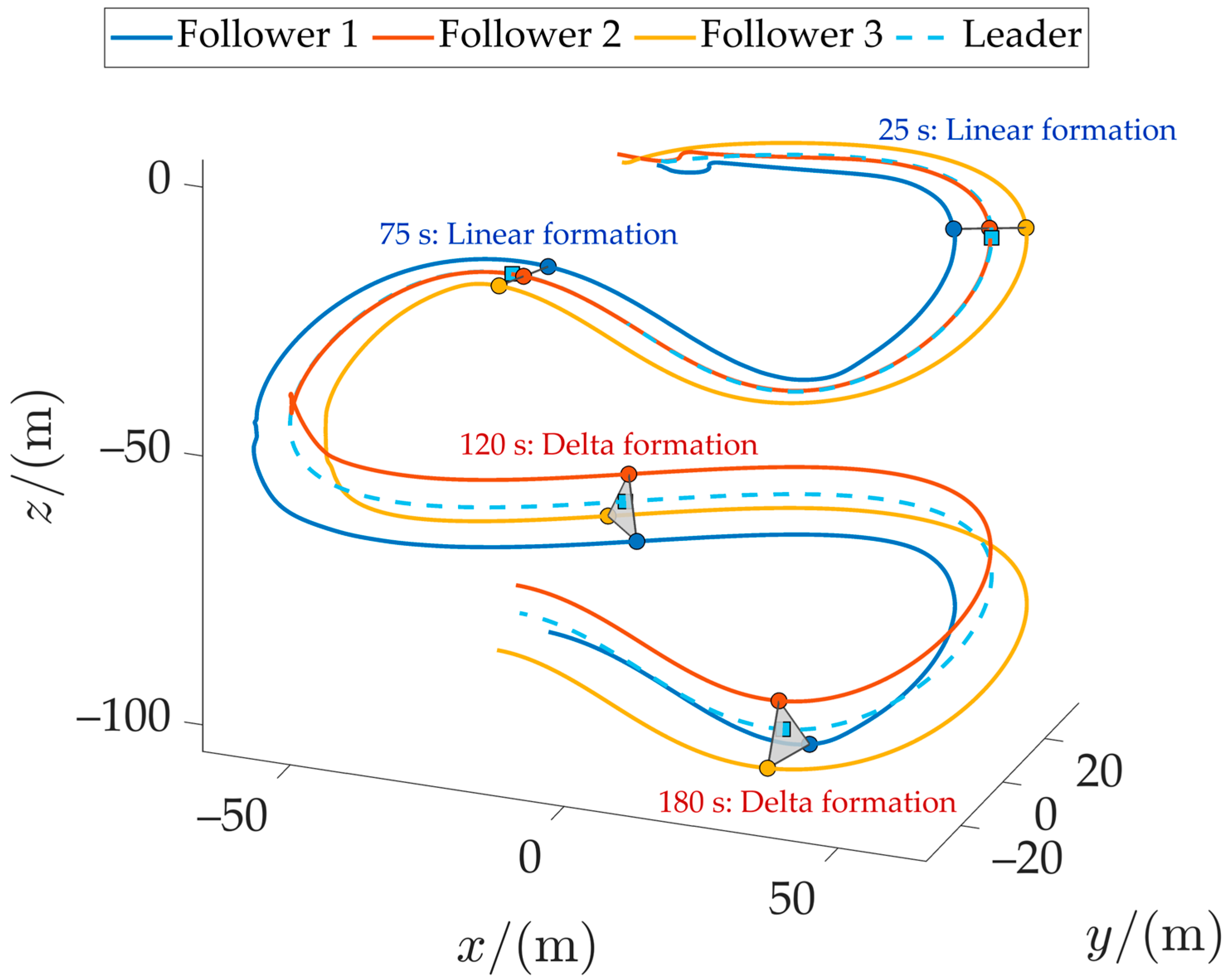
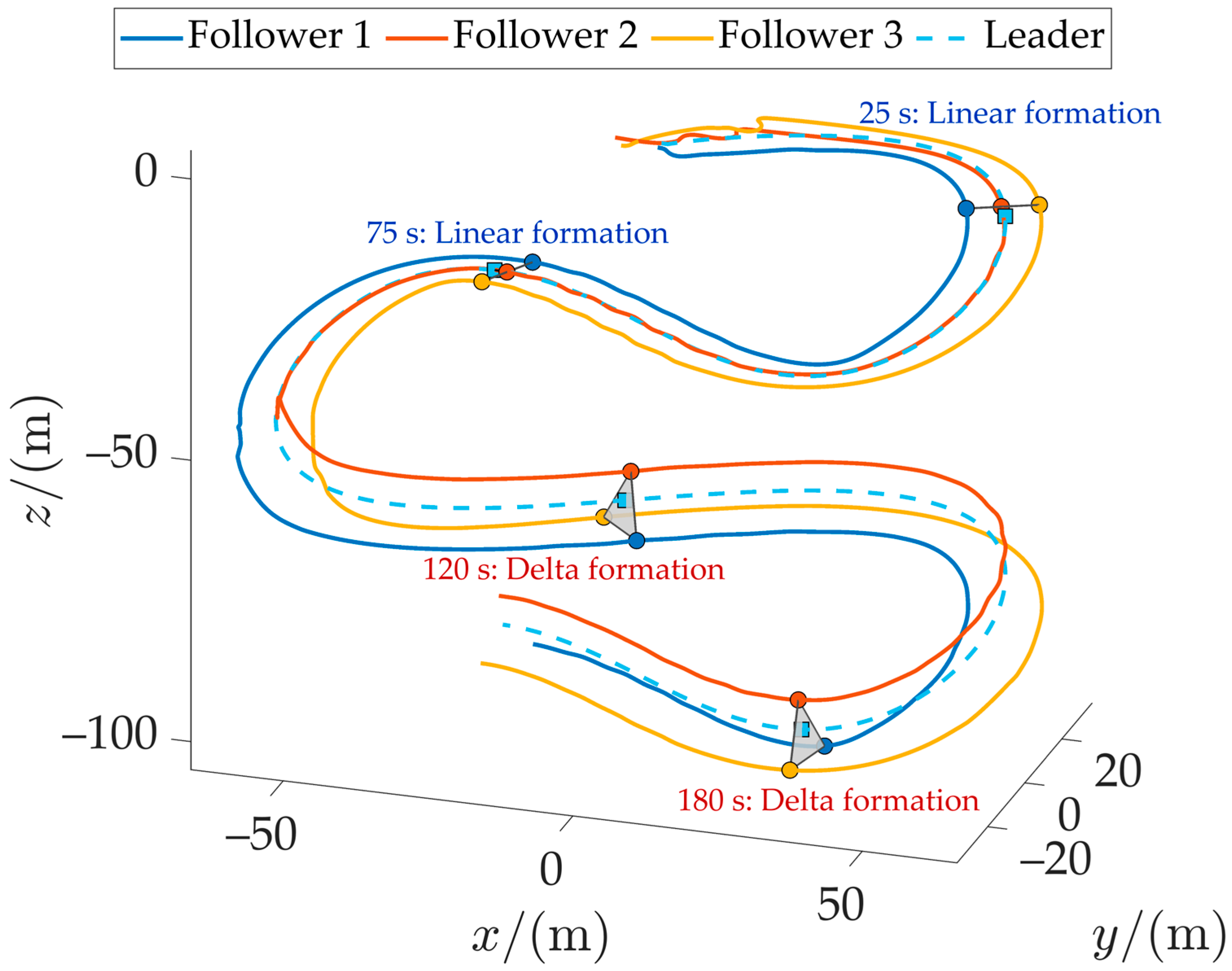
Phase 1 (0–100 s): The followers maintain a planar linear formation behind the leader. Formation values are given by , , .
Phase 2 (100–200 s): The formation transitions to a spatial triangular shape (delta formation), with the leader at the center. Formation values are given by , , .
The initial bit state of the leader is
, and the initial velocity is
. The initial bit state of the two followers is
,
,
and the initial velocity is
. The environmental disturbance is set as
To validate the effectiveness of the event-triggered mechanism and its communication efficiency, this study designs two comparative scenarios:
1. Formation tracking under periodic communication: The initial communication topology is set as AUV1 ↔ AUV2 ↔ AUV3. During t = 120–150 s, the link between Follower 1 and Follower 2 is disconnected, along with the direct connection between the leader and Follower 3. These links are restored at t = 150 s to assess the system’s ability to maintain formation under partial communication.
2. Formation tracking under dynamic event-triggered communication: Initial conditions remain identical to the periodic communication case. However, information exchange occurs only when predefined triggering conditions are met. The upper and lower limits for the event trigger threshold in the simulation are set to 0.2 m and 0.5 m.
Figure 9 and
Figure 10 illustrate the formation tracking performance of the four AUVs in three-dimensional space and horizontal projections, respectively. Different colored symbols indicate AUV positions at selected time instants (squares denote the leader, circles represent followers), with the gray area marking the formation coverage region of the followers. The formation remains stable in both straight-line and triangular configurations. The designed controller ensures rapid convergence to the desired trajectories. Although initial deviations occur due to starting position and formation errors, the system stabilizes quickly.
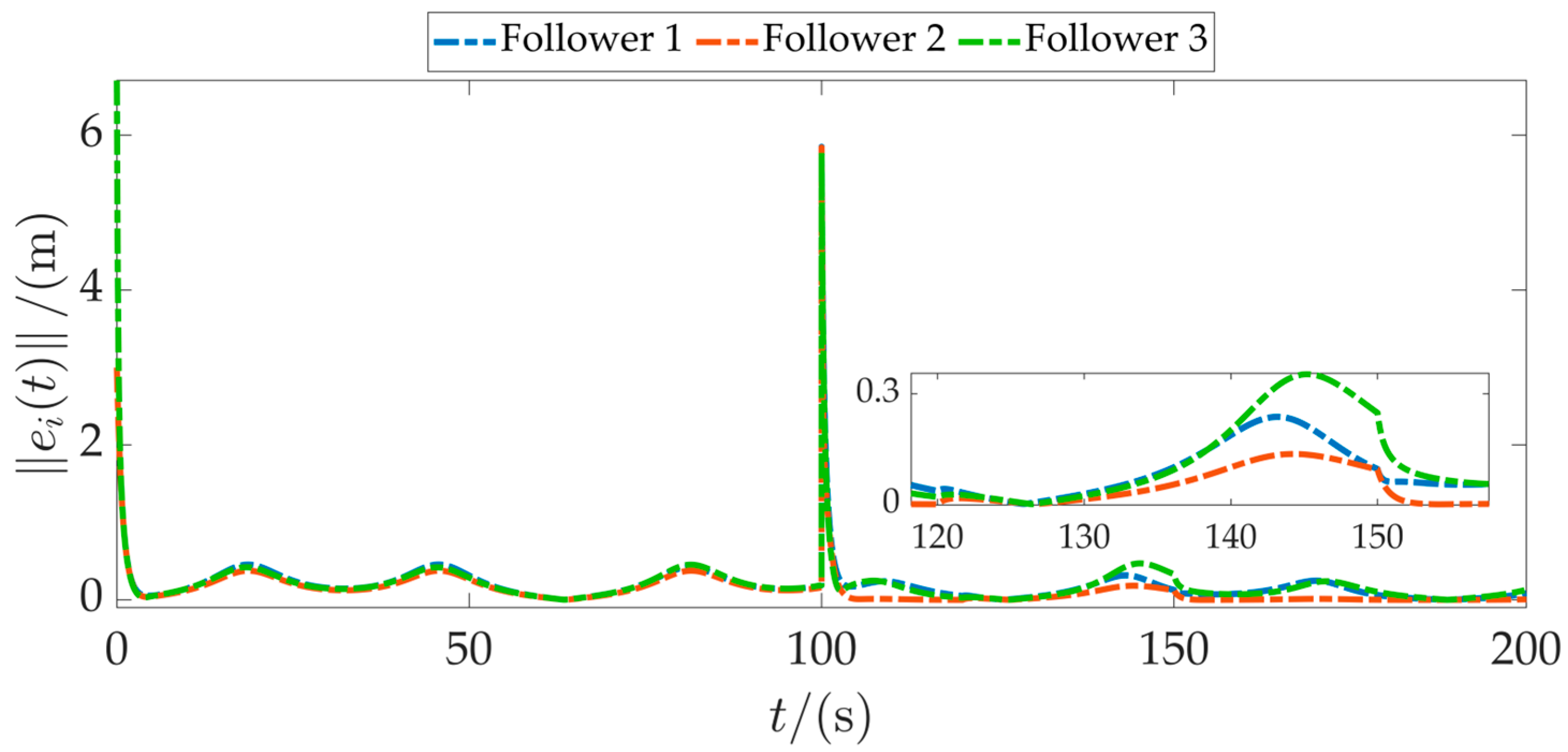
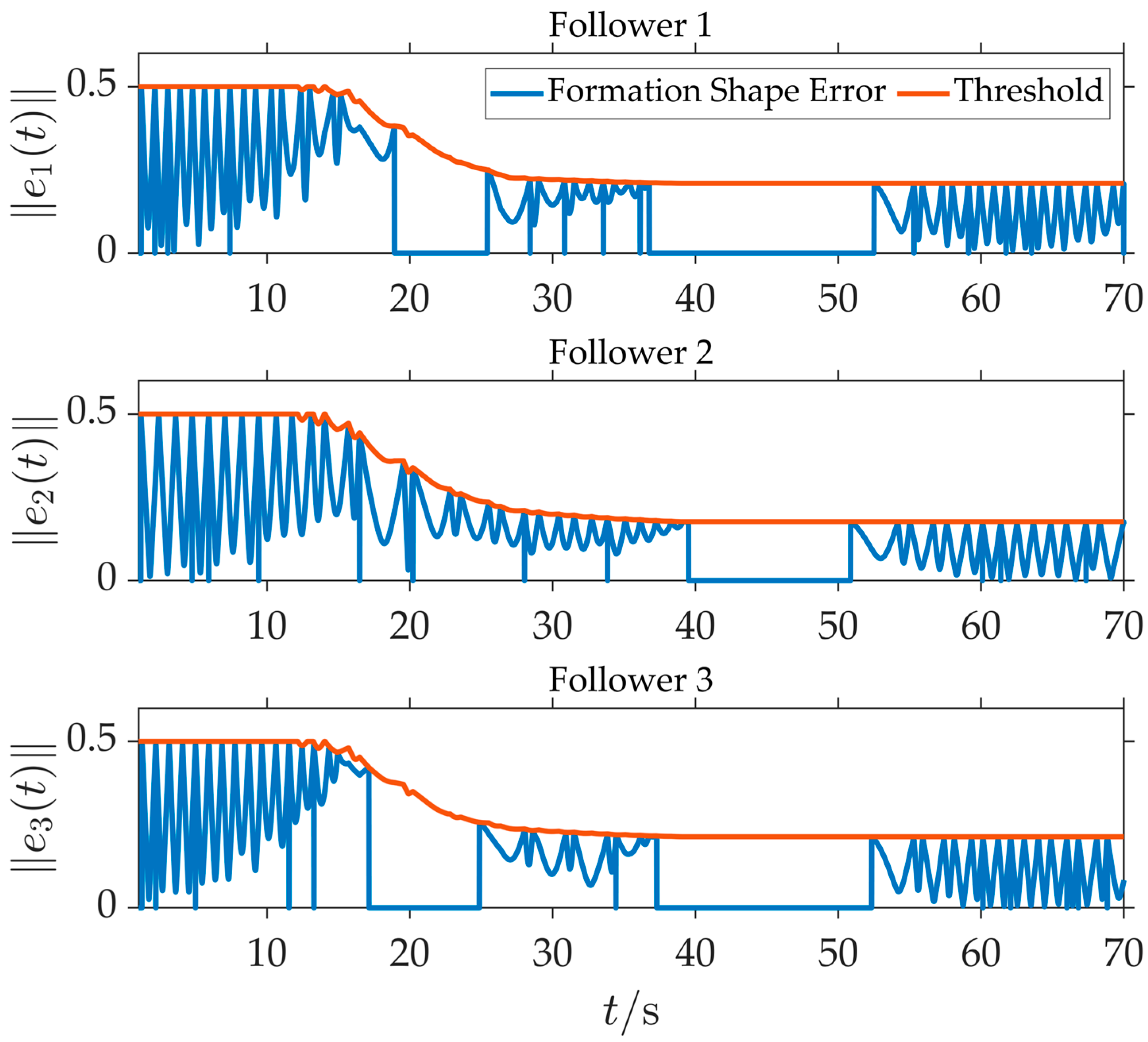
Figure 11 shows the formation error curves of the three followers. Errors increase slightly during the initial phase due to large starting deviations but are rapidly regulated within the threshold range through the trajectory negotiation mechanism. At
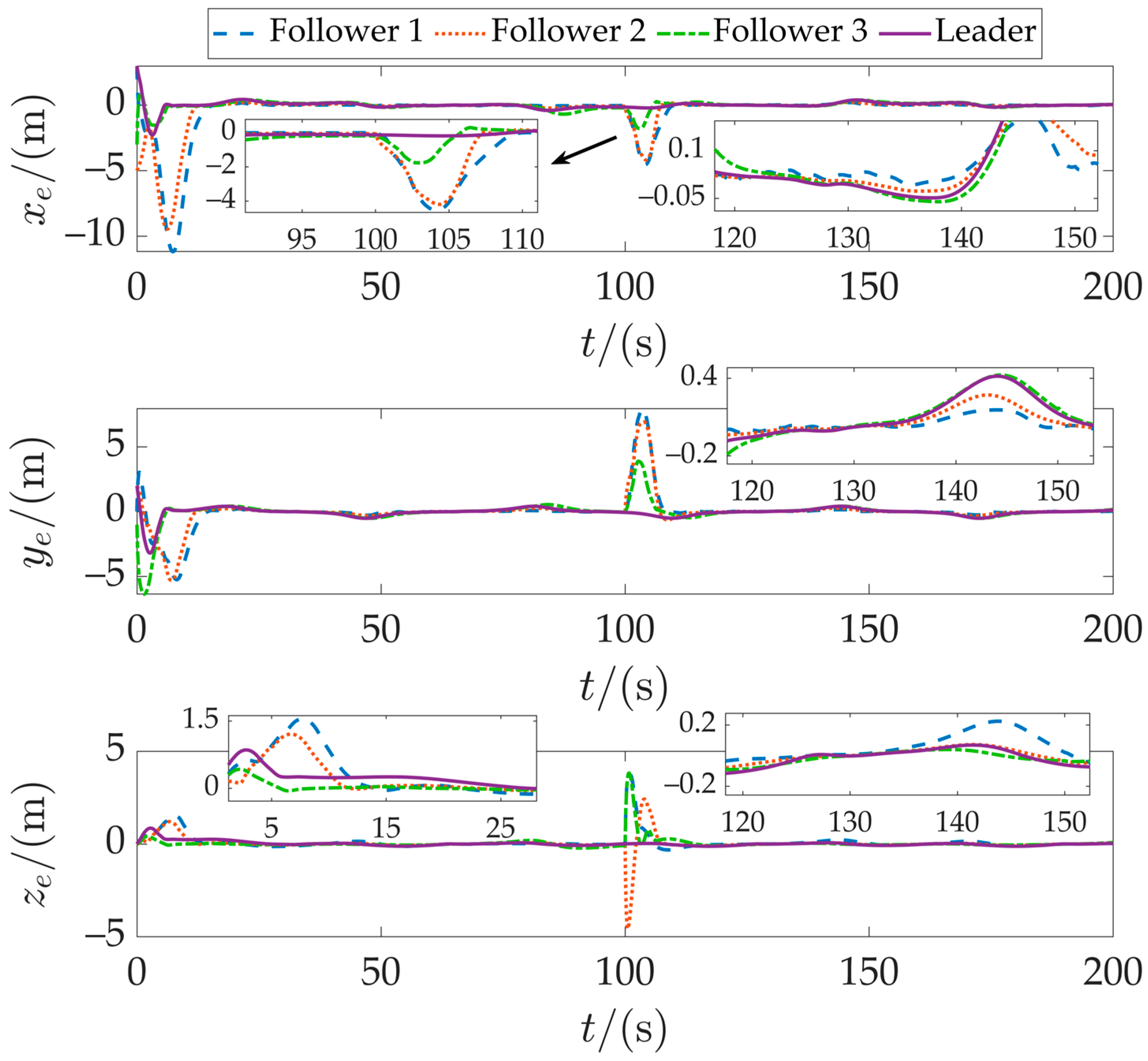
t = 100 s, when the formation shape changes, errors spike transiently but recover to a stable state quickly. Between 120 s and 150 s, during the communication topology change, Follower 3 exhibits slightly larger fluctuations than Followers 1 and 2, which aligns with the loss of partial neighbor information due to link disconnections. Nevertheless, all errors remain within acceptable bounds, confirming the distributed robustness of the algorithm.
Figure 12 further presents the position tracking errors of all four AUVs. The leader shows small and stable tracking errors. The followers initially exhibit larger errors owing to their deviated initial positions but converge rapidly. A brief error surge occurs during the formation switch at
t = 100 s, reflecting transient effects from trajectory reconfiguration, yet the system promptly restores tracking accuracy. The magnified view of the 120–150 s interval confirms that no error divergence occurs even under degraded communication, demonstrating consistent tracking performance under constrained conditions.
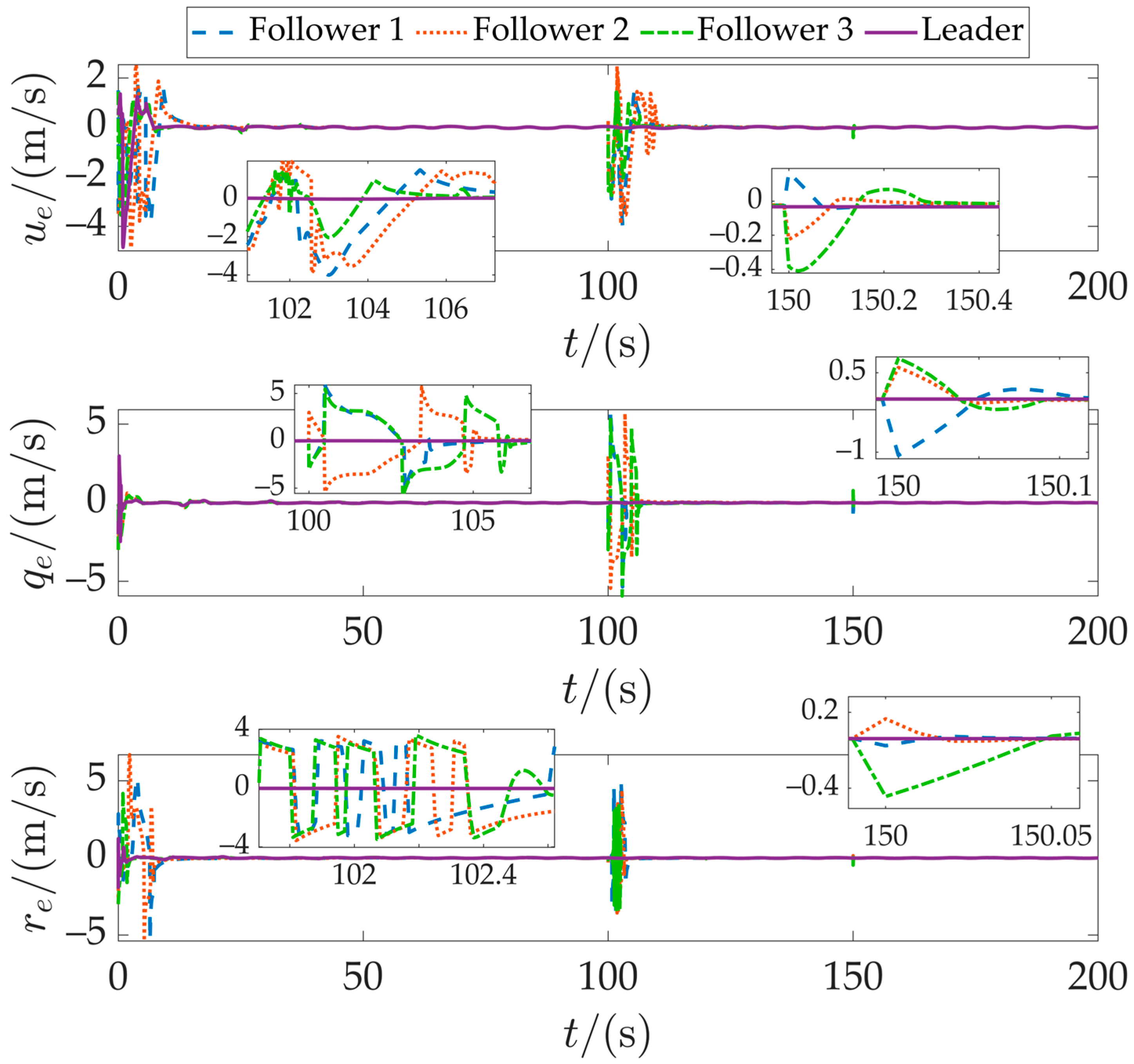
Figure 13 depicts the velocity error profiles. Despite starting from different initial positions, all AUVs rapidly reached steady-state operation. A transient oscillation in velocity error is observed during the formation reconfiguration at
t =1 00 s, reflecting necessary speed adjustments to align with the new formation geometry. The system demonstrated effective recovery, with errors converging to zero shortly after this transition. An enlarged view of the topology restoration phase around
t = 150 s reveals minor velocity fluctuations caused by communication link recovery. These disturbances were suppressed within 0.5 s without propagating to position tracking errors, confirming the robustness and disturbance rejection capability of the proposed formation coordination controller.
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18 and
Figure 19 present the simulation results under the dynamic event-triggered communication mechanism.
Figure 14 and
Figure 15 show the formation evolution of the four AUVs in three-dimensional space and on the horizontal plane, respectively, using the same color coding and annotation conventions as in the periodic communication case. It can be observed that under event-triggered communication, the overall formation remains stable, with all AUVs converging rapidly to the desired trajectory. However, due to the discontinuous nature of information updates introduced by the triggering mechanism, the resulting trajectories exhibit slightly more fluctuation and are less smooth than those under periodic communication. Despite this, the system maintains strong dynamic coordination and high formation accuracy.
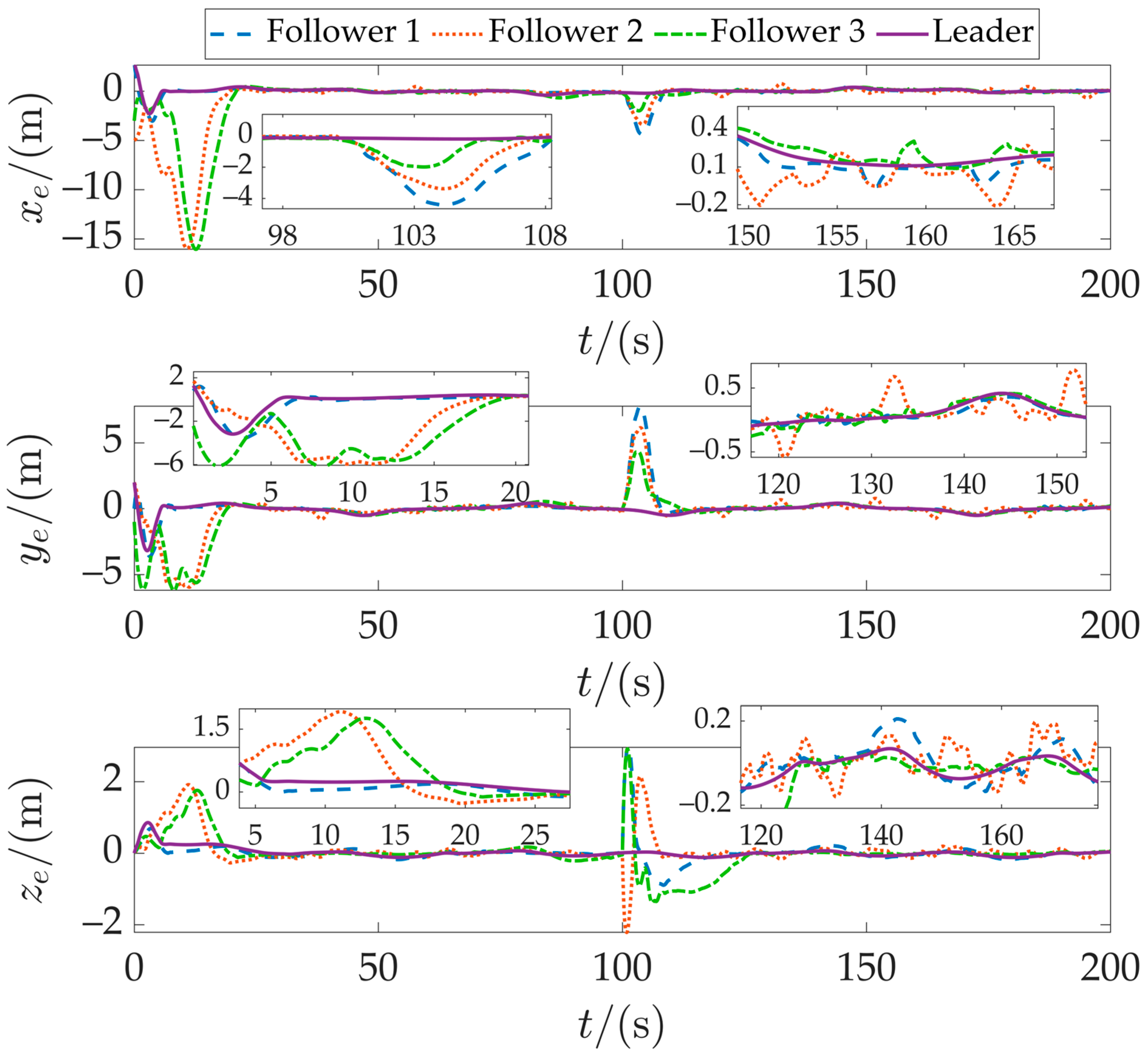
Figure 16 shows the position tracking error curves of the four AUVs. The three followers exhibit larger error amplitudes during both the initial transient phase and the formation switching at
t = 100 s, along with slightly extended convergence times, compared to the periodic communication case. This behavior results from the reduced frequency of neighbor information updates under the event-triggered mechanism. As the negotiated reference trajectory updates only when communication is triggered, it responds discontinuously to changes in state errors, leading to temporary fluctuations when errors remain within the triggering threshold and no communication occurs. Overall, the event-triggered mechanism achieves a significant reduction in communication frequency at the cost of a minor degradation in tracking accuracy.
To further illustrate the working pattern of the event-triggered mechanism,
Figure 17 zooms in on the time interval from
t = 1 s to
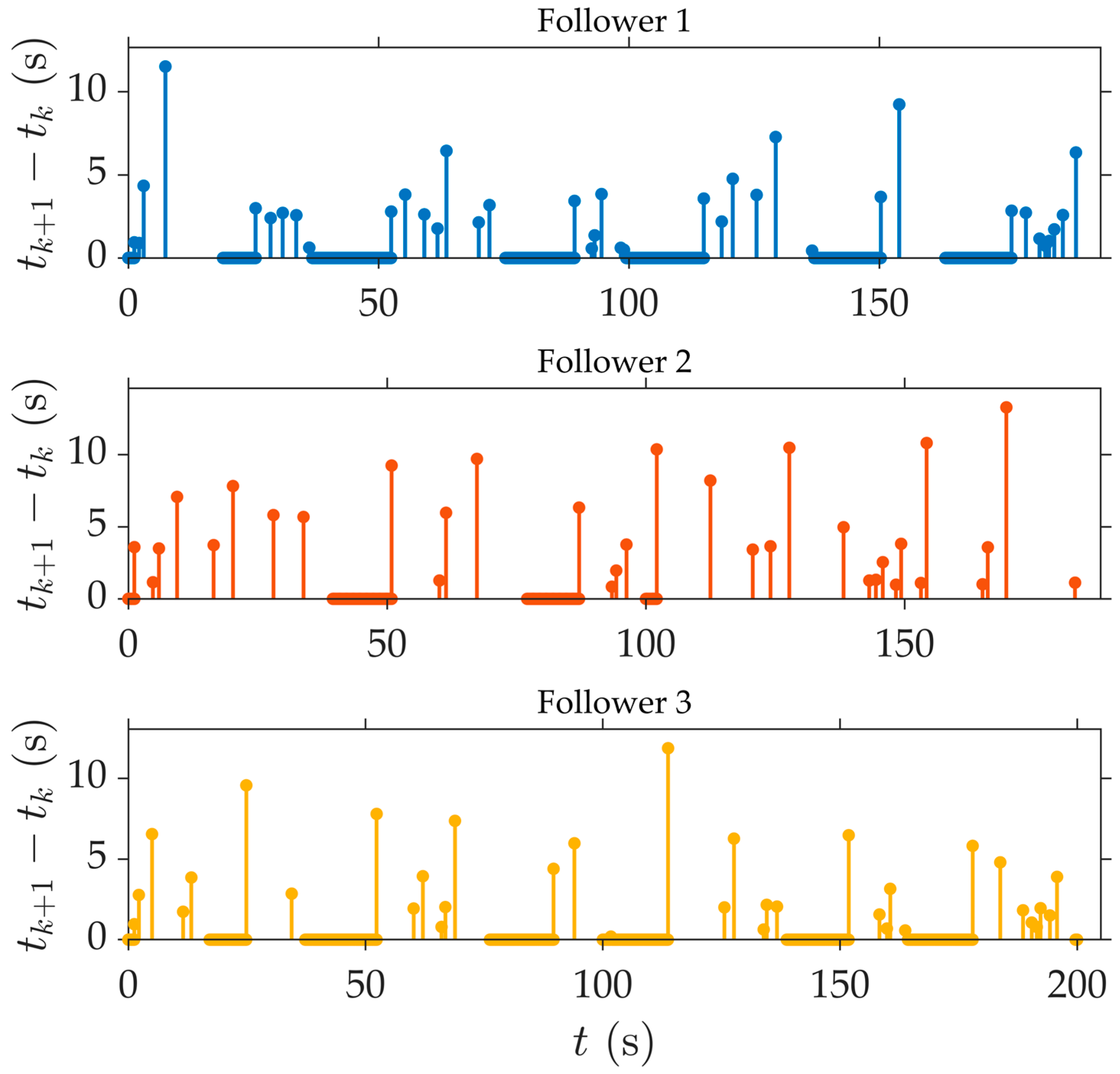
t = 70 s, which covers the transition from the transient phase to steady-state operation. The figure clearly reveals a typical triggering pattern: frequent controller updates during high-error periods (e.g., the initial phase) to ensure fast convergence, followed by significantly longer triggering intervals as the system enters steady state. This pattern demonstrates the mechanism’s ability to prolong communication silence during low-error periods, thereby effectively reducing the communication load.
Figure 18 and
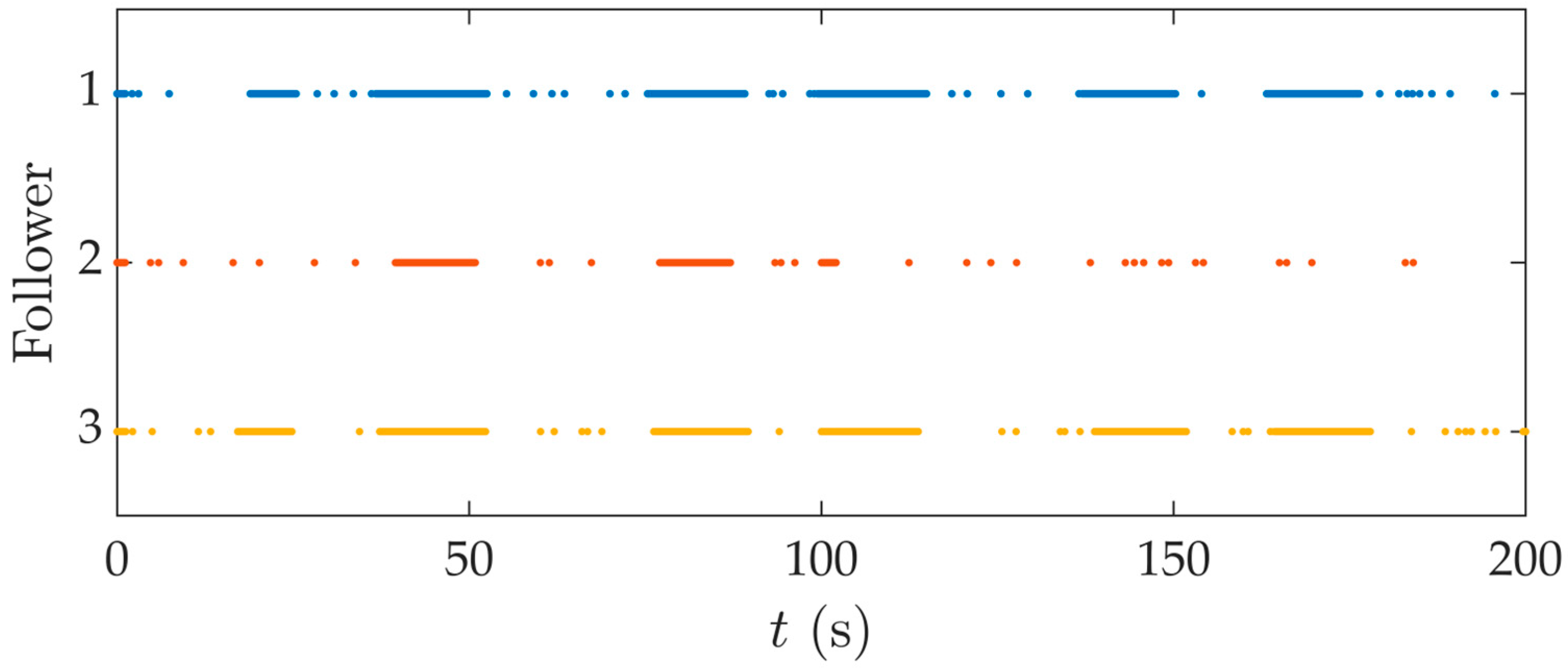
Figure 19 further illustrate the behavior of the dynamic event triggering mechanism.
Figure 18 shows the distribution of trigger moments for three followers throughout the entire operational cycle.
Figure 19 presents the variation curve of time intervals between trigger moments. The control strategy based on dynamic triggering increases the trigger interval, thereby reducing the number of triggers, verifying the characteristic of dynamically adjusting trigger frequency according to system state. As summarized in
Table 1, the total number of triggering instances under the dynamic event-triggered mechanism decreased by 65.2%, 87.5%, and 65.8%, respectively, compared to the periodic communication scheme. These results confirm that the proposed triggering strategy significantly reduces communication overhead while preserving control performance.
In summary, the simulation results comprehensively validate the effectiveness and robustness of the proposed method under dynamic formation changes, communication topology variations, and event-triggered communication. The system consistently maintains formation stability with limited communication resources, achieving high-precision trajectory tracking and substantial communication savings.