On Fractional Hermite–Hadamard-Type Inequalities for Harmonically s-Convex Stochastic Processes
Abstract
1. Introduction
2. Preliminaries
3. Auxiliary Results
4. Fractional Hermite–Hadamard Inequality for Harmonically -Convex Stochastic Processes
5. Midpoint-Type Inequalities
6. Illustrative Example and Application
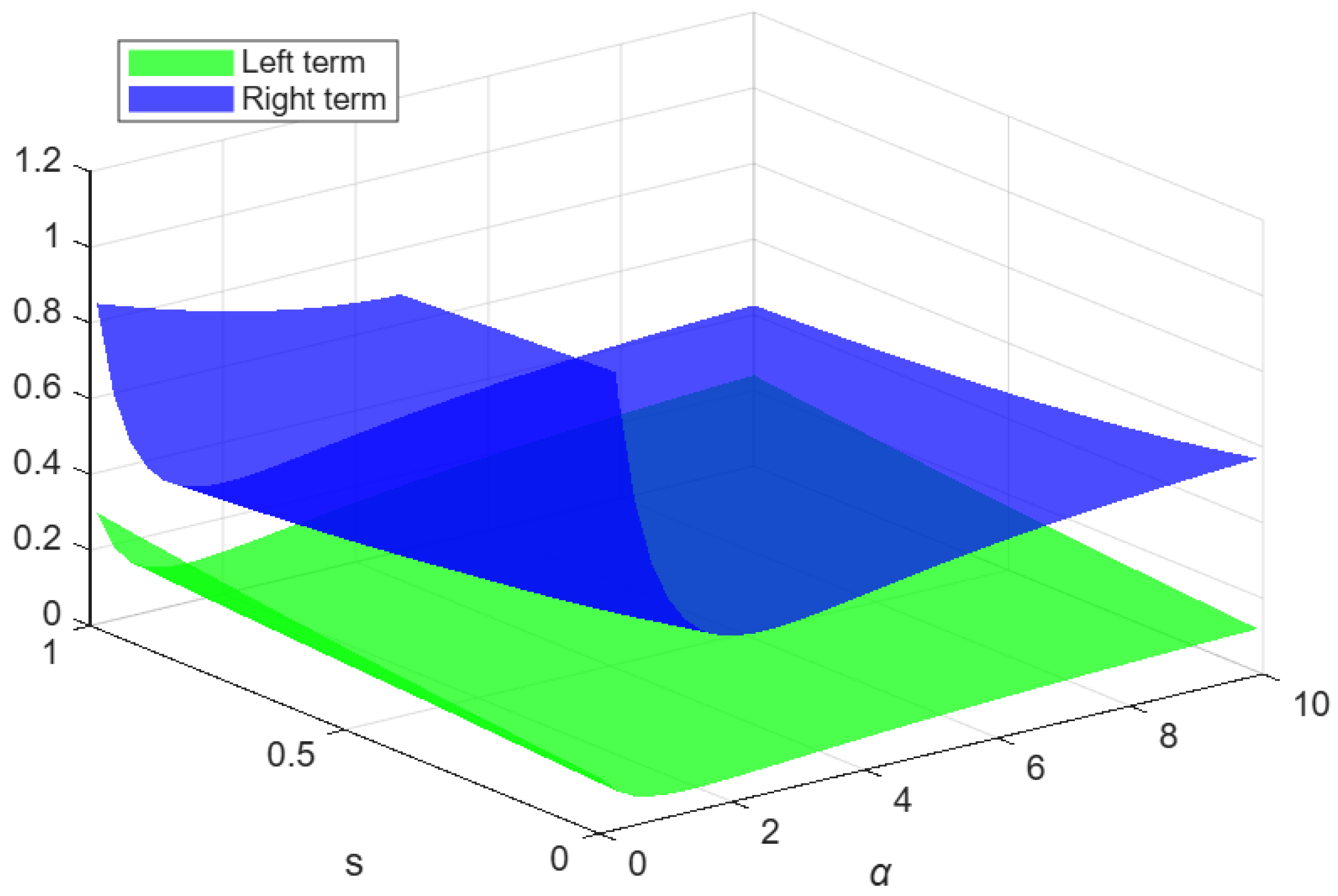
6.1. Numerical Example and Graphical Illustration
6.2. Application to Special Means
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lakhdari, A.; Budak, H.; Mlaiki, N.; Meftah, B.; Abdeljawad, T. New insights on fractal–fractional integral inequalities: Hermite–Hadamard and Milne estimates. Chaos Solitons Fractals 2025, 193, 116087. [Google Scholar] [CrossRef]
- Lakhdari, A.; Saleh, W. Multiplicative fractional Hermite–Hadamard-type inequalities in G-Calculus. Mathematics 2025, 13, 3426. [Google Scholar] [CrossRef]
- Li, H.; Meftah, B.; Saleh, W.; Xu, H.; Kiliçman, A.; Lakhdari, A. Further Hermite–Hadamard-type inequalities for fractional integrals with exponential kernels. Fractal Fract. 2024, 8, 345. [Google Scholar] [CrossRef]
- Saleh, W.; Meftah, B.; Awan, M.U.; Lakhdari, A. On Katugampola fractional multiplicative Hermite–Hadamard-type inequalities. Mathematics 2025, 13, 1575. [Google Scholar] [CrossRef]
- Kırmacı, U. Inequalities for differentiable mappings and applications to special means of real numbers and to midpoint formula. Appl. Math. Comput. 2004, 147, 137–146. [Google Scholar] [CrossRef]
- Hudzik, H.; Maligranda, L. Some remarks on s-convex functions. Aequationes Math. 1994, 48, 100–111. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Fitzpatrick, S. The Hadamard’s inequality for s-convex functions in the second sense. Demonstr. Math. 1999, 32, 687–696. [Google Scholar]
- Liu, Z. On inequalities of Hermite-Hadamard type involving an s-convex function with applications. Issues Anal. 2016, 5, 3–20. [Google Scholar] [CrossRef]
- İşcan, İ. Hermite–Hadamard type inequalities for harmonically convex functions. Hacet. J. Math. Stat. 2014, 43, 935–942. [Google Scholar] [CrossRef]
- İşcan, İ. Hermite-Hadamard and Simpson-like type inequalities for differentiable harmonically convex functions. J. Math. 2014, 2014, 346305. [Google Scholar] [CrossRef]
- İşcan, İ. Ostrowski type inequalities for harmonically s-convex functions. Konuralp J. Math. 2015, 3, 63–74. [Google Scholar]
- Latif, M.A.; Kalsoom, H.; Abidin, M.Z. Hermite–Hadamard-type inequalities involving harmonically convex function via the Atangana–Baleanu fractional integral operator. Symmetry 2022, 14, 1774. [Google Scholar] [CrossRef]
- Awan, M.U.; Akhtar, N.; Iftikhar, S.; Noor, M.A.; Chu, Y.M. New Hermite-Hadamard type inequalities for n-polynomial harmonically convex functions. J. Inequal. Appl. 2020, 2020, 125. [Google Scholar] [CrossRef]
- Butt, S.I.; Umar, M.; Khan, D.; Seol, Y.; Tipurić-Spužević, S. Hermite–Hadamard-type inequalities for harmonically convex functions via proportional Caputo-Hybrid operators with applications. Fractal Fract. 2025, 9, 77. [Google Scholar] [CrossRef]
- Nwaeze, E.R.; Khan, M.A.; Ahmadian, A.; Ahmad, M.N.; Mahmood, A.K. Fractional inequalities of the Hermite–Hadamard type for m-polynomial convex and harmonically convex functions. AIMS Math. 2021, 6, 1889–1904. [Google Scholar] [CrossRef]
- Şanlı, Z. Some midpoint type inequalities for Riemann Liouville fractional integrals. Appl. Appl. Math. 2019, 14, 58–73. [Google Scholar]
- İşcan, İ.; Wu, S.H. Hermite-Hadamard type inequalities for harmonically convex functions via fractional integrals. Appl. Math. Comput. 2014, 238, 237–244. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies; Elsevier Science B.V.: Amsterdam, The Nederlands, 2006. [Google Scholar]
- Nikodem, K. On convex stochastic processes. Aequationes Math. 1980, 20, 184–197. [Google Scholar] [CrossRef]
- Kotrys, D. Hermite-Hadamard inequality for convex stochastic processes. Aequationes Math. 2012, 83, 143–151. [Google Scholar] [CrossRef]
- Set, E.; Tomar, M.; Maden, S. Hermite-Hadamard type inequalities for s-convex stochastic processes in the second sense. Turk. J. Anal. Number Theory 2014, 2, 202–207. [Google Scholar] [CrossRef]
- Okur, N.; İşcan, İ.; Dizdar, E.Y. Hermite–Hadamard type inequalities for harmonically convex stochastic processes. Uluslararası İktisadi İdari İncelemeler Derg. 2018, 18, 281–292. [Google Scholar] [CrossRef]
- Agahi, H.; Babakhani, A. On fractional stochastic inequalities related to Hermite-Hadamard and Jensen types for convex stochastic processes. Aequationes Math. 2016, 90, 1035–1043. [Google Scholar] [CrossRef]
- Materano, J.; Merentes, N.; Valera-López, M. Some estimates on the Simpson’s type inequalities through s-convex and quasi-convex stochastic processes. Math. Aeterna 2015, 5, 673–705. [Google Scholar]
- Materano, J.; Merentes, N.; Valera-López, M. On Ostrowskis type inequalities via convex, s-convex and quasi-convex stochastic processes. Math. Aeterna 2016, 6, 47–85. [Google Scholar]
- Deng, J.; Wang, J. Fractional Hermite-Hadamard inequalities for (β,m)-logarithmically convex functions. J. Inequal. Appl. 2013, 2013, 364. [Google Scholar] [CrossRef]
- Afzal, W.; Botmart, T. Some novel estimates of Jensen and Hermite-Hadamard inequalities for h-Godunova-Levin stochastic processes. AIMS Math. 2023, 8, 7277–7291. [Google Scholar] [CrossRef]
- Meftah, B.; Benchettah, D.C.; Saleh, W.; Lakhdari, A. On k-Riemann-Liouville Maclaurin-type inequalities for s-convex stochastic processes. Math. Methods Appl. Sci. 2025, 1–12. [Google Scholar] [CrossRef]
- Sharma, N.; Mishra, R.; Hamdi, A. Hermite-Hadamard type integral inequalities for multidimensional general h-harmonic preinvex stochastic processes. Comm. Statist. Theory Methods 2022, 51, 6719–6740. [Google Scholar] [CrossRef]
- Hernández, J.E.; García, J.F.G. Hermite-Hadamard type inequalities, convex stochastic processes and Katugampola fractional integral. Rev. Integr. Temas Mat. 2018, 36, 133–149. [Google Scholar] [CrossRef]
- Hernández, J.E.H.; Gomez, J.F. Hermite-Hadamard type inequalities for (m, h1, h2)-convex stochastic processes using Katugampola fractional integral. Rev. Mat. Univ. Atl. 2019, 36, 133–149. [Google Scholar]
- Afzal, W.; Aloraini, N.M.; Abbas, M.; Ro, J.S.; Zaagan, A.A. Some novel Kulisch-Miranker type inclusions for a generalized class of Godunova-Levin stochastic processes. AIMS Math. 2024, 9, 5122–5146. [Google Scholar] [CrossRef]
- Jarad, F.; Sahoo, S.K.; Nisar, K.S.; Treanta, S.; Emadifar, H.; Botmart, T. New stochastic fractional integral and related inequalities of Jensen-Mercer and Hermite-Hadamard-Mercer type for convex stochastic processes. J. Inequal. Appl. 2023, 2023, 51. [Google Scholar] [CrossRef]
- Javed, M.Z.; Awan, M.U.; Ciurdariu, L.; Dragomir, S.S.; Almalki, Y. On extended class of totally ordered interval-valued convex stochastic processes and applications. Fractal Fract. 2024, 8, 577. [Google Scholar] [CrossRef]
- Set, E.; Sarıkaya, M.Z.; Tomar, M. Hermite-Hadamard type inequalities for coordinates convex stochastic processes. Math. Aeterna 2015, 5, 363–382. [Google Scholar]
- Sharma, N.; Mishra, R.; Hamdi, A. On strongly generalized convex stochastic processes. Comm. Statist. Theory Methods 2024, 53, 2908–2923. [Google Scholar] [CrossRef]
- Sobczyk, K. Stochastic Differential Equations; Mathematics and Its Applications (East European Series); Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Hafiz, F.M. The fractional calculus for some stochastic processes. Stoch. Anal. Appl. 2004, 22, 507–523. [Google Scholar] [CrossRef]
- Erdelyi, A. Higher Transcendental Functions; McGraw-Hill Book Company: New York, NY, USA, 1955; Volume III, Re-Issued 1981. [Google Scholar]
- Mitrinović, D.S.; Pečarić, J.E.; Fink, A.M. Classical and New Inequalities in Analysis; Mathematics and Its Applications (East European Series); Kluwer Academic Publishers Group: Dordrecht, The Netherlands, 1993. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzahrani, R.; Fakhfakh, R.; Alomani, G.; Meftah, B. On Fractional Hermite–Hadamard-Type Inequalities for Harmonically s-Convex Stochastic Processes. Fractal Fract. 2025, 9, 750. https://doi.org/10.3390/fractalfract9110750
Alzahrani R, Fakhfakh R, Alomani G, Meftah B. On Fractional Hermite–Hadamard-Type Inequalities for Harmonically s-Convex Stochastic Processes. Fractal and Fractional. 2025; 9(11):750. https://doi.org/10.3390/fractalfract9110750
Chicago/Turabian StyleAlzahrani, Rabab, Raouf Fakhfakh, Ghadah Alomani, and Badreddine Meftah. 2025. "On Fractional Hermite–Hadamard-Type Inequalities for Harmonically s-Convex Stochastic Processes" Fractal and Fractional 9, no. 11: 750. https://doi.org/10.3390/fractalfract9110750
APA StyleAlzahrani, R., Fakhfakh, R., Alomani, G., & Meftah, B. (2025). On Fractional Hermite–Hadamard-Type Inequalities for Harmonically s-Convex Stochastic Processes. Fractal and Fractional, 9(11), 750. https://doi.org/10.3390/fractalfract9110750





