The Hidden Order of Cosmic Rays: Fractal Scaling and Temporal Complexity
Abstract
1. Introduction
2. Materials and Methods
2.1. Observations
2.2. The Mono-Multifractal-Modified Detrended Fluctuation and Natural Time Analysis
- 1.
- Integrate the time series of N samples and divide it into boxes of equal length n.
- 2.
- In each box, fit a local trend (least squares line), subtract it, and calculate the RMS fluctuation.
- 3.
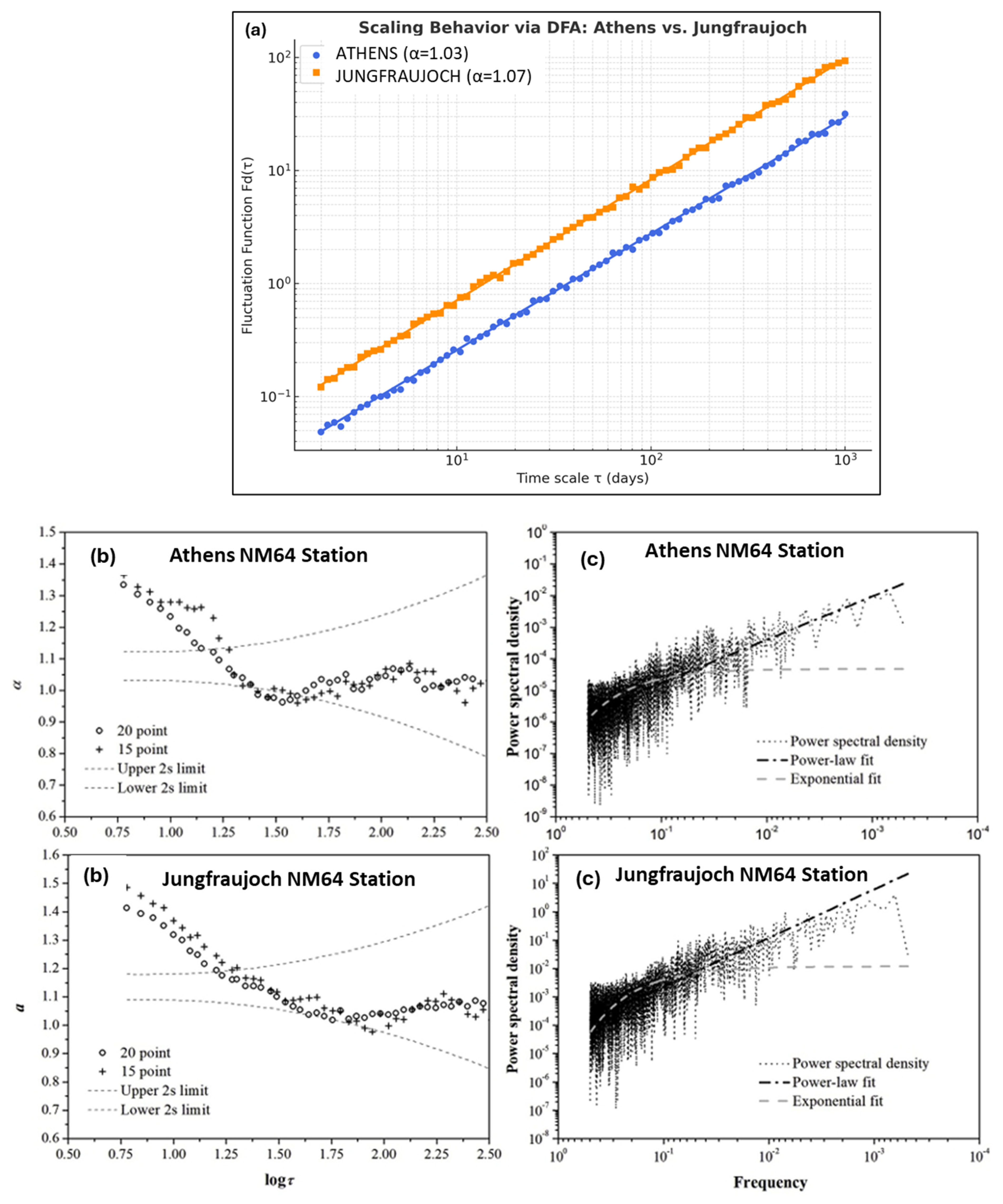
- Repeat for multiple box sizes. The function F(n) vs. n on a log–log plot gives the scaling exponent α.
- 0.5 < α < 1 persistent correlations exist (e.g., 1/f noise at α = 1).
- 0 < α < 0.5: anti-correlations (anti-persistence) prevail.
- α > 1: correlations not of power-law type exist (α = 1.5 indicates Brownian noise).
- Build the profile Y(i).
- Divide into Ns segments of length s.
- Detrend each segment using polynomial fits (DFA1, DFA2, …).
- Compute the q-order fluctuation function Fq(s).
- h(2) corresponds to the Hurst exponent.
- Positive q indicates scaling of large fluctuations, while negative q: small fluctuations.
- For monofractals, h(q) is independent of q; for multifractals, it varies.
3. Results and Discussion
3.1. The Long-Range Correlations in CR Dynamics
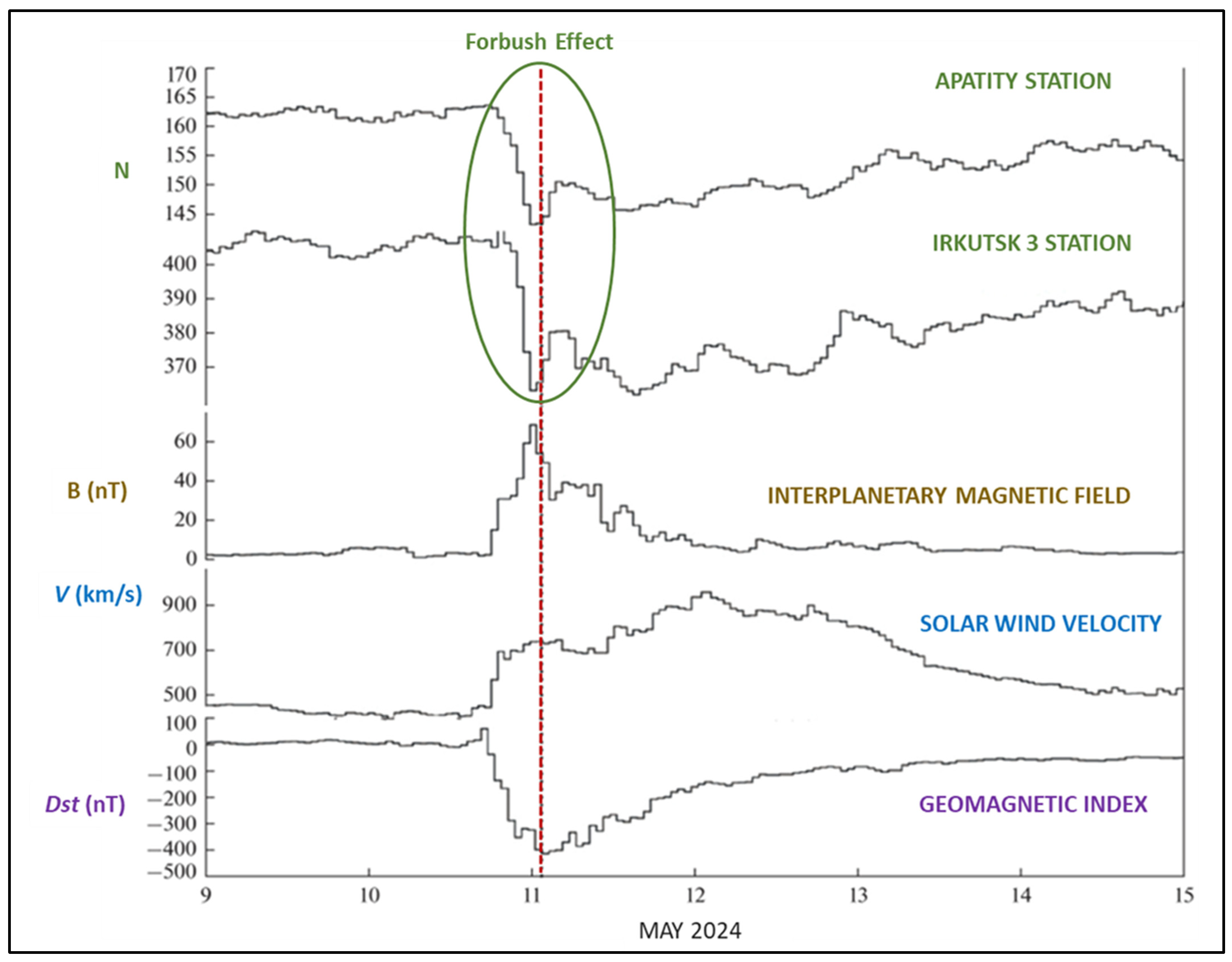
3.2. Warning Signatures of ECREs: The Forbush Effect of May 2024
3.2.1. Real-Time Fractal Behavior Analysis: The Importance of Order, Not Time, of ECRE Occurrence
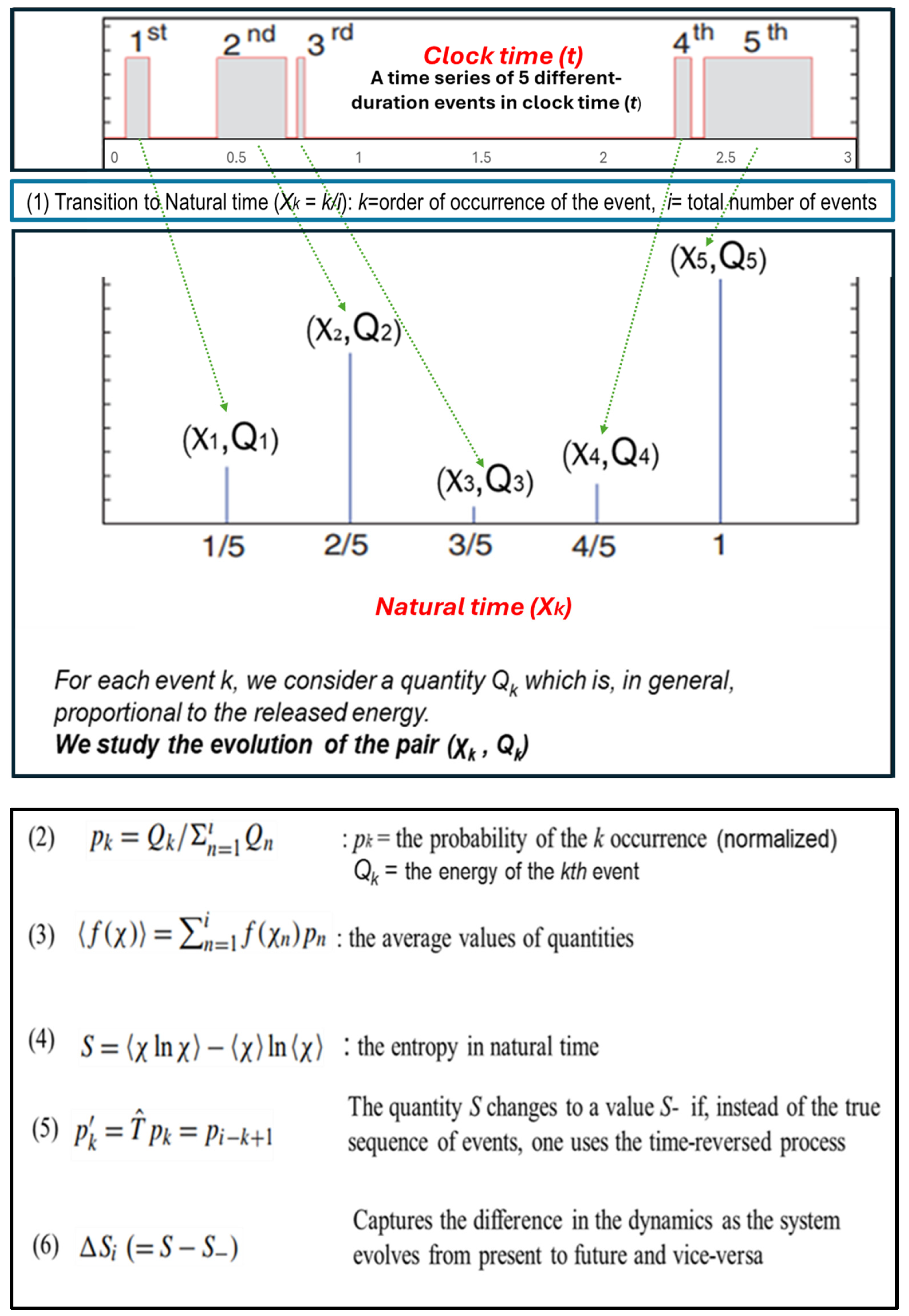
- Each event is assigned a normalized “natural time” χk = k/i, where k is the event index and i is the total number of events.
- The energy (or other quantity of interest) of each event is incorporated as a weight.
- The variance of natural time, κ1, is linked to correlations and criticality.
- The entropy S in natural time evaluates complexity and information content.
3.2.2. The Long-Term Signal for the Forbush Event Phase Transition
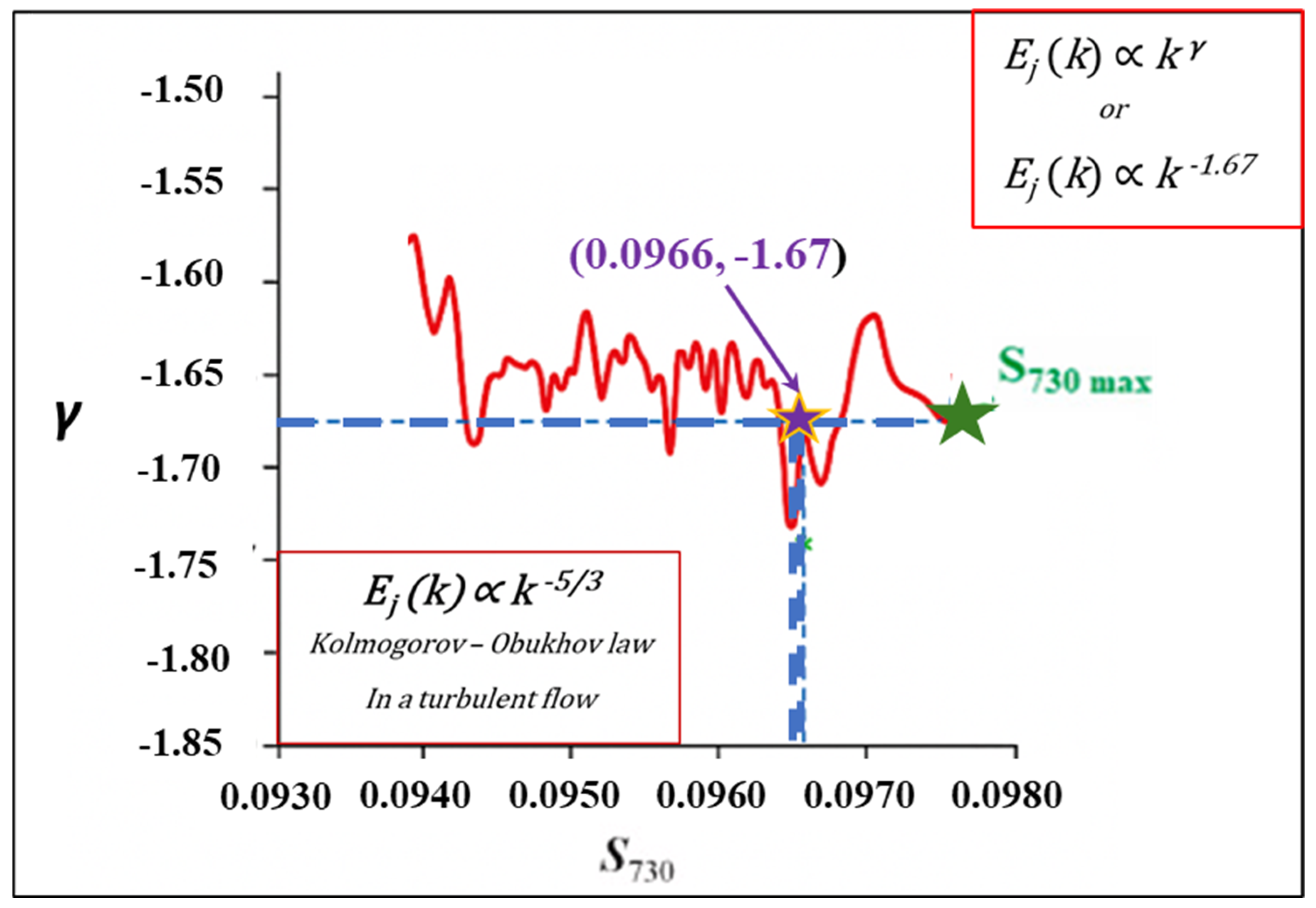
3.2.3. The Order of ECREs for the Future Occurrence Rate
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ginzburg, V.L. (Ed.) Astrophysics of Cosmic Rays; English ed.; North Holland Publ. Co.: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Malkov, M.A.; Diamond, P. Modern theory of Fermi acceleration: A new challenge to plasma physics. Phys. Plasmas 2001, 8, 2401–2406. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Golitsyn, G.S.; Efstathiou, M.; Sarlis, N. A new method of nowcasting extreme cosmic ray events. Remote Sens. Lett. 2023, 14, 576–584. [Google Scholar] [CrossRef]
- Golitsyn, G.; Varotsos, C. The Stochastic Nature of Environmental Phenomena and Processes; Springer: Berlin/Heidelberg, Germany, 2025. [Google Scholar] [CrossRef]
- Blümer, J.; Engel, R.; Hörandel, J.R. Cosmic rays from the knee to the highest energies. Prog. Part. Nucl. Phys. 2009, 63, 293–338. [Google Scholar] [CrossRef]
- Karelin, A.V.; Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Boneci, L.; Bongi, M.; Bonvicini, V.; et al. New measurements of the energy spectra of protons and helium nuclei of high-energy cosmic rays using a calorimeter in the PAMELA experiment. J. Exp. Theor. Phys. 2014, 119, 448–452. [Google Scholar] [CrossRef]
- Varotsos, C.; Tzanis, C.; Cracknell, A. The Enhanced Deterioration of the Cultural Heritage Monuments Due to Air Pollution. Environ. Sci. Pollut. Res. 2009, 16, 590–592. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, C.A.; Golitsyn, G.S.; Xue, Y.; Efstathiou, M.; Sarlis, N.; Voronova, T. On the relation between rain, clouds, and cosmic rays. Remote Sens. Lett. 2023, 14, 301–312. [Google Scholar] [CrossRef]
- Christodoulakis, J.; Varotsos, C.A.; Mavromichalaki, H.; Efstathiou, M.N.; Gerontidou, M. On the link between atmospheric cloud parameters and cosmic rays. J. Atmos. Sol.-Terr. Phys. 2019, 189, 98–106. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Golitsyn, G.S.; Efstathiou, M.; Sarlis, N. The remotely sensed geometric data of rain and clouds as a basis for studying extreme events. Remote Sens. Lett. 2023, 14, 558–564. [Google Scholar] [CrossRef]
- Loftfield, J.; Nowaczyk, N.; Lembke-Jene, L.; Frederichs, T.; Lachner, J.; Lamy, F.; Rugel, G.; Stübner, K.; Adolphi, F. Constraints on the use of cosmogenic beryllium isotopes for synchronizing marine sediments and ice cores. Earth Planet. Sci. Lett. 2025, 671, 119665. [Google Scholar] [CrossRef]
- CERN. CLOUD Challenges Current Understanding of Aerosol Particle Formation in Polar and Marine Regions. CERN, 15 December 2023. [Google Scholar]
- CERN. Cosmic Count Exceeds Expectation. CERN, 13 August 2024. [Google Scholar]
- Sierra-Porta, D. On the fractal properties of cosmic rays and Sun dynamics cross-correlations. Astrophys. Space Sci. 2022, 367, 116. [Google Scholar] [CrossRef]
- Efstathiou, M.N.; Tzanis, C.; Cracknell, A.P.; Varotsos, C.A. New features of land and sea surface temperature anomalies. Int. J. Remote Sens. 2011, 32, 3231–3238. [Google Scholar] [CrossRef]
- Giri, A.; Adhikari, B.; Dahal, S.; Paula, K.S.S.; Bolzan, M.J.A. Multifractal Analysis of Cosmic Rays over Mid- and High-Latitude Stations During Severe Geomagnetic Storms. Sol. Phys. 2024, 299, 148. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Golitsyn, G.S.; Mazei, Y.; Sarlis, N.V.; Xue, Y.; Mavromichalaki, H.; Efstathiou, M.N. On the observed time evolution of cosmic rays in a new time domain. Acta Astronaut. 2024, 225, 436–443. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Papaioannou, A.; Plainaki, C.; Sarlanis, C.; Souvatzoglou, G.; Gerontidou, M.; Tziotziou, K. Applications and usage of the real-time Neutron Monitor Database (NMDB). Adv. Space Res. 2011, 47, 2210–2222. [Google Scholar] [CrossRef]
- Steigies, C.T.; Fuller, N.; The NMDB Team. Accessing NMDB data using NEST and pandas. In Cosmic Ray Studies with Neutron Detectors; Kiel University: Kiel, Germany, 2023; Available online: https://macau.uni-kiel.de/receive/macau_mods_00003844 (accessed on 13 November 2025).
- Maejim, E. An introduction to the theory of self-similar stochastic processes. Int. J. Mod. Phys. B 2000, 14, 1399–1420. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Pachore, A.B.; Remesan, R.; Kumar, R. Multifractal characterization of meteorological to agricultural drought propagation over India. Sci. Rep. 2024, 14, 18889. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 2002, 66, 011902. [Google Scholar] [CrossRef]
- Maraun, D.; Rust, H.W.; Timmer, J. Tempting long-memory—On the interpretation of DFA results. Nonlinear Process Geophys. 2004, 11, 495–503. [Google Scholar] [CrossRef]
- Timmer, J.; Koenig, M. On generating power law noise. Astron. Astrophys. 1995, 300, 707. [Google Scholar]
- Stephens, M.A. EDF statistics for goodness of fit and some comparisons. J. Am. Stat. Assoc. 1974, 69, 730–737. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Makhmutov, V.S.; Bazilevskaya, G.A.; Philippov, M.V.; Stozhkov, Y.I.; Erkhov, V.I.; Morzabaev, A.K.; Tulekov, Y.A.; Raulin, J.P.; Tacza, J. Variations in Cosmic Rays during the Extreme Geomagnetic Disturbances of May 9–15, 2024. Bull. Russ. Acad. Sci. Phys. 2025, 89, 830–834. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Papailiou, M.C.; Livada, M.; Gerontidou, M.; Paschalis, P.; Stassinakis, A.; Abunina, M.; Shlyk, N.; Abunin, A.; Belov, A.; et al. Unusual forbush decreases and geomagnetic storms on 24 March, 2024 and 11 May, 2024. Atmosphere 2024, 15, 1033. [Google Scholar] [CrossRef]
- NASA. Annual Highlights of Results from the International Space Station. 2024. Available online: https://www.nasa.gov/wp-content/uploads/2025/02/ahr-2024-final.pdf (accessed on 13 November 2025).
- Borog, V.V.; Astapov, I.I.; Barbashina, N.S.; Mishutina, Y.N.; Shutenko, V.V. Analysis of Geoeffective Coronal Mass Ejections in the Flux of the Solar Wind and Cosmic Rays at Ground Level on May 10–12, 2024. Bull. Russ. Acad. Sci. Phys. 2025, 89, 821–825. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Order Parameter Fluctuations in Natural Time and B-Value Variation Before Large Earthquakes. Nat. Hazards Earth Syst. Sci. 2012, 12, 3473–3481. [Google Scholar] [CrossRef]
- Nikolopoulos, D.; Cantzos, D.; Alam, A.; Dimopoulos, S.; Petraki, E. Electromagnetic and radon earthquake precursors. Geosciences 2024, 14, 271. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Tanaka, H.A. Plausible Explanation of the B-Value in the Gutenberg-Richter Law from First Principles. Proc. Jpn. Acad. Ser. B 2004, 80, 429–434. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 1987, 59, 381. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 1988, 38, 364. [Google Scholar] [CrossRef] [PubMed]
- Blandford, R.; Eichler, D. Particle acceleration at astrophysical shocks: A theory of cosmic ray origin. Phys. Rep. 1987, 154, 1–75. [Google Scholar] [CrossRef]
- Caprioli, D. Cosmic-ray acceleration in supernova remnants: Non-linear theory revised. J. Cosmol. Astropart. Phys. 2012, 2012, 038. [Google Scholar] [CrossRef]
- Berezinskii, V.S.; Bulanov, S.V.; Dogiel, V.A.; Ginzburg, V.L.; Ptuskin, V.S. Astrophysics of Cosmic Rays; Izdatel’stvo Nauka: Moscow, Russia, 1984. [Google Scholar]
- Aschwanden, M.J. A macroscopic description of a generalized self-organized criticality system: Astrophysical applications. Astrophys. J. 2014, 782, 54. [Google Scholar] [CrossRef]
- Tsonis, A.A.; Deyle, E.R.; May, R.M.; Sugihara, G.; Swanson, K.; Verbeten, J.D.; Wang, G. Dynamical evidence for causality between galactic cosmic rays and interannual variation in global temperature. Proc. Natl. Acad. Sci. USA 2015, 112, 3253–3256. [Google Scholar] [CrossRef]
- Varotsos, C.; Sarlis, N.V.; Mazei, Y.; Saldaev, D.; Efstathiou, M. A composite tool for forecasting El Niño: The case of the 2023–2024 event. Forecasting 2024, 6, 187–203. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chattopadhyay, S. Exploring the Indian summer monsoon rainfall through multifractal detrended fluctuation analysis and the principle of entropy maximization. Earth Sci. Inform. 2021, 14, 1571–1577. [Google Scholar] [CrossRef]
- Pal, S.; Dutta, S.; Nasrin, T.; Chattopadhyay, S. Hurst exponent approach through rescaled range analysis to study the time series of summer monsoon rainfall over northeast India. Theor. Appl. Climatol. 2020, 142, 581–588. [Google Scholar] [CrossRef]
- Chakraborty, S.; Chattopadhyay, S. A probe into the behaviour of total ozone time series through multifractal detrended fluctuation analysis. Theor. Appl. Climatol. 2022, 148, 671–677. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varotsos, C. The Hidden Order of Cosmic Rays: Fractal Scaling and Temporal Complexity. Fractal Fract. 2025, 9, 748. https://doi.org/10.3390/fractalfract9110748
Varotsos C. The Hidden Order of Cosmic Rays: Fractal Scaling and Temporal Complexity. Fractal and Fractional. 2025; 9(11):748. https://doi.org/10.3390/fractalfract9110748
Chicago/Turabian StyleVarotsos, Costas. 2025. "The Hidden Order of Cosmic Rays: Fractal Scaling and Temporal Complexity" Fractal and Fractional 9, no. 11: 748. https://doi.org/10.3390/fractalfract9110748
APA StyleVarotsos, C. (2025). The Hidden Order of Cosmic Rays: Fractal Scaling and Temporal Complexity. Fractal and Fractional, 9(11), 748. https://doi.org/10.3390/fractalfract9110748





