B-Spline Wavelet Scheme for Multi-Term Time–Space Variable-Order Fractional Nonlinear Diffusion-Wave Equation
Abstract
1. Introduction
- Linearizing the M-TS-VFNDWE via quasilinearization;
- Discretizing the linearized equation using a collocation method to derive an algebraic system;
- Establishing a rigorous convergence analysis for the proposed scheme.
2. Preliminaries
2.1. Fractional Definitions
2.2. Semi-Orthogonal B-Spline Wavelets on a Bounded Interval
3. B-Spline Wavelet Scheme
| Algorithm 1 Semi-orthogonal B-spline wavelet collocation method. |
4. Convergence Analysis
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| V-FPDE | variable-order fractional partial differential equation |
| M-TS-VFNDWE | multi-term time–space variable-order fractional nonlinear diffusion-wave equation |
| M-TS-VFLDWE | multi-term time–space variable-order fractional linear diffusion-wave equation |
| SOBWCM | semi-orthogonal B-spline wavelet collocation method |
| BSWS | B-spline wavelet scheme |
| CWM | Chebyshev wavelet method |
| LDGM | local discontinuous Galerkin method |
References
- Soon, C.M.; Coimbra, C.F.M.; Kobayashi, M.H. The variable viscoelasticity oscillator. Ann. Phys. 2005, 14, 378–389. [Google Scholar] [CrossRef]
- Diaz, G.; Coimbra, C.F.M. Nonlinear dynamics and control of a variable order oscillator with application to the van der Pol equation. Nonlinear Dyn. 2009, 56, 145–157. [Google Scholar] [CrossRef]
- Pang, G.; Perdikaris, P.; Cai, W.; Karniadakis, G.E. Discovering variable fractional orders of advection-dispersion equations from field data using multi-fidelity Bayesian optimization. J. Comput. Phys. 2017, 348, 694–714. [Google Scholar] [CrossRef]
- Li, Z.; Wang, H.; Xiao, R.; Yang, S. A variable-order fractional differential equation model of shape memory polymers. Chaos Solitons Fractals 2017, 102, 473–485. [Google Scholar] [CrossRef]
- Lu, X.; Li, H.; Chen, N. An indicator for the electrode aging of lithium-ion batteries using a fractional variable order model. Electrochim. Acta 2019, 299, 378–387. [Google Scholar] [CrossRef]
- Samko, S. Fractional integration and differentiation of variable order. Anal. Math. 1995, 21, 213–236. [Google Scholar] [CrossRef]
- Coimbra, C.F.M. Mechanics with variable-order differential operators. Ann. Phys. 2003, 12, 692–703. [Google Scholar] [CrossRef]
- Lin, R.; Liu, F.; Anh, V.; Turner, I. Stability and convergence of a new explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Appl. Math. Comput. 2009, 212, 435–445. [Google Scholar] [CrossRef]
- Shen, S.; Liu, F.; Chen, J.; Turner, I.; Anh, V. Numerical techniques for the variable order time fractional diffusion equation. Appl. Math. Comput. 2012, 218, 10861–10870. [Google Scholar] [CrossRef]
- Sun, H.G.; Chen, W.; Li, C.P.; Chen, Y.Q. Finite difference schemes for variable-order time fractional diffusion equation. Int. J. Bifurc. Chaos 2012, 22, 1250085. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Khader, M.M.; Almarwm, H.M. Numerical studies for the variable-order nonlinear fractional wave equation. Fract. Calc. Appl. Anal. 2012, 15, 669–683. [Google Scholar] [CrossRef][Green Version]
- Xu, T.; Lu, S.J.; Chen, W.P.; Chen, H. Finite difference scheme for multi-term variable-order fractional diffusion equation. Adv. Differ. Equ. 2018, 2018, 103. [Google Scholar] [CrossRef]
- Zayernouri, M.; Karniadakis, G.E. Fractional spectral collocation methods for linear and nonlinear variable order FPDEs. J. Comput. Phys. 2015, 293, 312–338. [Google Scholar] [CrossRef]
- Jiang, W.; Li, H. A space-time spectral collocation method for the two-dimensional variable-order fractional percolation equations. Comput. Math. Appl. 2018, 75, 3508–3520. [Google Scholar] [CrossRef]
- Bhrawy, A.H.; Zaky, M.A. Highly accurate numerical schemes for multi-dimensional space variable-order fractional Schrödinger equations. Comput. Math. Appl. 2017, 73, 1100–1117. [Google Scholar] [CrossRef]
- Zaky, M.A.; Baleanu, D.; Alzaidy, J.F.; Hashemizadeh, E. Operational matrix approach for solving the variable-order nonlinear Galilei invariant advection-diffusion equation. Adv. Differ. Equ. 2018, 2018, 102. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z.; Mahmoudi, M.R. Chebyshev cardinal wavelets for nonlinear stochastic differential equations driven with variable-order fractional Brownian motion. Chaos Solitons Fractals 2019, 124, 105–124. [Google Scholar] [CrossRef]
- Heydari, M.H.; Avazzadeh, Z.; Haromi, M.F. A wavelet approach for solving multi-term variable-order time fractional diffusion-wave equation. Appl. Math. Comput. 2019, 341, 215–228. [Google Scholar] [CrossRef]
- Hosseininia, M.; Heydari, M.H.; Ghaini, F.M.M.; Avazzadeh, Z. A wavelet method to solve nonlinear variable-order time fractional 2D Klein-Gordon equation. Comput. Math. Appl. 2019, 78, 3713–3730. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Albalawi, A.O. A novel variable-order fractional nonlinear Klein Gordon model: A numerical approach. Numer. Methods Partial. Differ. Equ. 2019, 35, 1617–1629. [Google Scholar] [CrossRef]
- Doha, E.H.; Abdelkawy, M.A.; Amin, A.Z.M.; Lopes, A.M. A space-time spectral approximation for solving nonlinear variable-order fractional sine and Klein-Gordon differential equations. Comput. Appl. Math. 2018, 37, 6212–6229. [Google Scholar] [CrossRef]
- Lakestani, M.; Razzaghi, M.; Dehghan, M. Numerical solution of the controlled Duffing oscillator by semi-orthogonal spline wavelets. Phys. Scr. 2006, 74, 362–366. [Google Scholar] [CrossRef]
- Ahmadinia, M.; Safari, Z. Analysis of local discontinuous Galerkin method for time-space fractional sine-Gordon equations. Appl. Numer. Math. 2020, 148, 1–17. [Google Scholar] [CrossRef]
- Bellman, R.E.; Kalaba, R.E. Quasilinearization and Nonlinear Boundary-Value Problems; American Elsevier Publishing Company: New York, NY, USA, 1965. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Chui, C.K.; Quak, E. Wavelets on a Bounded Interval. In Numerical Methods in Approximation Theory; Braess, D., Schumaker, L.L., Eds.; Birkhäuser-Verlag, Basel: College Station, TX, USA, 1992; pp. 53–75. [Google Scholar]
- Liu, C.; Zhang, X.M.; Wu, B.Y. Numerical solution of fractional differential equations by semiorthogonal B-spline wavelets. Math. Methods Appl. Sci. 2019, 44, 2697–2710. [Google Scholar] [CrossRef]
- Maleknejad, K.; Nouri, K.; Sahlan, M.N. Convergence of approximate solution of nonlinear Fredholm-Hammerstein integral equations. Commun. Nonlinear Sci. 2010, 15, 1432–1443. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Liu, C.; Zhang, X.; Wu, B. Quasilinearized semi-orthogonal B-spline wavelet method for solving multi-term non-linear fractional order equations. Mathematics 2020, 8, 1549. [Google Scholar] [CrossRef]


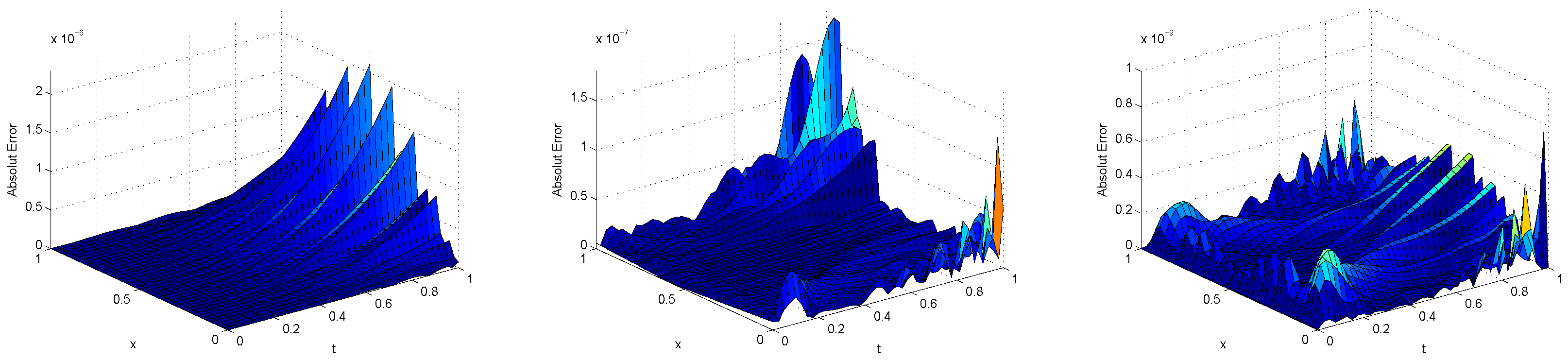
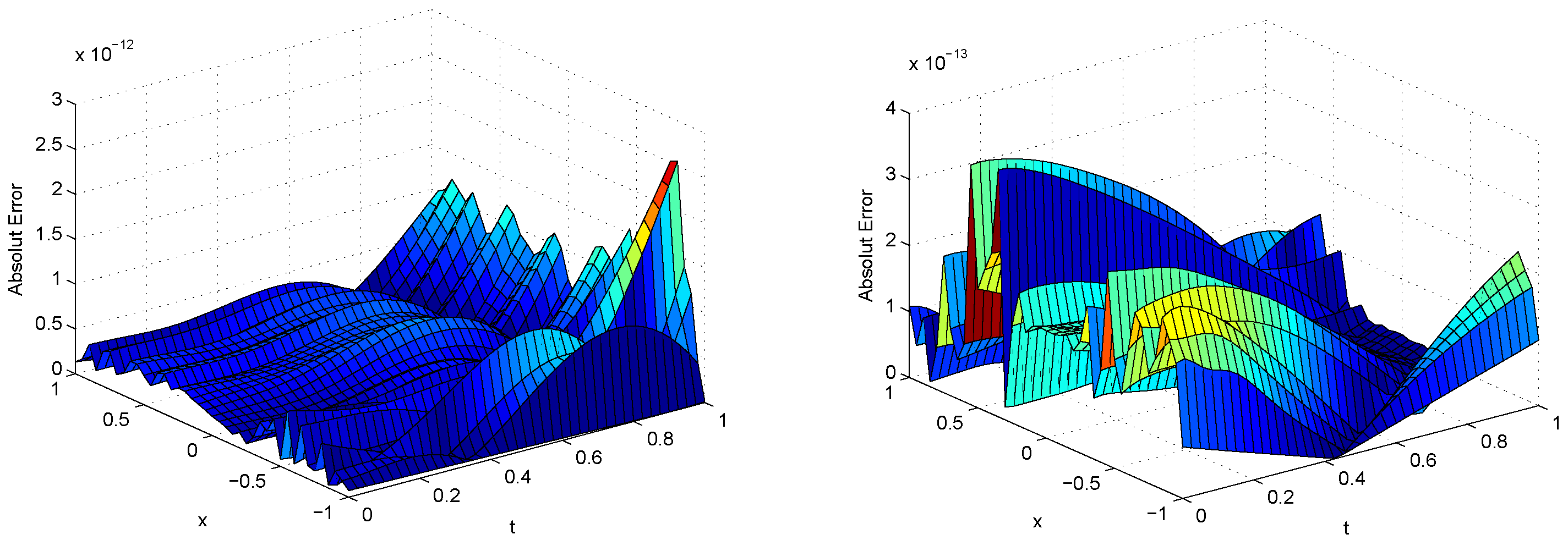
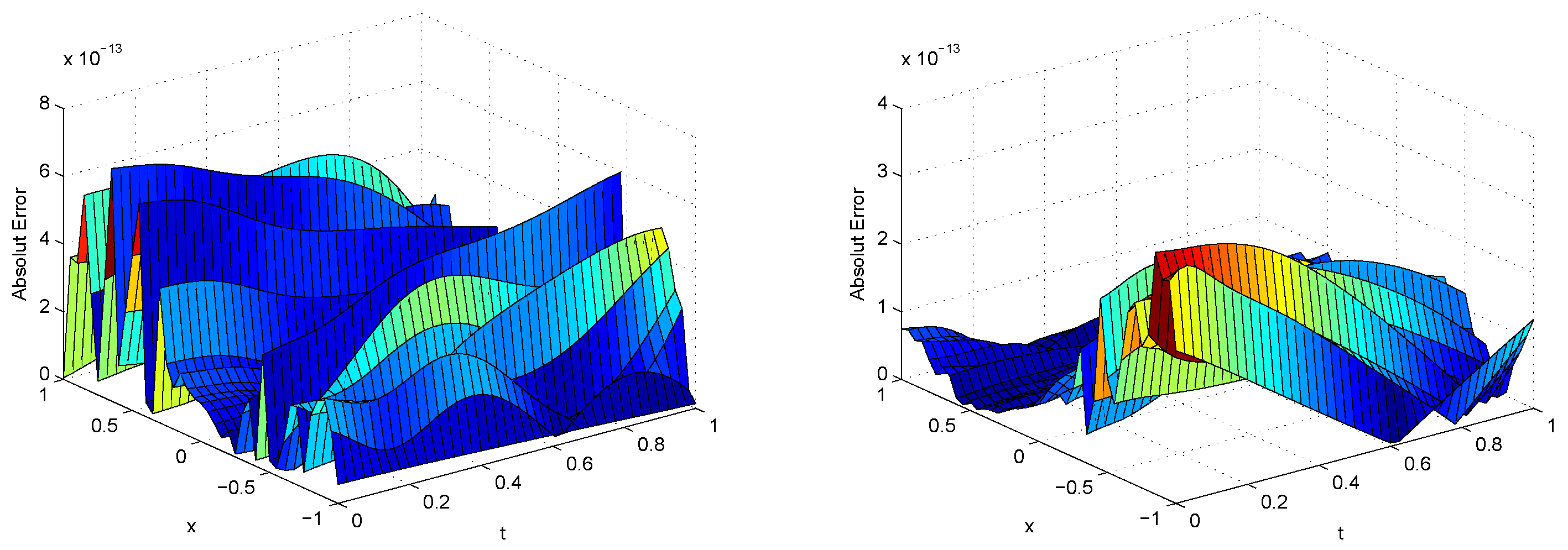
| BSWS | CWM | ||||||
|---|---|---|---|---|---|---|---|
| (0.1,0.1) | 4.4070 | 1.1338 | 4.7947 | 4.1355 | 3.2005 | 1.3326 | 9.4321 |
| (0.2,0.2) | 3.0324 | 5.8055 | 9.5953 | 2.7010 | 3.1341 | 1.9025 | 3.9248 |
| (0.3,0.3) | 7.6473 | 2.9594 | 7.9989 | 1.1969 | 5.3652 | 5.4423 | 5.1393 |
| (0.4,0.4) | 9.8438 | 2.8004 | 5.4350 | 1.3484 | 3.0927 | 3.3837 | 3.2847 |
| (0.5,0.5) | 3.6230 | 2.5739 | 1.6525 | 1.0421 | 2.6813 | 3.7564 | 8.2481 |
| (0.6,0.6) | 3.8095 | 9.7979 | 1.8443 | 4.5529 | 1.5741 | 2.0331 | 3.1398 |
| (0.7,0.7) | 1.3502 | 4.1117 | 1.0687 | 1.5270 | 4.9913 | 5.4594 | 1.0362 |
| (0.8,0.8) | 4.1153 | 3.7428 | 7.8339 | 1.7238 | 8.3473 | 2.5894 | 3.1942 |
| (0.9,0.9) | 7.1112 | 2.2003 | 1.7268 | 3.4461 | 5.1754 | 9.4243 | 1.4991 |
| Error | ||||
|---|---|---|---|---|
| -error | 3.6721 | 2.1475 | 3.1287 | 2.5657 |
| -error | 2.1118 | 1.7879 | 8.0679 | 5.9673 |
| BSWS | LDGM | ||||
|---|---|---|---|---|---|
| -Error | -Error | -Error | -Error | ||
| 1.5 | 1.5 | 2.9439 | 5.3268 | 5.01 | 5.39 |
| 1.2 | 1.8 | 5.4306 | 1.0356 | 5.65 | 7.56 |
| 1.1 | 5.7490 | 1.6542 | 6.27 | 6.83 | |
| 1.5 | 3.6974 | 8.7014 | 4.76 | 6.64 | |
| 1.8 | 7.8701 | 1.5864 | 5.01 | 6.85 | |
| 1.1 | 4.7225 | 9.0807 | 3.78 | 3.83 | |
| 1.7 | 5.4626 | 1.0390 | 3.58 | 3.75 | |
| 1.1 | 4.7200 | 2.5482 | 4.16 | 4.27 | |
| 1.7 | 1.2201 | 3.7397 | 4.00 | 4.19 | |
| BSWS | LDGM | ||||
|---|---|---|---|---|---|
| -Error | -Error | -Error | -Error | ||
| 1.8 | 1.5 | 8.6691 | 2.1058 | 3.97 | 5.31 |
| 1.3 | 4.8126 | 1.2434 | 2.40 | 2.36 | |
| 1.8 | 3.0802 | 6.5317 | 2.74 | 2.77 | |
| 1.3 | 7.6324 | 2.6229 | 2.44 | 2.41 | |
| 1.8 | 7.6085 | 3.8211 | 2.76 | 2.80 | |
| 1.3 | 2.2781 | 6.8752 | 3.65 | 5.05 | |
| 1.8 | 2.2781 | 6.8752 | 3.95 | 5.62 | |
| 1.5 | 2.3111 | 3.9605 | 4.41 | 6.22 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Yu, Z.; Zhang, X. B-Spline Wavelet Scheme for Multi-Term Time–Space Variable-Order Fractional Nonlinear Diffusion-Wave Equation. Fractal Fract. 2025, 9, 707. https://doi.org/10.3390/fractalfract9110707
Fang J, Yu Z, Zhang X. B-Spline Wavelet Scheme for Multi-Term Time–Space Variable-Order Fractional Nonlinear Diffusion-Wave Equation. Fractal and Fractional. 2025; 9(11):707. https://doi.org/10.3390/fractalfract9110707
Chicago/Turabian StyleFang, Jinwei, Zhe Yu, and Xinming Zhang. 2025. "B-Spline Wavelet Scheme for Multi-Term Time–Space Variable-Order Fractional Nonlinear Diffusion-Wave Equation" Fractal and Fractional 9, no. 11: 707. https://doi.org/10.3390/fractalfract9110707
APA StyleFang, J., Yu, Z., & Zhang, X. (2025). B-Spline Wavelet Scheme for Multi-Term Time–Space Variable-Order Fractional Nonlinear Diffusion-Wave Equation. Fractal and Fractional, 9(11), 707. https://doi.org/10.3390/fractalfract9110707






