On Some Novel Soliton Structures for the Beta-Time Fractional Benjamin–Ono Dynamical Equation in Fluids

Abstract

This paper consists of an exploration of the wave structures of the Benjamin–Ono equation along with a $\beta$-time fractional derivative. The model concerned is utilized to demonstrate internal waves of deep-stratified fluids. Bright, rational, periodic, and many more kinds of solutions for waves are achieved by utilizing the extended sinh-Gordon equation expansion (EShGEE) technique and the improved $G^{\prime }/G$-expansion scheme. An influence of fractional-order derivatives was also explored which gives the non-existing results. The Mathematica tool is utilized to gain and verify the results. The results are represented by 3-D, 2-D, and contour graphs. A stability analysis is utilized to confirm that results are precise as well as exact. Modulation instability (MI) is also performed for the steady-state solutions to the concerned model.

1. Introduction

Many naturally occurring phenomena are expressed as mathematical models. Many models are constructed as a shape of partial fractional differential equations (FPDEs) in various areas of engineering as well as science, for instance, the fractional paraxial Schrödinger equation [1], fractional Westervelt equation [2], and many others. Fractional calculus plays a significant role across various domains of science and engineering. Different methods have been introduced, including the generalized Riccati expansion technique [3], the Khater II scheme [4], the $(G^{\prime }/G,1/G)$-expansion approach [5], and the modified sub-ODE technique [6], among others.

In this research work, the authors utilized two useful and reliable techniques: the EShGEE and the improved $(G^{\prime }/G)$-expansion methods. The techniques concerned are utilized for various equations. For example, the extended ShGEE scheme is utilized for the generalized nonlinear Schrödinger model [7], the Kundu–Eckhaus model [8], the Schrödinger model along anti-cubic non-linearity [9], and the generalized Bretherton model [10]. In the same way, the improved $(G^{\prime }/G)$-expansion approach is applied to the breaking soliton model [11], the Kaup–Kupershmidt model [12], the modified Kawahara model [13], the Estevez–Mansfield–Clarkson model [14], and many more.

The aim of our research is to discover the distinct results of the fractional Benjamin–Ono model. Furthermore, dynamical analysis is discussed in the form of stability as well as MI analysis.

The motivation of our research is to explore the novel types of wave structures of the Benjamin–Ono model in relation to a $\beta$-time fractional derivative. The use of a fractional derivative represents the model in a more prominent form as well as providing more accurate results than the ordinary derivative. The techniques used provide different types of soliton solutions without any limitations/assumptions. Moreover, stability analysis and modulation instability analysis provide us with the stability as well as the accuracy of the solutions and model. The obtained solutions are useful in fluid dynamics and mathematical physics to study wave interaction, wave pattern, wave breaking, ocean engineering, etc.

The rest of the paper is structured as follows. The fractional calculus is introduced in Section 2, while the governing model is shown in Section 3. The analytical strategies are described in Section 4, the scientific computations are carried out in Section 5, the stability process is performed in Section 6, the MI analysis is performed in Section 7, graphical explanations are explored in Section 8, results and discussion are given in Section 9, and we conclude in Section 10.

2. The $\mathit{\beta }$-Time Fractional Derivative

The fractional derivative denotes global connectivity compared to the integer order derivative, suggesting that it could represent the dynamic processes involved in function evolution more precisely. In contrast to traditional calculus, which only examines the problem as it stands, mathematical modeling of these situations uses a fractional derivative, which explains why the models are nonlocal. Many researchers have recently examined many types of conformable fractional derivatives that describe various applications [15]. Fractional Taylor power series expansions, the chain rule, Linear differential systems, Laplace transforms, integration by parts, and Gronwall’s inequality were some of the concepts that Abdeljawad worked on [16]. Numerous significant physical mechanisms have been described in the literature using a range of fractional derivatives [17]. These include the Atangana [18], the Caputo [19], the modified Riemann–Liouville given by Jumarie [20], and the Beta derivative [21].

Suppose that $v(t)$ is defined ∀$t\ge 0$. Therefore, the $\beta$-time fractional derivative of v with order $\Delta$ is given in [22].

$$\begin{array}{c}\hfill D^{\Delta }(v(y))={\displaystyle \frac{d^{\Delta }v(y)}{d{t}^{\Delta }}}=\underset{ϵ\to 0}{lim}{\displaystyle \frac{v(y+ϵ{(y+\frac{1}{\Gamma (\Delta )})}^{1-\Delta })-v(y)}{ϵ}},0<\Delta \le 1.\end{array}$$

Suppose that $v(y)$ and $u(y)$ are $\Delta$-time differential functions ∀ y$>0$ and $\Delta \in (0,1]$, then the given properties are fulfilled [23,24]:

$$\begin{array}{ccc}\hfill D^{\Delta }(av(y)+bu(y))& =& a{D}^{\Delta }(v(y))+b{D}^{\Delta }(u(y)),\forall a,b\in \Re .\hfill \\ \hfill D^{\Delta }(v(y)u(y))& =& u(y)D^{\Delta }(v(y))+v(y)D^{\Delta }(u(y)),\hfill \\ \hfill D^{\Delta }({\displaystyle \frac{v(y)}{u(y)}})& =& {\displaystyle \frac{u(y)D^{\Delta }(v(y))-v(y)D^{\Delta }(u(y))}{{(u(y))}^2}},\hfill \\ \hfill D^{\Delta }(v(y))& =& {\left(y+{\displaystyle \frac{1}{\Gamma (\Delta )}}\right)}^{1-\Delta }{\displaystyle \frac{dv(y)}{d\Delta }}.\hfill \end{array}$$

3. The Governing Model Presentation

Consider a (1+1)-dimensional non-linear Benjamin–Ono (BO) model given as [25]

$$v_t+\mu v_{xx}+v{v}_x=0,$$

(1)

$v=v(x,t)$ indicates the wave profile of spatial variablex and temporal variable t. The parameter $\mu$ denotes the Hilbert transform operator, which is given as $\mu ={\displaystyle \frac{p.\nu }{\pi }}.{\int }_{-\infty }^{\infty }{\displaystyle \frac{\tau (y)}{y-\chi }}dy.$ Equation (1) was initially proposed by Benjamin and Ono to describe the internal waves of deep-stratified fluids. In ocean engineering, the fractional Benjamin–Ono equation is usually utilized in computer simulation for the water waves in deep water and open seas [26]. Different types of techniques are applied to determine the various exact solitons including the extended truncated expansion technique [25], the Jacobi elliptic expansion function scheme [26], the new generalized ($G^{\prime }/G)$-expansion technique [27], the $exp(-\varphi (\zeta ))$-expansion technique [28], $(G^{\prime }/G^2)$-expansion method [29], and many others.

The (1+1)-dimensional non-linear Benjamin–Ono model in $\beta$-time fractional derivative, which describes the internal single wave event in the atmosphere or water [30], is shown as

$${\displaystyle \frac{{\partial }^{\Delta }v}{\partial t^{\Delta }}}+\mu {\displaystyle \frac{{\partial }^{2\Delta }v}{\partial x^{2\Delta }}}+v{\displaystyle \frac{{\partial }^{\Delta }v}{\partial x^{\Delta }}}=0.$$

(2)

In the literature, different researchers have discussed the concerned equation; for example, F. Alizadeh et al. adopted the lie symmetries [31], while B. Sagar and S. Saha Ray implemented the unity method [32], whereas B. Babajanov applied the functional variable method [33] and H. Yang et al. employed the multi-scale analysis and perturbation approach [34] to analyse the higher dimensional fractional model efficiently.

4. Methodology

4.1. The Extended ShGEE Technique

In this subsection, we outline the basic points for the technique concerned.

Stage 1:

Consider a non-linear FPDE:

$$Z(g,D_t^{\Delta }{g}^2,g^2{g}_x,g_x,\cdots )=0$$

(3)

Here, g denotes wave-function. Suppose the following

$$g(x,t)=G(\mho ),\mho =x+{\displaystyle \frac{\kappa }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }.$$

(4)

Inserting Equation (4) in Equation (3) yields

$$H(G,G^2{G}^{\prime },G^{″},\cdots )=0.$$

(5)

Stage 2:

Assuming the solutions of Equation (5) given below,

$$G(p)={\alpha }_0+\sum _{j=1}^m{({\beta }_{j}sinh(p)+{\alpha }_{j}cosh(p))}^j,$$

(6)

here, ${\alpha }_0$, ${\alpha }_j$, ${\beta }_j$$(j=1,2,3,...,m)$ denote the undetermined. Considering a new profile p of ℧ fulfills

$${\displaystyle \frac{dp}{d\mho }}=sinh(p).$$

(7)

A positive integer m is calculated by using the homogenous balance (HB) technique. Equation (7) is achieved from the equation below:

$$q_{xt}=\kappa sinh(v).$$

(8)

From [35], one obtains the results for Equation (8), providing

$$sinhp(\mho )=\pm csch(\mho )\mathrm{or}coshp(\mho )=\pm coth(\mho ),$$

(9)

and

$$sinhp(\mho )=\pm \iota sech(\mho )\mathrm{or}coshp(\mho )=\pm tanh(\mho ).$$

(10)

${\iota }^2=-1$.

Stage 3:

Using Equation (6) along with Equation (7) in Equation (5), results a set containing $p^{\prime a}(\mho ){sinh}^{b}p(\mho ){cosh}^{n}p(\mho )$$(a=0,1;b=0,1;n=0,1,2,...)$. Setting every coefficient of $p^{\prime a}(\mho ){sinh}^{b}p(\mho ){cosh}^{n}p(\mho )$ equal to zero achieves a set.

Stage 4:

After simplifying the gained set, we achieved the solutions for the undetermined. Using the achieved results, Equations (9) and (10) provide the results of Equation (5), given as

$$G(\mho )={\alpha }_0+\sum _{j=1}^m{(\pm {\beta }_{j}csch(\mho )\pm {\alpha }_{j}coth(\mho ))}^j$$

(11)

and

$$G(\mho )={\alpha }_0+\sum _{j=1}^m{(\pm \iota {\beta }_{j}sech(\mho )\pm {\alpha }_{j}tanh(\mho ))}^j.$$

(12)

With the use of this technique, we gain solutions consisting of sech, $csch$, tanh, and coth.

4.2. Improved $(G^{\prime }/G)$-Expansion Technique

This subsection consists on the basic concept of the scheme [36].

Stage 1: Consider a non-linear PFDE.

$$Z(g,D_t^{\Delta }g,g^2{g}_x,...)=0.$$

(13)

Stage 2: Assume the given transformation:

$$g(x,t)=G(\eta ),\eta =x-{\displaystyle \frac{\kappa }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }.$$

(14)

where $\kappa$ denotes the constant. Inserting Equation (14) in Equation (13) provides

$$Y(G,G^2{G}^{\prime },...)=0.$$

(15)

Stage 3: Assume the following solution of Equation (15):

$$Q(\eta )=\sum _{i=0}^m{\alpha }_i{\left({\displaystyle \frac{G^{\prime }(\eta )}{G(\eta )}}\right)}^i.$$

(16)

In Equation (16), ${\alpha }_i,(i=0,1,...,m)$ denote the undetermined. By utilizing the HB approach for Equation (15), we achieve m. A profile $G=G(\eta )$ satisfies the equation:

$$G{G}^{″}-{\kappa }_1{G}^2-{\kappa }_{2}G{G}^{\prime }-{\kappa }_3{(G^{\prime })}^2=0,$$

(17)

Here, ${\kappa }_1$, ${\kappa }_2$, and ${\kappa }_3$ denote the constants.

Stage 4:

Assume that Equation (17) has the following results:

Case 1: If ${\kappa }_2\ne 0$ and $\pi ={\kappa }_2^2+4{\kappa }_1-4{\kappa }_1{\kappa }_3>0$, then

$${\displaystyle \frac{G^{\prime }(\eta )}{G(\eta )}}={\displaystyle \frac{{\kappa }_2\sqrt{\pi }\left(C_{1}exp\left(\frac{1}{2}\sqrt{\pi }\eta \right)+C_{2}exp\left(\frac{1}{2}\left(-\sqrt{\pi }\right)\eta \right)\right)}{(2(1-{\kappa }_3))\left(C_{1}exp\left(\frac{1}{2}\sqrt{\pi }\eta \right)-C_{2}exp\left(\frac{1}{2}\left(-\sqrt{\pi }\right)\eta \right)\right)}}+{\displaystyle \frac{{\kappa }_2}{2(1-{\kappa }_3)}}.$$

(18)

Case 2: If ${\kappa }_2\ne 0$ and $\pi ={\kappa }_2^2+4{\kappa }_1-4{\kappa }_1{\kappa }_3<0$, then

$${\displaystyle \frac{G^{\prime }(\eta )}{G(\eta )}}={\displaystyle \frac{{\kappa }_2\sqrt{-\pi }(C_1\iota cos(\frac{1}{2}\sqrt{-\pi }\eta )-C_{2}sin(\frac{1}{2}\sqrt{-\pi }\eta ))}{(2(1-{\kappa }_3))(C_1\iota sin(\frac{1}{2}\sqrt{-\pi }\eta )+C_{2}cos(\frac{1}{2}\sqrt{-\pi }\eta ))}}+{\displaystyle \frac{{\kappa }_2}{2(1-{\kappa }_3)}}.$$

(19)

Case 3: If ${\kappa }_2=0$ and ${\kappa }_1-{\kappa }_1{\kappa }_3\ge 0$, this provides

$${\displaystyle \frac{G^{\prime }(\eta )}{G(\eta )}}={\displaystyle \frac{\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\left(C_{2}sin\left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)+C_{1}cos\left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)\right)}{(1-{\kappa }_3)\left(C_{1}sin\left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)-C_{2}cos\left(\eta \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}\right)\right)}}.$$

(20)

Case 4: If ${\kappa }_2=0$ and ${\kappa }_1-{\kappa }_1{\kappa }_3<0$, then

$${\displaystyle \frac{G^{\prime }(\eta )}{G(\eta )}}={\displaystyle \frac{\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\left(C_1\iota cosh\left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)-C_{2}sinh\left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)\right)}{(1-{\kappa }_3)\left(C_1\iota sinh\left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)-C_{2}cosh\left(\eta \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}\right)\right)}}.$$

(21)

here ${\kappa }_1$, ${\kappa }_2$, ${\kappa }_3$, $C_1$, and $C_2$ denote the parameters.

Stage 5:

Substitute Equation (16) with Equation (17) in Equation (15) and combine the coefficient of each order of $\left({\displaystyle \frac{G^{\prime }(\eta )}{G(\eta )}}\right)$. Setting them equal to zero, we achieve a set.

Step 6:

Utilize the Mathematica software to solve the gained set of equations.

Step 7:

Using solutions in Equation (16) results in different solitons for Equation (13).

5. Mathematical Analysis

Assuming the following,

$$v(x,t)=V(\zeta ),\zeta =({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+\lambda {\displaystyle \frac{1}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })$$

(22)

using Equation (22) into Equation (2) results in

$$\lambda V^{\prime }+\mu V^{″}+V{V}^{\prime }=0.$$

(23)

Taking the integration of Equation (23) w.r.t $\zeta$ and considering the constant of integration 0 results in the following ODE:

$$\lambda V+\mu V^{\prime }+{\displaystyle \frac{1}{2}}{V}^2=0.$$

(24)

The value of m is obtained by a homogenous balance approach in Equation (24), and balancing the terms $V^{\prime }$ and $V^2$, one obtains $m=1$.

5.1. Applications of the Extended ShGEE Technique

Equation (6) changes to the given form for $m=1$:

$$V(\mho )={\alpha }_0+{\alpha }_{1}cosh(f(\mho ))+{\beta }_{1}sinh(f(\mho )).$$

(25)

Using Equations (25) and (7) in Equation (24), we gain a system containing ${\alpha }_0$, ${\alpha }_1$, ${\beta }_1$, $\lambda$, and $\rho$. By manipulation, the results are given in the form of sets.

Set 1:

$$\left\{{\alpha }_0=-\mu ,{\alpha }_1=-\mu ,{\beta }_1=-\mu ,\lambda =\mu \right\}.$$

(26)

$$v_{11}(x,t)=-\mu (1\pm coth({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\pm \csc \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(27)

$$v_{12}(x,t)=-\mu (1\pm tanh({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\pm \iota \sec \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(28)

Set 2:

$$\left\{{\alpha }_0=\mu ,{\alpha }_1=-\mu ,{\beta }_1=-\mu ,\lambda =-\mu \right\}.$$

(29)

$$v_{21}(x,t)=-\mu (-1\pm coth({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\pm \csc \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+\lambda {\displaystyle \frac{1}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(30)

$$v_{22}(x,t)=-\mu (-1\pm tanh({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\pm \iota \sec \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+\lambda {\displaystyle \frac{1}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(31)

Set 3:

$$\left\{{\alpha }_0=-\mu ,{\alpha }_1=-\mu ,{\beta }_1=\mu ,\lambda =\mu \right\}.$$

(32)

$$v_{31}(x,t)=-\mu (1\pm coth({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\mp \csc \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(33)

$$v_{32}(x,t)=-\mu (1\pm tanh({\displaystyle \frac{1}{\tau }}{(x+{\displaystyle \frac{1}{\Gamma (\tau )}})}^{\tau }+{\displaystyle \frac{\mu }{\tau }}{(t+{\displaystyle \frac{1}{\Gamma (\tau )}})}^{\tau })\mp \iota \sec \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(34)

Set 4:

$$\left\{{\alpha }_0=\mu ,{\alpha }_1=-\mu ,{\beta }_1=\mu ,\lambda =-\mu \right\}.$$

(35)

$$v_{41}(x,t)=\mu (1\mp coth({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\pm \csc \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(36)

$$v_{42}(x,t)=\mu (1\mp tanh({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\pm \iota \sec \mathrm{h}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(37)

Set 5:

$$\left\{{\alpha }_0=-2\mu ,{\alpha }_1=-2\mu ,{\beta }_1=0,\lambda =2\mu \right\}.$$

(38)

$$v_{51}(x,t)=-2\mu (1\pm coth({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{2\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(39)

$$v_{52}(x,t)=-2\mu (1\pm tanh({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{2\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(40)

Set 6:

$$\left\{{\alpha }_0=2\mu ,{\alpha }_1=-2\mu ,{\beta }_1=0,\lambda =-2\mu \right\}.$$

(41)

$$v_{61}(x,t)=2\mu (1\mp coth({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{2\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(42)

$$v_{62}(x,t)=2\mu (1\mp tanh({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{2\mu }{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })).$$

(43)

5.2. Soliton Solutions via the Improved $(G^{\prime }/G)$-Expansion Technique

Equation (16) takes the form for $m=1$:

$$V(\zeta )={\alpha }_0+{\alpha }_1\left({\displaystyle \frac{G^{\prime }(\zeta )}{G(\zeta )}}\right).$$

(44)

Here, ${\alpha }_0$ and ${\alpha }_1$ denote undetermined.

Applying Equation (44) with Equation (17) in Equation (24), we achieve the following sets.

Set 1:

$$\left\{{\alpha }_0=-{\kappa }_2\mu -\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))},{\alpha }_1=-2({\kappa }_3-1)\mu ,\lambda =\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}\right\}.$$

(45)

Case 1:

$$\begin{array}{c}v(x,t)=-{\kappa }_2\mu -\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu (({\kappa }_2\sqrt{\pi }(C_{1}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ +{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{\pi })+C_{2}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })(-\sqrt{\pi }))))/((2(1-{\kappa }_3))(C_{1}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{\pi })-C_{2}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })(-\sqrt{\pi }))))+{\displaystyle \frac{{\kappa }_2}{2(1-{\kappa }_3)}}).\end{array}$$

(46)

Case 2:

$$\begin{array}{c}v(x,t)=-{\kappa }_2\mu -\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu (({\kappa }_2\sqrt{-\pi }(C_1\iota cos({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ +{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{-\pi })-C_{2}sin({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{-\pi })))/((2(1-{\kappa }_3))(C_1\iota sin({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{-\pi })+C_{2}cos({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{-\pi })))+{\displaystyle \frac{{\kappa }_2}{2(1-{\kappa }_3)}}).\end{array}$$

(47)

Case 3:

$$\begin{array}{c}v(x,t)=-\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu ((\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}(C_{2}sin(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ +{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})+C_{1}cos(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})))/((1-{\kappa }_3)(C_{1}sin(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})-C_{2}cos(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})))).\end{array}$$

(48)

Case 4:

$$\begin{array}{c}v(x,t)=-\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu ((\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}(C_1\iota cosh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ +{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})-C_{2}sinh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})))/((1-{\kappa }_3)(C_1\iota sinh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})-C_{2}cosh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }+{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})))).\end{array}$$

(49)

Set 2:

$$\left\{{\alpha }_0=-{\kappa }_2\mu +\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))},{\alpha }_1=-2({\kappa }_3-1)\mu ,\lambda =-\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}\right\}.$$

(50)

Case 1:

$$\begin{array}{c}v(x,t)=-{\kappa }_2\mu +\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu (({\kappa }_2\sqrt{\pi }(C_{1}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ -{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{\pi })+C_{2}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })(-\sqrt{\pi }))))/((2(1-{\kappa }_3))(C_{1}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{\pi })-C_{2}exp({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })(-\sqrt{\pi }))))+{\displaystyle \frac{{\kappa }_2}{2(1-{\kappa }_3)}}).\end{array}$$

(51)

Case 2:

$$\begin{array}{c}v(x,t)=-{\kappa }_2\mu +\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu (({\kappa }_2\sqrt{-\pi }(C_1\iota cos({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ -{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{-\pi })-C_{2}sin({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{{\kappa }_2^2-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{-(\pi )})))/((2(1-{\kappa }_3))(C_1\iota sin({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{-\pi })+C_{2}cos({\displaystyle \frac{1}{2}}({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{({\kappa }_2^2-4{\kappa }_1({\kappa }_3-1))}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{-\pi })))+{\displaystyle \frac{{\kappa }_2}{2(1-{\kappa }_3)}}).\end{array}$$

(52)

Case 3:

$$\begin{array}{c}v(x,t)=\mu \sqrt{4{\kappa }_1-4{\kappa }_1{\kappa }_3}-2({\kappa }_3-1)\mu ((\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3}(C_{2}sin(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ -{\displaystyle \frac{\mu \sqrt{4{\kappa }_1-4{\kappa }_1{\kappa }_3}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})+C_{1}cos(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{4{\kappa }_1-4{\kappa }_1{\kappa }_3}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})))/((1-{\kappa }_3)(C_{1}sin(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{4{\kappa }_1-4{\kappa }_1{\kappa }_3}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})-C_{2}cos(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{4{\kappa }_1-4{\kappa }_1{\kappa }_3}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1-{\kappa }_1{\kappa }_3})))).\end{array}$$

(53)

Case 4:

$$\begin{array}{c}v(x,t)=\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}-2({\kappa }_3-1)\mu ((\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1}(C_1\iota cosh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }\hfill \\ -{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})-C_{2}sinh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}\\ {(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})))/((1-{\kappa }_3)(C_1\iota sinh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\rho }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\\ \hfill \sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})-C_{2}cosh(({\displaystyle \frac{1}{\Delta }}{(x+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta }-{\displaystyle \frac{\mu \sqrt{-4{\kappa }_1({\kappa }_3-1)}}{\Delta }}{(t+{\displaystyle \frac{1}{\Gamma (\Delta )}})}^{\Delta })\sqrt{{\kappa }_1{\kappa }_3-{\kappa }_1})))).\end{array}$$

(54)

6. The Stability Analysis (SA)

Here, we discuss an important analysis of the equation concerned. It is applied for various models, including [37,38]. For Equation (24), the stability analysis, we use the following:

$$\begin{array}{c}\hfill \mathcal{S}={\displaystyle \frac{1}{2}}{\int }_{-\infty }^{\infty }{\mathit{v}}^{\mathit{2}}dx,\end{array}$$

(55)

here, $\mathcal{S}$ represents a factor of momentum and $\mathit{v}(\mathit{x},\mathit{t})$ indicates the possibility power. An important criterion of stable solution is shown as

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial \mathcal{S}}{\partial \lambda }}>0,\end{array}$$

(56)

here, $\lambda$ denotes a soliton velocity; substituting Equation (31) in Equation (55) yields

$$\mathcal{S}={\displaystyle \frac{1}{2}}{\int }_{-6}^6{(-\mu (1+coth(x+\mu t)+\csc \mathrm{h}(x+\mu t)))}^{2}dx$$

(57)

By using the criterion given in Equation (56), we get the following for $\mu =0.5$ and $t=1$:

$$\begin{array}{c}-{\mu }^2({\displaystyle \frac{1}{2}}ttanh(3-{\displaystyle \frac{\mu t}{2}})-{\displaystyle \frac{1}{2}}tcoth({\displaystyle \frac{\mu t}{2}}+3)-{\displaystyle \frac{1}{2}}tcoth(3-{\displaystyle \frac{\mu t}{2}})-tcoth(\mu t)-tcoth(6-\mu t)\hfill \\ -t{\csc \mathrm{h}}^2(\mu t+6)+t{\csc \mathrm{h}}^2(6-\mu t)-tcoth(\mu t+6)\csc \mathrm{h}(\mu t+6)+tcoth(6-\mu t)\csc \mathrm{h}(6-\mu t)\\ +sinh(\mu t+6)\csc \mathrm{h}(\mu t)\sec \mathrm{h}({\displaystyle \frac{\mu t}{2}}+3)(tcosh({\displaystyle \frac{\mu t}{2}}+3)cosh(\mu t)\csc \mathrm{h}(\mu t+6)+\\ \hfill {\displaystyle \frac{1}{2}}tsinh({\displaystyle \frac{\mu t}{2}}+3)sinh(\mu t)\csc \mathrm{h}(\mu t+6)-tsinh(\mu t)cosh({\displaystyle \frac{\mu t}{2}}+3)coth(\mu t+6)\csc \mathrm{h}(\mu t+6)))>0.\end{array}$$

(58)

Hence, Equation (24) indicates the existence of a stable nonlinear model, provided the condition is fulfilled.

7. The Modulation Instability Analysis

In a nonlinear dispersion medium, a continuous surface wave induces modulation instability, leading to self-modulation of phase and intensity. To achieve the steady-state solution for the Benjamin–Ono model, assume the following relation as in [39]:

$$v(x,t)=\left(\sqrt{\tau }+V(x,t)\right)e^{\iota \tau t}$$

(59)

Here, $\tau$ indicates the normalized optical power. Using Equation (59) in Equation (1) and by linearizing, we obtain

$$\iota {\tau }^{3/2}+V_t+\iota \tau V+\mu V_{\mathrm{xx}}=0.$$

(60)

Consider the result of Equation (60) given as

$$V(x,t)=A_1{e}^{\iota (px-qt)}+A_2{e}^{-\iota (px-qt)}.$$

(61)

Here, q and p indicate the perturbation frequency and normalization wave number. Inserting Equation (61) in Equation (60) and by collecting each coefficient of $e^{\iota (px-qt)}$ and $e^{-\iota (px-qt)}$, we get a dispersive solution by solving the determinant of the coefficient matrix:

$${\mu }^2{p}^4+q^2-{\tau }^2=0=0.$$

(62)

Finding the dispersion result of Equation (62) for q yields

$$q=\pm \sqrt{{\tau }^2-{\mu }^2{p}^4}.$$

(63)

The obtained dispersive result denotes the stable steady state solution. When q is not real, the steady-state result will become unstable due to the steady perturbation increase. When q is real then steady state changes the stable due to decrease in perturbation. A steady-state result will not be stable when

$${\tau }^2-{\mu }^2{p}^4<0.$$

(64)

The MI gain spectrum $G(p)$ is given as

$$G(p)=2Im(q)=\sqrt{{\tau }^2-{\mu }^2{p}^4}.$$

(65)

8. Physical Description

This section explores the physical explanation of solutions derived for a (1+1)-dimensional Benjamin–Ono equation along with a $\beta$-time fractional derivative and the previously mentioned methods. To validate the physical accuracy of the mathematical model, we performed visual analyses via 3D plots, density, and 2D illustrations of the solutions. We have also investigated how fractional derivatives and the selected solution methods affect the characteristics and behavior of the solutions. Figure 1 represents the MI gain spectrum of Equation (27) with $\mu =4$. Figure 2 (singular soliton) shows the 3-D (a), 2-D (b), and contour (c) plots with $\Delta =0.9$ and $\mu =0.5$ of $v(x,t)$. Singular soliton is useful in optical physics, fluid dynamics, and mathematical modeling in nonlinear system and dynamics. Figure 3 (dark soliton) shows the 3D (a), 2D (b), and contour (c) plots with $\Delta =0.1$ and $\mu =0.5$ of $v(x,t)$ that appear in Equation (28). Dark soliton solutions have applications in optical communications, sensing, nonlinear optics, etc. Figure 4 (rational wave solution) shows the 3D (a), 2D (b), and contour (c) plots with $\Delta =0.1,\mu =0.5,{\kappa }_1=-0.1,{\kappa }_2=0.2,$ ${\kappa }_3=1.5,C_1=0.5,$ and $C_2=-0.2$ of $v(x,t)$ which appear in Equation (46). The rational wave solution has applications in nonlinear optics, fluid dynamics, Bose–Einstein condensates, etc. Figure 5 (periodic wave solution) shows the 3D (a), 2D (b), and contour (c) plots with $\Delta =0.9,\mu =0.5,{\kappa }_1=-0.1,{\kappa }_2=0.2,{\kappa }_3=-1.5,C_1=0.5,$ and $C_2=-0.2$ of $v(x,t)$ that appear in Equation (47). The periodic wave solution has applications in optical fibers, fluid dynamics, etc. Figure 6 (periodic soliton) shows the 3D (a), 2D (b), and contour (c) plots with $\Delta =0.9,\mu =0.5,{\kappa }_1=-0.1,{\kappa }_2=0,{\kappa }_3=1.5,C_1=0.5,$ and $C_2=-0.2$ of $v(x,t)$ that appear in Equation (48). Figure 7 (kink-singular soliton) shows the 3D(a), 2D(b), and contour(c) plots with $\Delta =0.1,\mu =0.5,{\kappa }_1=-0.5,{\kappa }_2=0,{\kappa }_3=-0.1,C_1=-0.5,$ and $C_2=0.2$ of $v(x,t)$ which appear in Equation (49). Kink-singular soliton has applications in nonlinear optics, plasma physics, condensed matter physics, etc.

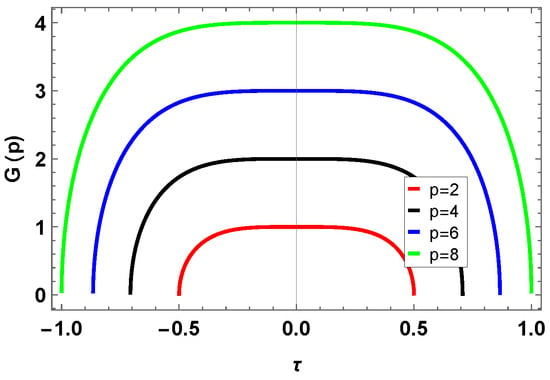
Figure 1. The MI gain spectrum for distinct values of p.

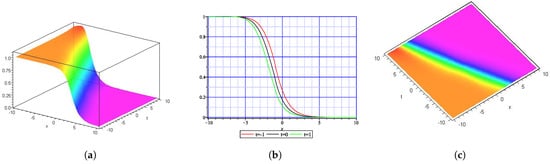
Figure 2. Physical interpretation of $v(x,t)$ is given in Equation (27). (a) represents the 3-D plot, (b) shows the 2-D graph at $t=-1,0,1$, and (c) represents the contour graph.

Figure 3. Physical interpretation of $v(x,t)$, as given in Equation (28). (a) represents the 3-D plot, (b) shows the 2-D graph at $t=-1,0,1$, and (c) represents the contour graph.

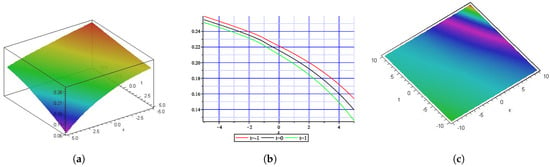
Figure 4. Graphical interpretation of $v(x,t)$, as shown in Equation (46). (a) represents the 3-D plot, (b) shows the 2-D graph at $t=-1,0,1$, and (c) represents the contour graph.

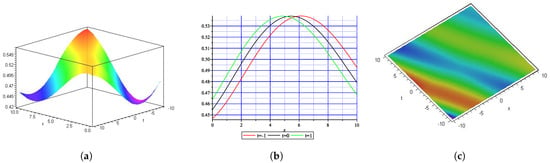
Figure 5. Graphical interpretation of $v(x,t)$, as shown in Equation (47). (a) represents the 3-D plot, (b) shows the 2-D graph at $t=-1,0,1$, and (c) represents the contour graph.

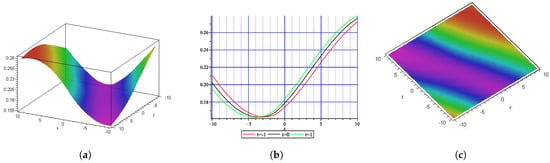
Figure 6. Graphical interpretation of $v(x,t)$, as shown in Equation (48). (a) represents the 3-D plot, (b) shows the 2-D graph at $t=-1,0,1$, and (c) represents the contour graph.

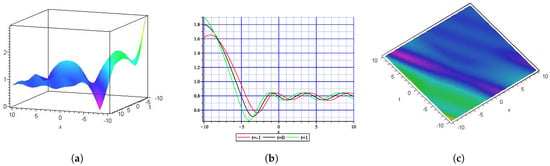
Figure 7. Graphical interpretation of $v(x,t)$, as shown in Equation (49). (a) represents the 3-D plot, (b) shows the 2-D graph at $t=-1,0,1$, and (c) represents the contour graph.

By investigating how fractional orders change the amplitude and phase components, researchers gain crucial information into wave propagation dynamics in harbor and coastal environments. The solitons in fluid dynamics are significant for understanding localized wave phenomena because the dynamics of solitons can mitigate wave energy and the modeling of wave behaviors in marine ecosystems. Some solitons in fluid dynamics have various practical applications and can predict oceanic processes, aiding in the management of offshore activities and marine environments.

9. Results and Discussion

In this section, we will compare the existing results and the results obtained in this research. In [25], the extended truncated expansion technique is used to obtain the kink wave solution. In [26], the Jacobi elliptic function expansion scheme is utilized to gain the same traveling wave solutions. In [27], the new generalized $(G^{\prime }/G)$-expansion technique is applied to obtain the different traveling soliton solutions. In [29], the $(G^{\prime }/G^2)$-expansion method is used to achieve the analytical solutions. Meanwhile, in our research, we utilized the EShGEE technique and the improved $(G^{\prime }/G)$-expansion method to obtain the novel kinds of exact solitons, including periodic, kink, dark, ratonal wave, and kink-singular soliton solutions of the $\beta$-time fractional Bejamin-Ono equation.

10. Conclusions

In this study, we have successfully developed a family of novel soliton structures to the Benjamin–Ono equation along beta-time fractional derivative. We obtained the results, achieving singular, singular-bright, dark, singular, singular-dark, kink, and many more solutions with the use of the EShGEE technique and the improved $(G^{\prime }/G)$-expansion technique. An effective sense of $\beta$-time fractional derivative yields different results compared to the existing results. The Mathematica tool is utilized to achieve as well as verify results. The results are represented by 2-D, 3-D, and contour graphs.

The (1+1)-dimensional nonlinear BO model is an integro-differential equation that explains one-dimensional internal waves in deep water. This equation is used in mathematical physics and dynamics to understand the nature of internal waves in a twin layer fluid. It has many applications in the studies of wave breaking, wave interactions, the evolution of wave patterns, and many more. Furthermore, the stability as well as modulation instability analysis of the concerned equation is also utilized to verify the stability and accuracy of the solutions obtained. Ultimately, the technique we used proved useful for handling NLFPDEs and larger systems of equations. The findings presented here offer substantial insight and potential applications in different scientific and engineering fields.