Fractal Technology for Sustainable Growth in the AI Era: Fractal Principles for Industry 5.0

Abstract

This study presents fractal technology as a foundational approach to sustainable growth in the artificial intelligence (AI) era and Industry 5.0. We explore how the principles of fractal geometry, including self-similarity and recursive properties, improve scalability, efficiency, and adaptability in AI-driven systems. Representative applications include neural networks, decentralized control, and intelligent manufacturing, where fractal-based design enables modularity, fault tolerance, and optimized resource use. Case studies and theoretical models demonstrate that a fractal frameworks provide a viable path toward long-term, self-organizing industrial innovation and sustainability-oriented vision of Industry 5.0. Theoretical perspectives are strengthened by connections to nonextensive Tsallis statistics and parallels with complex systems in quantum field theory, suggesting the universality of fractal laws across disciplines. Case studies confirm that fractal frameworks offer a viable path toward long-term, self-organizing industrial innovation, contributing to the emerging field of fractal engineering and providing a systems-level paradigm for sustainable technological evolution.

1. Introduction

The emergence of the artificial intelligence (AI) era is reshaping industries through intelligent automation, machine learning, and data-driven decision-making at an unprecedented pace. Built upon the foundations of digital and internet technologies, typically regarded as transformative milestones in human history, core systems and infrastructures from the pre-AI era are increasingly being replaced, integrated, or rendered obsolete by AI-based solutions [1,2].

This transformation is not only technological but also paradigmatic, providing a dual trajectory: sustainable industrial growth for those who adapt and obsolescence for those who do not. A common misconception is that AI is the inevitable driver of large-scale labor displacement through robotics, digitization, and automation. In reality, AI is redefining the industrial landscape by shifting value toward innovation, adaptability, and human–machine symbiosis. Within the broader vision of Industry 5.0- characterized by human-centricity, resilience, and sustainability- human creativity and problem-solving become indispensable assets [3].

Fractal geometry, first formalized by Mandelbrot (1982) [4], describes structures that exhibit self-similarity and recursive patterns across scales. These principles extend beyond mathematics, appearing in nature’s efficiencies—from branching rivers and trees to the organization of neural networks. Building on this foundation, we define fractal technology as the application of fractal design, scaling laws, and recursive simplicity to industrial systems and digital architectures in the AI and Industry 5.0 era [5,6,7,8,9].

Unlike traditional linear models, fractal-based approaches leverage recursive structures, scale-free networks, and hierarchical organization to enhance resilience, efficiency, and sustainability [2]. From deep neural networks that learn through iteration to generative AI models that reproduce self-similar patterns, fractal logic is already embedded in artificial intelligence. Recent studies further highlight the interdisciplinary reach of fractal principles, from statistical mechanics to complex adaptive systems and quantum field theory [10,11].

This study advances the thesis that fractal technology, which is the application of fractal principles such as self-similarity, scalability, and adaptive complexity, offers a foundational framework for next-generation, AI-integrated innovation. Fractal geometry (FG), originally formalized by Mandelbrot (1982) [4] to describe irregular yet patterned natural forms, provides not only mathematical tools but also philosophical insights into complex systems. Applied to industrial processes, fractal thinking enables decentralized control, recursive design strategies, and sustainable scalability from product conception to delivery [10].

We further contend that many AI technologies are grounded in fractal principles. AI typically mirrors the logic that underpins natural and fractal systems, from neural networks that learn through recursive patterns to generative models that mimic self-similar structures. Therefore, fractal technology can serve as both a conceptual and practical bridge between human imagination and AI, thereby enhancing creativity, responsiveness, and resilience across the value chain.

Ultimately, the success of industries in the AI and Industry 5.0 era will depend not only on technological capability but also on the wisdom with which it is applied. From this perspective, the rise in AI may be understood not as a threat, but as a blessing in disguise- a profound opportunity when applied with creativity and foresight.

2. Fractal Technology—Master Key to Sustainable Growth

2.1. Introduction

Fractal science provides a robust framework for understanding complexity in the AI era. Originating from the study of irregular natural patterns, fractal science reveals structure within apparent disorder, e.g., coastlines, clouds, and trees exhibit self-similarity across scales [4,6,7,8,9].

AI systems increasingly mirror such natural processes, with neural networks, genetic algorithms, and swarm intelligence extending biological principles into computation. Recognizing the geometry behind these patterns is critical for designing adaptive, intelligent systems. In this context, fractal technology—the practical application of fractal principles such as self-similarity, recursion, and scale-free organization—emerges as a bridge between natural laws and artificial intelligence, offering both a conceptual framework and a practical pathway for sustainable innovation in the AI era.

2.2. Fractal Technology: Characteristics

It is instructive to consider the classic problem posed by Richardson (1961) [12] regarding the measurement of the British coastline to understand FG characteristics. Richardson observed that the measured coastline length increased as the measuring unit became finer. In geometric terms, this implies that the measured length is scale-dependent and nonlinear.

Specifically, Richardson identified a linear relationship between the measured length (L) and the measuring unit (or ruler size) when plotted on a log-log scale (Figure 1). This plot is now commonly known as the Richardson plot or the box-counting method.

Figure 1 shows the Richardson plot, also known as the box-counting method.

This observation challenged the assumptions of classical Euclidean geometry, which assumes the following scale-invariant dimensions: a point (zero dimension), a line (one dimension), an area (two dimensions), and a volume (three dimensions). In contrast, Benoît Mandelbrot introduced the concept of fractal dimension to describe geometries that exhibit scale-dependent complexity. He defined the FD in terms of the slope of the Richardson plot as follows:

$$FD=1+\left|slope\right|.$$

(1)

In this context, the FD is not an integer because the slope is typically not. When the slope is zero, the FD equals 1, representing a straight line. For scale-dependent curves, the slope is greater than zero; thus, FD is greater than 1. In higher dimensions, the FD exceeds 2 and 3 for areas and volumes, respectively. Therefore, the FD can be interpreted as a quantitative measure of irregularity or deviation from Euclidean geometry.

Figure 1 shows a fundamental FG property: the measured length increases as the unit of measurement decreases, potentially approaching infinity. However, the area enclosed by the British coastline remains finite. This paradox, which is an infinite perimeter within a finite area, cannot be explained using conventional Euclidean models. It becomes intelligible only through the FG lens [5,12].

This framework challenged Euclidean assumptions by showing that a boundary can possess infinite length while enclosing a finite area—the so-called coastline paradox. The same principle extends to many complex systems: scale-free networks, internet topology, and metabolic pathways exhibit fractal dimensions that reflect their self-organizing efficiency [13,14]. Recent research further demonstrates the broad applicability of fractal dimension analysis: in artificial intelligence, it improves image recognition, edge detection, and pattern analysis in medical imaging and autonomous driving [15]; in engineering systems, it guides antenna design, porous media modeling, and nanostructured material science; and in complex systems, it links directly to power-law distributions and Tsallis statistics, which describe energy-efficient, nonextensive systems in physics and AI optimization [10].

In summary, fractal dimension is not only a mathematical construct but also a universal diagnostic tool for complexity. It provides quantitative insight into structures and processes ranging from coastlines to AI architectures, reinforcing the central role of fractal technology in both natural and engineered systems.

2.3. Mandelbrot Sets

Benoît Mandelbrot, typically regarded as the father of FG, expanded upon Richardson’s insight by formalizing the concept of fractals, which are structures that exhibit self-similarity across scales and reveal complex geometries through simple, recursive rules (Mandelbrot, Fractals: Form, Chance, and Dimension).

Among the many fractals studied by Mandelbrot, several foundational sets are extensively recognized and used to illustrate the FG principles. Representative sets are as follows: [4,16,17,18,19]

• Cantor Dust.
• Koch Snowflake.
• Sierpinski Carpet.
• Menger Sponge.

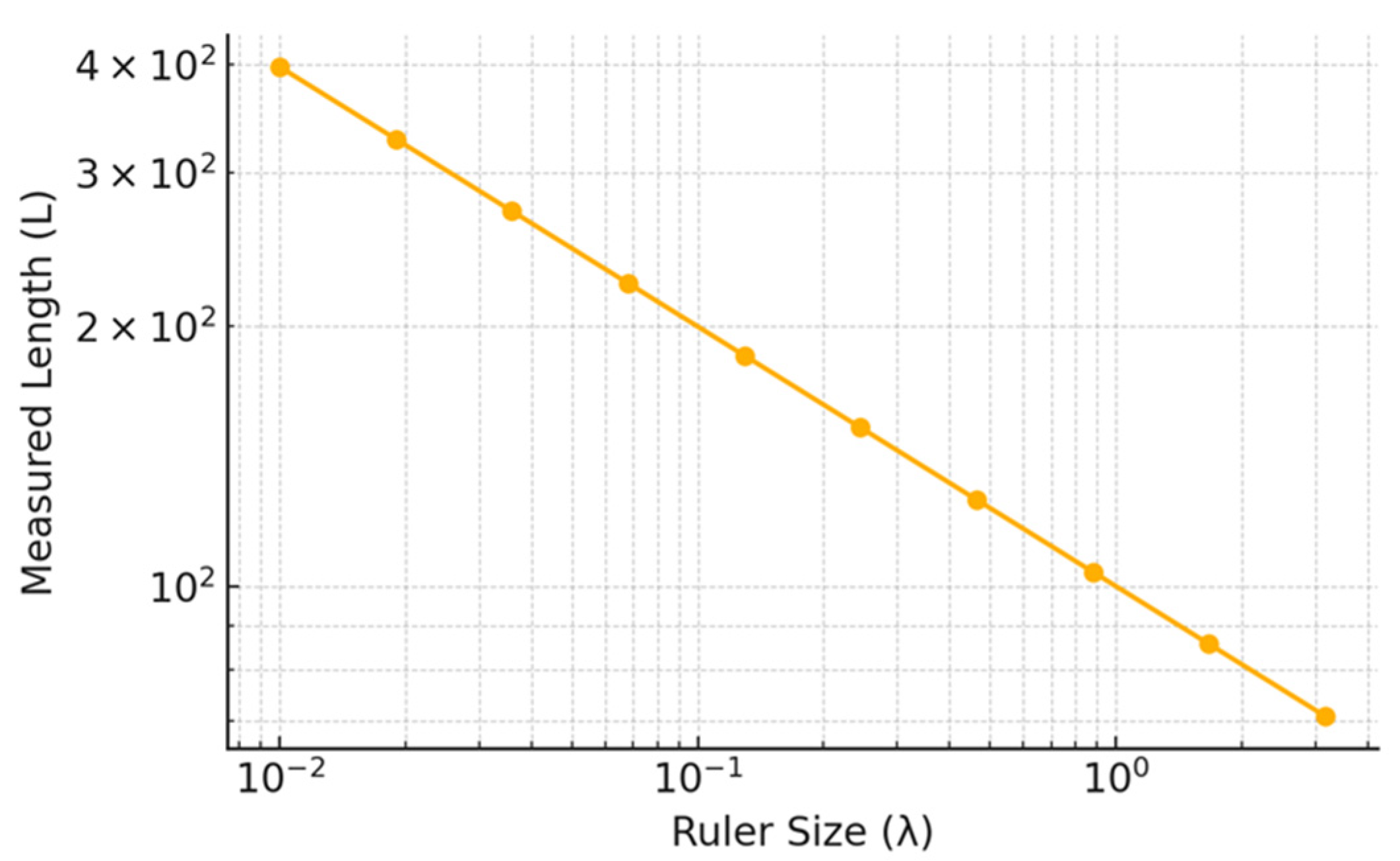
2.3.1. Example 1: Cantor Dust

Cantor Dust is one of the simplest yet most illustrative fractal examples. It is defined by self-similarity, recursion, and dimensional reduction. The structure is generated by iteratively removing the middle third from a line segment, thereby yielding a pattern that becomes increasingly fragmented with each iteration while preserving its underlying structure.

This infinite recursive process within a finite space exemplifies a core paradox of FG. With an FD of approximately 0.63, Cantor Dust exists in a space between a point set and a line, greater than zero dimension but less than one dimension. Unlike Euclidean geometry, where dimensions are integers, FG enables non-integer dimensions, allowing the nuance of irregular forms to be captured.

Figure 2 illustrates the iterative generation of the Cantor Dust fractal.

In the Cantor Fractal Geometry, the fractal dimension (FD) is calculated from:

$$FD=\log N/\log (1/L)$$

(2)

In this case, N = 2 (number of remaining self-similar segments), and L = 1/3 (length ratio of each segment to the original).

Substituting these values into Equation (2):

$$FD=\log 2/\log 3=0.63$$

The Cantor Dust structure also provides a metaphor for the evolution from analog to digital systems: longer segments resemble continuous analog waves and shorter fragments resemble discrete digital signals.

Similarly to actual dust, Cantor Dust appears as disconnected clusters. These fragmented clusters can contribute to signal noise, which is expected to decrease as the cluster size decreases, a phenomenon relevant in real-world systems.

These characteristics make Cantor Dust highly applicable in the following fields:

-

Signal processing.

-

Data compression.

-

Quantum computing.

-

Nanotechnology.

In each of these domains, scalable and recursive architectures are critical, and their development would not have been possible without the conceptual foundation of fractal technology.

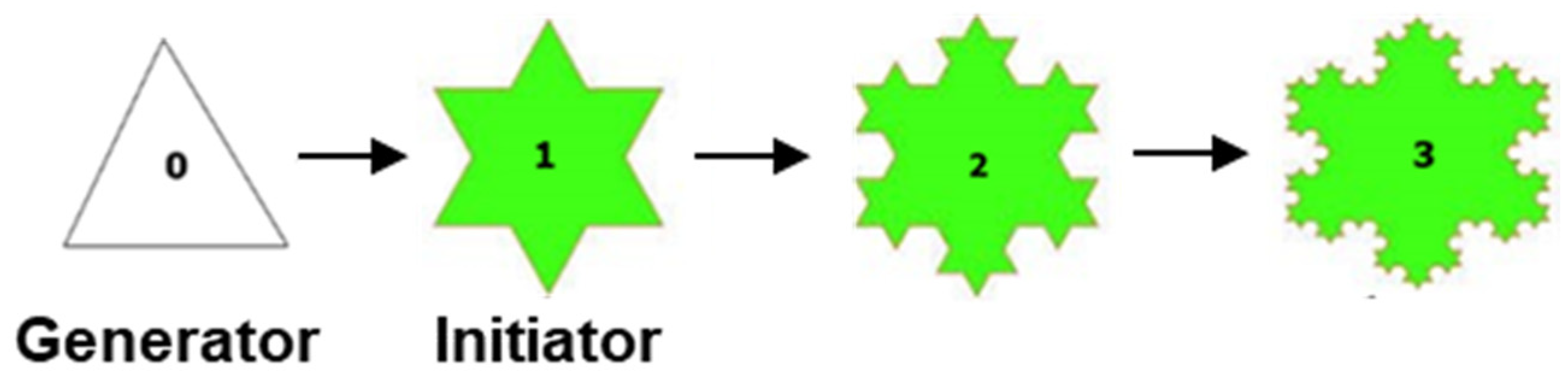
2.3.2. Example 2: Koch Snowflake

The Koch Snowflake is the next higher-order fractal after the Cantor Dust. It visually demonstrates how a simple geometric rule can evolve into infinite complexity. It is constructed by recursively adding equilateral triangles to the middle third of each line segment of the perimeter of a triangle.

With each iteration, the perimeter becomes longer, whereas the enclosed area remains bounded. As the number of iterations approaches infinity, the length of the boundary approaches infinity, whereas the enclosed area remains finite, which is an elegant contradiction to Euclidean expectations. This paradox reflects an essential trait of FG: infinite detail within finite bounds.

Figure 3 shows the iterative construction of the Koch snowflake.

In the Koch Fractal Geometry, the fractal dimension (FD) is calculated using the same Equation (1).

In this case, N = 4 (number of self-similar segments generated at each iteration), and L = 1/3 (length ratio of each new segment to the original).

Substituting these values into Equation (2):

$$FD=\log 4/\log 3=1.26$$

Similarly to Cantor Dust, the Koch Snowflake, like Cantor Dust, powerfully illustrates the fundamental characteristics of fractal technology. It demonstrates how an object can possess infinite length in a finite area—a concept that defies explanation through classical Euclidean geometry.

In this regard, the Koch snowflake provides a direct answer to Richardson’s coastline paradox: the measured length of a boundary increases without bound as the measuring scale decreases. Thus, the introduction of FG has opened an entirely new way of understanding complex shapes found in nature.

This insight has profound implications beyond mathematics. In biology, fractal principles are embedded in human organs:

-

Blood vessels must fit near-infinite circulatory paths within the limited space of the body.

-

Lungs must provide a maximal surface area for gas exchange within a confined thoracic cavity.

FG also provides critical engineering solutions, particularly where maximum efficiency in minimal space is required. Applications include

-

Surface design for heat exchangers.

-

Antenna miniaturization.

-

Material science, such as in porous media and lightweight foams.

These examples demonstrate how the Koch snowflake exemplifies the ability of FG to bridge theoretical insights and practical innovation, transforming our understanding of both natural systems and engineered technologies.

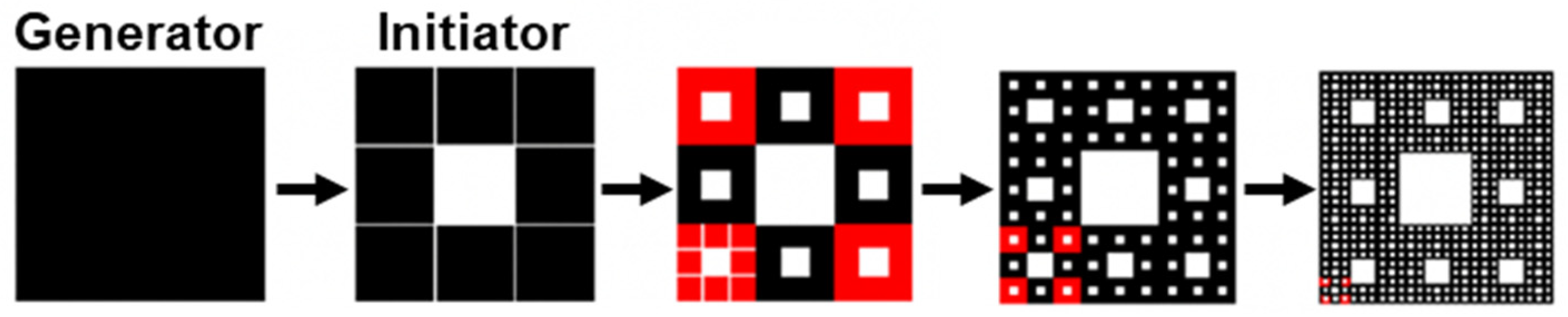
2.3.3. Example 3: Sierpinski Carpet

The Sierpinski carpet is the next higher-order fractal after the Koch Snowflake. It illustrates. It is generated by dividing a square into nine equal parts and removing the central square. This process is then repeated recursively on each of the remaining eight squares at each iteration. With each iteration, the length becomes longer, whereas the enclosed area remains bounded, which is another powerful example of fractal design.

Figure 4 shows the iterative development of the Sierpinski carpet.

In the Sierpinski Carpet Fractal Geometry, the fractal dimension (FD) is calculated using the same Equation (2):

In this case, N = 8 (number of self-similar squares remaining after each iteration), and L = 1/3 (length ratio of each smaller square to the original).

Substituting these values into Equation (2):

$$FD=\log 8/\log 3=1.89$$

Figure 4 illustrates a hierarchical design characterized by self-similarity. This fractal structure has broad applications in porous materials, such as filtration systems, surface science, and colloid engineering.

Its layered voids and structure-preserving recursion provide valuable models for hierarchical systems, such as neural networks, power grids, and data trees. The Sierpinski carpet demonstrates how the repeated application of simple rules across scales can result in complexity. This highlights a counterintuitive truth: complex designs do not necessarily originate from complex initial geometry.

The Sierpinski Carpet provides an effective model for energy and mass transfer. Its hierarchical structure, extending from nano- to macro-scale pores, represents one of the most efficient geometries in nature. Therefore, this fractal design should serve as a guiding principle for developing advanced transfer systems in the AI era.

2.3.4. Example 4: Menger Sponge

The Menger Sponge is a three-dimensional (3D) fractal generated by recursively removing the center cube and the center squares from each face of a larger cube (Figure 5). Similarly to the Sierpinski carpet, it exhibits a hierarchical design but is extended into three dimensions, thereby providing an even more robust model for both natural and engineering complex systems.

The structure becomes increasingly porous with each iteration, illustrating how void and solid coexist in perfect balance within the three-dimensional fractal geometry.

Figure 5 shows the Menger Sponge fractal.

In the Menger Sponge Fractal Geometry, the fractal dimension (FD) is calculated using the same Equation (2):

In this case, N = 20 (number of self-similar cubes remaining after each iteration), and L = 1/3 (length ratio of each smaller cube to the original).

Substituting these values into Equation (2):

$$FD=\log 20/\log 3=2.73$$

The high fractal dimension (FD) of 2.73 indicates that the Menger Sponge is a highly porous yet structurally dense fractal. Considering that the geometrical dimension of a solid cube is 3.0, this FD value reveals that the Menger Sponge retains a substantial solid volume even though it exhibits extreme porosity.

Just as the Koch Snowflake (FD = 1.26) and the Sierpinski Carpet (FD = 1.89) maximize length within a given area and surface porosity within a plane, respectively, the Menger Sponge (FD = 2.73) represents a three-dimensional counterpart—an architecture characterized by hierarchical pores at multiple scales while maintaining maximal solid connectivity.

Such a fractal design is highly desirable for efficient energy or fluid transfer, offering a model geometry for developing high-efficiency transfer systems in the AI era.

Its extensive surface area within a finite volume makes it particularly well-suited for modeling systems in which interface maximization is critical, such as in heat exchangers, catalytic reactors, acoustic dampening materials, and advanced porous media. Furthermore, the Menger sponge serves as an abstract model of recursive organization found in distributed networks, biological systems (such as alveoli in lungs), and multidimensional data storage, such as big data, a foundational technology in the AI era.

It challenges classical Euclidean assumptions by demonstrating how infinite boundaries and pathways can emerge from finite space. The Menger sponge highlights a central principle of fractal thinking: intricate complexity may not arise from complex beginnings but rather from the recursive application of simple rules across scales.

In summary, all Mandelbrot fractal sets demonstrate a hierarchical structure characterized by self-similar patterns replicated across various scales. The implications of this property are analyzed in a subsequent section.

2.4. FG and Log-Normal Distributions

As the saying goes that God does not create the world by tossing a coin; natural phenomena rarely follow uniform or Gaussian distributions. Instead, many natural processes, spanning from biological growth to sediment transport, follow log-normal distributions rather than Gaussian distributions [20]. This pattern suggests a strong link between fractal structures and log-normal statistics, both of which are signatures of multiplicative, self-organizing systems [17]

Representative examples are as follows:

-

Airborne dust particle distributions [20].

-

Pore size in cellulose fibers [17].

-

Contact angle variations on cellulose surfaces [21].

-

Fine particle aggregation [20].

In particular, Allan and Ko (1995) [22] used Derjaguin–Landau–Verwey–Overbeek (DLVO) theory to explain the log-normal pore distribution in cellulose, demonstrating how competing van der Waals and electrostatic forces lead to thermodynamically stable, energy-efficient configurations [22,23]. This reflects a broader natural tendency toward low-energy, self-organizing states, as posited by Emerson: “Nature works by short ways… through the principle of least action” [24].

Moreover, fractal analysis methods such as the Richardson plot typically reveal power-law relationships that are closely associated with log-normal behavior. Thus, when a system exhibits log-normal frequency distributions, the underlying FG is typically implied [22].

Recent research confirms their broad relevance, appearing in scale-free networks, financial systems, ecological structures, and artificial intelligence models [25]. For instance, the distribution of neural weights in deep learning, scaling laws in large language models, and fluctuations in medical imaging noise all exhibit log-normal or power-law behavior, reflecting recursive, fractal-like dynamics.

Summary

FG is not merely a mathematical abstraction but a universal design principle embedded in nature. Its consistent alignment with log-normal statistics reveals a deeper truth: nature does not evolve through randomness but through hierarchical, energy-efficient structures that enable adaptive function across multiple scales. This principle governs energy flow, structure formation, and complexity emergence in both living and physical systems.

2.5. Living Systems Are Fractal

Recognizing the fact that fractal technology has evolved from multiple intellectual traditions long before Benoît Mandelbrot coined the term fractal is both fascinating and significant. Various visionary thinkers have observed the self-similar and hierarchical patterns found in nature and the human body.

Swedenborg envisioned the human body as a system of embedded structures, such as “tongues within tongues,” “hearts within hearts,” a concept that mirrors the fractal architecture now recognized in lungs, blood vessels, and neural networks. These forms optimize functions through self-similar branching. For example, the human lung, featuring 23 airway bifurcation levels, achieves a surface area of approximately 70 m². These are contained within the chest’s confined volume. Optimization is a hallmark of fractal design.

More remarkably, Swedenborg envisioned this structure not merely as a form but as a dynamic process. Today, developmental biology and morphogenesis confirm that life unfolds through recursive rules, echoing the patterns he once described. As modern science now understands, FG underlies not only biological form but also growth, differentiation, and adaptation [26].

By bridging ancient insights with modern science, FG affirms a profound unity between form, function, and the generative structure of AI. The implications extend far beyond biology. Bio-inspired artificial intelligence increasingly draws on these same principles: neural networks echo fractal branching in brain architecture; robotics applies fractal morphology for adaptability and resilience; and medical imaging leverages fractal analysis to detect early signs of disease in lungs, blood vessels, and neural tissue [15]. These parallels affirm a central truth: both life and intelligence are fractal processes, shaped by recursive, scale-free organization.

As Emerson advised, “Learn from Nature,” a statement that calls us to understand and apply the principles of FG. Nature demonstrates that sustainability is not an abstract goal but a consequence of simple, recursive, energy-efficient systems. This principle should guide the development of technologies in the AI era.

Ultimately, FG is not designed to exhibit beauty but to ensure sustainable growth. It is the simplest and most energy-efficient structure. Consequently, many modern AI technologies are built upon fractal principles, whether consciously or unconsciously.

3. Role of AI in Industrial Innovation

AI is a foundational technology driving the next wave of industrial transformation and the transition to Industry 5.0. By simulating cognitive functions such as learning and decision-making, AI enables intelligent automation, predictive maintenance, and adaptive process control—already reshaping manufacturing, logistics, and energy systems. AI enhances efficiency, reduces waste, and supports self-organizing supply chains while advancing the human-centric and sustainable goals of Industry 5.0. As routine work becomes automated, human roles will shift toward creativity, systems thinking, and innovation—areas where fractal-based design and reasoning provide distinct advantages. In Industry 5.0, AI adoption converges with emerging digital technologies whose effectiveness often reflects fractal principles of scalability, decentralization, and recursive feedback. These principles support modular production systems, fault-tolerant operations, and resource-efficient innovation, demonstrating how fractal technology can serve as a bridge between human ingenuity and AI-driven industrial growth.

3.1. Blockchain Technologies

Blockchain is a decentralized ledger system that enables secure, transparent, and tamper-resistant data exchange across distributed networks. Within the framework of Industry 5.0, it supports key objectives such as traceability, sustainability, and system resilience by ensuring the integrity of transactions and data flows throughout complex value chains [3,27,28,29,30]

Representative emerging applications include:

-

Sustainable Resource Management: Tracking materials from origin to end use to ensure legal, ethical, and environmental compliance.

-

Circular Economy Integration: Verifying recycled and reused content to meet regulatory and sustainability standards.

-

Supply Chain Transparency: Automating audit trails to enhance accountability and ESG (Environmental, Social, and Governance) reporting.

-

Carbon and Energy Accounting: Linking process data with emission metrics for accurate sustainability assessments.

By embedding trust, transparency, and automation into industrial ecosystems, blockchain complements AI-driven systems and advances the human-centric, sustainable, and resilient goals of Industry 5.0. Integrated with AI, blockchain enables more robust certification systems, real-time monitoring, and next-generation ESG reporting [3,27,28,29,30,31,32].

From a fractal perspective, blockchain networks operate through distributed nodes that mirror self-similar structures, where each part reflects the whole. This recursive organization ensures resilience, scalability, and trust without central control—making blockchain not only a technological innovation but also a fractal model of decentralized, sustainable governance for Industry 5.0.

3.2. Three-Dimensional Printing Technology: Adaptive Manufacturing

3D printing, also known as additive manufacturing, is a digital fabrication technology that constructs structures layer by layer. It enables precise material usage and minimal waste, aligning with the circular economy and sustainability principles of Industry 5.0 [33,34,35].

Representative emerging applications are as follows:

-

Rapid prototyping of new products.

-

Localized and on-demand fabrication for supply chain resilience.

-

Precision production of high-value or complex components.

The use of renewable and biodegradable materials, such as bio-based polymers, cellulose, and nanocellulose, further enhances its environmental performance. In addition, 3D printing connects research, design, and manufacturing through integrated digital workflows, reducing time, cost, and risk compared with conventional trial-and-error methods [36,37].

By enabling flexible, decentralized, and sustainable production, 3D printing supports human-centric, resilient, and intelligent manufacturing systems—core attributes of Industry 5.0. From a fractal perspective, its layer-by-layer construction embodies recursive self-similarity, where simple units are iteratively combined to generate complex structures. This fractal logic enhances scalability, adaptability, and design freedom, reinforcing the principles of sustainable innovation and co-creation between humans and intelligent machines.

3.3. Internet of Things (IoT)

The Internet of Things (IoT) interconnects machines, sensors, and systems to enable real-time monitoring, data exchange, and autonomous control. It serves as a foundational infrastructure for intelligent, adaptive manufacturing—integrating the physical and digital worlds to enhance efficiency, transparency, and sustainability [38].

Representative emerging applications are as follows:

-

Predictive Maintenance: Smart sensors detect anomalies in equipment to prevent unplanned downtime and reduce maintenance costs.

-

Process Optimization: IoT-enabled systems adjust operational parameters in real time to improve energy efficiency, precision, and product quality.

-

Supply Chain Integration: Connected devices and RFID tracking enhance visibility, traceability, and responsiveness across the value chain.

-

Environmental Monitoring: Networked sensors collect emissions and resource data, supporting sustainability reporting and regulatory compliance.

By connecting all layers of production and logistics, IoT creates a responsive and human-centric ecosystem that aligns with the principles of Industry 5.0—collaboration between humans and intelligent systems, resilience through decentralization, and sustainability through data-driven optimization.

From a fractal perspective, IoT networks embody recursive self-similarity, where local interactions between devices scale into global system intelligence. This distributed architecture enhances adaptability, fault tolerance, and holistic optimization, demonstrating how fractal organization underpins the evolution of complex, human-aligned industrial systems.

3.4. Robot Technologies

Robotics is emerging as a key enabler of Industry 5.0, enhancing safety, efficiency, and precision across manufacturing and logistics. Robots perform high-risk, repetitive, and labor-intensive tasks as modular, self-similar units within intelligent production systems, reflecting fractal principles of scalability, adaptability, and recursive functionality [15,39].

Representative emerging applications are as follows:

-

Automated Material Handling: Robotic arms and autonomous guided vehicles (AGVs) transport materials and components, improving safety, workflow, and efficiency.

-

Packaging and Assembly: End-of-line robots perform wrapping, labeling, and assembly with sensor-guided accuracy, increasing throughput and reducing defects.

-

Vision-Guided Inspection: AI-enabled robotic systems identify surface defects and process deviations in real time, enabling continuous quality assurance and minimizing waste.

-

Maintenance and Safety Operations: Mobile robots equipped with thermal and gas sensors conduct cleaning, inspection, and diagnostics in hazardous or confined areas, improving occupational safety and operational reliability.

When integrated with AI, IoT, and digital twin technologies, robotics enables predictive maintenance, process optimization, and autonomous decision-making. These systems enhance human–machine collaboration, allowing people to focus on creativity, design, and high-level supervision—core values of Industry 5.0.

From a fractal perspective, robotic systems demonstrate how simple, self-contained operational units can combine recursively to form complex, adaptive networks. This fractal organization promotes modularity, fault tolerance, and continuous learning across scales, aligning robotics with the human-centric, sustainable, and intelligent ecosystem envisioned by Industry 5.0.

3.5. Drone Applications

Drone technologies—comprising unmanned aerial vehicles (UAVs) equipped with GPS, sensors, cameras, and AI—are emerging as versatile tools across the Industry 5.0 value chain. By extending industrial oversight into the aerial dimension, drones enable real-time data acquisition, faster response times, and safer, more efficient operations [40,41,42].

Representative emerging applications are as follows:

-

Inspection and Monitoring: Drones equipped with high-resolution cameras and thermal sensors conduct infrastructure and equipment inspections, reducing downtime and improving safety.

-

Environmental and Resource Management: Aerial data support precision monitoring of forests, crops, emissions, and environmental impact.

-

Agile Logistics: Autonomous drones facilitate rapid delivery and material transport within industrial sites, enhancing flexibility and efficiency.

-

Disaster and Safety Management: Real-time aerial surveillance supports emergency response, hazard detection, and risk prevention.

By integrating AI, IoT, and robotics, drones evolve from isolated aerial survey tools into intelligent, connected nodes within adaptive industrial ecosystems. These systems strengthen agility, resilience, and sustainability—key goals of Industry 5.0—while reducing human exposure to hazardous environments.

From a fractal perspective, drone networks exemplify distributed intelligence: each autonomous unit operates independently yet contributes to a coordinated, self-similar whole.

This recursive organization enhances scalability, responsiveness, and adaptability, reflecting the fractal logic of Industry 5.0, where technology and human insight converge to achieve harmony between innovation, safety, and sustainability.

4. Fractal Technology for AI Technology Development

Many foundational AI technologies reflect the principles of FG, particularly similarity, hierarchy, and recursive structure across scales. These technologies demonstrate measurable fractal-like properties such as power-law scaling, self-similar architectures, and emergent complexity [43]. Recent studies in complex systems, Tsallis statistics, and Quantum Field Theory (notably Quantum Chromodynamics) also suggest that fractal behavior is a fundamental organizational principle, linking physical and digital domains [44]. Below, representative AI technologies are aligned with their corresponding fractal characteristics.

4.1. Blockchain

Blockchain reflects fractal principles of recursive structure and decentralized hierarchy. Its cryptographically linked blocks form a self-similar ledger, while each node mirrors the structure of the whole.

This hierarchical decentralization underpins blockchain’s resilience, while its scalability emerges through iterative extension without altering its foundational design—a property parallel to fractal growth rules [45,46].

4.2. Big Data

Big data embodies fractal traits of scale invariance and infinite resolution. Patterns recur across temporal and spatial scales—whether in millisecond-level sensor inputs or long-term social dynamics—often following power-law or log-normal distributions. Recursive analytics in deep learning further reflects fractal iteration, where insights at one scale inform patterns at another [43,47,48,49,50].

4.3. Additive Manufacturing (3D Printing)

Additive manufacturing (3D printing) is emerging as a core AI-enabled technology essential for Industry 5.0, offering a sustainable alternative to conventional, capital-intensive manufacturing. Unlike subtractive processes—such as pulp production, where unwanted material is progressively removed—3D printing employs an additive, fractal-inspired layering technique, depositing only the required material to form complex structures. This recursive design maximizes efficiency, reduces waste, and enables production across micro-to-macro scales, with significant implications for packaging and other Industry 5.0 applications [33,34,51,52].

4.4. Deep Learning and Neural Networks

Deep learning and neural networks embody fractal characteristics of hierarchical representation and emergent complexity. Each layer extracts increasingly abstract features, while recursive backpropagation refines the system much like fractal iteration adds detail. The network’s intelligence arises from repeated, layered interactions rather than individual nodes, reflecting self-similar dynamics. Recent studies further link neural architectures to scale-free topologies in natural systems, underscoring their fractal organization [43,53].

4.5. IoT

The Internet of Things (IoT) reflects fractal principles of distributed networks and nested scales. Local sensor data aggregates into higher-level insights, mirroring fractal nesting from micro to macro patterns. Its adaptive responsiveness at multiple levels exemplifies self-similar adjustment across scales, positioning IoT as a scale-free network that embodies fractal organization [50,54,55,56].

4.6. Cloud Computing

Cloud computing demonstrates fractal characteristics of recursive and scalable resource allocation. Its layered architecture—spanning virtual machines, containers, and distributed services—maintains structural integrity from individual to planetary scale, reflecting fractal invariance under magnification. Elastic scalability and mirrored deployment of nodes reinforce self-similar patterns, enabling robust, adaptable infrastructures that align with fractal logic [57,58].

5. Fractal Characteristics in Core AI Technologies

FG provides a powerful conceptual framework for understanding the structural and functional characteristics of many core technologies driving the AI era. These technologies exhibit self-similarity, hierarchical organization, recursive processes, and scalability, which are fundamental traits of fractal systems.

Table 1. Fractal Characteristics of Core AI Technologies.

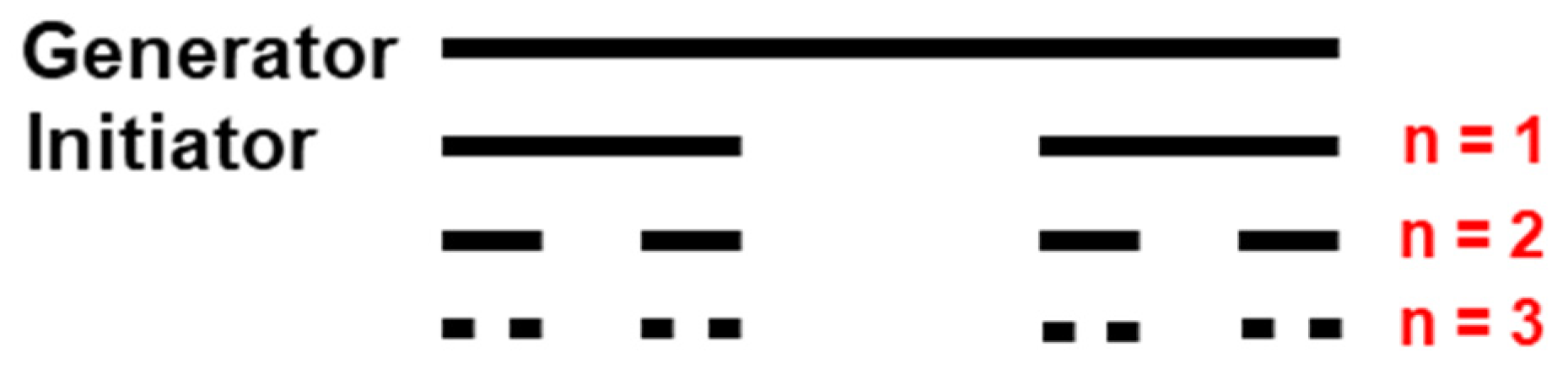
Core AI Technology	Fractal Characteristics	Explanation
Blockchain	Recursive structure, decentralized hierarchy, scalability	Blockchain forms a chain of data blocks, each linked recursively to the previous block. Each node mirrors the logic of the entire system, which is an inherently fractal design.
Big Data	Scale-invariance, power-law distribution, recursive pattern recognition	Big data analytics reveals patterns that repeat across temporal and spatial scales. Data distributions typically follow log-normal or power-law forms, reflecting fractal behavior.
3D Printing	Layered construction, material efficiency, micro-to-macro precision	3D printing iteratively builds objects layer by layer, mirroring fractal growth processes in nature that optimize form and function from the bottom up.
Deep Learning and Neural Networks	Hierarchical layers, recursive learning, emergent complexity	Deep neural networks are organized in layers, with each layer refining the information from the previous layer, similar to how fractals evolve complexity through iteration.
IoT	Distributed networks, local-to-global feedback, adaptive scaling	IoT systems mirror fractal systems by integrating small, locally intelligent devices that generate large-scale insights through decentralized interactions.
Cloud Computing	Scalable architecture, mirrored resource layers, elastic responsiveness	Cloud computing relies on recursive, layered resource allocation across distributed servers. This ensures consistency in form and function across scale.

outlines the alignment between major AI technologies and their corresponding fractal principles.

These examples illustrate that fractal thinking is not merely theoretical mathematics but a practical design logic for achieving scalability, resilience, and complexity in real-world systems. The recurrence of these principles across domains suggests that FG underlies not only natural evolution but also technological innovation.

Power spectral density (PSD)/fast Fourier transform (FFT)-based analytical techniques are particularly aligned with this fractal perspective. In these methods, structure is not confined to a single level but is distributed across multiple scales in both the time and frequency domains. This results in the concept of “fractal cycles,” which encapsulates the core fractal properties of self-similarity and recurrence across different scales or cycles.

Recent research has also highlighted intriguing connections between fractal geometry, Tsallis non-extensive statistics, and Quantum Field Theory—particularly Quantum Chromodynamics (QCD) [10]. While beyond the immediate scope of this paper, such connections underscore the fundamental role of fractal principles in unifying physical, informational, and technological systems.

Summary

AI technologies form the foundation of intelligent and human-centric transformation in the Industry 5.0 era. Moving beyond the automation focus of previous industrial stages, Industry 5.0 emphasizes the synergy between advanced technologies and human creativity. In a world shaped by global competition, environmental challenges, and demographic shifts, the convergence of AI with 3D printing, extended reality (XR), biotechnology, 5G, and advanced energy systems establishes a sustainable pathway toward resilient and inclusive growth.

The true strength of Industry 5.0 lies in technological convergence—where data, automation, and intelligent infrastructure operate as interconnected, self-similar systems across scales. Realizing this vision requires visionary leadership, cross-sector collaboration, and sustained investment in innovation and education.

As industries evolve from the pre-AI paradigm, they are not merely adapting to change but shaping it. By embracing convergent and fractal technologies, they can lead the transition toward systems that are adaptive, regenerative, and symbiotic with both human and natural ecosystems.

Fractal technology provides a unifying conceptual framework for Industry 5.0—designing processes and networks that mirror nature’s recursive efficiency. It offers a roadmap for building intelligent, scalable, and sustainable systems that harmonize technological progress with human values and planetary balance.

6. Future Trends in AI and Industry 5.0

In the emerging Industry 5.0 era, all sectors—ranging from traditional manufacturing industries such as oil, pulp and paper, and automotive, to emerging digital enterprises—face significant challenges in achieving sustainable growth under the transformative impact of artificial intelligence. AI is no longer an isolated tool but a global megatrend, integrating seamlessly with emerging technologies such as the Internet of Things (IoT), 3D printing, extended reality (XR), biotechnology, and renewable energy systems [59].

This section examines these prospects within the broader landscape of industrial and technological convergence, emphasizing the need for adaptive strategies that integrate innovation, sustainability, and human-centric design.

In analogy with Prof. Levitt’s classic article Marketing Myopia (1960) [60], it is not AI technologies themselves that determine whether an industry prospers or declines, but whether it embraces a long-term, visionary strategy [61,62]. Like a fractal cycle—continuous, ceaseless, and timeless, always striving upward—sustainable growth in Industry 5.0 depends on foresight and adaptability. Ultimately, the success or failure of Industry 5.0 will hinge on how deliberately industries apply the principles of fractal design.

6.1. Challenges Ahead

AI has become a megatrend, converging with transformative technologies such as 3D printing, extended reality (XR), the Internet of Things (IoT), and biotechnology. In the era of Industry 5.0, sustainable growth requires more than technological modernization—it demands a holistic realignment of industrial systems with emerging technological, environmental, and societal imperatives [26,59,63,64].

However, many organizations remain constrained by legacy thinking, exemplifying what Levitt termed marketing myopia—the failure to anticipate and evolve with future needs. The core challenge of Industry 5.0 is therefore not merely adopting advanced technologies but transforming mindsets. Creativity, adaptability, and visionary leadership are vital to ensure industries actively shape the future of intelligent, human-centered, and sustainable innovation [60,61,62,65,66].

6.2. Visionary Leadership in the AI Era

Levitt’s warning against short-term thinking remains highly relevant; however, the AI era demands a redefinition of leadership itself. Leadership is no longer confined to hierarchical authority—it now emerges across all levels of an organization, driven by data-informed decision-making, collaboration, and agility.

As AI transforms core functions such as maintenance, supply chain management, and customer service, the absence of visionary leadership poses a critical risk. As Kuhn (1962) [67] emphasized, true transformation arises from paradigm shifts rather than incremental reforms. In this context, sustainable growth depends on cultivating leaders who champion innovation, adaptability, and creative problem-solving, enabling organizations to thrive amid continuous technological and social change [67,68,69].

6.3. From Industry 3.0 Through Industry 4.0 to Industry 5.0

The trajectory of industrial development is best understood as a continuum. Industry 3.0 introduced automation through electronics, computers, and IT systems. Industry 4.0 built upon this foundation by integrating digitalization, cyber–physical systems, IoT, cloud computing, robotics, and smart factories. Now, industries are advancing toward Industry 5.0, which emphasizes intelligent, human-centric, and sustainable systems.

In this transition, the convergence of AI and fractal modeling represents a transformative shift. AI enables real-time analytics, predictive control, and adaptive learning, while fractal science provides insight into the hierarchical and energy-efficient structures that govern material and process behaviors.

Together, these technologies offer significant benefits:

-

Optimization of energy and resource utilization.

-

Reduction in downtime through predictive and adaptive control.

-

Improvement in product customization and quality assurance.

Stronger alignment with circular economy and sustainability goals

This transformation extends beyond technical integration—it signifies a strategic imperative. AI should not be viewed as a replacement for human insight but as a collaborator in creative reinvention. As repetitive tasks become automated, creativity, imagination, and critical thinking emerge as the true competitive advantages of Industry 5.0—uniquely human capabilities that remain beyond the reach of machines [70,71,72].

Concluding Remarks

The prospects of Industry 5.0 highlight both opportunities and challenges. The convergence of AI with fractal modeling offers powerful tools for real-time analytics, predictive control, and adaptive system design, enabling industries to optimize resources while advancing sustainability goals. Yet, the true success of Industry 5.0 will not depend solely on technological adoption but on cultivating visionary leadership, fostering creativity, and embracing human–AI collaboration.

Ultimately, Industry 5.0 represents a strategic shift from efficiency-driven automation to human-centric, adaptive, and sustainable innovation. By applying fractal principles of self-similarity, hierarchy, and recursive growth, industries can position themselves not just to adapt to change, but to lead in shaping the next industrial era.

7. Conclusions

In the AI era, industries worldwide face tremendous challenges in achieving sustainable growth. Meeting these demands requires more than incremental improvements; it requires a constructive transformation and an entirely new paradigm. A simple paradigm shift is no longer sufficient.

It is striking and promising that many AI technologies are inherently built on fractal principles. This alignment is not coincidental. The sustainable growth of industry in the AI era depends on how the timeless principles of fractal technology are implemented.

FG reflects the deepest efficiencies of nature: hierarchical organization, self-similarity, and recursive simplicity. As an open book, nature reveals a profound lesson: simple is good, simpler is better, and simplest is best. This is exemplified by the foundation of fractal design, which begins not with complexity but with the most basic shapes, i.e., lines, triangles, squares, and circles, from which infinite complexity emerges through iteration.

Remark. Recent work suggests that fractal models intersect with Tsallis non-extensive statistics and emerging frameworks in Quantum Field Theory and Quantum Chromodynamics. Although beyond the scope of this paper, such connections highlight the universality of fractal principles and their potential to unify natural and technological systems.