An Efficient High-Accuracy RBF-HFD Scheme for Caputo Time-Fractional Sub-Diffusion Problems with Integral Boundaries

Abstract

This study presents an efficient high-order radius function Hermite finite difference (RBF-HFD) scheme for the numerical solution of Caputo time-fractional sub-diffusion equations with integral boundary conditions. The spatial derivatives are approximated using a fourth-order RBF-HFD scheme, while the Caputo fractional derivative in time is discretized via the L$2-1_{\sigma }$ formula. To ensure global fourth-order spatial accuracy, the integral boundary conditions are discretized with the composite Simpson rule. As a result, we obtain an unconditionally stable numerical scheme that achieves fourth-order convergence in space and second-order convergence in time. The solvability, stability, and convergence of the scheme are rigorously established using the discrete energy method. The proposed method is validated through three numerical examples and is compared with existing approaches. The numerical results demonstrate that the proposed scheme achieves higher accuracy than the methods available in the literature.

1. Introduction

We consider the Caputo-type time-fractional diffusion equation that satisfies the following initial and boundary conditions:

$$\left\{\begin{array}{c}{}_0{}^{C}D_t^{\alpha }v(x,t)-a_x{\displaystyle \frac{{\partial }^{2}v}{\partial x^2}}(x,t)=f(x,t),0<x<L,0<t\le T, \left(a\right)\hfill \\ v(x,0)=v_0\left(x\right),0\le x\le L,\left(b\right)\hfill \\ v(0,t)={\alpha }_1\underset{0}{\overset{L}{\int }}\phi \left(x\right)v(x,t)dx+{\beta }_1{g}_1\left(t\right),\left(c\right)\hfill \\ v(L,t)={\alpha }_2\underset{0}{\overset{L}{\int }}\psi \left(x\right)v(x,t)dx+{\beta }_2{g}_2\left(t\right),0<t\le T.\left(d\right)\hfill \end{array}\right.$$

(1)

where $a_x$,${\alpha }_1,{\alpha }_2,{\beta }_1,{\beta }_2$ are constants and $\phi ,\psi ,g_1,g_2,v_0$ are known functions. When ${\alpha }_1={\alpha }_2=0$, Equation (1) is subject to Dirichlet boundary conditions. When ${\alpha }_1={\alpha }_2\ne 0$, Equation (1) is subject to integral boundary conditions. The above system describes a one-dimensional Caputo-type time-fractional diffusion equation with non-local integral boundary conditions. Equation (a) governs the diffusion process, where ${}_0{}^{C}D_t^{\alpha }v(x,t)$ denotes the Caputo fractional derivative of order $0<\alpha <1$, the Caputo fractional derivative is defined as ${}_0{}^{C}D_t^{\alpha }v\left(t\right)={\displaystyle \frac{1}{\Gamma (1-\alpha )}}{\int }_0^t{\displaystyle \frac{v^{\prime }\left(s\right)}{{(t-s)}^{\alpha }}}ds$, where $\Gamma (·)$ denotes the Gamma function, which satisfies $\Gamma (1-\alpha )={\int }_0^{\infty }{\xi }^{-\alpha }{e}^{-\xi }d\xi$, capturing memory and hereditary effects, $a_x\frac{{\partial }^{2}v}{\partial x^2}(x,t)$ represents the classical diffusion operator with diffusion coefficient $a_x>0$, and $f(x,t)$ is a given source term. The initial condition (b) prescribes the solution at $t=0$. Unlike standard local boundary conditions, the conditions at $x=0$ and $x=L$, given by (c) and (d), are integral in nature, involving weighted averages of the solution over the spatial domain through kernel functions $\phi \left(x\right)$ and $\psi \left(x\right)$, together with boundary data $g_1\left(t\right)$ and $g_2\left(t\right)$. These non-local boundary constraints incorporate global spatial information into the boundary behavior, making the problem more challenging and suitable for modeling physical processes where the boundary response depends on the overall state of the system [1]. Time-fractional diffusion equations with integral boundary conditions frequently arise in thermo-elasticity problems. These integral boundary conditions impose constraints on the integral over the boundary, and strict conditions must be satisfied, namely, ${\int }_0^1\left|\phi \left(x\right)\right|dx<1$ and ${\int }_0^1\left|\psi \left(x\right)\right|dx<1$ [2]. Such conditions allow for the incorporation of more boundary information when solving the diffusion equation, leading to more accurate predictions of the temperature distribution within the domain. Since diffusion problems with integral boundary conditions often involve complex geometries or inhomogeneous properties, their numerical treatment poses significant challenges. In [3], Yunkang Liu proposed a second-order $\theta$-difference scheme for diffusion equations with integral boundary conditions, employing the $\theta$-difference method in space and the Crank–Nicolson (C-N) method in time, achieving overall second-order accuracy. Mehdi Dehghan [4] applied the central difference method for spatial discretization and utilized three time-stepping approaches—the C-N method, the implicit method, and the Padé approximation formula—to solve the equation. Building on previous work, Cui [5] developed a compact difference scheme for integer-order diffusion equations with integral boundary conditions, using a fourth-order compact difference in space and backward Euler or C-N methods in time, thus obtaining first-order temporal and fourth-order spatial precision, with unconditional stability and convergence established via the energy inequality method.

The radial basis function (RBF) is a real-valued function that depends solely on the distance from a specified central point. The fundamental concept is to represent the solution of a given problem as a linear combination of a series of RBFs, with the coefficients of this combination determined to approximate the true solution. In 1990, Edward Kansa first applied RBFs to solve partial differential equations, introducing what is now known as the Kansa method [6,7]. Later, in 2004, Fornberg and Wright proposed an algorithm for computing RBFs across all values of the shape parameter. Since then, researchers have developed and applied various RBF-based approaches for solving partial differential equations, including the RBF-QR method [8], the RBF-DQ method [9], and the RBF-PUM method [10].

In 2011, Wright, Tolstykh, and others introduced the Radial Basis Function Finite Difference (RBF-FD) method, which was subsequently applied to complex models such as Asian option pricing. Their work also contributed theoretical advances in stability and convergence analysis. In reference [11], Bhatia provided a comprehensive summary of common RBFs, deriving weight formulas and specific coefficient values for different node configurations. Building on these developments, Fazlollah Soleymani applied a finite difference scheme based on inverse multiquadric RBFs to the American options problem [12,13]. He further proposed a general framework for deriving approximate weights in the integrated RBF (IRBF) method [14], thereby enabling investigations into high-order convergence properties of node sets and extending the method to high-dimensional PDEs.

Continuing in this direction, In reference [15], Yin Yang addressed the worthless options problem using the RBF-HFD method constructed with multiquadric RBFs. Similarly, Mehdi Tatari combined RBFs with the collocation method to solve integer-order diffusion equations with integral boundary conditions [16]. Majid Haghi applied the RBF-HFD method to the cubic–quintic complex Ginzburg–Landau equation, demonstrating its superior accuracy and efficiency [17]. Extending the applications further, Mohammad Ilati employed the local RBF-Compact Finite Difference (RBF-CFD) method to solve multi-dimensional Sobolev equations arising in fluid mechanics [18]. Building on this foundation, Majid Haghi and Mohammad Ilati jointly studied two-dimensional, distributed-order, time-fractional cable equations over irregular domains [19], offering a robust alternative for tackling such problems.

The common methods for solving Caputo-type time-fractional problems include the $L1$ approximation formula [20], the $L1-2$ approximation formula [21], the $L2-1_{\sigma }$ approximation formula [22], and Finite Element Method [23]. Among these, the $L2-1_{\sigma }$ approximation formula has been widely applied to the numerical solution of Caputo-type time-fractional partial differential equations, such as diffusion equation [24], sub-diffusion equation [25], Burgers’ equation [22], KdV–Burgers’ equation [20,26], etc. As it effectively captures heat conduction phenomena with memory and non-local effects while achieving uniform second-order accuracy. For instance, it has been employed to solve the two-dimensional space–time fractional diffusion equation [27,28], the time-fractional nonlinear slow-diffusion equation [29,30], a high order difference method for fractional sub-diffusion equations with the spatially variable coefficients [31] and the time-fractional telegraph equation [32]. In reference [33], Mingrong Cui further developed a fourth-order compact difference scheme for the time-fractional diffusion equation with integral boundary conditions, adopting the $L1$ approximation in the temporal direction to attain $2-\alpha$ accuracy in time.

A given literature reveals that the Hermite finite difference schemes based on radial basis functions, together with their theoretical analysis for time-fractional diffusion equations with integral boundary conditions, remain largely unexplored. Motivated by reference [33], this paper introduces a Hermite difference scheme using radial basis functions in the spatial direction for such equations. The composite Simpson’s formula is employed to handle the integral boundary conditions, enabling the scheme to achieve fourth-order spatial accuracy. To ensure stability and uniform convergence, the $L2-1_{\sigma }$ approximation is applied in the temporal direction, leading to the construction of an unconditionally stable $RBFHFD-L2-1_{\sigma }$ numerical scheme. Furthermore, a comprehensive analysis of solvability, stability, and convergence is provided, supported by numerical experiments. Since the choice of shape parameters in radial basis functions significantly affects the quality of numerical solutions, this study also investigates their influence and identifies optimal parameter values.

Moreover, the proposed RBFHFD-L2-1_$\sigma$ scheme addresses a research gap by providing a stable, accurate, and efficient framework for solving time-fractional diffusion equations with integral boundary conditions. Its robustness and flexibility also make it well-suited for future extension to more complex, high-dimensional fractional models of parabolic and hyperbolic type, involving the Caputo fractional derivative for orders $1<\alpha <2$ [3].

The organization of this paper is as follows: Section 2 introduces the construction of the proposed scheme in both spatial and temporal directions, including the treatment of integral boundary conditions. Section 3 provides a detailed analysis of the theoretical properties of the scheme. Numerical experiments and illustrative examples are presented in Section 4.

2. Discrete Scheme

2.1. Spatial Discretization

For the Equation (1), we introduce a set of uniformly spaced grid points $(x_i,t_n)$ defined by $x_i=i\Delta x$ with $i=0,1,2,\dots ,N$ and $t_n=n\Delta t$ with $n=0,1,2,\dots ,M$, where N and M are positive integers, $\Delta x={\displaystyle \frac{L}{2N}}$ is the spatial grid width, $\Delta t={\displaystyle \frac{T}{M}}$ is the time step size, and any grid function $v(x_i,t_n)$ is denoted as $v_i^n$; to facilitate the construction of the subsequent numerical scheme, we further define $\varsigma =1-{\displaystyle \frac{\alpha }{2}}$, $t_{n-1+\varsigma }=(n-1+\varsigma )\Delta t$, $d={\displaystyle \frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}}$, ${\sigma }_x{v}_i^n=v_{i+1}^n-v_i^n$, and ${\sigma }_x^2{v}_i^n=v_{i-1}^n-2v_i^n+v_{i+1}^n$.

The numerical approximation performance of various radial basis functions (RBFs) including the Gaussian function ${\phi }_G$, multiquadric function ${\phi }_M$, and inverse multiquadric function ${\phi }_{IM}$ depends critically on the optimal selection of the following:

• Basis function centers ${\left\{{\mathbf{x}}_i\right\}}_{i=1}^N$;
• Shape parameters $\omega$.

These commonly employed RBF types can achieve fourth-order spatial accuracy in numerical implementations. For our analysis, we focus on the Gaussian RBF defined as

$${\phi }_G\left(r\right)=exp(-\omega r^2),r=\parallel \mathbf{x}-{\mathbf{x}}_i\parallel$$

(2)

where r represents the Euclidean distance from the center ${\mathbf{x}}_i$, and $\omega >0$ denotes the shape parameter.

Following the RBF-based Hermite finite difference (RBF-HFD) framework [12], we obtain the second derivative approximation at node ${\mathbf{x}}_i$ using a three-point stencil:

$$v^{″}\left({\mathbf{x}}_i\right)\approx {\widehat{v}}^{″}\left({\mathbf{x}}_i\right)={\lambda }_{1}v({\mathbf{x}}_i-\Delta x)+{\lambda }_{2}v\left({\mathbf{x}}_i\right)+{\lambda }_{3}v({\mathbf{x}}_i+\Delta x)+{\mu }_1{\widehat{v}}^{″}({\mathbf{x}}_i-\Delta x)+{\mu }_3{\widehat{v}}^{″}({\mathbf{x}}_i+\Delta x)$$

(3)

where the weights ${\left\{{\lambda }_k\right\}}_{k=1}^3$ and ${\left\{{\mu }_k\right\}}_{k\in \{1,3\}}$ are determined by the RBF-HFD formulation.

By approximating the function v using Gaussian radial basis functions centered at the nodal points $x_{i-1}$, $x_i$, and $x_{i+1}$ (where $x_{i\pm 1}=x_i\pm \Delta x$), we derive the following system of five linear equations.

$$\left\{\begin{array}{c}{\lambda }_1+{\lambda }_2{e}^{-\omega {(\Delta x)}^2}+{\lambda }_3{e}^{-\omega {(2\Delta x)}^2}-2\omega {\mu }_1+(4{\omega }^2{(2\Delta x)}^2-2\omega )e^{-\omega {(2\Delta x)}^2}{\mu }_3=(4{\omega }^2{(\Delta x)}^2-2\omega )e^{-\omega {(\Delta x)}^2}\hfill \\ {\lambda }_1{e}^{-\omega {(\Delta x)}^2}+{\lambda }_2+{\lambda }_3{e}^{-\omega {(\Delta x)}^2}+(4{\omega }^2{(\Delta x)}^2-2\omega )e^{-\omega {(\Delta x)}^2}{\mu }_1+(4{\omega }^2{(\Delta x)}^2-2\omega )e^{-\omega {(\Delta x)}^2}{\mu }_3=-2\omega \hfill \\ {\lambda }_1{e}^{-\omega {(2\Delta x)}^2}+{\lambda }_2{e}^{-\omega {(\Delta x)}^2}+{\lambda }_3+(4{\omega }^2{(2\Delta x)}^2-2\omega )e^{-\omega {(2\Delta x)}^2}{\mu }_1-2\omega {\mu }_3=(4{\omega }^2{(\Delta x)}^2-2\omega )e^{-\omega {(\Delta x)}^2}\hfill \\ -2\omega \Delta x{e}^{-\omega {(\Delta x)}^2}{\lambda }_2-2\omega (2\Delta x)e^{-\omega {(2\Delta x)}^2}{\lambda }_3+(12{\omega }^2(2\Delta x)-8{\omega }^3{(2\Delta x)}^3)e^{-\omega {(2\Delta x)}^2}{\mu }_3=(12{\omega }^2\Delta x-8{\omega }^3\Delta x^3)e^{-\omega {(\Delta x)}^2}\hfill \\ -2\omega (2\Delta x)e^{-\omega {(2\Delta x)}^2}{\lambda }_1-2\omega \Delta x{e}^{-\omega {(\Delta x)}^2}{\lambda }_2+(12{\omega }^2(2\Delta x)-8{\omega }^3{(2\Delta x)}^3)e^{-\omega {(2\Delta x)}^2}{\mu }_1=(12{\omega }^2\Delta x-8{\omega }^3\Delta x^3)e^{-\omega {(\Delta x)}^2}\hfill \end{array}\right.$$

The solution to the above system, obtained using Maple, is

$${\lambda }_1=-{\displaystyle \frac{4{\omega }^2{(\Delta x)}^2{e}^{-\omega {(\Delta x)}^2}}{2{\left(e^{-\omega {(\Delta x)}^2}\right)}^2-e^{-4\omega {(\Delta x)}^2}-1}}$$

$${\lambda }_2=-{\displaystyle \frac{2\omega (4\omega {(\Delta x)}^2{(e^{-\omega {(\Delta x)}^2})}^2-2{(e^{-\omega {(\Delta x)}^2})}^2+e^{-4\omega {(\Delta x)}^2}+1)}{2{\left(e^{-\omega {(\Delta x)}^2}\right)}^2-e^{-4\omega {(\Delta x)}^2}-1}}$$

$${\lambda }_3=-{\displaystyle \frac{4{\omega }^2{(\Delta x)}^2{e}^{-\omega {(\Delta x)}^2}}{2{\left(e^{-\omega {(\Delta x)}^2}\right)}^2-e^{-4\omega {(\Delta x)}^2}-1}}$$

$${\mu }_1=-{\displaystyle \frac{4{\omega }^2{(\Delta x)}^2{e}^{-\omega {(\Delta x)}^2}}{2{\left(e^{-\omega {(\Delta x)}^2}\right)}^2-e^{-4\omega {(\Delta x)}^2}-1}}$$

$${\mu }_3=-{\displaystyle \frac{4{\omega }^2{(\Delta x)}^2{e}^{-\omega {(\Delta x)}^2}}{2{\left(e^{-\omega {(\Delta x)}^2}\right)}^2-e^{-4\omega {(\Delta x)}^2}-1}}$$

Expanding and simplifying the above coefficients using Taylor series expansions yields

$${\lambda }_1={\lambda }_3={\displaystyle \frac{6}{5\Delta x^2}}+{\displaystyle \frac{9\omega }{25}};{\lambda }_2=-2{\lambda }_1=-{\displaystyle \frac{12}{5\Delta x^2}}-{\displaystyle \frac{18\omega }{25}};{\mu }_1={\mu }_3=-{\displaystyle \frac{1}{10}}-{\displaystyle \frac{9\omega \Delta x^2}{5}}$$

By means of Taylor series expansion, the error equation can be derived as

$$R_1\left(x_i\right)=v^{″}\left(x_i\right)-{\widehat{v}}^{″}\left(x_i\right)=\left(({\displaystyle \frac{81}{25\Delta x^2}}+{\displaystyle \frac{76\omega }{125}})v^{″}(x_i)+({\displaystyle \frac{177}{100}}+{\displaystyle \frac{19\omega \Delta x^2}{375}})v^{\left(4\right)}\left(x_i\right)\right)\Delta x^4+o(\Delta x^5)$$

(4)

2.2. Time Discretization

For the $\alpha$-order Caputo derivative where $0<\alpha <1$, the standard $L1$ approximation formula achieves a uniform convergence order of $(2-\alpha )$. In contrast, the $L1$-2 formula utilizes an increased number of computational nodes, which elevates the convergence order to $(3-\alpha )$. As research in fractional calculus has advanced, scholars have disscussed the $L1$-2 formula to identify super-convergent interpolation points, leading to the development of the $L2$-$1_{\sigma }$ approximation formula [33].

We begin by expressing the fractional-order derivative as a sum of integrals over subintervals:

$${}_0{}^{C}D_t^{\alpha }v\left(t\right)\left|t=t_{n-1+\varsigma }\right.={\displaystyle \frac{1}{\Gamma (1-\alpha )}}\left[{\displaystyle \sum _{j=1}^{n-1}}{\int }_{t_{j-1}}^{t_j}{\displaystyle \frac{v^{\prime }\left(t\right)}{{(t_{n-1+\varsigma }-t)}^{\alpha }}}dt+{\int }_{t_{n-1}}^{t_{n-1+\varsigma }}{\displaystyle \frac{v^{\prime }\left(t\right)}{{(t_{n-1+\varsigma }-t)}^{\alpha }}}\right].$$

(5)

We use the quadratic interpolation polynomials $L_{2,j}\left(t\right)$ ($1\le j\le n-1$) and $L_{1,n}\left(t\right)$, constructed from three points on the interval $[t_{j-1},t_j]$ as given in Reference [24], to approximate Equation (4). This yields

$$\begin{array}{c}{}_0{}^{C}D_t^{\alpha }v\left(t\right)\left|t=t_{n-1+\varsigma }\right.\approx {\displaystyle \frac{1}{\Gamma (1-\alpha )}}\left[{\displaystyle \sum _{j=1}^{n-1}}{\int }_{t_{j-1}}^{t_j}{\displaystyle \frac{{L^{\prime }}_{2,j}\left(t\right)}{{(t_{n-1+\varsigma }-t)}^{\alpha }}}dt+{\int }_{t_{n-1}}^{t_{n-1+\varsigma }}{\displaystyle \frac{{L^{\prime }}_{1,n}\left(t\right)}{{(t_{n-1+\varsigma }-t)}^{\alpha }}}dt\right]\hfill \\ ={\displaystyle \frac{\Delta t^{1-\alpha }}{\Gamma (1-\alpha )}}\left\{\left[{\int }_0^1({\displaystyle \frac{3}{2}}-\theta ){(n-1+\varsigma -\theta )}^{-\alpha }d\theta \right]{\displaystyle \frac{v^1-v^0}{\Delta t}}\right.+{\displaystyle \sum _{j=2}^{n-1}}\left[{\int }_0^1({\displaystyle \frac{3}{2}}-\theta ){(n-j+\varsigma -\theta )}^{-\alpha }d\theta \right.\hfill \\ +\left.{\int }_0^{1/2}\theta \left(\alpha {\int }_{-\theta }^{\theta }{(n-j+{\displaystyle \frac{1}{2}}+\varsigma +\xi )}^{-\alpha -1}d\xi \right)d\theta \right]{\displaystyle \frac{v^j-v^{j-1}}{\Delta t}}\hfill \end{array}$$

(6)

Denote $s_0^{(1,\alpha )}={\varsigma }^{1-\alpha }$, when $n\ge 2$, gives

$$\left\{\begin{array}{c}{s}_0^{(n,\alpha )}=(1-\alpha ){\int }_0^{1/2}\theta \left(\alpha {\int }_{-\theta }^{\theta }{({\displaystyle \frac{1}{2}}+\varsigma +\xi )}^{-\alpha -1}d\xi \right)d\theta +{\varsigma }^{1-\alpha }\hfill \\ s_j^{(n,\alpha )}=(1-\alpha )\left[{\int }_0^1({\displaystyle \frac{3}{2}}-\theta ){(j+\varsigma -\theta )}^{-\alpha }d\theta +\left.{\int }_0^{1/2}\theta \left(\alpha {\int }_{-\theta }^{\theta }{(j+{\displaystyle \frac{1}{2}}+\varsigma +\xi )}^{-\alpha -1}d\xi \right)d\theta \right],1\le j\le n-2.\right.\hfill \\ s_{n-1}^{(n,\alpha )}=(1-\alpha ){\int }_0^1({\displaystyle \frac{3}{2}}-\theta ){(n-1+\varsigma -\theta )}^{-\alpha }d\theta ,\hfill \end{array}\right.$$

Equation (5) can be written as follows

$${▹}_t^{\alpha }{v}^{n-1+\varsigma }={\displaystyle \frac{\Delta t^{1-\alpha }}{\Gamma (2-\alpha )}}\sum _{j=1}^n{s}_{n-j}^{(n,\alpha )}{\displaystyle \frac{v^j-v^{j-1}}{\Delta t}}={\displaystyle \frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}}\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}(v^{n-j}-v^{n-j-1}),1\le j\le M.$$

(7)

Equation (6) is the $L2-1_{\sigma }$ approximation formula, and the specific calculation results of the coefficients are as follows. When $n\ge 2$,

$$\left\{\begin{array}{c}{s}_0^{(n,\alpha )}={\displaystyle \frac{{(1+\varsigma )}^{2-\alpha }-{\varsigma }^{2-\alpha }}{2-\alpha }}-{\displaystyle \frac{{(1+\varsigma )}^{1-\alpha }-{\varsigma }^{1-\alpha }}{2}},\hfill \\ s_j^{(n,\alpha )}={\displaystyle \frac{1}{2-\alpha }}\left[{(j+1+\varsigma )}^{2-\alpha }-2{(j+\varsigma )}^{2-\alpha }+{(j-1+\varsigma )}^{2-\alpha }\right]-{\displaystyle \frac{1}{2}}\left[{(j+1+\varsigma )}^{1-\alpha }-2{(j+\varsigma )}^{1-\alpha }+{(j-1+\varsigma )}^{2-\alpha }\right]\hfill \\ s_{n-1}^{(n,\alpha )}={\displaystyle \frac{1}{2}}\left[3{(n-1+\varsigma )}^{1-\alpha }-{(n-2+\varsigma )}^{1-\alpha }\right]-{\displaystyle \frac{1}{2-\alpha }}\left[{(n-1+\varsigma )}^{2-\alpha }-{(n-2+\varsigma )}^{2-\alpha }\right].\hfill \end{array}\right.$$

According to the characteristics of the construction format, this paper defines the following operator:

$${\mathrm{H}}_{xx}{v}_i=-{\mu }_1{v}_{i-1}+v_i-{\mu }_3{v}_{i+1},{\mathrm{H}}_{\left(x\right)}{v}_i={\lambda }_1{v}_{i-1}+{\lambda }_2{v}_i+{\lambda }_3{v}_{i+1};1\le i\le 2N-1.$$

Based on the results from Section 2.1, the following can be deduced:

$$\begin{array}{c}\begin{array}{c}{\displaystyle {\mathrm{H}}_{xx}{v}_i=-{\mu }_1{v}_{i-1}+v_i-{\mu }_3{v}_{i+1}=v_i+\left(\frac{1}{10}+\frac{9\omega \Delta x^2}{5}\right)\left(v_{i-1}+v_{i+1}\right)}\hfill \\ {\displaystyle =\left(\frac{1}{10}+\frac{9\omega \Delta x^2}{5}\right)\left(v_{i-1}-2v_i+v_{i+1}\right)+2·\left(\frac{1}{10}+\frac{9\omega \Delta x^2}{5}\right)v_i+v_i}\hfill \\ {\displaystyle =\left(\frac{6}{5}+\frac{18\omega {(\Delta x)}^2}{5}\right)v_i+\left(\frac{1}{10}+\frac{9\omega {(\Delta x)}^2}{5}\right)(v_{i-1}-2v_i+v_{i+1})}\hfill \end{array}\hfill \\ {\displaystyle =\left[\left(\frac{6}{5}+\frac{18\omega {(\Delta x)}^2}{5}\right)+\left(\frac{1}{10}+\frac{9\omega {(\Delta x)}^2}{5}\right){\sigma }_x^2\right]v_i;}\hfill \end{array}$$

$${\mathrm{H}}_{\left(x\right)}{v}_i={\lambda }_1{v}_{i-1}+{\lambda }_2{v}_i+{\lambda }_3{v}_{i+1}=\left({\displaystyle \frac{6}{5{(\Delta x)}^2}}+{\displaystyle \frac{9\omega }{25}}\right)\left(v_{i-1}-2v_i+v_{i+1}\right)=\left({\displaystyle \frac{6}{5{(\Delta x)}^2}}+{\displaystyle \frac{9\omega }{25}}\right){\sigma }_x^2{v}_i;$$

Substituting these results into Equation (2), we obtain

$${\mathrm{H}}_{xx}{v}_i^{″}={\mathrm{H}}_{\left(x\right)}{v}_i\Rightarrow \left[\left({\displaystyle \frac{6}{5}}+{\displaystyle \frac{18\omega {(\Delta x)}^2}{5}}\right)+\left({\displaystyle \frac{1}{10}}+{\displaystyle \frac{9\omega {(\Delta x)}^2}{5}}\right){\sigma }_x^2\right]v_i^{″}=\left({\displaystyle \frac{6}{5{(\Delta x)}^2}}+{\displaystyle \frac{9\omega }{25}}\right){\sigma }_x^2{v}_i.$$

Consequently, it follows that

$${\left({\displaystyle \frac{{\partial }^{2}v}{\partial x^2}}\right)}_i={\displaystyle \frac{\left(\frac{6}{5{(\Delta x)}^2}+\frac{9\omega }{25}\right){\sigma }_x^2}{\left[\left(\frac{6}{5}+\frac{18\omega {(\Delta x)}^2}{5}\right)+\left(\frac{1}{10}+\frac{9\omega {(\Delta x)}^2}{5}\right){\sigma }_x^2\right]}}{v}_{i,j}+o(\Delta x^4);$$

Considering Equation (1.a) at point $(x_i,t_{n-1+\varsigma })$, we obtain

$${}_0{}^{C}D_t^{\alpha }{v}_i^{n-1+\varsigma }-a_x\left\{{\displaystyle \frac{\left(\frac{6}{5{(\Delta x)}^2}+\frac{9\omega }{25}\right){\sigma }_x^2}{\left[\left(\frac{6}{5}+\frac{18\omega {(\Delta x)}^2}{5}\right)+\left(\frac{1}{10}+\frac{9\omega {(\Delta x)}^2}{5}\right){\sigma }_x^2\right]}}\right\}{v}_i^{n-1+\varsigma }=f_i^{n-1+\varsigma }.$$

(8)

Based on the above derivations, Equation (1) can be rearranged as

$$\left\{\begin{array}{c}{\displaystyle {\mathrm{H}}_{xx}\left({}_0{}^{C}D_t^{\alpha }{v}_i^{n-1+\varsigma }\right)-a_x{\mathrm{H}}_{\left(x\right)}{v}_i^{n-1+\varsigma }}\hfill \\ {\displaystyle ={\mathrm{H}}_{xx}{f}_i^{n-1+\varsigma }+R_2\left(x_i\right),1\le i<2N-1,1\le n\le M, \left(a\right)}\hfill \\ {\displaystyle v_i^0=v_0\left(x_i\right),0\le i<2N,\left(b\right)}\hfill \\ {\displaystyle v_0^{n-1+\varsigma }={\alpha }_1{\int }_0^1\phi \left(x_i\right)v_i^{n-1+\varsigma }dx+{\beta }_1{g}_1\left(t_{n-1+\varsigma }\right), \left(c\right)}\hfill \\ v_N^{n-1+\varsigma }={\alpha }_2{\int }_0^1\psi \left(x_i\right)v_i^{n-1+\varsigma }dx+{\beta }_2{g}_2\left(t_{n-1+\varsigma }\right),1\le n\le M; \left(d\right)\hfill \end{array}\right.$$

(9)

Among them, for $R_2\left(x_i\right)=a_x{\mathrm{H}}_{xx}{R}_1\left(x_i\right)+{\mathrm{H}}_{xx}{\displaystyle \frac{(4\varsigma -1){\varsigma }^{-\alpha }}{12\Gamma (2-\alpha )}}\underset{t_0\le t\le t_n}{max}\left|v^{‴}\left(t\right)\right|\Delta t^{3-\alpha }.$ let

$$\rho =max\left\{{\displaystyle \frac{(4\varsigma -1){\varsigma }^{-\alpha }}{12\Gamma (2-\alpha )}}\underset{(x,t)\in D}{max}\left|{\displaystyle \frac{{\partial }^{3}v(x,t)}{\partial t^3}}\right|,({\displaystyle \frac{81}{25\Delta x^2}}+{\displaystyle \frac{76\omega }{125}})\underset{(x,t)\in D}{max}\left|{\displaystyle \frac{{\partial }^{2}v(x,t)}{\partial x^2}}\right|+({\displaystyle \frac{177}{100}}+{\displaystyle \frac{19\omega \Delta x^2}{375}})\underset{(x,t)\in D}{max}\left|{\displaystyle \frac{{\partial }^{4}v(x,t)}{\partial x^4}}\right|\right\}$$

Then, we have

$$\left|R_2\left(x_i\right)\right|\le \rho (\Delta t^2+\Delta x^4),1\le i\le 2N-1,0\le n\le M-1.$$

(10)

By applying Equation (6) to discretize the time-fractional order derivative in Equation (9.a), we can obtain

$$\begin{array}{c}{\displaystyle {\mathrm{H}}_{xx}\left({}_0{}^{C}D_t^{\alpha }{v}_i^{n-1+\varsigma }\right)=\frac{\Delta t^{-\alpha }}{\Gamma (2-\alpha )}\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({\mathrm{H}}_{xx}{v}_i^{n-j}-{\mathrm{H}}_{xx}{v}_i^{n-j-1}\right)}\hfill \\ {\displaystyle =d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({\mathrm{H}}_{xx}{v}_i^{n-j}-{\mathrm{H}}_{xx}{v}_i^{n-j-1}\right)}\hfill \end{array}$$

(11)

Thus, Equation (9.a) can be processed as

$$d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({\mathrm{H}}_{xx}{v}_i^{n-j}-{\mathrm{H}}_{xx}{v}_i^{n-j-1}\right)=a_x\left(\varsigma {\mathrm{H}}_{\left(x\right)}{v}_i^n+(1-\varsigma ){\mathrm{H}}_{\left(x\right)}{v}_i^{n-1}\right)+{\mathrm{H}}_{xx}{f}_i^{n-1+\varsigma }$$

(12)

The Hermite difference scheme based on radial basis functions achieves fourth-order accuracy. To maintain this level of precision, the composite Simpson’s formula is applied for handling the non-local boundary conditions, thereby ensuring that the overall scheme retains fourth-order accuracy.

The composite Simpson’s formula [32] is given by

$${\int }_0^{L}K(x_i,t_n)dx\approx {\displaystyle \frac{\Delta x}{3}}{K}_0^n+{\displaystyle \frac{4\Delta x}{3}}\sum _{k=0}^{N-1}{K}_{2k+1}^n+{\displaystyle \frac{2\Delta x}{3}}\sum _{k=1}^{N-1}{K}_{2k}^n+{\displaystyle \frac{\Delta x}{3}}{K}_{2N}^n\equiv \Delta x\sum _{k=0}^{2N}{q}_k{K}_k^n$$

(13)

where the coefficients are defined as $q_0=q_{2N}={\displaystyle \frac{1}{3}},q_{2k}={\displaystyle \frac{2}{3}},q_{2k+1}={\displaystyle \frac{4}{3}}(1\le k\le N-1)$. Therefore, Equation (12) can be expressed as

$${\int }_0^{L}K(x_i,t_n)dx=\Delta x\sum _{k=0}^{2N}{q}_k{K}_k^n-{\displaystyle \frac{\Delta x^4}{180}}{\displaystyle \frac{{\partial }^{5}K}{\partial x^5}}(\xi ,t_n),\xi \in (0,L)$$

By incorporating these results, the $RBFHFD-L2-1_{\sigma }$ scheme of the equation is obtained:

$$\left\{\begin{array}{c}{\displaystyle \left(1-\frac{\Delta x}{3}{\phi }_0{\alpha }_1\right)v_0^n-\frac{4\Delta x}{3}{\alpha }_1\sum _{k=0}^{N-1}{\phi }_{2k+1}{v}_{2k+1}^n-\frac{2\Delta x}{3}{\alpha }_1\sum _{k=1}^{N-1}{\phi }_{2k}{v}_{2k}^n-\frac{\Delta x}{3}{\alpha }_1{\phi }_{2N}{v}_{2N}^n={\beta }_1{g}_1^n,}\hfill \\ {\displaystyle d{s}_0^{(n,\alpha )}\left(-{\mu }_1{v}_{i-1}^n+v_i^n-{\mu }_3{v}_{i+1}^n\right)-\varsigma a_x\left({\lambda }_1{v}_{i-1}^n+{\lambda }_2{v}_i^n+{\lambda }_3{v}_{i+1}^n\right)=}\hfill \\ {\displaystyle d{s}_0^{(n,\alpha )}\left(-{\mu }_1{v}_{i-1}^{n-1}+v_i^{n-1}-{\mu }_3{v}_{i+1}^{n-1}\right)+(1-\varsigma )a_x\left({\lambda }_1{v}_{i-1}^{n-1}+{\lambda }_2{v}_i^{n-1}+{\lambda }_3{v}_{i+1}^{n-1}\right)}\hfill \\ {\displaystyle -d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left[(-{\mu }_1{v}_{i-1}^{n-j}+v_i^{n-j}-{\mu }_3{v}_{i+1}^{n-j})-(-{\mu }_1{v}_{i-1}^{n-j-1}+v_i^{n-j-1}-{\mu }_3{v}_{i+1}^{n-j-1})\right]}\hfill \\ {\displaystyle +\varsigma H_{xx}{f}_i^n+(1-\varsigma )H_{xx}{f}_i^{n-1},}\hfill \\ {\displaystyle -\frac{\Delta x}{3}{\alpha }_2{\psi }_0{v}_0^n-\frac{4\Delta x}{3}{\alpha }_2\sum _{k=0}^{N-1}{\psi }_{2k+1}{v}_{2k+1}^n-\frac{2\Delta x}{3}{\alpha }_2\sum _{k=1}^{N-1}{\psi }_{2k}{v}_{2k}^n+\left(1-\frac{\Delta x}{3}{\alpha }_2{\psi }_{2N}\right)v_{2N}^n={\beta }_2{g}_2^n}\hfill \end{array}\right.$$

(14)

3. Theoretical Analysis

In this section, we establish the unique solvability, stability, and convergence of the proposed scheme through a series of theorems and their corresponding proofs.

3.1. Solvability

Theorem 1.  

The difference scheme (14) admits a unique solution.

Proof. 

Let $v^n=(v_0^n,v_1^n,\cdots v_{2N-1}^n,v_{2N}^n)$. From Equation (9.b), the initial value $v^0$ on the 0-th layer is known. Assume that the values $v^{n-1}$ at the $n-1$-th layer have already been determined. Then, the difference scheme for computing $v^n$ at the n-th layer is given by Equation (14), which can be written in the following matrix form:

$$P{V}^n=Q{V}^{n-1}-d\sum _{j=1}^{n-1}{s}_j^{(n,\alpha )}M+G.$$

Denote:

$$\begin{array}{c}{\displaystyle {\alpha }_{21}=-{\mu }_{1}d{s}_0^{(n,\alpha )}-\varsigma a_x{\lambda }_1;{\alpha }_{22}=d{s}_0^{(n,\alpha )}-\varsigma a_x{\lambda }_2;{\alpha }_{23}=-{\mu }_{3}d{s}_0^{(n,\alpha )}-\varsigma a_x{\lambda }_3;}\hfill \\ {\displaystyle {\beta }_{21}=-{\mu }_{1}d{s}_0^{(n,\alpha )}+(1-\varsigma )a_x{{\lambda }_1}_1;{\beta }_{22}=d{s}_0^{(n,\alpha )}+(1-\varsigma )a_x{\lambda }_2;{\beta }_{23}=-{\mu }_{3}d{s}_0^{(n,\alpha )}+(1-\varsigma )a_x{\lambda }_3;}\hfill \end{array}$$

Let

$$V={\left[v_0,v_1,\cdots v_{2N-1},v_{2N}\right]}^T;$$

Then the coefficient matrices and vectors in the difference scheme can be written as

$$P=\left(\begin{array}{cccccc}1-{\displaystyle \frac{\Delta x}{3}}{\alpha }_1{\phi }_0& -{\displaystyle \frac{4\Delta x}{3}}{\alpha }_1{\phi }_1& -{\displaystyle \frac{2\Delta x}{3}}{\alpha }_1{\phi }_2& \cdots & -{\displaystyle \frac{4\Delta x}{3}}{\alpha }_1{\phi }_{2N-1}& -{\displaystyle \frac{\Delta x}{3}}{\alpha }_1{\phi }_{2N}\\ {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}& 0& \cdots & 0\\ & \ddots & \ddots & \ddots & & \\ & & \ddots & \ddots & \ddots & \\ 0& \cdots & 0& {\alpha }_{21}& {\alpha }_{22}& {\alpha }_{23}\\ -{\displaystyle \frac{\Delta x}{3}}{\alpha }_2{\psi }_0& -{\displaystyle \frac{4\Delta x}{3}}{\alpha }_2{\psi }_1& -{\displaystyle \frac{2\Delta x}{3}}{\alpha }_2{\psi }_2& \cdots & -{\displaystyle \frac{4\Delta x}{3}}{\alpha }_2{\psi }_{2N-1}& 1-{\displaystyle \frac{\Delta x}{3}}{\alpha }_2{\psi }_{2N}\end{array}\right);$$

$$M=\left(\begin{array}{c}0\\ (-{\mu }_1{v}_0^{n-j}+v_1^{n-j}-{\mu }_3{v}_2^{n-j})-(-{\mu }_1{v}_0^{n-j-1}+v_1^{n-j-1}-{\mu }_3{v}_2^{n-j-1})\\ ⋮\\ ⋮\\ (-{\mu }_1{v}_{2N-2}^{n-j}+v_{2N-1}^{n-j}-{\mu }_3{v}_{2N}^{n-j})-(-{\mu }_1{v}_{2N-2}^{n-j-1}+v_{2N-1}^{n-j-1}-{\mu }_3{v}_{2N}^{n-j-1})\\ 0\end{array}\right);$$

and

$$Q=\left(\begin{array}{cccccc}0& 0& 0& \cdots & 0& 0\\ {\beta }_{21}& {\beta }_{22}& {\beta }_{23}& 0& \cdots & 0\\ & \ddots & \ddots & \ddots & & \\ & & \ddots & \ddots & \ddots & \\ 0& \cdots & 0& {\beta }_{21}& {\beta }_{22}& {\beta }_{23}\\ 0& 0& 0& \cdots & 0& 0\end{array}\right);G=\left(\begin{array}{c}{\beta }_1{g}_1^n\\ \varsigma {\mathrm{H}}_{xx}{f}_1^n+(1-\varsigma ){\mathrm{H}}_{xx}{f}_1^{n-1}\\ \begin{array}{c}⋮\\ ⋮\end{array}\\ \begin{array}{c}\varsigma {\mathrm{H}}_{xx}{f}_{2N-1}^n+(1-\varsigma ){\mathrm{H}}_{xx}{f}_{2N}^{n-1}\\ {\beta }_2{g}_2^n\end{array}\end{array}\right)$$

As mentioned in Reference [3], if the boundary conditions satisfy $\Delta x{\displaystyle \sum _{k=0}^{2N}}{q}_k\left|{\phi }_k^n\right|<1$ and $\Delta x{\displaystyle \sum _{k=0}^{2N}}{q}_k\left|{\psi }_k^n\right|<1$, then the first and last rows of P satisfy the following:

$$\begin{array}{c}\left|P_{1,1}\right|=\left|1-{\displaystyle \frac{\Delta x}{3}}{\alpha }_1{\phi }_0\right|>\left|\Delta x{\alpha }_1{\displaystyle \sum _{k=0}^{2N}}{q}_k\left|{\phi }_k^n\right|-{\displaystyle \frac{\Delta x}{3}}{\alpha }_1{\phi }_0\right|={\displaystyle \sum _{j=2}^{2N}}\left|P_{1,j}\right|;\hfill \\ \left|P_{2N,2N}\right|=\left|1-{\displaystyle \frac{\Delta x}{3}}{\alpha }_2{\psi }_{2N}\right|>\left|\Delta x{\alpha }_2{\displaystyle \sum _{k=0}^{2N}}{q}_k\left|{\psi }_k^n\right|-{\displaystyle \frac{\Delta x}{3}}{\alpha }_2{\psi }_{2N}\right|={\displaystyle \sum _{j=1}^{2N-1}}\left|P_{2N,j}\right|;\hfill \end{array}$$

The elements of the other rows in the matrix $\mathit{P}$ satisfy the following:

$$\begin{array}{c}\left|P_{i,i}\right|=\left|{\alpha }_{22}\right|=\left|d{s}_0^{(n,\alpha )}-a_x\varsigma {\lambda }_2\right|=\left|d{s}_0^{(n,\alpha )}+2a_x\varsigma {\lambda }_1\right|\hfill \\ >\left|-{\mu }_{1}d{s}_0^{(n,\alpha )}-\varsigma a_x{\lambda }_1+(-{\mu }_{3}d{s}_0^{(n,\alpha )}-\varsigma a_x{\lambda }_3)\right|=\left|2{\mu }_{1}d{s}_0^{(n,\alpha )}+2\varsigma a_x\lambda \right|={\displaystyle \sum _{j=2,j\ne i}^{2N-1}}\left|P_{i,j}\right|.\hfill \end{array}$$

Consequently, the full coefficient matrix is strictly diagonally dominant and therefore non-singular. Hence, the difference scheme admits a unique solution. □

3.2. Stability

To simplify the analysis of the stability and convergence of the subsequent scheme, we introduce the following notations:

$$\left(u,v\right)=\Delta x\sum _{l=1}^{2N-1}{u}_l{v}_l;∥v∥=\sqrt{\left(v,v\right)};{\left|v\right|}_1=\sqrt{\left({\sigma }_{x}v,{\sigma }_{x}v\right)}$$

Lemma 1  

([33]). Let Ω be an inner product space with inner product $(·,·)$ and induced norm $\parallel ·\parallel$. For $0\le \alpha <1$, assume the sequence $\left\{s_j^{(n,\alpha )}\right|0\le j\le n-1,n\ge 1\}$ satisfies

$$s_0^{(n,\alpha )}>s_1^{(n,\alpha )}>\cdots >s_{n-1}^{(n,\alpha )}>0,(2\varsigma -1)s_0^{(n,\alpha )}-\varsigma s_1^{(n,\alpha )}>0.$$

Then, for any $v^0,v^1,\dots ,v^n\in \Omega$,

$$\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}(v^{n-j}-v^{n-j-1},\varsigma v^n+(1-\varsigma )v^{n-1})\ge {\displaystyle \frac{1}{2}}\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}(\parallel v^{n-j}{\parallel }^2-\parallel v^{n-j-1}{\parallel }^2).$$

Lemma 2  

([33]). For $\alpha \in (0,1)$ and $\varsigma =1-{\displaystyle \frac{\alpha }{2}}$, the coefficients $\left\{s_j^{(n,\alpha )}\right\}$ satisfy

$$s_0^{(n,\alpha )}>s_1^{(n,\alpha )}>\cdots >s_{n-1}^{(n,\alpha )}>(1-\alpha )n^{-\alpha },(2\varsigma -1)s_0^{(n,\alpha )}-\varsigma s_1^{(n,\alpha )}>0.$$

Hence,

$${\displaystyle \frac{1}{d{s}_{n-1}^{(n,\alpha )}}}\le {\displaystyle \frac{\Delta t^{\alpha }\Gamma (2-\alpha )}{(1-\alpha )n^{-\alpha }}}\le t_n^{\alpha }\Gamma (1-\alpha ).$$

Theorem 2.  

Let $\left\{v_i^n\left|0\le i\le 2N,0\le n\le \left.M\right\}\right.\right.$ be the solution of the system of difference equations:

$$\left\{\begin{array}{c}{\displaystyle d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}{\mathrm{H}}_{xx}(v_i^{n-j}-v_i^{n-j-1})=a_x\varsigma {\mathrm{H}}_{\left(x\right)}{v}_i^n}\hfill \\ {\displaystyle +a_x(1-\varsigma ){\mathrm{H}}_{\left(x\right)}{v}_i^{n-1}+q_i^n,1\le i\le 2N-1;1\le n\le M.\left(a\right)}\hfill \\ {\displaystyle v_i^0=v_0\left(x_i\right),1\le i\le 2N-1,\left(b\right)}\hfill \\ {\displaystyle v_0^n=0,v_{2N_x}^n=0,1\le n\le M.\left(c\right)}\hfill \end{array}\right.$$

(15)

Then, we have

$${∥v^n∥}^2\le {∥v^0∥}^2+{\displaystyle \frac{5\Gamma (1-\alpha )}{9a_x(6-25\omega )}}\underset{1\le j\le n}{max}\left\{t_j^{\alpha }{∥q^j∥}^2\right\}$$

(16)

$${∥{\sigma }_x{v}^n∥}^2\le {∥{\sigma }_x{v}^0∥}^2+{\displaystyle \frac{25\Gamma (1-\alpha )}{8a_x(6-25\omega )}}\underset{1\le j\le n}{max}\left\{t_j^{\alpha }{∥q^j∥}^2\right\}$$

(17)

Proof (16). 

Taking the inner product of $\varsigma v^n+(1-\varsigma )v^{n-1}$ with both sides of Equation (15.a), we obtain

$$\begin{array}{c}{\displaystyle d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}{\mathrm{H}}_{xx}\left(v^{n-j}-v^{n-j-1},\varsigma v^n+(1-\varsigma )v^{n-1}\right)}\hfill \\ {\displaystyle =a_x{\mathrm{H}}_{\left(x\right)}\left(\varsigma v^n+(1-\varsigma )v^{n-1},\varsigma v^n+(1-\varsigma )v^{n-1}\right)+\left(q^n,\varsigma v^n+(1-\varsigma )v^{n-1}\right)}\hfill \end{array}$$

(18)

By estimating each term in Equation (18) and applying the inequality $\left|v\right|\le \frac{L}{\sqrt{6}}{\left|v\right|}_1$ [33], the right-hand side of Equation (18) is obtained as

$$\begin{array}{c}{\displaystyle a_x\left(\frac{6}{5{(\Delta x)}^2}+\frac{9\omega }{25}\right){\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1},\varsigma v^n+(1-\varsigma )v^{n-1}\right)+\left(q^n,\varsigma v^n+(1-\varsigma )v^{n-1}\right)}\hfill \\ {\displaystyle =-a_x\left(\frac{6}{5{(\Delta x)}^2}+\frac{9\omega }{25}\right){∥{\sigma }_x\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)∥}^2+\left(q^n,\varsigma v^n+(1-\varsigma )v^{n-1}\right)}\hfill \\ {\displaystyle \le -\frac{6a_x}{L^2}\left(\frac{6}{5}+\frac{9\omega }{25}\right){∥\varsigma v^n+(1-\varsigma )v^{n-1}∥}^2+\left[\frac{6a_x}{L^2}\left(\frac{6}{5}+\frac{9\omega }{25}\right){∥\varsigma v^n+(1-\varsigma )v^{n-1}∥}^2+\frac{L^2}{24a_x}·\frac{25}{(30+9\omega )}{∥q^n∥}^2\right]}\hfill \\ {\displaystyle =\frac{25}{24a_x(30+9\omega )}{∥q^n∥}^2}\hfill \end{array}$$

Applying Lemma 1 to the left-hand side of Equation (18) and according to $\left({\left|v\right|}_1^2\le 4{∥v∥}^2\right)$ [33], we derive the following estimate:

$$\begin{array}{c}\left[\left({\displaystyle \frac{6}{5}}+{\displaystyle \frac{18\omega {(\Delta x)}^2}{5}}\right)+\left({\displaystyle \frac{1}{10}}+{\displaystyle \frac{9\omega {(\Delta x)}^2}{5}}\right){\sigma }_x^2\right]d{\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left(v^{n-j}-v^{n-j-1},\varsigma v^n+(1-\varsigma )v^{n-1}\right)\hfill \\ =\left({\displaystyle \frac{6}{5}}+{\displaystyle \frac{18\omega {(\Delta x)}^2}{5}}\right)d{\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left(v^{n-j}-v^{n-j-1},\varsigma v^n+(1-\varsigma )v^{n-1}\right)\hfill \\ +\left({\displaystyle \frac{1}{10}}+{\displaystyle \frac{9\omega {(\Delta x)}^2}{5}}\right)d{\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left({\sigma }_x^2(v^{n-j}-v^{n-j-1}),\varsigma v^n+(1-\varsigma )v^{n-1}\right)\hfill \\ \ge {\displaystyle \frac{d}{2}}\left({\displaystyle \frac{6}{5}}+{\displaystyle \frac{18\omega }{5}}\right){\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left({∥v^{n-j}∥}^2-{∥v^{n-j-1}∥}^2\right)-{\displaystyle \frac{d}{2}}\left({\displaystyle \frac{1}{10}}+{\displaystyle \frac{9\omega }{5}}\right){\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)\hfill \\ \ge {\displaystyle \frac{d}{2}}{\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left[\left({\displaystyle \frac{6}{5}}+{\displaystyle \frac{18\omega }{5}}\right)\left({∥v^{n-j}∥}^2-{∥v^{n-j-1}∥}^2\right)-4\left({\displaystyle \frac{1}{10}}+{\displaystyle \frac{9\omega }{5}}\right)\left({∥v^{n-j}∥}^2-{∥v^{n-j-1}∥}^2\right)\right]\hfill \\ ={\displaystyle \frac{d}{2}}{\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left({\displaystyle \frac{4}{5}}-{\displaystyle \frac{18\omega }{5}}\right)\left({∥v^{n-j}∥}^2-{∥v^{n-j-1}∥}^2\right)=d\left({\displaystyle \frac{2}{5}}-{\displaystyle \frac{9\omega }{5}}\right){\displaystyle \sum _{j=0}^{n-1}}{s}_j^{(n,\alpha )}\left({∥v^{n-j}∥}^2-{∥v^{n-j-1}∥}^2\right)\hfill \end{array}$$

By organizing the above equations, it can be known that

$$d\left({\displaystyle \frac{2}{5}}-{\displaystyle \frac{9\omega }{5}}\right)\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({∥v^{n-j}∥}^2-{∥v^{n-j-1}∥}^2\right)\le {\displaystyle \frac{25}{24a_x(30+9\omega )}}{∥q^n∥}^2,1\le n\le M.$$

(19)

Therefore, Equation (19) can be rewritten as

$$\begin{array}{c}{\displaystyle s_0^{(n,\alpha )}{∥v^n∥}^2\le \sum _{j=1}^{n-1}(s_{j-1}^{(n,\alpha )}-s_j^{(n,\alpha )}){∥v^{n-j}∥}^2+s_{n-1}^{(n,\alpha )}{∥v^0∥}^2+\frac{25}{48a_x(6-25\omega )d}{∥q^n∥}^2}\hfill \\ {\displaystyle =\sum _{j=1}^{n-1}(s_{j-1}^{(n,\alpha )}-s_j^{(n,\alpha )}){∥v^{n-j}∥}^2+s_{n-1}^{(n,\alpha )}\left({∥v^0∥}^2+\frac{25}{48a_x(6-25\omega )}·\frac{1}{d{s}_{n-1}^{(n,\alpha )}}{∥q^n∥}^2\right)}\hfill \\ {\displaystyle \le \sum _{j=1}^{n-1}(s_{j-1}^{(n,\alpha )}-s_j^{(n,\alpha )}){∥v^{n-j}∥}^2+s_{n-1}^{(n,\alpha )}\left({∥v^0∥}^2+\frac{5}{9a_x(6-25\omega )}·t_n^{\alpha }\Gamma (1-\alpha ){∥q^n∥}^2\right)}\hfill \end{array}$$

(20)

By applying the mathematical induction and organizing the relevant expressions, we can obtain

$${∥v^n∥}^2\le {∥v^0∥}^2+{\displaystyle \frac{5\Gamma (1-\alpha )}{9a_x(6-25\omega )}}\underset{1\le j\le n}{max}\left\{t_j^{\alpha }{∥q^j∥}^2\right\}$$

□

Proof (17). 

Take the inner product of $-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)$ with both sides of Equation (15.a), and we obtain

$$\begin{array}{c}{\displaystyle d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}{\mathrm{H}}_{xx}\left(v^{n-j}-v^{n-j-1},-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)=}\hfill \\ {\displaystyle a_x{\mathrm{H}}_{\left(x\right)}\left(\varsigma v^n+(1-\varsigma )v^{n-1},-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)-\left(q^n,{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)}\hfill \end{array}$$

(21)

Estimate the right-hand side term of Equation (21), and we can obtain

$$\begin{array}{c}{\displaystyle a_x{\mathrm{H}}_{\left(x\right)}\left(\varsigma v^n+(1-\varsigma )v^{n-1},-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)-\left(q^n,{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)}\hfill \\ {\displaystyle a_x\left(\frac{6}{5{(\Delta x)}^2}+\frac{9\omega }{25}\right){\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1},-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)-\left(q^n,{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)}\hfill \\ {\displaystyle =a_x\left(\frac{6}{5{(\Delta x)}^2}+\frac{9\omega }{25}\right){∥{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)∥}^2-\left(q^n,{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)}\hfill \\ {\displaystyle \le a_x\left(\frac{6}{5}+\frac{9\omega }{25}\right){∥{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)∥}^2+\left(a_x\left(\frac{6}{5}+\frac{9\omega }{25}\right){∥{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)∥}^2+\frac{25}{4a_x(30+9\omega )}{∥q^n∥}^2\right)}\hfill \\ {\displaystyle =\frac{25}{4a_x(30+9\omega )}{∥q^n∥}^2}\hfill \end{array}$$

For the left-hand side term of Equation (21), first apply the partial summation formula, and then apply Lemmas 1 and 2. The following estimation can be obtained:

$$\begin{array}{c}{\displaystyle \left[\left(\frac{6}{5}+\frac{18\omega {(\Delta x)}^2}{5}\right)+\left(\frac{1}{10}+\frac{9\omega {(\Delta x)}^2}{5}\right){\sigma }_x^2\right]d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}(v^{n-j}-v^{n-j-1},-{\delta }_x^2(\varsigma v^n+(1-\varsigma )v^{n-1}))}\hfill \\ {\displaystyle =\left(\frac{6}{5}+\frac{18\omega {(\Delta x)}^2}{5}\right)d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left(v^{n-j}-v^{n-j-1},-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)+}\hfill \\ {\displaystyle +\left(\frac{1}{10}+\frac{9\omega {(\Delta x)}^2}{5}\right)d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({\sigma }_x^2(v^{n-j}-v^{n-j-1}),-{\sigma }_x^2\left(\varsigma v^n+(1-\varsigma )v^{n-1}\right)\right)}\hfill \\ {\displaystyle \ge \frac{d}{2}\left(\frac{6}{5}+\frac{18\omega }{5}\right)\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)-\frac{d}{2}\left(\frac{1}{10}+\frac{9\omega }{5}\right)\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({∥{\sigma }_x^2{v}^{n-j}∥}^2-{∥{\sigma }_x^2{v}^{n-j-1}∥}^2\right)}\hfill \\ {\displaystyle \ge \frac{d}{2}\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left[\left(\frac{6}{5}+\frac{18\omega }{5}\right)\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)-4\left(\frac{1}{10}+\frac{9\omega }{5}\right)\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)\right]}\hfill \\ {\displaystyle =\frac{d}{2}\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left(\frac{4}{5}-\frac{18\omega }{5}\right)\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)=d\left(\frac{2}{5}-\frac{9\omega }{5}\right)\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)}\hfill \end{array}$$

By arranging the above two equations, we can obtain

$$d\left({\displaystyle \frac{2}{5}}-{\displaystyle \frac{9\omega }{5}}\right)\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}\left({∥{\sigma }_x{v}^{n-j}∥}^2-{∥{\sigma }_x{v}^{n-j-1}∥}^2\right)\le {\displaystyle \frac{25}{4a_x(30+9\omega )}}{∥q^n∥}^2$$

(22)

Rewrite Equation (22) as

$$\begin{array}{c}{\displaystyle s_0^{(n,\alpha )}{∥{\sigma }_x{v}^n∥}^2\le \sum _{j=1}^{n-1}(s_{j-1}^{(n,\alpha )}-s_j^{(n,\alpha )}){∥{\sigma }_x{v}^{n-j}∥}^2+s_{n-1}^{(n,\alpha )}{∥{\sigma }_x{v}^0∥}^2+\frac{25}{8a_x(6-25\omega )d}{∥q^n∥}^2}\hfill \\ {\displaystyle =\sum _{j=1}^{n-1}(s_{j-1}^{(n,\alpha )}-s_j^{(n,\alpha )}){∥{\sigma }_x{v}^{n-j}∥}^2+s_{n-1}^{(n,\alpha )}\left({∥{\sigma }_x{v}^0∥}^2+\frac{25}{8a_x(6-25\omega )}·\frac{1}{d{s}_{n-1}^{(n,\alpha )}}{∥q^n∥}^2\right)}\hfill \\ {\displaystyle \le \sum _{j=1}^{n-1}(s_{j-1}^{(n,\alpha )}-s_j^{(n,\alpha )}){∥{\sigma }_x{v}^{n-j}∥}^2+s_{n-1}^{(n,\alpha )}\left({∥{\sigma }_x{v}^0∥}^2+\frac{25}{8a_x(6-25\omega )}·t_n^{\alpha }\Gamma (1-\alpha ){∥q^n∥}^2\right)}\hfill \end{array}$$

By applying mathematical induction and arranging the relevant expressions, it can be obtained that

$${∥{\sigma }_x{v}^n∥}^2\le {∥{\sigma }_x{v}^0∥}^2+{\displaystyle \frac{25\Gamma (1-\alpha )}{8a_x(6-25\omega )}}\underset{1\le j\le n}{max}\left\{t_j^{\alpha }{∥q^j∥}^2\right\}$$

□

3.3. Convergence

Theorem 3.  

Let $\left\{v(x,t)\left|(x,t)\in D\right.\right\}$ be the solution of the well-posed problem (1), and $\left\{v_i^n\left|0\le i\le 2N,0\le n\le M\right.\right\}$ be the solution of the difference scheme (8), then we have

$$∥{\sigma }_x{e}^n∥\le {\displaystyle \frac{5}{2}}\sqrt{{\displaystyle \frac{T^{\alpha }\Gamma (1-\alpha )}{2a_x(6-25\omega )}}}·\rho (\Delta t^2+\Delta x^4),1\le n\le M.$$

(23)

$${∥e^n∥}_{\infty }\le {\displaystyle \frac{5}{4}}\sqrt{{\displaystyle \frac{L{T}^{\alpha }\Gamma (1-\alpha )}{2a_x(6-25\omega )}}}\rho (\Delta t^2+\Delta x^4),1\le n\le M.$$

(24)

Proof. 

Denote $e_i^n=v(x_i,t_n)-v_i^n$. Subtract Equation (9) from Equation (1), and then the error system of equations can be obtained

$$\left\{\begin{array}{c}{\displaystyle d\sum _{j=0}^{n-1}{s}_j^{(n,\alpha )}{\mathrm{H}}_{xx}(e_i^{n-j}-e_i^{n-j-1})=a_x\varsigma {\mathrm{H}}_{\left(x\right)}{e}_i^n+a_x(1-\varsigma ){\mathrm{H}}_{\left(x\right)}{e}_i^{n-1}}\hfill \\ {\displaystyle +{\left(R_2\right)}_i^n,1\le i\le 2N-1;1\le n\le M,}\hfill \\ {\displaystyle e_i^0=0,1\le i\le 2N-1,}\hfill \\ {\displaystyle e_0^n=0,e_{2N}^n=0,1\le n\le M.}\hfill \end{array}\right.$$

Applying Theorem 2 and the error Formula (10), we obtain

$${∥{\sigma }_x{e}^n∥}^2\le {∥{\sigma }_x{e}^0∥}^2+{\displaystyle \frac{25\Gamma (1-\alpha )}{8a_x(6-25\omega )}}\underset{1\le j\le n}{max}\left\{t_j^{\alpha }{∥{\left(R_2\right)}^j∥}^2\right\}\le {\displaystyle \frac{25\Gamma (1-\alpha )}{8a_x(6-25\omega )}}{T}^{\alpha }{\left(\rho (\Delta t^2+\Delta x^4)\right)}^2,1\le n\le M.$$

Take the square root on both sides, and we obtain

$$∥{\sigma }_x{e}^n∥\le {\displaystyle \frac{5}{2}}\sqrt{{\displaystyle \frac{T^{\alpha }\Gamma (1-\alpha )}{2a_x(6-25\omega )}}}·\rho (\Delta t^2+\Delta x^4),1\le n\le M.$$

(25)

Also, due to ${∥v∥}_{\infty }\le {\displaystyle \frac{\sqrt{L}}{2}}·∥{\sigma }_{x}v∥$, for further details see i.e., [33]. it might be known that

$${∥e^n∥}_{\infty }\le {\displaystyle \frac{\sqrt{L}}{2}}∥{\sigma }_x{e}^n∥\le {\displaystyle \frac{\sqrt{L}}{2}}·{\displaystyle \frac{5}{2}}\sqrt{{\displaystyle \frac{T^{\alpha }\Gamma (1-\alpha )}{2a_x(6-25\omega )}}}·\rho (\Delta t^2+\Delta x^4)={\displaystyle \frac{5}{4}}\sqrt{{\displaystyle \frac{L{T}^{\alpha }\Gamma (1-\alpha )}{2a_x(6-25\omega )}}}\rho (\Delta t^2+\Delta x^4),1\le n\le M.$$

□

Remark 1.  

The above analysis establishes the well-posedness of the proposed difference scheme by demonstrating its unique solvability, stability, and convergence. These theoretical guarantees form a rigorous foundation for the subsequent numerical experiments, ensuring that the computed results are both mathematically consistent and reliable.

4. Numerical Experiment

This section presents numerical experiments validating the proposed RBFHFD-L2-1$\sigma$ scheme for time-fractional diffusion equations. The results confirm the theoretical convergence rates, demonstrating fourth-order spatial and second-order temporal accuracy across various fractional orders ($\alpha =0.1,0.5,0.9$). For instance, in Example 1 with Dirichlet conditions, the scheme achieved errors as low as $1.29\times {10}^{-8}$, significantly outperforming the method in [1]. Example 2, featuring non-local boundary conditions, further highlighted this superiority, where our method obtained errors an order of magnitude smaller than those in [33]. The robustness of the scheme was also confirmed by Example 3 with more complex integral boundaries, showing excellent agreement with the exact solution. Furthermore, parameter analysis identified an optimal shape parameter ($\omega =2.07$) that minimizes numerical errors, establishing the method’s reliability and efficiency for practical applications. The error norms are defined as

$$L_{\infty }(\Delta x,\Delta t)=\underset{1\le i\le N}{max}\left|v(x_i,t_n)-v_i^n\right|,L_2(\Delta x,\Delta t)=\sqrt{\Delta x\sum _{i=1}^N{\left|v(x_i,t_n)-v_i^n\right|}^2}.$$

The convergence rates are measured by

$$Ord1={log}_2\left({\displaystyle \frac{L(\Delta x,\Delta t)}{L(2^{-\frac{4}{2-\alpha }}\Delta x,\Delta t)}}\right),Ord2={log}_2\left({\displaystyle \frac{L(\Delta x,\Delta t)}{L(\Delta x,2^{-\frac{4}{2-\alpha }}\Delta t)}}\right).$$

The test problems are reconstructed with reference to their integer-order counterparts. The Mittag–Leffler function with two parameters is given by

$$E_{\alpha ,\beta }\left(\gamma \right)=\sum _{j=0}^{\infty }{\displaystyle \frac{{\gamma }^j}{\Gamma (\alpha j+\beta )}},\alpha >0,\beta >0.$$

In the computations, the precision of $\gamma$ is set to ${10}^{-10}$. All experiments are carried out using MATLAB (R2024a) on a Lenovo system with Intel(R) i5-1035G1 CPU and 8 GB memory.

Example 1 

([1]). Consider the case where ${\alpha }_1={\alpha }_2=0,{\beta }_1={\beta }_2=1$, in which the equation is subject to Dirichlet boundary conditions.

$$\left\{\begin{array}{c}{}_0{}^{C}D_t^{\alpha }v(x,t)-{\displaystyle \frac{{\partial }^{2}v}{\partial x^2}}(x,t)=exp\left(x\right)\left[\Gamma (2+\alpha )t-t^{1+\alpha }\right],0<x<1,0<t\le T\hfill \\ v(x,0)=0,\hfill \\ v(0,t)=t^{1+\alpha };v(1,t)=e{t}^{1+\alpha }.\hfill \end{array}\right.$$

Its exact solution is $v(x,t)=exp\left(x\right)t^{1+\alpha }$.

The numerical results summarized in

Table 1. A comparison of the spatial convergence accuracy, errors, and CPU time between the proposed scheme and the scheme in Reference [1] is conducted for $T=\omega =1$ with time step $\Delta t=\Delta x^{(4/2-\alpha )}$.

		Method of [1]				$\mathit{RBFHFD}-\mathit{L}2-1_{\mathit{\sigma }}$
$\mathbf{\alpha }$	$\mathit{N}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathit{s}\right)$		${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathit{s}\right)$
0.1	5	4.4370e-05		0.0099		3.1157e-06		0.0111
	10	2.8402e-06	3.9655	0.0925		2.0252e-07	3.9734	0.1009
	20	1.7887e-07	3.9890	2.1832		1.2909e-08	3.9816	2.1969
	40	1.1230e-08	3.9934	12.694		8.1549e-09	3.9946	13.987
0.5	5	4.4552e-05		0.0567		2.6994e-06		0.0728
	10	2.8223e-06	3.9591	2.3964		1.7904e-07	3.9805	2.4892
	20	1.7661e-07	3.9808	12.068		1.1499e-08	3.9982	13.137
	40	1.1040e-08	3.9909	21.098		7.2802e-09	3.9997	24.100
0.9	5	2.6846e-05		3.8925		2.4014e-06		4.1502
	10	1.7999e-05	3.8987	11.929		1.5512e-07	3.9221	13.442
	20	1.1635e-06	3.9515	23.047		9.9039e-08	3.9617	25.126
	40	7.3985e-07	3.9750	55.164		6.2766e-09	3.9790	58.943

and

Table 2. A comparison of the temporal convergence accuracy and errors between the proposed scheme and the scheme in Reference [1] is conducted for $T=\omega =1$ with spatial step $\Delta x=0.01$.

		Method of [1]				Present
$\mathbf{\alpha }$	$\mathit{M}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{2}$	${\mathit{L}}_{\mathbf{2}}$	$\mathit{Ord}\mathbf{2}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{2}$	${\mathit{L}}_{\mathbf{2}}$	$\mathit{Ord}\mathbf{2}$
0.1	5	1.8450e-03		1.8600e-03		2.7907e-04		2.0304e-04
	10	4.3705e-04	1.8078	4.4061e-04	1.8082	6.6085e-05	2.0082	4.8091e-05	2.0079
	20	1.0229e-04	1.8151	1.0315e-04	1.8168	1.5462e-05	2.0056	1.1255e-05	2.0052
	40	2.3758e-05	1.8262	2.3981e-05	1.8299	3.5899e-06	2.0067	2.6137e-06	2.0063
0.5	5	2.3772e-03		2.3965e-03		3.5665e-04		2.6098e-04
	10	3.8351e-04	1.5319	3.8665e-04	1.5318	5.7281e-05	2.0384	4.2048e-05	2.0338
	20	5.9784e-05	1.4814	6.0298e-05	1.4848	8.8789e-06	2.0896	6.5436e-06	2.0839
	40	9.0109e-06	1.5300	9.1142e-06	1.5259	1.3289e-06	2.0402	9.8417e-07	2.0331
0.9	5	3.3879e-04		3.4156e-04		5.0122e-05		3.7054e-05
	10	4.3500e-05	1.1613	4.3880e-05	1.1605	6.3956e-06	1.9703	4.7473e-06	1.9845
	20	6.8626e-06	1.1342	6.9454e-06	1.1295	1.0144e-06	1.9865	7.4996e-07	1.9922
	40	1.3134e-06	1.1255	1.3538e-06	1.1090	1.9675e-07	2.0061	1.4406e-07	2.0002

indicate that the proposed scheme achieves fourth-order accuracy in space and second-order accuracy in time, which is fully consistent with the theoretical analysis. A comparative study with the numerical results in Figure 1, demonstrates the advantages of our method, showing that it yields more accurate numerical solutions with higher computational efficiency.

Figure 2 and Figure 3 presents the absolute errors under three fractional orders: $\alpha =0.1$, $\alpha =0.5$ and $\alpha =0.9$ with $\Delta x=0.01$, $\Delta t=0.025$ at $L\left(T\right)\in \{0.1,0.3,0.5,0.7,0.9\}$. The investigation into the dependence of errors on $\alpha$ and on the spatial and temporal discretization serves to enrich the experimental results.

Example 2 

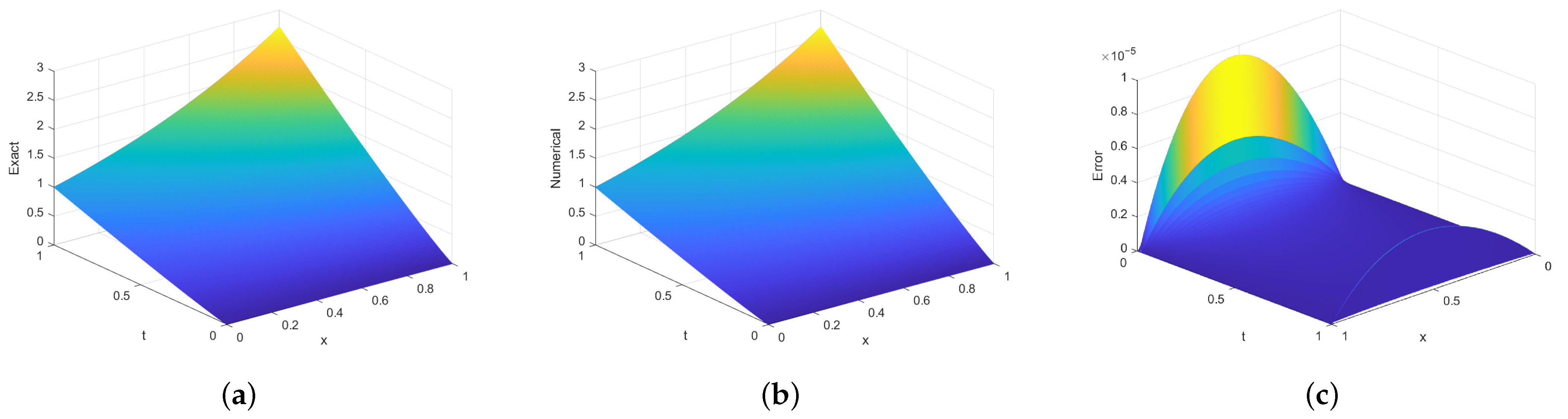
([33]). Consider the case where ${\alpha }_1={\alpha }_2=1,{\beta }_1={\beta }_2=0$, in which the equation is subject to non-local boundary conditions.

$$\left\{\begin{array}{c}{\displaystyle {}_0{}^{C}D_t^{\alpha }v(x,t)-\frac{{\partial }^{2}v}{\partial x^2}(x,t)=t^{-\alpha }\left[E_{1,1-\alpha }(-t)-\frac{1}{\Gamma (1-\alpha )}\right]\left[x(x-1)+\frac{\sigma }{\sigma (1+\sigma )}\right]-2e^{-t},0<x<1,0<t\le T}\hfill \\ {\displaystyle v(x,0)=x(x-1)+\frac{\sigma }{6(1+\sigma )},0\le x\le 1}\hfill \\ {\displaystyle v(0,t)={\int }_0^1-\sigma v(x,t)dx,}\hfill \\ {\displaystyle v(1,t)={\int }_0^1-\sigma v(x,t)dx,0<t\le T.}\hfill \end{array}\right.$$

Its exact solution is $v(x,t)=e^{-t}\left[x(x-1)+{\displaystyle \frac{\sigma }{6(1+\sigma )}}\right]$ and $\sigma =0.0144$.

Figure 4 presents the exact solution and the numerical solution at $T\in \{0.2,0.4,0.6,0.8,1.0\}$ for $\alpha =0.1$ with $\Delta x=0.01$, $\Delta t=0.001$. The results demonstrate that the proposed method achieves high numerical accuracy, showing excellent agreement with the analytical solution.

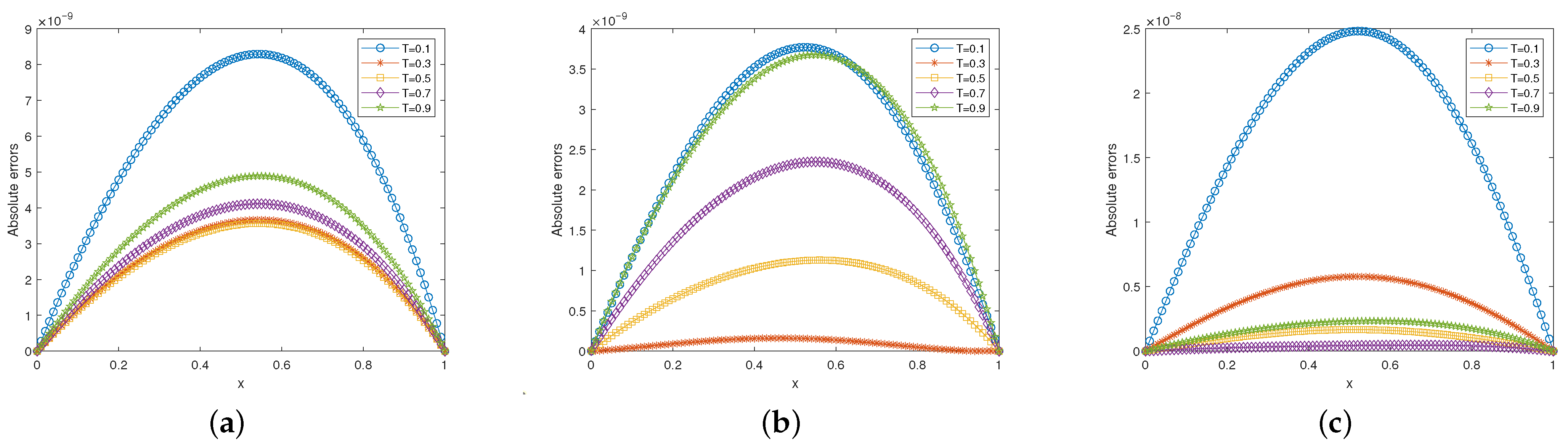
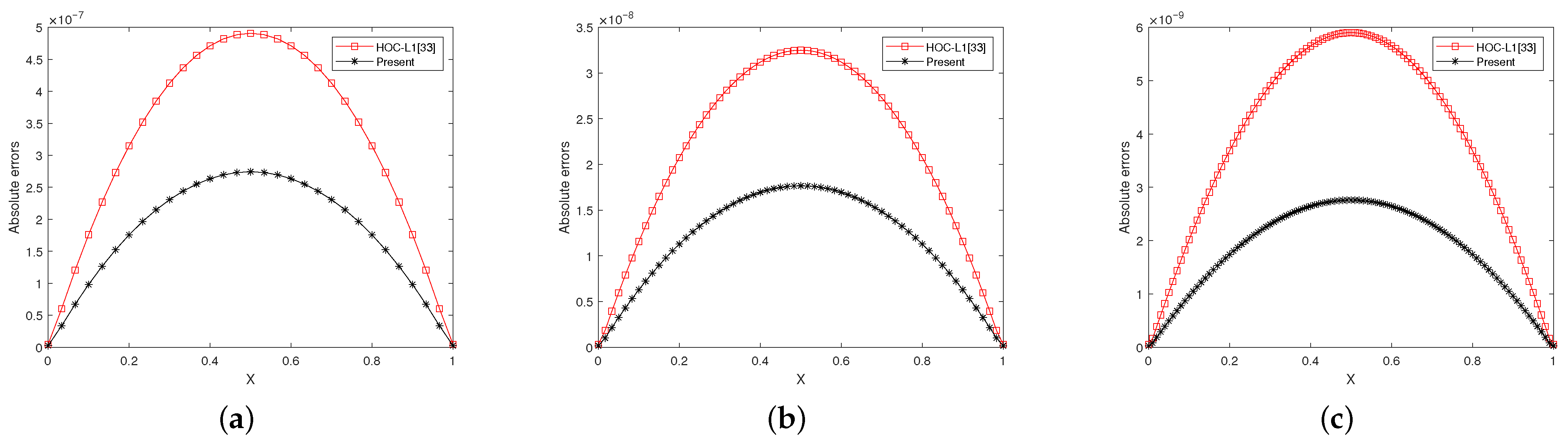
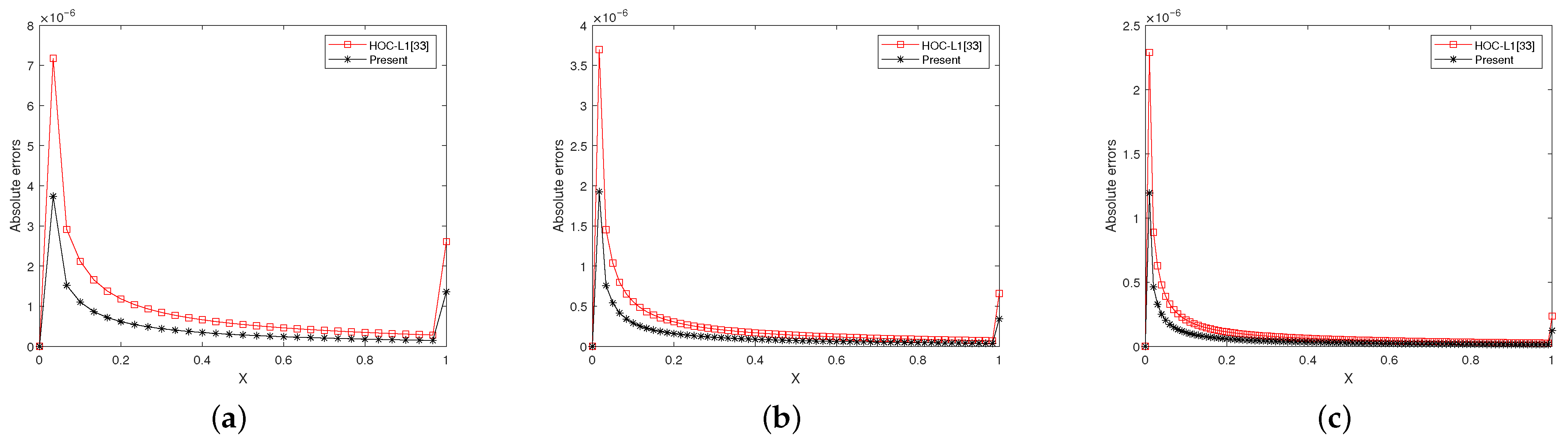
Figure 5 and Figure 6 present a comparison of the absolute errors between the $RBFHFD-L2-1_{\sigma }$ scheme proposed in this work and the method described in Reference [33] under different spatial (time) step sizes. The results demonstrate that the computational accuracy of the present method is significantly superior to that of the method in [33].

From the above Table 1 and Table 2 and figures, the following conclusions can be drawn. The radial basis function Hermite difference scheme developed in this paper proves to be an effective approach for solving time-fractional diffusion equations with non-local boundary conditions, as confirmed by the strong agreement observed in the numerical experiments. Moreover,

Table 3. A comparison of the spatial convergence accuracy, errors, and CPU time between the proposed scheme and the scheme in Reference [33] is conducted for $T=\omega =1$ with time step $\Delta t=\Delta x^{(4/2-\alpha )}$.

		Method of [33]				$\mathit{RBFHFD}-\mathit{L}2-1_{\mathit{\sigma }}$
$\mathbf{\alpha }$	$\mathit{N}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathit{s}\right)$		${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathit{s}\right)$
0.1	5	6.9610e-06		0.0105		3.4409e-07		0.0146
	10	5.4183e-07	3.6834	0.1436		2.1724e-08	3.9854	0.1579
	20	3.9562e-08	3.7757	2.4152		1.3709e-09	3.9861	2.5024
	40	2.7818e-09	3.8300	14.284		8.6369e-10	3.9884	16.062
0.5	5	9.5732e-06		0.0690		3.9935e-07		0.0869
	10	6.4552e-07	3.8905	2.4099		2.5091e-08	3.9925	2.7710
	20	4.1727e-08	3.9514	14.067		1.5696e-09	3.9987	16.001
	40	2.6372e-09	3.9839	26.015		9.8043e-10	4.0008	28.334
0.9	5	5.0360e-06		3.9898		6.9610e-06		4.1859
	10	3.2384e-06	3.9589	11.997		5.4183e-07	3.9712	13.681
	20	2.0332e-07	3.9935	22.191		3.9562e-08	3.9959	25.436
	40	1.2712e-08	3.9995	57.172		2.7818e-09	4.0171	59.076

and

Table 4. A comparison of the temporal convergence accuracy and errors between the proposed scheme and the scheme in Reference [33] is conducted for $T=\omega =1$ with spatial step $\Delta x=0.002$.

		Method of [33]				Present
$\mathbf{\alpha }$	$\mathit{M}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{2}$	${\mathit{L}}_{\mathbf{2}}$	$\mathit{Ord}\mathbf{2}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{2}$	${\mathit{L}}_{\mathbf{2}}$	$\mathit{Ord}\mathbf{2}$
0.1	5	5.7098e-04		4.0389e-04		3.7528e-05		2.6551e-05
	10	1.6292e-04	1.8093	1.1524e-04	1.8093	9.8202e-06	1.9341	6.9481e-06	1.9341
	20	4.6198e-05	1.8182	3.2679e-05	1.8182	2.5011e-06	1.9732	1.7696e-06	1.9732
	40	1.3023e-06	1.8268	9.2120e-06	1.8268	6.2765e-07	1.9945	4.4412e-07	1.9944
0.5	5	7.0765e-04		5.0044e-04		8.0384e-05		7.3588e-05
	10	2.4857e-04	1.5094	1.7578e-04	1.5094	2.2995e-05	2.0150	1.6311e-05	2.0136
	20	8.7590e-05	1.5048	6.1941e-05	1.5048	4.6844e-06	2.0204	3.3278e-06	2.0185
	40	3.0913e-05	1.5026	2.1860e-05	1.5026	8.5685e-07	2.1507	6.1038e-07	2.1468
0.9	5	3.6994e-04		2.6153e-04		2.2847e-05		9.4354e-05
	10	1.6958e-04	1.1253	1.1988e-04	1.1253	1.9194e-05	1.9427	1.3107e-05	1.9477
	20	7.8384e-05	1.1133	5.5413e-05	1.1133	2.1940e-06	1.9894	1.5373e-06	2.0038
	40	3.6392e-05	1.1069	2.5727e-05	1.1069	1.2162e-06	2.0114	8.5540e-07	2.0077

demonstrate that, compared with the scheme in Reference [33], the proposed method achieves higher accuracy and smaller errors in both the spatial and temporal directions, thereby highlighting its superior efficiency and clear advantages.

Example 3. 

$$\left\{\begin{array}{c}{\displaystyle {}_0{}^{C}D_t^{\alpha }v(x,t)-\frac{{\partial }^{2}v}{\partial x^2}(x,t)=t^{-\alpha }\left[E_{1,1-\alpha }(-t)-\frac{1}{\Gamma (1-\alpha )}\right]\left[sin\left(\pi x\right)+cos\left(\pi x\right)\right]+{\pi }^2{e}^{-t}\left[sin\left(\pi x\right)+cos\left(\pi x\right)\right]}\hfill \\ {\displaystyle v(x,0)=sin\left(\pi x\right)+cos\left(\pi x\right),0\le x\le 1}\hfill \\ {\displaystyle v(0,t)={\int }_0^{1}2sin\left(\pi x\right)v(x,t)dx,}\hfill \\ {\displaystyle v(1,t)={\int }_0^1-2cos\left(\pi x\right)v(x,t)dx,0<x<1,0<t\le T}\hfill \end{array}\right.$$

The exact solution is $v(x,t)=e^{-t}(sin\left(\pi x\right)+cos\left(\pi x\right))$.

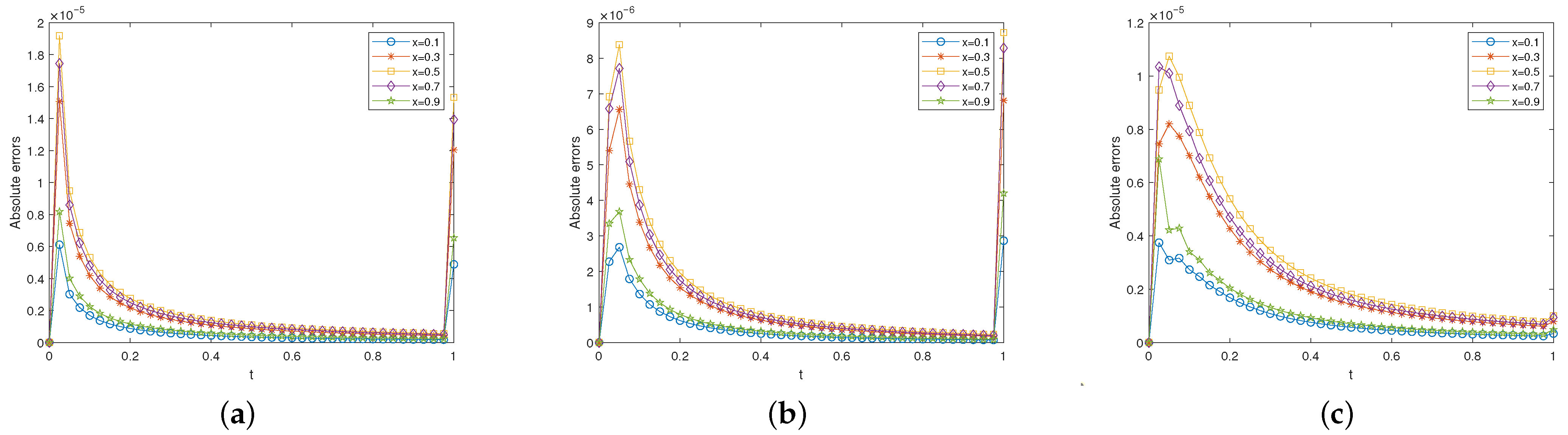
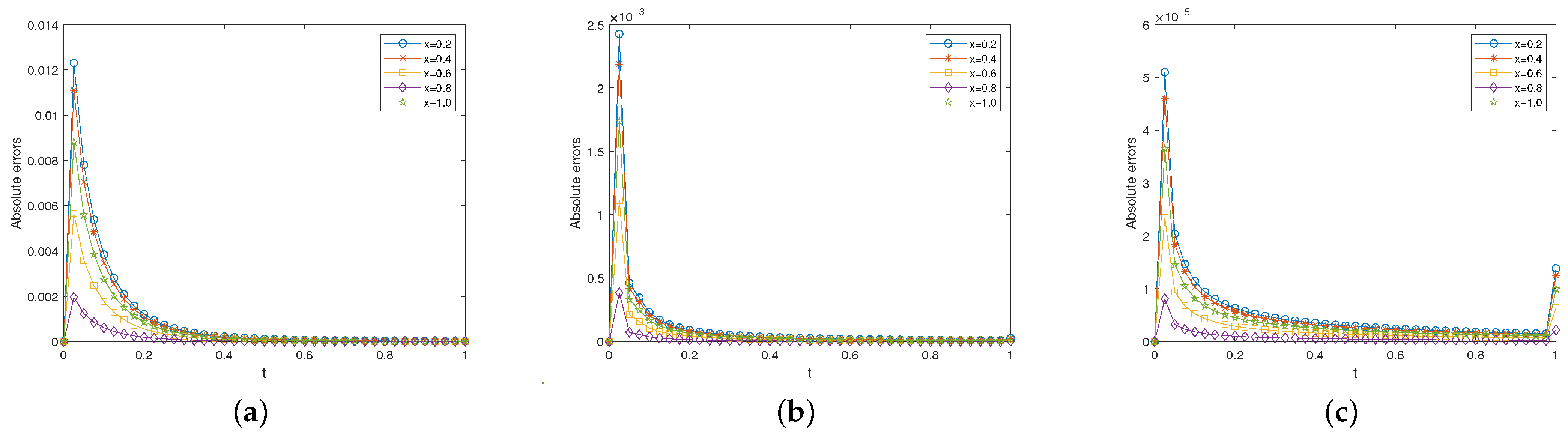
Figure 7 and Figure 8 present the absolute errors under three fractional orders: $\alpha =0.1$, $\alpha =0.5$ and $\alpha =0.9$ with $\Delta x=0.01$, $\Delta t=0.025$ at $L\left(T\right)\in \{0.2,0.4,0.6,0.8,1.0\}$. The above results thus establish the robustness of the present method for fractional calculus problems.

From the

Table 5. For $T=1$ and $\omega =1$, comparison of the maximum error and convergence order of the proposed scheme for different spatial step sizes $\Delta x$.

	$\mathit{\alpha }=0.1$				$\mathit{\alpha }=0.5$				$\mathit{\alpha }=0.9$
$\mathit{N}$	${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathbf{s}\right)$		${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathit{s}\right)$		${\mathit{L}}_{\infty }$	$\mathit{Ord}\mathbf{1}$	$\mathit{CPU}\left(\mathbf{s}\right)$
5	1.5661e-05		0.0170		1.5432e-05		0.0651		1.1048e-05		4.0168
10	9.8289e-07	3.9940	0.1233		9.8017e-07	3.9768	2.5814		6.9308e-07	3.9947	13.224
20	6.0792e-08	4.0151	2.3814		6.1358e-08	3.9977	13.002		4.3387e-08	3.9977	27.028
40	3.7634e-09	4.0138	13.794		3.8398e-09	3.9982	25.317		2.7151e-09	3.9992	60.011

and

Table 6. For $T=1$ and $\omega =1$, comparison of the maximum error and convergence order of the proposed scheme for different spatial step sizes $\Delta x$.

		$\mathit{\alpha }=0.1$				$\mathit{\alpha }=0.5$				$\mathit{\alpha }=0.9$
$\mathit{M}$		${\mathit{L}}_{\infty }$		$\mathit{Ord}\mathbf{2}$		${\mathit{L}}_{\infty }$		$\mathit{Ord}\mathbf{2}$		${\mathit{L}}_{\infty }$		$\mathit{Ord}\mathbf{2}$
5		2.1057e-04				5.8147e-04				7.2060e-05
10		5.5100e-05		1.9342		1.2867e-04		2.0760		1.1297e-05		2.0733
20		1.4032e-05		1.9733		2.6188e-05		2.0967		1.2544e-05		2.1107
40		3.5212e-06		1.9946		4.7836e-06		2.1528		6.9344e-06		2.1414

and Figure 8 and Figure 9, the following observations can be made. The $RBFHFD-L2-1_{\sigma }$ scheme proposed in this paper consistently achieves second-order accuracy in time and fourth-order accuracy in space, in agreement with the theoretical predictions. Furthermore, the numerical solutions closely match the analytical solutions for the two examples considered, demonstrating the accuracy and reliability of the scheme. During the computations, the chosen shape parameter $\omega =1$ is found to significantly influence the numerical results, highlighting the importance of parameter selection in the radial basis function. In the following, we will examine the effect of varying the shape parameter $\omega$.

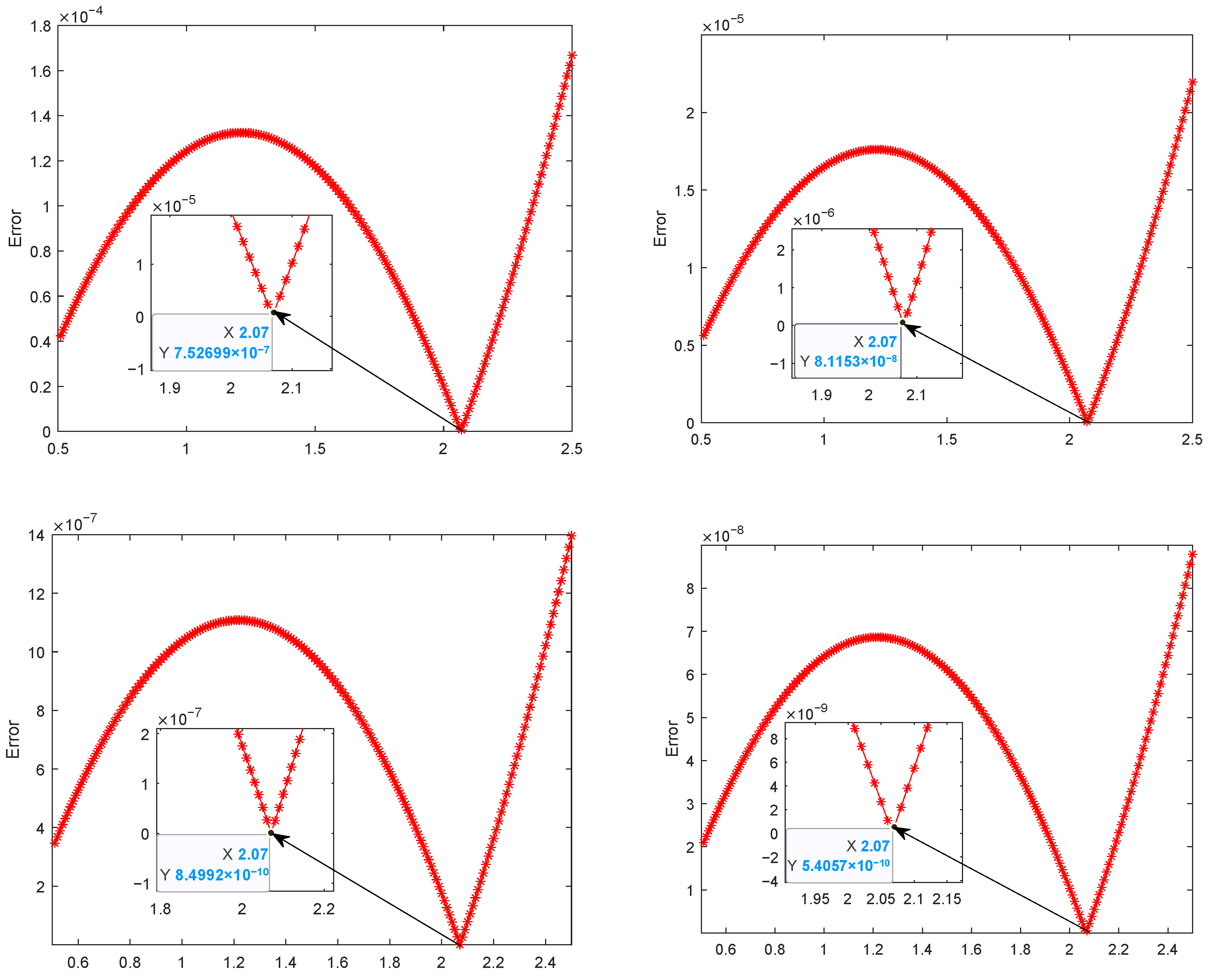
From the above Figure 8 and Figure 9, the following conclusions can be drawn. With the temporal step size fixed and the spatial step size varying, testing the shape parameter $\omega$ over the range $\left[0.5,2.5\right]$ shows that the error is minimized at $\omega =2.07$. Therefore, the optimal value of $\omega$ is 2.07.

Table 7. $T=1,\Delta x=0.002$, A comparison of the minimum values of the maximum errors for various T.

		$\mathit{\alpha }=0.1$			$\mathit{\alpha }=0.5$			$\mathit{\alpha }=0.9$
$\mathit{M}$		$\mathit{\omega }=\mathbf{1}$	$\mathit{\omega }=\mathbf{2}.\mathbf{07}$		$\mathit{\omega }=\mathbf{1}$	$\mathit{\omega }=\mathbf{2}.\mathbf{07}$		$\mathit{\omega }=\mathbf{1}$	$\mathit{\omega }=\mathbf{2}.\mathbf{07}$
5		3.9721e-04	2.1057e-05		3.7990e-04	3.2026e-05		5.4069e-04	2.8656e-05
10		5.5149e-05	4.5100e-06		8.5773e-05	8.1931e-06		1.5427e-05	1.4870e-06
20		6.8825e-05	1.4032e-06		9.7855e-05	1.6676e-07		4.0624e-06	2.1576e-07
40		4.4718e-06	3.5212e-07		5.4191e-06	3.0460e-07		1.7981e-06	1.1121e-07

presents a comparison of the minimum values of the maximum errors for different values of the fractional orders $\alpha \in \{0.1,0.5,0.9\}$ under two frequency parameters, $\omega =1$ and $\omega =2.07$. As M increases, the errors decrease significantly for all cases, demonstrating the convergence and accuracy of the proposed time-fractional numerical scheme. For smaller fractional orders (e.g., $\alpha =0.1$), the decay of error with increasing M is evident, though the convergence rate is slightly slower than that for higher fractional orders. At $\alpha =0.9$, the method achieves the smallest maximum errors, particularly for $\omega =2.07$, where the error drops from $2.8656\times {10}^{-5}$ at $M=5$ to $1.1121\times {10}^{-7}$ at $M=40$. This consistent reduction in error across all parameter sets confirms both the robustness and high precision of the scheme for varying fractional orders and frequency parameters.

5. Conclusions

In this study, we have developed an effective and stable $\mathrm{RBFHFD}-L2-1_{\sigma }$ scheme for solving time-fractional diffusion equations with integral boundary conditions. The integral boundary condition is discretized using the composite Simpson formula, ensuring both accuracy and computational efficiency. The proposed scheme achieves fourth-order spatial accuracy, and its stability and convergence have been rigorously established through the energy inequality method. Numerical experiments on benchmark problems confirm its high accuracy, reduced error levels, and robustness. In addition, the influence of shape parameters in radial basis functions has been systematically analyzed, providing insights into their optimal selection for improved numerical performance. The successful integration of this method with the Alternating Direction Implicit (ADI) technique further demonstrates its strong adaptability to high-dimensional problems, underscoring its general applicability. This work can be extended to higher-order fractional derivatives in parabolic and hyperbolic models using the L2 scheme with $\alpha \in (1,2)$. Further directions include the finite element method [34,35,36], adaptive shape parameter strategies, machine learning-assisted error control, and large-scale simulations on irregular domains, broadening the applicability and practical relevance of the proposed scheme. The RBF-HFD method [37,38,39,40,41] exhibits superior accuracy and computational efficiency, which is important for solving complex equations, as it provides a high-accuracy and unconditionally stable numerical differentiation approach.