Advancements in Sustainable Mobility: Fractional-Order FOC of IM in an Electric Vehicle Powered by an Autonomous PV Battery System

Abstract

This paper presents a novel fractional-order field-oriented control (FO-FOC) strategy for induction motor drives in electric vehicles (EVs) powered by an autonomous photovoltaic (PV) battery energy system. The proposed control approach integrates a fractional-order sliding mode controller (FO-SMC) into the conventional FOC framework to enhance dynamic performance, improve robustness, and reduce sensitivity to parameter variations. The originality of this work lies in the combined use of fractional-order control and real-time adaptive parameter updating, applied within a PV battery-powered EV platform. This dual-layer control structure allows the system to effectively reject disturbances, maintain torque and flux tracking, and mitigate the effects of component aging or thermal drift. Furthermore, to address the chattering phenomenon typically associated with sliding mode control, a continuous saturation function was employed, resulting in smoother voltage and current responses more suitable for real-time implementation. Extensive simulation studies were conducted under ideal conditions, with parameter mismatch, and with the proposed adaptive update laws. Results confirmed the superiority of the FO-based approach over classical integer-order designs in terms of speed tracking, flux regulation, torque ripple reduction, and system robustness. The proposed methodology offers a promising solution for next-generation sustainable mobility systems requiring high-performance, energy-efficient, and fault-tolerant electric drives.

1. Introduction

Many complex systems in engineering and science are described by nonlinear partial differential equations that exhibit fractional-order dynamics. These fractional characteristics have led to the development of fractional-order control strategies, which provide more precise and flexible control compared to traditional integer-order methods [1]. Fractional-order controllers are particularly effective in managing systems with nonlinearity and memory effects, making them highly applicable across various domains, including renewable energy systems and electric vehicle (EV) applications [1,2].

Recent research has shown that many renewable energy and storage systems are inherently described by nonlinear partial differential equations (PDEs), which capture complex dynamics and memory effects. For example, electrochemical models of lithium-ion batteries are governed by diffusion–convection PDEs that describe ion transport and state-of-charge evolution under varying loads [3,4]. Similarly, the thermal behavior of photovoltaic (PV) modules is modeled through nonlinear heat transfer PDEs that account for irradiance fluctuations and temperature gradients [5]. In stand-alone PV battery systems, coupled nonlinear PDEs are essential for analyzing the interaction between PV generation, battery dynamics, and load demand, often exhibiting fractional-order characteristics that complicate real-time control [6,7]. These studies motivate the adoption of advanced control methods capable of addressing nonlinearities and uncertainties, providing the foundation for fractional-order sliding mode control strategy.

Induction motors are widely regarded as a viable solution for EV propulsion due to their robustness, cost efficiency, and minimal maintenance requirements. Among the available control methods, field-oriented control (FOC) is extensively used for torque regulation in induction motors because of its ability to decouple torque and flux, allowing precise and dynamic control [8,9]. Despite its advantages, conventional FOC methods face challenges, such as torque and flux ripples, which reduce motor efficiency and introduce undesirable noise and vibrations. These issues are particularly pronounced in EV systems powered by standalone renewable energy sources, such as photovoltaic (PV) and battery systems, where dynamic operating conditions further complicate control.

To address these challenges, researchers have explored advanced control methods. Fractional-order control, leveraging the unique properties of fractional derivatives, offers significant advantages in improving dynamic stability and mitigating flux and torque ripples. Previous studies have employed techniques such as adaptive sliding mode controllers and fuzzy logic enhancements to improve the performance of induction motors [10,11]. However, most of these approaches either lack rigorous stability analysis or do not fully utilize the potential of fractional-order control in managing nonlinearities inherent in induction motor systems [2,12,13]. In fact, in these references, stability has been primarily verified through simulation results, which illustrate controller performance under selected scenarios but do not provide a general theoretical guarantee. Such simulation-based validation, while useful, remains limited in scope, as it cannot fully capture the robustness of the system against parameter variations and external disturbances.

In this work, a novel fractional-order sliding mode control (FO-SMC) strategy was proposed for the field-oriented control (FOC) of induction motors (IMs) in electric vehicles powered by an autonomous photovoltaic (PV) battery system. The originality of this study lies in the integration of fractional-order dynamics into both the current and speed control loops, combined with a real-time adaptive parameter updating mechanism. This hybrid framework was designed to improve tracking accuracy, mitigate torque and flux ripples, and enhance robustness against system uncertainties and parameter variations.

The proposed control structure establishes a rigorous stability proof employing the Lyapunov theory. This analytical approach ensures global stability of the closed-loop system, thereby strengthening the theoretical foundation of the proposed control strategy and highlighting its contribution beyond existing work. Unlike conventional integer-order or non-adaptive controllers, the FO-SMC approach demonstrated superior adaptability to thermal and electrical parameter shifts commonly encountered in electric vehicle operation, particularly under fluctuating renewable energy conditions.

The simulation results further confirmed the advantages of the proposed method, including faster convergence, reduced chattering through continuous saturation functions, and strong resilience against resistive and inductive mismatches. This work advances the field of sustainable transportation by providing a high-performance, energy-sensitive, and disturbance-resilient control solution for electric vehicle propulsion systems.

Section 1 introduces the overall electric vehicle propulsion architecture, describing the energy flow from the PV battery system to the induction motor. It explains the mechanical model based on tractive effort, covering key resistive forces such as rolling resistance, aerodynamic drag, and road gradient. The connection between vehicle dynamics and motor load torque is established through gear ratios and wheel parameters.

Section 2 provides the modeling foundation, including the mathematical description of the induction motor in the d–q reference frame. It details the relationships between stator/rotor currents and fluxes and introduces the mechanical equation and electromagnetic torque expression. The concept of slip speed and its influence on flux generation is outlined, followed by a brief review of the DTC-SVM technique for comparison.

Section 3 presents the core of the research: the proposed adaptive FO-SMC control law. This section details the design of fractional sliding surfaces, the continuous control formulation to reduce chattering, and the integration of an adaptive law for online parameter estimation. The Lyapunov-based proof of stability ensures theoretical soundness.

Section 4 discusses simulation results under various operating scenarios, including ideal conditions, parameter mismatches, and adaptive updates. Performance metrics such as speed tracking, flux regulation, voltage smoothness, and torque precision are compared with and without adaptation. The results validate the controller’s effectiveness in maintaining performance despite disturbances.

Section 5 concludes the paper by summarizing key findings and emphasizing the potential of fractional-order adaptive control in future electric vehicle systems. Recommendations are made for experimental validation and further exploration of fractional calculus in distributed energy-based transportation frameworks.

2. Fundamentals of Electric Vehicle Propulsion

Figure 1 illustrates a simplified diagram of an electric vehicle (EV) propulsion system, showing the critical components involved in converting electrical energy into mechanical motion to propel the vehicle. The propulsion system integrates several essential components. The transmission links the induction motor (IM) to the vehicle’s wheels, often incorporating a gearbox to modulate the motor’s output speed and torque according to driving demands. The IM serves as the primary actuator, transforming electrical energy into mechanical energy for vehicle propulsion. To power the motor, the inverter converts direct current (DC) from the battery or photovoltaic (PV) system to alternating current (AC) that is compatible with the motor’s operation. The optional photovoltaic system supplements energy from solar sources, enhancing the overall efficiency and sustainability of the system.

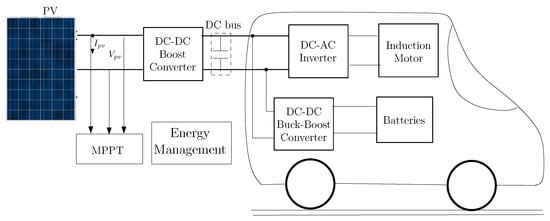
Figure 1. Architecture of the PV battery-powered EV with FO-FOC control.

The control system is centered on a robust control mechanism, integrating sophisticated algorithms and logic (see Figure 2). The fractional-order sliding mode (FO-SM) control technique is implemented to optimize the motor’s dynamic performance. Inputs from the driver, such as the position of the accelerator pedal, and from sensors, such as speed measurements, are processed by the control system to determine the desired motor torque and speed. The control signals are then sent to the inverter, which adjusts the AC voltage and frequency supplied to the induction motor. The motor generates the required torque, transmitted through the transmission to drive the wheels. In addition, the photovoltaic system, when included, can supplement the power of the system, further improving energy utilization and reducing the dependence on the battery.

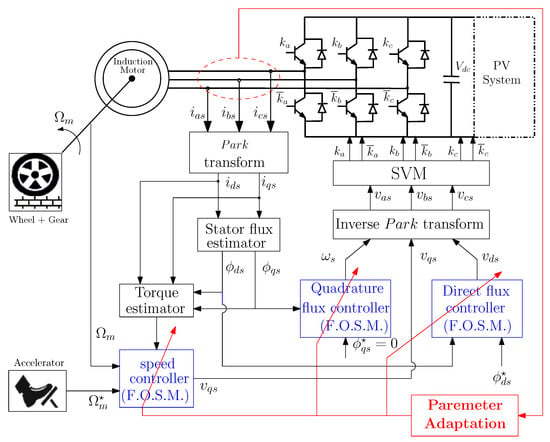
Figure 2. Block representation of FO-FOC scheme for induction motor control.

The relationship between the motor speed (${\mathrm{\Omega }}_m$) and the vehicle speed $V_v$ is given by: $V_v=R_{g}r{\mathrm{\Omega }}_m$. Substituting this into the load torque equation, we obtain the following: $T_L=f_0+f_2{\mathrm{\Omega }}_m^2$, where $f_0=k_0$ and $f_2=k_2{\left(R_{g}r\right)}^2$. This equation simulates the motor behavior under various conditions [14].

3. Energy Management Algorithm Between PV Technology and Batteries

To ensure continuity of service (the load has been supplied by a continuous fixed voltage), a management algorithm between the PV technology/battery system and the load will be proposed.

The energy management algorithm is used to supervise the energy exchanges between the elements of the installation, as well as to regulate the charge/discharge of the storage system (protection against overloads and deep discharges) to preserve the physicochemical battery properties and the extension of its lifetime. The proposed energy management algorithm is based on the following two scenarios:

• Power supply of the load and the storage system by PV panels if the photovoltaic energy is sufficient;
• Power supply of loads only from the storage system if the PV energy is insufficient.

The perfect functioning of the autonomous photovoltaic system requires optimal management of the energy flow exchanged between the different components of the system. Therefore, it is necessary to introduce a management system. To supervise the entire photovoltaic installation, the batteries are assumed to be initially charged. The management system is mainly responsible for supplying the load and protecting the batteries (we take a minimum state of charge, SOC_min = 30%, and a maximum state of charge, SOC_max = 95%). There are four operating modes in a photovoltaic battery system (see Table 1):

Table 1. The different operating modes of the PV technology/batteries system.

Mode	Production	S1	S2	S3	SOC
Mode 1	excess	1	1	0	SOC ≥ SOCmax
Mode 2	excess	1	1	1	SOC < SOCmax
Mode 3	lack	1	0	0	SOC > SOCmin
Mode 4	lack	0	0	0	SOC ≤ SOCmin

• Excess PV energy

  –

  Mode 1: Batteries are charged (SOC ≥ SOC_max). The photovoltaic generator is sufficient to satisfy the load ($P_{pv}\ge P_L$).

  –

  Mode 2: The photovoltaic generator is sufficient to satisfy the load ($P_{pv}=P_L$). Excess energy production will be stored in the batteries.

• Lack of PV energy

  –

  Mode 3: Only the batteries supply the load ($P_{bat}=P_L$).

  –

  Mode 4: Fully discharged batteries (SOC < SOC_min) and no photovoltaic production.

The proposed energy management algorithm plays a central role in balancing photovoltaic (PV) generation and battery storage to ensure a continuous power supply. Its main advantages include improved system stability through smooth power sharing, reduced energy losses by optimizing charging/discharging cycles, and extended battery lifetime via controlled depth-of-discharge. However, it also presents some limitations, such as sensitivity to parameter uncertainties and the need for reliable real-time measurements, which increase computational requirements. These aspects underline the importance of developing robust control strategies that can adapt to fluctuating operating conditions.

4. Modeling Induction Machine with FOC

The dynamic model of an induction machine may be expressed in terms of the d–q reference frame rotating at a synchronous speed. The electrical equations of the induction machine are as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{i}_{ds}}{dt}}={\displaystyle \frac{1}{\gamma l_s}}\left[-R_{sm}{i}_{ds}+{\omega }_s\gamma l_s{i}_{qs}+{\displaystyle \frac{r_{r}M}{l_r^2}}{\varphi }_{dr}+{\displaystyle \frac{M}{l_r}}{\omega }_m{\varphi }_{qr}+v_{ds}\right]\hfill \\ \hfill \\ {\displaystyle \frac{d{i}_{qs}}{dt}}={\displaystyle \frac{1}{\gamma l_s}}\left[-R_{sm}{i}_{qs}-{\omega }_s\gamma l_s{i}_{ds}+{\displaystyle \frac{r_{r}M}{l_r^2}}{\varphi }_{qr}-{\displaystyle \frac{M}{l_r}}{\omega }_m{\varphi }_{dr}+v_{qs}\right]\hfill \end{array}\right.\end{array}$$

(1)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{\varphi }_{dr}}{dt}}=-{\displaystyle \frac{r_r}{l_r}}{\varphi }_{dr}+\left({\omega }_s-{\omega }_m\right){\varphi }_{qr}+{\displaystyle \frac{r_{r}M}{l_r}}{i}_{ds}\hfill \\ \hfill \\ {\displaystyle \frac{d{\varphi }_{qr}}{dt}}=-{\displaystyle \frac{r_r}{l_r}}{\varphi }_{qr}-\left({\omega }_s-{\omega }_m\right){\varphi }_{dr}+{\displaystyle \frac{r_{r}M}{l_r}}{i}_{qs}\hfill \end{array}\right.\end{array}$$

(2)

where $R_{sm}=\left(r_s+{\displaystyle \frac{r_r{M}^2}{l_r^2}}\right)$.

The mechanical differential equation is:

$$\begin{array}{ccc}\hfill J{\displaystyle \frac{d{\mathrm{\Omega }}_m}{dt}}& =& T_{em}-T_L\hfill \end{array}$$

(3)

The electromagnetic torque is given by the following:

$$\begin{array}{c}\hfill T_{em}=N_p{\displaystyle \frac{M}{l_r}}\left({\varphi }_{dr}{i}_{qs}-{\varphi }_{qr}{i}_{ds}\right)\end{array}$$

(4)

If $N_p$ represents the number of pole pairs, we have ${\omega }_m=N_p{\mathrm{\Omega }}_m$. Equations (1)–(3) yield to a fifth-order system with three controls (${\omega }_s$, $v_{ds}$, $v_{qs}$). The idea is to decompose this system into three interconnected subsystems. With a suitable change of control variables, these subsystems become independent. Ideal decoupling can be achieved by aligning the rotor flux vector to the d-axis and setting the rotor flux linkage to be constant (${\varphi }_{dr}={\varphi }_{dr}^{\star }$, ${\varphi }_{qr}=0$).

• Control of the quadrature flux—for ${\varphi }_{qr}=0$, ${\dot{\varphi }}_{qr}=0$, we obtain the following:

  $$\begin{array}{c}\hfill {\displaystyle \frac{d{\varphi }_{qr}}{dt}}=-{\displaystyle \frac{r_r}{l_r}}{\varphi }_{qr}-\left({\omega }_s-{\omega }_m\right){\varphi }_{dr}+{\displaystyle \frac{r_{r}M}{l_r}}{i}_{qs}\end{array}$$

  (5)

  which should have ${\varphi }_{qr}$ goes to zero for an adequate control law of ${\omega }_s$ within a fast transient.
• Control of the direct flux ${\varphi }_{dr}={\varphi }_{dr}^{\star }$ is calculated as follows:

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{\varphi }_{dr}}{dt}}=-{\displaystyle \frac{r_r}{l_r}}{\varphi }_{dr}+{\displaystyle \frac{r_{r}M}{l_r}}{i}_{ds}+e_{dq1}\hfill \\ \hfill \\ {\displaystyle \frac{d{i}_{ds}}{dt}}={\displaystyle \frac{1}{\gamma l_s}}\left[-R_{sm}{i}_{ds}+{\displaystyle \frac{r_{r}M}{l_r^2}}{\varphi }_{dr}+\gamma l_s{\omega }_s{i}_{qs}+v_{ds}\right]+e_{dq2}\hfill \end{array}\right.\end{array}$$

  (6)
  With an adequate control $v_{ds}$, the desired direct flux should reach its desired value within a fast transient.
• Control of the machine speed ${\mathrm{\Omega }}_m$ is calculated as follows:

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{d{\mathrm{\Omega }}_m}{dt}}={\displaystyle \frac{1}{J}}\left[N_p{\displaystyle \frac{M}{l_r}}{\varphi }_N{i}_{qs}-T_L\right]+e_{dq3}\hfill \\ \hfill \\ {\displaystyle \frac{d{i}_{qs}}{dt}}={\displaystyle \frac{1}{\gamma l_s}}\left(-R_{sm}{i}_{qs}-{\omega }_s\gamma l_s{i}_{ds}+{\displaystyle \frac{r_{r}M}{l_r^2}}{\varphi }_{qr}-{\displaystyle \frac{M}{l_r}}{\omega }_m{\varphi }_{dr}+v_{qs}\right)\hfill \end{array}\right.\end{array}$$

  (7)

  with

  $$T_L=f\left({\mathrm{\Omega }}_m\right)=(f_0+f_2{\mathrm{\Omega }}_m^2)sign{\mathrm{\Omega }}_m+f_1{\mathrm{\Omega }}_m$$

  (8)
  The error quantities $e_{dq1}$, $e_{dq2}$, and $e_{dq3}$ are expressed as follows:

  $$\begin{array}{ccc}\hfill e_{dq1}& =& ({\omega }_s-{\omega }_m){\varphi }_{qr}=o\left({\varphi }_{qr}\right)\hfill \end{array}$$

  (9)

  $$\begin{array}{ccc}\hfill e_{dq2}& =& {\displaystyle \frac{M}{\gamma l_s{l}_r}}{\omega }_m{\varphi }_{qr}=o\left({\varphi }_{qr}\right)\hfill \end{array}$$

  (10)

  $$\begin{array}{ccc}\hfill e_{dq3}& =& N_p{\displaystyle \frac{M}{J{l}_r}}\left[({\varphi }_{dr}-{\varphi }_{dr}^{\star })i_{qs}-{\varphi }_{qr}{i}_{ds}\right]=o\left(\mathrm{\Delta }\varphi \right)\hfill \end{array}$$

  (11)

  with $\mathrm{\Delta }\varphi =({\varphi }_{dr}-{\varphi }_{dr}^{\star },{\varphi }_{qr}-0)$. These quantities go to zero after converging ${\varphi }_{qr}$ to zero and ${\varphi }_{dr}$ to ${\varphi }_{dr}^{\star }$.

5. Proposed Control

5.1. Background on Fractional Calculus

Several well-known mathematical definitions for fractional-order derivatives have been cited in many references, such as the (i) Riemann–Liouville, (ii) Grünwald–Letnikov, and (iii) Caputo approaches. They are commonly discussed in the literature [15,16,17].

In this work, we take into consideration the following Caputo definitions of fractional differentiation and integration of a function $g\left(t\right)$ for order $\sigma \in ]0,1[$:

$$\begin{array}{ccc}\hfill D_t^{-\sigma }g\left(t\right)& =& {\displaystyle \frac{1}{\mathrm{\Gamma }\left(\sigma \right)}}{\int }_0^t{(t-v)}^{\sigma -1}g\left(v\right)dv\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill D_t^{\sigma }g\left(t\right)& =& D_t^1\left(D_t^{-(1-\sigma )}g\left(t\right)\right)\hfill \end{array}$$

(13)

$$\begin{array}{ccc}& =& {\displaystyle \frac{d}{dt}}\left[{\displaystyle \frac{1}{\mathrm{\Gamma }(1-\sigma )}}{\int }_0^t{(t-v)}^{-\sigma }g\left(v\right)dv\right]={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\sigma )}}{\int }_0^t{(t-v)}^{-\sigma }{\displaystyle \frac{dg}{dv}}dv\hfill \end{array}$$

(14)

with the $\mathrm{\Gamma }$ function written as

$$\mathrm{\Gamma }\left(\eta \right)={\int }_0^{\infty }{t}^{\eta -1}{e}^{-t}dt$$

(15)

5.2. Quadrature Flux Controller

Let us consider the following sliding function:

$$S_{\varphi q}={\varphi }_{qr}+{\lambda }_{\varphi q}{D}_t^{-\alpha }{\varphi }_{qr}$$

(16)

The chosen dynamic behavior of the sliding function of the quadrature flux is chosen as follows:

$${\dot{S}}_{\varphi q}=-({\eta }_{1\varphi q}sign{S}_{\varphi q}+{\eta }_{2\varphi q}{S}_{\varphi q}+{\eta }_{3\varphi q}|S_{\varphi q}{|}^{{\sigma }_q}sign{S}_{\varphi q})$$

(17)

The control law is then expressed as follows:

$${\omega }_s={\displaystyle \frac{1}{{\varphi }_{dr}^{\star }}}\left[({\eta }_{1\varphi q}sign{S}_{\varphi q}+{\eta }_{2\varphi q}{S}_{\varphi q}+{\eta }_{3\varphi q}|S_{\varphi q}{|}^{{\sigma }_q}sign{S}_{\varphi q})-{\displaystyle \frac{r_r}{l_r}}{\varphi }_{qr}+{\omega }_m{\varphi }_{dr}+{\displaystyle \frac{r_{r}M}{l_r}}{i}_{qs}\right]$$

(18)

Theorem 1.

We have the following:

$$\underset{t⟶+\infty }{lim}{S}_{\varphi q}=0$$

(19)

and then

$$\underset{t⟶+\infty }{lim}{\varphi }_{qr}=0$$

(20)

Proof. 

Let us consider the following first Lyapunov equation:

$$V_{1\varphi q}={\displaystyle \frac{1}{2}}{S}_{\varphi q}^2>0$$

(21)

Its derivative verifies the following:

$${\dot{V}}_{1\varphi q}={\dot{S}}_{\varphi q}{S}_{\varphi q}=-({\eta }_{1\varphi q}|S_{\varphi q}|+{\eta }_{2\varphi q}{S}_{\varphi q}^2+{\eta }_{3\varphi q}|S_{\varphi q}{|}^{{\sigma }_q+1})<0$$

(22)

This shows that $S_{\varphi q}$ converges to 0.

After having $S_{\varphi q}=0$, and then $D_t^{\alpha }{S}_{\varphi q}=0$, we can write the following:

$$D_t^{\alpha }{\varphi }_{qr}=-{\lambda }_{\varphi q}{\varphi }_{qr}$$

(23)

Let us consider the following second Lyapunov function:

$$V_{2\varphi q}={\displaystyle \frac{1}{2}}{\varphi }_{qr}^2$$

(24)

Its quadrature derivative verifies the following:

$$D_t^{\alpha }{V}_{2\varphi q}\le {\varphi }_{qr}{D}_t^{\alpha }{\varphi }_{qr}=-{\lambda }_{\varphi q}{\varphi }_{qr}^2<0$$

(25)

This shows that ${\varphi }_{qr}$ converges to 0. □

5.3. Direct Flux Controller

Keeping ${\varphi }_{qr}=0$, the direct flux ${\varphi }_{dr}$ can be described by the following differential equation:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d^2{\varphi }_{dr}}{d{t}^2}}& =& -{\displaystyle \frac{r_r}{l_r}}\left(-{\displaystyle \frac{r_r}{l_r}}{\varphi }_{dr}+{\displaystyle \frac{r_{r}M}{l_r}}{i}_{ds}\right)+{\displaystyle \frac{r_{r}M}{\gamma l_s{l}_r}}\left(-R_{sm}{i}_{ds}+{\displaystyle \frac{r_{r}M}{l_r^2}}{\varphi }_{dr}+\gamma l_s{\omega }_s{i}_{qs}+v_{ds}\right)+e_{dq}\hfill \\ & =& a_1{\varphi }_{dr}-a_2{i}_{ds}+a_3{\omega }_s{i}_{qs}+a_4{v}_{ds}+e_{dq}\hfill \end{array}$$

(26)

where $e_{dq}=o\left({\varphi }_{qr}\right)$ and

$$\begin{array}{ccc}\hfill a_1& =& {\displaystyle \frac{r_r^2}{l_r^2}}\times {\displaystyle \frac{l_s{l}_r}{l_s{l}_r-M^2}}\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill a_2& =& {\displaystyle \frac{r_r{R}_{sm}M}{l_s{l}_s-M^2}}+{\displaystyle \frac{M{r}_r^2}{l_r^2}}\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill a_3& =& {\displaystyle \frac{M{r}_r}{l_r}}\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill a_4& =& {\displaystyle \frac{r_{r}M}{l_s{l}_r-M^2}}\hfill \end{array}$$

(30)

without forgetting

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{\varphi }_{dr}}{dt}}& =& -{\displaystyle \frac{r_r}{l_r}}{\varphi }_{dr}+{\displaystyle \frac{M{r}_r}{l_r}}{i}_{ds}+e_{dq1}=-a_5{\varphi }_{dr}+a_3{i}_{ds}+e_{dq1}\hfill \end{array}$$

(31)

where

$$\begin{array}{ccc}\hfill a_5& =& {\displaystyle \frac{r_r}{l_r}}\hfill \end{array}$$

(32)

Let us define the errors $e_d$, ${\epsilon }_d$, and sliding function $S_{\varphi d}$ as follows:

$$\begin{array}{ccc}\hfill e_d& =& {\varphi }_{dr}-{\varphi }_{dr}^{\star }\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill {\epsilon }_d& =& {\dot{e}}_d+{\lambda }_{1\varphi d}{e}_d\hfill \end{array}$$

(34)

$$\begin{array}{ccc}\hfill S_{\varphi d}& =& {\epsilon }_d+{\lambda }_{1\varphi d}{D}_t^{-\alpha }{\epsilon }_d\hfill \end{array}$$

(35)

with ${\varphi }_{dr}^{\star }=1$ Wb.

The chosen dynamical behavior of the sliding function of the direct flux is chosen as follows:

$${\dot{S}}_{\varphi d}=-({\eta }_{1\varphi d}+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d})sign{S}_{\varphi d}-{\eta }_{2\varphi d}{S}_{\varphi d}$$

(36)

This gives the following control law:

$$\begin{array}{ccc}\hfill v_{ds}& =& {\displaystyle \frac{1}{a_4}}[-({\eta }_{1\varphi d}+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d})sign{S}_{\varphi d}-{\eta }_{2\varphi d}{S}_{\varphi d}\hfill \\ & & -a_1{\varphi }_{dr}+a_2{i}_{ds}-a_3{\omega }_s{i}_{qs}-{\lambda }_{1\varphi d}{\dot{e}}_d-{\lambda }_{2\varphi d}{D}_t^{1-\alpha }{\epsilon }_d]\hfill \end{array}$$

(37)

Theorem 2.

We have the following:

$$\underset{t⟶+\infty }{lim}{S}_{\varphi d}=0$$

(38)

and then

$$\underset{t⟶+\infty }{lim}{\varphi }_{dr}={\varphi }_{dr}^{\star }$$

(39)

Proof. 

Let us consider the following Lyapunov function:

$$V_{1\varphi d}={\displaystyle \frac{1}{2}}{S}_{\varphi d}^2>0$$

(40)

Its derivatives verifies the following:

$${\dot{V}}_{1\varphi d}={\dot{S}}_{\varphi d}{S}_{\varphi d}=-({\eta }_{1\varphi d}|S_{\varphi d}|+{\eta }_{2\varphi d}{S}_{\varphi d}^2+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d+1})<0$$

(41)

This shows that $S_{\varphi d}$ converges asymptotically to 0.

After having $S_{\varphi d}=0$, and then $D_t^{\alpha }{S}_{\varphi q}=0$, we can write the following:

$$D_t^{\alpha }{\epsilon }_d=-{\lambda }_{2\varphi d}{\epsilon }_d$$

(42)

Then, consider the following Lyapunov equation:

$$V_{2\varphi d}={\displaystyle \frac{1}{2}}{\epsilon }_d^2>0$$

(43)

Its fractional derivatives verifies the following:

$$D_t^{\alpha }{V}_{2\varphi d}\le {\epsilon }_d{D}_t^{\alpha }{\epsilon }_d=-{\lambda }_{2\varphi d}{\epsilon }_d^2<0$$

(44)

This ensures that ${\epsilon }_d$ converges asymptotically to 0.

Now, consider the third Lyapunov function, written as follows:

$$V_{3\varphi d}={\displaystyle \frac{1}{2}}{e}_d^2>0$$

(45)

Or, after the convergence of ${\epsilon }_d$ to 0, we can write: ${\dot{e}}_d=-{\lambda }_{1\varphi d}{e}_d$. This shows that the time derivatives of the third Lyapunov function $V_{3\varphi d}$ verifies the following:

$${\dot{V}}_{3\varphi d}={\dot{e}}_d{e}_d=-{\lambda }_{1\varphi d}{e}_d^2<0$$

(46)

which ensures that the error $e_d$ converges asymptotically to zero, and consequently, the direct flux ${\varphi }_{dr}$ converges converges asymptotically to ${\varphi }_{dr}^{\star }$. □

5.4. Speed Controller

After having ${\varphi }_{dr}={\varphi }_{dr}^{\star }$ and ${\varphi }_{qr}=0$, the speed is described by the following differential equation:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d^2{\mathrm{\Omega }}_m}{d{t}^2}}& =& {\displaystyle \frac{N_{p}M{\varphi }_{dr}^{\star }}{J{l}_r}}{\displaystyle \frac{d{i}_{qs}}{dt}}-{\displaystyle \frac{1}{J}}{\displaystyle \frac{d{T}_L}{dt}}\hfill \\ & =& {\displaystyle \frac{N_{p}M{\varphi }_{dr}^{\star }}{J\gamma l_s{l}_r}}\left(-R_{sm}{i}_{qs}-{\displaystyle \frac{N_{p}M{\varphi }_{dr}^{\star }}{l_r}}{\mathrm{\Omega }}_m-{\omega }_s\gamma l_s{i}_{ds}+v_{qs}\right)-{\displaystyle \frac{1}{J}}{\displaystyle \frac{d{T}_L}{dt}}\hfill \end{array}$$

(47)

First, let us consider the following generalized error:

$${\epsilon }_{\mathrm{\Omega }}={\dot{e}}_{\mathrm{\Omega }}+{\lambda }_{1\mathrm{\Omega }}{e}_{\mathrm{\Omega }}$$

(48)

with the error

$$e_{\mathrm{\Omega }}={\omega }_m-{\omega }_m^{\star }$$

(49)

and the following sliding function

$$S_{\mathrm{\Omega }}={\epsilon }_{\mathrm{\Omega }}+{\lambda }_{2\mathrm{\Omega }}{D}_t^{-\alpha }{\epsilon }_{\mathrm{\Omega }}$$

(50)

The dynamical behaviour of the sliding function is chosen as follows:

$${\dot{S}}_{\mathrm{\Omega }}=-({\eta }_{1\mathrm{\Omega }}+{\eta }_{3\mathrm{\Omega }}|S_{\mathrm{\Omega }}{|}^{{\sigma }_{\mathrm{\Omega }}})sign{S}_{\mathrm{\Omega }}-{\eta }_{2\mathrm{\Omega }}{S}_{\mathrm{\Omega }}$$

(51)

with: ${\eta }_{1\mathrm{\Omega }}>0$, ${\eta }_{2\mathrm{\Omega }}>0$, ${\eta }_{3\mathrm{\Omega }}>0$ and $0<{\sigma }_{\mathrm{\Omega }}<1$.

In this case, the control law verifies the following:

$$\begin{array}{ccc}\hfill v_{qs}& =& R_{sm}{i}_{qs}+{\displaystyle \frac{N_{p}M{\varphi }_{dr}^{\star }}{l_r}}{\mathrm{\Omega }}_m+{\omega }_s\gamma l_s{i}_{ds}+{\displaystyle \frac{J\gamma l_s{l}_r}{N_{p}M{\varphi }_{dr}^{\star }}}({\displaystyle \frac{1}{J}}{\displaystyle \frac{d{T}_L}{dt}}+{\displaystyle \frac{d^2{\mathrm{\Omega }}_m^{\star }}{d{t}^2}}{\epsilon }_{\mathrm{\Omega }}\hfill \\ & & -{\lambda }_{1\mathrm{\Omega }}{\dot{e}}_{\mathrm{\Omega }}-{\lambda }_{2\mathrm{\Omega }}{D}_t^{1-\alpha }-({\eta }_{1\mathrm{\Omega }}+{\eta }_{3\mathrm{\Omega }}|S_{\mathrm{\Omega }}{|}^{{\sigma }_{\mathrm{\Omega }}})sign{S}_{\mathrm{\Omega }}-{\eta }_{2\mathrm{\Omega }}{S}_{\mathrm{\Omega }})\hfill \end{array}$$

(52)

with

$${\displaystyle \frac{d{T}_L}{dt}}=\left(f_1+2f_2|{\mathrm{\Omega }}_m|\right){\displaystyle \frac{d{\mathrm{\Omega }}_m}{dt}}$$

(53)

Theorem 3.

We have the following:

$$\underset{t⟶+\infty }{lim}{S}_{\mathrm{\Omega }}=0$$

(54)

and then

$$\underset{t⟶+\infty }{lim}{\mathrm{\Omega }}_m={\mathrm{\Omega }}_m^{\star }$$

(55)

Proof. 

Let us consider the following Lyapounov function:

$$V_{1\mathrm{\Omega }}={\displaystyle \frac{1}{2}}{S}_{\mathrm{\Omega }}^2$$

(56)

Its derivative verifies the following:

$$\begin{array}{c}\hfill {\dot{V}}_{1\mathrm{\Omega }}=S_{\mathrm{\Omega }}{\dot{S}}_{\mathrm{\Omega }}=-({\eta }_{1\mathrm{\Omega }}|S|+{\eta }_{2\mathrm{\Omega }}{S}^{T}S+{\eta }_{3\mathrm{\Omega }}{|S|}^{{\sigma }_{\mathrm{\Omega }}+1}) <0\end{array}$$

(57)

This shows that S converges to 0.

After imposing $S_{\mathrm{\Omega }}=0$, then $D_t^{\alpha }{S}_{\mathrm{\Omega }}=0$, we can write the following:

$$D_t^{\alpha }{\epsilon }_{\mathrm{\Omega }}=-{\lambda }_{2\mathrm{\Omega }}{\epsilon }_{\mathrm{\Omega }}$$

(58)

In order to ensure that the trajectory error goes to zero, we consider the subsequent Lyapunov function:

$$V_{2\mathrm{\Omega }}\left(\epsilon \right)={\displaystyle \frac{1}{2}}{\epsilon }_{\mathrm{\Omega }}^2>0$$

(59)

Its fractional derivatives with respect to time, noted $D_t^{\gamma }{V}_{2\mathrm{\Omega }}$, is expressed by the following:

$$\begin{array}{ccc}\hfill D_t^{\alpha }{V}_{2\mathrm{\Omega }}\left(\epsilon \right)& \le & {\epsilon }_{\mathrm{\Omega }}{D}_t^{\alpha }{\epsilon }_{\mathrm{\Omega }}=-{\lambda }_{2\mathrm{\Omega }}{\epsilon }_{\mathrm{\Omega }}^2<0\hfill \end{array}$$

(60)

Thus, we have shown that $S_{\mathrm{\Omega }}$ goes to 0, and ${\epsilon }_{\mathrm{\Omega }}=({\dot{e}}_{\mathrm{\Omega }}+{\lambda }_{1\mathrm{\Omega }}{e}_{\mathrm{\Omega }})$ goes to zero, and consequently, $e_{\mathrm{\Omega }}$ converges to zero, and the system attains its desired trajectory. □

Remark 1.

We should choose: ${\lambda }_{1\varphi d}={\lambda }_{1\varphi q}\gg {\lambda }_{1\mathrm{\Omega }}$, and ${\lambda }_{2\varphi d}={\lambda }_{2\varphi q}\gg {\lambda }_{2\mathrm{\Omega }}$. In fact, the direct and quadrature fluxes should reach their desired values rapidly to apply a vector control of the speed.

Moreover, parameter ${\eta }_{3\varphi q}={\eta }_{3\varphi d}>0$ and ${\eta }_{3\mathrm{\Omega }}>0$ are introduced in order to have the convergence of sliding surfaces in finite times.

5.5. Adaptive Approcah to Remedy Flux Rotor

We have defined the error on ${\varphi }_{dr}$ as $e_d={\varphi }_{dr}-{\varphi }_{dr}^{\star }$ and the generalized error as ${\epsilon }_d={\dot{e}}_d+{\lambda }_1{e}_d$. The differential of $e_d$ is calculated as a function of parameters $r_r$, $r_s$, and M, which are not the real parameters of the machine. Then, we should update their values as follows: We define ${\overline{r}}_r$, ${\overline{r}}_s$, and $\overline{M}$ using the updated values of ill-known variables $r_r$, $r_s$, and M. The control law $v_{ds}$ is calculated in terms of parameters ${\overline{a}}_i$, which are functions of ${\overline{r}}_r$, ${\overline{r}}_s$, and $\overline{M}$:

$$\begin{array}{ccc}\hfill {\overline{v}}_{ds}& =& {\displaystyle \frac{1}{{\overline{a}}_4}}[-({\eta }_{1\varphi d}+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d})sign{S}_{\varphi d}-{\eta }_{2\varphi d}{S}_{\varphi d}\hfill \\ & & -{\overline{a}}_1{\varphi }_{dr}+{\overline{a}}_2{i}_{ds}-{\overline{a}}_3{\omega }_s{i}_{qs}-{\lambda }_{1\varphi d}(a_3{i}_{ds}-a_5{\varphi }_{dr}))-{\lambda }_{2\varphi d}{D}_t^{1-\alpha }{\epsilon }_d]\hfill \end{array}$$

(61)

The expression of ${\epsilon }_d$ becomes the following:

$${\epsilon }_d={\dot{e}}_d+{\lambda }_1{e}_d=-a_5{\varphi }_{dr}+a_3{i}_{ds}+{\lambda }_1{e}_d$$

(62)

The derivative of the sliding function $S_d$ is expressed by the following:

$$\begin{array}{ccc}\hfill {\dot{S}}_d& =& {\dot{\epsilon }}_d+{\lambda }_{1\varphi d}{D}_t^{1-\alpha }{\epsilon }_d\hfill \\ & =& {\displaystyle \frac{d^2{\varphi }_{dr}}{d{t}^2}}+{\lambda }_{1\varphi d}{\displaystyle \frac{d{\varphi }_{dr}}{dt}}+{\lambda }_{1\varphi d}{D}_t^{1-\alpha }{\epsilon }_d\hfill \\ & =& a_1{\varphi }_{dr}-a_2{i}_{ds}+a_3{\omega }_s{i}_{qs}+a_4{v}_{ds}+{\lambda }_{1\varphi d}(a_3{i}_{ds}-a_5{\varphi }_{dr})+{\lambda }_{1\varphi d}{D}_t^{1-\alpha }{\epsilon }_d\hfill \end{array}$$

(63)

By applying the control ${\overline{v}}_{ds}$ instead $v_{ds}$, the derivative of the sliding function $S_d$ becomes the following:

$$\begin{array}{ccc}\hfill {\overline{\dot{S}}}_d& =& a_1{\varphi }_{dr}-a_2{i}_{ds}+a_3{\omega }_s{i}_{qs}+a_4{\overline{v}}_{ds}+{\lambda }_{1\varphi d}(a_3{i}_{ds}-a_5{\varphi }_{dr})+{\lambda }_{1\varphi d}{D}_t^{1-\alpha }{\epsilon }_d\hfill \end{array}$$

(64)

While ${\dot{S}}_d$ is a linear function of parameters $a_i$, we can write the following:

$${\dot{S}}_d={\overline{\dot{S}}}_d+\sum _i{\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_i}}\mathrm{\Delta }{a}_i$$

(65)

with $\mathrm{\Delta }{a}_i=a_i-{\overline{a}}_i$ and

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_1}}& =& {\varphi }_{dr}\hfill \end{array}$$

(66)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_2}}& =& -i_{ds}\hfill \end{array}$$

(67)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_3}}& =& {\lambda }_{1\varphi d}{i}_{ds}+{\omega }_s{i}_{qs}\hfill \end{array}$$

(68)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_4}}& =& {\overline{v}}_{ds}\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_5}}& =& -{\lambda }_{1\varphi d}{\varphi }_{dr}\hfill \end{array}$$

(70)

Finally, applying the control law ${\overline{v}}_{ds}$, we can write the following:

$${\dot{S}}_d=-({\eta }_{1\varphi d}+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d})sign{S}_{\varphi d}-{\eta }_{2\varphi d}{S}_{\varphi d}+\sum _i{\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_i}}\mathrm{\Delta }{a}_i$$

(71)

Theorem 4.

The control law (61) with the following adaptive laws ($i=1\dots 5)$, is written as follows:

$${\dot{\overline{a}}}_i={\rho }_i{S}_d{\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_i}}$$

(72)

with ${\rho }_i>0$, we ensure the convergence of ${\varphi }_{dr}$ to ${\varphi }_{dr}^{\star }$.

Proof. 

Let us consider the following Lyapunov equation:

$$\begin{array}{c}\hfill V_{4\varphi d}={\displaystyle \frac{1}{2}}{S}_d^2+{\displaystyle \frac{1}{2}}\sum _{i=1}^5{\displaystyle \frac{1}{{\rho }_i}}{\left(\mathrm{\Delta }{a}_i\right)}^2\end{array}$$

(73)

Its derivatives are as follows:

$$\begin{array}{ccc}\hfill {\dot{V}}_{4\varphi d}& =& S_d\left[-({\eta }_{1\varphi d}+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d})sign{S}_{\varphi d}-{\eta }_{2\varphi d}{S}_{\varphi d}+\sum _{i=1}^5{\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_i}}\mathrm{\Delta }{a}_i\right]+\sum _{i=1}^5{\displaystyle \frac{1}{{\rho }_i}}\mathrm{\Delta }{a}_i\mathrm{\Delta }{\dot{a}}_i\hfill \\ & =& -({\eta }_{1\varphi d}|S_{\varphi d}|+{\eta }_{2\varphi d}{S}_{\varphi d}^2+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d+1})+\sum _{i=1}^5{\displaystyle \frac{1}{{\rho }_i}}\mathrm{\Delta }{a}_i\underset{=0}{\underbrace{\left[\mathrm{\Delta }{\dot{a}}_i+{\rho }_i{S}_d{\displaystyle \frac{\partial {\dot{S}}_d}{\partial a_i}}\right]}}\hfill \\ & =& -({\eta }_{1\varphi d}|S_{\varphi d}|+{\eta }_{2\varphi d}{S}_{\varphi d}^2+{\eta }_{3\varphi d}|S_{\varphi d}{|}^{{\sigma }_d+1})\le 0\hfill \end{array}$$

(74)

In fact, for constant variables $a_i$ or for their slow variations, we can write ${\dot{a}}_i\simeq 0$, then $\mathrm{\Delta }{\dot{a}}_i={\dot{a}}_i-{\dot{\overline{a}}}_i\simeq -{\dot{\overline{a}}}_i$.

This guarantees the stability of the system and the convergence of $S_d$ to 0, then ${\varphi }_d$ to ${\varphi }_d^{\star }$. □

Remark 2.

We have chosen to update 5 parameters $a_i$ instead of three parameters $r_r$, $r_s$ and M because the control law $v_{qs}$ and the time derivative of the sliding function ${\dot{s}}_d$ are nonlinear functions of the machine parameters, but they are linear in terms of composite parameters $a_i$.

6. Simulation Results

In the following, we will present some simulations in the following cases:

• Supposing all parameters are well known and using the sign function as described above (the ideal case);
• Replacing the sign function with a smooth function, which is a saturation function, in order to eliminate the chattering phenomenon (elimination of the chattering);
• Applying $+100\%$ on stator resistance and rotor resistance caused by heating in the motor and applying $-50\%$ on the magnetizing inductance M caused by saturation of magnetic circuits (parameter’s variations).

6.1. Ideal Case

Figure 3 shows how well the proposed FO-SMC controller synchronizes the motor’s rotational speed with the linear velocity of the vehicle. The response is fast and steady, suggesting that the fractional-order controller offers good transient handling and helps maintain accuracy without overshooting, which is crucial for the drivability of electric vehicles.

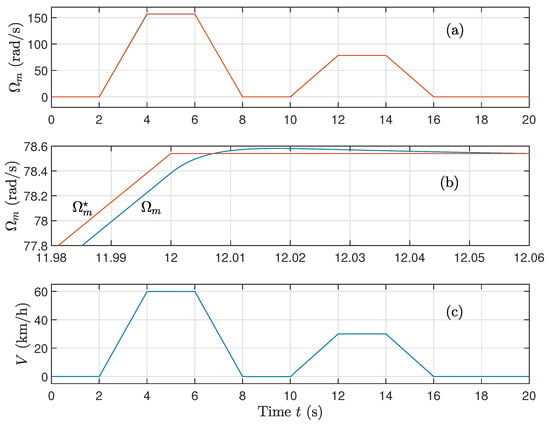
Figure 3. (a) Rotating speed, (b) Zoom of rotating speed, and (c) Velocity of the vehicle, for well-known parameters using sign function on the control.

In Figure 4, we see the effectiveness of field-oriented control. The direct-axis flux stays consistent, while the quadrature-axis flux quickly falls to zero, confirming the decoupling. The fractional-order terms appear to enhance the smoothness and speed of convergence compared to classical integer-order methods.

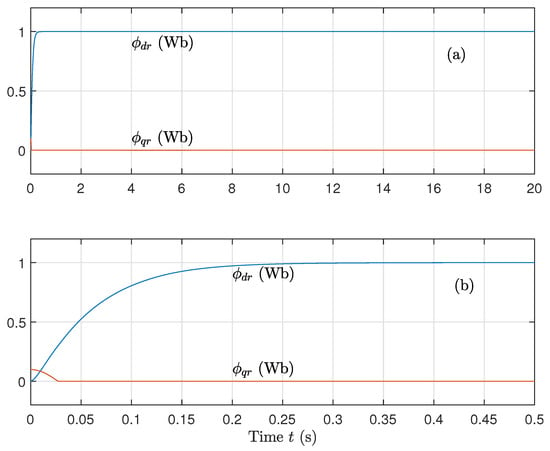
Figure 4. (a) Direct flux component and (b) Quadrature flux component, for well-known parameters using the sign function on the control.

Figure 5 illustrates the behavior of the voltage and current outputs under ideal conditions. Although the system responds quickly, some chattering is visible, likely due to the discontinuous control action. This highlights a trade-off between speed and signal smoothness in sliding mode control, especially in its basic form.

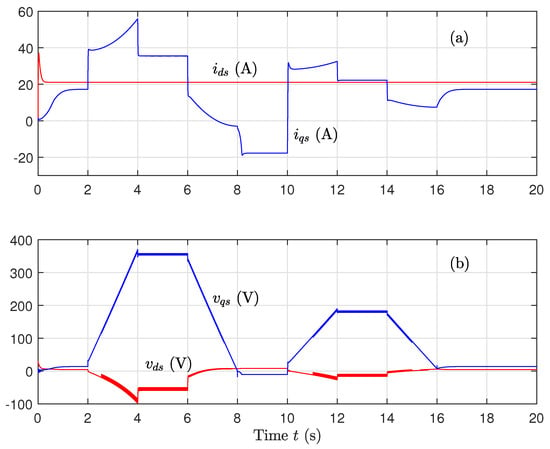
Figure 5. (a) Direct and quadrature voltage components and (b) Direct and quadrature current components, for well-known parameters using the sign function on the control.

In Figure 6, the torque produced by the motor closely follows the load torque, indicating a strong control precision. The stator frequency remains stable throughout, showing that the controller maintains synchronization even under dynamic load variations.

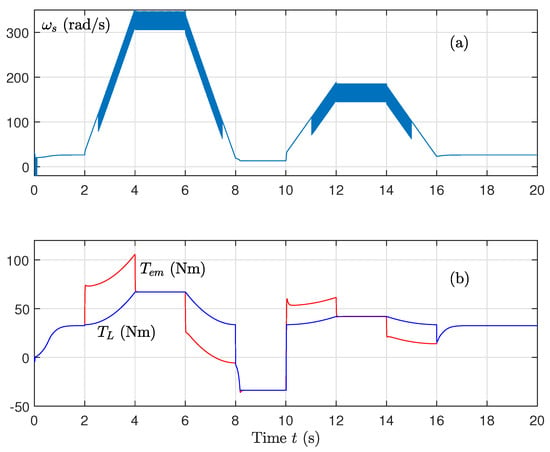
Figure 6. (a) Stator pulsation and (b) Torques (electromagnetic and load), for well-known parameters using the sign function on the control.

6.2. Elimination of the Chattering

We obtain the same results except for the dynamical behavior of quadrature rotor flux ${\varphi }_{qr}$, stator voltages $v_{ds}$ and $v_{qs}$, and stator pulsation ${\omega }_s$.

By replacing the sign function with a smoother saturation function, Figure 7 shows improved flux behavior. The quadrature component converges more smoothly, and signal quality improves without significantly compromising performance.

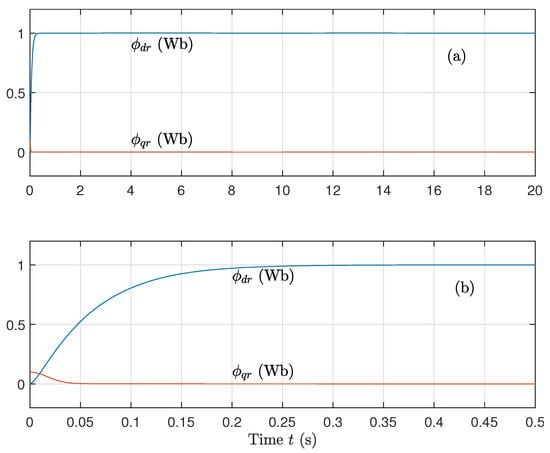
Figure 7. (a) Direct flux component and (b) Quadrature flux component, for well-known parameters using the sat function on the control.

In Figure 8, the voltage output is noticeably smoother compared to Figure 5. This confirms the benefit of using continuous functions to reduce chattering, making the controller more suitable for hardware implementation in EV applications.

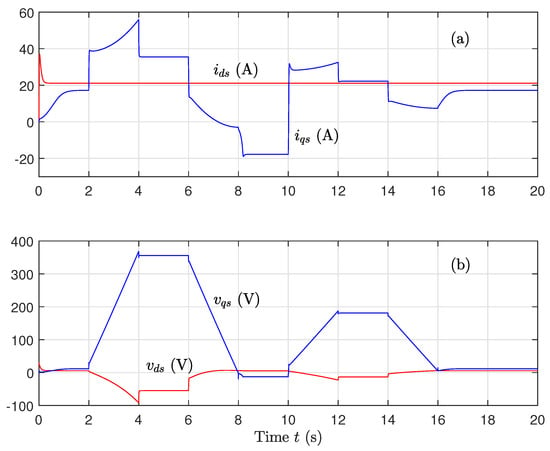
Figure 8. (a) Direct and quadrature voltage components and (b) Direct and quadrature current components, for well-known parameters using the sat function in the control.

The frequency signal becomes cleaner, with fewer oscillations, supporting the effectiveness of the modified control law. It is a practical improvement that makes the system more robust to switching and noise-related effects (see Figure 9).

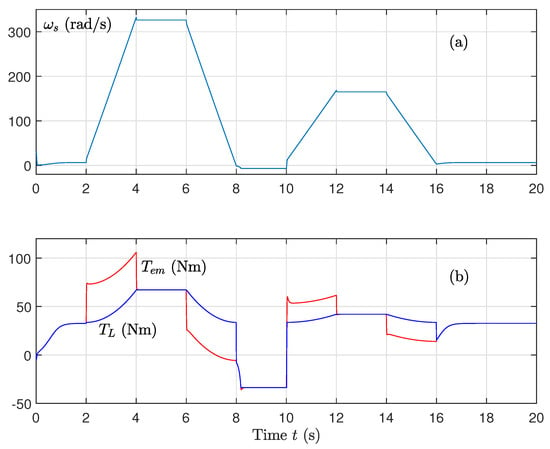
Figure 9. (a) Stator pulsation and (b) Torques (electromagnetic and load) for well-known parameters using the sat function on the control.

6.3. Parameter’s Variations

Despite significant changes in resistance and inductance, the motor and vehicle still follow their reference trajectories with minor deviations. This highlights the inherent robustness of the FO controller to parameter mismatches (see Figure 10).

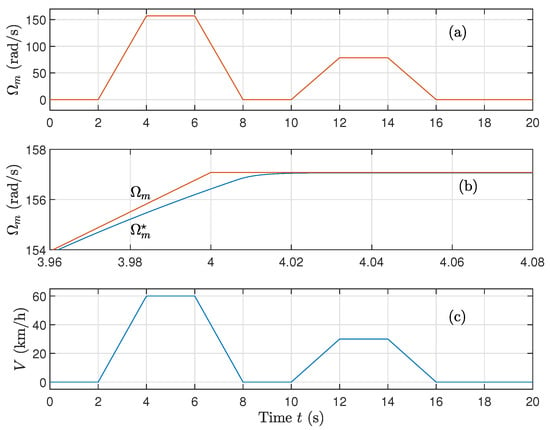
Figure 10. (a) Rotating speed, (b) Zoom of rotating speed, and (c) Velocity of the vehicle, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control.

The flux trajectories (Figure 11) remain well controlled, showing that the system preserves field orientation even under large uncertainties of parameters. This is key for reliable torque production in real driving conditions.

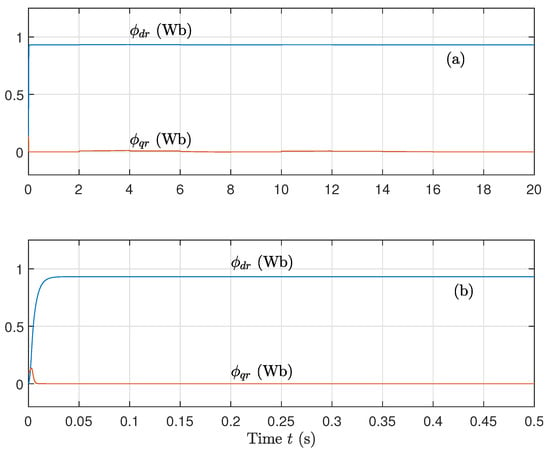
Figure 11. (a) Direct flux component and (b) Quadrature flux component, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control.

Although some distortions appear, overall control is maintained. The voltage and current profiles, in Figure 12 and Figure 13, remain within acceptable ranges, showing that the system handles uncertainties without instability.

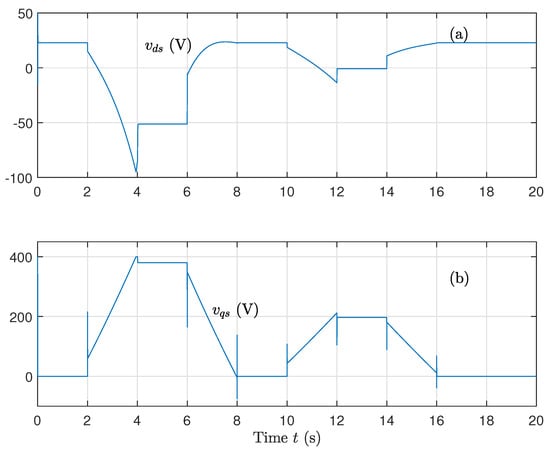
Figure 12. (a) Direct voltage component and (b) Quadrature voltage component, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control.

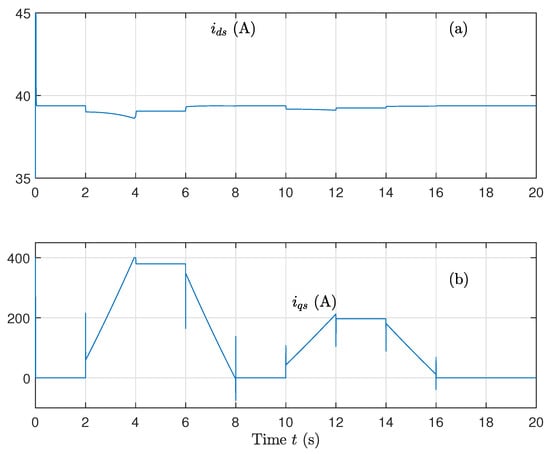
Figure 13. (a) Direct current component and (b) Quadrature current component, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control.

The torque output remains responsive and tracks the load even with disturbed parameters (see Figure 14). This result confirms that the fractional-order sliding mode controller can manage both mechanical and electrical inconsistencies effectively.

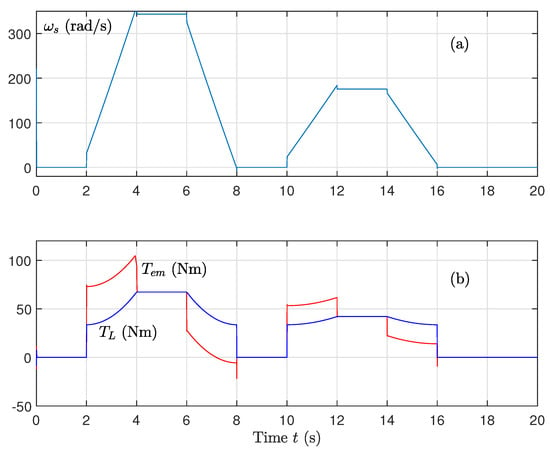
Figure 14. (a) Stator pulsation and (b) Torques (electromagnetic and load) for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control.

6.4. Parameter’s Adaptation

Adding adaptive laws helps restore performance almost perfectly. The system quickly corrects deviations caused by parameter variations, which confirms the practical value of online parameter estimation in EV systems (see Figure 15).

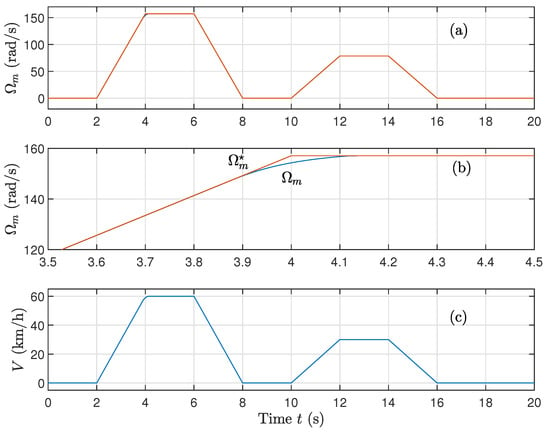
Figure 15. (a) Rotating speed, (b) Zoom of rotating speed, and (c) velocity of the vehicle for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control and updated parameters.

With adaptation, both flux components return to their ideal behavior (Figure 16). This reinforces the controller’s ability to automatically recover field orientation, even after significant model degradation.

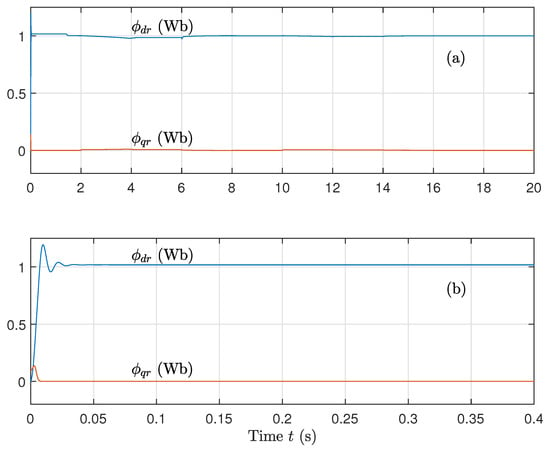
Figure 16. (a) Direct flux component and (b) Quadrature flux component, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control and updated parameters.

Compared to earlier results, the voltage and current responses here are much cleaner and better controlled. This is a strong indicator of the success of the adaptive layer in correcting the behavior of the system under uncertainty (Figure 17 and Figure 18).

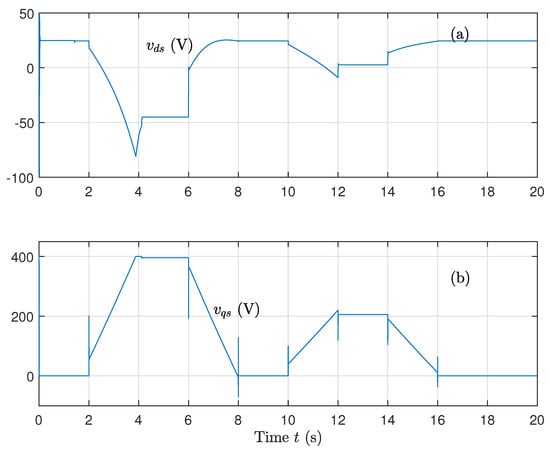
Figure 17. (a) Direct voltage component and (b) Quadrature voltage component, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control and updated parameters.

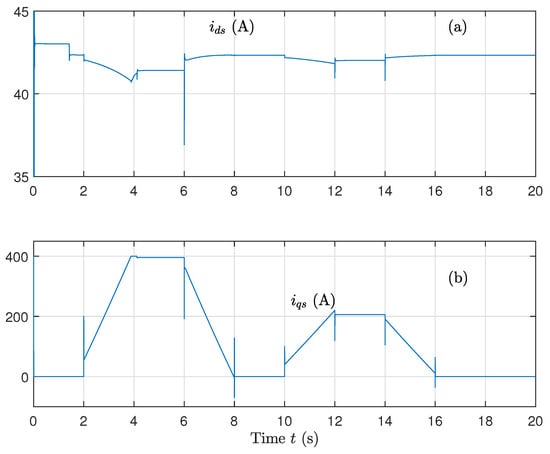
Figure 18. (a) Direct current component and (b) Quadrature current component, for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control and updated parameters.

The system fully regains its tracking ability, and the torque output remains stable (Figure 19). The combined effect of fractional control and adaptation results in a high-performance, fault-tolerant drive suitable for EV applications.

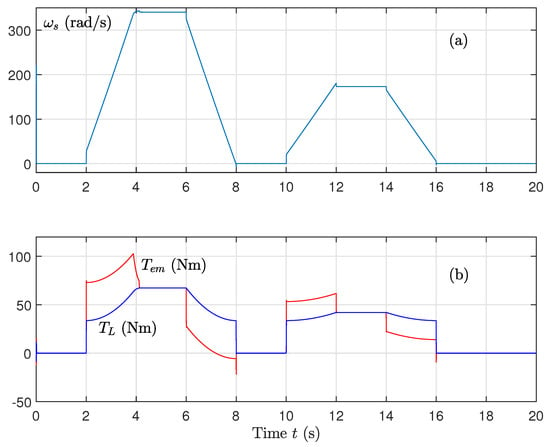
Figure 19. (a) Stator pulsation and (b) torques (electromagnetic and load) for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using the sat function on the control and updated parameters.

Regarding Figure 20, it is clear that the variations of parameters $a_1$, $a_2$, and $a_4$ are not important. In fact, the variations of these parameters perturb the second derivatives ${\ddot{\varphi }}_{rd}$. However, these variations are compensated by the control law that contains the term ${\eta }_{1\varphi d}$ (multiplied by $sign{S}_{\varphi d}$ or $sat{S}_{\varphi d}$). However, only the parameter $a_3$ has been updated. In fact, the defluxation problem is originated by the first derivative ${\dot{\varphi }}_{rd}$. This results from the equation ${\dot{S}}_{\varphi d}=0$, which contains ${\dot{\varphi }}_{rd}$, containing parameters $a_3$ and $a_5$. If these parameters are perturbed, the convergence of ${\dot{\varphi }}_{rd}$ to 0 leads to the convergence of ${\varphi }_{rd}$ to a value different from the derived ${\varphi }_{rd}^{\star }$. Regarding Figure 20f, we can conclude that the ratio between the updated values of $a_3$ and $a_5$ converge to their desired ratio. This can be explained by the fact that if these parameters converge to $k{a}_3$ and $k{a}_5$, k is a positive constant, and Equation (42) becomes the following:

$$k{D}_t^{\alpha }{\epsilon }_d=-{\lambda }_{2\varphi d}{\epsilon }_d$$

(75)

which is similar to Equation (42) after replacing ${\lambda }_{2\varphi d}$ with ${\displaystyle \frac{{\lambda }_{2\varphi d}}{k}}$.

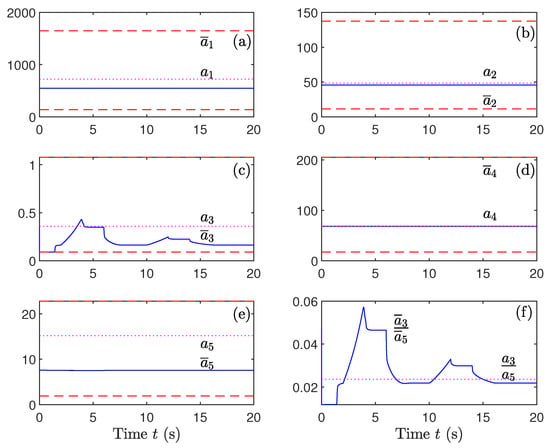
Figure 20. (a) Evolution of the updated parameter $a_1$, (b) Evolution of the updated parameter $a_2$, (c) Evolution of the updated parameter $a_3$, (d) Evolution of the updated parameter $a_4$, (e) Evolution of the updated parameter $a_5$, and (f) The ratio ${\displaystyle \frac{a_3}{a_5}}$ for $+100\%$ variations on rotor and stator resistances and $-50\%$ variations on the magnetizing inductance using “sat” function on the control.

The following should be noted:

$${\displaystyle \frac{a_3}{a_5}}=M$$

(76)

In the simulation conditions, M takes $50\%$ of its nominal value, that is, $M=0.5\times 0.047=0.0235$. In a steady state, the value of ${\displaystyle \frac{{\overline{a}}_3}{{\overline{a}}_5}}$ is 0.02183, which is close to its real value.

Knowing that $l_r=M+l_{rr}$, with $l_{rr}\ll M$, parameter $a_3$ is expressed as follows:

$$a_3={\displaystyle \frac{M{r}_r}{l_r}}={\displaystyle \frac{M{r}_r}{M+l_{rr}}}={\displaystyle \frac{r_r}{1-{\displaystyle \frac{l_{rr}}{M}}}}\simeq r_r$$

(77)

This confirms that the only parameter that influences the obtained results is the rotor resistance, and it should be updated in a practical case due to the heating effect.

7. Conclusions

This study presented a robust control approach for electric vehicle propulsion systems powered by a standalone photovoltaic battery configuration. A fractional-order sliding mode controller (FO-SMC) was integrated into a field-oriented control (FOC) scheme for an induction motor (IM) drive, with the aim of enhancing performance under both nominal and uncertain conditions.

The results demonstrated that the proposed fractional-order control strategy improved speed tracking accuracy, reduced torque ripple, and ensured stable flux regulation compared to conventional integer-order controllers. The FO-based system also exhibited strong robustness against parameter variations such as changes in stator resistance and magnetizing inductance, which commonly occurred due to thermal or operational factors in electric vehicle applications.

To address the chattering effects associated with the classical sliding-mode control, a continuous saturation function was employed. This modification effectively smoothed the control signals without compromising dynamic response, improving suitability for real-time power electronic implementations. Additionally, the incorporation of adaptive laws allowed the controller to update key parameters in real time, which restored ideal performance even under severe mismatches and system uncertainties.

The originality of this work lies in the novel combination of fractional-order sliding-mode control with adaptive parameter tuning, applied within an energy-autonomous electric vehicle framework powered by a PV battery source. Unlike conventional approaches, the proposed method not only addressed robustness and precision in motor control but also ensured compatibility with practical implementation constraints in renewable-powered EV platforms.

Overall, the proposed FO-FOC framework proved to be a reliable and adaptable solution for sustainable electric mobility. Future work may focus on real-time experimental validation and extending the methodology to multi-drive systems and integrated energy management using fractional-order models.