Dynamics in a Fractional-Order Four-Species Food Web System with Top Predator and Delays

Abstract

The predator–prey model is a fundamental mathematical tool in ecology used to understand the dynamic relationship between predator and prey populations. This study develops a fractional-order delayed dynamical model for a four-species food web, which includes an intermediate predator feeding on two prey species and a top predator preying on all three species. The boundedness of the system’s solutions is first rigorously established using the Laplace transform method. Next, a nonlinear dynamical analysis is performed to determine the existence conditions and local stability of both the trivial and positive equilibrium points. In particular, by treating the time delay as a bifurcation control parameter, explicit criteria for the onset of Hopf bifurcation are derived. Theoretically, when the delay magnitude exceeds a critical threshold, the system loses stability and exhibits sustained oscillatory behavior. Finally, systematic numerical simulations are performed under specific parameter settings. The effects of varying fractional orders and delay magnitudes on the system’s dynamics are quantitatively explored, and the results show strong agreement with the theoretical predictions.

1. Introduction

The predator–prey model serves as a fundamental mathematical tool in ecology for exploring the interactions between two biological populations, particularly the dynamic equilibrium between predators and their prey [1,2]. These models not only reveal inherent patterns in population fluctuations but also offer a theoretical basis for understanding ecosystem stability, assessing the effectiveness of biological control, and addressing broader ecological challenges. Through ongoing refinement and development, these models allow researchers to explore the complex dynamic behavior of ecosystems more deeply, thereby supporting biodiversity conservation and informing ecosystem management decisions.

The four-dimensional predator–prey model represents substantial advancement over the classical Lotka–Volterra model. By incorporating additional variables, it captures more intricate ecological interactions [3,4]. This class of models is particularly effective for simulating integrated ecosystems involving multiple resources, multiple predators, and environmental influences. Studies have shown that four-dimensional models provide distinct advantages in assessing the impact of environmental changes on ecosystems [5] and predicting long-term population dynamics [6,7]. Specifically, these models capture the complex network of relationships among predators, various biological resources, competitors, and environmental disturbances. For example, Shang et al. [8] developed a four-species food web model that systematically examined the influence of fear effects and nonlinear foraging behavior by top predators on system dynamics. Similarly, Farhan et al. [9] proposed a four-dimensional model involving two prey and two predators, offering a detailed analysis of solution existence, boundedness, and the stability of multiple equilibrium states. In both ecological research and applied contexts, the four-dimensional predator–prey model offers significant theoretical insight and practical relevance [10]. It provides novel perspectives for understanding the functional mechanisms of complex ecosystems and serves as a robust analytical framework for addressing increasingly urgent ecological and environmental challenges.

The functional response function is a foundational mathematical model in ecology that characterizes the relationship between predator foraging behavior and prey population density. It quantitatively describes how predation rates dynamically respond to fluctuations in prey density. Based on specific predator behavioral traits, functional responses are generally classified into standard types such as the Holling [11] and Beddington–DeAngelis (B-D) [12,13] types, each reflecting distinct ecological mechanisms. In theoretical research, Dai et al. [14] incorporated the B-D-type functional response into a predator–prey system governed by advection–reaction–diffusion equations, thereby expanding the model’s applicability. Danane et al. [15] further developed the B-D framework by introducing stochastic noise terms, enhancing its ability to represent environmental uncertainty. Recent studies indicate that the B-D-type functional response carries considerable theoretical importance and practical utility in population dynamics modeling, ecosystem stability analysis, and optimizing biological control strategies [16,17,18]. This model functions as a robust quantitative tool for deepening insights into interspecific interactions and forecasting ecological evolutionary trends.

On the other hand, the integer-order predator–prey model serves as the foundation and preliminary work for studying the fractional-order predator–prey model. Therefore, when constructing the fractional-order predator–prey model, we still need to start our discussion from the already studied integer-order model. For instance, Farhan et al. [9] developed an integer-order predator–prey model within an extended framework encompassing two prey species and two predator species. The prey populations occupy distinct habitats and exhibit group defense mechanisms, while the predator species employ differential foraging strategies: one predator engages in cross-habitat predation with prey-switching behavior, whereas the other is a specialist restricted to a single prey species. The full system is mathematically formulated as follows:

$$\begin{array}{c}{\dot{x}}_1=x_1\left(g_1\left(1-{\displaystyle \frac{x_1}{k_1}}\right)-{\displaystyle \frac{{\alpha }_1{x}_2^n{y}_1}{x_1^n+x_2^n}}-\beta y_2\right),\hfill \\ {\dot{x}}_2=x_2\left(g_2\left(1-{\displaystyle \frac{x_2}{k_2}}\right)-{\displaystyle \frac{{\alpha }_2{x}_1^n{y}_1}{x_1^n+x_2^n}}\right),\hfill \\ {\dot{y}}_1=y_1\left(-{\mu }_1+{\displaystyle \frac{{\delta }_1{x}_1{x}_2^n}{x_1^n+x_2^n}}+{\displaystyle \frac{{\delta }_2{x}_1^n{x}_2}{x_1^n+x_2^n}}\right),\hfill \\ {\dot{y}}_2=y_2\left(-{\mu }_2+\gamma x_1\right),\hfill \end{array}$$

where $x_1\left(t\right)$ and $x_2\left(t\right)$ denote the population densities of the prey species at time t, while $y_1\left(t\right)$ and $y_2\left(t\right)$ represent the population densities of two distinct predator species at time t. Specifically, predator $y_1\left(t\right)$ preys on both $x_1\left(t\right)$ and $x_2\left(t\right)$, and predator $y_2\left(t\right)$ preys on $x_1\left(t\right)$; $g_1$ and $g_2$ denote the intrinsic growth rates of the populations $x_1$ and $x_2$, respectively. ${\mu }_1$ and ${\mu }_2$ denote the intrinsic growth rates of populations $y_1$ and $y_2$, respectively. $k_1$ and $k_2$ denote the environmental carrying capacities of populations $x_1$ and $x_2$, respectively. ${\alpha }_1$ and ${\alpha }_2$ denote the predation rates of predator $y_1$, and ${\beta }_2$ denotes the predation rate of predator $y_2$. ${\delta }_1$ and ${\delta }_2$ denote the conversion rates of predator $y_1$, and $\gamma$ denotes the conversion rate of predator $y_2$. Building on the predator characteristics outlined in the aforementioned model, we formulate a four-dimensional fractional-order predator–prey system. The integration of fractional derivatives allows for more precise characterization of historical dependence and memory effects in population dynamics. While classical integer-order derivatives assume system states depend exclusively on instantaneous conditions, our fractional-order framework captures the influence of past states on current ecological processes (e.g., cumulative resource depletion effects and the accumulation of predator experience), thereby significantly enhancing biological realism. Additionally, time-delay terms directly model critical ecological lags, addressing the idealized instantaneous-response assumption inherent in conventional models. Furthermore, we adopt B-D functional responses, which offer superior ecological interpretability compared to classical Holling-type responses. Consequently, we obtain the following fractional-order four-species food web system incorporating a top predator and time delays:

$$\begin{array}{c}{}^{c}D^q{x}_1\left(t\right)=x_1\left(t\right)\left[r_1-a_1{x}_2\left(t\right)-b_{1}y\left(t\right)-b_{2}z\left(t\right)-c_1{x}_1\left(t\right)\right],\hfill \\ {}^{c}D^q{x}_2\left(t\right)=x_2\left(t\right)\left[r_2-a_2{x}_1\left(t\right)-b_{3}y\left(t\right)-b_{4}z\left(t\right)-c_2{x}_2\left(t\right)\right],\hfill \\ {}^{c}D^{q}y\left(t\right)=y\left(t\right)\left[e_1{x}_1\left(t\right)+e_2{x}_2\left(t\right)-{\displaystyle \frac{f_{1}z(t-\tau )}{1+k_{1}y(t-\tau )+k_{2}z(t-\tau )}}-d_1\right],\hfill \\ {}^{c}D^{q}z\left(t\right)=z\left(t\right)\left[e_3{x}_1\left(t\right)+e_4{x}_2\left(t\right)+{\displaystyle \frac{f_{2}y(t-\tau )}{1+k_{1}y(t-\tau )+k_{2}z(t-\tau )}}-d_2\right],\hfill \end{array}$$

(1)

where the interpretation of the symbols used in model (1) is given in

Table 1. Biological meaning of parameters in system (1).

Parameter	Biological Interpretation
$r_1$	Intrinsic growth rate of prey $x_1\left(t\right)$.
$r_2$	Intrinsic growth rate of prey $x_2\left(t\right)$.
$a_1$	Competitive effect of $x_2\left(t\right)$ on $x_1\left(t\right)$.
$a_2$	Competitive effect of $x_1\left(t\right)$ on $x_2\left(t\right)$.
$b_1$	Attack rate of predator $y\left(t\right)$ on prey $x_1\left(t\right)$.
$b_2$	Attack rate of predator $z\left(t\right)$ on prey $x_1\left(t\right)$.
$b_3$	Attack rate of predator $y\left(t\right)$ on prey $x_2\left(t\right)$.
$b_4$	Attack rate of predator $z\left(t\right)$ on prey $x_2\left(t\right)$.
$c_1$	Intraspecific competition coefficient of $x_1\left(t\right)$.
$c_2$	Intraspecific competition coefficient of $x_2\left(t\right)$.
$f_1$	Predation rate of top predator $z\left(t\right)$ on $y\left(t\right)$.
$f_2$	Benefit coefficient from consuming $y\left(t\right)$.
$d_1$	Natural mortality rate of $y\left(t\right)$.
$d_2$	Natural mortality rate of $z\left(t\right)$.
$k_1$	Intra-predator interference among $y\left(t\right)$ individuals.
$k_2$	Intra-predator interference among $z\left(t\right)$ individuals.
$e_1$	Efficiency of converting $x_1\left(t\right)$ into $y\left(t\right)$.
$e_2$	Efficiency of converting $x_2\left(t\right)$ into $y\left(t\right)$.
$e_3$	Efficiency of converting $x_1\left(t\right)$ into $z\left(t\right)$.
$e_4$	Efficiency of converting $x_2\left(t\right)$ into $z\left(t\right)$.
$\tau$	Time delay representing predation lag or digestive processing time.

.

Building on existing theoretical research, this paper proposes the above four-dimensional fractional-order delayed predator–prey model designed to capture the complex dynamics of grassland ecosystems. The model constructs a food web comprising four trophic levels, represented by the following four populations: Hares (primary consumers), which feed on grass, with their population growth shaped by resource availability, competition, and predation; voles (primary consumers), which compete with hares for plant resources; raptors (obligate predators), which primarily prey on hares and voles; and foxes (facultative predators), which consume both hares and voles and occasionally prey on raptors. This model integrates the B-D type functional response with fractional-order differential equations to more accurately characterize the temporal delay effects and non-local properties inherent in interspecific interactions. Through this model, we systematically analyze dynamic behaviors within the grassland ecosystem, such as steady-state equilibria, periodic oscillations, and population collapse, thereby providing a theoretical foundation for ecosystem conservation and management.

2. Preliminaries

In system (1), $x_1\left(t\right)$ and $x_2\left(t\right)$ denote the population densities of the prey species at time t, while $y\left(t\right)$ and $z\left(t\right)$ represent the population densities of two distinct predator species at time t. Specifically, predator $y\left(t\right)$ preys on both $x_1\left(t\right)$ and $x_2\left(t\right)$, whereas the top predator $z\left(t\right)$ feeds on $x_1\left(t\right)$, $x_2\left(t\right)$, and $y\left(t\right)$, with its predation on $y\left(t\right)$ adhering to the Beddington–DeAngelis (B-D) functional response. The biological meanings of all other parameters in system (1) are given in Table 1.

For system (1), we have the following initial condition:

$$\begin{array}{c}x\left(0\right)>0,y\left(0\right)>0,z\left(0\right)>0,\hfill \end{array}$$

The following are the important definitions and lemmas required for this paper.

Definition 1 

([19]). The Caputo fractional derivative operator is given by the following expression:

$${}^{c}D^{q}f\left(t\right)={\displaystyle \frac{1}{\Gamma (m-\phi )}}{\int }_0^t{(t-\tau )}^{m-\phi -1}f\left(\tau \right)d\tau ,$$

where $m-1<\phi <m$ for some $m\in {\mathbb{Z}}^{*}$, and and $\Gamma (·)$ denotes the Gamma function, mathematically characterized as

$$\Gamma \left(\alpha \right)={\int }_0^{\infty }{e}^{-v}{v}^{\alpha -1}dv.$$

The Laplace transform of the Caputo fractional-order derivative is expressed as

$$\mathcal{L}\left\{{}^{c}D^{q}f\left(t\right);s\right\}=s^{q}F\left(s\right)-\sum _{i=0}^{n-1}{s}^{q-i-1}{f}^{\left(i\right)}\left(0\right),$$

where $F\left(s\right)=\mathcal{L}\left\{f\right(t\left)\right\}$ represents the Laplace transform of $f\left(t\right)$. In the specific case where the initial derivatives satisfy $f^{\left(i\right)}\left(0\right)=0$ for all $i=0,1,\dots ,n-1$, the transform simplifies to $\mathcal{L}{\left\{{}^{c}D^{q}f\left(t\right)\right\}}_s=s^{q}F\left(s\right)$.

Lemma 1 

([20]). For any positive real numbers $c>0$ and $d>0$ and a matrix $K\in C^{n\times n}$, the following Laplace transform relation holds:

$$\mathcal{L}\left\{t^{d-1}{E}_{c,d}\left(K{t}^c\right)\right\}={\displaystyle \frac{p^{c-d}}{p^c-K}},\mathrm{for}\mathfrak{R}\left(p\right)>{\parallel K\parallel }^{{\displaystyle \frac{1}{c}}},$$

where $\mathfrak{R}\left(p\right)$ denotes the real part of the complex number p, and $E_{c,d}$ represents the Mittag–Leffler function, which is defined as $E_{c,d}\left(z\right)={\sum }_{n=0}^{\infty }{\displaystyle \frac{z^n}{\Gamma (cn+d)}}$.

Lemma 2 

([21]). Consider the following fractional-order dynamical system:

$${}^{c}D^{q}x\left(t\right)=f\left(x\right),x\left(0\right)=x_0,$$

where $q\in (0,1)$ and $x\in {\mathbb{R}}^n$. The equilibrium points of this system are determined by the solutions of the equation $f\left(x\right)=0$. An equilibrium point of the system is locally asymptotically stable if, for the Jacobian matrix $J={\displaystyle \frac{\partial f}{\partial x}}$ evaluated at this equilibrium point, all its eigenvalues ${\lambda }_j$ satisfy the condition $\left|arg\left({\lambda }_j\right)\right|>{\displaystyle \frac{q\pi }{2}}$.

3. Main Results

This section investigates the dynamical properties of system (1) under zero time delay ($\tau =0$), including the boundedness of solutions, the existence of equilibrium points, and their local asymptotic stability. First, we establish the boundedness of solutions to the system.

Theorem 1. 

All trajectories of system (1) remain uniformly bounded within the domain ζ, which is defined precisely as follows:

$$\zeta =\left\{(x_1,x_2,y,z)\in {\mathbb{R}}_{+}^4\mid 0<x_1+x_2+y+z\le {\displaystyle \frac{r_3^2}{4c_{1}K}}+\epsilon ,\epsilon >0\right\}.$$

Proof. 

For our analysis, we introduce the following function:

$$\begin{array}{c}\mathfrak{R}\left(t\right)=x_1\left(t\right)+x_2\left(t\right)+y\left(t\right)+z\left(t\right).\hfill \end{array}$$

(2)

By evaluating the Caputo fractional derivative of the candidate function (2), we derive the following expression:

$$\begin{array}{cc}\hfill {}^{c}D^q\mathfrak{R}\left(t\right)& ={}^{c}D^q{x}_1\left(t\right)+{}^{c}D^q{x}_2\left(t\right)+{}^{c}D^{q}y\left(t\right)+{}^{c}D^{q}z\left(t\right)\hfill \\ \hfill & =x_1\left(t\right)\left[r_1-a_1{x}_2\left(t\right)-b_{1}y\left(t\right)-b_{2}z\left(t\right)-c_1{x}_1\left(t\right)\right]\hfill \\ \hfill & +x_2\left(t\right)\left[r_2-a_2{x}_1\left(t\right)-b_{3}y\left(t\right)-b_{4}z\left(t\right)-c_2{x}_2\left(t\right)\right]\hfill \\ \hfill & +y\left(t\right)\left[e_1{x}_1\left(t\right)+e_2{x}_2\left(t\right)-{\displaystyle \frac{f_{1}z(t-\tau )}{1+k_{1}y(t-\tau )+k_{2}z(t-\tau )}}-d_1\right]\hfill \\ \hfill & +z\left(t\right)\left[e_3{x}_1\left(t\right)+e_4{x}_2\left(t\right)+{\displaystyle \frac{f_{2}y(t-\tau )}{1+k_{1}y(t-\tau )+k_{2}z(t-\tau )}}-d_2\right]\hfill \\ \hfill & \le r_1{x}_1\left(t\right)-c_1{x}_1^2\left(t\right)+r_2{x}_2\left(t\right)-c_2{x}_2^2\left(t\right)-d_{1}y\left(t\right)-d_{2}z\left(t\right).\hfill \end{array}$$

If $\Lambda =min\left\{r_2,d_1,d_2\right\},r_3=r_1+\Lambda$. Consequently, the following identity holds:

$$\begin{array}{c}{}^{c}D^q\mathfrak{R}\left(t\right)+\Lambda \mathfrak{R}\left(t\right)\le r_3{x}_1\left(t\right)-c_1{x}_1^2\left(t\right)=-c_1{\left[x_1\left(t\right)-{\displaystyle \frac{r_3}{2c_1}}\right]}^2+{\displaystyle \frac{r_3^2}{4c_1}}\le {\displaystyle \frac{r_3^2}{4c_1}}.\hfill \end{array}$$

(3)

Applying the Laplace transform to Equation (3) and denoting $F\left(s\right)=\mathcal{L}\left\{\mathfrak{R}\right(t\left)\right\}$, we obtain the following fundamental inequality:

$$\begin{array}{c}{s}^{q}F\left(s\right)-s^{q-1}\mathfrak{R}\left(0\right)+KF\left(s\right)\le {\displaystyle \frac{r_3^2}{4c_{1}s}}.\hfill \end{array}$$

(4)

From the above inequality (4), we can deduce that

$$\begin{array}{c}F\left(s\right)\le \mathfrak{R}\left(0\right){\displaystyle \frac{s^{q-1}}{s^q+K}}+{\displaystyle \frac{r_3^2}{4c_{1}s\left(s^q+K\right)}}.\hfill \end{array}$$

(5)

Applying the inverse Laplace transform to both sides of Equation (5) yields

$$\mathfrak{R}\left(t\right)\le \mathfrak{R}\left(0\right){\mathcal{L}}^{-1}\left\{{\displaystyle \frac{s^{q-1}}{s^q+K}}\right\}+{\displaystyle \frac{r_3^2}{4c_1}}{\mathcal{L}}^{-1}\left\{{\displaystyle \frac{s^{q-(q+1)}}{s^q+K}}\right\}.$$

By Lemma 1, we obtain

$$\begin{array}{c}\mathfrak{R}\left(t\right)\le \mathfrak{R}\left(0\right)E_{q,1}\left\{-K{t}^q\right\}+{\displaystyle \frac{r_3^2}{4c_1}}{t}^q{E}_{q,q+1}\left\{-K{t}^q\right\}.\hfill \end{array}$$

Based on the fundamental properties of the Mittag–Leffler function, we derive the following relationship:

$$E_{q,1}\left\{-K{t}^q\right\}=\left(-K{t}^q\right)E_{q,q+1}\left\{-K{t}^q\right\}+{\displaystyle \frac{1}{\Gamma \left(1\right)}}.$$

Equivalently, we have the following:

$$t^q{E}_{q,q+1}\left\{-K{t}^q\right\}=-{\displaystyle \frac{1}{K}}\left[E_{q,1}\left\{-K{t}^q\right\}-1\right].$$

Consequently, we derive

$$\mathfrak{R}\left(t\right)\le \left\{\mathfrak{R}\left(0\right)-{\displaystyle \frac{r_3^2}{4c_{1}K}}\right\}{E}_{q,1}\left\{-K{t}^q\right\}+{\displaystyle \frac{r_3^2}{4c_{1}K}}.$$

Given that $E_{q,1}\to 0$ as $t\to \infty$, system (1) possesses the property that all solutions are ultimately confined to the positively invariant region:

$$\zeta =\left\{(x_1,x_2,y,z)\in {\mathbb{R}}_{+}^4\mid 0<x_1+x_2+y+z\le {\displaystyle \frac{r_3^2}{4c_{1}K}}+\epsilon ,\epsilon >0\right\}.$$

□

Next, we analyze the existence and local asymptotic stability of equilibrium points of system (1).

Theorem 2. 

The trivial equilibrium $E_0=(0,0,0,0)$ is locally asymptotically stable.

Proof. 

The Jacobian matrix of system (1) evaluated at the trivial equilibrium point $E_0$ takes the following form:

$$\begin{array}{c}{J}_0=\left[\begin{array}{cccc}{r}_1& 0& 0& 0\\ 0& r_2& 0& 0\\ 0& 0& -d_1& 0\\ 0& 0& 0& -d_2\end{array}\right],\hfill \end{array}$$

yielding the characteristic equation

$$\begin{array}{c}(\lambda -r_1)(\lambda -r_2)(\lambda +d_1)(\lambda +d_2)=0,\hfill \end{array}$$

(6)

The eigenvalues of (6) are

$$\begin{array}{c}{\lambda }_1=r_1,{\lambda }_2=r_2,{\lambda }_3=-d_1,{\lambda }_4=-d_2.\hfill \end{array}$$

A direct analysis reveals that

$$\begin{array}{c}\left|arg\left({\lambda }_{1,2}\right)\right|=\pi >{\displaystyle \frac{\pi q}{2}},\left|arg\left({\lambda }_{3,4}\right)\right|=0<{\displaystyle \frac{\pi q}{2}}.\hfill \end{array}$$

Consequently, the necessary conditions for the local asymptotic stability of $E_0$ are not satisfied, thereby proving that $E_0$ is unstable. □

Theorem 3. 

The coexisting equilibrium $E_{*}=(x_1^{*},x_2^{*},y^{*},z^{*})$ exhibits local asymptotic stability provided that Hypotheses 1–3, as defined herein, are satisfied:

Hypothesis 1. 

$T_1+Q_1{y}^{*}+R_1{z}^{*}>0$.

Hypothesis 2. 

$T_2+Q_2{y}^{*}+R_2{z}^{*}>0$.

Hypothesis 3. 

$B_1>0$, $B_2>0$, $B_3>0$, ${\Delta }_2>0$, ${\Delta }_3>0$, and ${\Delta }_4>0$.

Here,

$$\begin{array}{c}{\Delta }_2=\left|\begin{array}{cc}{B}_1& 1\\ B_3& B_2\end{array}\right|,{\Delta }_3=\left|\begin{array}{ccc}{B}_1& 1& 0\\ B_3& B_2& B_1\\ 0& B_4& B_3\end{array}\right|,{\Delta }_4=B_4{\Delta }_3,\hfill \end{array}$$

and $B_i$ (for $i=1,2,3,4$) are defined in the proof.

Proof. 

First, we establish the existence of the coexisting equilibrium of the system.

By solving system (1), $x_1^{*},x_2^{*},y^{*},$ and $z^{*}$ are subjects to the following relationship:

$$\begin{array}{c}{r}_1-a_1{x}_2^{*}-b_1{y}^{*}-b_2{z}^{*}-c_1{x}_1^{*}=0,\hfill \\ r_2-a_2{x}_1^{*}-b_3{y}^{*}-b_4{z}^{*}-c_2{x}_2^{*}=0,\hfill \\ e_1{x}_1^{*}+e_2{x}_2^{*}-{\displaystyle \frac{f_1{z}^{*}}{1+k_1{y}^{*}+k_2{z}^{*}}}-d_1=0,\hfill \\ e_3{x}_1^{*}+e_4{x}_2^{*}+{\displaystyle \frac{f_2{y}^{*}}{1+k_1{y}^{*}+k_2{z}^{*}}}-d_2=0.\hfill \end{array}$$

(7)

Solving the first two equations in (7) for $x_1^{*}$ and $x_2^{*}$ yields:

$$\begin{array}{c}{x}_1^{*}=T_1+Q_1{y}^{*}+R_1{z}^{*},\hfill \\ x_2^{*}=T_2+Q_2{y}^{*}+R_2{z}^{*},\hfill \end{array}$$

(8)

where

$$\begin{array}{c}{T}_1={\displaystyle \frac{r_1{c}_2-r_2{a}_1}{c_1{c}_2-a_1{a}_2}},T_2={\displaystyle \frac{r_2{c}_1-r_1{a}_2}{c_1{c}_2-a_1{a}_2}},Q_1={\displaystyle \frac{b_3{a}_1-b_1{c}_2}{c_1{c}_2-a_1{a}_2}},\hfill \\ Q_2={\displaystyle \frac{b_1{a}_2-b_3{c}_1}{c_1{c}_2-a_1{a}_2}},R_1={\displaystyle \frac{a_1{b}_4-b_2{c}_2}{c_1{c}_2-a_1{a}_2}},R_2={\displaystyle \frac{a_2{b}_2-b_4{c}_1}{c_1{c}_2-a_1{a}_2}}.\hfill \end{array}$$

By inserting (8) into the remaining two relations in (7), we obtain

$$\begin{array}{c}{R}_3+M_1{y}^{*}+N_1{z}^{*}=d_1+{\displaystyle \frac{f_1{z}^{*}}{1+k_1{y}^{*}+k_2{z}^{*}}},\hfill \\ R_4+M_2{y}^{*}+N_2{z}^{*}+{\displaystyle \frac{f_2{y}^{*}}{1+k_1{y}^{*}+k_2{z}^{*}}}=d_1,\hfill \end{array}$$

(9)

where

$$\begin{array}{c}{R}_3=e_1{T}_1+e_2{T}_2,R_4=e_3{T}_1+e_4{T}_2,N_1=e_1{R}_1+e_2{R}_2,\hfill \\ N_2=e_3{R}_1+e_4{R}_2,M_1=e_1{Q}_1+e_2{Q}_2,M_2=e_3{Q}_1+e_4{Q}_2.\hfill \end{array}$$

Using Equation (9), we numerically demonstrate the existence of positive solutions $y^{*},z^{*}$ through numerical simulations with $y^{*},z^{*}$ as the horizontal and vertical coordinates, respectively. The results are presented in Figure 1.

From the above analysis and Figure 1, we can conclude that the coexisting equilibrium $E_{*}=(x_1^{*},x_2^{*},y^{*},z^{*})$ exists if Hypotheses 1 and 2 are satisfied.

Next, we establish the local asymptotic stability of the coexisting equilibrium $E_{*}=(x_1^{*},x_2^{*},y^{*},z^{*})$ of system (1).

The Jacobian matrix of system (1) evaluated at the coexisting equilibrium $E_{*}$ is given by the following block structure:

$$J_{E^{*}}=\left[\begin{array}{cccc}{k}_{11}\hfill & k_{12}\hfill & k_{13}\hfill & k_{14}\hfill \\ k_{21}\hfill & k_{22}\hfill & k_{23}\hfill & k_{24}\hfill \\ k_{31}\hfill & k_{32}\hfill & k_{33}\hfill & k_{34}\hfill \\ k_{41}\hfill & k_{42}\hfill & k_{43}\hfill & k_{44}\hfill \end{array}\right],$$

where

$$\begin{array}{c}{k}_{11}=r_1-a_1{x}_2^{*}-b_1{y}^{*}-b_2{z}^{*}-2c_1{x}_1^{*},\hfill \\ k_{12}=-a_1{x}_2^{*},k_{13}=-b_1{x}_1^{*},k_{14}=-b_2{x}_1^{*},k_{21}=-a_2{x}_2^{*},\hfill \\ k_{22}=r_2-a_2{x}_1^{*}-b_3{y}^{*}-b_4{z}^{*}-2c_2{x}_2^{*},k_{23}=-b_3{y}^{*},k_{24}=-b_4{x}_2^{*},\hfill \\ k_{31}=e_1{y}^{*},k_{32}=e_2{y}^{*},k_{33}=e_1{x}_1^{*}+e_2{x}_2^{*}-{\displaystyle \frac{f_1{z}^{*}(1+k_2{z}^{*})}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}}-d_1,\hfill \\ k_{34}=-{\displaystyle \frac{f_1{y}^{*}(1+k_1{y}^{*})}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}},k_{41}=e_3{z}^{*},k_{42}=e_4{z}^{*},\hfill \\ k_{43}={\displaystyle \frac{f_2{z}^{*}(1+k_2{z}^{*})}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}},k_{44}=e_3{x}_1^{*}+e_4{x}_2^{*}+{\displaystyle \frac{f_2{y}^{*}(1+k_1{y}^{*})}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}}-d_2.\hfill \end{array}$$

Consequently, the characteristic equation corresponding to the linearized system (denoted as Equation (10)) assumes the following form:

$$\begin{array}{c}{\lambda }^4+B_1{\lambda }^3+B_2{\lambda }^2+B_3\lambda +B_4=0,\hfill \end{array}$$

(10)

where

$$\begin{array}{c}{B}_1=-(k_{11}+k_{22}+k_{33}+k_{44}),\hfill \\ B_2={\displaystyle \sum _{i<j}}(k_{ii}{k}_{jj}-k_{ij}{k}_{ji}),\hfill \\ B_3=-{\displaystyle \sum _{i<j<l}}\left|\begin{array}{ccc}{k}_{ii}& k_{ij}& k_{il}\\ k_{ji}& k_{jj}& k_{jl}\\ k_{li}& k_{lj}& k_{ll}\end{array}\right|,\hfill \\ B_4=\left|\begin{array}{cccc}{k}_{11}& k_{12}& k_{13}& k_{14}\\ k_{21}& k_{22}& k_{23}& k_{24}\\ k_{31}& k_{32}& k_{33}& k_{34}\\ k_{41}& k_{42}& k_{43}& k_{44}\end{array}\right|.\hfill \end{array}$$

Through application of Hypotheses 1–3 and the Routh–Hurwitz criterion, we establish that all roots of the characteristic Equation (10) possess strictly negative real parts. Consequently, the coexisting equilibrium $E_{*}$ is locally asymptotically stable in the absence of time delay $\tau =0$. This completes the proof. □

4. Hopf Bifurcation

In this section, we discuss the Hopf bifurcation of system (1). To derive the Hopf bifurcation of the system, we first present the necessary preliminary work and conduct key discussions and analyses prior to drawing conclusions about the Hopf bifurcation.

To enhance analytical tractability, we implement the following coordinate transformation:

$$\begin{array}{c}{x}_1=u_1+x_1^{*},x_2=u_2+x_2^{*},y=v+y^{*},z=w+z^{*}.\hfill \end{array}$$

Under this transformation, system (1) takes the following equivalent form:

$$\begin{array}{c}{}^{c}D^q{x}_1\left(t\right)=\left(u_1\left(t\right)+x_1^{*}\right)\left[r_1-a_1(u_2\left(t\right)+x_2^{*})-b_1(v\left(t\right)+y^{*})-b_2(w\left(t\right)+z^{*})-c_1(u_1\left(t\right)+x_1^{*})\right],\hfill \\ {}^{c}D^q{x}_2\left(t\right)=\left(u_2\left(t\right)+x_2^{*}\right)\left[r_2-a_2(u_1\left(t\right)+x_1^{*})-b_3(v\left(t\right)+y^{*})-b_4(w\left(t\right)+z^{*})-c_2(u_2\left(t\right)+x_2^{*})\right],\hfill \\ {}^{c}D^{q}y\left(t\right)=\left(v\left(t\right)+y^{*}\right)\left[e_1(u_1\left(t\right)+x_1^{*})+e_2(u_2\left(t\right)+x_2^{*})-{\displaystyle \frac{f_1(w(t-\tau )+z^{*})}{1+k_1(v(t-\tau )+y^{*})+k_2(w(t-\tau )+z^{*})}}-d_1\right],\hfill \\ {}^{c}D^{q}z\left(t\right)=\left(w\left(t\right)+z^{*}\right)\left[e_3(u_1\left(t\right)+x_1^{*})+e_4(u_2\left(t\right)+x_2^{*})+{\displaystyle \frac{f_2(v(t-\tau )+y^{*})}{1+k_1(v(t-\tau )+y^{*})+k_2(w(t-\tau )+z^{*})}}-d_2\right].\hfill \end{array}$$

Consequently, we obtain the following principal result:

$$\begin{array}{c}{}^{c}D^q{u}_1\left(t\right)=h_{11}{u}_1\left(t\right)+h_{12}{u}_2\left(t\right)+h_{13}v\left(t\right)+h_{14}w\left(t\right),\hfill \\ {}^{c}D^q{u}_2\left(t\right)=h_{21}{u}_1\left(t\right)+h_{22}{u}_2\left(t\right)+h_{23}v\left(t\right)+h_{24}w\left(t\right),\hfill \\ {}^{c}D^{q}v\left(t\right)=h_{31}{u}_1\left(t\right)+h_{32}{u}_2\left(t\right)+h_{33}v\left(t\right)+p_{33}v(t-\tau )+p_{34}w(t-\tau ),\hfill \\ {}^{c}D^{q}w\left(t\right)=h_{41}{u}_1\left(t\right)+h_{42}{u}_2\left(t\right)+h_{44}w\left(t\right)+p_{43}v(t-\tau )+p_{44}w(t-\tau ).\hfill \end{array}$$

(11)

where

$$\begin{array}{c}{h}_{11}=r_1-a_1{x}_2^{*}-b_1{y}^{*}-b_2{z}^{*}-2c_1{x}_1^{*},h_{12}=-a_1{x}_1^{*},h_{13}=-b_1{x}_1^{*},\hfill \\ h_{14}=-b_2{x}_1^{*},h_{21}=-a_2{x}_2^{*},h_{22}=r_2-a_2{x}_1^{*}-b_3{y}^{*}-b_4{z}^{*}-2c_2{x}_2^{*},\hfill \\ h_{23}=-b_3{x}_2^{*},h_{24}=-b_4{x}_2^{*},h_{31}=e_1{y}^{*},h_{32}=e_2{y}^{*},\hfill \\ h_{33}=e_1{x}_1^{*}+e_2{x}_2^{*}-{\displaystyle \frac{f_1{z}^{*}}{1+k_1{y}^{*}+k_2{z}^{*}}}-d_1,h_{41}=e_3{z}^{*},h_{42}=e_4{z}^{*},\hfill \\ h_{44}=e_3{x}_1^{*}+e_4{x}_2^{*}-{\displaystyle \frac{f_2{y}^{*}}{1+k_1{y}^{*}+k_2{z}^{*}}}-d_2,p_{33}={\displaystyle \frac{f_1{k}_1{y}^{*}{z}^{*}}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}},\hfill \\ p_{34}={\displaystyle \frac{f_1{y}^{*}(1+k_1{y}^{*})}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}},p_{43}={\displaystyle \frac{f_2{z}^{*}(1+k_2{z}^{*})}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}},p_{44}=-{\displaystyle \frac{f_2{k}_2{y}^{*}{z}^{*}}{{(1+k_1{y}^{*}+k_2{z}^{*})}^2}}.\hfill \end{array}$$

Using the Laplace transform $\mathcal{L}\left(u_1\left(t\right)\right)=U_1\left(s\right),\mathcal{L}\left(u_2\left(t\right)\right)=U_2\left(s\right),\mathcal{L}\left(v\left(t\right)\right)=V\left(s\right),\mathcal{L}\left(w\left(t\right)\right)=W\left(s\right)$ on (11), we can get

$$\begin{array}{cc}\hfill s^q{U}_1\left(s\right)-s^{q-1}{u}_1\left(0\right)& =h_{11}{U}_1\left(s\right)+h_{12}{U}_2\left(s\right)+h_{13}V\left(s\right)+h_{14}W\left(s\right),\hfill \\ \hfill s^q{U}_2\left(s\right)-s^{q-1}{u}_2\left(0\right)& =h_{21}{U}_1\left(s\right)+h_{22}{U}_2\left(s\right)+h_{23}V\left(s\right)+h_{24}W\left(s\right),\hfill \\ \hfill s^{q}V\left(s\right)-s^{q-1}v\left(0\right)& =h_{31}{U}_1\left(s\right)+h_{32}{U}_2\left(s\right)+h_{33}V\left(s\right)\hfill \\ \hfill & +p_{33}{e}^{-s\tau }\left(V\left(s\right)+{\int }_{-\tau }^0{e}^{-st}v\left(t\right)dt\right)\hfill \\ \hfill & +p_{34}{e}^{-s\tau }\left(W\left(s\right)+{\int }_{-\tau }^0{e}^{-st}w\left(t\right)dt\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill s^{q}W\left(s\right)-s^{q-1}w\left(0\right)& =h_{41}{U}_1\left(s\right)+h_{42}{U}_2\left(s\right)+h_{44}W\left(s\right)\hfill \\ \hfill & +p_{34}{e}^{-s\tau }\left(V\left(s\right)+{\int }_{-\tau }^0{e}^{-st}v\left(t\right)dt\right)\hfill \\ \hfill & +p_{44}{e}^{-s\tau }\left(W\left(s\right)+{\int }_{-\tau }^0{e}^{-st}w\left(t\right)dt\right).\hfill \end{array}$$

The characteristic equation corresponding to the linearized system (11) is expressed as

$$\begin{array}{c}|\Delta \left(s\right)|=\left|\begin{array}{cccc}{s}^q-h_{11}& -h_{12}& -h_{13}& -h_{14}\\ -h_{21}& s^q-h_{22}& -h_{23}& -h_{24}\\ -h_{31}& -h_{32}& s^q-h_{33}-p_{33}{e}^{-st}& -p_{34}{e}^{-st}\\ -h_{41}& -h_{42}& -p_{43}{e}^{-st}& s^q-h_{44}-p_{44}{e}^{-st}\end{array}\right|=0.\hfill \end{array}$$

(12)

Equation (12) can be reformulated as follows:

$$\begin{array}{c}{\Gamma }_1\left(s\right)+{\Gamma }_2\left(s\right)e^{-st}=0,\hfill \end{array}$$

(13)

where

$$\begin{array}{cc}\hfill {\Gamma }_1\left(s\right)=& s^{4q}+s^{3q}(-h_{11}-h_{22}-h_{33}-h_{44})\hfill \\ \hfill & +s^{2q}(h_{11}{h}_{22}+h_{11}{h}_{33}+h_{11}{h}_{44}+h_{22}{h}_{33}+h_{22}{h}_{44}+h_{33}{h}_{44}\hfill \\ \hfill & -h_{12}{h}_{21}-h_{13}{h}_{31}-h_{14}{h}_{41}-h_{23}{h}_{32}-h_{24}{h}_{42}-h_{34}{h}_{43})\hfill \\ \hfill & +s^q(h_{11}{h}_{22}{h}_{33}-h_{11}{h}_{22}{h}_{44}-h_{11}{h}_{33}{h}_{44}-h_{22}{h}_{33}{h}_{44}\hfill \\ \hfill & +h_{11}{h}_{23}{h}_{32}+h_{11}{h}_{24}{h}_{42}+h_{22}{h}_{13}{h}_{31}+h_{22}{h}_{14}{h}_{41}\hfill \\ \hfill & +h_{33}{h}_{12}{h}_{21}+h_{33}{h}_{14}{h}_{41}+h_{44}{h}_{12}{h}_{21}+h_{44}{h}_{13}{h}_{31}\hfill \\ \hfill & +h_{12}{h}_{24}{h}_{41}+h_{13}{h}_{34}{h}_{41}+h_{14}{h}_{31}{h}_{43}+h_{21}{h}_{33}{h}_{42})\hfill \\ \hfill & +h_{11}{h}_{22}{h}_{33}{h}_{44}-h_{11}{h}_{22}{h}_{34}{h}_{43}-h_{11}{h}_{23}{h}_{32}{h}_{44}\hfill \\ \hfill & -h_{11}{h}_{24}{h}_{33}{h}_{42}+h_{11}{h}_{24}{h}_{32}{h}_{43}+h_{12}{h}_{21}{h}_{33}{h}_{44}\hfill \\ \hfill & -h_{12}{h}_{21}{h}_{34}{h}_{43}-h_{12}{h}_{23}{h}_{31}{h}_{44}+h_{12}{h}_{24}{h}_{31}{h}_{43}\hfill \\ \hfill & -h_{13}{h}_{21}{h}_{32}{h}_{44}+h_{13}{h}_{24}{h}_{31}{h}_{42}+h_{14}{h}_{21}{h}_{32}{h}_{43}\hfill \\ \hfill & -h_{14}{h}_{22}{h}_{31}{h}_{43}-h_{14}{h}_{23}{h}_{31}{h}_{42}.\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\Gamma }_2\left(s\right)=& s^{2q}(p_{33}+p_{44})\hfill \\ \hfill & +s^q(-h_{11}{p}_{33}-h_{11}{p}_{44}-h_{22}{p}_{33}-h_{22}{p}_{44}-h_{33}{p}_{44}\hfill \\ \hfill & -h_{44}{p}_{33}+p_{34}{h}_{43}+p_{43}{h}_{34})\hfill \\ \hfill & +h_{11}{h}_{22}{p}_{33}+h_{11}{h}_{22}{p}_{44}+h_{11}{h}_{33}{p}_{44}+h_{22}{h}_{33}{p}_{44}\hfill \\ \hfill & +h_{11}{h}_{44}{p}_{33}+h_{22}{h}_{44}{p}_{33}-h_{11}{h}_{23}{p}_{43}-h_{11}{h}_{24}{p}_{34}\hfill \\ \hfill & -h_{22}{h}_{13}{p}_{43}-h_{22}{h}_{14}{p}_{34}-h_{12}{h}_{21}{p}_{33}-h_{12}{h}_{21}{p}_{44}\hfill \\ \hfill & -h_{11}{p}_{34}{h}_{42}-h_{22}{p}_{34}{h}_{41}-h_{12}{h}_{24}{p}_{33}+h_{14}{h}_{21}{p}_{34}.\hfill \end{array}$$

denoted as

$$\begin{array}{c}{\Gamma }_1\left(s\right)=s^{4q}+m_1{s}^{3q}+m_2{s}^{2q}+m_3{s}^q+m_4,\hfill \\ {\Gamma }_2\left(s\right)=m_5{s}^{3q}+m_6{s}^{2q}+m_7{s}^q+m_8.\hfill \end{array}$$

Suppose the pure imaginary root of Equation (13) is $s=i\omega$ ($\omega >0$). Substituting $s=i\omega$ into Equation (13) and equating the real and imaginary parts separately, we derive the following expressions:

$$\begin{array}{cc}\hfill & {\left(iw\right)}^{4q}+m_1{\left(iw\right)}^{3q}+m_2{\left(iw\right)}^{2q}+m_3{\left(iw\right)}^q+m_4\hfill \\ \hfill & +\left(m_5{\left(iw\right)}^{3q}+m_6{\left(iw\right)}^{2q}+m_6\right)e^{-i\widehat{i}\tau }=0\hfill \\ \hfill & w^{4q}\left(cos2q\pi +isin2q\pi \right)\hfill \\ \hfill & +m_1{w}^{3q}\left(cos{\displaystyle \frac{3q\pi }{2}}+isin{\displaystyle \frac{3q\pi }{2}}\right)\hfill \\ \hfill & +m_2{w}^{2q}\left(cos\left(q\pi \right)+isin\left(q\pi \right)\right)\hfill \\ \hfill & +m_3{w}^q\left(cos{\displaystyle \frac{q\pi }{2}}+isin{\displaystyle \frac{q\pi }{2}}\right)+m_4\hfill \\ \hfill & +m_5\left(cos{\displaystyle \frac{3q\pi }{2}}+isin{\displaystyle \frac{3q\pi }{2}}\right)(cos\left(w\tau \right)-isin\left(w\tau \right))\hfill \\ \hfill & +m_6\left(cos\left(q\pi \right)+isin\left(q\pi \right)\right)(cos\left(w\tau \right)-isin\left(w\tau \right))\hfill \\ \hfill & +m_7\left(cos{\displaystyle \frac{q\pi }{2}}+isin{\displaystyle \frac{q\pi }{2}}\right)(cos\left(w\tau \right)-isin\left(w\tau \right))\hfill \\ \hfill & +m_8(cos\left(w\tau \right)-isin\left(w\tau \right))=0.\hfill \end{array}$$

The resulting expression can be decomposed into its respective real and imaginary components as follows:

$$\begin{array}{c}{E}_{1}cos\left(w\tau \right)+F_{1}sin\left(w\tau \right)=-E_2,\hfill \\ F_{1}cos\left(w\tau \right)-E_{1}sin\left(w\tau \right)=-F_2,\hfill \end{array}$$

where

$$\begin{array}{c}{E}_1=m_{5}cos\left({\displaystyle \frac{3q\pi }{2}}\right)+m_{6}cos\left(q\pi \right)+m_{7}cos\left({\displaystyle \frac{q\pi }{2}}\right)+m_8,\hfill \\ E_2=w^{4q}cos\left(2q\pi \right)+m_1{w}^{3q}cos{\displaystyle \frac{3q\pi }{2}}+m_2{w}^{2q}cos\left(q\pi \right)+m_3{w}^{q}cos{\displaystyle \frac{q\pi }{2}}+m_4,\hfill \\ F_1=m_{5}sin\left({\displaystyle \frac{3q\pi }{2}}\right)+m_{6}sin\left(q\pi \right)+m_{7}sin\left({\displaystyle \frac{q\pi }{2}}\right),\hfill \\ F_2=w^{4q}sin\left(2q\pi \right)+m_1{w}^{3q}sin{\displaystyle \frac{3q\pi }{2}}+m_2{w}^{2q}sin\left(q\pi \right)+m_3{w}^{q}sin{\displaystyle \frac{q\pi }{2}}.\hfill \end{array}$$

We obtain

$$\begin{array}{c}cos\left(w\tau \right)=-{\displaystyle \frac{E_1{E}_2+F_1{F}_2}{E_1{}^2+F_1^2}}=g_1\left(w\right),\hfill \\ sin\left(w\tau \right)={\displaystyle \frac{E_1{F}_2-E_2{F}_1}{E_1{}^2+F_1^2}}=g_2\left(w\right),\hfill \end{array}$$

using the Pythagorean trigonometric identity ${sin}^2\left(w\tau \right)+{cos}^2\left(w\tau \right)=1$ and derive the following relationship:

$$g_1^2\left(w\right)+g_2^2\left(w\right)=1,$$

where $g_1\left(w\right)=cos\left(w\tau \right)$. Solving for the time delay $\tau$ from the argument of the cosine function, we obtain the following family of solutions:

$${\tau }^{\left(k\right)}={\displaystyle \frac{1}{w}}\left[arccos{g}_1\left(w\right)+2k\pi \right](k=0,1,2,\dots ),$$

where k indexes the countably infinite set of periodic solutions induced by the cosine functions periodicity.

The critical delay value triggering a Hopf bifurcation is characterized by the smallest positive solution in this family, defined as

$${\tau }_0=min\left\{{\tau }^{\left(k\right)}\mid k\in {\mathbb{N}}_0\right\},$$

where ${\mathbb{N}}_0=\{0,1,2,\dots \}$ denotes the set of non-negative integers. This value ${\tau }_0$ represents the smallest delay parameter for which pure imaginary roots exist, serving as the bifurcation threshold for the emergence of oscillatory behavior in the system.

For characterizing the emergence of Hopf bifurcations, we introduce the following necessary condition as our working hypothesis:

Hypothesis 4. 

${\displaystyle \frac{X_1{Y}_1+X_2{Y}_2}{Y_1^2+Y_2^2}}\ne 0$ where the expressions for $X_i$ and $Y_i$ ($i=1,2$) are defined in (14).

Theorem 4. 

Let $s\left(\tau \right)=\alpha \left(\tau \right)+i\eta \left(\tau \right)$ denote the root of (12) such that near the critical delay $\tau ={\tau }_0$, it satisfies $\alpha \left({\tau }_0\right)=0$ and $\eta \left({\tau }_0\right)={\eta }_0$, where ${\eta }_0>0$ is the angular frequency at the bifurcation point. Under these conditions and by Hypothesis 4, the transversal condition

$${\left.Re\left[{\displaystyle \frac{ds}{d\tau }}\right]\right|}_{(\tau ={\tau }_0,\omega ={\omega }_0)}\ne 0$$

is satisfied, ensuring that the eigenvalue crosses the imaginary axis with non-zero speed as τ varies through ${\tau }_0$.

Proof. 

The verification of the transversality condition for Hopf bifurcation is carried out by differentiating both sides of the characteristic Equation (13) relative to the time delay $\tau$, which gives

$$\begin{array}{c}{\Gamma }_1^{\prime }\left(s\right){\displaystyle \frac{ds}{d\tau }}+{\Gamma }_2^{\prime }\left(s\right){\displaystyle \frac{ds}{d\tau }}{e}^{-s\tau }-\tau {\Gamma }_2\left(s\right){\displaystyle \frac{ds}{d\tau }}{e}^{-s\tau }-s{\Gamma }_2\left(s\right)e^{-s\tau }=0,\hfill \end{array}$$

simplified to

$$\begin{array}{c}{\displaystyle \frac{ds}{d\tau }=\frac{s{\Gamma }_2\left(s\right)e^{-s\tau }}{{\Gamma }_1^{\prime }\left(s\right)+{\Gamma }_2{}^{\prime }\left(s\right)e^{-s\tau }-\tau {\Gamma }_2\left(s\right)e^{-s\tau }},}\hfill \end{array}$$

As stipulated by Hypothesis 4, we obtain

$$\begin{array}{c}{\displaystyle Re\left[\frac{ds}{d\tau }\right]=\frac{X_1{Y}_1+X_2{Y}_2}{Y_1^2+Y_2^2}\ne 0,}\hfill \end{array}$$

where

$$\begin{array}{c}{X}_1=Re\left[{\Gamma }_2\left(i{w}_0\right)e^{-i{w}_0{\tau }_0}i{w}_0\right],\hfill \\ X_2=Im\left[{\Gamma }_2\left(i{w}_0\right)e^{-i{w}_0{\tau }_0}i{w}_0\right],\hfill \\ Y_1=Re\left[{\Gamma }_1^{\prime }\left(i{w}_0\right)+{\Gamma }_2^{\prime }\left(i{w}_0\right)e^{-i{w}_0{\tau }_0}-{\Gamma }_2\left(i{w}_0\right)e^{-i{w}_0{\tau }_0}{\tau }_0\right],\hfill \\ Y_2=Im\left[{\Gamma }_1^{\prime }\left(i{w}_0\right)+{\Gamma }_2^{\prime }\left(i{w}_0\right)e^{-i{w}_0{\tau }_0}-{\Gamma }_2\left(i{w}_0\right)e^{-i{w}_0{\tau }_0}{\tau }_0\right].\hfill \end{array}$$

(14)

This concludes the proof. □

Based on the above discussions, analyses, and Theorem 3, we draw the following summary conclusions.

Theorem 5. 

The subsequent results for system (1) are established under Hypotheses 1–4:

(i) 

If τ$\in [0,{\tau }_0)$, then the $E_{*}$ of system (1) is asymptotically stable.

(ii) 

The $E_{*}$ of system (1) is unstable when $\tau >{\tau }_0.$

(iii) 

If $\tau ={\tau }_0$, then system (1) undergoes a Hopf bifurcation.

5. Numerical Simulations

This section implements numerical simulations to both validate the theoretical results and systematically examine the fractional order’s role in bifurcation onset. The following parameter values are used in our computations:

$$\begin{array}{c}{r}_1=1.8,r_2=1.5,a_1=0.15,a_2=0.15,b_1=0.18,b_2=0.05,b_3=0.05,\hfill \\ b_4=0.18,c_1=0.3,c_2=0.3,e_1=0.35,e_2=0.2,e_3=0.2,e_4=0.35,\hfill \\ d_1=0.5,d_2=0.5,f_1=0.01,f_2=0.01,k_1=0.12,k_2=0.08.\hfill \end{array}$$

(15)

Through direct computation, we verify that Hypotheses 1–4 are satisfied under the specified parameter configuration. The coexisting equilibrium point is numerically determined to be $E^{*}=(x_1^{*},x_2^{*},y^{*},z^{*})=(1.08,0.75,6.45,4.52)$, with existence rigorously confirmed through analytical and numerical methods. For our simulations, we adopt the initial condition vector $(x_1\left(0\right),x_2\left(0\right),y\left(0\right),z\left(0\right))=(1.8,2.5,1.2,1.5)$ to examine transient dynamics.

Case 1: A systematic investigation is conducted to examine the impact of fractional orders on the stability region of the system.

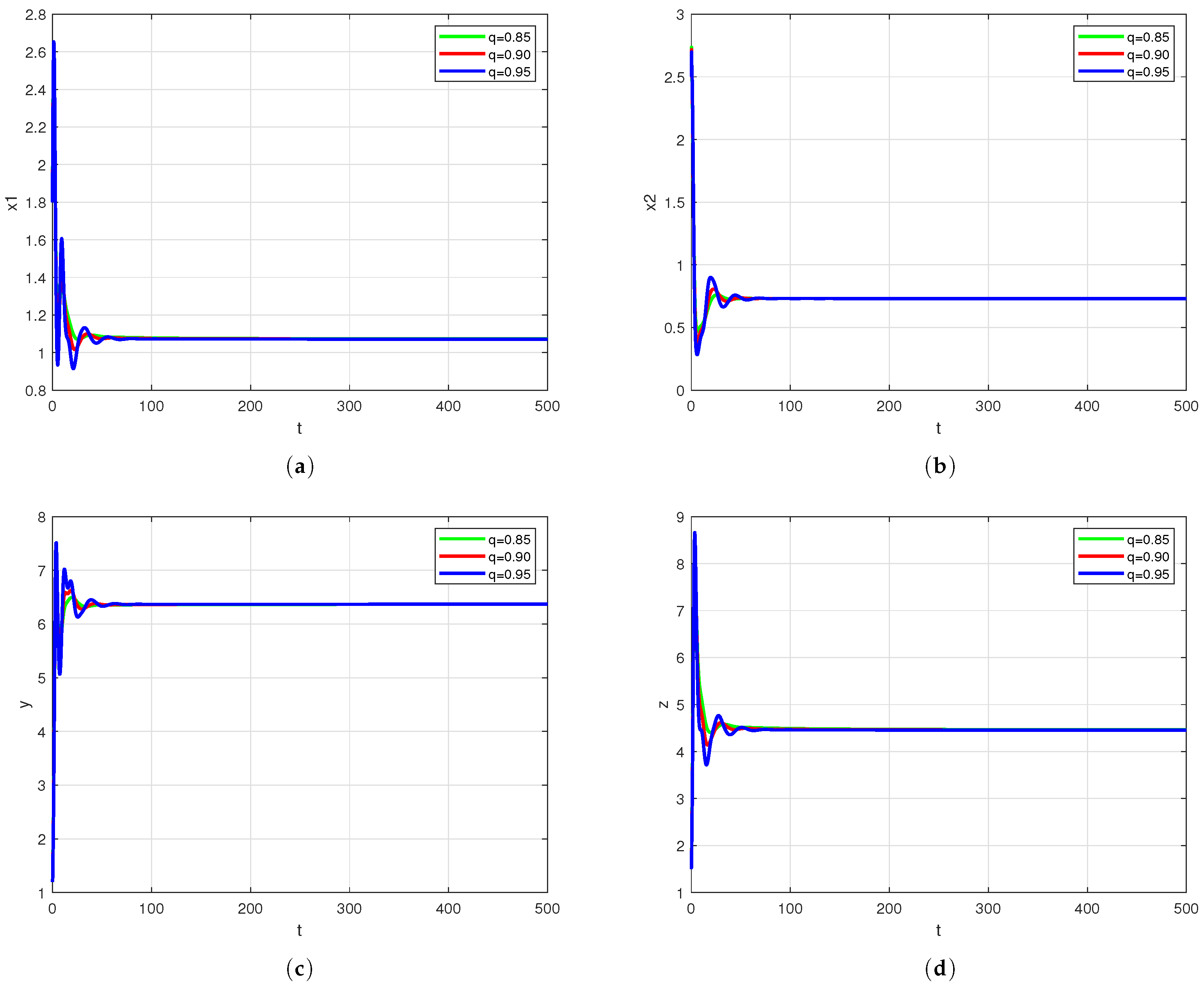
In the absence of time delay $\tau =0$, we first analyze how the fractional order influences the solution’s convergence rate toward equilibrium. Figure 2 illustrates the oscillatory behavior exhibited by system solutions for different fractional orders.

Figure 2 clearly illustrates the enhanced oscillatory behavior of solutions with increasing fractional order. A marked intensification in both amplitude and frequency is observed as the order rises from 0.85 to 0.95, demonstrating the fractional order’s pivotal influence on stability region modulation.

Figure 3 demonstrates the local asymptotic stability characteristics of the system’s equilibrium point for distinct fractional orders: Figure 3a–c correspond to q = 0.95, while Figure 3d–f illustrate the case for q = 0.99.

When fractional order $q=1.00$, the fractional-order dynamical system degenerates into an integer-order system. Given that the fractional-order system exhibits instability at $q=0.99$, its integer-order counterpart must be unstable under identical parametric conditions. This observation highlights that the stability region of the fractional-order system is significantly broader than that of its integer-order counterpart. From a biological perspective, this phenomenon can be interpreted as follows: the population dynamics incorporate a "memory effect," where historical behavioral patterns (analogous to the fractional-order system’s past-state dependence) influence current interactions. This inherent memory property, which is fundamentally embedded in fractional-order dynamical operators, mathematically encodes the biological mechanism whereby organisms utilize temporally integrated experience to adaptively regulate current behavioral responses. Such mnemonic dynamics confer significant evolutionary fitness benefits through two principal mechanisms:

(i)

Enhancement of population stability via historical state-dependent feedback;

(ii)

Improvement of ecological adaptability through continuous behavioral optimization.

Case 2: We systematically investigate how time delays affect the stability characteristics of the system and govern the emergence of Hopf bifurcations.

In this section, we systematically analyze the stability of equilibrium $E^{*}$ and the emergence of Hopf bifurcation by considering the time delay $\tau$ as the bifurcation parameter. For a fixed fractional order $q=0.80$, analytical determination of the characteristic equation yields the critical bifurcation threshold ${\tau }_0=1.405$. This computation establishes that system (1) experiences a Hopf bifurcation at equilibrium $E^{*}$ precisely when $\tau$ crosses the critical value ${\tau }_0=1.405$, as numerically verified in Figure 4a–d.

Consistent with Theorem 5, it follows that $E^{*}$ is locally asymptotically stable when the delay parameter $\tau =1.39$ is less than the critical value ${\tau }_0$. This stability is visualized in Figure 5a–c, which display the time series plots and phase portraits, respectively. Conversely, when $\tau =1.45$ exceeds ${\tau }_0$, $E^{*}$ loses stability, as illustrated in Figure 5d–f, where the corresponding time series and phase diagrams exhibit divergent behavior.

Remark 1. 

In comparing studies such as [13,14,15,16,17,18,19,21], the uniqueness and contributions of this study can be condensed into three aspects: First is ecological scenario innovation: Breaking through the existing simplified two/three-species framework, we constructed a four-species food web model including a top predator. This is the first study to analyze multi-trophic cascade effects and indirect interactions, focusing on the coupling mechanism between the fractional-order memory effect of the top predator and the B-D response and on a core ecological process that cannot be covered by low-species-number models. Second is the breakthrough in mathematical analysis: We coupled three elements ("four-species trophic structure, species-specific delays, and fractional derivatives"), abandoning the simplification of a single global delay. We derived the fractional characteristic equation and Hopf bifurcation criteria for the four-species system and revealed the bifurcation mechanism co-driven by "memory effect multiple delays trophic competition". The depth of mathematical treatment far exceeds that of existing studies on low-species-number and single-factor-driven systems. Third is this study’s value in advancing knowledge: It fills the gap in the dynamics of four-species fractional-order food webs. Theoretically, it clarifies the regulatory rules of memory–delay coupling on system stability; practically, it provides a quantitative basis for multi-species ecological management.

6. Conclusions

This study analyzes a 4D fractional-order delayed predator–prey model with B-D functional response. Using Caputo fractional derivatives (integrating memory effects for more realistic population dynamics than integer-order systems) and Laplace transforms (rigorously confirming solution boundedness and existence), it reveals that equilibrium behaviors depend on fractional order and time delay: the coexistence equilibrium $E_{*}$ is locally asymptotically stable under specific parameters if $\tau$ < ${\tau }_0$. Numerical simulations verify the model’s robustness.

Bifurcation analysis reveals Hopf bifurcation ($\tau >$ ${\tau }_0$), underscoring delays’ destabilizing role in memory-involved predator–prey interactions. Numerical tests show higher fractional orders boost oscillation amplitude/frequency, and the system has a wider stability range than integer-order counterparts emphasizing memory-driven dynamics’ biological significance. Its fractional derivative-embedded “memory effect” reflects real ecological adaptations, matching observations (e.g., predator foraging shaped by historical prey availability).

The findings of this study are significant for ecological modeling and conservation, especially in multi-species systems like grasslands. Its model integrates fractional calculus and time delays, providing a versatile framework for exploring complex trophic networks (including indirect interactions and delayed feedback). However, This model employs a single global delay ($\tau$) to characterize the time lag in ecological processes. The limitations of this simplifying assumption are primarily reflected in two core dimensions: ecological realism and dynamic analysis. First, at the ecological level: it fails to accurately distinguish species-specific time lag differences. In real grassland ecosystems, the key time-dependent processes of the four species exhibit significant heterogeneity; for instance, the resource response lag of prey and the foraging decision-making and digestive processing lags of predators all differ. However, a single global delay “averages out” these heterogeneous lags, making it difficult to precisely depict the time-dependent characteristics of different species. Second, at the dynamic level: it obscures the interactive regulatory effects between multiple delays. The single-delay assumption can only reveal the simple monotonic relationship of “delay magnitude system stability,” yet it cannot capture the potential synergistic (jointly exacerbating instability) or antagonistic (mutually offsetting disturbances) effects of various delays (such as predation lag and population feedback lag) in real ecological systems, which limits the in-depth analysis of the system’s complex dynamic mechanisms.

Future research will advance around model optimization and mechanism deepening: First, through incorporating multi-species-specific delays, the simplification bias of the single global delay will be addressed, and the ecological realism of the model will be significantly enhanced. Second, a sensitivity analysis covering the biologically plausible ranges of key parameters will be conducted to systematically verify the robustness of the conclusions and their universality boundaries beyond a single case. Finally, the application of the nonlinear B-D (Beddington–DeAngelis) functional response will be extended to all predators to construct a more comprehensive fractional-order predator–prey dynamic framework, with a focus on analyzing its core dynamic characteristics such as bifurcation and oscillation.