Iterative Investigation of the Nonlinear Fractional Cahn–Allen and Fractional Clannish Random Walker’s Parabolic Equations by Using the Hybrid Decomposition Method
Abstract
1. Introduction
Advantages and Disadvantages of the Hybrid Decomposition Method (HDM)
- Advantages:
- -
- Handles fractional operators naturally via the Laplace transform (clean initial condition embedding) and treats nonlinearity by decomposition, yielding rapidly convergent series with few terms.
- -
- Achieves low truncation/residual errors and robust performance across fractional orders ; recovers the classical model smoothly as .
- -
- Moderate computational cost; analytic-like series enable easy parameter sweeps and clear physical interpretation.
- -
- Avoids the full complexity of polynomial generation in purely ADM-type schemes; hybridization improves stability/accuracy.
- Disadvantages:
- -
- Convergence is problem- and domain-dependent; accuracy may deteriorate for large time/spatial ranges or strong nonlinearities unless more terms are retained.
- -
- Requires Laplace inversion and smooth data; complex boundary conditions, external forcing, or irregular geometries can complicate the pipeline.
- -
- Truncation-error control is empirical unless a contraction proof is available; residual checks are needed to certify accuracy.
- -
- Extension to higher dimensions or discontinuous solutions (e.g., shocks) can reduce efficiency and may require additional stabilization.
2. Preliminaries
2.1. Definition
2.2. Definition
2.3. Definition
2.4. Definition
3. Solution Procedure for FCRWP-Equation via HDM
4. Solution Procedure for the NFCA Equation via HDM
Theorem [3]
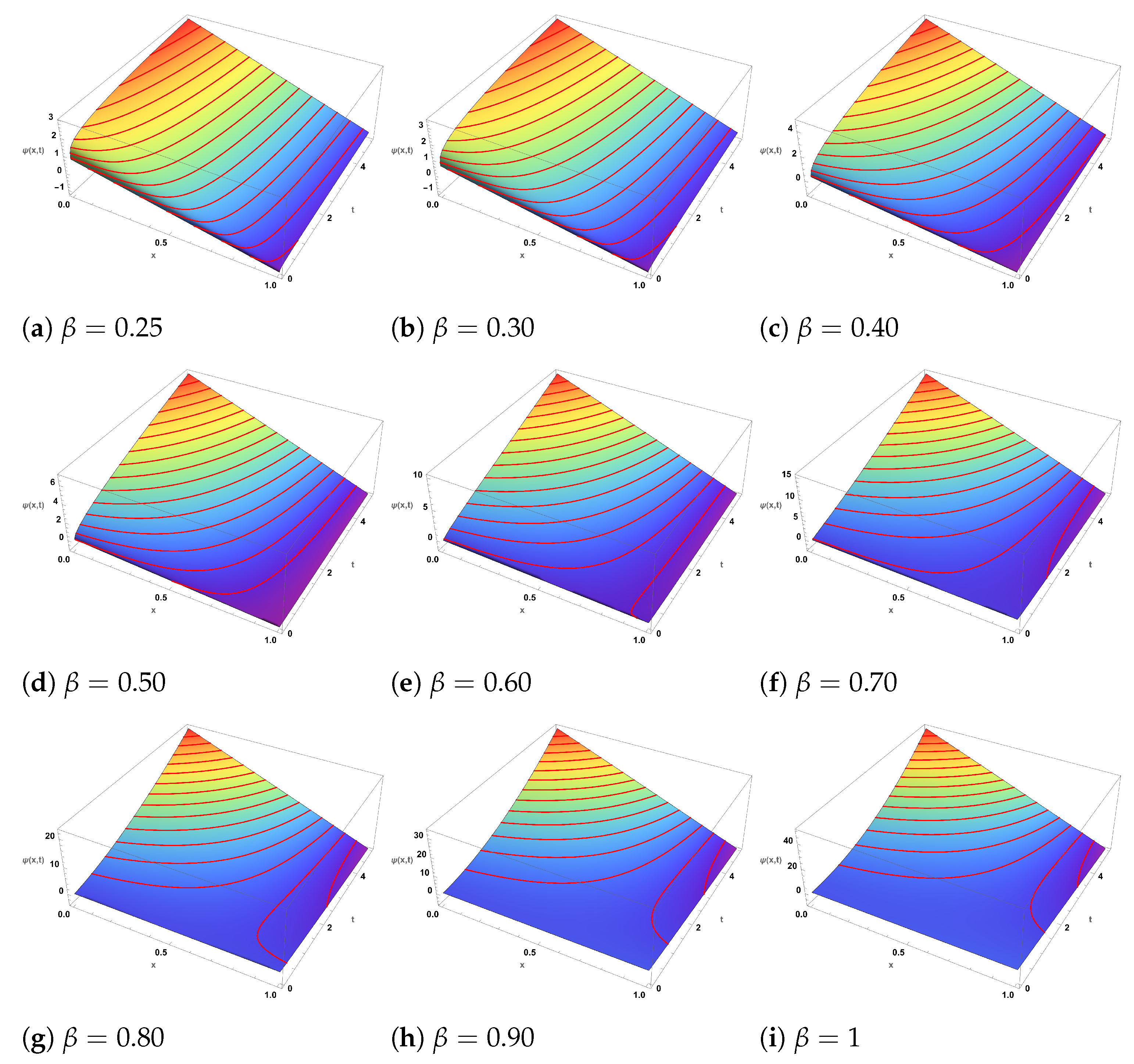
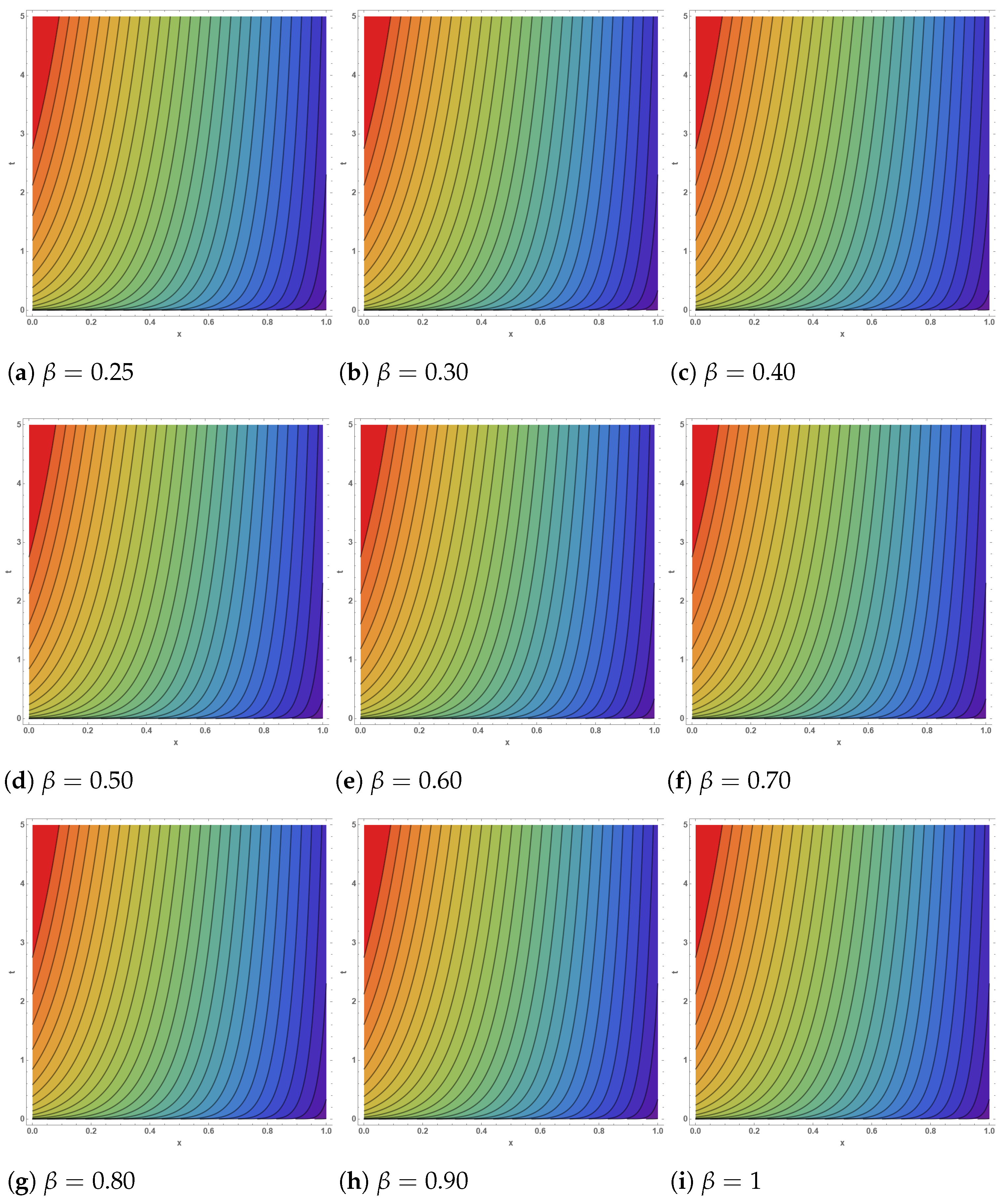
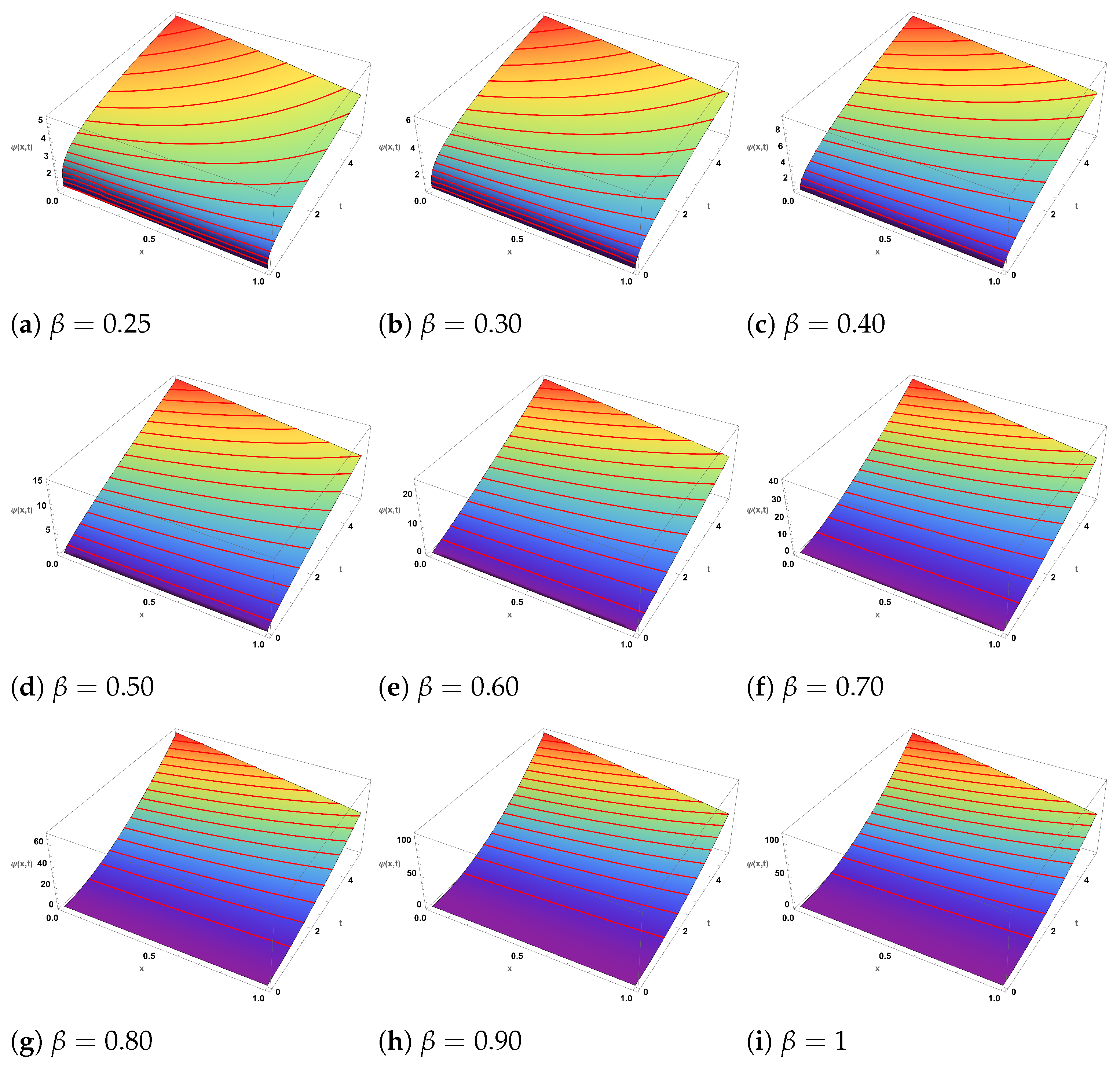
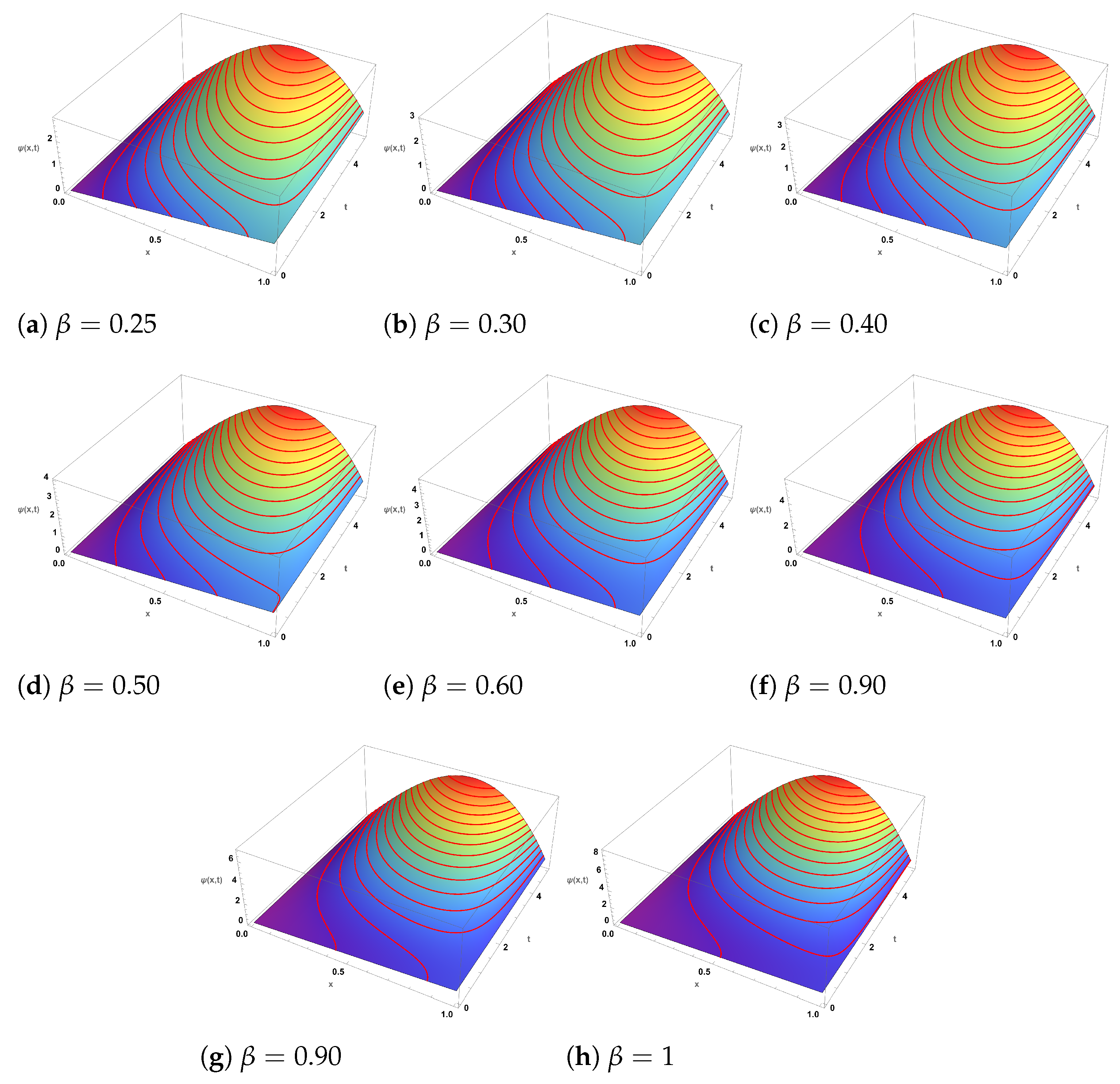
5. Discussion and Applications
5.1. Example
5.2. Example
5.3. Example
6. Error Analysis and Residual Verification
7. Comparative Numerical Discussion
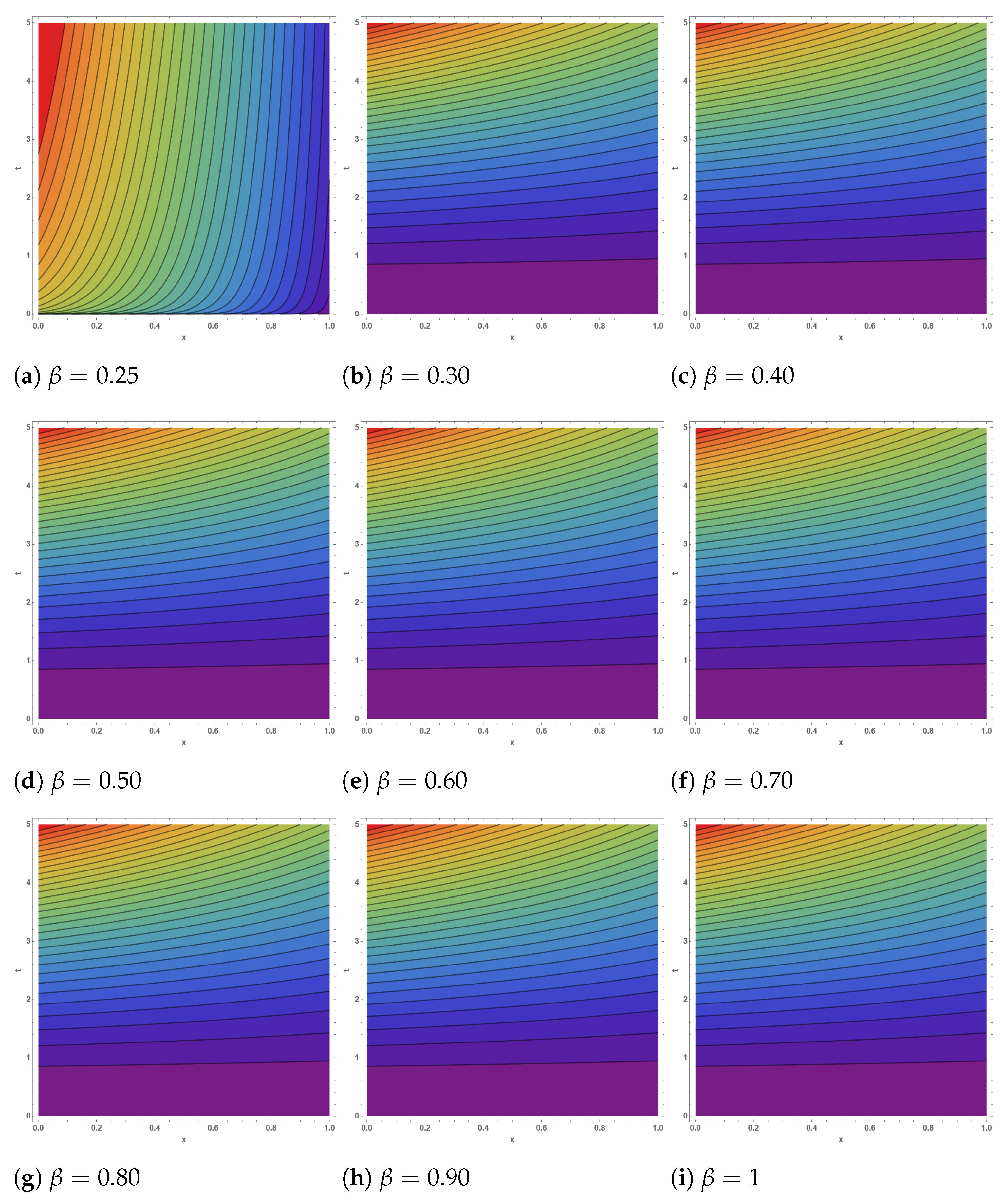
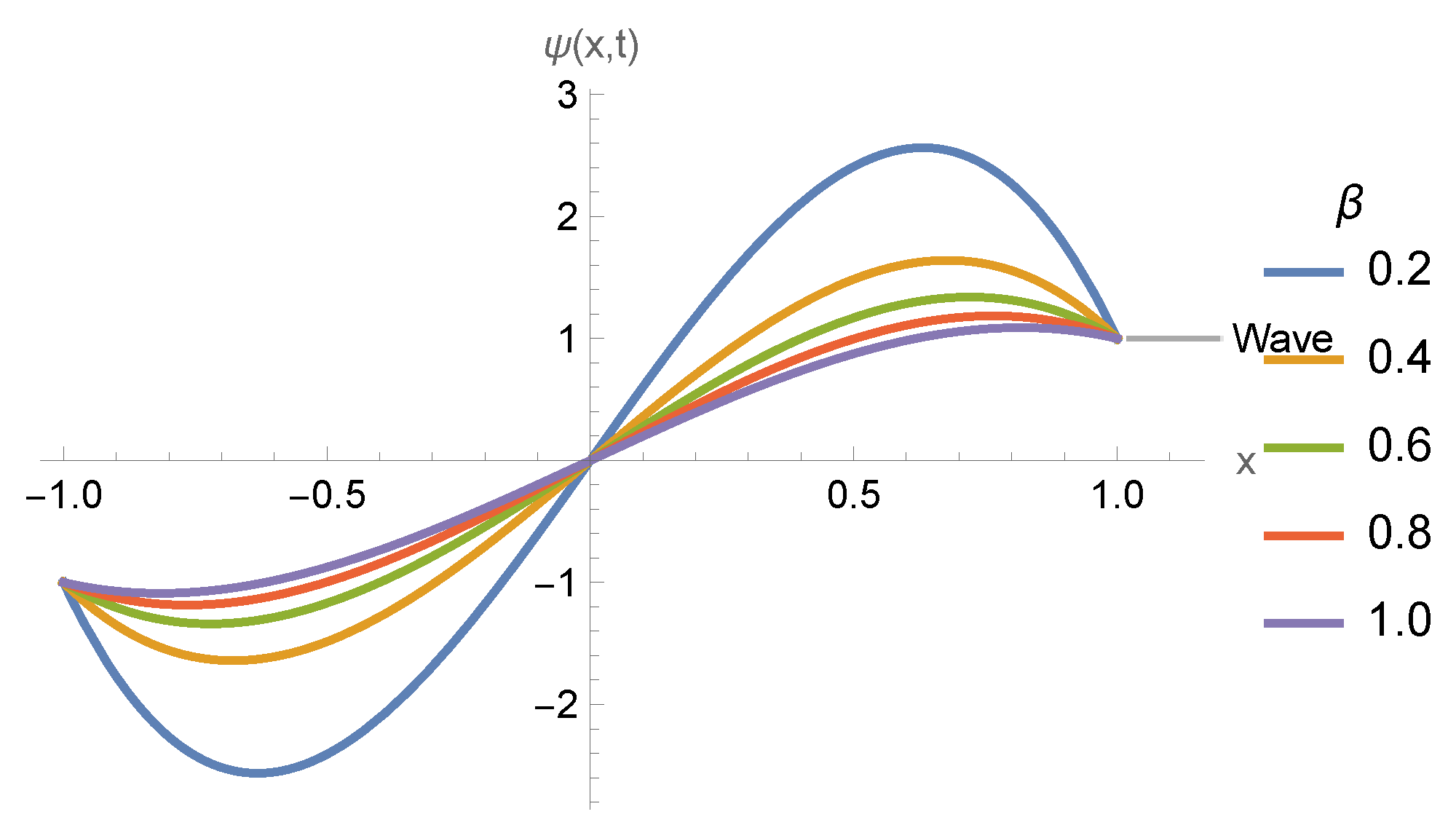
8. Physical Interpretation of the Fractional Order
9. Result and Observations
10. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seadawy, A.R.; Rizvi, S.T.; Mustafa, B.; Ali, K.; Althubiti, S. Chirped periodic waves for an cubic-quintic nonlinear Schrödinger equation with self steepening and higher order nonlinearities. Chaos Solitons Fractals 2022, 156, 111804. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Naqvi, S.K.; Althubiti, S. Multi lump and interaction solutions for Atangana conformable Boussinesq-like equation. Results Phys. 2022, 34, 105187. [Google Scholar] [CrossRef]
- Wang, G.; Ren, X.; Bai, Z.; Hou, W. Radial symmetry of standing waves for nonlinear fractional Hardy–Schrodinger equation. Appl. Math. Lett. 2019, 96, 131–137. [Google Scholar] [CrossRef]
- Chen, C.; Jiang, Y.; Wang, Z.; Wu, J. Dynamical behavior and exact solutions for time-fractional nonlinear Schrödinger equation with parabolic law nonlinearity. Optik 2020, 222, 165331. [Google Scholar] [CrossRef]
- Zheng, B.; Kai, Y.; Xu, W.; Yang, N.; Zhang, K.; Thibado, P.M. Exact traveling and non-traveling wave solutions of the time fractional reaction–diffusion equation. Phys. A 2019, 532, 121780. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Liu, W. The dynamic characteristics of pure-quartic solitons and soliton molecules. Appl. Math. Model. 2022, 102, 305–312. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, T.; Biswas, A.; Liu, W. Nonlinear control of logic structure of all-optical logic devices using soliton interactions. Nonlinear Dyn. 2022, 107, 1215–1222. [Google Scholar] [CrossRef]
- Zhang, R.F.; Li, M.C.; Gan, J.Y.; Li, Q.; Lan, Z.Z. Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Solitons Fractals 2022, 154, 111692. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Bibi, I.; Younis, M.; Bekir, A. Interaction properties of solitons for a couple of nonlinear evolution equations. Chin. Phys. B 2021, 30, 010502. [Google Scholar] [CrossRef]
- Rehman, H.U.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R.; Anwar, I.; Baber, M.Z.; Althobaiti, A. Weakly nonlinear electron-acoustic waves in the fluid ions propagated via a (3 + 1)-dimensional generalized Korteweg–de-Vries–Zakharov–Kuznetsov equation in plasma physics. Results Phys. 2022, 33, 105069. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M.; Alshomrani, A.S.; Baleanu, D. The deterministic and stochastic solutions of the Schrodinger equation with time conformable derivative in birefrigent fibers. AIMS Math. 2020, 5, 2326. [Google Scholar] [CrossRef]
- Aliyu, A.I.; Alshomrani, A.S.; Inc, M.; Baleanu, D. Optical solitons for TrikiBiswas equation by two analytic approaches. AIMS Math. 2020, 5, 1001. [Google Scholar] [CrossRef]
- Korpinar, Z.; Inc, M.; Baleanu, D. On the fractional model of Fokker-Planck equations with two different operator. AIMS Math. 2020, 5, 236. [Google Scholar] [CrossRef]
- Younas, U.; Younis, M.; Seadawy, A.R.; Rizvi, S.T.R.; Althobaiti, S.; Sayed, S. Diverse exact solutions for modified nonlinear Schrödinger equation with conformable fractional derivative. Results Phys. 2021, 20, 103766. [Google Scholar] [CrossRef]
- Akram, U.; Seadawy, A.R.; Rizvi, S.T.R.; Younis, M.; Althobaiti, S.; Sayed, S. Traveling wave solutions for the fractional Wazwaz–Benjamin–Bona–Mahony model in arising shallow water waves. Results Phys. 2021, 20, 103725. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Bilal, M.; Younis, M.; Rizvi, S.T.R.; Althobaiti, S. Analytical mathematical approaches for the double-chain model of DNA by a novel computational technique. Chaos Solitons Fractals 2021, 144, 110669. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rehman, S.; Younis, M.; Rizvi, S.T.R.; Althobaiti, S.; Makhlouf, M.M. Modulation instability analysis and longitudinal wave propagation in an elastic cylindrical rod modelled with Pochhammer-Chree equation. Phys. Scr. 2021, 96, 045202. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rizvi, S.T.R.; Ahmad, S.; Younis, M.; Baleanue, D. Lump, lump one stripe, multiwaves and breather solutions for the Hunter Sexton equation. Open Phys. 2021, 19, 1–20. [Google Scholar] [CrossRef]
- Chita, F.; Ayadi, S.; Erden Ege, M.; Ege, O.; Ramaswamy, R. A Novel Approach for Solving Fractional Differential Equations via a Multistage Telescoping Decomposition Method. Fractal Fract. 2025, 9, 65. [Google Scholar] [CrossRef]
- Chakraverty, S.; Jena, R.M. (Eds.) Computation and Modeling for Fractional Order Systems; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Amilo, D.; Sadri, K.; Hincal, E. Comparative analysis of Caputo and variable-order fractional derivative algorithms across various applications. Int. J. Appl. Comput. Math. 2025, 11, 80. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, İ. Examples and Applications of Global Fractional Differential Equations. In Fractional Differential and Integral Operators with Respect to a Function: Theory Methods and Applications; Springer Nature: Singapore, 2025; Volume 1, p. 409. [Google Scholar]
- Boukedroun, M.; Ayadi, S.; Chita, F.; Erden Ege, M.; Ege, O.; Ramaswamy, R. Solutions of Nonlinear Fractional-Order Differential Equation Systems Using a Numerical Technique. Axioms 2025, 14, 233. [Google Scholar] [CrossRef]
- Banihashemi, S.; Jafaria, H.; Babaei, A. A novel collocation approach to solve a nonlinear stochastic differential equation of fractional order involving a constant delay. Discret. Contin. Dyn. Syst.-S 2022, 15, 339. [Google Scholar] [CrossRef]
- Sharif, A.A. On psi-Caputo Fractional Nonlinear Volterra-Fredholm Integro-Differential Equations. Discontinuity Nonlinearity Complex. 2022, 11, 97–106. [Google Scholar]
- Banihashemi, S.; Jafari, H.; Babaei, A. A stable collocation approach to solve a neutral delay stochastic differential equation of fractional order. J. Comput. Appl. Math. 2022, 403, 113845. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Amin, A.Z.; Lopes, A.M.; Hashim, I.; Babatin, M.M. Shifted Fractional-Order Jacobi Collocation Method for Solving Variable-Order Fractional Integro-Differential Equation with Weakly Singular Kernel. Fractal Fract. 2022, 6, 19. [Google Scholar] [CrossRef]
- Tverdyi, D.; Parovik, R. Investigation of Finite-Difference Schemes for the Numerical Solution of a Fractional Nonlinear Equation. Fractal Fract. 2022, 6, 23. [Google Scholar] [CrossRef]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. A novel method for carbon emission forecasting based on Gompertz’s law and fractional grey model: Evidence from American industrial sector. Renew. Energy 2022, 181, 803–819. [Google Scholar] [CrossRef]
- Fendzi-Donfack, E.; Kumar, D.; Tala-Tebue, E.; Nana, L.; Nguenang, J.P.; Kenfack-Jiotsa, A. Construction of exotical soliton-like for a fractional nonlinear electrical circuit equation using differential-difference Jacobi elliptic functions sub-equation method. Results Phys. 2022, 32, 105086. [Google Scholar] [CrossRef]
- Arqu, O.A.; Al-Smadi, M.; Almusawa, H.; Baleanu, D.; Hayat, T.; Alhodaly, M.; Osman, M.S. A novel analytical algorithm for generalized fifth-order time-fractional nonlinear evolution equations with conformable time derivative arising in shallow water waves. Alex. Eng. J. 2022, 61, 5753–5769. [Google Scholar] [CrossRef]
- Rupa, M.L.; Aruna, K. Soliton solutions of time fractional seventh-order Korteweg–de Vries equations arises in applied sciences. Int. J. Appl. Comput. Math. 2025, 11, 119. [Google Scholar] [CrossRef]
- Rupa, M.L.; Aruna, K.; Raghavendar, K. Insights into the time fractional Belousov–Zhabotinsky system arises in thermodynamics. Int. J. Theor. Phys. 2024, 63, 222. [Google Scholar] [CrossRef]
- Rupa, M.L.; Aruna, K. Optical solitons of time fractional Kundu–Eckhaus equation and massive Thirring system arises in quantum field theory. Opt. Quantum Electron. 2024, 56, 460. [Google Scholar] [CrossRef]
- Manikandan, K.; Aravinthan, D.; Sudharsan, J.B.; Reddy, S.R.R. Soliton and rogue wave solutions of the space–time fractional nonlinear Schrödinger equation with PT-symmetric and time-dependent potentials. Optik 2022, 266, 169594. [Google Scholar] [CrossRef]
- Rupa, M.L.; Aruna, K. Optical soliton solutions of nonlinear time fractional Biswas–Milovic equation. Optik 2022, 270, 169921. [Google Scholar] [CrossRef]
- Rupa, M.L.; Aruna, K.; Raghavendar, K. The impact of time-fractional Cahn–Hilliard equation that arises during the process of digital picture reconstruction. Bol. Soc. Parana. Mat. 2025, 43. [Google Scholar] [CrossRef]
- Odabasi, M.; Misirli, E. On the solutions of the nonlinear fractional differential equations via the modified trial equation method. Math. Methods Appl. Sci. 2018, 41, 904–911. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A.; Unsal, O. Two reliable methods for solving the time fractional Clannish Random Walker’s Parabolic equation. Optik 2016, 127, 9571–9577. [Google Scholar] [CrossRef]
- Alam, M.; Talib, I.; Bazighifan, O.; Chalishajar, D.N.; Almarri, B. An Analytical Technique Implemented in the Fractional Clannish Random Walker’s Parabolic Equation with Nonlinear Physical Phenomena. Mathematics 2021, 9, 801. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Ali, A.; Raddadi, M.H. Exact and solitary wave solutions of conformable time fractional Clannish Random Walker’s Parabolic and Ablowitz-Kaup-Newell-Segur equations via modified mathematical methods. Results Phys. 2021, 26, 104374. [Google Scholar] [CrossRef]
- Atilgan, E.; Taşbozan, O.; Ali, K.U.R.T.; Mohyud-Din, S.T. Approximate Analytical Solutions of Conformable Time Fractional Clannish Random Walker’s Parabolic (CRWP) Equation and Modified Benjamin-Bona-Mahony (BBM) equation. Univers. J. Math. Appl. 2020, 3, 61–68. [Google Scholar]
- Wang, P.; Shan, W.; Wang, Y.; Li, Q. Lie symmetry analysis, explicit solutions and conservation laws of the time fractional Clannish Random Walker’s Parabolic equation. Mod. Phys. Lett. B 2021, 35, 2150074. [Google Scholar] [CrossRef]
- Korkmaz, A. Explicit exact solutions to some one-dimensional conformable time fractional equations. Waves Random Complex Media 2019, 29, 124–137. [Google Scholar] [CrossRef]
- Bulut, H. Exact solutions for some fractional nonlinear partial differential equations via Kudryashov method. Phys. Sci. 2013, 8, 24–63. [Google Scholar]
- Rawashdeh, M.S. A reliable method for the space-time fractional Burgers and time-fractional Cahn-Allen equations via the FRDTM. Adv. Differ. Equ. 2017, 2017, 99. [Google Scholar] [CrossRef]
- Guner, O.; Bekir, A.; Cevikel, A.C. A variety of exact solutions for the time fractional Cahn-Allen equation. Eur. Phys. J. Plus 2015, 130, 146. [Google Scholar] [CrossRef]
- Inc, M.; Yusuf, A.; Aliyu, A.I.; Baleanu, D. Time-fractional Cahn–Allen and time-fractional Klein–Gordon equations: Lie symmetry analysis, explicit solutions and convergence analysis. Phys. A Stat. Mech. Its Appl. 2018, 493, 94–106. [Google Scholar] [CrossRef]
- Khater, M.M.; Bekir, A.; Lu, D.; Attia, R.A. Analytical and semi-analytical solutions for time-fractional Cahn–Allen equation. Math. Methods Appl. Sci. 2021, 44, 2682–2691. [Google Scholar] [CrossRef]
- Liao, H.L.; Tang, T.; Zhou, T. An Energy Stable and Maximum Bound Preserving Scheme with Variable Time Steps for Time Fractional Allen–Cahn Equation. SIAM J. Sci. Comput. 2021, 43, A3503–A3526. [Google Scholar] [CrossRef]
- Hou, D.; Zhu, H.; Xu, C. Highly efficient schemes for time-fractional Allen-Cahn equation using extended SAV approach. Numer. Algorithms 2021, 88, 1077–1108. [Google Scholar] [CrossRef]
- Akram, G.; Arshed, S.; Sadaf, M. Extraction of new exact soliton solutions and Painlevé-test for fractional Cahn–Allen equation. Opt. Quantum Electron. 2022, 54, 46. [Google Scholar] [CrossRef]

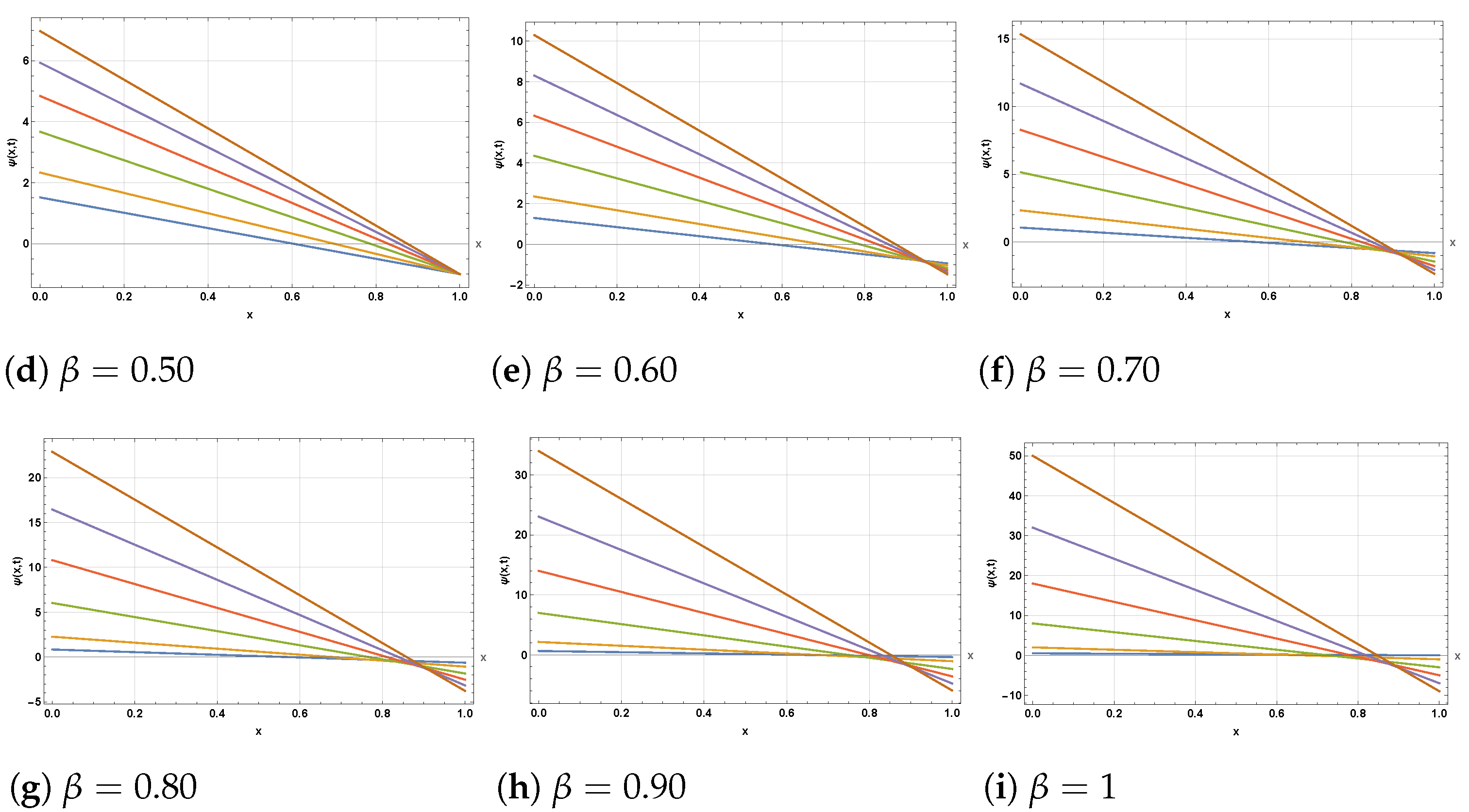
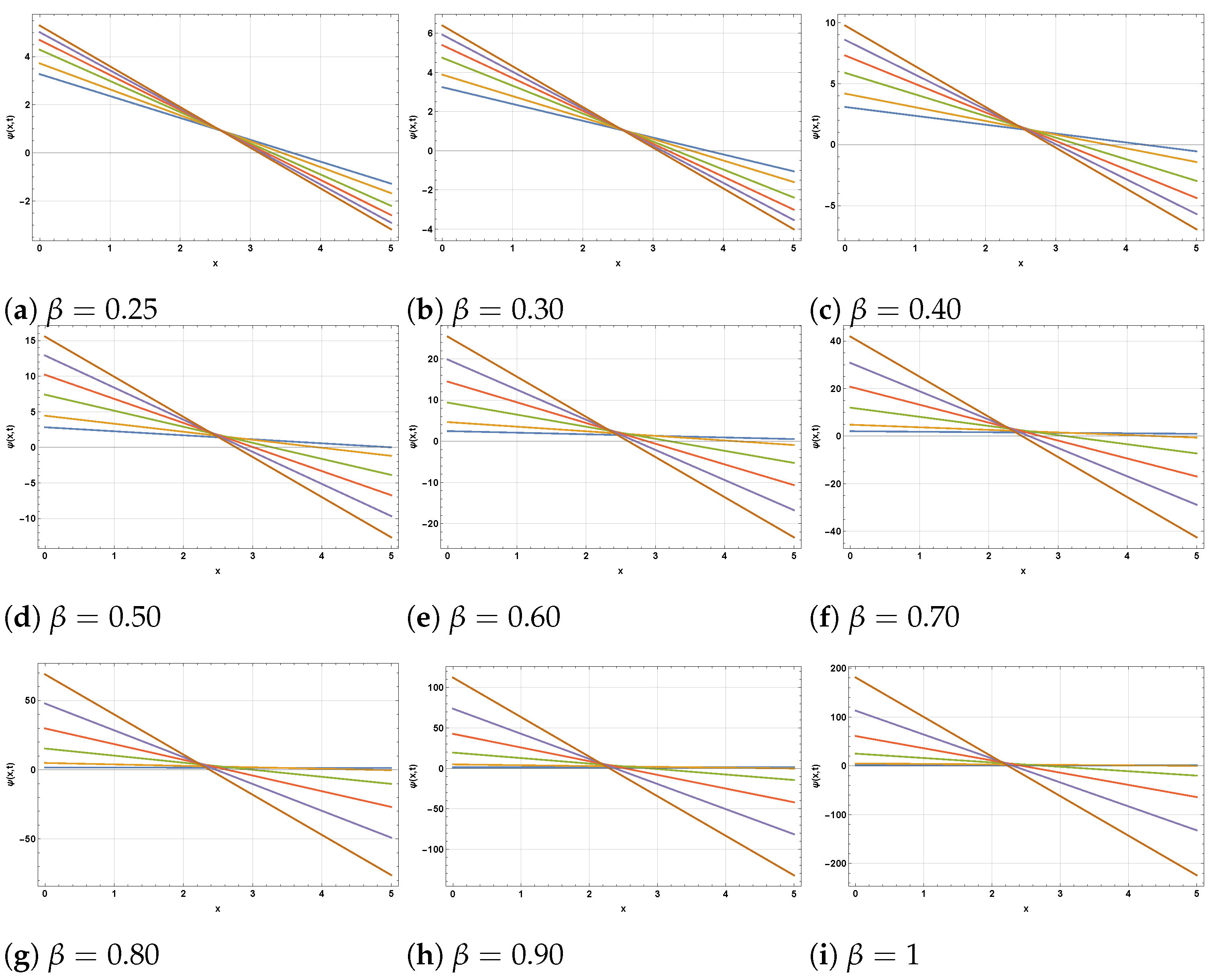

| Author(s) and Year | Method Used | Findings / Limitations |
|---|---|---|
| Guner et al. [39] | Two reliable methods for FCRWP | Exact/solitary-type solutions; no Caputo fractional setting; uniqueness not addressed. |
| Alam et al. [40] | Analytical technique (governing model) | Closed-form analysis; restricted to classical form; lacks fractional memory and numerical validation. |
| Seadawy et al. [41] | Modified mathematical methods | New exact and solitary waves for FCRWP; no uniqueness or comparative numerics. |
| Odabaşi et al. [38] | Modified trial-equation method | New solutions for FCRWP; fractional calculus and Laplace-based framework not considered. |
| Atilgan et al. [42] | Approximate analytical solutions | Approximations for FCRWP; no Caputo derivative or uniqueness analysis. |
| Wang et al. [43] | Lie symmetries; explicit solutions; conservation laws | Rich symmetry results for FCRWP; limited fractional/Caputo treatment and numerics. |
| Korkmaz [44] | Explicit exact solutions | Closed-form families for FCRWP; no fractional memory or uniqueness proofs. |
| Bulut [45] | Kudryashov method (fractional NPDEs) | Exact solutions for related fractional NPDEs; not specific to FCRWP/NFCA; minimal numerical study. |
| Rawashdeh [46] | Reliable method for time-fractional Cahn–Allen | Fractional analysis on a different model; techniques not tailored to FCRWP/NFCA. |
| Guner et al. [47] | Distinct exact solutions for NFCA | Solution families only; no uniqueness or Laplace-based fractional framework. |
| Inc et al. [48] | Lie symmetry; convergence; explicit solutions (NFCA) | Solid theory; HDM/ABFD not used; uniqueness for stated models not established. |
| Khater et al. [49] | Analytical and semi-analytical solutions (NFCA) | Accurate approximations; limited treatment of Caputo memory + Laplace coupling. |
| Liao et al. [50] | Energy-stable, maximum-bound-preserving scheme (NFCA) | Strong scheme properties; uniqueness and HDM/ABFD pipeline not the focus. |
| Hou et al. [51] | Highly efficient schemes (NFCA) | Efficiency emphasized; lacks Caputo–Laplace framework or uniqueness proofs. |
| Akram et al. [52] | New exact solutions (NFCA) | Broader classical solutions; little numerical comparison; no HDM/ABFD or uniqueness. |
| Present Work (2025) | HDM + ABFD in Caputo sense with Laplace transform | Uniqueness and numerical study for both FCRWP and NFCA equations within a unified Caputo–Laplace framework; complements prior solution-only works with rigorous uniqueness and systematic numerics. |
| Iteration n | ||||
|---|---|---|---|---|
| 0 | 0.2000 | 0.5000 | 1.0000 | 1.5000 |
| 1 | 0.0450 | 0.0780 | 0.1100 | 0.1500 |
| 2 | 0.0102 | 0.0175 | 0.0250 | 0.0330 |
| 3 | 0.0024 | 0.0042 | 0.0058 | 0.0078 |
| 4 | 0.0006 | 0.0010 | 0.0014 | 0.0018 |
| 5 | 0.0001 | 0.0002 | 0.0003 | 0.0004 |
| Iteration n | |||
|---|---|---|---|
| 0 | 0.5000 | 0.3500 | 0.2200 |
| 1 | 0.1200 | 0.0850 | 0.0530 |
| 2 | 0.0280 | 0.0195 | 0.0120 |
| 3 | 0.0068 | 0.0047 | 0.0030 |
| 4 | 0.0016 | 0.0011 | 0.0007 |
| 5 | 0.0004 | 0.0003 | 0.0002 |
| Iteration n | ||||
|---|---|---|---|---|
| 0 | 0.1000 | 0.5000 | 1.0000 | 1.5000 |
| 1 | 0.0220 | 0.0950 | 0.1850 | 0.2900 |
| 2 | 0.0052 | 0.0225 | 0.0450 | 0.0680 |
| 3 | 0.0013 | 0.0057 | 0.0115 | 0.0168 |
| 4 | 0.0003 | 0.0014 | 0.0029 | 0.0042 |
| 5 | 0.00007 | 0.0003 | 0.0007 | 0.0010 |
| Iteration n | |||
|---|---|---|---|
| 0 | 0.4800 | 0.3200 | 0.2000 |
| 1 | 0.1050 | 0.0700 | 0.0420 |
| 2 | 0.0250 | 0.0170 | 0.0100 |
| 3 | 0.0060 | 0.0040 | 0.0025 |
| 4 | 0.0015 | 0.0010 | 0.0006 |
| 5 | 0.0004 | 0.0003 | 0.0002 |
| Iteration (n) | Truncation Error (NFCA) | Truncation Error (FCRWPE) |
|---|---|---|
| 5 | ||
| 10 | ||
| 15 | ||
| 20 | ||
| 25 |
| Iteration (n) | Residual Norm (NFCA) | Residual Norm (FCRWPE) |
|---|---|---|
| 5 | ||
| 10 | ||
| 15 | ||
| 20 | ||
| 25 |
| Method | Accuracy | Residual Error | Computational Cost/Robustness |
|---|---|---|---|
| HDM | Very High (errors –) | Lowest among the compared methods | Moderate cost; robust |
| ADM | Moderate (errors –) | Higher than HDM | Low cost; may diverge |
| FRDTM | High (errors –) | Close to HDM but slightly higher | Higher computational cost |
| Amplitude Decay | Oscillation Period | Propagation Speed | Physical Interpretation | |
|---|---|---|---|---|
| 0.2 | Very slow decay () | 1.65 × classical period | 0.65 × classical speed | Strong memory; oscillations persist much longer, delayed wavefront. |
| 0.4 | Slow decay () | 1.35 × classical period | 0.75 × classical speed | Significant memory effect; wave spreads slower. |
| 0.6 | Moderate decay () | 1.15 × classical period | 0.85 × classical speed | Transitional regime. |
| 0.8 | Faster decay () | 1.05 × classical period | 0.93 × classical speed | Memory effect weak; dynamics close to integer-order. |
| 1.0 | Exponential-like decay () | Classical period | Classical speed | No memory; recovers classical PDE. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; Aldawish, I.; Rizvi, S.T.R.; Seadawy, A.R. Iterative Investigation of the Nonlinear Fractional Cahn–Allen and Fractional Clannish Random Walker’s Parabolic Equations by Using the Hybrid Decomposition Method. Fractal Fract. 2025, 9, 656. https://doi.org/10.3390/fractalfract9100656
Ahmed S, Aldawish I, Rizvi STR, Seadawy AR. Iterative Investigation of the Nonlinear Fractional Cahn–Allen and Fractional Clannish Random Walker’s Parabolic Equations by Using the Hybrid Decomposition Method. Fractal and Fractional. 2025; 9(10):656. https://doi.org/10.3390/fractalfract9100656
Chicago/Turabian StyleAhmed, Sarfaraz, Ibtisam Aldawish, Syed T. R. Rizvi, and Aly R. Seadawy. 2025. "Iterative Investigation of the Nonlinear Fractional Cahn–Allen and Fractional Clannish Random Walker’s Parabolic Equations by Using the Hybrid Decomposition Method" Fractal and Fractional 9, no. 10: 656. https://doi.org/10.3390/fractalfract9100656
APA StyleAhmed, S., Aldawish, I., Rizvi, S. T. R., & Seadawy, A. R. (2025). Iterative Investigation of the Nonlinear Fractional Cahn–Allen and Fractional Clannish Random Walker’s Parabolic Equations by Using the Hybrid Decomposition Method. Fractal and Fractional, 9(10), 656. https://doi.org/10.3390/fractalfract9100656







