1. Introduction
Recent advances in mathematical biology highlight the importance of incorporating time delays into models. Such delays represent real-life phenomena more accurately, including feeding cycles, maturation periods, resource replenishment, and delayed responses. These delays introduce memory-driven dynamics into the system, significantly shaping its behavior over time. Both early and modern studies—such as [
1,
2,
3,
4]—have shown that delay differential equations (DDEs) produce rich dynamical outcomes. These include instabilities, bifurcation phenomena, and persistent oscillatory behavior, mainly due to the influence of past system states on present evolution. For instance, the research presented in [
5] utilized the Caputo–Fabrizio fractional operator to investigate nonlinear models involving both constant and state-proportional delays. Further relevant studies are discussed in [
6,
7,
8].
Classical DDEs often rely on constant or predetermined delays, which may not adequately capture the evolving nature of many real-world processes. In biological, physical, and engineering systems, the delay experienced by the system is often influenced by the current state or time, and the underlying dynamics exhibit memory effects and nonlocal behavior. Traditional integer-order models are limited in describing such complex systems.
Traditional integer-order models often fall short in describing complex systems, particularly when accounting for memory-dependent or hereditary traits. To bridge this gap, fractional-order differential models were introduced, employing nonlocal operators that are defined through integral kernels. The growing interaction between fractional calculus and practical modeling has significantly advanced the field, establishing fractional differential equations (FDEs) as an essential tool in modern applied mathematics. These equations are now widely employed in multiple domains (see [
9,
10,
11]). However, classical fractional formulations may prove insufficient in scenarios involving irregular geometries, fractal media, or anomalous transport phenomena. This growing interest has led to the adoption of fractal–fractional derivatives, particularly in the Caputo sense, which employ power-law memory kernels. Such derivatives provide a dual capability: modeling time-dependent feedback while capturing structural complexity. These operators have the ability to capture both memory effects and scale-dependent behaviors in complex systems [
12]. In ref. [
13], the authors utilized fractal–fractional calculus to apply analytical methods for examining the dynamics of a breast cancer model, uncovering significant insights into disease progression. A similar approach was adopted in ref. [
14], where a waterborne disease model was analyzed using fractal–fractional operators. The work focused on both theoretical development and numerical simulations to better understand the system’s behavior. In ref. [
15], a model involving liver fibrosis was constructed within the framework of fractal–fractional derivatives, emphasizing transitions across subintervals and providing mathematical interpretations. Likewise, the study described in ref. [
16] investigated the spread of Ebola using a
-piecewise hybrid fractional derivative framework. These developments reflect the growing reliance on advanced mathematical modeling to interpret and predict complex biological phenomena.
The study of coupled systems of differential equations also plays a crucial role in modeling complex phenomena where multiple dynamical components interact over time (see [
17]). Coupled systems of DEs with two state variables have widely been studied, as in [
18,
19,
20]. In particular, triply coupled systems arise naturally in various fields such as mathematical biology, engineering, epidemiology, and economics. Classical triply coupled system models have been considered by many researchers (for instance, see [
21,
22]). However, triply coupled systems in which the state of each variable depends on the delayed states of all other variables are rarely investigated. Unlike classical coupled systems, triply coupled models with time-dependent delays capture more realistic interactions, including feedback, memory, and nonlocal effects that occur in real-world processes. Furthermore, incorporating fractal–fractional derivatives in the Caputo sense enhances the model’s ability to describe systems with hereditary properties and anomalous dynamics. This framework not only generalizes classical differential equations but also accommodates both the fractal nature of the time domain and the fading memory that is inherent in many physical and biological systems. The present work analyzes the existence, uniqueness, and stability of solutions for such systems using fixed point theory. This provides a rigorous mathematical foundation for further analytical and numerical investigations.
We propose the following triply coupled system of DEs involving fractal–fractional Caputo (FFC) derivatives and time-dependent delays:
subject to the initial conditions:
where
Here, is a fractal–fractional Caputo differential operator; is the fractional order, is the fractal dimension, the functions represent bounded time-dependent delays, represents the time, and define the coupling dynamics among the state variables . The system exhibits interaction under memory and fractal effects, governed by the FFC operator.
Novelty and Main Contributions
The novelty and main contributions of this work are as follows:
The present work advances the existing literature on fractional-order systems with delays by introducing time-dependent delays in the framework of fractal–fractional Caputo DEs. While most earlier studies have focused on constant or fixed delays, time-dependent delays provide a more realistic description of dynamical processes in which the lag evolves in relation to time, capturing memory and hereditary effects more accurately. Furthermore, our study develops theoretical guarantees for existence, uniqueness, and stability under this generalized setting, which to the best of our knowledge have not been systematically established in previous works. On the computational side, we employ the Adams–Bashforth scheme adapted to the fractal–fractional Caputo derivative with time-dependent delays and validate the model through a biologically relevant food-chain system. This combined theoretical and numerical framework highlights both the originality and practical applicability of our contribution.
We divide the manuscript into several sections as follows:
Section 2 outlines the essential preliminary concepts.
Section 3 addresses the existence results for the proposed model.
Section 4 addresses sthe tability findings.
Section 5 is devoted to numerical solution.
Section 6 is devoted to the application of the key findings to a general numerical problem and a real-world three-species food-chain model. In
Section 7, we present our conclusions.
3. Investigation of Existence and Uniqueness Results
Let us define the Banach space:
equipped with the following norm:
Define the operator
by
where for
,
and for
, we define the following:
To establish the existence and uniqueness of solutions to the system (
1) and (
2), we impose the following assumptions:
Assumption 1. The functionsare continuous. Assumption 2. There exist constants such that for all and for all real numbers , Assumption 3. The time delay functions are continuous on and satisfy Assumption 4. The functions are bounded and continuous.
Assumption 5. There exist constants such that Theorem 2. If (A1)
–(A5)
hold true, then the proposed triply coupled system (
1) and (
2)
, with time-dependent delays, admits a minimum of one solution. Proof. For the proof of this result, we apply Theorem 1.
Step 1: Continuity.
Let
in
as
. Define
By uniform convergence and continuity of delay functions
, we have pointwise convergence:
,
, and
. By assumption (A5), each function is bounded. Moreover, the kernel
is integrable on
. Using the dominated convergence theorem,
and similarly for
and
. Thus,
is continuous.
Step 2: Boundedness.
Let
be a constant, and define the closed ball:
For
, using assumption (A5),
Consider the integral
Letting
, the integral becomes
where
is the beta function. Thus,
Similarly,
and
Combining the three bounds on
,
, and
into a single bound for the whole operator, we have
Therefore,
, where
.
Step 3: Equicontinuity.
Let
, with
. Then, for
,
Each term tends to zero as
; therefore,
is equicontinuous. This is similar for
and
. Hence,
is equicontinuous.
By the Arzelà–Ascoli Theorem and Steps 1–3, is compact.
Step 4: A priori boundedness.
Let
for some
. Then,
Using the transformation,
we have
Similarly,
and
Thus, the set
is bounded.
All the conditions of Schaefer’s Fixed Point Theorem are satisfied. Hence,
has a fixed point in
, which corresponds to a solution of the triply coupled system (
1) and (
2). □
Theorem 3. Let (A1)
–(A3)
hold true and suppose that f, g, and h satisfy the Lipschitz conditions in (A2)
. If then the triply coupled system (
1) and (
2)
with time-dependent delays admits a unique solution on . Proof. Let
. For all
, we consider
Using the Lipschitz condition (A2), we have
Taking the maximum over
and using the norm definition
, we get the following:
Now, using the identity
we get
Similarly,
and
Thus, combining the three yields the following:
If
then
is a contraction on
.
By the Banach Fixed Point Theorem, admits a unique fixed point in , which corresponds to a unique solution of the triply coupled system. □
6. Numerical Application
This section is further divided into two subsections. In the first subsection, we apply our theoretical results to a general triply coupled system of DEs with time-dependent delays. In the second subsection, we apply the concept of time-varying delays to a real-world model of a three-species food-chain. Numerical simulations are performed using the extended ABM numerical method and MATLAB R2024a.
6.1. A General Triply Coupled System of DEs with Time-Dependent Delays
In this subsection, we consider a triply coupled system of DEs with time-dependent delays in the FFC sense:
with the following initial conditions:
where
First, we estimate the Lipschitz constants for
f:
Similarly, for
g, we estimate the Lipschitz constants as
And for
h, the Lipschitz constants are estimated as
Using the condition of
for
,
, and
:
Therefore, applying Theorem 3, it is guaranteed that (
17) has a unique solution.
6.2. Application to Three-Species Food-Chain Model
In this subsection, we apply the concept of time-dependent delays to a real-world model of a three-species food-chain.
We consider a three-species food-chain model with the lowest trophic level
, the middle trophic level
, and the highest trophic level
. The governing system is given by the fractional differential equations with time-dependent delays:
The time-dependent delays are given by
The parameter values used in the numerical simulations of the application model are listed in
Table 1.
The initial conditions for
are given by the history functions:
In addition to the existing literature on fractional-order food-chain models, we note the closely related study by Das and Samanta [
29], where a delayed fractional-order food-chain model with fear effects and prey refuge was investigated. Their work focuses primarily on ecological extensions through the incorporation of behavioral factors such as fear and refuge, while the delay considered is constant. By contrast, the present study develops a more general theoretical framework by incorporating time-dependent delays within the setting of fractal–fractional Caputo differential equations. Furthermore, our approach is not restricted to ecological dynamics but can be adapted to other applied domains, such as disease modeling and population dynamics in health sciences. From the numerical perspective, while our examples are less complex than those in [
29], they are intentionally chosen to demonstrate the feasibility and robustness of the newly developed theoretical framework. Extending this analysis to richer ecological settings remains a promising avenue for future research.
The proposed model example is simulated for multiple cases:
First, we analyze the effects of time-varying delays on the lowest, middle, and highest trophic species.
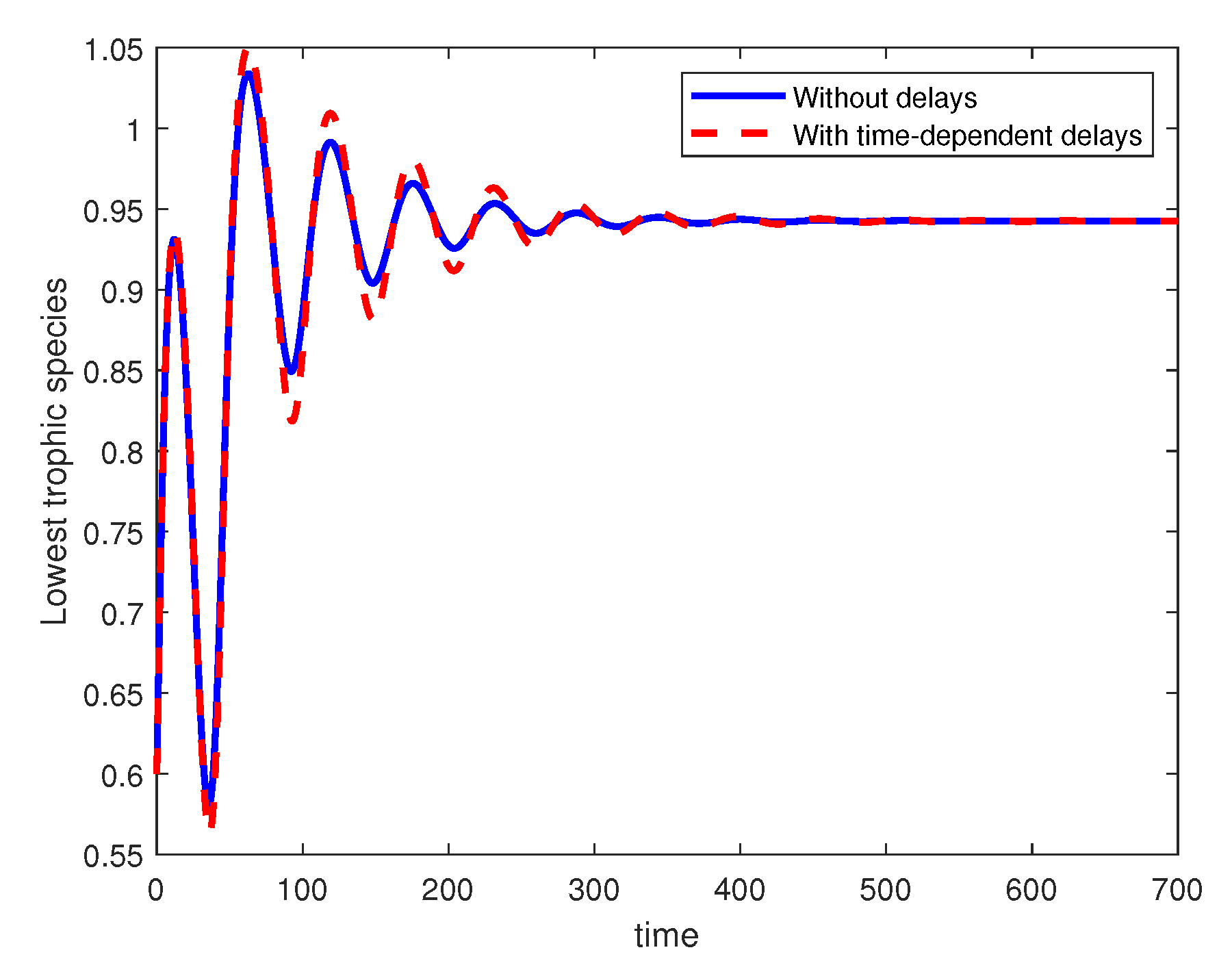
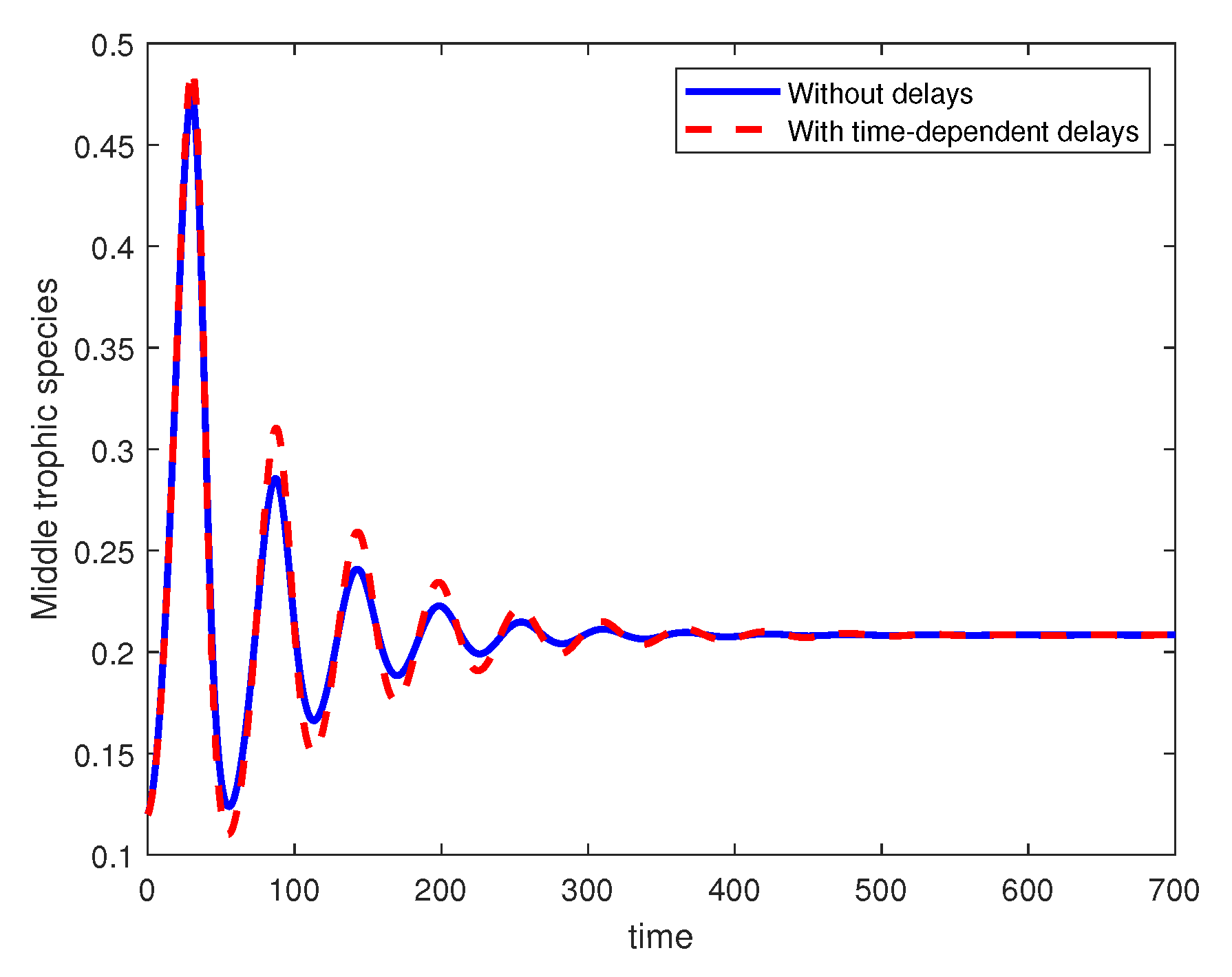
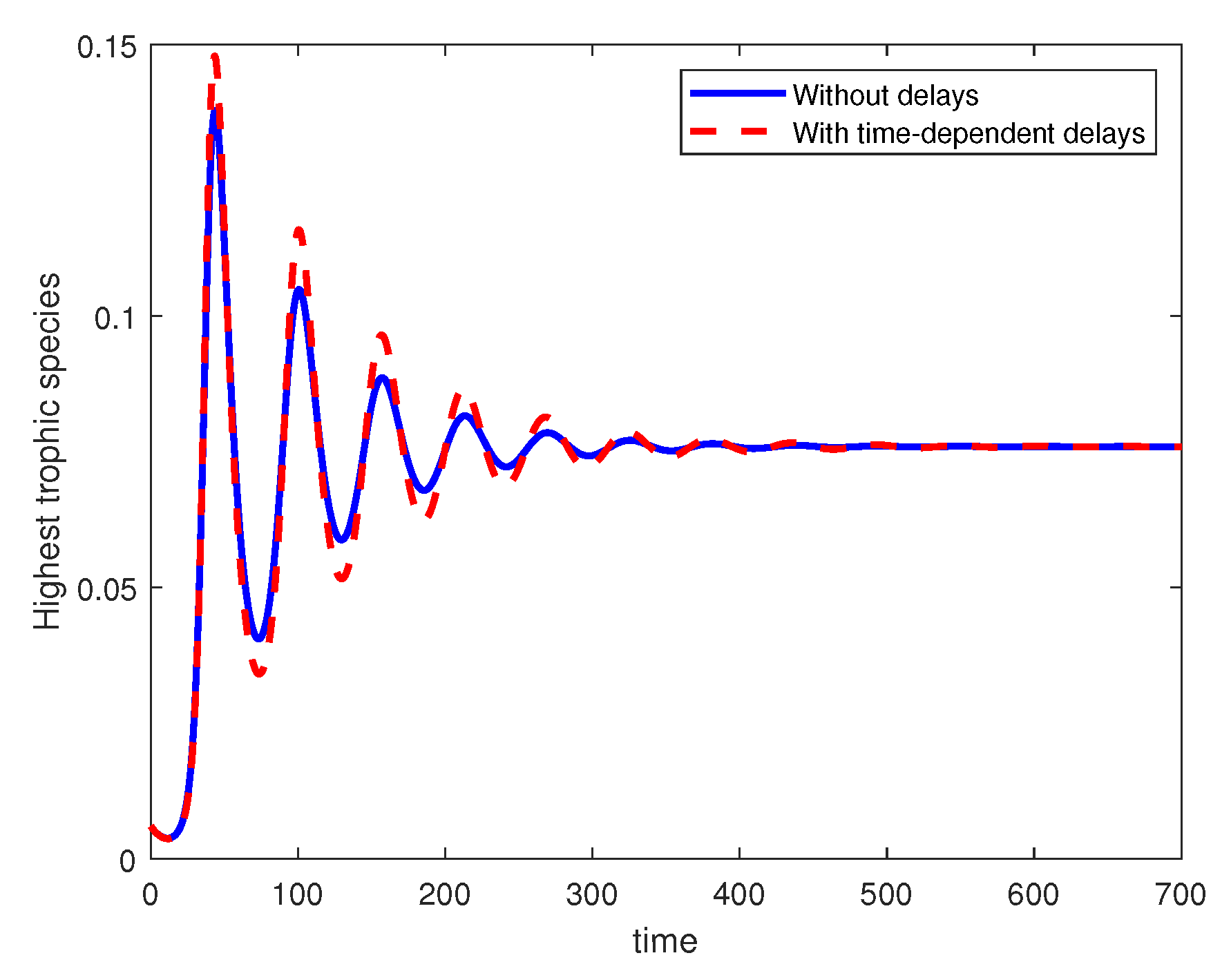
From the plots in
Figure 1,
Figure 2 and
Figure 3, we observe that both cases—without delays (blue solid line) and with time-dependent delays (red dashed line)—exhibit similar qualitative dynamics. Starting from the same initial condition, the solutions undergo oscillations before eventually converging to the steady-state value of
. We observe that the oscillations in the delayed case show slightly higher amplitudes during certain cycles (e.g., around
and
). This suggests that time-dependent delays add small perturbations to the transient dynamics.
It can be observed that the presence of time-dependent delays does not destabilize the system. Both cases dampen oscillations at a similar rate, and the steady-state value is unchanged, meaning that the long-term equilibrium is robust to such delays.
The main visible effects are a subtle shift and amplitude modulation in the oscillations during the transient phase; however, the asymptotic behavior remains essentially the same.
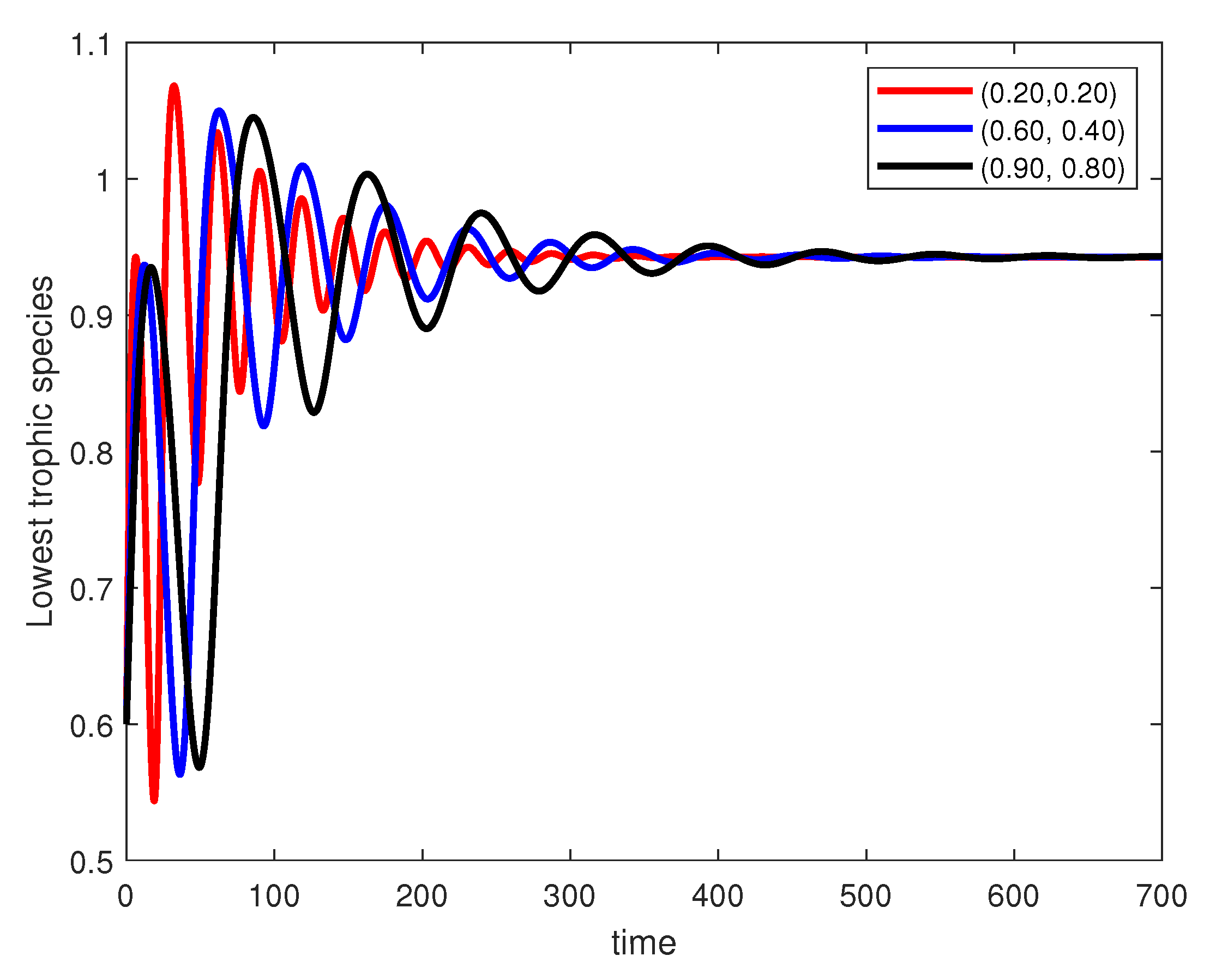
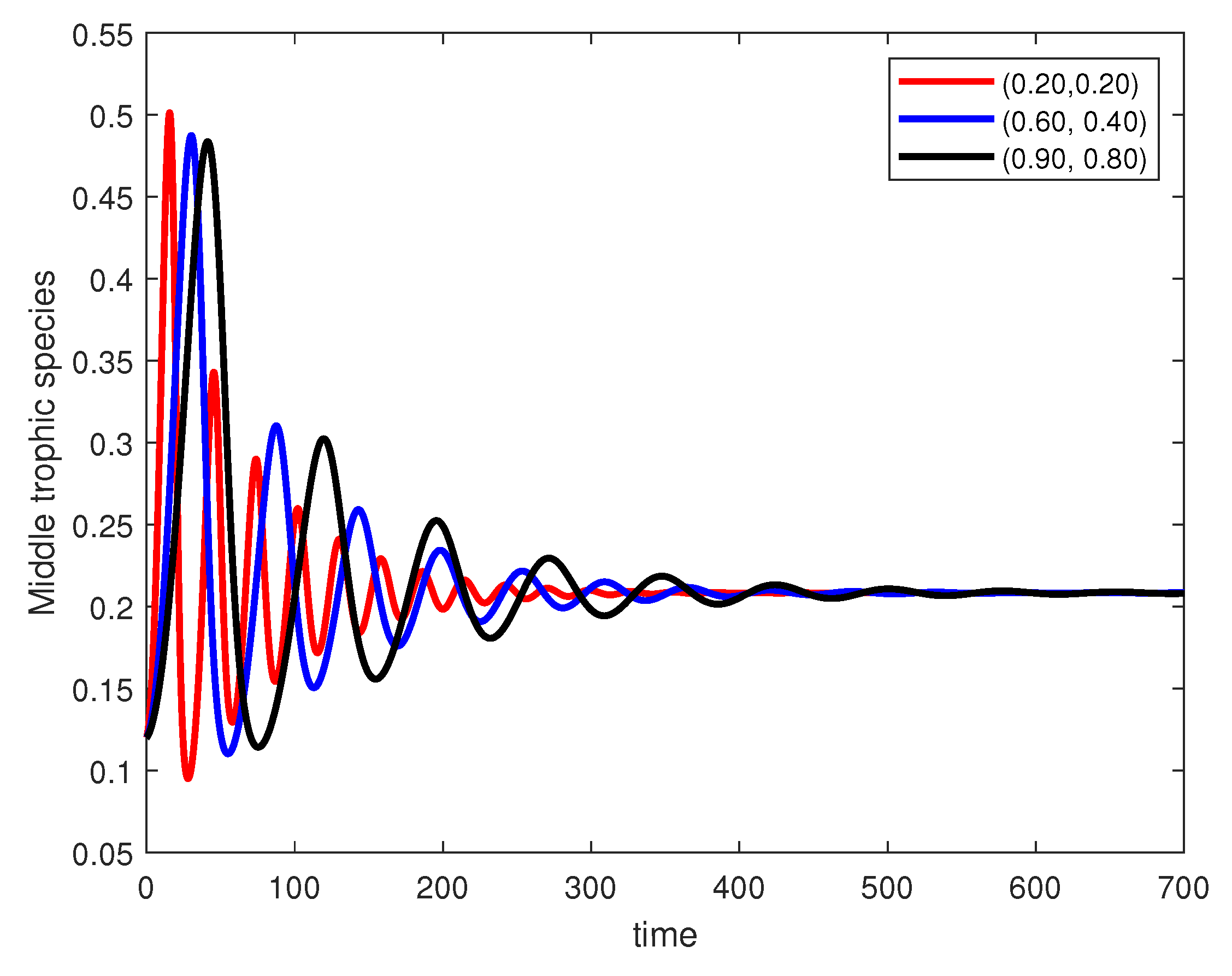
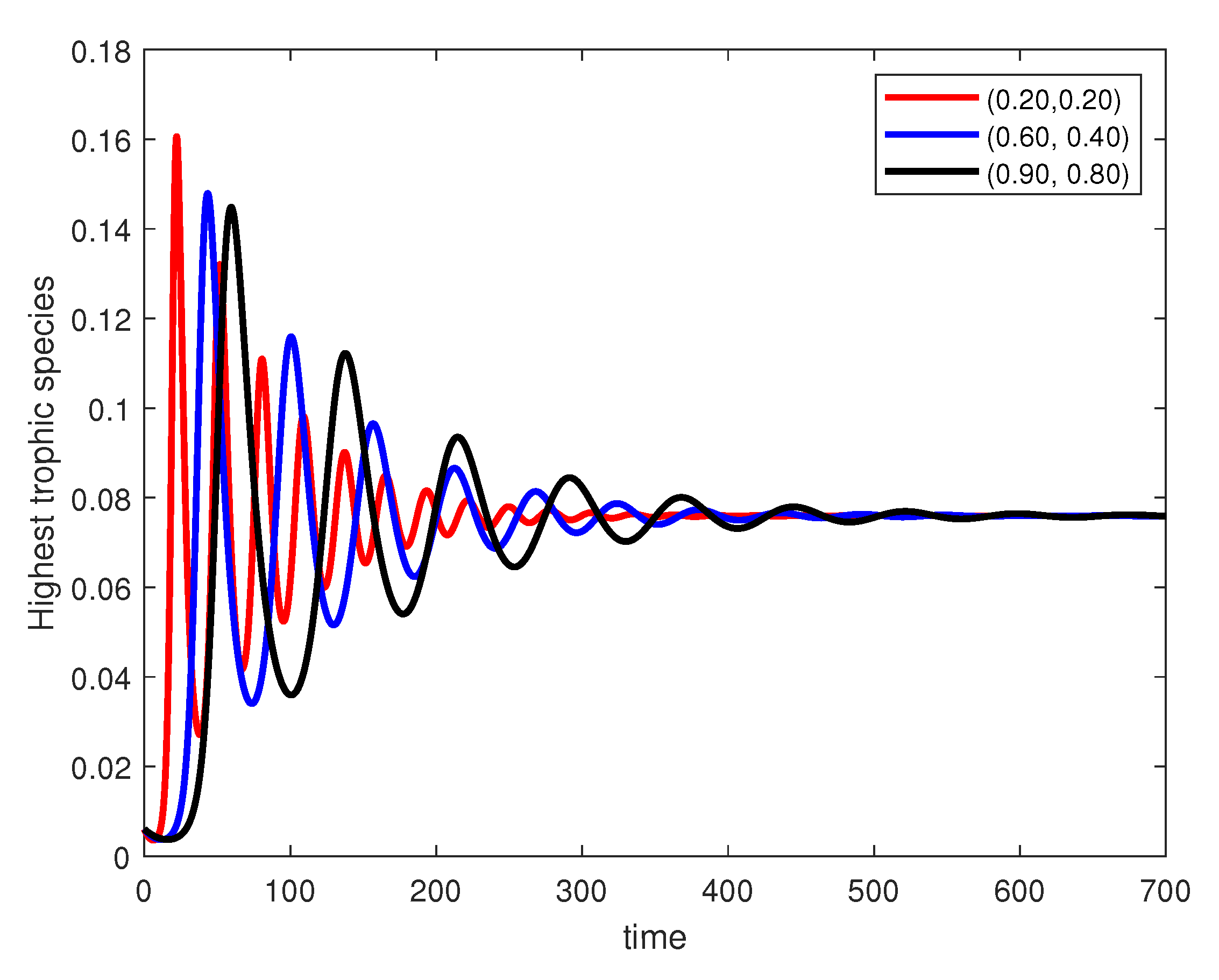
In the following figures, we analyze the impact of fractal–fractional order values on dynamical behaviors of the lowest, middle, and highest trophic species.
From
Figure 4, we observe dampened oscillatory growth toward a steady state, with lower fractional orders and fractal dimensions leading to faster stabilization. From
Figure 5, we can observe that the middle trophic species exhibits predator–prey-type oscillations that decay over time. Lower fractional orders and fractal dimensions again smooth out dynamics faster. Similarly, in
Figure 6, the highest trophic species follow similar delayed oscillatory patterns before stabilizing.
Discussion of Numerical Method’s Limitations
In this study, we employ the Adams–Bashforth method (ABM), an explicit multi-step scheme, to approximate the solutions of the fractal–fractional Caputo system with time-dependent delays. Although the method is straightforward to implement and computationally efficient, it also presents certain limitations. In particular, explicit schemes are prone to stability issues in stiff systems and may perform poorly in high-dimensional models with strong nonlinear interactions. Furthermore, achieving satisfactory accuracy requires the use of small step sizes, which increases computational costs. These limitations point to the need for future research on more robust numerical techniques. Potential directions include implicit predictor–corrector methods, adaptive-step solvers, and exponential integrators, which may provide improved stability and efficiency for large-scale or stiff problems.
7. Conclusions
In this study, we developed and analyzed a triply coupled system of fractal–fractional Caputo differential equations with time-dependent delays. This framework provides a more realistic representation of dynamical processes with evolving memory and delay effects. The theoretical analysis confirmed the existence, uniqueness, and HU stability of the solutions.
The proposed ABM scheme effectively approximated the intricate dynamics of the system. Numerical simulations, including a three-species food-chain model, revealed that incorporating time-dependent delays can significantly alter system behavior compared with systems without delays. These results highlight the importance of time-dependent delays in modeling real-world phenomena.
Overall, this study contributes to a deeper understanding of fractional-order systems with dynamic memory effects and opens new directions for future research in nonlinear dynamical modeling with time-dependent delays.