Abstract
This paper investigates the problem of observer-based control for a class of nonlinear systems described by the Caputo–Hadamard fractional-order derivative. Given the growing interest in fractional-order systems for their ability to capture complex dynamics, ensuring their practical stability remains a significant challenge. We propose a novel concept of practical stability tailored to nonlinear Hadamard fractional-order systems, which guarantees that the system solutions converge to a small ball containing the origin, thereby enhancing their robustness against perturbations. Furthermore, we introduce a practical observer design that extends the classical observer framework to fractional-order systems under an enhanced One-Sided Lipschitz (OSL) condition. This extended OSL condition ensures the convergence of the proposed practical observer, even in the presence of significant nonlinearities and disturbances. Notably, the novelty of our approach lies in the extension of both the practical observer and the stability criteria, which are innovative even in the integer-order case. Theoretical results are substantiated through numerical examples, demonstrating the feasibility of the proposed method in real-world control applications. Our contributions pave the way for the development of robust observers in fractional-order systems, with potential applications across various engineering domains.
Keywords:
practical stability; Caputo–Hadamard fractional-order derivative; control; observer; observer-based control MSC:
93C10; 34A08; 93B07
1. Introduction
Fractional-order systems have emerged as a powerful tool for modeling complex dynamics that cannot be captured by classical integer-order models. These systems have been widely used in various fields such as control theory, signal processing, and even biomedical engineering due to their ability to describe memory and the hereditary properties inherent in many physical processes. The classical fractional-order derivatives, such as the Caputo and Riemann–Liouville derivatives, have received considerable attention in these applications. However, the Caputo–Hadamard fractional-order derivative, despite its potential broad applicability, remains underexplored in both theory and practice [,]. The Caputo–Hadamard fractional-order derivative offers a unique perspective in modeling systems with nonlocal behavior, memory effects, and processes that evolve over irregular time scales or domains. Unlike the more commonly used Caputo and Riemann–Liouville derivatives, which are well-suited for modeling phenomena with smooth and regular memory effects, the Caputo–Hadamard derivative is particularly effective in describing processes where the rate of change depends not just on the current state, but also on the logarithmic scale of past states. The Caputo–Hadamard derivative is particularly well-suited for modeling processes in fractal or irregular media []. Many physical systems exhibit fractal properties, such as porous media, geological formations, and certain biological tissues. In these cases, traditional fractional derivatives may not adequately capture the irregularities in the media, whereas the Caputo–Hadamard derivative, with its logarithmic scaling, can more accurately represent the dynamics of these systems. Anomalous diffusion [], where the mean square displacement of particles deviates from the linear behavior predicted by classical Brownian motion, is observed in various complex systems, including heterogeneous materials, plasma physics, and financial markets. The Caputo–Hadamard derivative can model such phenomena more effectively by incorporating the nonlocal and irregular nature of the diffusion process. Also, in systems with long-term memory, such as viscoelastic materials, where their current state depends on the entire history of their stress–strain relationship, the Caputo–Hadamard derivative offers an advantage by considering their history on a logarithmic scale []. This makes it possible to model systems where the influence of past states decays at a rate that varies with the logarithm of time, rather than at a constant rate.
The motivation behind adopting the Caputo–Hadamard fractional-order derivative lies in its ability to provide a more flexible and accurate mathematical framework for describing systems with complex, nonlocal, and irregular dynamics. As the use of fractional-order models continues to grow in fields such as engineering, physics, and biology, the need for derivatives like the Caputo–Hadamard, which can better capture the nuances of real-world systems, becomes increasingly important. The introduction of this derivative into observer design not only extends our theoretical understanding of fractional calculus but also opens up new possibilities for practical applications where traditional derivatives may fall short.
In the context of control systems, observer design is crucial for estimating the unmeasured states of a system, particularly when full-state measurements are impractical or costly. Traditionally, the focus has been on integer-order systems, where a rich body of literature exists on observer design methodologies such as the Luenberger observer [], sliding mode observers [], and Kalman filters []. These techniques have been refined over decades to ensure their stability, robustness, and accuracy in various applications ranging from aerospace to industrial automation [].
With the growing interest in fractional-order systems, several studies have extended observer design techniques to this domain. Recent contributions include the development of fractional-order observers based on the Caputo derivative [], as well as sliding mode observers for fractional systems with uncertain dynamics []. These efforts aim to bridge the gap between classical and fractional-order control, yet they largely ignore the practical considerations essential for real-world applications. In particular, most designs do not address practical stability—a key feature ensuring that the system solutions converge toward a desired equilibrium within a specified bounded region, even in the presence of perturbations and modeling inaccuracies.
Another significant gap in the literature is the extension of stability conditions, such as the OSL condition, to fractional-order systems. The OSL and Quasi-One-Sided Lipschitz (QOSL) conditions have been successfully applied in nonlinear observer designs for integer-order systems, where they play a critical role in ensuring observer convergence by restricting the growth rate of nonlinearities []. However, there is a lack of work extending this condition to fractional-order systems, particularly in the context of practical stability. Ensuring practical stability is essential when dealing with fractional-order systems due to their inherent sensitivity to perturbations and initial conditions [].
Numerous studies have explored observer design for fractional-order systems, primarily focusing on the Caputo and Riemann–Liouville fractional derivatives. In [], a fractional-order Luenberger observer was proposed for a class of linear fractional-order systems. This observer was shown to achieve asymptotic stability under specific conditions on the system matrices. However, the scope of these results was limited to linear systems, and their robustness to perturbations and practical stability were not addressed.
In [], a sliding mode observer was designed for nonlinear fractional-order systems using the Caputo derivative. This design introduced robustness to uncertainties but lacked the ability to handle nonlinearities under practical stability constraints. The observer was designed with global asymptotic stability in mind, but no provision was made for ensuring convergence to a bounded region, which is crucial in real-world implementations where perfect convergence may not be achievable due to system disturbances.
Compared to these existing designs, our proposed observer framework introduces practical stability concepts in the context of Caputo–Hadamard fractional-order systems for the first time. The extension of the OSL condition to fractional-order systems offers a novel mechanism for ensuring that the observer error remains bounded, even under nonlinear and uncertain conditions. Unlike [,], our design explicitly addresses practical stability, making it more suitable for systems where perturbations or modeling inaccuracies are present.
Observer designs for nonlinear integer-order systems have been extensively studied. In [], an observer for nonlinear systems was developed using the OSL condition, ensuring that the observer error converges to zero under specific conditions. While effective in the integer-order domain, this approach does not extend naturally to fractional-order systems, whose memory effects and non-local properties require different analytical tools.
In [], a robust observer design for nonlinear systems based on backstepping was introduced. This design achieved global asymptotic stability but was not adapted to fractional-order dynamics. Moreover, practical considerations such as bounded error convergence were not considered. The methods in [,] assume ideal system models without considering perturbations, making them less practical for real-world applications.
Our proposed method extends the classical OSL-based observer designs by incorporating practical stability into the analysis of fractional-order systems. The practical observer we introduce is novel, even in the integer-order case, and provides a robustness feature that traditional methods lack. Additionally, our method leverages the Caputo–Hadamard derivative, which offers a new perspective on fractional-order dynamics not covered in the integer-order frameworks of [,].
The Caputo and Riemann–Liouville derivatives are the most common choices in fractional calculus for control and observer design. However, the Caputo–Hadamard derivative offers distinct advantages, particularly when dealing with systems that exhibit non-local behavior and memory effects over irregular intervals.
In [], the Caputo derivative was applied to a fractional-order PID controller, demonstrating its effectiveness in improving the control performance of systems with long memory. However, no attempt was made to extend this to observer design. In contrast, our work utilizes the Caputo–Hadamard derivative, which provides more flexibility in capturing the irregularities of real-world dynamics. This is particularly advantageous in control applications where classical fractional derivatives may not adequately capture system behavior over irregular domains.
By focusing on the Caputo–Hadamard derivative, our design benefits from enhanced modeling capabilities, which are essential in complex, nonlinear systems. This offers a distinct advantage over existing designs that rely solely on the Caputo or Riemann–Liouville derivatives.
Most existing observer designs for fractional-order systems aim to achieve asymptotic stability, ensuring that the observer error converges to zero as time approaches infinity. However, asymptotic stability may not always be feasible in practical applications, where disturbances, noise, and modeling inaccuracies are unavoidable. In such cases, achieving practical stability—where the observer error converges to a bounded region rather than zero—is often more realistic and sufficient for ensuring satisfactory system performance.
In [], practical stability was explored for integer-order systems. While this approach was effective for dealing with uncertainties, it was not extended to fractional-order systems. Our work introduces practical stability for nonlinear Caputo–Hadamard fractional-order systems, providing a robust framework that ensures bounded error convergence. This makes the observer more resilient to perturbations and modeling uncertainties, thus making it more applicable in real-world scenarios.
In this work, we propose several novel contributions that address critical gaps in the existing literature:
- Novel Extension to Practical Observers: We extend the classical observer design to a practical observer, ensuring its robustness under real-world implementation conditions. This novel contribution is significant even for integer-order systems and particularly impactful for fractional-order systems.
- Caputo–Hadamard Fractional-Order Derivative: We introduce the Caputo–Hadamard fractional-order derivative into the observer design framework. Despite its potential for describing complex nonlocal properties, this derivative has not been fully explored in control theory, making our work a pioneering effort in this direction.
- Practical Stability of Nonlinear Fractional-Order Systems: We propose the concept of practical stability for nonlinear Hadamard fractional-order systems. Practical stability ensures that the system solutions converge toward a small ball around the origin, providing robustness against disturbances and perturbations—a vital characteristic for real-world applications.
- Extension of the OSL Condition: We extend the OSL condition, which is widely used in nonlinear observer design, to fractional-order systems. This ensures that the practical observer converges even in the presence of nonlinearities and disturbances, offering a new stability criterion for fractional-order control systems.
These contributions open up new avenues for designing robust and practical observers in fractional-order systems, significantly enhancing their applicability in control engineering.
2. Preliminaries
In this section, some definitions and lemmas are presented [,].
Definition 1
[]. The Hadamard integral of a locally integrable function x of order is given by
Definition 2
[]. The Caputo–Hadamard fractional derivative of an absolutely continuous is given by
Lemma 1
[]. Let and be a constant and symmetric definite positive matrix. Then,
Definition 3
[]. The Mittag–Leffler (ML) functions can be defined with one or two parameters, respectively, as follows:
Consider the system
Definition 4
[]. The system (*) is called practically ML stable if
such that for the of (*), the inequality
is satisfied, where
, and
is a locally given Lipschitz function.
In this work, we consider the nonlinear fractional-order system
where , , , , , , , . In this case, we have .
Assumption 1.
The unknown disturbance is an essentially bounded function, i.e.,
In the rest of the paper, assumption 1 is considered for all results.
3. Observer Design for Lipschitz Fractional-Order Systems
In this section, we introduce the necessary assumptions, provide key definitions, and present a theorem that establishes the main result of observer design in Lipschitz fractional-order systems.
Assumption 2.
(A, C) is observable and such that
when .
Definition 5.
is Lipschitz continuous with a Lipschitz constant
, meaning that there exists a constant
such that for all
Given the system described in Equation (1), where certain state variables cannot be directly measured, and under Assumption 2, we propose the following observer to estimate the state:
where
Theorem 1 presents practical stability under condition (3).
Theorem 1.
If condition (3) is met and Assumption 2 holds, and if
then (4) is a practical observer of system (1).
Proof.
See Appendix A. □
4. Observer Design for OSL and Quasi-OSL Fractional-Order Systems
In this section, we provide essential definitions and present theorems that establish the primary result for observer design in OSL fractional-order systems.
Definition 6.
is an OSL in with an OSL constant , meaning that for any
, the following inequality holds:
We introduce the theorem.
Theorem 2.
If condition (6) is satisfied and Assumption 2 holds, and if
then (4) is a practical observer of system (1).
Proof.
See Appendix B. □
Now, when a quasi-OSL condition is introduced, we have the following definition:
Definition 7.
is a quasi-OSL in with an OSL constant symmetric matrix
, i.e.,
where M is a real symmetric matrix.
Theorem 3.
Consider system (1) under the quasi-OSL condition (8). If Assumption 2 holds and if
then (4) yields practical stable for (1).
Proof.
If one supposes where , then we have
Then, using (10), one can have
Then, (9) guarantees the practical stability of the considered observer. □
5. Separation Principle
In this section, we outline the necessary assumptions, introduce a key lemma, and present a theorem that encapsulates the main result for the separation principle in fractional-order systems. In our case, we assume that the nominal linear component of the system is controllable. A review of the literature reveals that several studies have addressed more complex nonlinear scenarios, as discussed in references [,].
Assumption 3.
The pair (A, B) is stabilizable. There exists a matrix such that , and a Lyapunov function for the linear system can be chosen as
, where , such that
We present Lemma 2.
Lemma 2.
Assume that Assumption 3 and condition (3) are satisfied, and the constant fulfills the inequality
Thus, the feedback control law
globally stabilizes system (1) in the sense of Mittag–Leffler stability.
Proof.
See Appendix C. □
Now, consider system (1) with the given in Lemma 2, where . Thus, Theorem 4 is presented.
Theorem 4.
Condition (3) is fulfilled and if assumptions (2) and (3) are satisfied, and if
then the system
is practically stable.
Proof.
One defines and .
One supposes the function
where . Then, we have
From (13) and Lemma 1, it follows that
Now, considering (10) and the Cauchy–Schwarz inequality,
knowing that and using condition (3),
If (12) is satisfied, we have presented in the proof of Theorem 3.1 that
So, one has
where
Thus, if we choose such that , system (13) is practically stable. □
6. Illustrative Examples
Example 1.
One supposes
where
We can present system (1) as , where
Using Lemma 2, we show that practically stabilizes the nominal part. In fact, by solving (10) and choosing , one obtains
Furthermore, we have , thus the feedback system is practically stable. With , is observable. By solving (2), we find
where , and one has , thus, (12) holds. Based on Theorem 4, system (16) is practically stabilizable throughout . By fixing , Figure 1 and Figure 2 show the curves’ evolution for both the actual and estimated states when . These figures clearly demonstrate the practical stability of all signals, thereby validating our theoretical results.
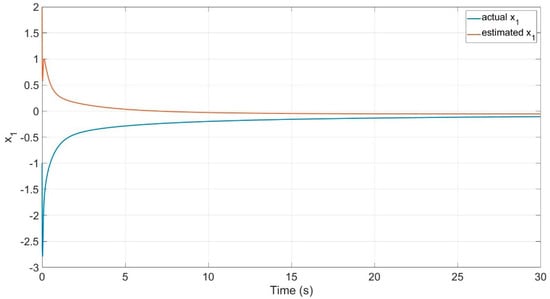
Figure 1.
The actual state and its corresponding estimate for Example 1.
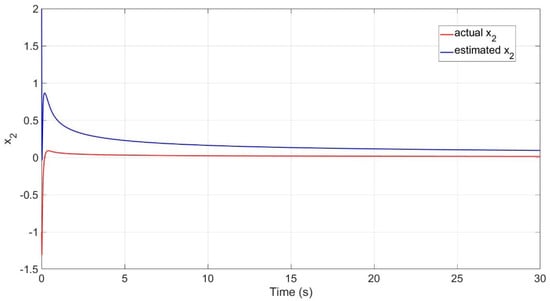
Figure 2.
The actual state and its corresponding estimate for Example 1.
In Figure 1, the actual state and its corresponding estimate for Example 1 are plotted over time. This figure depicts how the states converge towards a small neighborhood around the origin, indicating practical stability. Despite the presence of the nonlinear terms and external disturbance , the error between the actual state and its estimate stabilizes, demonstrating the effectiveness of the control law.
Figure 2 displays the evolution of the actual state and its estimate over time, starting from initial conditions and . The graph illustrates that the estimated states converge to the actual states, thereby validating the effectiveness of the observer design. The closeness of the estimated states to the actual states over time reinforces the practical stability of the system when the observer is applied.
Example 2.
Consider the system
where
We can present system (15) as , where
Based on Lemma 2, the control law practically stabilizes the nominal part. In fact, by solving (10) and choosing , one obtains:
Furthermore, we have , thus, the feedback system is practically stable. On the other hand, with , solving Equation (2) yields
where . We have , so condition (12) holds, and, based on Theorem 4, system (15) is practically stabilizable throughout . Fixing .
Figure 3 depicts the actual states and and their estimates for Example 2, with . These figures demonstrate the practical stability of all signals, thereby confirming the theoretical results.
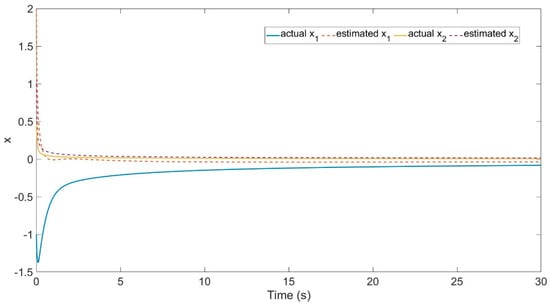
Figure 3.
Actual states and and their estimates for Example 2.
7. Conclusions
This paper addresses the observer-based control problem for nonlinear systems governed by the Caputo–Hadamard fractional-order derivative. By introducing the novel concept of practical stability, we ensure that the system solutions converge towards a small ball around the origin, thus enhancing their robustness to disturbances. A practical observer design is developed under the OSL condition, which is extended to fractional-order systems. This novel approach guarantees convergence despite nonlinearities and disturbances. Our theoretical findings are supported by numerical examples, offering new insights for robust observer design in fractional-order systems and paving the way for future research in areas such as adaptive control and fault-tolerant systems. Moreover, this work opens up potential applications in various engineering fields, including the control of complex industrial processes, autonomous systems, and biomedical engineering. The concepts presented could also be adapted to address emerging challenges in the control of systems with time-varying delays and uncertainties, contributing to the development of more resilient and flexible control strategies.
Author Contributions
Conceptualization: R.I., O.N. and M.T.; Methodology: A.B.M., O.N. and M.T.; Software: M.T.; Validation: A.B.M. and M.T.; Formal analysis: L.M. and M.T.; Investigation: O.N. and M.T.; Resources: M.T.; Writing—original draft preparation: R.I. and M.T.; Writing—review and editing: R.I. and M.T.; Visualization: O.N. and M.T.; Supervision: O.N. and M.T.; Project administration: M.T. Funding acquisition: M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Saud University through Researchers Supporting Project number (RSPD2024R685), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
The authors confirm that no data were generated or analyzed during the current study. Therefore, data sharing is not applicable to this article.
Acknowledgments
The authors acknowledge “Researchers Supporting Project number (RSPD2024R685), King Saud University, Riyadh, Saudi Arabia”.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
Appendix A
Proof of Theorem 1.
If one supposes
then
where . One also supposes
Based on Lemma 1, one obtains
We have
And so
Using Assumption 1, we deduce that
Let . Using the fact that
then, using (5), one can have
Thus, if (5) is fulfilled, we have with
Similar to the proof of Theorem 1 in [], we find the practical stability of the error system. □
Appendix B
Proof of Theorem 2.
The proof of Theorem 2 follows a similar approach to that of Theorem 1. One supposes that , so
Consider . Based on Lemma 1, we have
Now using (6), we have
Using Assumption 1, we deduce that
Let . Using the fact that
then, using (6), one can have
If (7) is fulfilled, we have with .
Thus, the origin of the error equation is practically stable. □
Appendix C
Proof of Lemma 2.
One supposes and solves (10) for . One considers system (1), where , and one chooses . One then finds that
Using condition (3) and Assumption 1 and knowing that , then
Let . Using the fact that
it yields
If (11) is fulfilled, then practically stabilizes the system (1). □
References
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Hadamard, J. Essai sur l’étude des fonctions données par leur développement de Taylor. J. Math. Pures Appl. 1892, 8, 101–186. [Google Scholar]
- Erochenkova, G.; Lima, R. A fractional diffusion equation for a marker in porous media. Chaos Interdiscip. J. Nonlinear Sci. 2001, 11, 495–499. [Google Scholar] [CrossRef] [PubMed]
- Del-Castillo-Negrete, D. Fractional diffusion models of anomalous transport. In Anomalous Transport: Foundations and Applications; Wiley: Hoboken, NJ, USA, 2008; pp. 163–212. [Google Scholar]
- Teka, W.W.; Upadhyay, R.K.; Mondal, A. Fractional-order leaky integrate-and-fire model with long-term memory and power law dynamics. Neural Netw. 2017, 93, 110–125. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Gómez, Á.; Langarica-Cordoba, D.; Martinez-Rodriguez, P.R.; González-Aguilar, H.; Guilbert, D.; Saldivar, B. Design and implementation of the Luenberger observer for estimating the voltage response of a PEM electrolyzer during supply current variations. IEEE Access. 2024, 12, 68266–68277. [Google Scholar] [CrossRef]
- Borja-Jaimes, V.; Coronel-Escamilla, A.; Escobar-Jiménez, R.F.; Adam-Medina, M.; Guerrero-Ramírez, G.V.; Sánchez-Coronado, E.M.; García-Morales, J. Fractional-Order Sliding Mode Observer for Actuator Fault Estimation in a Quadrotor UAV. Mathematics 2024, 12, 1247. [Google Scholar] [CrossRef]
- Park, G. Optimal vehicle position estimation using adaptive unscented Kalman filter based on sensor fusion. Mechatronics 2024, 99, 103144. [Google Scholar] [CrossRef]
- Moroz, V.V.; Gavriushin, S.S.; Murashov, M.V.; Baulina, L.V. Industrial Automation for Regulating the Technological Process of High-Pressure Hydrogen Generation. In Proceedings of the IEEE 25th International Conference of Young Professionals in Electron Devices and Materials (EDM), Altai, Russia, 28 June–2 July 2024; pp. 1680–1683. [Google Scholar]
- Jmal, A.; Naifar, O.; Ben Makhlouf, A.; Derbel, N.; Hammami, M.A. On observer design for nonlinear Caputo fractional-order systems. Asian J. Control 2018, 20, 1533–1540. [Google Scholar] [CrossRef]
- Echi, N.; Mabrouk, F. Observer based control for practical stabilization of one-sided Lipschitz nonlinear systems. Rocky Mt. J. Math. 2024, 54, 109–120. [Google Scholar] [CrossRef]
- Naifar, O.; Makhlouf, A.B. Fractional Order Systems—Control Theory and Applications, Fundamentals and Applications. In Studies in Systems, Decision and Control Series; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Marzougui, S.; Bedoui, S.; Atitallah, A.; Abderrahim, K. Parameter and state estimation of nonlinear fractional-order model using Luenberger observer. Circuits Syst. Signal Process. 2022, 41, 5366–5391. [Google Scholar] [CrossRef]
- Iqbal, W.; Ghous, I.; Ansari, E.A.; Duan, Z.; Imran, M.; Khan, A.A.; Humayun, M.T. Robust nonlinear observer-based controller design for one-sided Lipschitz switched systems with time-varying delays. J. Frankl. Inst. 2023, 360, 2046–2067. [Google Scholar] [CrossRef]
- Su, B.; Zhang, F.; Huang, P. Observer-based adaptive backstepping control and the application for a class of multi-input multi-output nonlinear systems with structural uncertainties and perturbations. Int. J. Robust Nonlinear Control. 2023, 33, 6211–6232. [Google Scholar] [CrossRef]
- He, J.; Xiao, M.; Lu, Y.; Wang, Z.; Zheng, W.X. Fractional-order PID control of tipping in network congestion. Int. J. Syst. Sci. 2023, 54, 1873–1891. [Google Scholar] [CrossRef]
- Damak, H.; Hammami, M.A.; Heni, R. Input-to-state practical stability criteria of non-autonomous infinite-dimensional systems. J. Control. Decis. 2024, 11, 190–200. [Google Scholar] [CrossRef]
- Jothimani, K.; Valliammal, N.; Vijayakumar, V. An exploration of controllability on Hilfer fractional system via integral contractor. Math. Methods Appl. Sci. 2023, 46, 16156–16169. [Google Scholar] [CrossRef]
- Jothimani, K.; Valliammal, N.; Alsaeed, S.; Nisar, K.S.; Ravichandran, C. Controllability results of Hilfer fractional derivative through integral contractors. Qual. Theory Dyn. Syst. 2023, 22, 137. [Google Scholar] [CrossRef]
- Gassara, H.; Iben Ammar, I.; Ben Makhlouf, A.; Mchiri, L.; Rhaima, M. Design of Polynomial Observer-Based Control of Fractional-Order Power Systems. Mathematics 2024, 11, 4450. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).