Leveraging the Performance of Integrated Power Systems with Wind Uncertainty Using Fractional Computing-Based Hybrid Method
Abstract
1. Introduction
- The Gaussian probability distribution function is used in scenario-based optimum RPD to provide an effective characterization of wind power output and load uncertainty.
- The modeling of a novel integrated optimization mechanism, namely FHPSO, based on the collaboration of Shanon entropy, fractional calculus, PSO, and GSA, is shown as an alternate method for solving probabilistic RPD problems.
- The computational intelligence and rich pedigree of FHPSO versions based on various fractional orders are demonstrated by minimizing the voltage deviation index and line losses while fulfilling operational constraints and scenario power demand in electric networks.
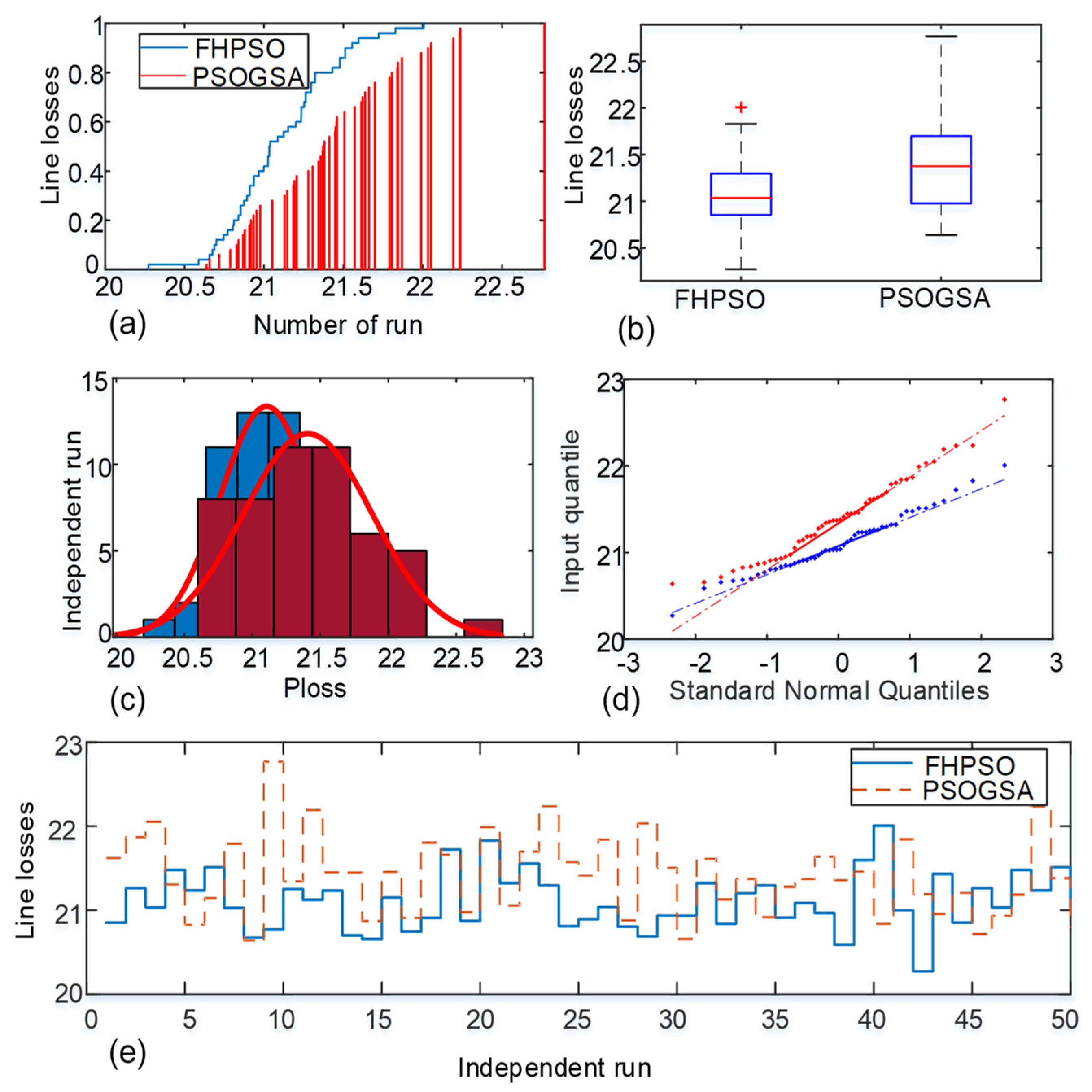
- A detailed statistical comparison of the proposed FHPSO and original FPSOGSA-EE based on cumulative distribution function graph, boxplot illustration, quantile-quantile plot, and histograms to validate the consistency, stability, efficacy, and scalability of the FHPSO. The remainder of this research document is organized as follows.
| Ref. | Methods | Objectives | Year | Ref. | Methods | Objectives | Year |
|---|---|---|---|---|---|---|---|
| [44] | Evolutionary programming | f1 | 1995 | [45] | Enhanced firefly | f1, f2 | 2015 |
| [46] | Adaptive genetic algorithm | f1 | 1998 | [47] | Differential evolution | f1 | 2015 |
| [48] | PSO | f1 | 2000 | [49] | Backtracking search | f1, f2 | 2016 |
| [50] | Multi-agent PSO | f1, f1 | 2005 | [10] | Chaotic krill herd | f1, f2 | 2016 |
| [51] | Improved GA | f1 | 2005 | [52] | Exchange market algorithm | f1, f2, stability | 2016 |
| [53] | GA-interior point method | f1 | 2006 | [54] | Quasi-oppositional DE | f1, f2, stability | 2016 |
| [55] | Modified PSO | Stability | 2007 | [56] | Oppositional krill herd | f1, f2 | 2016 |
| [57] | Turbulent crazy PSO | f1, f2 | 2009 | [58] | Two-point estimate method | f1, f2, stability | 2016 |
| [59] | Self-adaptive real-coded GA | f1 | 2009 | [60] | Moth-flame optimization | f1 | 2017 |
| [61] | Comprehensive learning PSO | f1 | 2010 | [62] | GBWC | f1, f2 | 2017 |
| [63] | MNSGA-II | f1, stability | 2011 | [12] | Chemical reaction | f1, f2, stability | 2018 |
| [64] | Ant colony optimization | f1 | 2011 | [8] | ABC-FF | f1, f2, stability | 2018 |
| [65] | Biogeography optimization | f1, f2 | 2011 | [66] | Whale optimization | f1 | 2018 |
| [67] | Harmony search algorithm | f1, f2, f3 | 2011 | [68] | Sine cosine algorithm | f1, f2 | 2019 |
| [69] | Adaptive approaches | f1, f2 | 2012 | [70] | Moth Swarm Algorithm | f1, f2 | 2019 |
| [71] | HFMOEA | f1, stability | 2013 | [72] | ALC-PSO algorithm | f1, f2 | 2019 |
| [73] | Opposition-based GSA | f1, f2, stability | 2013 | [74] | Lightning Attachment | f1 | 2019 |
| [75] | MICA-IWO | f1 | 2014 | [76] | Enhanced GWO | f1, f2 | 2019 |
| [77] | Teaching learning | f1 | 2015 | [78] | Artificial bee colony | f1, f2, stability | 2020 |
| [79] | Hybrid firefly algorithm | f1, f2 | 2015 | [80] | Chaotic Bat Algorithm | f1, f2, stability | 2020 |
| [81] | Gray wolf optimizer (GWO) | f1, f2 | 2015 |
2. System Model
2.1. Uncertainty Characterization
2.2. Problem Formulation
2.2.1. Voltage Deviation Index (VDI)
2.2.2. Power Loss Minimization
- •
- x2 represents vector of the controlling parameters such as the transformers tap setting (T1, T2, …, TNT), generators voltage magnitude (VG1, VG2, …, VGNPV), reactive power compensators (QC1, QC2, …, QCNC).
- •
- x1 represents the dependent parameters such as the reactive power of the generator (QG1, QG2, …, QGNPV), load voltages (VL1, VL2, …, VLNL) and line loading (SL1, SL2, …, SLNL).
- •
- R represents the total branches in power system.
- •
- f (x1, x2) is power loss minimization function.
- •
- gr represents the line conductance.
- •
- Vj and Vi are, respectively, the receiving and sending end voltages.
- •
- δi and δj are the sending and receiving end voltage angles, respectively.
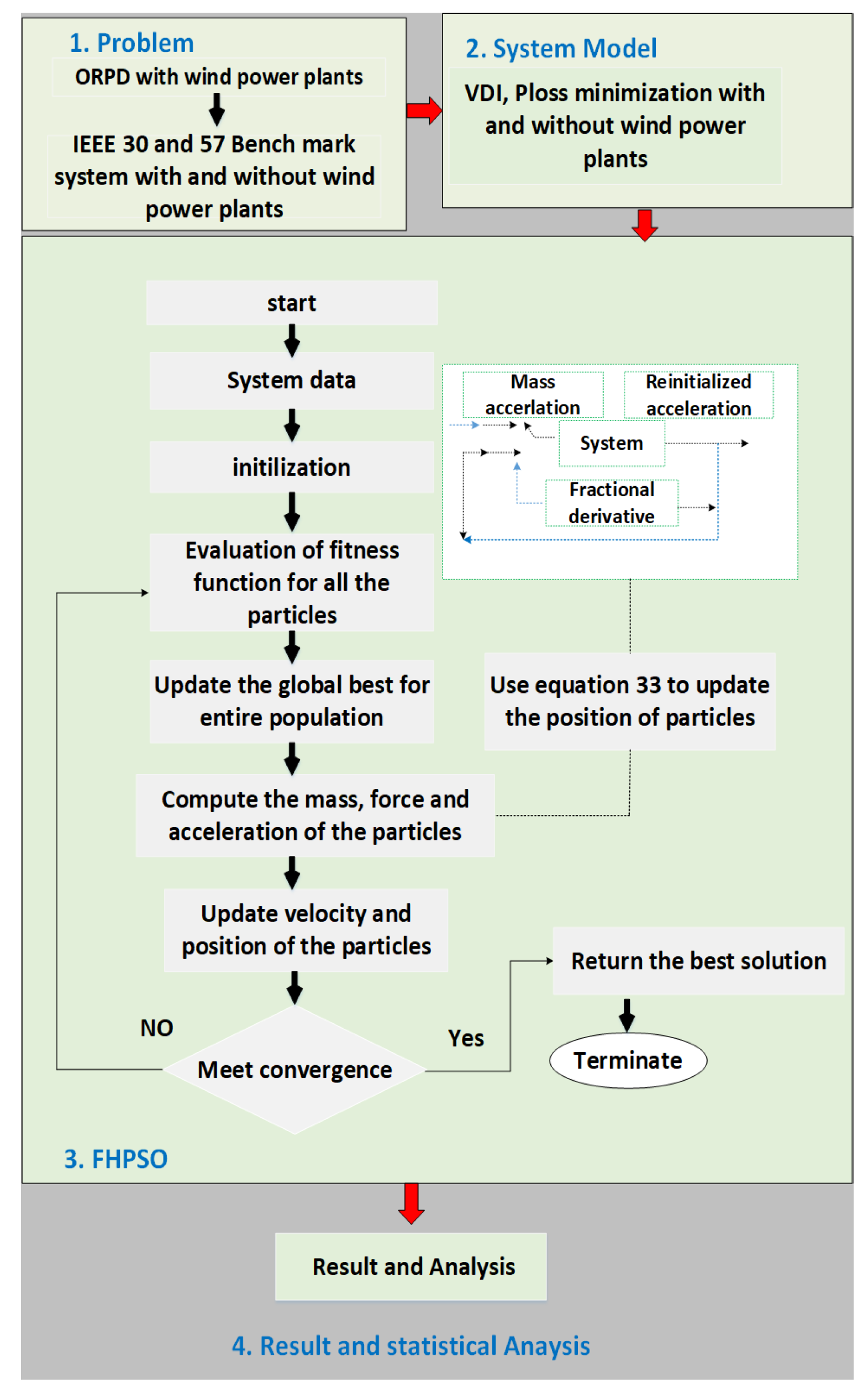
3. Design Methodology
3.1. Conventional GSA
3.2. Traditional PSO
3.3. The Hybrid PSOGSA
3.4. Fractional Calculus
3.5. Fractional PSO
3.6. Entropy
3.7. Fractional Hybrid PSO
3.8. VCPI Method
4. Case Study and Simulation Results
4.1. Reactive Power Dispatch under Wind/Load Uncertainties
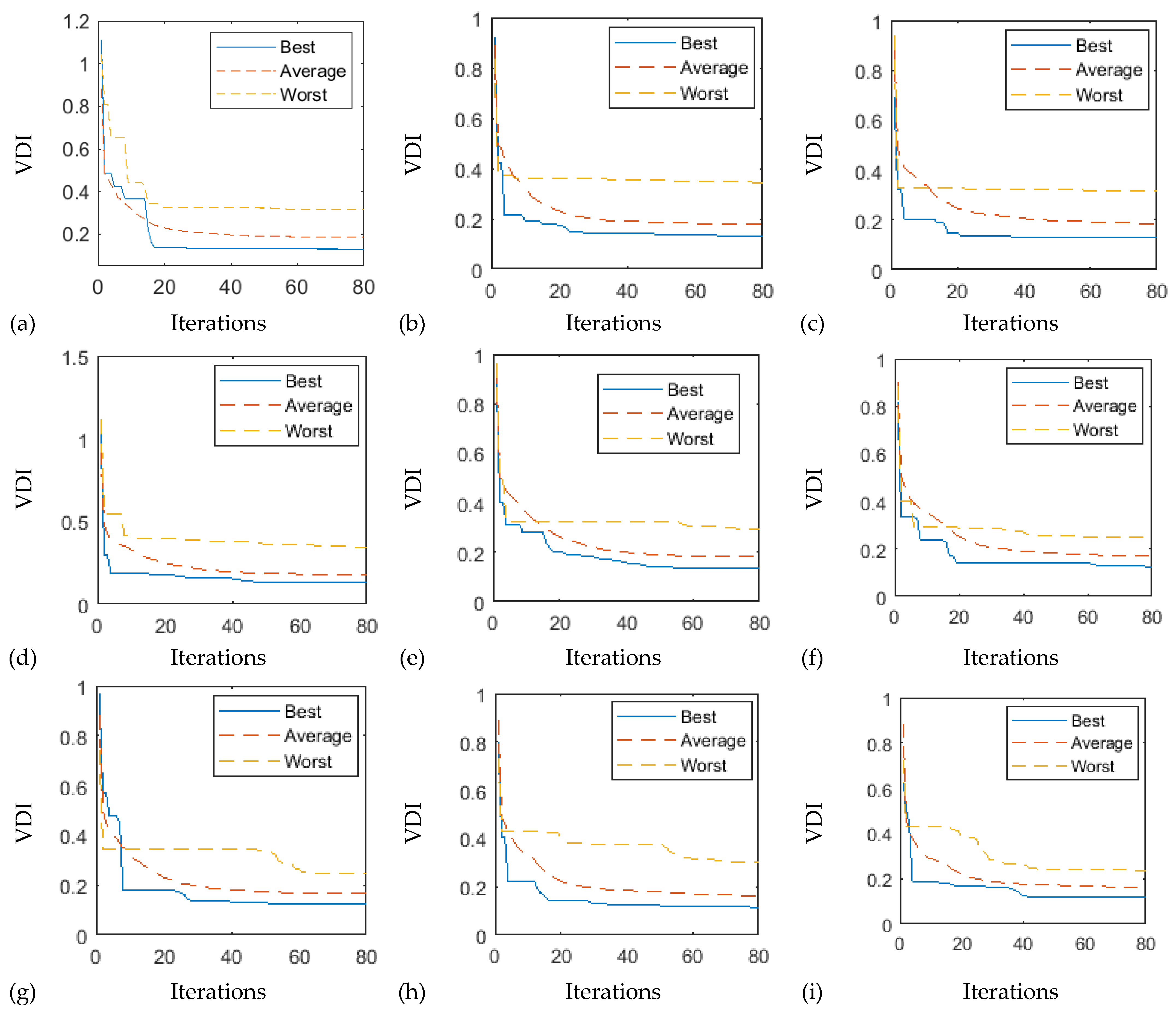
4.2. V DI Minimization in the IEEE 30 Bus
4.3. VDI Minimization Considering WPPs in IEEE 30 Bus
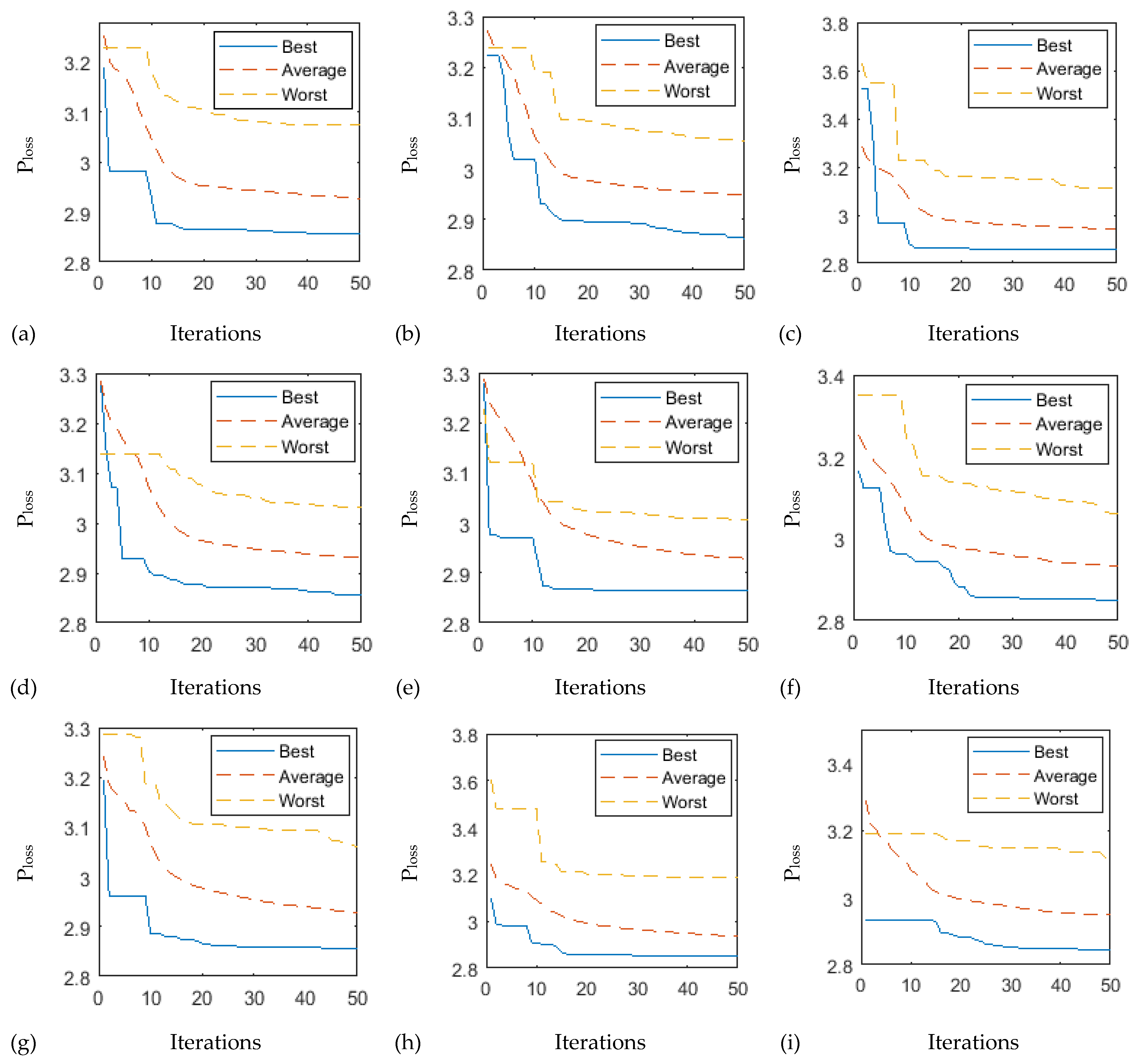
4.4. Ploss Minimization Considering WPPs
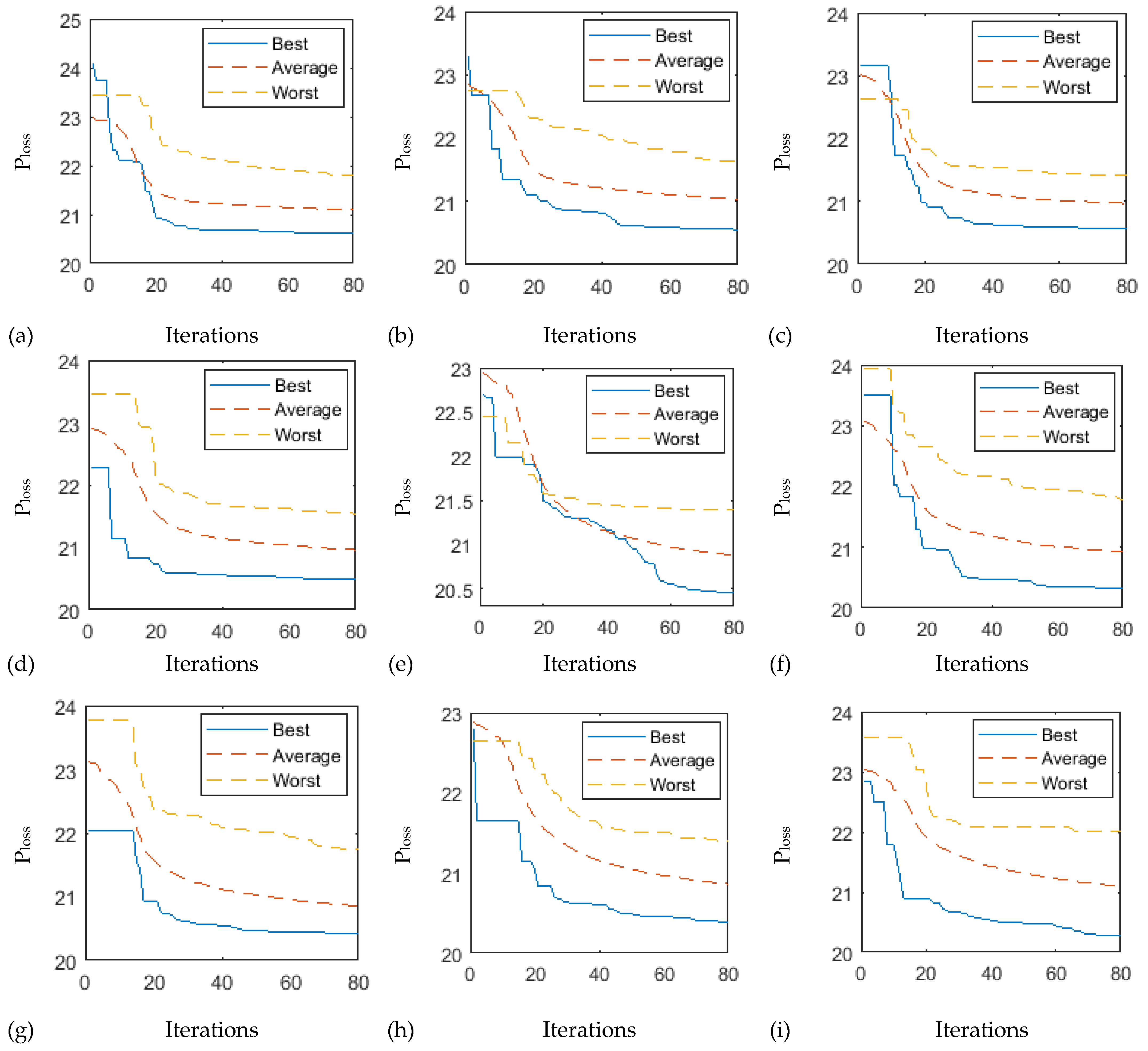
4.5. Ploss Minimization Considering WPPs in IEEE 57 Bus
4.6. Traditional Optimal RPD Problems (without Considering Wind Power Plants)
5. Discussion and Statistical Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ali, A.; Abbas, G.; Keerio, M.U.; Touti, E.; Ahmed, Z.; Alsalman, O.; Kim, Y.-S. A Bi-Level Techno-Economic Optimal Reactive Power Dispatch Considering Wind and Solar Power Integration. IEEE Access 2023, 11, 62799–62819. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Multi-objective optimal power flow solutions using a constraint handling technique of evolutionary algorithms. Soft Comput. 2020, 24, 2999–3023. [Google Scholar] [CrossRef]
- Papazoglou, G.; Biskas, P. Review and Comparison of Genetic Algorithm and Particle Swarm Optimization in the Optimal Power Flow Problem. Energies 2023, 16, 1152. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Fatahi, A.; Zamani, H.; Mirjalili, S.; Oliva, D. Hybridizing of Whale and Moth-Flame Optimization Algorithms to Solve Diverse Scales of Optimal Power Flow Problem. Electronics 2022, 11, 831. [Google Scholar] [CrossRef]
- Wais, D.S.; Majeed, W.S. The gravitational search algorithm for incorporating TCSC devices into the system for optimum power flow. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 4678–4688. [Google Scholar] [CrossRef]
- Kumar, L.; Kar, M.K.; Kumar, S. Statistical analysis based reactive power optimization using improved differential evolutionary algorithm. Expert Syst. 2023, 40, e13091. [Google Scholar] [CrossRef]
- Sarhan, S.; Shaheen, A.; El-Sehiemy, R.; Gafar, M. An Augmented Social Network Search Algorithm for Optimal Reactive Power Dispatch Problem. Mathematics 2023, 11, 1236. [Google Scholar] [CrossRef]
- Badi, M.; Mahapatra, S.; Raj, S. Hybrid BOA-GWO-PSO algorithm for mitigation of congestion by optimal reactive power management. Optim. Control Appl. Methods 2023, 44, 935–966. [Google Scholar] [CrossRef]
- Chary, G.V.B.; Rosalina, K.M. Least Squares Regression Based Ant Lion Optimizer to Solve Optimal Reactive Power and Economic Load Dispatch Problems. J. Electr. Eng. Technol. 2023, 18, 3391–3413. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Kamel, S.; Hassan, M.H.; Zeinoddini-Meymand, H. CAVOA: A chaotic optimization algorithm for optimal power flow with facts devices and stochastic wind power generation. IET Gener. Transm. Distrib. 2024, 18, 121–144. [Google Scholar] [CrossRef]
- Kar, M.K.; Kumar, S.; Singh, A.K.; Panigrahi, S. Reactive power management by using a modified differential evolution algorithm. Optim. Control Appl. Methods 2023, 44, 967–986. [Google Scholar] [CrossRef]
- Hazra, S.; Shukla, R.D.; Roy, P.K.; Metia, S. Oppositional Chemical Reaction Optimization Applied to Renewable-Hydro-Thermal Energy Systems. In Proceedings of the 2024 IEEE 3rd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 25–27 January 2024; pp. 331–336. [Google Scholar]
- Xia, W.; Che, J.; Hu, K.; Xu, Y. A synchronized multi-step wind speed prediction with adaptive features and parameters selection: Insights from an interaction model. Expert Syst. Appl. 2024, 255, 124764. [Google Scholar] [CrossRef]
- Lv, M.; Wang, J.; Niu, X.; Lu, H. A newly combination model based on data denoising strategy and advanced optimization algorithm for short-term wind speed prediction. J. Ambient Intell. Humaniz. Comput. 2022, 14, 8271–8290. [Google Scholar] [CrossRef]
- Niu, X.; Wang, J. A combined model based on data preprocessing strategy and multi-objective optimization algorithm for short-term wind speed forecasting. Appl. Energy 2019, 241, 519–539. [Google Scholar] [CrossRef]
- Wadood, A.; Ahmed, E.; Khan, S.; Ali, H. Fraction order particle swarm optimization for parameter extraction of triple-diode photovoltaic models. Eng. Res. Express 2024, 6, 025316. [Google Scholar] [CrossRef]
- Ates, A.; Alagoz, B.B.; Kavuran, G.; Yeroglu, C. Implementation of fractional order filters discretized by modified fractional order Darwinian particle swarm optimization. Measurement 2017, 107, 153–164. [Google Scholar] [CrossRef]
- Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A. A Novel Feature Selection Approach Based on FODPSO and SVM. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2935–2947. [Google Scholar] [CrossRef]
- Couceiro, M.S.; Rocha, R.P.; Ferreira, N.M.F.; Machado, J.A.T. Introducing the fractional-order Darwinian PSO. Signal Image Video Process. 2012, 6, 343–350. [Google Scholar] [CrossRef]
- Łegowski, A.; Niezabitowski, M. Robot path control based on pso with fractional-order velocity. In Proceedings of the 2016 International Conference on Robotics and Automation Engineering (ICRAE), Jeju, Republic of Korea, 27–29 August 2016; pp. 21–25. [Google Scholar]
- Akbar, S.; Zaman, F.; Asif, M.; Rehman, A.U.; Raja, M.A.Z. Novel application of fo-dpso for 2-d parameter estimation of electromagnetic plane waves. Neural Comput. Appl. 2019, 31, 3681–3690. [Google Scholar] [CrossRef]
- Wadood, A.; Sattar Khan, B.; Albalawi, H.; Alatwi, A.M. Design of the Novel Fractional Order Hybrid Whale Optimizer for Thermal Wind Power Generation Systems with Integration of Chaos Infused Wind Power. Fractal Fract. 2024, 8, 379. [Google Scholar] [CrossRef]
- Wadood, A.; Park, H. A Novel Application of Fractional Order Derivative Moth Flame Optimization Algorithm for Solving the Problem of Optimal Coordination of Directional Overcurrent Relays. Fractal Fract. 2024, 8, 251. [Google Scholar] [CrossRef]
- Wadood, A.; Ahmed, E.; Rhee, S.B.; Khan, B.S. A Fractional-Order Archimedean Spiral Moth–Flame Optimization Strategy to Solve Optimal Power Flows. Fractal Fract. 2024, 8, 225. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Wang, J.; Shu, H.; Li, D.; Zeng, C.; Chen, Y.; Zhang, X.; Yu, T. Robust fractional-order pid control of su-percapacitor energy storage systems for distribution network applications: A perturbation compensation based approach. J. Clean. Prod. 2021, 279, 123362. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Wang, J.; Yang, R. Online simultaneous identification of parameters and order of a fractional order battery model. J. Clean. Prod. 2020, 247, 119147. [Google Scholar] [CrossRef]
- Lai, X.; He, L.; Wang, S.; Zhou, L.; Zhang, Y.; Sun, T.; Zheng, Y. Co-estimation of state of charge and state of power for lithium-ion batteries based on fractional variable-order model. J. Clean. Prod. 2020, 255, 120203. [Google Scholar] [CrossRef]
- Zhao, H.; Lifeng, W. Forecasting the non-renewable energy consumption by an adjacent accumulation grey model. J. Clean. Prod. 2020, 275, 124113. [Google Scholar] [CrossRef]
- Paliwal, K.; Singh, S.; Gaba, P. Feature selection approach of hyperspectral image using GSA-FODPSO-SVM. In Proceedings of the 2017 International Conference on Computing, Communication and Automation (ICCCA), Greater Noida, India, 5–6 May 2017; pp. 1070–1075. [Google Scholar]
- Ghamisi, P.; Couceiro, M.S.; Benediktsson, J.A. Classification of hyperspectral images with binary fractional order Darwinian PSO and random forests. In Image and Signal Processing for Remote Sensing XIX, Proceedings of the SPIE Remote Sensing 2013, Dresden, Germany, 23–25 September 2013; International Society for Optics and Photonics: Bellingham, WA, USA; p. 88920S.
- Wang, Y.-Y.; Peng, W.-X.; Qiu, C.-H.; Jiang, J.; Xia, S.-R. Fractional-order Darwinian PSO-based feature selection for media-adventitia border detection in intravascular ultrasound images. Ultrasonics 2019, 92, 1–7. [Google Scholar] [CrossRef]
- Ates, A.; Kavuran, G.; Alagoz, B.B.; Yeroglu, C. Improvement of IIR filter discretization for fractional order filter by discrete stochastic optimization. In Proceedings of the 2016 39th International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016; pp. 583–586. [Google Scholar]
- Guo, F.; Peng, H.; Zou, B.; Zhao, R.; Liu, X. Localisation and segmentation of optic disc with the fractional-order Darwinian particle swarm optimisation algorithm. IET Image Process. 2018, 12, 1303–1312. [Google Scholar] [CrossRef]
- Yokoya, N.; Ghamisi, P. Land-cover monitoring using time-series hyperspectral data via fractional-order Darwinian particle swarm optimization segmentation. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–5. [Google Scholar]
- Wadood, A.; Yousaf, A.-F.; Alatwi, A.M. An Enhanced Multiple Unmanned Aerial Vehicle Swarm Formation Control Using a Novel Fractional Swarming Strategy Approach. Fractal Fract. 2024, 8, 334. [Google Scholar] [CrossRef]
- Katal, N.; Narayan, S. Design of robust fractional order pid controllers for coupled tank systems using multi-objective particle swarm optimisation. Int. J. Syst. Control. Commun. 2017, 8, 250–267. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Fractional order sliding mode pid controller/observer for continuous nonlinear switched systems with pso parameter tuning. In The International Conference on Advanced Machine Learning Technologies and Applications, Proceedings of the 2018 International Conference on Advanced Machine Learning Technologies and Applications (AMLTA 2018), Cairo, Egypt, 22–24 February 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 13–22. [Google Scholar]
- Li, X.; Wang, Y.; Li, N.; Han, M.; Tang, Y.; Liu, F. Optimal fractional order PID controller design for automatic voltage regulator system based on reference model using particle swarm optimization. Int. J. Mach. Learn. Cybern. 2017, 8, 1595–1605. [Google Scholar] [CrossRef]
- Guezgouz, M.; Jurasz, J.; Bekkouche, B.; Ma, T.; Javed, M.S.; Kies, A. Optimal hybrid pumped hydro-battery storage scheme for off-grid renewable energy systems. Energy Convers. Manag. 2019, 199, 112046. [Google Scholar] [CrossRef]
- Gao, M.; Yang, H.; Xiao, Q.; Goh, M. A novel fractional grey Riccati model for carbon emission prediction. J. Clean. Prod. 2021, 282, 124471. [Google Scholar] [CrossRef]
- Kosari, M.; Teshnehlab, M. Non-linear fractional-order chaotic systems identification with approximated fractional-order derivative based on a hybrid particle swarm optimization-genetic algorithm method. J. AI Data Min. 2018, 6, 365–373. [Google Scholar]
- Abdulkhader, H.K.; Jacob, J.; Mathew, A.T. Fractional-order leadlag compensator-based multi-band power system stabiliser design using a hybrid dynamic ga-pso algorithm. IET Gener. Transm. Distrib. 2018, 12, 3248–3260. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, N.; Awan, S.E.; Raja, M.A.Z.; Chaudhary, N.I.; Kiani, A.K.; Ullah, F.; Shu, C.-M. Fractional memetic computing paradigm for reactive power management involving wind-load chaos and uncertainties. Chaos, Solitons Fractals 2022, 161, 112285. [Google Scholar] [CrossRef]
- Wu, Q.; Ma, J. Power system optimal reactive power dispatch using evolutionary programming. IEEE Trans. Power Syst. 1995, 10, 1243–1249. [Google Scholar] [CrossRef]
- Liang, R.-H.; Wang, J.-C.; Chen, Y.-T.; Tseng, W.-T. An enhanced firefly algorithm to multi-objective optimal active/reactive power dispatch with uncertainties consideration. Int. J. Electr. Power Energy Syst. 2015, 64, 1088–1097. [Google Scholar] [CrossRef]
- Wu, Q.; Cao, Y.; Wen, J. Optimal reactive power dispatch using an adaptive genetic algorithm. Int. J. Electr. Power Energy Syst. 1998, 20, 563–569. [Google Scholar] [CrossRef]
- Amrane, Y.; Boudour, M.; Ladjici, A.A.; Elmaouhab, A. Optimal VAR control for real power loss minimization using differential evolution algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 262–271. [Google Scholar] [CrossRef]
- Yoshida, H.; Kawata, K.; Fukuyama, Y.; Takayama, S.; Nakanishi, Y. A particle swarm optimization for reactive power and voltage control considering voltage security assessment. IEEE Trans. Power Syst. 2000, 15, 1232–1239. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Optimal reactive power dispatch using backtracking search algorithm. Aust. J. Electr. Electron. Eng. 2016, 13, 200–210. [Google Scholar] [CrossRef]
- Zhao, B.; Guo, C.X.; Cao, Y.J. A multiagent-based particle swarm optimization approach for optimal reactive power dispatch. IEEE Trans. Power Syst. 2005, 20, 1070–1078. [Google Scholar] [CrossRef]
- Durairaj, S.; Kannan, P.S.; Devaraj, D. Application of genetic algorithm to optimal reactive power dispatch including voltage stability constraint. J. Energy Environ. 2005, 4, 7. [Google Scholar]
- Rajan, A.; Malakar, T. Exchange market algorithm based optimum reactive power dispatch. Appl. Soft Comput. 2016, 43, 320–336. [Google Scholar] [CrossRef]
- Yan, W.; Liu, F.; Chung, C.; Wong, K. A Hybrid Genetic Algorithm–Interior Point Method for Optimal Reactive Power Flow. IEEE Trans. Power Syst. 2006, 21, 1163–1169. [Google Scholar] [CrossRef]
- Basu, M. Quasi-oppositional differential evolution for optimal reactive power dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 29–40. [Google Scholar] [CrossRef]
- Cai, G.; Ren, Z.; Yu, T. Optimal Reactive Power Dispatch Based on Modified Particle Swarm Optimization Considering Voltage Stability. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–5. [Google Scholar]
- Dutta, S.; Mukhopadhyay, P.; Roy, P.K.; Nandi, D. Unified power flow controller based reactive power dispatch using oppositional krill herd algorithm. Int. J. Electr. Power Energy Syst. 2016, 80, 10–25. [Google Scholar] [CrossRef]
- Roy, P.K.; Ghoshal, S.P.; Thakur, S. Turbulent crazy particle swarm optimization technique for optimal reactive power dispatch. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 1219–1224. [Google Scholar]
- Mohseni-Bonab, S.M.; Rabiee, A.; Mohammadi-Ivatloo, B.; Jalilzadeh, S.; Nojavan, S. A two-point estimate method for uncertainty modeling in multi-objective optimal reactive power dispatch problem. Int. J. Electr. Power Energy Syst. 2016, 75, 194–204. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar] [CrossRef]
- Mahadevan, K.; Kannan, P. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- Heidari, A.A.; Abbaspour, R.A.; Jordehi, A.R. Gaussian barebones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. 2017, 57, 657–671. [Google Scholar] [CrossRef]
- Jeyadevi, S.; Baskar, S.; Babulal, C.; Iruthayarajan, M.W. Solving multiobjective optimal reactive power dispatch using modified NSGA-II. Int. J. Electr. Power Energy Syst. 2011, 33, 219–228. [Google Scholar] [CrossRef]
- El-Ela, A.A.A.; Kinawy, A.M.; El-Sehiemy, R.A.; Mouwafi, M.T. Optimal reactive power dispatch using ant colony optimization algorithm. Electr. Eng. 2011, 93, 103–116. [Google Scholar] [CrossRef]
- Roy, P.K.; Ghoshal, S.P.; Thakur, S.S. Optimal reactive power dispatch considering flexible ac transmission system devices using bio-geography-based optimization. Electr. Power Compon. Syst. 2011, 39, 733–750. [Google Scholar] [CrossRef]
- Ben Oualid Medani, K.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Sivasubramani, S.; Swarup, K. Multi-objective harmony search algorithm for optimal power flow problem. Int. J. Electr. Power Energy Syst. 2011, 33, 745–752. [Google Scholar] [CrossRef]
- Abdel-Fatah, S.; Ebeed, M.; Kamel, S. Optimal reactive power dispatch using modified sine cosine algorithm. In Proceedings of the 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 2–4 February 2019; pp. 510–514. [Google Scholar]
- Mallipeddi, R.; Jeyadevi, S.; Suganthan, P.; Baskar, S. Efficient constraint handling for optimal reactive power dispatch problems. Swarm Evol. Comput. 2012, 5, 28–36. [Google Scholar] [CrossRef]
- Abdel-Fatah, S.; Ebeed, M.; Kamel, S.; Nasrat, L. Moth Swarm Algorithm for Reactive Power Dispatch Considering Stochastic Nature of Renewable Energy Generation and Load. In Proceedings of the 2019 21st International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 17–19 December 2019; pp. 594–599. [Google Scholar]
- Saraswat, A.; Saini, A. Multi-objective optimal reactive power dispatch considering voltage stability in power systems using HFMOEA. Eng. Appl. Artif. Intell. 2013, 26, 390–404. [Google Scholar] [CrossRef]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S. Optimal reactive power dispatch by particle swarm optimization with an aging leader and challengers. Appl. Soft Comput. 2015, 29, 298–309. [Google Scholar] [CrossRef]
- Shaw, B.; Mukherjee, V.; Ghoshal, S. Solution of reactive power dispatch of power systems by an opposition-based gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 29–40. [Google Scholar] [CrossRef]
- Abdel-Fatah, S.; Ebeed, M.; Kamel, S.; Yu, J. Reactive Power Dispatch Solution with Optimal Installation of Renewable Energy Resources Considering Uncertainties. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 118–123. [Google Scholar]
- Ghasemi, M.; Ghavidel, S.; Ghanbarian, M.M.; Habibi, A. A new hybrid algorithm for optimal reactive power dispatch problem with discrete and continuous control variables. Appl. Soft Comput. 2014, 22, 126–140. [Google Scholar] [CrossRef]
- Kamel, S.; Abdel-Fatah, S.; Ebeed, M.; Yu, J.; Xie, K.; Zhao, C. Solving optimal reactive power dispatch problem considering load uncertainty. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1335–1340. [Google Scholar]
- Ghasemi, M.; Taghizadeh, M.; Ghavidel, S.; Aghaei, J.; Abbasian, A. Solving optimal reactive power dispatch problem using a novel teaching–learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2015, 39, 100–108. [Google Scholar] [CrossRef]
- Ettappan, M.; Vimala, V.; Ramesh, S.; Kesavan, V.T. Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using artificial bee colony algorithm. Microprocess. Microsyst. 2020, 76, 103085. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Optimal reactive power dispatch using hybrid Nelder–Mead simplex based firefly algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 9–24. [Google Scholar] [CrossRef]
- Mugemanyi, S.; Qu, Z.; Rugema, F.X.; Dong, Y.; Bananeza, C.; Wang, L. Optimal Reactive Power Dispatch Using Chaotic Bat Algorithm. IEEE Access 2020, 8, 65830–65867. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S.; Wang, G.-G.; Coelho, L.D.S. Binary optimization using hybrid particle swarm optimization and gravitational search algorithm. Neural Comput. Appl. 2014, 25, 1423–1435. [Google Scholar] [CrossRef]
- Pires, E.J.S.; Machado, J.A.T.; De Moura Oliveira, P.B.; Cunha, J.B.; Mendes, L. Particle swarm optimization with fractional-order velocity. Nonlinear Dyn. 2010, 61, 295–301. [Google Scholar] [CrossRef]
- McBride, A. Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ortigueira, M.D.; Machado, J.A.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- De Oliveira, E.C.; Machado, J.A.T. A review of definition for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 1–7. [Google Scholar] [CrossRef]
- Davison, M.; Essex, C. Fractional differential equations and initial value problems. Math. Sci. 1998, 23, 108–116. [Google Scholar]
- Usta, I.; Arik, I.; Yenilmez, I.; Kantar, Y.M. A new estimation approach based on moments for estimating weibull parameters in wind power applications. Energy Convers. Manag. 2018, 164, 570–578. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A.; Mohammadi-Ivatloo, B. Voltage stability constrained multi-objective optimal reactive power dispatch under load and wind power uncertainties: A stochastic approach. Renew. Energy 2016, 85, 598–609. [Google Scholar] [CrossRef]
- Muhammad, Y.; Khan, R.; Raja, M.A.Z.; Ullah, F.; Chaudhary, N.I.; He, Y. Design of fractional swarm intelligent computing with entropy evolution for optimal power flow problems. IEEE Access 2020, 8, 111401–111419. [Google Scholar] [CrossRef]
- Muhammad, Y.; Chaudhary, N.I.; Sattar, B.; Siar, B.; Awan, S.E.; Raja, M.A.Z.; Shu, C.-M. Fractional order swarming intelligence for multi-objective load dispatch with photovoltaic integration. Eng. Appl. Artif. Intell. 2024, 137, 109073. [Google Scholar] [CrossRef]
- Muhammad, Y.; Raja, M.A.Z.; Altaf, M.; Ullah, F.; Chaudhary, N.I.; Shu, C.-M. Design of fractional comprehensive learning PSO strategy for optimal power flow problems. Appl. Soft Comput. 2022, 130, 109638. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hassan, M.H.; Mahdy, M.A.; Kamel, S. Development and application of equilibrium optimizer for optimal power flow calculation of power system. Appl. Intell. 2023, 53, 7232–7253. [Google Scholar] [CrossRef]
- Abaci, K.; Yetgin, Z.; Yamacli, V.; Isiker, H. Modified effective butterfly optimizer for solving optimal power flow problem. Heliyon 2024, 10, e32862. [Google Scholar] [CrossRef]
- Maheshwari, A.; Sood, Y.R.; Jaiswal, S. A Comprehensive Review on Stochastic Optimal Power Flow Problems and Solution Methodologies. IETE Tech. Rev. 2024, 41, 147–174. [Google Scholar] [CrossRef]

| Inputs [43] | Probabilities [43] | Outputs | |||||
|---|---|---|---|---|---|---|---|
| Scenario | Wind% | Load% | πd | πw | πs | EPloss | EVDI |
| S-25 | 100 | 105 | 0.025 | 0.1227 | 0.0031 | 0.0181 | 0.0006 |
| S-24 | 86.83 | 105 | 0.025 | 0.1992 | 0.005 | 0.0281 | 0.0015 |
| S-23 | 49.37 | 105 | 0.025 | 0.4048 | 0.0101 | 0.0588 | 0.0018 |
| S-22 | 12.87 | 105 | 0.025 | 0.2044 | 0.0051 | 0.0291 | 0.0008 |
| S-21 | 0 | 105 | 0.025 | 0.0689 | 0.0017 | 0.0097 | 0.0006 |
| S-20 | 100 | 103 | 0.135 | 0.1227 | 0.0166 | 0.0973 | 0.0033 |
| S-19 | 86.83 | 103 | 0.135 | 0.1992 | 0.0269 | 0.1516 | 0.0097 |
| S-18 | 49.37 | 103 | 0.135 | 0.4048 | 0.0546 | 0.3094 | 0.0176 |
| S-17 | 12.87 | 103 | 0.135 | 0.2044 | 0.0276 | 0.1580 | 0.0048 |
| S-16 | 0 | 103 | 0.135 | 0.0689 | 0.0093 | 0.0535 | 0.0044 |
| S-15 | 100 | 100 | 0.680 | 0.1227 | 0.0834 | 0.4752 | 0.0144 |
| S-14 | 86.83 | 100 | 0.680 | 0.1992 | 0.1355 | 0.7928 | 0.0548 |
| S-13 | 49.37 | 100 | 0.680 | 0.4048 | 0.2753 | 0.002811 | 0.0028 |
| S-12 | 12.87 | 100 | 0.680 | 0.2044 | 0.139 | 0.0166 | 0.0028 |
| S-11 | 0 | 100 | 0.680 | 0.0689 | 0.0469 | 0.2386 | 0.0160 |
| S-10 | 100 | 97 | 0.135 | 0.1227 | 0.0166 | 0.0992 | 0.0060 |
| S-09 | 86.83 | 97 | 0.135 | 0.1992 | 0.0269 | 0.0048 | 0.0079 |
| S-08 | 49.37 | 97 | 0.135 | 0.4048 | 0.0546 | 0.3125 | 0.0187 |
| S-07 | 12.87 | 97 | 0.135 | 0.2044 | 0.0276 | 0.0564 | 0.0017 |
| S-06 | 0 | 97 | 0.135 | 0.0689 | 0.0093 | 0.0527 | 0.0020 |
| S-05 | 100 | 95 | 0.025 | 0.1227 | 0.0031 | 0.0178 | 0.0012 |
| S-04 | 86.83 | 95 | 0.025 | 0.1992 | 0.005 | 0.0291 | 0.0024 |
| S-03 | 49.37 | 95 | 0.025 | 0.4048 | 0.0101 | 0.0592 | 0.0046 |
| S-02 | 12.87 | 95 | 0.025 | 0.2044 | 0.0051 | 0.0291 | 0.0012 |
| S-01 | 0 | 95 | 0.025 | 0.0689 | 0.0017 | 0.0098 | 0.0004 |
| Control Variables | Fractional Order | Integer Order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.1 | α = 0.2 | α = 0.3 | α = 0.4 | α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| V1 | 1.009997 | 1.01 | 1.00996 | 1.009357 | 1.008535 | 1.009993 | 1.01 | 1.01 | 1.009943 | 1.01 |
| V2 | 1.01 | 1.01 | 1.009976 | 1.009766 | 1.01 | 1.01 | 1.01 | 1.009989 | 1.009999 | 1.01 |
| V5 | 1.01 | 1.009526 | 1.01 | 1.009884 | 1.009977 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| V8 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.009263 |
| V11 | 0.997338 | 0.979931 | 1.01 | 1.009941 | 1.009756 | 1.00507 | 1.01 | 1.009878 | 0.998376 | 1.009335 |
| V13 | 1.007964 | 1.009966 | 1.008925 | 1.01 | 1.009993 | 1.009386 | 1.01 | 1.00106 | 1.01 | 1.00638 |
| T11 | 0.968603 | 0.958173 | 0.974194 | 0.963291 | 0.993197 | 0.951334 | 0.97888 | 0.994752 | 0.959817 | 0.980802 |
| T12 | 0.950104 | 0.95 | 0.950052 | 0.950978 | 0.950601 | 0.975811 | 0.95 | 0.951426 | 0.95 | 0.95 |
| T15 | 0.963189 | 0.970253 | 0.973144 | 0.969639 | 0.952203 | 0.973865 | 0.96685 | 0.962683 | 0.976754 | 0.978289 |
| T36 | 0.971012 | 0.964969 | 0.950336 | 0.952066 | 0.950982 | 0.951319 | 0.953682 | 0.962722 | 0.960634 | 0.973938 |
| Qc10 | 3.897704 | 4.437704 | 4.501827 | 4.873459 | 2.345744 | 3.217345 | 2.705423 | 4.786584 | 4.999846 | 2.378371 |
| Qc12 | 4.954354 | 3.819101 | 4.069773 | 0.090632 | 0.60293 | 1.636259 | 0.079362 | 4.566777 | 2.296087 | 3.541337 |
| Qc15 | 1.490825 | 4.079146 | 4.128829 | 2.989181 | 1.899343 | 2.995714 | 4.520463 | 4.855639 | 4.717713 | 4.999899 |
| Qc17 | 4.287732 | 2.549029 | 2.310929 | 1.523325 | 3.706118 | 3.27968 | 1.87727 | 3.362823 | 0.000793 | 4.997936 |
| Qc20 | 4.76726 | 3.66755 | 4.716818 | 4.989153 | 4.908928 | 4.696337 | 3.475392 | 4.92343 | 5 | 3.721863 |
| Qc21 | 4.62632 | 3.132631 | 1.729241 | 4.117648 | 4.537567 | 4.841364 | 4.828549 | 4.96083 | 5 | 5 |
| Qc23 | 4.931755 | 4.861373 | 4.949557 | 4.041004 | 4.448722 | 4.914961 | 4.503106 | 3.958634 | 5 | 5 |
| Qc24 | 2.723139 | 4.944161 | 2.525881 | 3.056695 | 3.419034 | 4.99979 | 4.659123 | 3.936695 | 3.35988 | 4.560676 |
| Qc29 | 4.930604 | 3.955492 | 1.165535 | 1.229564 | 1.326223 | 0.941414 | 2.153882 | 2.634725 | 2.576249 | 4.41817 |
| VDI (p.u.) | 0.130052 | 0.132484 | 0.128501 | 0.131554 | 0.133731 | 0.126458 | 0.124852 | 0.11517 | 0.117782 | 0.1174 |
| Control Variables | Fractional Order | Integer Order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.1 | α = 0.2 | α = 0.3 | α = 0.4 | α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| V1 | 1.009598 | 0.992727 | 1.000642 | 0.998938 | 1.003732 | 1.009926 | 1.000825 | 1.009964 | 0.984796 | 0.998802 |
| V2 | 0.980401 | 1.005783 | 1.006349 | 1.009831 | 0.994001 | 1.000287 | 1.01 | 1.008954 | 1.01 | 1.01 |
| V5 | 1.009361 | 1.009923 | 1.008598 | 1.007585 | 1.009853 | 1.01 | 1.01 | 1.009888 | 1.01 | 1.01 |
| V8 | 1.002166 | 1.008009 | 1.000658 | 0.998546 | 1.009409 | 1.001073 | 0.999756 | 0.995423 | 0.994774 | 1.005358 |
| V11 | 1.008156 | 0.952376 | 0.99613 | 0.993479 | 0.974025 | 1.01 | 0.950909 | 1.001683 | 1.01 | 0.95 |
| V13 | 1.007451 | 1.009774 | 0.989689 | 0.996711 | 0.994486 | 1.003881 | 1.006022 | 1.005176 | 1.00953 | 0.999609 |
| T11 | 1.017491 | 0.959128 | 0.994153 | 0.992835 | 0.967558 | 1.011877 | 0.952593 | 0.996736 | 1.012935 | 0.950322 |
| T12 | 1.038584 | 1.008402 | 1.044878 | 1.037886 | 1.04449 | 1.026261 | 1.001931 | 1.049976 | 1.05 | 1.030283 |
| T15 | 0.966919 | 0.969242 | 0.952456 | 0.957599 | 0.958898 | 0.95 | 0.972916 | 0.95 | 0.981771 | 0.95 |
| T36 | 0.959815 | 0.954373 | 0.953198 | 0.954614 | 0.971034 | 0.950509 | 0.963596 | 0.965718 | 0.950554 | 0.952637 |
| Qc10 | 4.997096 | 2.773556 | 2.026303 | 0.187836 | 0.015959 | 2.767962 | 1.270832 | 2.910785 | 3.441165 | 0.931014 |
| Qc12 | 1.709004 | 3.638932 | 4.197716 | 3.198421 | 3.007224 | 2.958404 | 4.723731 | 0 | 1.644165 | 4.789313 |
| Qc15 | 2.729187 | 0.026141 | 3.850031 | 1.14113 | 4.992537 | 0.354864 | 2.589197 | 3.58932 | 3.008114 | 2.762203 |
| Qc17 | 2.918021 | 4.584324 | 4.732506 | 4.926041 | 0.866615 | 2.621195 | 0.279706 | 0.601639 | 3.70388 | 3.496858 |
| Qc20 | 0.965048 | 0.096781 | 0.016877 | 3.120113 | 0.659116 | 0.566124 | 1.213956 | 0.212836 | 1.804096 | 0 |
| Qc21 | 3.708417 | 0.864623 | 4.381865 | 3.699563 | 4.28813 | 2.309885 | 3.33615 | 4.076081 | 3.018913 | 4.385511 |
| Qc23 | 4.376691 | 4.730329 | 4.632192 | 4.011251 | 4.975529 | 1.5858 | 4.999824 | 2.219595 | 4.992568 | 1.881586 |
| Qc24 | 2.400727 | 2.130312 | 2.166979 | 4.266552 | 4.879632 | 3.842694 | 2.741557 | 4.48471 | 3.8594 | 1.640443 |
| Qc29 | 1.786826 | 0.882162 | 1.627655 | 1.005825 | 2.563779 | 0.638681 | 2.544383 | 3.030669 | 0.942991 | 1.086004 |
| VDI (p.u.) | 3.18 × 10−4 | 3.08 × 10−4 | 3.05 × 10−4 | 3.18 × 10−4 | 3.16 × 10−4 | 3.26 × 10−4 | 3.22 × 10−4 | 3.18 × 10−4 | 3.08 × 10−4 | 3.23 × 10−4 |
| Control Variables | Fractional Order | Integer Order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.1 | α = 0.2 | α = 0.3 | α = 0.4 | α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| V1 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| V2 | 1.009139 | 1.008497 | 1.008984 | 1.01 | 1.008663 | 1.009636 | 1.008175 | 1.009719 | 1.009871 | 1.01 |
| V5 | 0.991447 | 0.991898 | 0.991027 | 0.991812 | 0.991838 | 0.993039 | 0.990261 | 0.989737 | 0.991319 | 0.993865 |
| V8 | 0.997199 | 0.997331 | 0.997572 | 0.997876 | 0.997914 | 0.999895 | 0.995167 | 0.996172 | 0.999264 | 0.998556 |
| V11 | 1.00973 | 1.00532 | 1.009439 | 1.00381 | 1.009616 | 1.009975 | 1.01 | 1.009219 | 1.01 | 1.01 |
| V13 | 1.009999 | 1.01 | 1.009974 | 1.01 | 1.009523 | 1.01 | 1.01 | 1.00982 | 1.01 | 1.01 |
| T11 | 1.016388 | 0.977609 | 0.96998 | 1.007841 | 0.952357 | 1.016355 | 0.994707 | 0.988959 | 0.993752 | 1.003823 |
| T12 | 0.950022 | 1.040717 | 1.016363 | 0.95 | 1.04808 | 0.971971 | 0.958049 | 0.95 | 0.951116 | 0.95 |
| T15 | 0.952916 | 0.979169 | 0.956783 | 0.950151 | 0.950167 | 0.952517 | 0.952476 | 0.950043 | 0.95 | 0.95 |
| T36 | 0.952993 | 0.967388 | 0.955043 | 0.964451 | 0.960877 | 0.964672 | 0.950321 | 0.953925 | 0.95 | 0.964321 |
| Qc10 | 1.30842 | 3.039407 | 2.498887 | 1.555517 | 2.800039 | 1.654898 | 2.300174 | 1.436268 | 3.06738 | 4.531357 |
| Qc12 | 2.615445 | 1.235816 | 3.616906 | 4.946201 | 2.364442 | 4.952389 | 1.625983 | 4.763014 | 4.155678 | 4.119073 |
| Qc15 | 3.412006 | 0.497456 | 0.023099 | 0.062106 | 0.412725 | 2.592019 | 2.132699 | 3.850767 | 1.129889 | 0.563277 |
| Qc17 | 4.467295 | 3.882846 | 4.646732 | 3.051384 | 3.0589 | 4.987051 | 1.646051 | 1.685549 | 2.839364 | 1.796974 |
| Qc20 | 0.030214 | 0.149475 | 1.461066 | 0.081318 | 1.6133.4 | 1.182738 | 1.04643 | 0.325587 | 1.111193 | 0.001759 |
| Qc21 | 4.09634 | 0.366882 | 2.671941 | 2.722601 | 2.976372 | 2.691452 | 1.728655 | 3.369179 | 1.938579 | 1.365593 |
| Qc23 | 1.136409 | 4.274631 | 3.394322 | 0.07818 | 2.136938 | 2.679618 | 4.984786 | 1.087084 | 2.861772 | 2.223829 |
| Qc24 | 1.584408 | 4.784188 | 2.545824 | 4.507205 | 3.78813 | 4.872162 | 4.340718 | 2.614785 | 4.340777 | 4.421699 |
| Qc29 | 0.00929 | 1.466873 | 1.008741 | 2.111019 | 1.079646 | 2.444771 | 1.523108 | 2.092179 | 1.129839 | 3.253818 |
| Ploss | 2.858 | 2.8631 | 2.858735 | 2.855258 | 2.864563 | 2.850616 | 2.856476 | 2.850347 | 2.845852 | 2.849088 |
| Control Variables | Fractional Order | Integer Order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| α = 0.1 | α = 0.2 | α = 0.3 | α = 0.4 | α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| V_G1 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 |
| V_G2 | 1.007645 | 1.009223 | 1.007051 | 1.009654 | 1.01 | 1.01 | 1.009446 | 1.01 | 1.01 | 1.00946 |
| V_G3 | 0.998833 | 0.999628 | 0.998998 | 1.002971 | 1.000687 | 1.000615 | 0.998295 | 1.001342 | 1.002205 | 0.996966 |
| V_G6 | 0.992719 | 0.995446 | 0.99835 | 1.003004 | 0.992987 | 0.996591 | 0.991579 | 0.992051 | 0.993074 | 0.984087 |
| V_G8 | 1.009946 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.01 | 1.009723 | 1.009934 | 1.003579 |
| V_G9 | 0.997128 | 0.994634 | 0.995134 | 0.997333 | 0.998467 | 0.999352 | 0.994094 | 0.995522 | 0.996622 | 0.98164 |
| V_G12 | 0.990462 | 0.989106 | 0.988193 | 0.9942 | 0.993211 | 0.98976 | 0.990659 | 0.991376 | 0.995006 | 0.980991 |
| T_4-18 | 0.97723 | 0.960907 | 0.988011 | 1.022341 | 1.002013 | 1.030412 | 1.031282 | 1.045078 | 0.95 | 0.95 |
| T_4-18 | 1.030279 | 0.970857 | 1.0337 | 1.043736 | 1.0281 | 0.95 | 0.985417 | 0.964339 | 1.05 | 1.013221 |
| T_21-20 | 1.024093 | 1.007874 | 0.98204 | 1.047049 | 1.049585 | 1.039553 | 1.025576 | 1.05 | 1.05 | 1.005138 |
| T_24-26 | 0.983092 | 1.047792 | 0.988998 | 1.004138 | 0.991509 | 0.998622 | 0.977219 | 1.020306 | 0.994999 | 1.05 |
| T_7-29 | 0.962191 | 0.995391 | 0.959904 | 0.959586 | 0.953988 | 0.955238 | 0.95 | 0.961194 | 0.95 | 0.999998 |
| T_34-32 | 0.989965 | 0.97816 | 1.04373 | 1.011779 | 0.951606 | 0.967364 | 0.961342 | 1.027341 | 0.950826 | 1.05 |
| T_11-41 | 1.017831 | 0.952886 | 0.957979 | 1.043545 | 1.043317 | 1.049826 | 1.045441 | 0.951355 | 0.961136 | 0.973287 |
| T_15-45 | 0.973424 | 0.950198 | 0.991595 | 0.95 | 0.952318 | 0.966384 | 0.966524 | 0.95 | 0.950071 | 0.95 |
| T_14-46 | 0.98882 | 0.97591 | 0.984263 | 0.951325 | 0.979581 | 0.951056 | 0.970844 | 0.951524 | 0.95 | 0.953992 |
| T_10-51 | 0.980632 | 0.966671 | 0.976927 | 0.969647 | 0.979036 | 0.953734 | 0.965839 | 0.95 | 0.950288 | 0.95 |
| T_13-49 | 0.958235 | 0.950137 | 0.980628 | 0.950435 | 0.950164 | 0.95007 | 0.959208 | 0.95 | 0.95 | 0.95 |
| T_11-43 | 0.955294 | 1.046944 | 0.953916 | 0.952371 | 0.960695 | 0.95 | 0.950002 | 1.036775 | 0.95 | 0.95 |
| T_40-56 | 0.981962 | 1.049014 | 1.05 | 1.013506 | 1.05 | 0.95 | 1.018456 | 0.95 | 0.977272 | 0.95 |
| T_39-57 | 0.959673 | 0.972857 | 0.953979 | 0.952371 | 0.968534 | 1.013002 | 1.031243 | 1.005092 | 0.992674 | 0.95 |
| T_9-55 | 0.964146 | 0.990958 | 0.957799 | 0.963741 | 0.954701 | 0.968277 | 0.950565 | 0.95 | 0.95 | 0.992709 |
| Q_C18 | 9.183823 | 4.919385 | 1.200194 | 0.404448 | 2.517985 | 1.488137 | 3.61981 | 0.004937 | 3.707711 | 4.043883 |
| Q_C25 | 13.89894 | 4.966403 | 3.745585 | 6.312066 | 4.020983 | 9.6559 | 10.68565 | 9.398614 | 13.0572 | 9.531845 |
| Q_C53 | 11.59676 | 10.84459 | 10.61797 | 7.870676 | 11.99991 | 13.02508 | 7.088589 | 11.87762 | 11.46538 | 10.52381 |
| Ploss | 20.60795 | 20.55402 | 20.56932 | 20.49348 | 20.45659 | 20.3324 | 20.41443 | 20.39718 | 20.27219 | 20.63867 |
| Parameter | Algorithms | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ALC-PSO | FAHL CPSO | GSA | OGSA | PSO | ABC | SGA (2) | CKHA | NGB WCA | KHA | PSOGSA | FPSOGSA | FHPSO | |
| V1 | 1.05 | 1.1 | 1.071652 | 1.05 | 1.1 | 1.05 | 1.05 | 1.05 | 1.0502 | 1.05 | 1.01 | 1.01 | 1.01 |
| V2 | 1.0384 | 1.0387 | 1.022199 | 1.041 | 1.0425 | 1.0615 | 1.0445 | 1.0473 | 1.0382 | 1.0381 | 1.01 | 1.01 | 1.009989 |
| V5 | 1.0108 | 1.0161 | 1.040094 | 1.0154 | 1.0871 | 1.0711 | 1.024 | 1.0293 | 1.0107 | 1.011 | 1.01 | 1.01 | 1.01 |
| V8 | 1.021 | 1.029 | 1.050721 | 1.0267 | 1.0859 | 1.0849 | 1.026 | 1.035 | 1.0212 | 1.025 | 1.01 | 1.009263 | 1.01 |
| V11 | 1.05 | 1.0123 | 0.977122 | 1.0082 | 1.0647 | 1.1 | 1.05 | 1.05 | 1.0503 | 1.05 | 1.01 | 1.009335 | 1.009878 |
| V13 | 1.05 | 1.1 | 0.96765 | 1.05 | 1.081 | 1.0665 | 1.05 | 1.05 | 1.05 | 1.05 | 1.01 | 1.00638 | 1.00106 |
| T11 | 0.9521 | 1.0223 | 1.09845 | 1.0585 | 1.0255 | 0.97 | 1.049 | 0.9916 | 0.952 | 0.9541 | 1.016833 | 0.980802 | 0.994752 |
| T12 | 1.0299 | 0.9107 | 0.982481 | 0.9089 | 0.95 | 1.05 | 0.9 | 0.9538 | 1.0295 | 1.0412 | 0.95 | 0.95 | 0.951426 |
| T15 | 0.9721 | 1.0098 | 1.095909 | 1.0141 | 1.0021 | 0.99 | 0.988 | 0.9603 | 0.972 | 0.9514 | 0.95 | 0.978289 | 0.962683 |
| T36 | 0.9657 | 0.9744 | 1.059339 | 1.0182 | 1.0416 | 0.99 | 0.965 | 0.967 | 0.9661 | 0.9541 | 0.970105 | 0.973938 | 0.862722 |
| Qc10 | 0.009 | 0.034125 | 1.6537 | 0.033 | 2.6425 | 5 | 0.05 | 0.0092 | 0.0097 | 0.0089 | 4.03815 | 2.378371 | 4.786584 |
| Qc12 | 0.0126 | 0.05 | 4.372261 | 0.0249 | 4.7822 | 5 | 0.05 | 0 | 0.0125 | 0 | 4.948908 | 3.541337 | 4.566777 |
| Qc15 | 0.0209 | 0.020981 | 0.119957 | 0.0177 | 4.4309 | 5 | 0.05 | 0.0153 | 0.0212 | 0.0141 | 2.870865 | 4.999899 | 4.855639 |
| Qc17 | 0.05 | 0.05 | 2.087617 | 0.05 | 4.3706 | 5 | 0.05 | 0.0497 | 0.0541 | 0.04989 | 4.7608 | 4.997936 | 3.362823 |
| Qc20 | 0.0031 | 0.035512 | 0.357729 | 0.0334 | - | 0.05 | 0.05 | 0.0302 | 0.0043 | 0.0314 | 4.981661 | 3.721863 | 4.92343 |
| Qc21 | 0.0293 | 0.004001 | 0.260254 | 0.0403 | - | 0.05 | 0.05 | 0.05 | 0.0289 | 0.0345 | 3.335246 | 5 | 4.96083 |
| Qc23 | 0.0226 | 5 | 0 | 0.0269 | - | 0.05 | 0.036 | 5 | 0.0229 | 0.0241 | 4.998355 | 4.998355 | 3.958634 |
| Qc24 | 0.05 | 0.0488 | 1.383953 | 0.05 | - | 0.05 | 0.05 | 5 | 0.0498 | 0.05 | 4.560676 | 4.560676 | 3.936695 |
| Qc29 | 0.0107 | 0.021 | 5.5372 | 0.000317 | - | 0.0256 | 0.0275 | 3.52052 | 0.0106 | 0.0107 | 4.41817 | 4.41817 | 2.634725 |
| VDI (p.u.) | 0.3001 | 0.7914 | 1.6552 | 0.854 | - | 1.6815 | 0.7372 | 0.3524 | 0.3003 | 0.2963 | 0.1258 | 0.1174 | 0.11517 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albalawi, H.; Muhammad, Y.; Wadood, A.; Khan, B.S.; Zainab, S.T.; Alatwi, A.M. Leveraging the Performance of Integrated Power Systems with Wind Uncertainty Using Fractional Computing-Based Hybrid Method. Fractal Fract. 2024, 8, 532. https://doi.org/10.3390/fractalfract8090532
Albalawi H, Muhammad Y, Wadood A, Khan BS, Zainab ST, Alatwi AM. Leveraging the Performance of Integrated Power Systems with Wind Uncertainty Using Fractional Computing-Based Hybrid Method. Fractal and Fractional. 2024; 8(9):532. https://doi.org/10.3390/fractalfract8090532
Chicago/Turabian StyleAlbalawi, Hani, Yasir Muhammad, Abdul Wadood, Babar Sattar Khan, Syeda Taleeha Zainab, and Aadel Mohammed Alatwi. 2024. "Leveraging the Performance of Integrated Power Systems with Wind Uncertainty Using Fractional Computing-Based Hybrid Method" Fractal and Fractional 8, no. 9: 532. https://doi.org/10.3390/fractalfract8090532
APA StyleAlbalawi, H., Muhammad, Y., Wadood, A., Khan, B. S., Zainab, S. T., & Alatwi, A. M. (2024). Leveraging the Performance of Integrated Power Systems with Wind Uncertainty Using Fractional Computing-Based Hybrid Method. Fractal and Fractional, 8(9), 532. https://doi.org/10.3390/fractalfract8090532







