An 8D Hyperchaotic System of Fractional-Order Systems Using the Memory Effect of Grünwald–Letnikov Derivatives
Abstract
1. Introduction
- By introducing fractional-order derivatives, the fractional-order Chen system provides a more generalized framework that can capture a wider array of dynamical behaviors, making it a powerful tool in various applications requiring nonlocal memory effects.
- The fractional-order operators provide a more flexible and accurate representation of the memory and hereditary properties inherent in many real-world systems. Unlike classical integer-order models, which assume local interactions, fractional-order models account for the history of the state variables, allowing for more accurate modeling of processes with long-range temporal correlations.
- The introduction of fractional-order derivatives can lead to more complex dynamical behaviors, such as a wider range of chaotic attractors and bifurcation scenarios. This increased complexity allows the fractional-order Chen system to better capture the nuances of the chaotic phenomena observed in physical, biological, and engineering systems.
- The fractional-order Chen system can exhibit chaos at lower parameter values compared to the classical system, which can be advantageous in designing systems that require chaotic behavior for performance, such as in cryptography or random number generation.
2. Mathematical Formulation and Methodology
2.1. Basic Idea
2.2. Proposed Methodology
| Algorithm 1 Simulation of fractional-order system |
|
3. Numerical Analysis of the Proposed Methodology
3.1. Analysis of FOs (1) for the Set of Orders at
3.2. Analysis of FOs (1) for the Set of Orders at
4. Chaotic Characteristics and Complexity Analysis
4.1. Perron Effect
4.2. Kolmogorov–Sinai (KS) Entropy
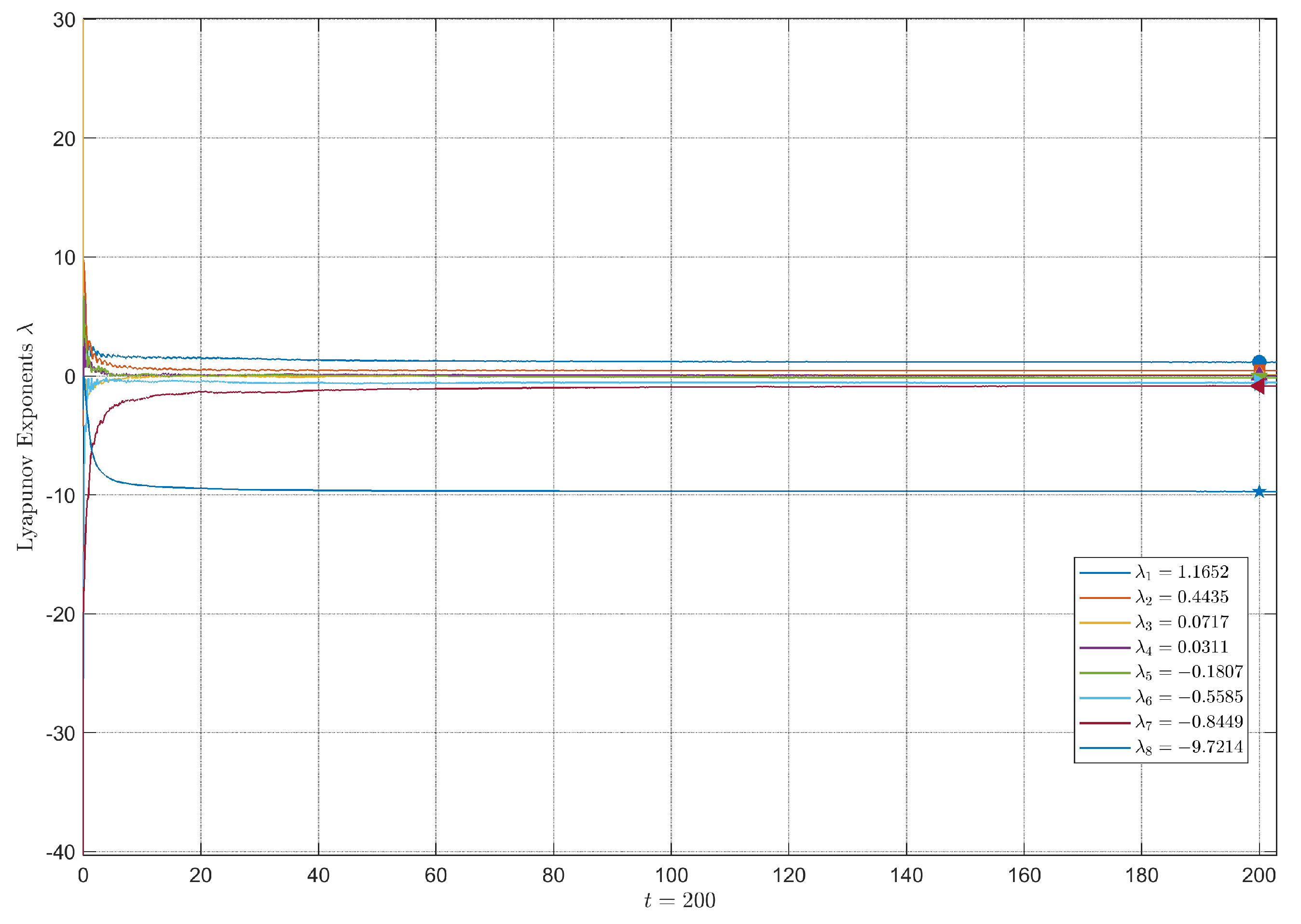
4.3. Lyapunov Exponents and Kaplan–Yorke Dimension
| Algorithm 2 Calculate Kaplan–Yorke dimension |
|
4.4. 0–1 Test for Chaos
- •
- is the value of the ith state variable at time step k.
- •
- and are the translation variables obtained from the time series of the dynamical system. They are computed by projecting the time series onto two orthogonal directions defined by a randomly chosen angle.
- •
- is the total number of time points in the time series from to .
- •
- is the total number of data points in the time series, and it defines the upper limit of the summation.
- •
- represents the average squared displacement of the points in the space over a time lag n.
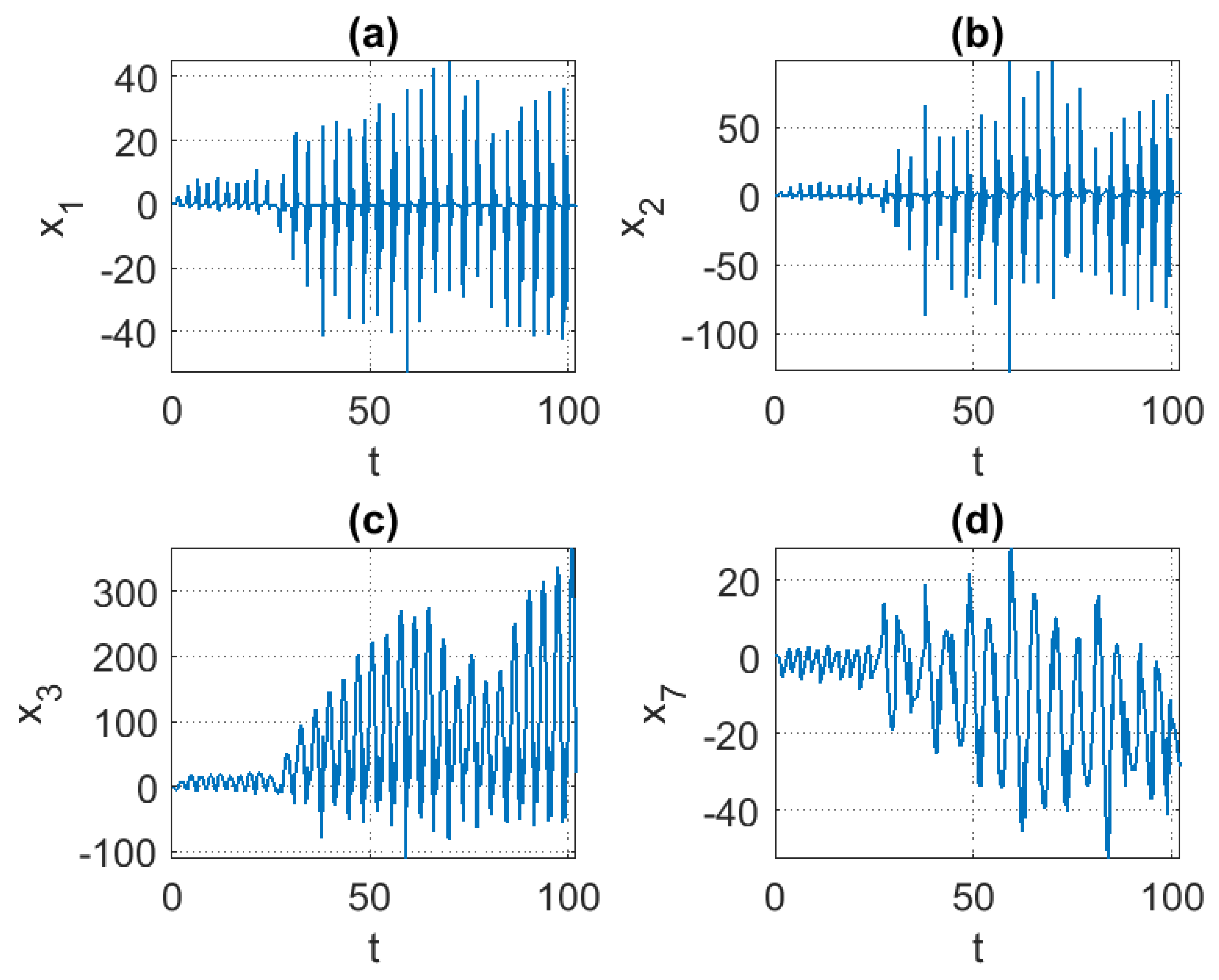
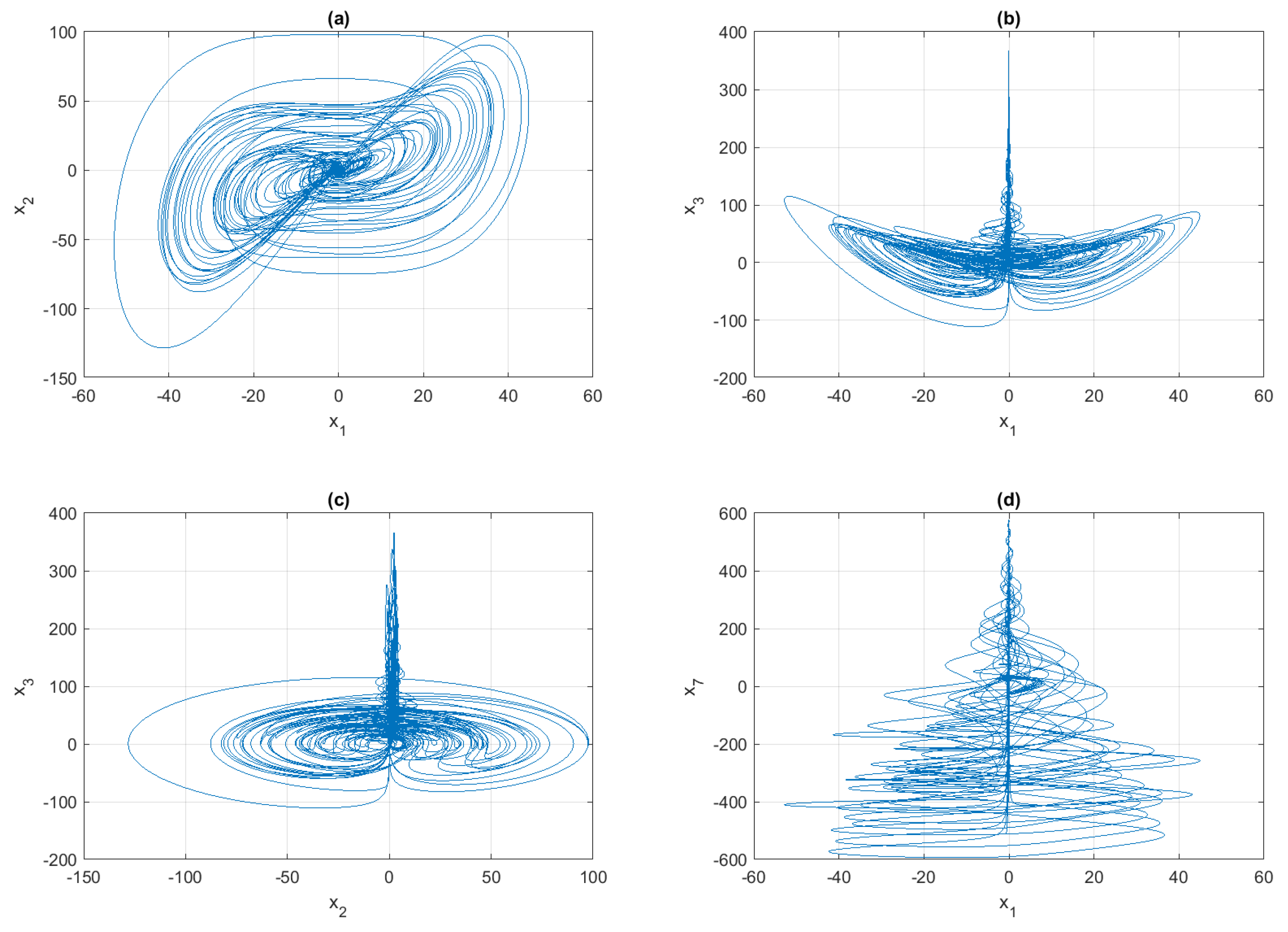
5. Results and Discussions
6. Conclusions
7. Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 1994. [Google Scholar]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hilfer, R. Fractional diffusion based on Riemann-Liouville fractional derivatives. J. Phys. Chem. B 2000, 104, 3914–3917. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 000010151520150081. [Google Scholar] [CrossRef]
- Syam, M.I.; Mohammed, A.-R. Fractional differential equations with Atangana–Baleanu fractional derivative: Analysis and applications. Chaos Solitons Fractals 2019, X 2, 100013. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Grunwald, A.K. Ueber “begrenzte” Derivationen und deren Anwendung. Z. FüR Angew. Math. Und Phys. 1867, 12, 441–480. [Google Scholar]
- Letnikov, A.V. Theory of differentiation of fractional order. Mat. Sb. 1868, 3, 1868. [Google Scholar]
- Qin, H.; Li, L.; Li, Y.; Chen, X. Time-Stepping Error Estimates of Linearized Grünwald–Letnikov Difference Schemes for Strongly Nonlinear Time-Fractional Parabolic Problems. Fractal Fract. 2024, 8, 390. [Google Scholar] [CrossRef]
- Abdel Aal, M. New Perturbation–Iteration Algorithm for Nonlinear Heat Transfer of Fractional Order. Fractal Fract. 2024, 8, 313. [Google Scholar] [CrossRef]
- Tian, H.; Zhao, M.; Liu, J.; Wang, Q.; Yu, X.; Wang, Z. Dynamic Analysis and Sliding Mode Synchronization Control of Chaotic Systems with Conditional Symmetric Fractional-Order Memristors. Fractal Fract. 2024, 8, 307. [Google Scholar] [CrossRef]
- Dehingia, K.; Boulaaras, S. The Stability of a Tumor–Macrophages Model with Caputo Fractional Operator. Fractal Fract. 2024, 8, 394. [Google Scholar] [CrossRef]
- Kuznetsov, N.V. Lyapunov Functions and Exponents in the Analysis of Dynamical Systems. Ph.D. Thesis, 2010. [Google Scholar]
- Oseledets, V.I. A multiplicative ergodic theorem. Characteristic Ljapunov, exponents of dynamical systems. Trans. Mosc. Math. Soc. 1968, 19, 197–231. [Google Scholar]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.M. Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them. Part 1: Theory. Meccanica 1980, 15, 9–20. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Habib, S.; Ryne, R.D. Symplectic calculation of Lyapunov exponents. Phys. Rev. Lett. 1995, 74, 70. [Google Scholar] [CrossRef]
- Lorenz, E.N. The local structure of a chaotic attractor in four dimensions. Phys. D 1984, 13, 90–104. [Google Scholar] [CrossRef]
- Bryant, P.; Brown, R.; Abarbanel, H.D. Lyapunov exponents from observed time series. Phys. Rev. Lett. 1990, 65, 1523. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Eykholt, R.; Pielke, R. Estimating the Lyapunov-exponent spectrum from short time series of low precision. Phys. Rev. Lett. 1991, 66, 3229. [Google Scholar] [CrossRef]
- Balcerzak, M.; Dabrowski, A.; Blazejczyk-Okolewska, B.; Stefanski, A. Determining Lyapunov exponents of non-smooth systems: Perturbation vectors approach. Mech. Syst. Signal Process. 2020, 141, 106734. [Google Scholar] [CrossRef]
- Soriano, D.C.; Fazanaro, F.I.; Suyama, R.; de Oliveira, J.R.; Attux, R.; Madrid, M.K. A method for Lyapunov spectrum estimation using cloned dynamics and its application to the discontinuously-excited FitzHugh–Nagumo model. Nonlinear Dyn. 2012, 67, 413–424. [Google Scholar] [CrossRef]
- Stefanski, A. Estimation of the largest Lyapunov exponent in systems with impacts. Chaos Solitons Fractals 2000, 11, 2443–2451. [Google Scholar] [CrossRef]
- Wang, G.; Ding, H.; Chen, L. Nonlinear normal modes and optimization of a square root nonlinear energy sink. Nonlinear Dyn. 2021, 104, 1069–1096. [Google Scholar] [CrossRef]
- Vogl, M.; Rötzel, P.G. Chaoticity versus stochasticity in financial markets: Are daily S and P 500 return dynamics chaotic? Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106218. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, C.; Liu, C.; Yong, H.; Zhang, X. Optically triggered chaotic vortex avalanches in superconducting films. Phys. Rev. A 2020, 13, 024036. [Google Scholar] [CrossRef]
- Li, H.; Shen, Y.; Yang, S.; Peng, M.; Han, Y. Simultaneous primary and super-harmonic resonance of Duffing oscillator. Acta Phys. Sin. 2021, 70, 040502. [Google Scholar]
- Valério, D.; Machado, J.T.; Kiryakova, V. Some pioneers of the applications of fractional calculus. Fract. Calc. Appl. Anal. 2014, 17, 552–578. [Google Scholar] [CrossRef]
- Naim, M.; Lahmidi, F.; Namir, A.; Kouidere, A. Dynamics of a fractional SEIR epidemic model with infectivity in latent period and general nonlinear incidence rate. Chaos Solitons Fractals 2021, 152, 111456. [Google Scholar] [CrossRef]
- Higazy, M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals 2020, 138, 110007. [Google Scholar] [CrossRef]
- Kamal, F.; Elsonbaty, A.; Elsaid, A. A novel fractional nonautonomous chaotic circuit model and its application to image encryption. Chaos Solitons Fractals 2021, 144, 110686. [Google Scholar] [CrossRef]
- Wang, S.; Hong, L.; Jiang, J.; Li, X. Synchronization precision analysis of a fractional-order hyperchaos with application to image encryption. AIP Adv. 2020, 10, 105316. [Google Scholar] [CrossRef]
- Sun, L.; Chen, Y. Numerical analysis of variable fractional viscoelastic column based on two-dimensional Legendre wavelets algorithm. Chaos Solitons Fractals 2021, 152, 111372. [Google Scholar] [CrossRef]
- Meral, F.; Royston, T.; Magin, R. Fractional calculus in viscoelasticity: An experimental study. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 939–945. [Google Scholar] [CrossRef]
- Hou, J.; Niu, J.; Shen, Y.; Yang, S.; Zhang, W. Dynamic analysis and vibration control of two-degree-of-freedom boring bar with fractional-order model of magnetorheological fluid. J. Vib. Control 2022, 28, 3001–3018. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, Y.; Baleanu, D.; Chen, W.; Chen, Y. A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 2018, 64, 213–231. [Google Scholar] [CrossRef]
- Diethelm, K.; Kiryakova, V.; Luchko, Y.; Machado, J.; Tarasov, V.E. Trends, directions for further research, and some open problems of fractional calculus. Nonlinear Dyn. 2022, 107, 3245–3270. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y. Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 2013, 71, 621–633. [Google Scholar] [CrossRef]
- Li, C.; Gong, Z.; Qian, D.; Chen, Y. On the bound of the Lyapunov exponents for the fractional differential systems. Chaos 2010, 20, 013127. [Google Scholar] [CrossRef]
- Grigorenko, I.; Grigorenko, E. Chaotic dynamics of the fractional Lorenz system. Phys. Rev. Lett. 2003, 91, 034101. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, X. Simple estimation method for the largest Lyapunov exponent of continuous fractional-order differential equations. Phys. A Stat. Mech. Its Appl. 2021, 563, 125478. [Google Scholar] [CrossRef]
- Danca, M.F. Matlab code for Lyapunov exponents of fractional-order systems, Part II: The noncommensurate case. Int. J. Bifurc. Chaos 2021, 31, 2150187. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, W.; Xiao, X.; Yao, W.; Cai, S.; Zhang, J.; Wang, C.; Li, Y. Dynamic Analysis and Field-Programmable Gate Array Implementation of a 5D Fractional-Order Memristive Hyperchaotic System with Multiple Coexisting Attractors. Fractal Fract. 2024, 8, 271. [Google Scholar] [CrossRef]
- Mahmoud, E.E.; Higazy, M.; Al-Harthi, T.M. A New Nine-Dimensional Chaotic Lorenz System with Quaternion Variables: Complicated Dynamics, Electronic Circuit Design, Anti-Anticipating Synchronization, and Chaotic Masking Communication Application. Mathematics 2019, 7, 877. [Google Scholar] [CrossRef]
- Zhu, J.L.; Dong, J.; Gao, H.Q. Nine-Dimensional Eight-Order Chaotic System and its Circuit Implementation. Appl. Mech. Mater. 2014, 716–717, 1346–1351. [Google Scholar] [CrossRef]
- Jianliang, Z.; Shouqiang, K.; Huaqiang, G.; Yujing, W. Ten-dimensional nine-order chaotic system and its circuit implementation. In Proceedings of the IEEE 12th International Conference on Electronic Measurement and Instruments, ICEMI, Qingdao, China, 16–18 July 2015; pp. 964–968. [Google Scholar]
- Lu, T.; Li, C.; Wang, X.; Tao, C.; Liu, Z. A memristive chaotic system with offset-boostable conditional symmetry. Eur. Phys. J. Spec. Top. 2020, 229, 1059–1069. [Google Scholar] [CrossRef]
- Benkouider, K.; Bouden, T.; Sambas, A.; Lekouaghet, B.; Mohamed, M.A.; Ibrahim Mohammed, S.; Ahmad, M.Z. A new 10-D hyperchaotic system with coexisting attractors and high fractal dimension: Its dynamical analysis, synchronization and circuit design. PLoS ONE 2022, 17, e0266053. [Google Scholar] [CrossRef]
- Biban, G.; Chugh, R.; Panwar, A. Image encryption based on 8D hyperchaotic system using Fibonacci Q-Matrix. Chaos Solitons Fractals 2023, 170, 113396. [Google Scholar] [CrossRef]
- Chen, Z.M. A note on Kaplan-Yorke-type estimates on the fractal dimension of chaotic attractors. Chaos Solitons Fractals 1993, 3, 575–582. [Google Scholar] [CrossRef]
- Hu, Z.; Chan, C.K. A 7-D hyperchaotic system-based encryption scheme for secure fast-OFDM-PON. J. Light. Technol. 2018, 36, 3373–3381. [Google Scholar] [CrossRef]
- Yang, Q.; Zhu, D.; Yang, L. A new 7D hyperchaotic system with five positive Lyapunov exponents coined. Int. J. Bifurc. Chaos 2018, 28, 1850057. [Google Scholar] [CrossRef]
- Yu, W.; Wang, J.; Wang, J.; Zhu, H.; Li, M.; Li, Y.; Jiang, D. Design of a New Seven-Dimensional Hyperchaotic Circuit and Its Application in Secure Communication. IEEE Access 2019, 7, 125586–125608. [Google Scholar] [CrossRef]
- Lagmiri, S.N.; Amghar, M.; Sbiti, N. Seven Dimensional New Hyperchaotic Systems: Dynamics and Synchronization by a High Gain Observer Design. Int. J. Control Autom. 2017, 10, 251–266. [Google Scholar] [CrossRef]
- Varan, M.; Akgul, A. Control and synchronisation of a novel seven-dimensional hyperchaotic system with active control. Pramana 2018, 90, 1–8. [Google Scholar] [CrossRef]
- Falconer, I.; Gottwald, G.A.; Melbourne, I.; Wormnes, K. Application of the 0–1 test for chaos to experimental data. SIAM J. Appl. Dyn. Syst. 2007, 6, 395–402. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. On the implementation of the 0–1 test for chaos. SIAM J. Appl. Dyn. Syst. 2009, 8, 129–145. [Google Scholar] [CrossRef]
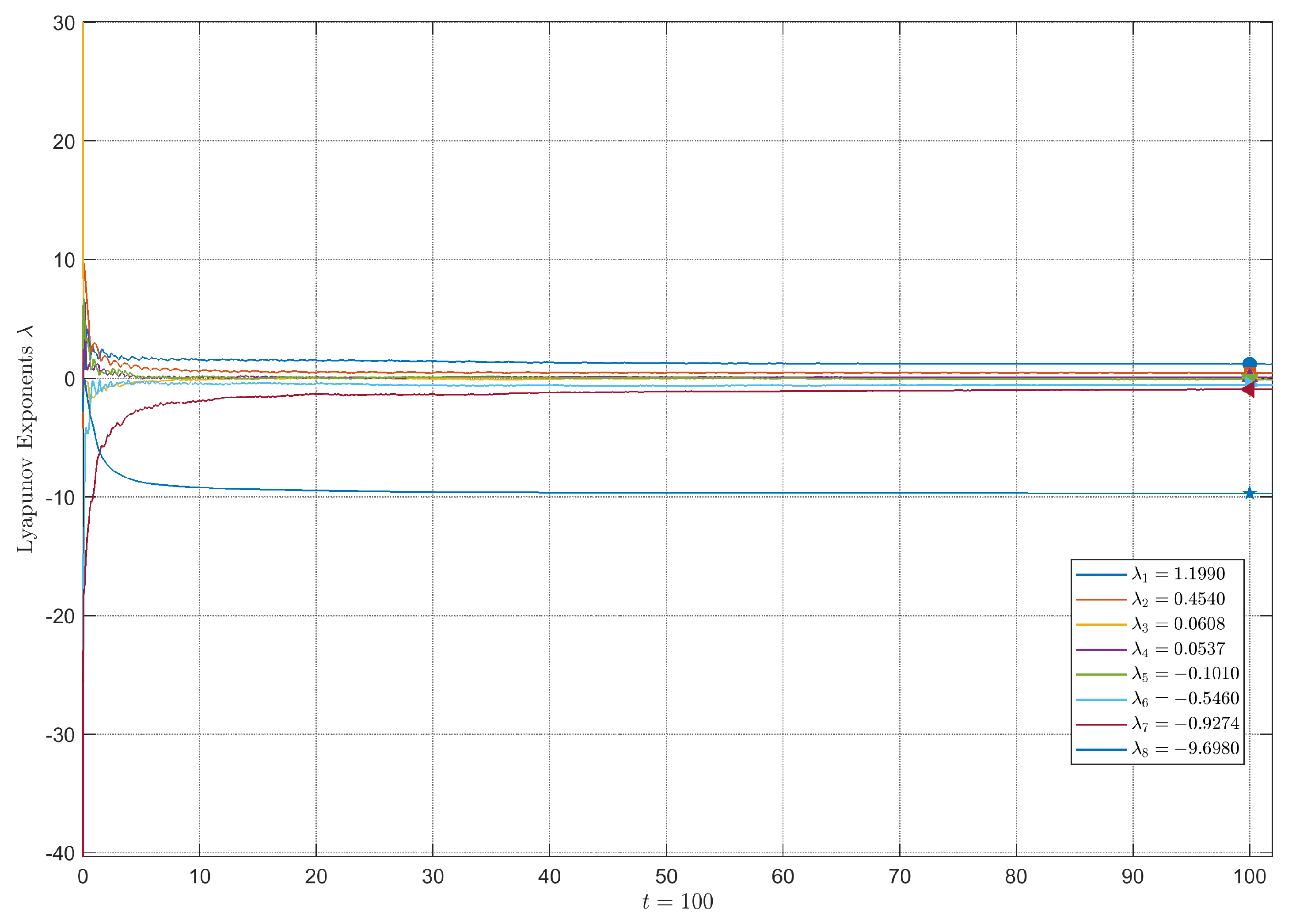

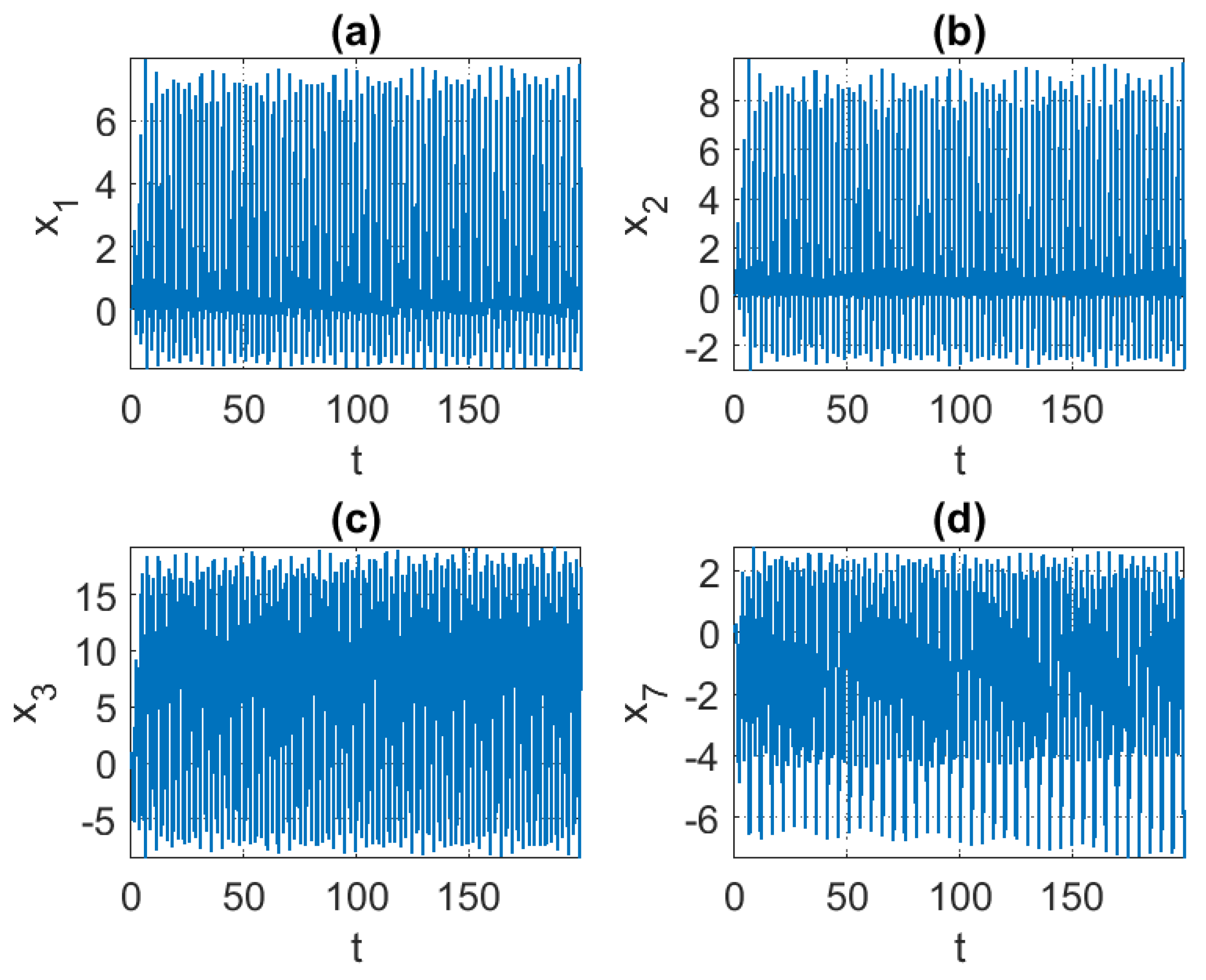
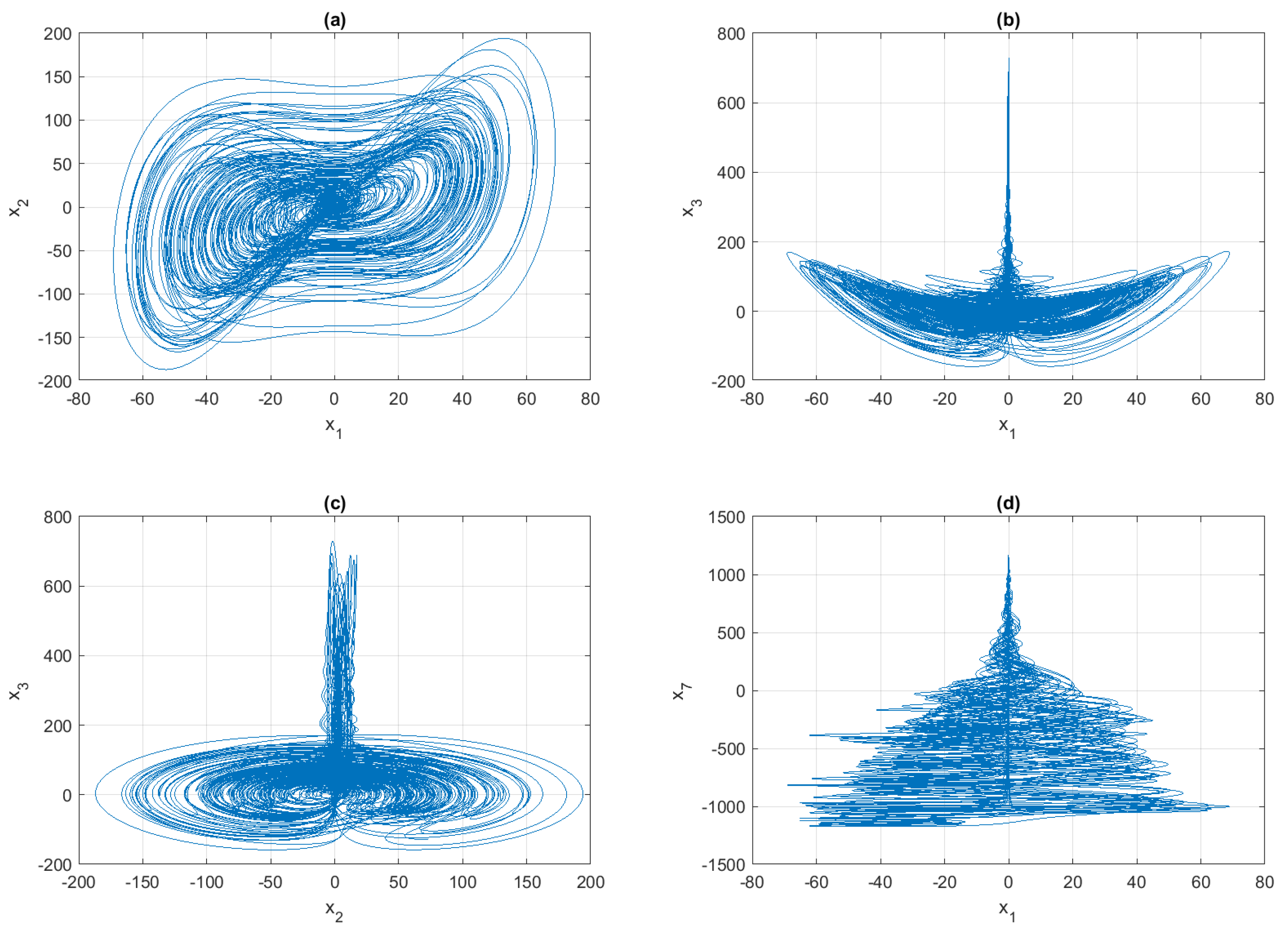

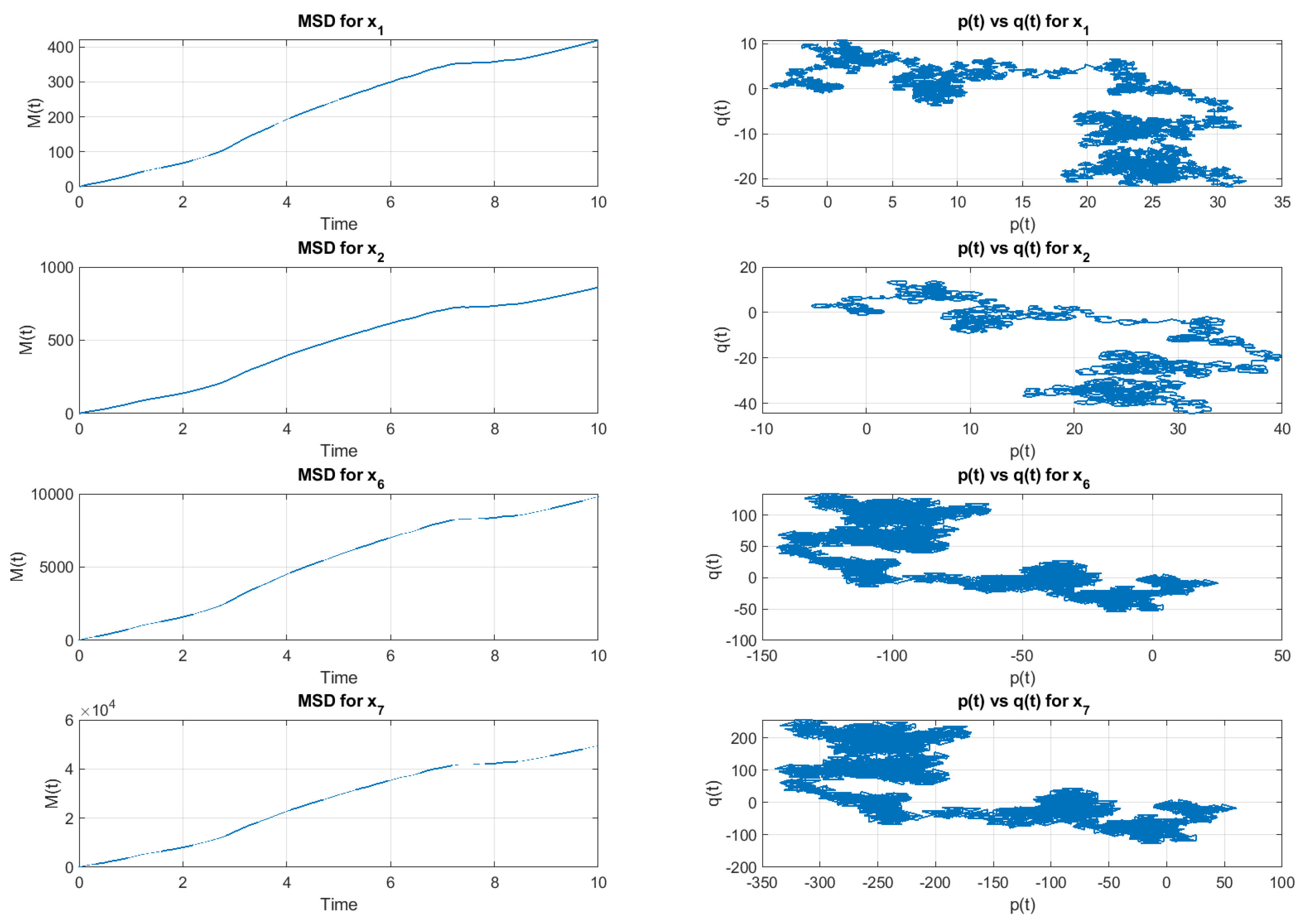
| Orders | Limit Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| FO1 | 1.868 | 1.118 | 0.240 | 0.097 | −0.133 | −0.325 | −2.326 | −9.684 | Hyperchaos |
| FO2 | 1.348 | 0.469 | 0.121 | 0.058 | −0.316 | −0.747 | −0.776 | −9.755 | Hyperchaos |
| FO3 | 1.199 | 0.454 | 0.061 | 0.054 | −0.101 | −0.546 | -0.927 | −9.698 | Hyperchaos |
| Orders | Limit Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| FO1 | 1.519 | 0.552 | 0.147 | 0.126 | 0.0393 | −0.169 | −1.660 | −9.677 | Hyperchaos |
| FO2 | 1.331 | 0.463 | 0.064 | 0.100 | −0.335 | −0.696 | −0.736 | −9.780 | Hyperchaos |
| FO3 | 1.165 | 0.444 | 0.072 | 0.031 | −0.181 | −0.558 | −0.845 | −9.721 | Hyperchaos |
| ODE Systems | Fractal Dimensions |
|---|---|
| 7D Hu and Chan system [54] | 6.732 |
| 7D Yang system [55] | 6.149 |
| 7D Yu system [56] | 5.278 |
| 7D Lagmiri system [57] | 2.091 |
| 7D Varan system [58] | 2.175 |
| 8D Biban system [52] | 7.13 |
| 9D Mahmoud system [47] | 5.128 |
| 9D Zhu system [48] | 2.171 |
| 10D Jianliang system [49] | 2.429 |
| Proposed 8D FOs1 | 7.05 |
| Proposed 8D FOs2 | 7.019 |
| Proposed 8D FOs3 | 7.013 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarfraz, M.; Zhou, J.; Ali, F. An 8D Hyperchaotic System of Fractional-Order Systems Using the Memory Effect of Grünwald–Letnikov Derivatives. Fractal Fract. 2024, 8, 530. https://doi.org/10.3390/fractalfract8090530
Sarfraz M, Zhou J, Ali F. An 8D Hyperchaotic System of Fractional-Order Systems Using the Memory Effect of Grünwald–Letnikov Derivatives. Fractal and Fractional. 2024; 8(9):530. https://doi.org/10.3390/fractalfract8090530
Chicago/Turabian StyleSarfraz, Muhammad, Jiang Zhou, and Fateh Ali. 2024. "An 8D Hyperchaotic System of Fractional-Order Systems Using the Memory Effect of Grünwald–Letnikov Derivatives" Fractal and Fractional 8, no. 9: 530. https://doi.org/10.3390/fractalfract8090530
APA StyleSarfraz, M., Zhou, J., & Ali, F. (2024). An 8D Hyperchaotic System of Fractional-Order Systems Using the Memory Effect of Grünwald–Letnikov Derivatives. Fractal and Fractional, 8(9), 530. https://doi.org/10.3390/fractalfract8090530







