Fuzzy Adaptive Approaches for Robust Containment Control in Nonlinear Multi-Agent Systems under False Data Injection Attacks
Abstract
1. Introduction
- The development of a novel fuzzy adaptive control strategy specifically designed for nonlinear multi-agent systems under FDI attacks
- A detailed stability analysis that validates the effectiveness of the proposed method
- Extensive simulations that compare our method with existing approaches show significant improvements in both adaptability and robustness.
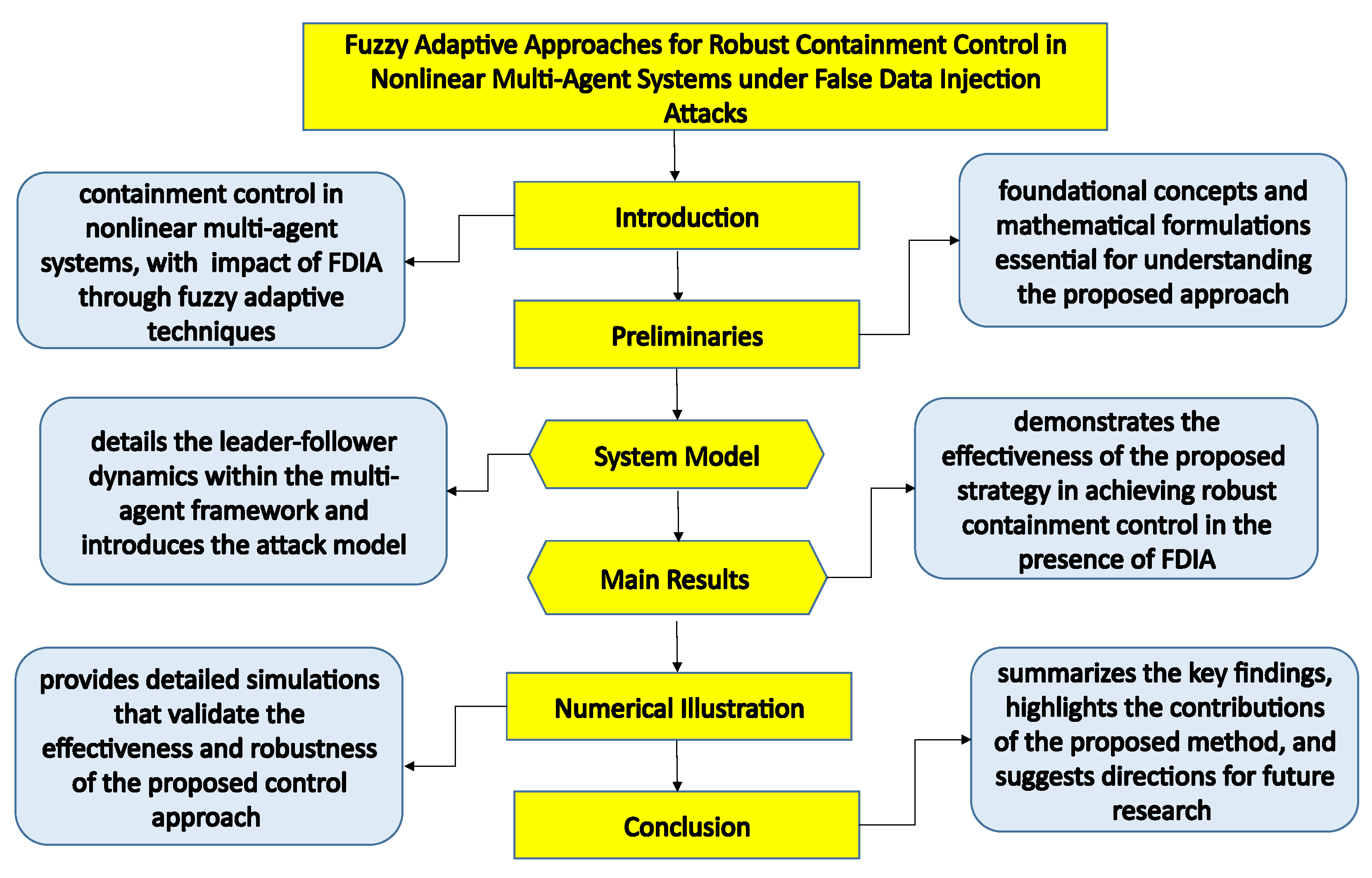
- We introduce our work in Section 1.
- In Section 2, graph theory is explained for the communication of agents. Some lemmas and definitions are provided.
- Section 3 provides a system model that explains the dynamic of leaders and followers.
- In Section 4, main results are presented.
- Section 5 provides a numerical experiment, and two examples are provided for the effectiveness of the results.
- In Section 6, we draw conclusions.
2. Preliminaries
2.1. Definition and Lemmas
2.2. Introduction to Interval Type-II Fuzzy Systems
3. System Model
- denotes the fractional derivative of order ,
- is the state vector of the p-th follower,
- represents the nonlinear dynamics of the system,
- is the saturated control input,
- denotes false data injected by the adversary.
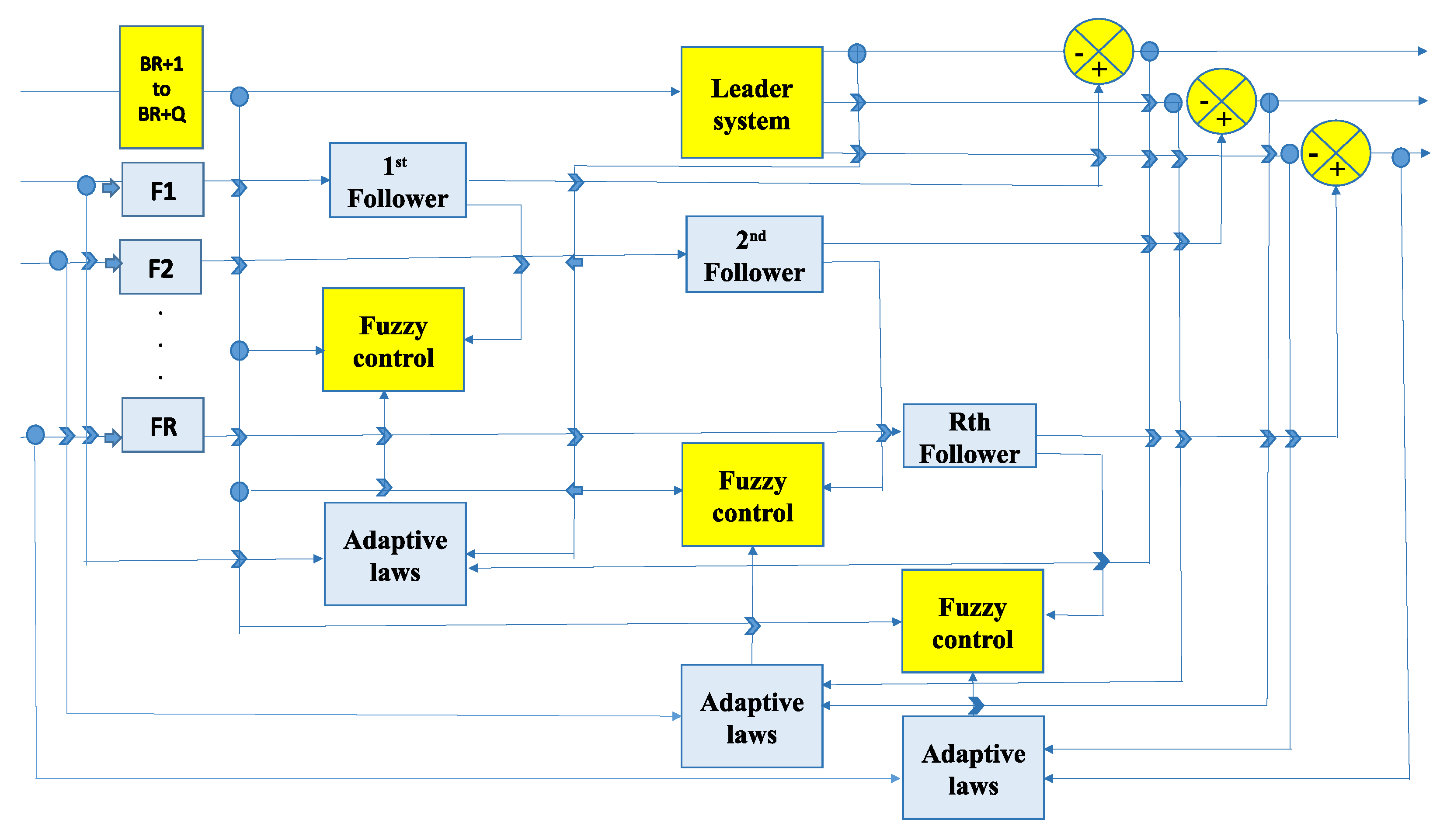
- Leader Dynamics: In the diagram, the leader dynamics are represented as the driving force of the system. The leader agents provide the desired trajectories or reference signals that guide the follower agents. These trajectories represent the target behaviors that the followers aim to achieve. The leader dynamics set the objectives for the system, which are tracked by the followers through feedback control mechanisms.
- Follower Dynamics: The follower agents are represented in the block diagram as systems that track the leaders’ behavior. Each follower adjusts its state based on both its local interactions and the leader’s state. The dynamics of these followers are influenced by the control inputs received from the fuzzy controller. Followers work together to reach the leaders’ trajectories while maintaining a desired formation or coordinated behavior.
- Fuzzy Controller: The fuzzy controller is shown as the primary decision-making block that processes input information from both the leaders and followers. It maps the input errors (the difference between the leader and follower states) to appropriate control actions using fuzzy logic rules. The fuzzy controller helps manage uncertainties and nonlinearities in the system by generating adaptive control signals that adjust the behavior of the followers.
- Adaptive Laws: The adaptive laws are depicted as a mechanism that adjusts the parameters of the fuzzy controller over time. They allow the system to adapt to unknown or changing dynamics within the leader–follower interactions, ensuring robustness against disturbances or modeling inaccuracies. Adaptive laws ensure that the control gains are modified continuously based on system performance, allowing the system to remain stable and achieve the desired tracking performance.
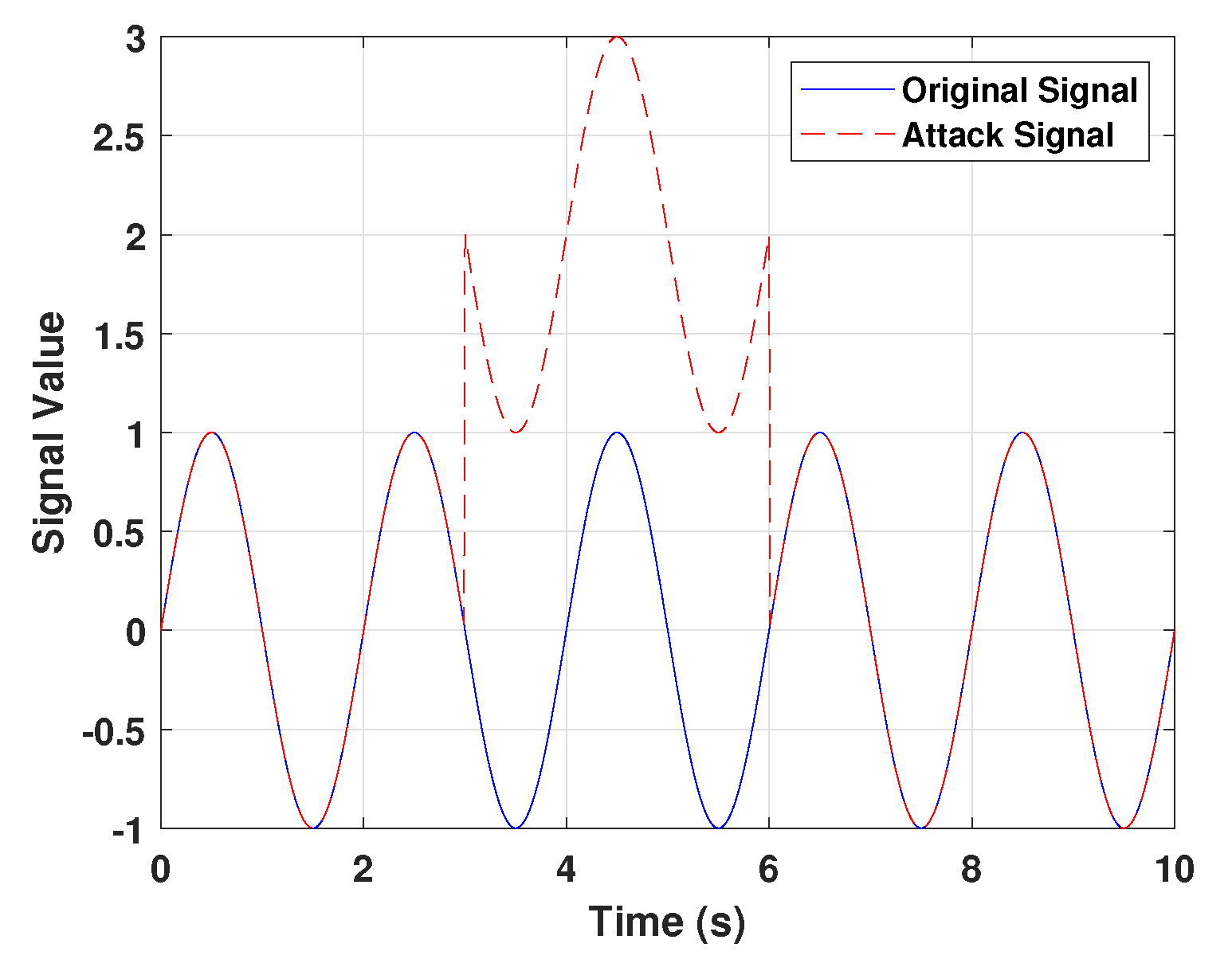
3.1. Attack Model
3.1.1. Nature of FDI Attacks
3.1.2. Mechanisms of Injection
3.2. Impact on System Dynamics
- is the state vector of the k-th leader,
- represents the dynamics of the leader.
- , , , ,
- , , , , .
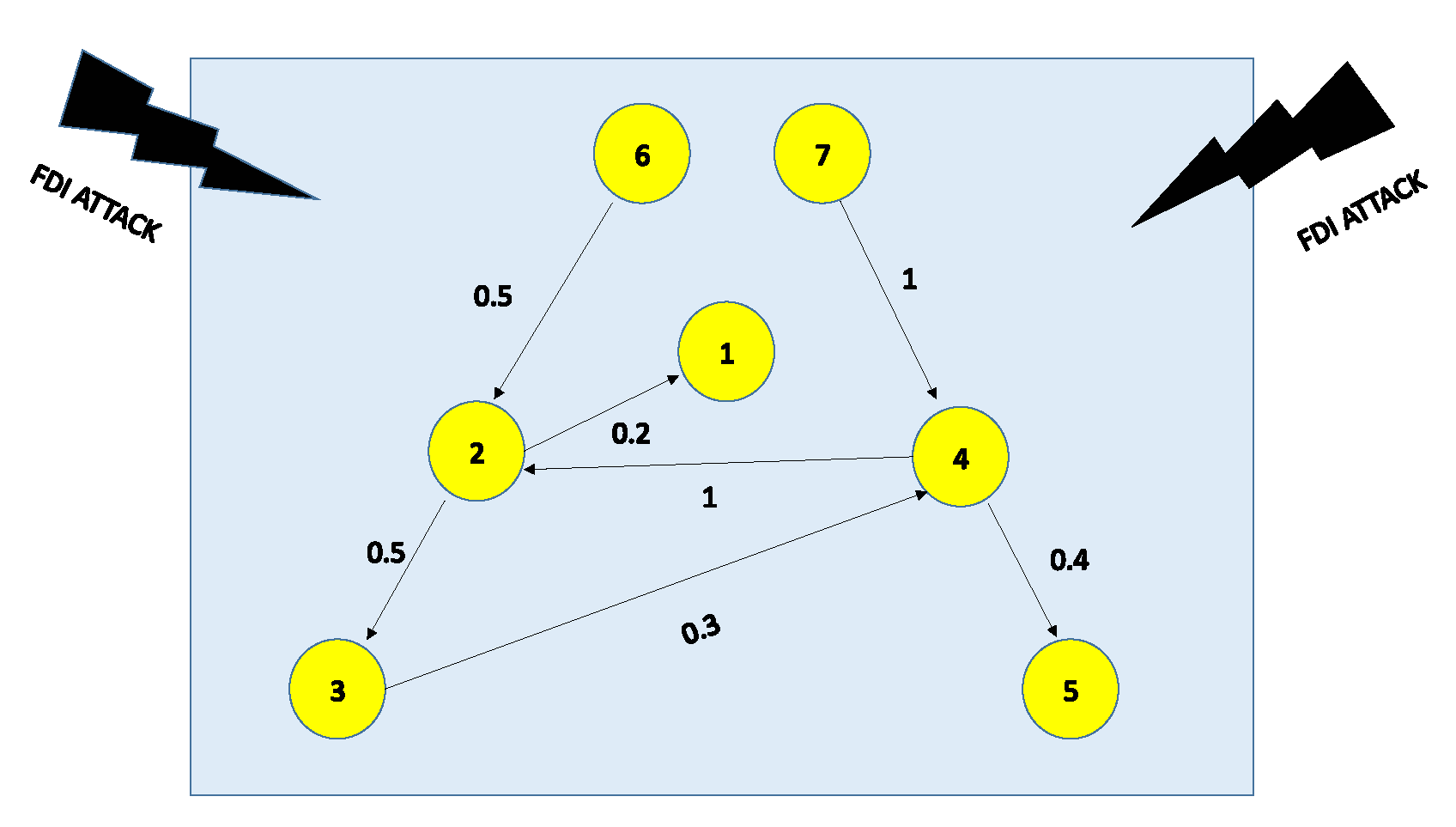
- The set of values represents the adjacent neighbors of agents .
- The position is guided to converge towards the convex hull defined by the positions of the leader agents. This convergence is expressed by:where denotes the convex hull formed by the positions of the leader agents.
- The controller of each follower agent p is constrained to remain within a specified range, . Here, and are predetermined constants, with being negative and being positive.
4. Main Results
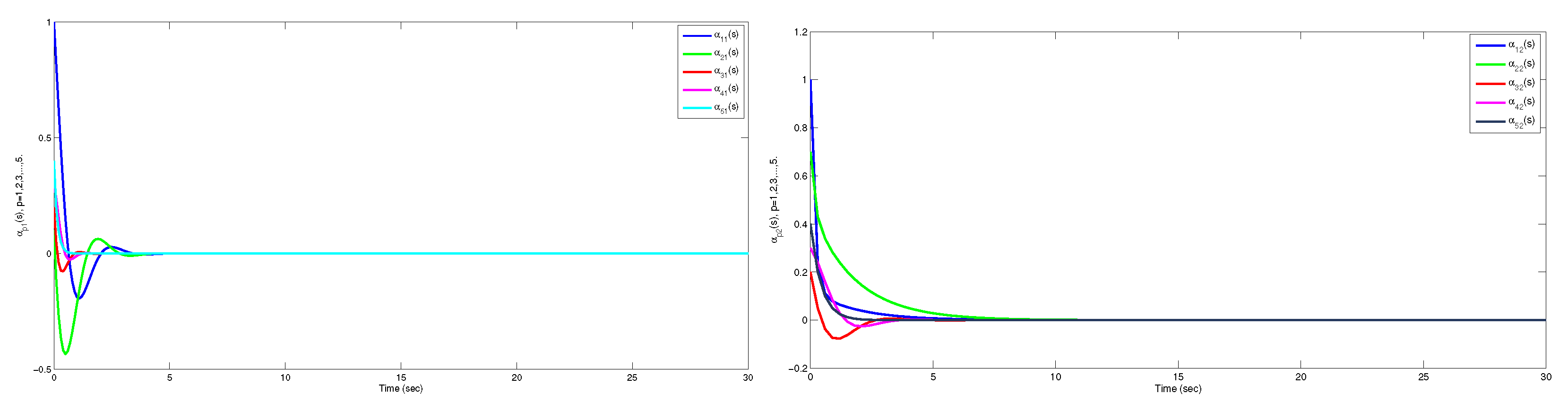
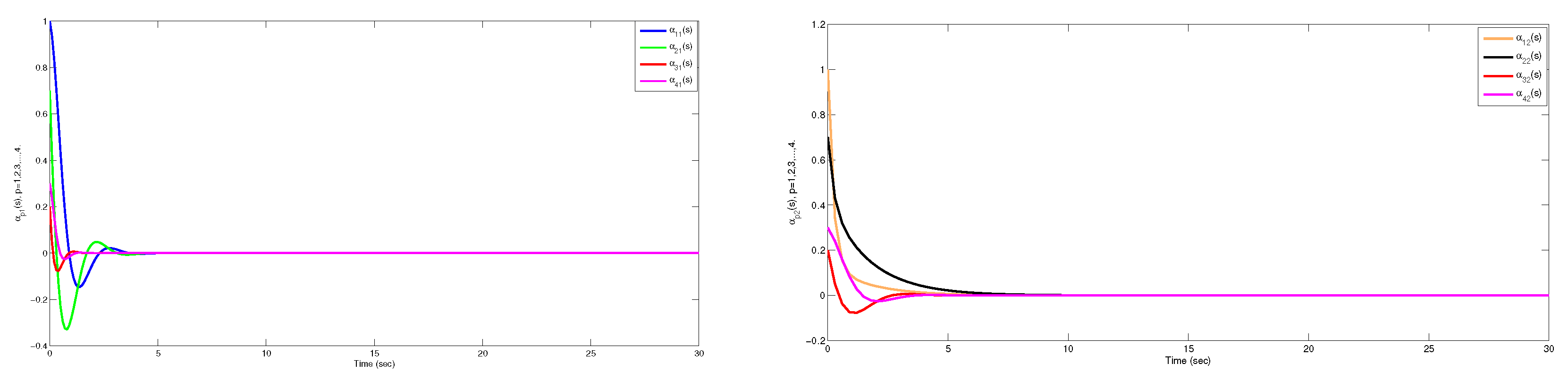
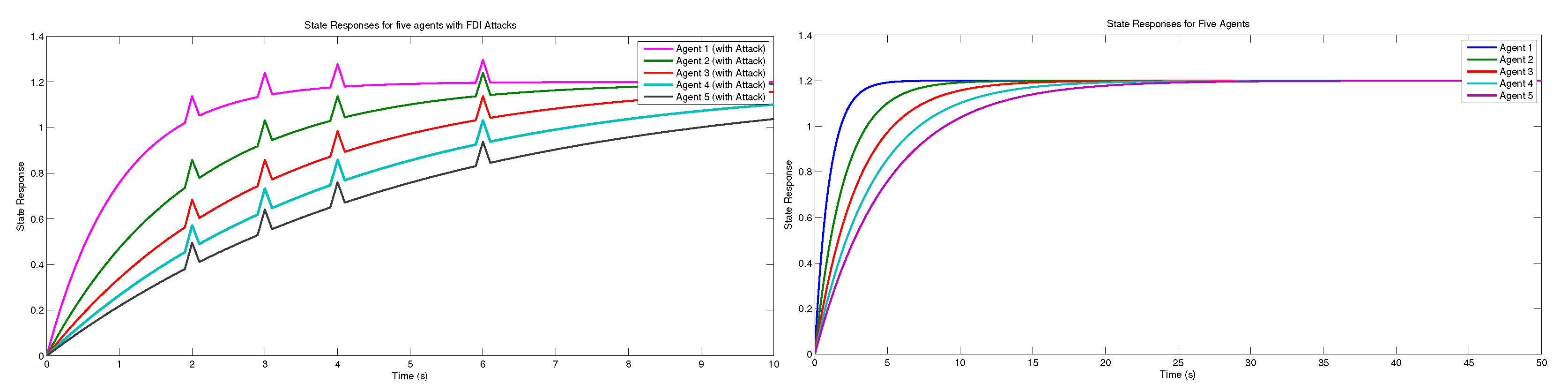
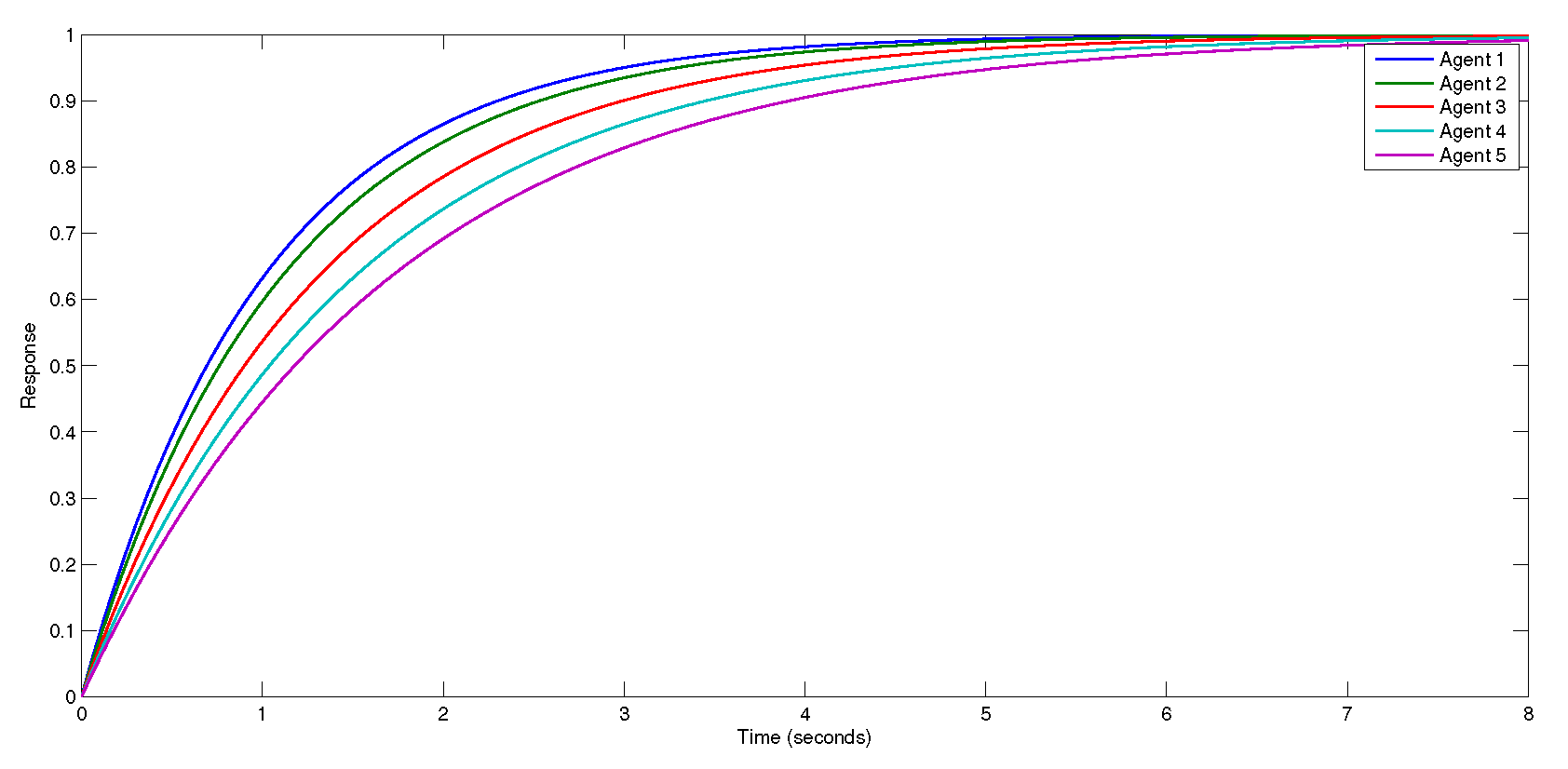
5. Numerical Illustration
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, X.; Zhao, C.; Fang, C.; He, J. Submodularity-based false data injection attack scheme in multi-agent dynamical systems. Automatica 2024, 160, 111426. [Google Scholar] [CrossRef]
- Li, J.; Sun, Y.; Su, Q. Security control of integral sliding modes for multi-agent systems under false data injection attacks. J. Frankl. Inst. 2024, 361, 106613. [Google Scholar] [CrossRef]
- Lv, Y.; Liu, Y.J.; Liu, L.; Yu, D.; Chen, Y. Distributed Nash equilibrium searching for multi-agent games under false data injection attacks. Neurocomputing 2024, 570, 127134. [Google Scholar] [CrossRef]
- Fei, C.; Shen, J.; Qiu, H.; Zhang, Z.; Xing, W. Learning Secure Control Design for Cyber-Physical Systems under False Data Injection Attacks. IEEE Trans. Ind.-Cyber-Phys. Syst. 2024, 2, 60–68. [Google Scholar] [CrossRef]
- Sun, L.; Wu, T.; Zhang, Y. A defense strategy for false data injection attacks in multi-agent systems. Int. J. Syst. Sci. 2023, 54, 3071–3084. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, X.; Li, Y.; Gorbachev, S.; Yue, D. Adaptive resilient tracking control with dual-terminal dynamic-triggering for a linear multi-agent system against false data injection attacks. IEEE Trans. Signal Inf. Process. Over Netw. 2023, 9, 1–12. [Google Scholar] [CrossRef]
- Wang, M.; Hu, J.; Cao, J. Resilient Consensus Control for Linear Multi-agent System Against the False Data Injection Attacks. Int. J. Control. Autom. Syst. 2023, 21, 2112–2123. [Google Scholar] [CrossRef]
- Wang, Z.; Shi, S.; He, W.; Xiao, M.; Cao, J.; Gorbachev, S. Observer-based asynchronous event-triggered bipartite consensus of multi-agent systems under false data injection attacks. IEEE Trans. Control. Netw. Syst. 2023, 10, 1603–1615. [Google Scholar] [CrossRef]
- Duan, Z.; Wei, A.; Zhang, X.; Mu, R. Sampled-data consensus control for nonlinear time-delay multi-agent systems under false data injection attacks. Nonlinear Dyn. 2023, 111, 12253–12266. [Google Scholar] [CrossRef]
- Hu, J.; Sun, Q.; Zhai, M.; Wang, B. Privacy Preserving Consensus Strategy for Secondary Control in Microgrids Against Multi-link False Data Injection Attacks. IEEE Trans. Ind. Inform. 2023, 19, 10334–10343. [Google Scholar] [CrossRef]
- Burgos-Mellado, C.; Zuñiga-Bauerle, C.; Muñoz-Carpintero, D.; Arias-Esquivel, Y.; Càrdenas-Dobson, R.; DragiČević, T.; Watson, A. Reinforcement learning-based method to exploit vulnerabilities of false data injection attack detectors in modular multilevel converters. IEEE Trans. Power Electron. 2023, 38, 8907–8921. [Google Scholar] [CrossRef]
- Habib, A.A.; Hasan, M.K.; Alkhayyat, A.; Islam, S.; Sharma, R.; Alkwai, L.M. False data injection attack in smart grid cyber physical system: Issues, challenges, and future direction. Comput. Electr. Eng. 2023, 107, 108638. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, L.; Bao, Z.; Liu, Y.; Yin, L.; Yao, W.; Wu, L. Secure Control Against Multiplicative And Additive False Data Injection Attacks. IEEE Trans. Ind.-Cyber-Phys. Syst. 2023, 1, 92–100. [Google Scholar] [CrossRef]
- Chen, L.; Tong, S. Observer-based adaptive fuzzy consensus control of nonlinear multi-agent systems encountering deception attacks. IEEE Trans. Ind. Informatics. 2023, 20, 1808–1818. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, T.; Su, X.; Ma, X. Impulsive Consensus of One-Sided Lipschitz Multi-Agent Systems with Deception Attacks and Stochastic Perturbation. IEEE Trans. Artif. Intell. 2023, 5, 1328–1338. [Google Scholar] [CrossRef]
- Pan, Z.; Chi, R.; Hou, Z. Distributed Model-Free Adaptive Predictive Control for MIMO Multi-Agent Systems With Deception Attack. IEEE Trans. Signal Inf. Process. Over Networks. 2024, 10, 32–47. [Google Scholar] [CrossRef]
- Ying, C.; Zheng, R.; Wu, Y.; Xu, M.; Zhang, W.A. Privacy-preserving adaptive resilient consensus for multi-agent systems under cyber attacks. IEEE Trans. Ind. Informatics. 2023, 20, 1630–1640. [Google Scholar] [CrossRef]
- Kharchouf, I.; Mohammed, O.A. Controller Hardware-in-the-Loop Testbed of a Distributed Consensus Multi-Agent System Control under Deception and Disruption Cyber-Attacks. Energies 2024, 17, 1669. [Google Scholar] [CrossRef]
- Niu, B.; Gao, Y.; Zhang, G.; Zhao, X.; Wang, H.; Wang, D.; Liu, C. Adaptive Prescribed-Time Consensus Tracking Control Scheme of Nonlinear Multi-Agent Systems Under Deception Attacks. IEEE Trans. Autom. Sci. Eng. 2024. [CrossRef]
- Wan, Q.; Chen, W.H.; Lu, X. Secure consensus tracking of multi-agent systems with network-induced delays under deception attacks via guaranteed performance impulsive control. Nonlinear Dyn. 2023, 111, 12213–12232. [Google Scholar] [CrossRef]
- Ahmed, Z.; Ali, R.; Zhang, W. H2 resilient consensus control of multiagent systems under deception attack. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 2530–2534. [Google Scholar] [CrossRef]
- Janani, V.M.; Visakamoorthi, B.; Muthukumar, P.; Hur, S.H. Reachable set estimation of multi-agent systems under packet losses and deception attacks. J. Appl. Math. Comput. 2024, 70, 3555–3574. [Google Scholar] [CrossRef]
- Gao, Y.; Zhou, W.; Riu, B.; Kao, Y.; Wang, H.; Sun, R. Distributed Prescribed-Time Consensus Tracking for Heterogeneous Nonlinear Multi-Agent Systems Under Deception Attacks and Actuator Faults. IEEE Trans. Autom. Sci. Eng. 2023. [Google Scholar] [CrossRef]
- Han, S.; Zhu, H.; Zhong, Q.; Shi, K.; Kwon, O.M. Secure Sampled-Data Consensus of Multi-Agent Systems Under Asynchronous Deception Attacks With Application to Unmanned Surface Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 25, 5462–5473. [Google Scholar] [CrossRef]
- Sayghe, A.; Hu, Y.; Zografopoulos, I.; Liu, X.; Dutta, R.G.; Jin, Y.; Konstantinou, C. Survey of machine learning methods for detecting false data injection attacks in power systems. IET Smart Grid 2020, 3, 581–595. [Google Scholar] [CrossRef]
- Reda, H.T.; Anwar, A.; Mahmood, A. Comprehensive survey and taxonomies of false data injection attacks in smart grids: Attack models, targets, and impacts. Renew. Sustain. Energy Rev. 2022, 163, 112423. [Google Scholar] [CrossRef]
- Aboelwafa, M.M.; Seddik, K.G.; Eldefrawy, M.H.; Gadallah, Y.; Gidlund, M. A machine-learning-based technique for false data injection attacks detection in industrial IoT. IEEE Internet Things J. 2020, 7, 8462–8471. [Google Scholar] [CrossRef]
- Choraria, M.; Chattopadhyay, A.; Mitra, U.; Ström, E.G. Design of false data injection attack on distributed process estimation. IEEE Trans. Inf. Forensics Secur. 2022, 17, 670–683. [Google Scholar] [CrossRef]
- Pang, Z.H.; Fan, L.Z.; Sun, J.; Liu, K.; Liu, G.P. Detection of stealthy false data injection attacks against networked control systems via active data modification. Inf. Sci. 2021, 546, 192–205. [Google Scholar] [CrossRef]
- Lu, A.Y.; Yang, G.H. False data injection attacks against state estimation without knowledge of estimators. IEEE Trans. Autom. Control. 2022, 67, 4529–4540. [Google Scholar] [CrossRef]
- Li, Y.; Wei, X.; Li, Y.; Dong, Z.; Shahidehpour, M. Detection of false data injection attacks in smart grid: A secure federated deep learning approach. IEEE Trans. Smart Grid 2022, 13, 4862–4872. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Ye, D. False data injection attacks with complete stealthiness in cyber–physical systems: A self-generated approach. Automatica 2020, 120, 109117. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Chen, B. Detecting false data injection attacks in smart grids: A semi-supervised deep learning approach. IEEE Trans. Smart Grid 2020, 12, 623–634. [Google Scholar] [CrossRef]
- Lu, A.Y.; Yang, G.H. False data injection attacks against state estimation in the presence of sensor failures. Inf. Sci. 2020, 508, 92–104. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Kammoun, A.; Debbah, M.; Poor, H.V. Data-driven false data injection attacks against power grids: A random matrix approach. IEEE Trans. Smart Grid 2020, 12, 635–646. [Google Scholar] [CrossRef]
- Abbaspour, A.; Yen, K.K.; Noei, S.; Sargolzaei, A. Detection of fault data injection attack on uav using adaptive neural network. Procedia Comput. Sci. 2016, 95, 193–200. [Google Scholar] [CrossRef]
- Luo, X.; Bai, M.; Wang, X.; Sun, X. Square-root Extended Kalman Filter-based Detection of False Data Injection Attack in Smart Grids. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; pp. 2376–2381. [Google Scholar]
- Ju, Z.; Zhang, H.; Li, X.; Chen, X.; Han, J.; Yang, M. A survey on attack detection and resilience for connected and automated vehicles: From vehicle dynamics and control perspective. IEEE Trans. Intell. Veh. 2022, 7, 815–837. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, B.; Yu, L. Intermediate-variable-based estimation for FDI attacks in cyber-physical systems. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 2762–2766. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Shen, H.; Cao, J.; Rutkowski, L. Fuzzy H∞ control of discrete-time nonlinear Markov jump systems via a novel hybrid reinforcement Q-learning method. IEEE Trans. Cybern. 2022, 53, 7380–7391. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Y.; Wang, J.; Park, J.H. A fuzzy-model-based approach to optimal control for nonlinear Markov jump singularly perturbed systems: A novel integral reinforcement learning scheme. IEEE Trans. Fuzzy Syst. 2023, 31, 3734–3740. [Google Scholar] [CrossRef]
- Wang, J.; Wang, D.; Yan, H.; Shen, H. Composite Anti-Disturbance H∞ Control for Hidden Markov Jump Systems With Multi-Sensor Against Replay Attacks. IEEE Trans. Autom. Control. 2023, 59, 1760–1766. [Google Scholar]
- Khan, A.; Niazi, A.U.K.; Rehman, S.; Ahmed, S. Hostile-based bipartite containment control of nonlinear fractional multi-agent systems with input delays: A signed graph approach under disturbance and switching networks. Aims Math. 2024, 9, 12678–12699. [Google Scholar] [CrossRef]
- Huong, D.C.; Thuan, M.V. Mixed H∞ and passive control for fractional-order nonlinear systems via LMI approach. Acta Appl. Math. 2020, 170, 37–52. [Google Scholar] [CrossRef]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Xia, Z.; Mou, J. IT2 fuzzy adaptive containment control for fractional-order heterogeneous multi-agent systems with input saturation. J. Intell. Fuzzy Syst. 2023, 45, 4361–4370. [Google Scholar] [CrossRef]
- Mendel, J.M. Explainable Uncertain Rule-Based Fuzzy Systems; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Deng, X.; Cui, Y. Adaptive fuzzy containment control for nonlinear multi-agent systems with input delay. Int. J. Syst. Sci. 2021, 52, 1633–1645. [Google Scholar] [CrossRef]
- Li, Y.; Qu, F.; Tong, S. Observer-based fuzzy adaptive finite-time containment control of nonlinear multiagent systems with input delay. IEEE Trans. Cybern. 2020, 51, 126–137. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Wang, Y.; Liang, H. Adaptive containment control for fractional-order nonlinear multi-agent systems with time-varying parameters. IEEE/CAA J. Autom. Sin. 2022, 9, 1627–1638. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, H.; Sun, J.; Wang, Y. Event-triggered adaptive finite-time containment control for fractional-order nonlinear multiagent systems. IEEE Trans. Cybern. 2022, 54, 1250–1260. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsinai, A.; Al-Shamiri, M.M.A.; Ul Hassan, W.; Rehman, S.; Niazi, A.U.K. Fuzzy Adaptive Approaches for Robust Containment Control in Nonlinear Multi-Agent Systems under False Data Injection Attacks. Fractal Fract. 2024, 8, 506. https://doi.org/10.3390/fractalfract8090506
Alsinai A, Al-Shamiri MMA, Ul Hassan W, Rehman S, Niazi AUK. Fuzzy Adaptive Approaches for Robust Containment Control in Nonlinear Multi-Agent Systems under False Data Injection Attacks. Fractal and Fractional. 2024; 8(9):506. https://doi.org/10.3390/fractalfract8090506
Chicago/Turabian StyleAlsinai, Ammar, Mohammed M. Ali Al-Shamiri, Waqar Ul Hassan, Saadia Rehman, and Azmat Ullah Khan Niazi. 2024. "Fuzzy Adaptive Approaches for Robust Containment Control in Nonlinear Multi-Agent Systems under False Data Injection Attacks" Fractal and Fractional 8, no. 9: 506. https://doi.org/10.3390/fractalfract8090506
APA StyleAlsinai, A., Al-Shamiri, M. M. A., Ul Hassan, W., Rehman, S., & Niazi, A. U. K. (2024). Fuzzy Adaptive Approaches for Robust Containment Control in Nonlinear Multi-Agent Systems under False Data Injection Attacks. Fractal and Fractional, 8(9), 506. https://doi.org/10.3390/fractalfract8090506







