Analysis of Impact Crushing Characteristics of Steel Fiber Reinforced Recycled Aggregate Concrete Based on Fractal Theory

Abstract

The fractal theory can effectively describe the complexity and multi-scale of concrete under impact load and provide a scientific basis for evaluating concrete’s impact resistance. Therefore, based on the fractal theory, this study carried out the fragmentation size analysis by weighing the quality of SFRRAC fragments, disclosed the distribution characteristics of impact fragmentation size of steel fiber reinforced recycled aggregate concrete (SFRRAC) specimens under different recycled coarse aggregate (RCA) replacement ratio, different steel fiber (SF) contents and different impact pressures. The results indicate that the fractal dimension can describe the degree of fragmentation of the specimen. The greater the fractal dimension, the more the amount of fragmentation of the specimen subjected to impact load, the lesser the fragmentation size, and the greater the degree of fragmentation. Under the impact load, the fractal dimension of SFRRAC is between 1.36 and 2.28. As the impact pressure increases, the energy consumption increases, and the fractal dimension decreases. With the growth in replacement ratio, the fractal dimension gradually increases, and the energy consumption is negatively correlated with the fractal dimension. Along with the growth of SF content, the energy consumption gradually increases, and the fractal dimension continuously decreases. A new metric angle is provided to explore the inherent law between the impact-crushing characteristics of SFRRAC and the dynamic load, thereby offering foundational support for the application of SFRRAC in practical engineering.

1. Introduction

1.1. Research Background

With the rapid development of urban construction in China, many old buildings have achieved their service life. In addition to the renovation of urban areas, a large amount of concrete is removed every year, and the amount of concrete removed tends to increase every year. Most of the waste concrete blocks are conveyed to the suburbs for open stacking, wasting resources and polluting the environment [1,2,3]. Recycled aggregate concrete (RAC) is a sort of concrete that is prepared by crushing, cleaning, grading, and mixing the waste concrete as a fraction or all of the aggregate in place of natural coarse aggregate (NCA) [4,5,6]. The crushing of waste concrete as RCA not only solves the problem of lack of NCA but also realizes the recycling of resources in the concrete production process [7,8,9].

1.2. State of the Art

1.2.1. RAC

As one of the green and environmentally friendly building materials, RAC has a good application prospect. For a long time, scholars have conducted wide research on RAC. Choi et al. [10] examined in relation to the mechanical properties of RAC columns, and the investigation demonstrates that in the wake of growth in the replacement ratios of RCA, the carrying capacity of RAC columns was 6%~8% inferior to that of ordinary concrete columns. Meng et al. [11,12] explored the triaxial compressive property of RAC after exposure to high temperatures. The exploration revealed that the performance of RAC continuously decreases with the growth in temperature. The best replacement ratio of RAC was 70%, and the increase of lateral restraint can effectively improve the triaxial compression performance of RAC. Abdelgadir [13], Roumiana [14], Otsuki [15], Evangelista [16], and so on have studied the durability of RAC. The investigation pointed out that the anti-carbonization performance of RAC was lesser than that of natural aggregate concrete (NAC) in the same context. The frost resistance of RAC was lower in comparison to NAC. The impermeability of RAC was commonly inferior to that of NAC and related to water-cement ratio, RAC strength, and age. Sami [17], Padmini [18], Amnon [19], and Sasha [20] studied the mechanical properties of RAC under uniaxial compression. The research demonstrated that the strength of RAC was inferior to that of NAC under the same conditions, but there was a certain fluctuation, and the change range was within 20%. In comparison with NAC, the brittleness of RAC increases. The compressive strength of RAC was relevant to the replacement ratio, the intensity of the original concrete, the source of RCA, the water-cement ratios, and aggregate gradation. All in all, the mechanical properties of RAC made of RCA are inferior to those of NAC made of ordinary aggregate.

1.2.2. Steel Fiber Reinforced Recycled Aggregate Concrete (SFRRAC)

The method of improving the behavior of RAC has attracted much attention in recent years [21,22,23], in which adding SF to RAC is an efficient approach to make up for the defects of RCA [24,25]. Therefore, it is beneficial to the application and promotion of RAC to examine the advancement effect of SF on the mechanical property of RAC. With respect to static property, Carneiro et al.’s [26] test results demonstrate that RAC mixed with SF enhances the mechanical strength and fracture property of RAC. SF can markedly strengthen the toughness and ductility of RAC. Li et al. [27] carried out hydrostatic pressure and dynamic axial loading tests on cylindrical SFRRAC specimens in a triaxial box. It is found that SF has little impact on the failure mode of SFRRAC, but dramatically enhances the ductility and toughness. Gao et al. [28] explored the compressive properties of SFRRAC. The finding indicated that the toughness index of SFRRAC gradually increases in the wake of the increase in SF volume content, but it decreases with the rising of the replacement ratios of RCA. Kazmi et al. [29] found that the peak stress and peak strain of the SFRRAC specimen increased along with the growth in SF content, and the reinforcement effect of SF on RAC was better than that of NAC. In terms of dynamic performance. Omidinasab et al. [30] showed that the addition of SF can offset the negative influence RCA made on the impact performance of RAC; 1% SF can increase the splitting tensile strength and flexural strength of RAC by 89.9% and 101.45%, respectively. Sun et al. [31] research demonstrated that the compressive toughness increased greatly as the increase in SF content, indicating that SF can effectively improve the compressive toughness of RAC. Xia et al. [32] found that with the growth in SF content, the compressive strength and impact resistance of RAC presents an upward trend. In summary, in terms of static performance, the incorporation of SF can enhance the strength, toughness, and ductility of RAC. In terms of dynamic performance, SF improves the compressive strength and compressive toughness, and the impact resistance of RAC significantly improves.

1.2.3. Fractal Theory

A large number of meso-damage elements, such as pores and cracks, are randomly distributed inside the SFRRAC. In the process of high-speed impact load, the internal microscopic damage of SFRRAC may develop and intersect, which ultimately results in the macroscopic failure of SFRRAC. The distribution state and geometric shape of failed SFRRAC may have obvious statistical self-similarity within a certain measure range. Moreover, the object of research in fractal theory is self-similar irregular curves and shapes. Consequently, based on the fractal theory, this study investigated the impact of replacement ratio, SF content, and impact pressure on SFRRAC. However, there are few studies on the impact failure characteristics of SFRRAC based on fractal theory. Only some scholars used fractal theory to analyze the characteristics of concrete materials.

Lü [33], Gao [34], and Xie et al. [35] test results demonstrated that assessing the complex performance indexes of RCA and the correlated RAC by means of the fractal method was effective. Konkol and Wang et al. [36,37] found that as the water–cement ratio increased, the corresponding structural porosity of the aggregate–cement paste transition zone and the crack propagation speed increased, and the crack propagation path bypassed the aggregate particles, thereby increasing the surface roughness of the fracture and increasing the fractal dimension. Zamen [38], Yin [39], and He et al. [40] showed that fractal dimension could be used to reveal the development of cracks and the evolution process of structural damage. Zarnaghi [41] and Han et al. [42] suggested that the fractal dimension can be viewed as a comprehensive parameter of pore shape and spatial distribution of pore structure. Ding et al. [43] demonstrated that the fractal dimension of the fracture depended on different parameters, including the tensile strength of the concrete, the cross-sectional area of the structure, the ratio of the elastic modulus of the steel bar to that of the concrete, and the reinforcement ratio. Li [44], Yang [45], Li [46], and Zhao et al. [47] found that the fractal dimension of concrete fragmentation was positively correlated with dissipated energy. Ren et al. [48] explored the fractal characteristics of concrete fragmentation at impact load. The results indicated that the greater the degree of fragmentation, the more the fractal dimension; the change of fractal dimension essentially relied on the development of internal cracks and the compactness of concrete. Chrysanidis et al. [49] found that a larger rebar content led to greater concrete disorganization and, thus, to a larger number of cracks appearing for the same normalized degrees of elongation. Carpinteri et al. [50] examined the fracture resistance of fiber-reinforced concrete by fractal dimension. Akhavan et al. [51] analyzed the width, curvature, and surface roughness of concrete surface cracks by fractal theory and found that the curvature and roughness of concrete surface cracks satisfied self-similarity. Wood et al. [52] considered that the automatic damage assessment method based on the distribution of concrete cracks could use fractal dimension analysis to track the damage degree of structures and members, and the method could track the non-uniform damage process during the earthquake. Tang et al. [53] found a relationship between carbonation depth and fractal dimension of cracks and pores; the carbonation depth of concrete increased in the wake of the decrease of fractal dimension. The aforementioned literature indicates that the application of fractal dimension is primarily concentrated on the crack morphology of concrete, and there are few studies on the distribution characteristics of concrete fragments, as well as the relationship between distribution characteristics and concrete strength. As the most intuitive reflection of the impact damage degree for concrete, the distribution characteristics of fragmentation size can reasonably describe the fragmentation behavior of concrete under dynamic loading.

1.3. Research Content

The fractal theory can effectively describe the complexity and multi-scale of concrete under impact load and provide a scientific basis for evaluating concrete’s impact resistance. Therefore, this study investigated the impact process of SFRRAC specimens based on fractal theory, revealed the influence law of fractal dimension by taking the volume content of SF, replacement ratio of RCA, and impact pressure as the changing parameters, and investigated the relationship between energy consumption and fractal dimension. The present research aims to explore the inherent law between the impact-crushing characteristics of SFRRAC and the dynamic load, providing basic support for the application of SFRRAC in practical engineering.

2. Materials and Method

2.1. Raw Materials

In this test, the SF shown in Figure 1 was used, 100% without fracture, and the basic performance index is shown in

Table 1. Basic performance indexes of SF.

Length/mm	Diameter/mm	Tensile Strength/MPa	Elastic Modulus/GPa	Poisson Ratio
13	0.22	3193	40–60	0.19–0.24

. RCA was prepared by artificial crushing, screening, and cleaning of damaged reinforced concrete beams with an original concrete strength grade of C25. Natural gravel was selected as the NCA. The gradation of both the aggregates was satisfactory, and the physical properties are listed in

Table 2. The basic physical performance of coarse aggregate.

Coarse Aggregate Type	Particle Size/mm	Apparent Density/(kg/m3)	Water Content/%	Water Absorption/%
Natural	5~10	2798	0.7	0.1
Recycle	5~10	2486	1.8	4.5

. Natural river sand was selected as the fine aggregate. The determined apparent density, bulk density, and fineness modulus were 2631 kg/m³, 1532 kg/m³, and 2.73, respectively. P•O 42.5R cement was applied in the test, and the fineness, loss on ignition, compressive strength, flexural strength, and initial/final setting time of the cement were 1.3%, 2.4%, 51 MPa, 9 MPa, and 185/270 min, respectively. With fineness, density, water content, and loss on ignition of 48 μm, 2.4 g/cm³, 0.25%, and 2.4, respectively, the fly ash of grade II was used., accounting for 20% of the cement content. Naphthalene superplasticizer was used with a water-reduction ratio of 15%, and the dosage made up 0.5% of the cementitious material. The test water was tap water.

2.2. Method

2.2.1. Mix Proportion and Specimen Design

In accordance with the “Ordinary Concrete Mix Design Specification” (JGJ55-2011), the mix proportion design of C40 SFRRAC specimens was carried out. Firstly, the appropriate water-binder ratio and the amount of each material were determined. Then, in accordance with the quality percentage of RCA in the total coarse aggregate, the mix proportions under the three replacement ratios of 0%, 50%, and 100% were designed, respectively, and the amount of additional water was considered according to the amount of RCA, the moisture content and water absorption of RCA. The measured concrete slump was 70 mm~180 mm. The designed mix proportion of RAC is presented in

Table 3. RAC mix proportion.

R (%)	W	SR (%)	C (kg/m3)	MW (kg/m3)	AW (kg/m3)	RCA (kg/m3)	NCA (kg/m3)	S (kg/m3)	FA (kg/m3)	WR (kg/m3)
0	0.47	32	346	191	1.22	0.0	1224.9	577	69.2	2.04
50	0.47	32	346	191	28.17	612.5	612.5	577	69.2	2.04
100	0.47	32	346	191	55.12	1224.9	0.0	577	69.2	2.04

Note: R represents the replacement ratio of RCA, W denotes the water–binder ratio, SR refers to the sand ratio, C denotes the cement, MW stands for the mixing water, AW refers to the additional water, S denotes the sand, FA stands for fly ash, and WR represents the water reducer.

.

In this study, for different replacement ratios (0%, 50%, 100%) and SF contents (0.5%, 1%, 1.5%, 2%), 12 groups of 150 mm × 150 mm × 150 mm standard cube specimen were designed for coring and grinding, then the cylindrical specimen with a diameter of 50 mm and thickness of 25 mm were extracted. There were 3 specimens in a group, a total of 36. Specimen parameters are shown in

Table 4. SFRRAC specimen parameters.

Specimen NO.	Replacement Ratio (%)	SF (kg/m3)	Impact pressure (MPa)
R0SF0.5	0	39	0.4, 0.5, 0.6
R0SF1	0	78	0.4, 0.5, 0.6
R0SF1.5	0	117	0.4, 0.5, 0.6
R0SF2	0	156	0.4, 0.5, 0.6
R50SF0.5	50	39	0.4, 0.5, 0.6
R50SF1	50	78	0.4, 0.5, 0.6
R50SF1.5	50	117	0.4, 0.5, 0.6
R50SF2	50	156	0.4, 0.5, 0.6
R100SF0.5	100	39	0.4, 0.5, 0.6
R100SF1	100	78	0.4, 0.5, 0.6
R100SF1.5	100	117	0.4, 0.5, 0.6
R100SF2	100	156	0.4, 0.5, 0.6

. Among them, taking R0SF0.5 as an example, R denotes the replacement ratio of RCA, 0 denotes the replacement ratios of 0%, SF represents the content of steel fiber, 0.5 denotes the SF content of 0.5%, and other specimens are named by analogy.

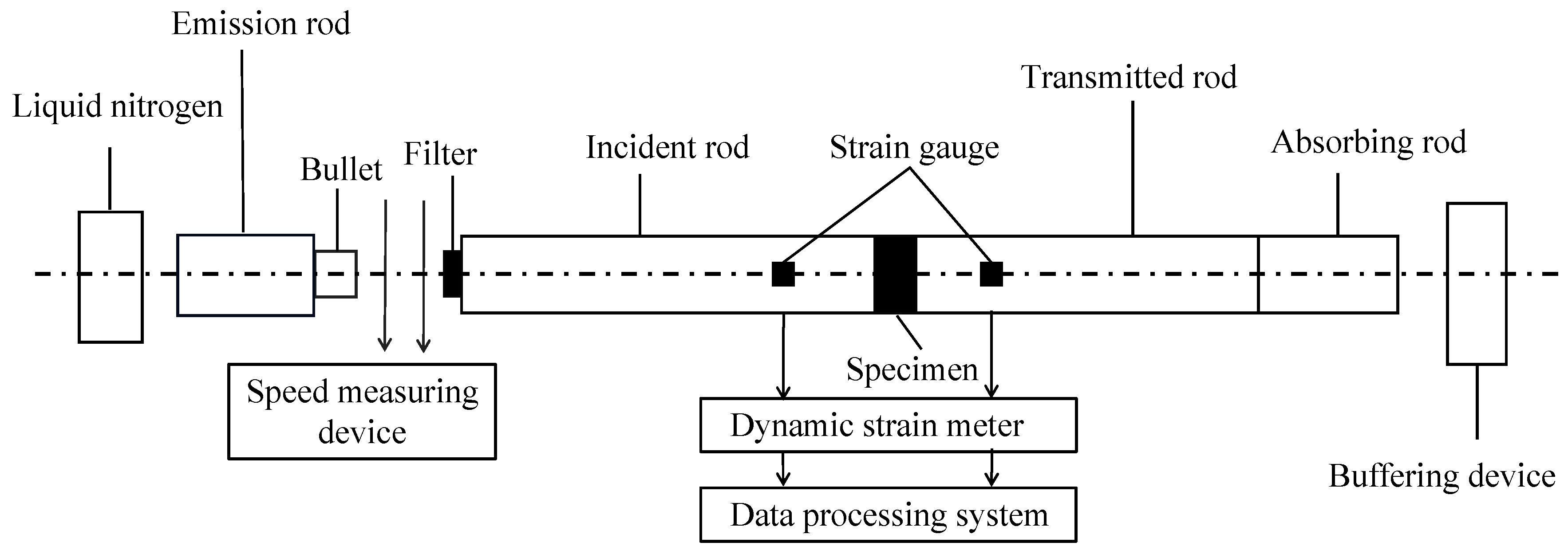
2.2.2. Test Method

The testing procedures graph is shown in Figure 2. The SHPB impact device consists of a gas pressurization system, elastic pressure bar system, buffer damping device, and data processing system, and the impact device is presented in Figure 3. Ordinary nitrogen was utilized in the test, and the air pressure controller employed to adjust different impact pressures is shown in Figure 4a.

The specimen is placed between the incident rod and the transmitted rod of the SHPB device to ensure that the specimen is in good contact with the end of the rod. When the bullet hits the incident rod, the incident wave ${\epsilon }_{\mathrm{I}}$ is generated in the incident rod. Due to the different wave impedance between the rod and the specimens, part of the incident wave traversed through the specimen to the transmitted rod, which is called the transmitted wave ${\epsilon }_{\mathrm{T}}$, and a portion of the incident wave is reflected in the incident rod, which is called the reflected wave ${\epsilon }_{\mathrm{R}}$, when the incident wave reaches the surface of the specimen. The strain signals of the incident wave, reflected wave, and transmitted wave are collected by strain gauges installed on the incident rod and the transmitted rod. The data are recorded by the dynamic strain gauge, as shown in Figure 4b.

Before the formal test, to prevent the impact pressure from being too large or too small to cause the specimen to be completely broken or damaged too lightly, the specimens were subjected to multiple pre-impacts to determine the appropriate impact pressure. After multiple impacts, the changing levels of impact pressure for the SFRRAC specimens were set to be 0.4 MPa, 0.5 MPa, and 0.6 MPa.

3. Test Result

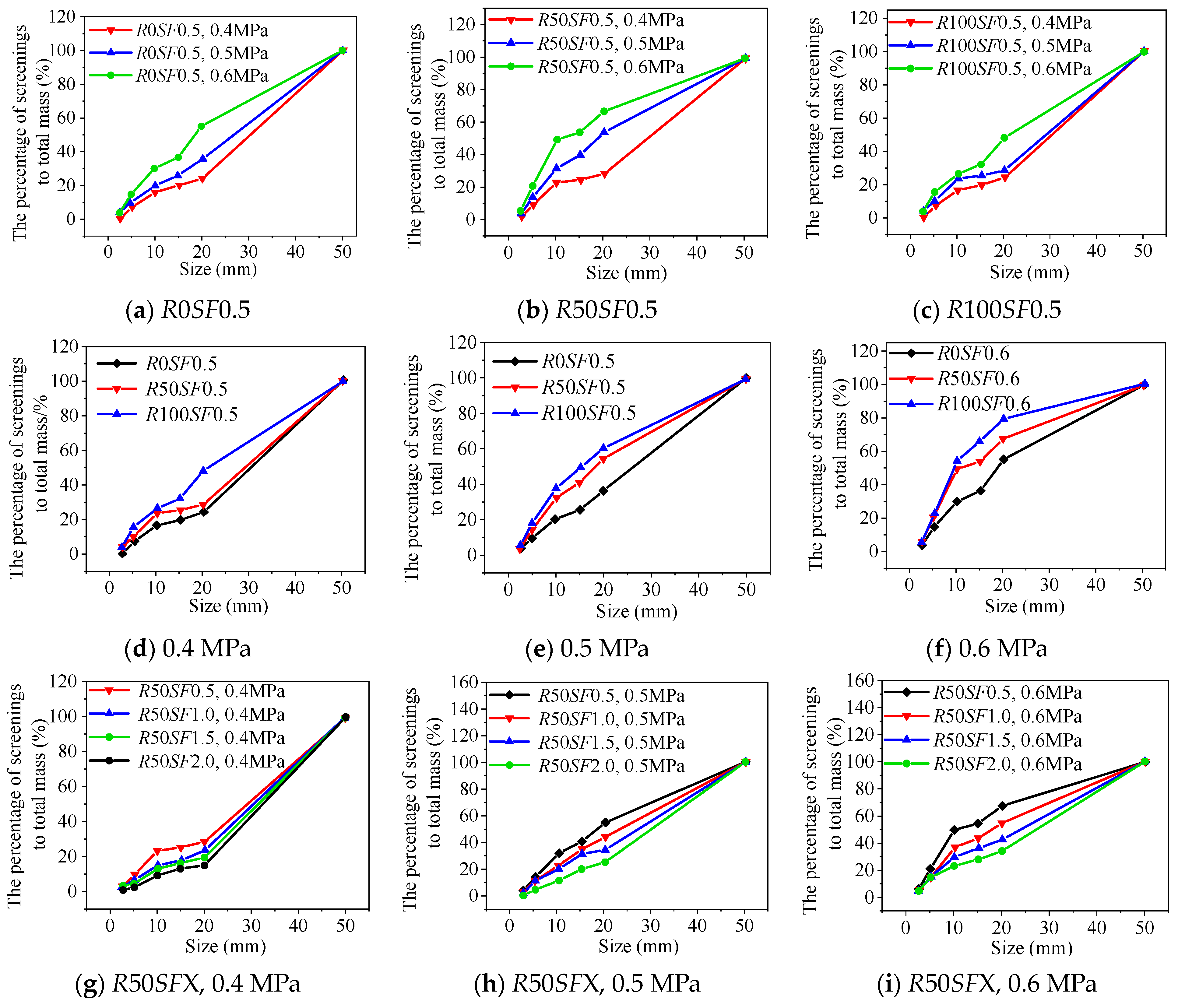
3.1. Distribution of Fragmentation Size

The SHPB impact test was conducted on SFRRAC specimens under various parameters, and the failure modes of some specimens are depicted in Figure 5. The fragmentation of SFRRAC after the impact test was collected and divided into six grades of 0~2.5 mm, 2.5~5 mm, 5~10 mm, 10~15 mm, 15~20 mm, and 20~50 mm by standard screens with the screen-mesh size of 2.5, 5, 10, 15, 20 and 50 mm. For the purpose of size analysis, the quality of SFRRAC fragmentation left on each grade screen was weighed by a high-precision sensitive electronic scale.

The fragmentation size distribution of partial SFRRAC within varying parameters is presented in Figure 6. Figure 3a–c shows that the fragmentation size distribution of SFRRAC is different under varying impact pressures. In the wake of the increase of impact pressure, the initial slope of the curves increases accordingly, indicating that the proportion of coarse particle size (above 20 mm) of the fragmentation gradually decreases, and the proportion of fine particle size (below 10 mm) gradually increases. As indicated in Figure 3d–f, following the increases in replacement ratios, the fragmentation degree of the specimens gradually increases, especially at the high pressure of 0.6 MPa, and the proportion of fine particle size of the fragments increases more noticeably. As found in Figure 6g–i, with the growth in SF content, the fragmentation degree of the specimens within the same replacement ratios and impact pressure is continuously weakened due to the toughening impact of the fiber in the mortar matrix.

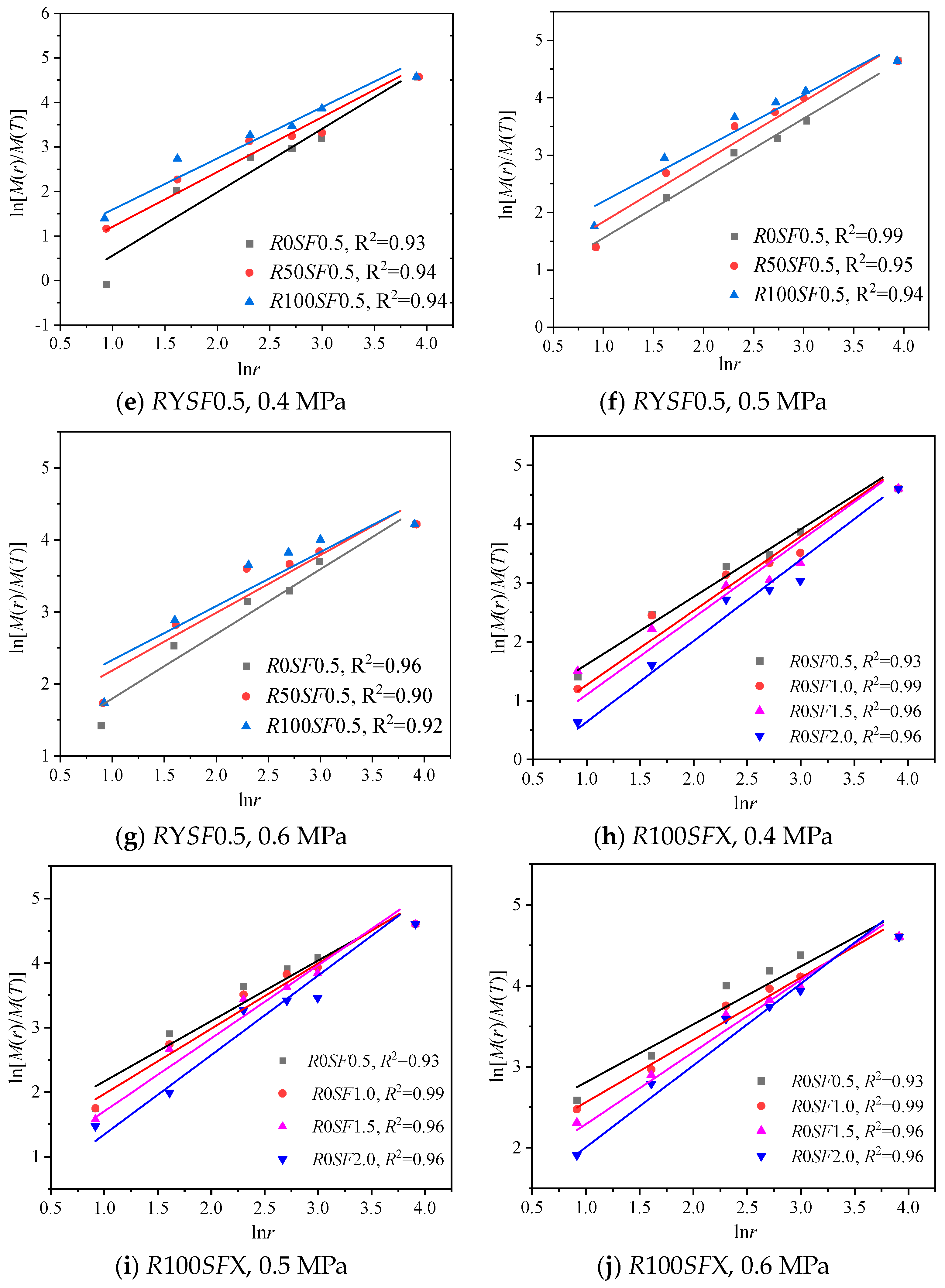
3.2. Calculation of Fractal Dimension of Fragments

In accordance with the relationship between mass and frequency [54], the distribution equation of the impact fragmentation size of SFRRAC can be drawn as shown in Equation (1).

$$y=M(r)/M_{\mathrm{T}}={\left(r/r_{\mathrm{m}}\right)}^b$$

(1)

where M(r) represents the cumulative quality of the fragments with particle size less than r, M_T is the overall quality of the fragments, r_m represents the maximum size of the fragments, and b denotes the distribution parameter.

The fractal dimension D_b can be computed by the linear characteristic size (particle size, r) of the fragments and the number (N) of fragments larger than the size (r), as shown in Equation (2).

$$N=r^{-D_{\mathrm{b}}}$$

(2)

Because of the difficulty of accurately estimating the number of fragments under each particle size, the relationship between the augmenter of fragment amount and the augmenter of fragment quality is introduced, as shown in Equation (3).

$$\mathrm{d}M\propto r^3\mathrm{d}N$$

(3)

Differentiating Equation (1) and Equation (2) and substituting them into Equation (3), the fractal dimension of the fragments ($D_b=3-b$) could be calculated by the particle size-mass method. Applying the logarithm to both sides of Equation (2), the result $\mathrm{In}\left[M(r)/M_T\right]-\mathrm{In}r=(3-D_b)\ln (r/r_m)$ was made, and the slope of the curve was (3 − D_b). As for the calculation of D_b, the characteristic sizes r were 2.5, 5, 10, 15, 20 and 50 mm. Figure 7 shows the $\mathrm{In}\left[M(r)/M_T\right]-\mathrm{In}r$ curves of partial SFRRAC under different changing parameters. It is observed that a satisfactory linear correlation is reached in the double logarithmic coordinates. The fragmentation size distribution of SFRRAC subjected to impact damage presents the power-law characteristics, which belongs to statistically fractal. The greater the fractal dimension, the greater the number of fragments of the specimens subjected to the impact load, the smaller the fragmentation size, and the higher the degree of fragmentation.

4. Discussion

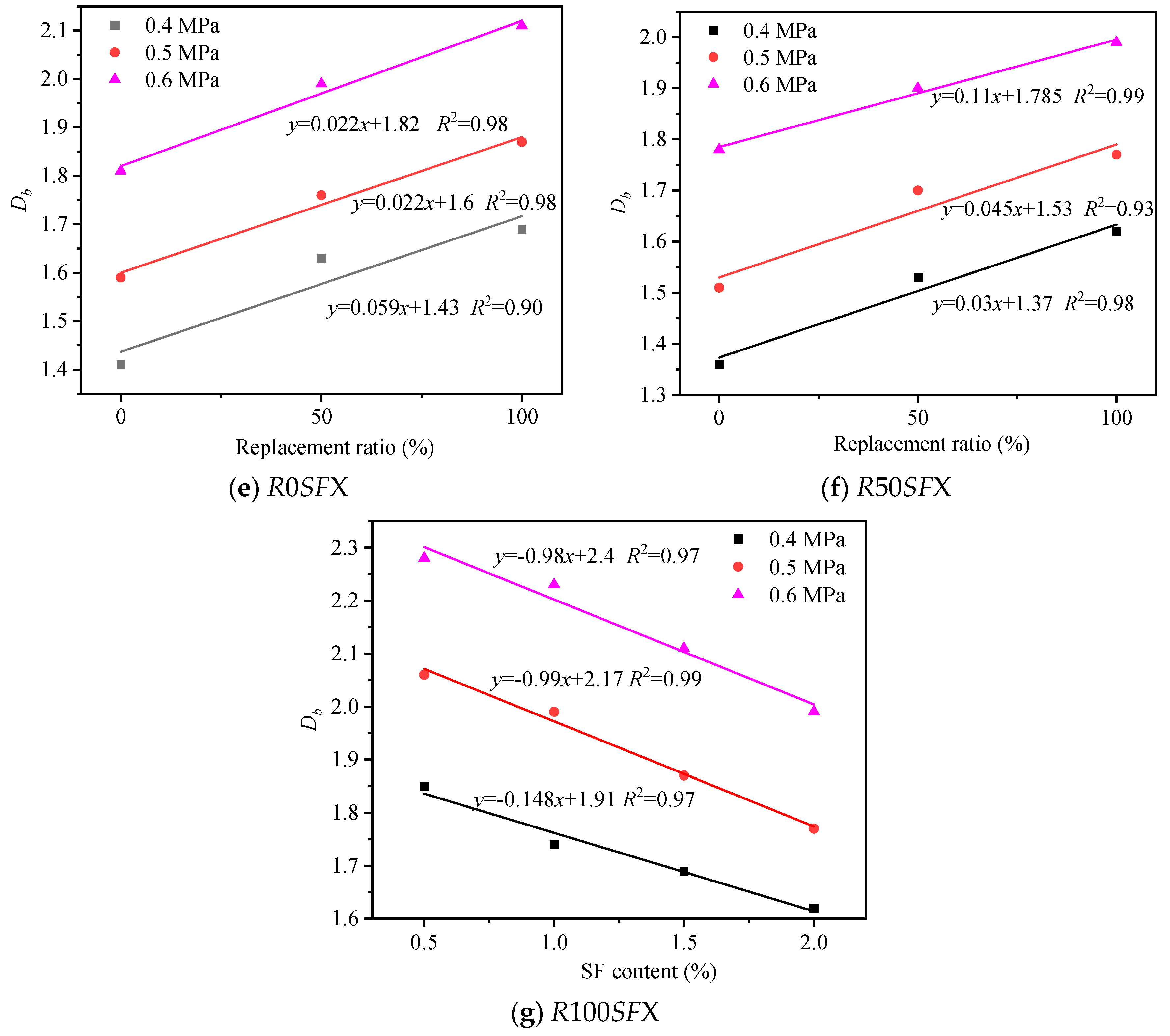
4.1. The Influence of Different Parameters on Fractal Dimension

Figure 8 shows the relationship curve between different changing parameters and fractal dimensions. It is found that under the same replacement ratio and the same SF content, the fractal dimension increases in the wake of the increase of impact pressure and presents an obvious strain ratio effect. When the impact pressure reached 0.4 MPa, the fractal dimension was between 1.36 and 1.85. When the impact pressure stood at 0.5 MPa, the fractal dimension was between 1.51 and 2.06. When the impact pressure reached 0.6 MPa, the fractal dimension was between 1.78 and 2.28. This is because when the impact ratio increases, the number of micro-cracks in the specimens increases rapidly in a short time. When the specimens are destroyed, the fragmentation size decreases, the number of fragments increases, and the fractal dimension increases.

The analysis of Figure 8a–d shows that within the same SF content and impact pressure, the fractal dimension increases with the growth in replacement ratios. The main cause is that compared with the NCA, the interior of RCA inevitably produces microcracks during crushing, and most of the RCA surface attachment the old mortar. Hence, not only does the interface transition zone between aggregate and mortar exist in RAC, but also the interface weak zone between new mortar and old mortar exists. The uniformity and compactness of the RAC specimens are less than those of ordinary concrete, and the mortar matrix is loose and porous. When subjected to impact load, the higher the replacement ratio, the more the original damage accumulated inside the specimens. That is, in the wake of growth in the replacement ratio, the damage to specimens becomes more serious, and the fractal dimension gets larger and larger. When the SF content was 1.5%, following the growth of the replacement ratio, the increase in fractal dimension was the most obvious under the same impact pressure, which was between 9~13.4% and 3.5~5.8%, respectively.

Figure 8e–g illustrates that within the same replacement ratio and impact pressure, the fractal dimension decreases in the wake of an increase in SF content. This is primarily attributed to the fact that the SF can productively bond with the RAC matrix and give full play to the bridging effect. In the high–speed impact, the loading time is short, and the material deforms quickly. Due to the three–dimensional chaotic distribution state in the specimens, the anti-pulling effect of SF can potently inhibit the deformation of the specimens, delay the generation of cracks, improve the plasticity of the specimens, and decrease the damage degree of the specimens. Therefore, the fractal dimension is reduced. When the replacement ratio was 0%, the fractal dimension decreased most significantly. When the impact pressure is 0.4 MPa, 0.5 MPa, and 0.6 MPa, the fractal dimension of the specimens is reduced by 8.8%, 9%, and 6%, respectively.

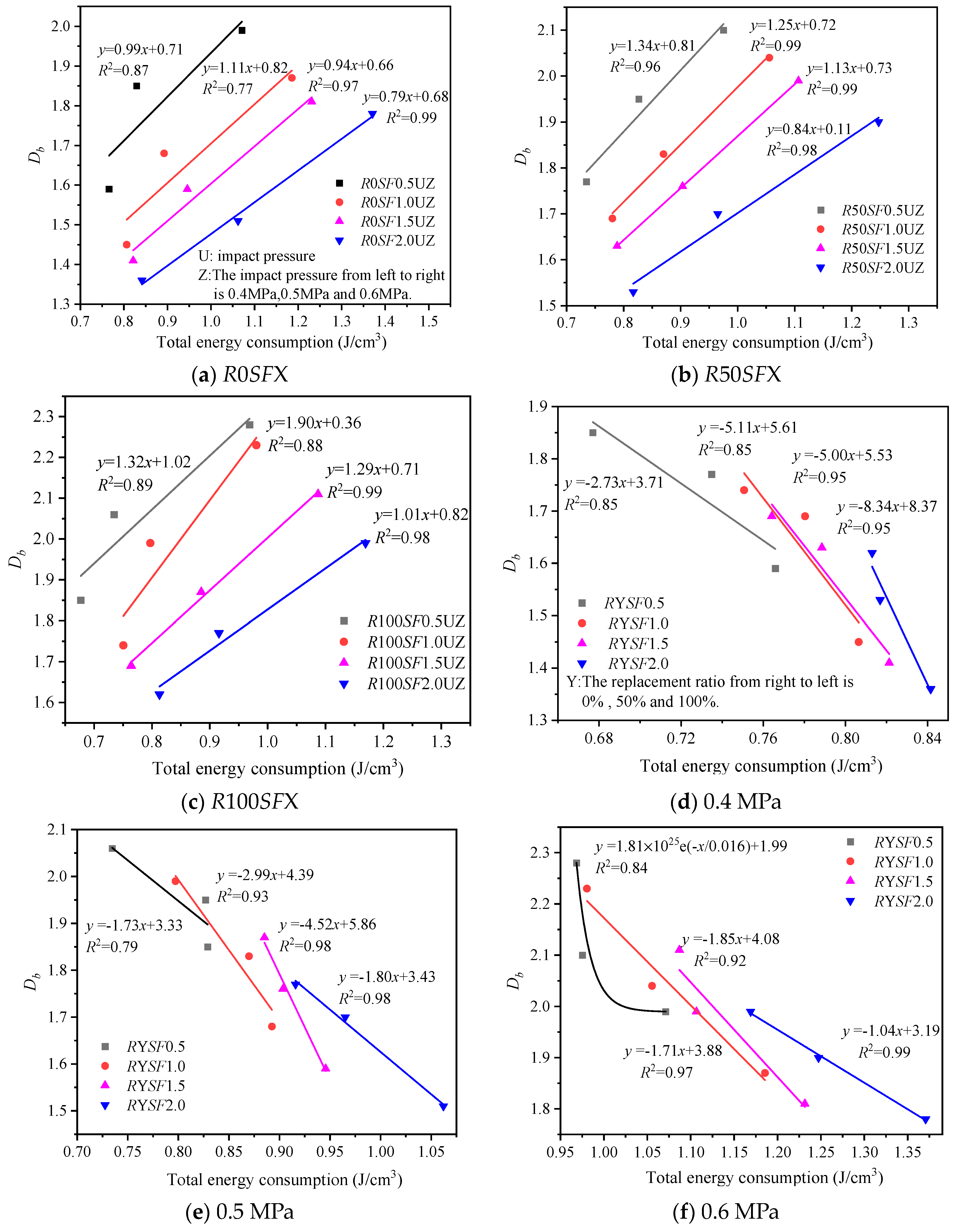
4.2. The Relationship between Fractal Dimension and Energy Absorption for SFRRAC Specimens

According to the theory of one-dimensional elastic stress wave, the pressure and velocity of the end face of the specimen can be expressed by incident wave (${\epsilon }_{\mathrm{I}}$), reflected wave (${\epsilon }_{\mathrm{R}}$), and transmitted wave (${\epsilon }_{\mathrm{T}}$). A₀, E, and C₀ is the cross-sectional area, the elastic modulus, and the propagation velocity of the stress wave in the compressive bar, respectively. The incident energy ($W_{\mathrm{I}}$), the reflected energy ($W_{\mathrm{R}}$) and the transmitted energy ($W_{\mathrm{T}}$) satisfy the Equations (4), (5) and (6), respectively.

$$W_{\mathrm{I}}=AE{C}_0{\displaystyle \int {\epsilon }_{\mathrm{I}}^2(t)dt}$$

(4)

$$W_{\mathrm{T}}=AE{C}_0{\displaystyle \int {\epsilon }_{\mathrm{R}}^2(t)dt}$$

(5)

$$W_{\mathrm{T}}=AE{C}_0{\displaystyle \int {\epsilon }_{\mathrm{T}}^2(t)dt}$$

(6)

According to the law of energy conservation, the total energy consumption ($W_D$) satisfies Equation (7), ignoring the energy loss between the incident rod, the transmitted rod, and the end face of the specimens.

$$W_{\mathrm{D}}=W_{\mathrm{I}}-W_R-W_{\mathrm{T}}$$

(7)

Figure 9 shows the relationship between the fractal dimension and the total energy consumption for SFRRAC. Figure 9a–c indicates that under the same replacement ratio and SF content, as the impact pressure increases, the energy consumption increases, and the fractal dimension also increases. The rationale is that, owing to the short time of impact loading, the crack development in the specimens is no longer like the expansion along a single main crack or multiple cracks under static load; as a result, a large number of microcracks appear when subjected to impact loading. As the defect initiates and expands to form a new crack, a certain amount of energy will be consumed. Therefore, the greater the impact pressure, the more micro-cracks appear in a short time, and the deeper the crack propagation and penetration, increasing fractal dimension and energy consumption.

Figure 9d–f shows the same impact pressure and SF content, along with the growth in replacement ratios, energy consumption, and fractal dimension in negative correlation. The cause is that the increase in the replacement ratio will inevitably contribute to the increase of meso-damages, such as micro–cracks in RAC. Therefore, under the high–speed impact, the internal cracks of SFRRAC develop rapidly and consume less energy compared with steel fiber–reinforced ordinary concrete. Because of the low overall stiffness of RAC and much original damage, the greater the replacement ratios, the more serious the failure of specimens, leading to a large fractal dimension.

Figure 9a–c indicates the same impact pressure and replacement ratio; in the wake of growth in SF content, the energy consumption increases, and the fractal dimension decreases. The reason is analyzed as follows. The randomly distributed SF in the mortar matrix are intertwined to form the fiber network, constraining the mortar matrix. Under high–speed impact, once cracks appeared in RAC, SF spanned among cracks and inhibited the further expansion of cracks due to the close bonding between SF and RAC matrix. When the stress was greater than the bonding force between fibers and the RAC matrix, the fibers were pulled out, consuming part of the energy. Therefore, with the growth in SF content, the total energy consumption of the specimen increased continuously. Then, the increase in SF content made the toughness of RAC larger and larger, which led to the fact that RAC is not prone to brittle failure. As a result, the integrity of SFRRAC was strong at the failure point, and the fractal dimension was continuously reduced.

5. Conclusions

Within the variation amplitude of design parameters, the SHPB impact resistance test of SFRRAC was carried out, and the fractal characteristics of the fragmentation size for the impacted specimens were examined. The primary conclusions are as outlined below:

• The fractal dimension can represent the degree of specimen fragmentation. The greater the fractal dimension, the higher the number of fragments of the specimens subjected to impact load, and the smaller the fragmentation size, indicating a higher degree of fragmentation;
• In the wake of the increases in impact pressure, the proportion of coarse particle size in the specimen fragments continuously decreases while the proportion of fine particle size gradually increases. As the replacement ratio grows, the degree of specimen fragmentation gradually increases, especially at the high pressure of 0.6 MPa, and the proportion of fine particle size of the fragments increases more significantly. As the SF content increases, the degree of specimen fragmentation decreases continuously under the same replacement ratio and impact pressure;
• As impact pressure rises, the fractal dimension increases between 1.36 and 2.28 for SFRRAC. Along with the replacement ratio increase, the fractal dimension increases continuously. When the SF content is 1.5%, the fractal dimension increase of up to 13.4% is the most evident. With the growth in SF content, the fractal dimension decreases;
• As impact pressure increases, the energy consumption increases. With the growth in replacement ratio, energy consumption, and fractal dimension are negatively correlated. In the wake of the increase in SF content, energy consumption is on the rise;
• In general, this study discusses the influence of different parameters on the fractal dimension and the relationship between energy consumption and the fractal dimension of SFRRAC. It provides an experimental basis for the application of SFRRAC in engineering structures under dynamic load. Currently, research on the impact-crushing characteristics of SFRRAC is relatively limited, and this study cannot be directly compared with other studies. However, this limitation also implies that the characteristics of impact fragmentation can be studied more deeply in the future. At the same time, different types of hybrid fibers can be introduced to explore the effects on the impact-crushing characteristics of RAC. This will help promote the wide application of RAC in construction engineering.