Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation
Abstract
1. Introduction
2. Model Description and Mathematical Analysis
3. Modified Extended Direct Algebraic Method and Its Application
Application
4. Improved -Expansion Technique and Its Application
Application
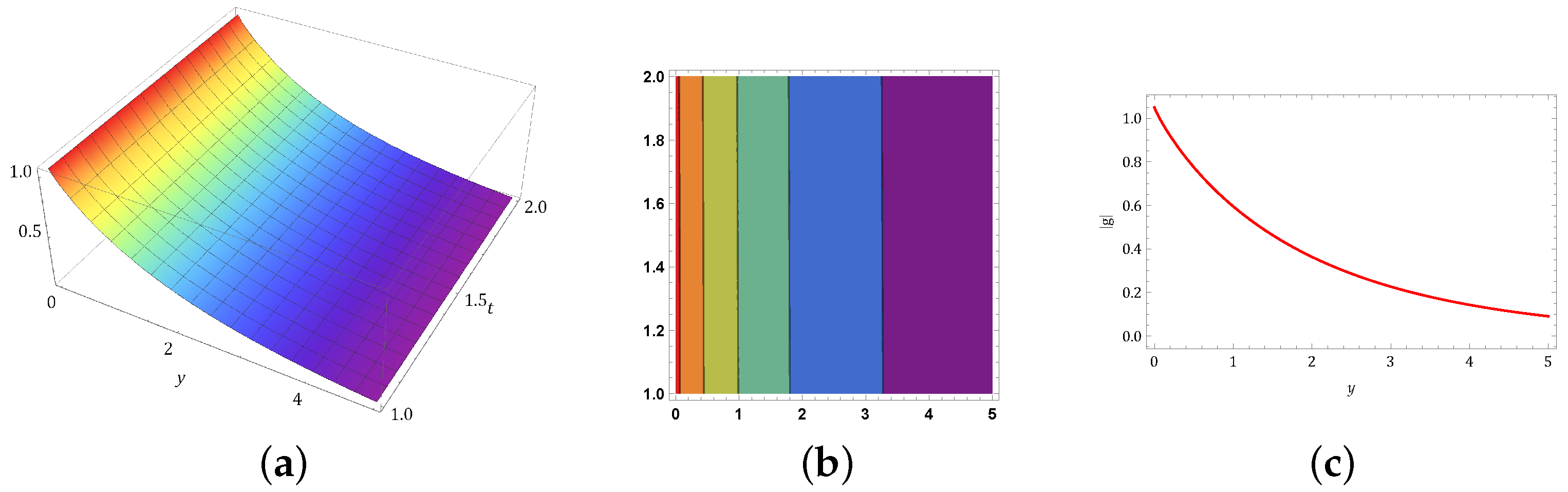
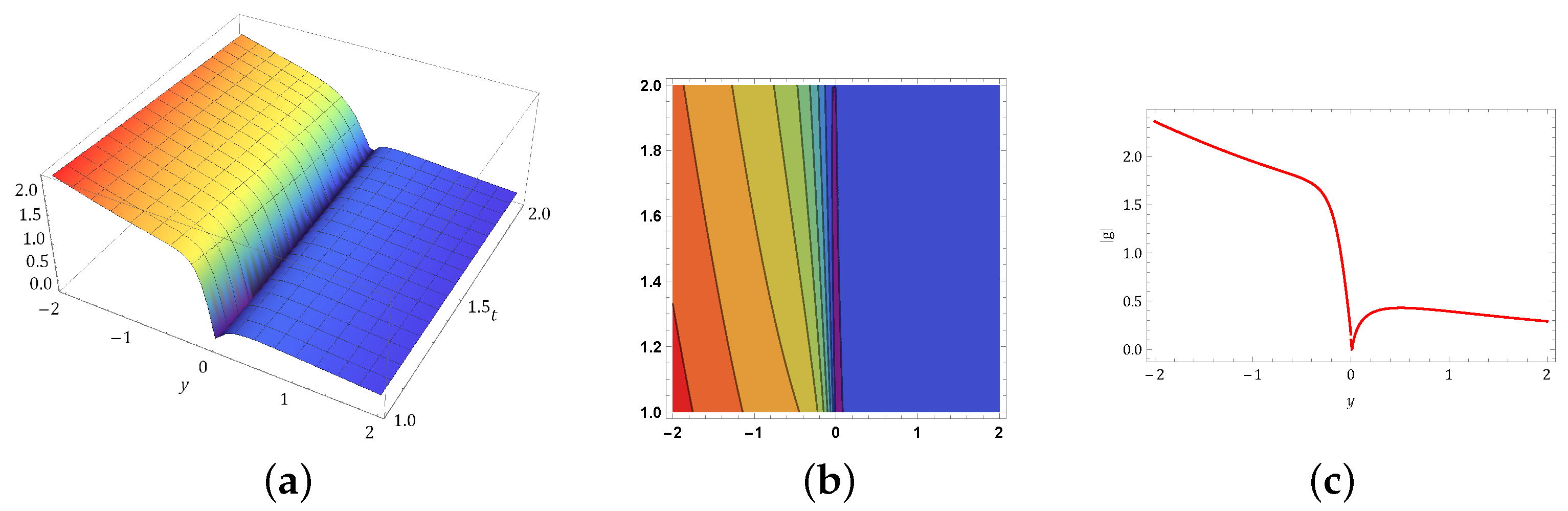
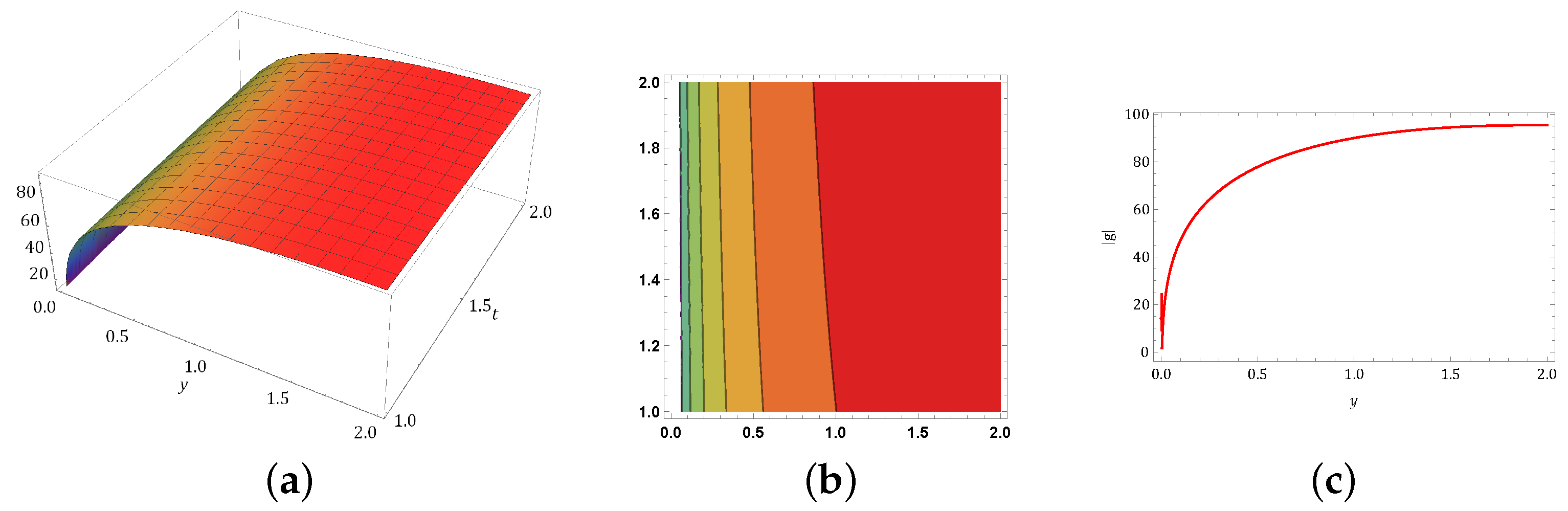
5. Physical Behavior of Solutions
6. Stability Analysis
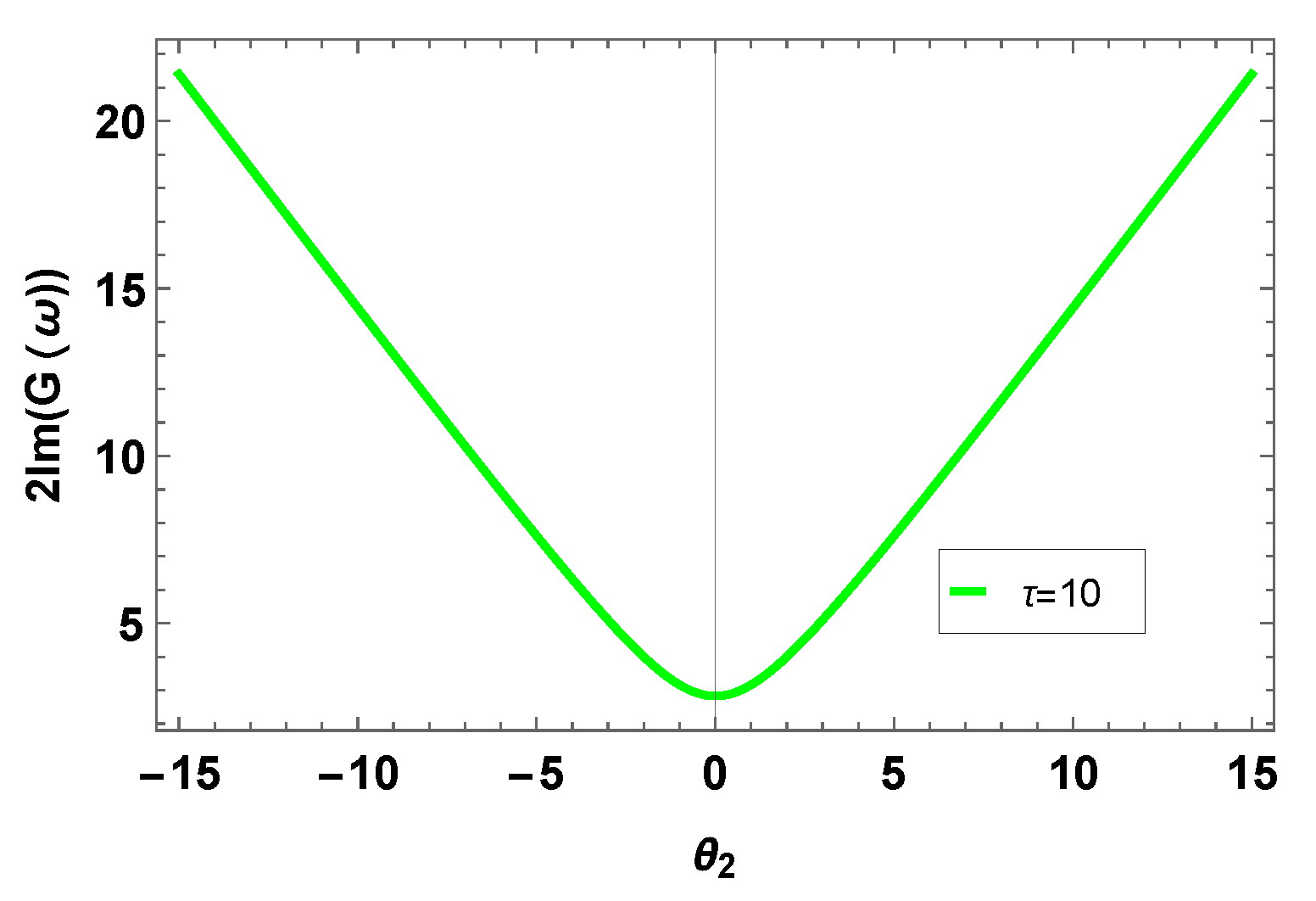
7. Modulation Instability Analysis
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ullah, M.S.; Abdeljabbar, A.; Roshid, H.O.; Ali, M.Z. Application of the unified method to solve the Biswas–Arshed model. Results Phys. 2022, 42, 105946. [Google Scholar] [CrossRef]
- Batiha, I.M.; Njadat, S.A.; Batyha, R.M.; Zraiqat, A.; Dababneh, A.; Momani, S. Design Fractional-order PID Controllers for Single-Joint Robot Arm Model. Int. J. Adv. Soft Comput. Appl. 2022, 14, 96–114. [Google Scholar] [CrossRef]
- Tuğba, A. Application of the generalized unified method to solve (2+1)-dimensional Kundu–Mukherjee–Naskar equation. Opt. Quantum Electron. 2023, 55, 534. [Google Scholar]
- Avazzadeh, Z.; Nikan, O.; Machado, J.A. Solitary wave solutions of the generalized Rosenau-KdV-RLW equation. Mathematics 2020, 8, 1601. [Google Scholar] [CrossRef]
- Jiang, S.; Zhang, J.; Zhang, Q.; Zhang, Z. Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun. Comput. Phys. 2017, 21, 650–678. [Google Scholar] [CrossRef]
- Erdal, B.; Ramazan, O. Real world applications of fractional models by Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 116, 121–125. [Google Scholar]
- Behzad, G.; Dumitru, B. New optical solutions of the fractional Gerdjikov-Ivanov equation with conformable derivative. Front. Phys. 2020, 8, 167. [Google Scholar]
- Mehmet, O.E. New exact solutions of some important nonlinear fractional partial differential Equations with beta derivative. Fractal Fract. 2022, 6, 173. [Google Scholar] [CrossRef]
- Qawaqneh, H.; Zafar, A.; Raheel, M.; Zaagan, A.A.; Zahran, E.H.; Cevikel, A.; Bekir, A. New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques. Opt. Quantum Electron. 2024, 56, 737. [Google Scholar] [CrossRef]
- Boubekeur, G.; Alaaeddin, M.; Yazid, M.; Lama, A.; Mehmet, B.H. Bifurcation and exact traveling wave solutions to a conformable nonlinear Schrödinger equation using a generalized double auxiliary equation method. Opt. Quantum Electron. 2024, 56, 18. [Google Scholar]
- Faridi, W.A.; Myrzakulova, Z.; Myrzakulov, R.; Akgül, A.; Osman, M.S. The construction of exact solution and explicit propagating optical soliton waves of Kuralay equation by the new extended direct algebraic and Nucci’s reduction techniques. Int. J. Model. Simul. 2024, 1–20. [Google Scholar] [CrossRef]
- Nasreen, N.; Rafiq, M.N.; Younas, U.; Arshad, M.; Abbas, M.; Ali, M.R. Stability analysis and dynamics of solitary wave solutions of the (3+1)-dimensional generalized shallow water wave equation using the Ricatti equation mapping method. Results Phys. 2024, 56, 107226. [Google Scholar] [CrossRef]
- Faridi, W.A.; Wazwaz, A.M.; Mostafa, A.M.; Myrzakulov, R.; Umurzakhova, Z. The Lie point symmetry criteria and formation of exact analytical solutions for Kairat-II equation: Paul-Painlevé approach. Chaos Solitons Fractals 2024, 182, 114745. [Google Scholar] [CrossRef]
- Wang, H. Exact traveling wave solutions of the generalized fifth-order dispersive equation by the improved Fan subequation method. Math. Methods Appl. Sci. 2024, 47, 1701–1710. [Google Scholar] [CrossRef]
- Arnous, A.H.; Hashemi, M.S.; Nisar, K.S.; Shakeel, M.; Ahmad, J.; Ahmad, I.; Jan, R.; Ali, A.; Kapoor, M.; Shah, N.A. Investigating solitary wave solutions with enhanced algebraic method for new extended Sakovich equations in fluid dynamics. Results Phys. 2024, 57, 107369. [Google Scholar] [CrossRef]
- Ramya, S.; Krishnakumar, K.; Ilangovane, R. Exact solutions of time fractional generalized burgers–Fisher equation using exp and exponential rational function methods. Int. J. Dyn. Control. 2024, 12, 292–302. [Google Scholar] [CrossRef]
- Eidinejad, Z.; Saadati, R.; Li, C.; Inc, M.; Vahidi, J. The multiple exp-function method to obtain soliton solutions of the conformable Date–Jimbo–Kashiwara–Miwa equations. Int. J. Mod. Phys. B 2024, 38, 2450043. [Google Scholar] [CrossRef]
- Ghayad, M.S.; Badra, N.M.; Ahmed, H.M.; Rabie, W.B. Derivation of optical solitons and other solutions for nonlinear Schrödinger equation using modified extended direct algebraic method. Alex. Eng. J. 2023, 64, 801–811. [Google Scholar] [CrossRef]
- Bilal, M.; Iqbal, J.; Ali, R.; Awwad, F.A.; AIsmail, E.A. Exploring Families of Solitary Wave Solutions for the Fractional Coupled Higgs System Using Modified Extended Direct Algebraic Method. Fractal Fract. 2023, 7, 653. [Google Scholar] [CrossRef]
- Hubert, M.B.; Betchewe, G.; Justin, M.; Doka, S.Y.; Crepin, K.T.; Biswas, A.; Zhou, Q.; Alshomrani, A.S.; Ekici, M.; Moshokoa, S.P.; et al. Optical solitons with Lakshmanan–Porsezian–Daniel model by modified extended direct algebraic method. Optik 2018, 162, 228–236. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Zaghrout, A.S.; Ahmed, H.M.; Arnous, A.H. Optical soliton perturbation of the Gerdjikov–Ivanov equation with spatio-temporal dispersion using a modified extended direct algebraic method. Optik 2022, 259, 168904. [Google Scholar] [CrossRef]
- Rabie, W.B.; Hussein, H.H.; Ahmed, H.M.; Alnahhass, M.; Alexan, W. Abundant solitons for highly dispersive nonlinear Schrödinger equation with sextic-power law refractive index using modified extended direct algebraic method. Alex. Eng. J. 2024, 86, 680–689. [Google Scholar] [CrossRef]
- Ali, M.H.; El-Owaidy, H.M.; Ahmed, H.M.; El-Deeb, A.A.; Samir, I. Solitons and other wave solutions for (2+1)-dimensional perturbed nonlinear Schrödinger equation by modified extended direct algebraic method. J. Opt. 2023, 53, 1–9. [Google Scholar] [CrossRef]
- Faisal, H.; Dipankar, K. A variety of exact analytical solutions of extended shallow water wave equations via improved (G′/G)-expansion method. Int. J. Phys. Res. 2017, 5, 21–27. [Google Scholar]
- Shakeel, M.; Mohyud-Din, S.T. Improved (G′/G)-expansion and extended tanh methods for (2+1)-dimensional Calogero–Bogoyavlenskii–Schiff equation. Alex. Eng. J. 2015, 54, 27–33. [Google Scholar] [CrossRef]
- Al-Sawalha, M.M.; Noor, S.; Alshammari, S.; Ganie, A.H.; Shafee, A. Analytical insights into solitary wave solutions of the fractional Estevez-Mansfield-Clarkson equation. Aims Math. 2024, 9, 13589–13606. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota- Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Vanterler, J.; Sousa, D.A.C.; Capelas, E.; Oliveira, D.E. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Sirasrete, P.; Weerachai, T. Wave effects of the fractional shallow water equation and the fractional optical fiber equation. Front. Appl. Math. Stat. 2022, 8, 900369. [Google Scholar]
- Barman, H.K.; Islam, M.E.; Akbar, M.A. A study on the compatibility of the generalized Kudryashov method to determine wave solutions. Propuls. Power Res. 2021, 10, 95–105. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S.; Abdou, M.A. New exact solutions for time-fractional Kaup-Kupershmidt equation using improved (G′/G)-expansion and extended (G′/G)-expansion methods. Alex. Eng. J. 2020, 59, 3105–3110. [Google Scholar] [CrossRef]
- Tariq, K.U.; Wazwaz, A.M.; Javed, R. Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel’d–Sokolov–Wilson model. Chaos Solitons Fractals 2023, 166, 112903. [Google Scholar] [CrossRef]
- Zulfiqar, H.; Aashiq, A.; Tariq, K.U.; Ahmad, H.; Almohsen, B.; Aslam, M.; Rehman, H.U. On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise. Optik 2023, 289, 171250. [Google Scholar] [CrossRef]
- Shafqat, U.R.; Jamshad, A. Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing. Alex. Eng. J. 2021, 60, 1339–1354. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qawaqneh, H.; Alrashedi, Y. Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation. Fractal Fract. 2024, 8, 467. https://doi.org/10.3390/fractalfract8080467
Qawaqneh H, Alrashedi Y. Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation. Fractal and Fractional. 2024; 8(8):467. https://doi.org/10.3390/fractalfract8080467
Chicago/Turabian StyleQawaqneh, Haitham, and Yasser Alrashedi. 2024. "Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation" Fractal and Fractional 8, no. 8: 467. https://doi.org/10.3390/fractalfract8080467
APA StyleQawaqneh, H., & Alrashedi, Y. (2024). Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation. Fractal and Fractional, 8(8), 467. https://doi.org/10.3390/fractalfract8080467





