Pavement Crack Detection Using Fractal Dimension and Semi-Supervised Learning
Abstract
1. Introduction
- Self-similarity characteristics within crack regions are identified by analyzing pavement crack images, leading to the development of a method for extracting candidate crack regions in pavement images using fractal dimensions.
- A semi-supervised learning-based automatic crack detection model, CrackSL-Net, is developed, which effectively achieves automatic crack detection in pavement images by employing a semantic similarity learning strategy and contrastive learning methods.
- Evaluation tests are performed on the GAPs384 and Crack500 datasets, and performance comparison experiments are conducted with various mainstream detection methods to assess the performance of the proposed method.
2. Methods
2.1. Crack Candidate Region Extraction
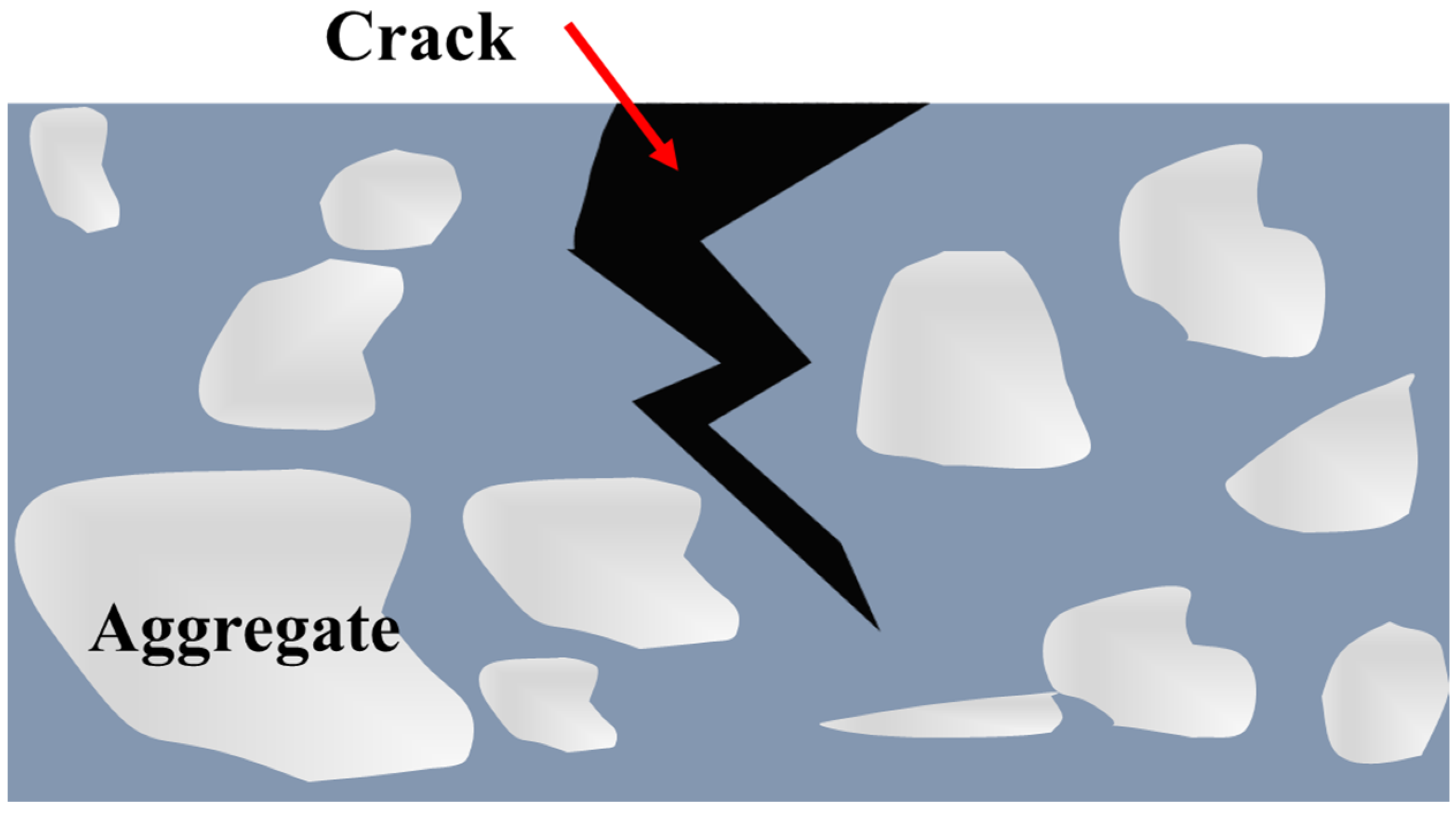
2.1.1. Fractal Nature of Crack
2.1.2. Crack Candidate Region Extraction Using Fractal Dimension
| Algorithm 1: Fractal Dimension-Based Crack Candidate Region Extraction |
| Input:
: Pavement image, b: Block size,
: Fractal dimension threshold Output: R: Crack candidate regions
|
2.2. Crack Detection Model
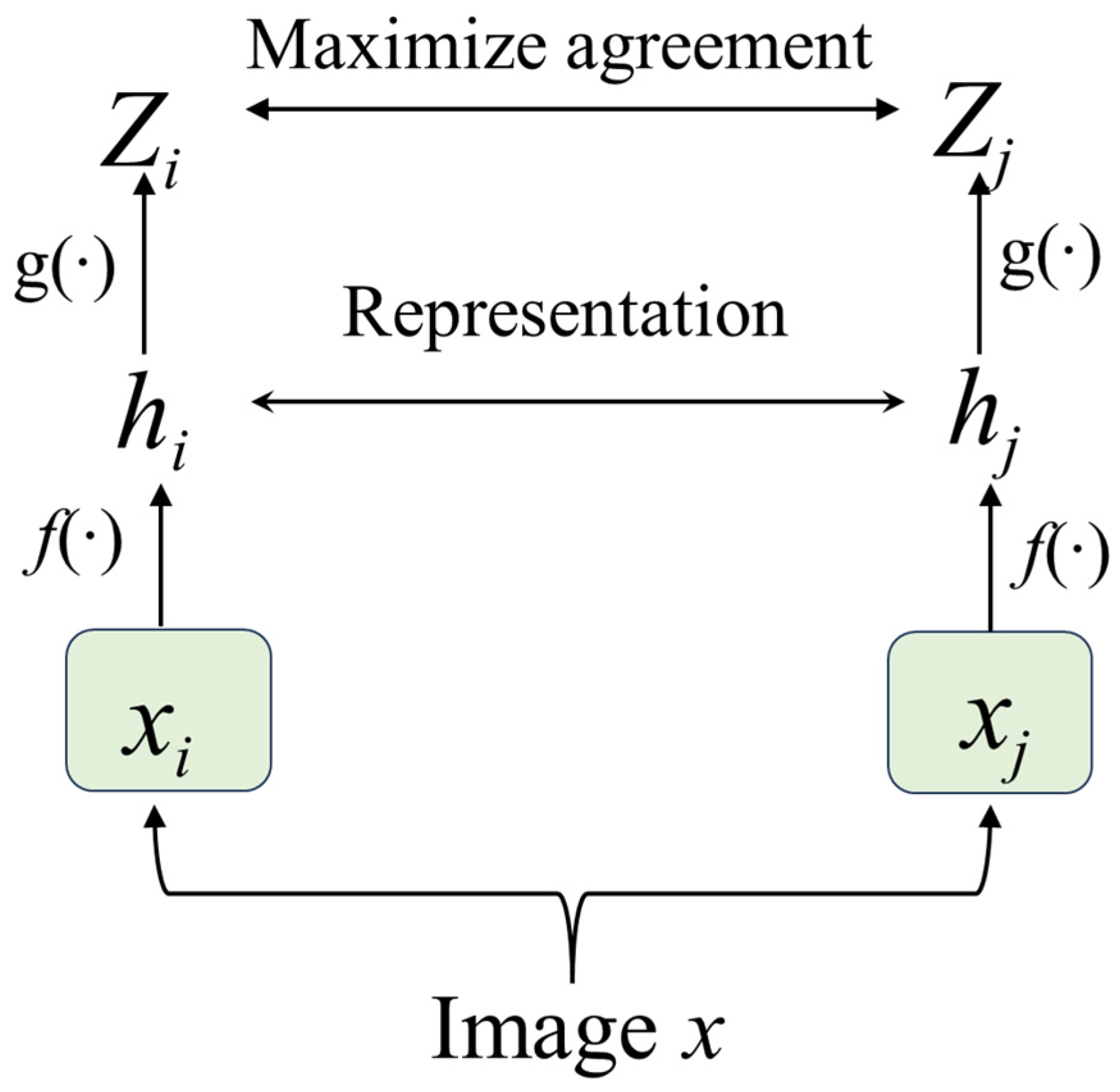
2.2.1. Contrastive Learning Model
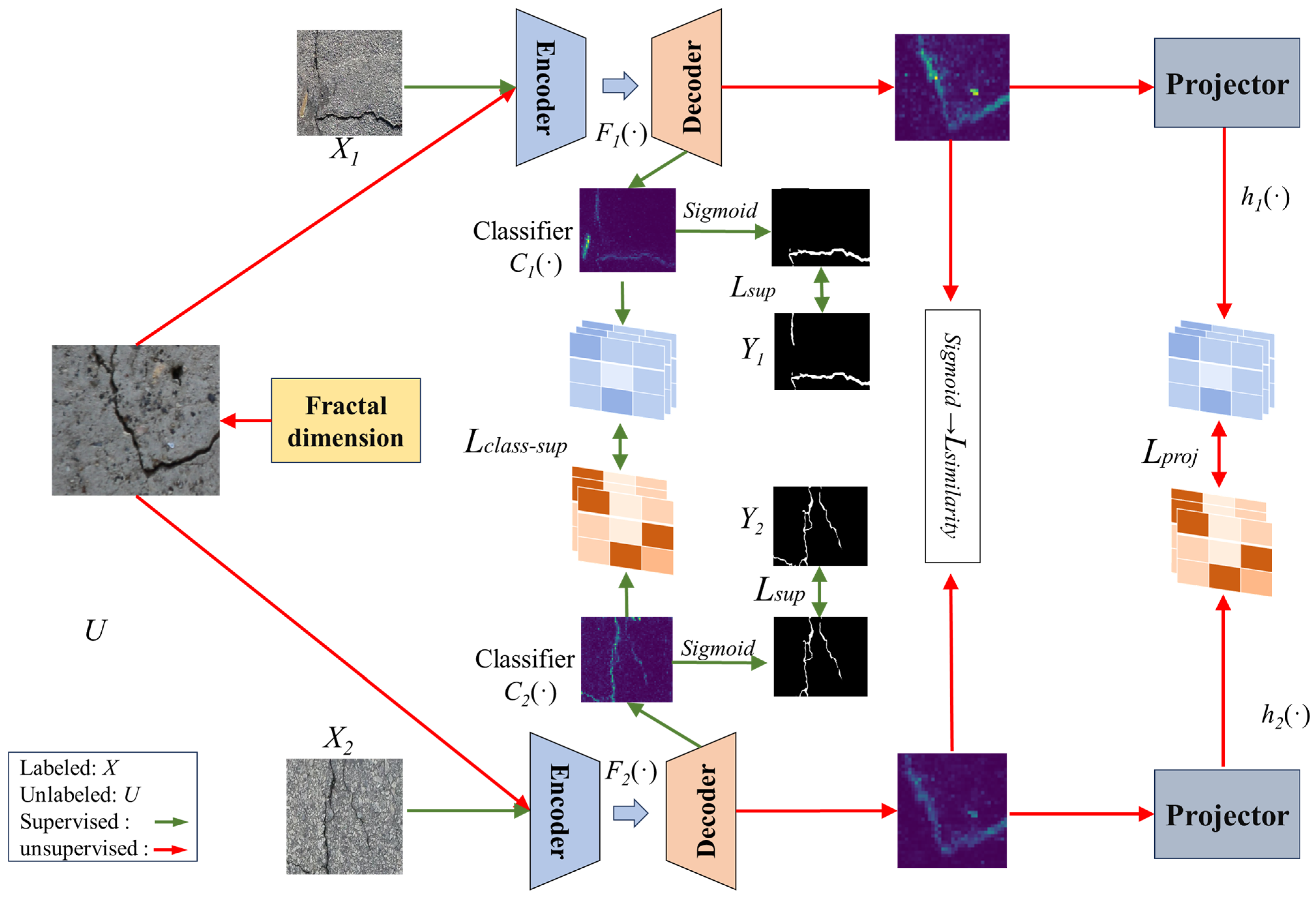
2.2.2. Structure of the Crack Detection Model
2.2.3. Loss Function
3. Implementation
3.1. Pavement Crack Data
3.2. Experimental Environment
3.3. Evaluation Indicators
4. Experiments and Analyses
4.1. Crack Detection Results and Analysis
4.1.1. Performance Comparison Analysis
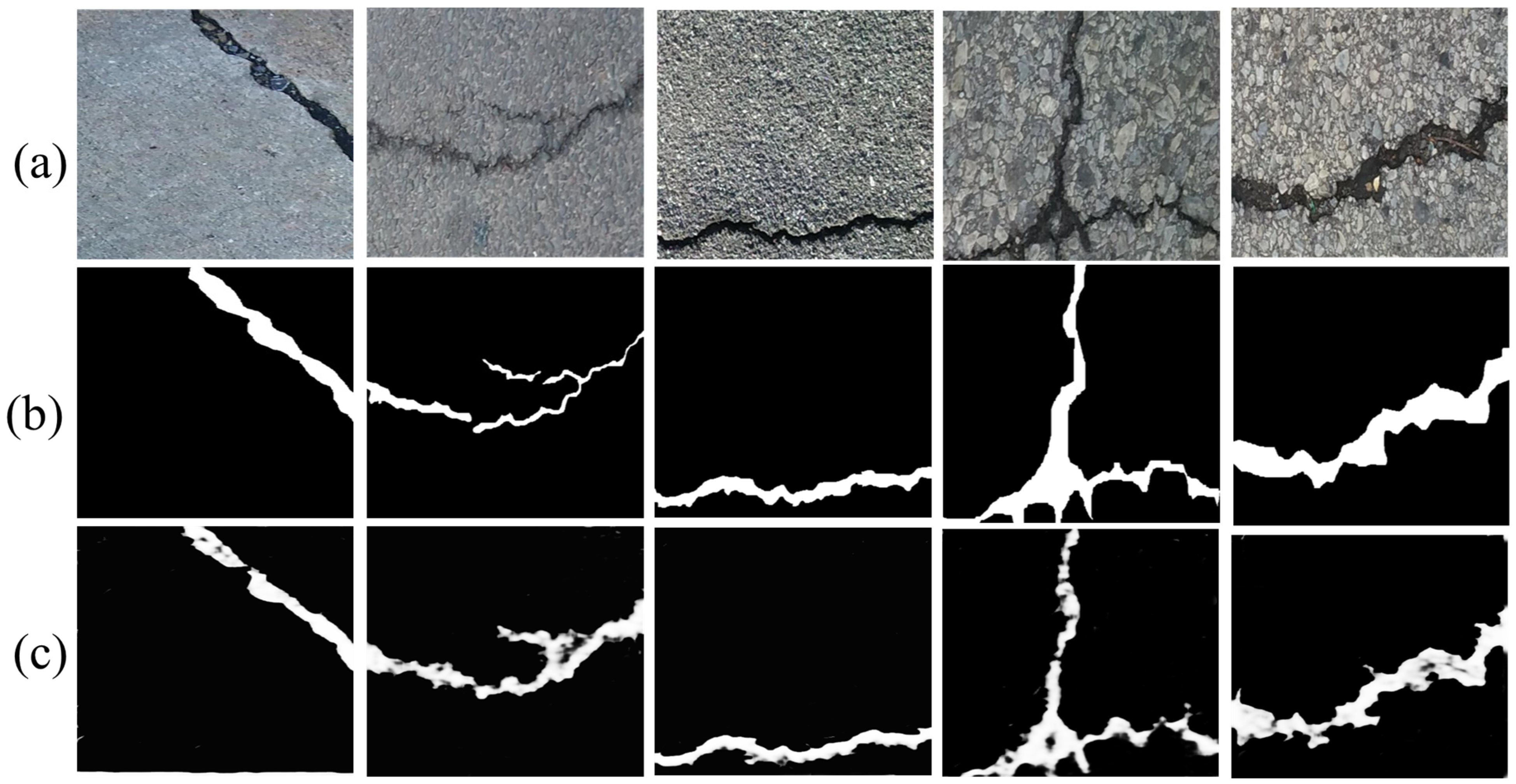
4.1.2. Comparative Analysis of Visualizations
4.2. Ablation Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ai, D.; Jiang, G.; Lam, S.K.; He, P.; Li, C. Computer vision framework for crack detection of civil infrastructure—A review. Eng. Appl. Artif. Intell. 2023, 117, 105478. [Google Scholar] [CrossRef]
- Yu, Y.; Guan, H.; Li, D.; Zhang, Y.; Jin, S.; Yu, C. CCapFPN: A Context-Augmented Capsule Feature Pyramid Network for Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3324–3335. [Google Scholar] [CrossRef]
- Zhang, D.; Zou, Q.; Lin, H.; Xu, X.; He, L.; Gui, R.; Li, Q. Automatic pavement defect detection using 3D laser profiling technology. Autom. Constr. 2018, 96, 350–365. [Google Scholar] [CrossRef]
- Guo, W.; Zhang, X.; Zhang, D.; Chen, Z.; Zhou, B.; Huang, D.; Li, Q. Detection and classification of pipe defects based on pipe-extended feature pyramid network. Autom. Constr. 2022, 141, 104399. [Google Scholar] [CrossRef]
- Sattar, S.; Li, S.; Chapman, M. Road surface monitoring using smartphone sensors: A review. Sensors 2018, 18, 3845. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar]
- Liu, Y.; Cheng, M.M.; Hu, X.; Bian, J.W.; Zhang, L.; Bai, X.; Tang, J. Richer Convolutional Features for Edge Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 1939–1946. [Google Scholar] [CrossRef] [PubMed]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Zhang, Z.; Li, Q.; Qi, X.; Wang, Q.; Wang, S. DeepCrack: Learning hierarchical convolutional features for crack detection. IEEE Trans. Image Process. 2019, 28, 1498–1512. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Liu, M.Y.; Kao, C.C.; Lee, T.Y. Deep active learning for civil infrastructure defect detection and classification. In Proceedings of the Congress on Computing in Civil Engineering, Proceedings; Mitsubishi Electric Research Laboratories, Inc.: Cambridge, MA, USA, 2017; pp. 298–306. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.-Y.; et al. Segment Anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023. [Google Scholar]
- Chaiyasarn, K.; Buatik, A.; Likitlersuang, S. Concrete crack detection and 3D mapping by integrated convolutional neural networks architecture. Adv. Struct. Eng. 2021, 24, 1480–1494. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, M.; Peng, Y.; Wu, L.; Wang, Y. HDCB-Net: A Neural Network with the Hybrid Dilated Convolution for Pixel-Level Crack Detection on Concrete Bridges. IEEE Trans. Ind. Inform. 2021, 17, 5485–5494. [Google Scholar] [CrossRef]
- Choi, W.; Cha, Y.J. SDDNet: Real-Time Crack Segmentation. IEEE Trans. Ind. Electron. 2020, 67, 8016–8025. [Google Scholar] [CrossRef]
- Kang, D.H.; Cha, Y.J. Efficient attention-based deep encoder and decoder for automatic crack segmentation. Struct. Health Monit. 2022, 21, 2190–2205. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zheng, T.; Xu, G.; Yang, Z.; Liu, H.; Cai, D. Training-time-friendly network for real-time object detection. In Proceedings of the AAAI 2020—34th AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 11685–11692. [Google Scholar] [CrossRef]
- Zhang, J.; Qian, S.; Tan, C. Automated bridge surface crack detection and segmentation using computer vision-based deep learning model. Eng. Appl. Artif. Intell. 2022, 115, 105225. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, L.; Yu, S.; Prokhorov, D.; Mei, X.; Ling, H. Feature Pyramid and Hierarchical Boosting Network for Pavement Crack Detection. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1525–1535. [Google Scholar] [CrossRef]
- Ye, X.W.; Jin, T.; Chen, P.Y. Structural crack detection using deep learning–based fully convolutional networks. Adv. Struct. Eng. 2019, 22, 3412–3419. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Fei, Y.; Wang, K.C.P.; Zhang, A.; Chen, C.; Li, J.Q.; Liu, Y.; Yang, G.; Li, B. Pixel-Level Cracking Detection on 3D Asphalt Pavement Images through Deep-Learning- Based CrackNet-V. IEEE Trans. Intell. Transp. Syst. 2020, 21, 273–284. [Google Scholar] [CrossRef]
- Bang, S.; Park, S.; Kim, H.; Kim, H. Encoder–decoder network for pixel-level road crack detection in black-box images. Comput. Civ. Infrastruct. Eng. 2019, 34, 713–727. [Google Scholar] [CrossRef]
- Nayyeri, F.; Hou, L.; Zhou, J.; Guan, H. Foreground–background separation technique for crack detection. Comput. Civ. Infrastruct. Eng. 2019, 34, 457–470. [Google Scholar] [CrossRef]
- Zhu, D.; Tang, A.; Wan, C.; Zeng, Y.; Wang, Z. Investigation on the flexural toughness evaluation method and surface cracks fractal characteristics of polypropylene fiber reinforced cement-based composites. J. Build. Eng. 2021, 43, 103045. [Google Scholar] [CrossRef]
- Yin, Y.; Ren, Q.; Lei, S.; Zhou, J.; Xu, L.; Wang, T. Mesoscopic crack pattern fractal dimension-based concrete damage identification. Eng. Fract. Mech. 2024, 296, 109829. [Google Scholar] [CrossRef]
- An, Q.; Chen, X.; Wang, H.; Yang, H.; Yang, Y.; Huang, W.; Wang, L. Segmentation of Concrete Cracks by Using Fractal Dimension and UHK-Net. Fractal Fract. 2022, 6, 95. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, Q.; Huang, X. An Algorithm for Crack Detection, Segmentation, and Fractal Dimension Estimation in Low-Light Environments by Fusing FFT and Convolutional Neural Network. Fractal Fract. 2023, 7, 820. [Google Scholar] [CrossRef]
- Nguyen, S.D.; Tran, T.S.; Tran, V.P.; Lee, H.J.; Piran, M.J.; Le, V.P. Deep Learning-Based Crack Detection: A Survey. Int. J. Pavement Res. Technol. 2023, 16, 943–967. [Google Scholar] [CrossRef]
- Liu, K.; Chen, B.M. Industrial UAV-Based Unsupervised Domain Adaptive Crack Recognitions: From Database Towards Real-Site Infrastructural Inspections. IEEE Trans. Ind. Electron. 2023, 70, 9410–9420. [Google Scholar] [CrossRef]
- Pang, X.; Lin, C.; Li, F.; Pan, Y. Bio-inspired XYW parallel pathway edge detection network. Expert Syst. Appl. 2024, 237, 121649. [Google Scholar] [CrossRef]
- Peiris, H.; Chen, Z.; Egan, G.; Harandi, M. Duo-SegNet: Adversarial Dual-Views for Semi-supervised Medical Image Segmentation. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2021; Volume 12902 LNCS, pp. 428–438. [Google Scholar]
- Ye, M.; Zhang, X.; Yuen, P.C.; Chang, S.F. Unsupervised embedding learning via invariant and spreading instance feature. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6203–6212. [Google Scholar] [CrossRef]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 9726–9735. [Google Scholar]
- Weng, X.; Huang, Y.; Li, Y.; Yang, H.; Yu, S. Unsupervised domain adaptation for crack detection. Autom. Constr. 2023, 153, 104939. [Google Scholar] [CrossRef]
- Jin, X.; Bu, J.; Yu, Z.; Zhang, H.; Wang, Y. FedCrack: Federated Transfer Learning With Unsupervised Representation for Crack Detection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11171–11184. [Google Scholar] [CrossRef]
- Wu, Y.; Hong, M.; Li, A.; Huang, S.; Liu, H.; Ge, Y. Self-Supervised Adversarial Learning for Domain Adaptation of Pavement Distress Classification. IEEE Trans. Intell. Transp. Syst. 2023, 25, 1966–1977. [Google Scholar] [CrossRef]
- Zhao, X.; Sheng, Y.; Lv, H.; Jia, H.; Liu, Q.; Ji, X.; Xiong, R.; Meng, J. Laboratory investigation on road performances of asphalt mixtures using steel slag and granite as aggregate. Constr. Build. Mater. 2022, 315, 125655. [Google Scholar] [CrossRef]
- Wu, J.; Jin, X.; Mi, S.; Tang, J. An effective method to compute the box-counting dimension based on the mathematical definition and intervals. Results Eng. 2020, 6, 100106. [Google Scholar] [CrossRef]
- Lou, A.; Tawfik, K.; Yao, X.; Liu, Z.; Noble, J. Min-Max Similarity: A Contrastive Semi-Supervised Deep Learning Network for Surgical Tools Segmentation. IEEE Trans. Med. Imaging 2023, 42, 2832–2841. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Qi, G.J. Contrastive Learning with Stronger Augmentations. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 5549–5560. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; He, K. Exploring simple Siamese representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 15745–15753. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, Virtual, 13–18 July 2020; Volume PartF16814, pp. 1575–1585. [Google Scholar]
- Gao, S.H.; Cheng, M.M.; Zhao, K.; Zhang, X.Y.; Yang, M.H.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef] [PubMed]
- Eisenbach, M.; Stricker, R.; Seichter, D.; Amende, K.; Debes, K.; Sesselmann, M.; Ebersbach, D.; Stoeckert, U.; Gross, H.M. How to get pavement distress detection ready for deep learning? A systematic approach. In Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 2039–2047. [Google Scholar]
- Lyu, C.; Hu, G.; Wang, D. Attention to fine-grained information: Hierarchical multi-scale network for retinal vessel segmentation. Vis. Comput. 2022, 38, 345–355. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, Y.; Cheng, H. Da CrackGAN: Pavement Crack Detection Using Partially Accurate Ground Truths Based on Generative Adversarial Learning. IEEE Trans. Intell. Transp. Syst. 2021, 22, 1306–1319. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]



| Methods | DSC | IoU | MAE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HED (fully) | 0.89 | 0.75 | 0.06 | ||||||
| RCF (fully) | 0.89 | 0.77 | 0.05 | ||||||
| U-Net (fully) | 0.91 | 0.88 | 0.05 | ||||||
| Label ratio lr | 5% | 20% | 50% | 5% | 20% | 50% | 5% | 20% | 50% |
| HED | 0.57 | 0.68 | 0.80 | 0.48 | 0.56 | 0.56 | 0.07 | 0.07 | 0.07 |
| RCF | 0.61 | 0.71 | 0.81 | 0.53 | 0.63 | 0.77 | 0.06 | 0.06 | 0.06 |
| U-Net | 0.64 | 0.72 | 0.81 | 0.60 | 0.76 | 0.78 | 0.07 | 0.06 | 0.06 |
| CrackSL-Net | 0.82 | 0.86 | 0.90 | 0.79 | 0.83 | 0.87 | 0.05 | 0.03 | 0.03 |
| Methods | DSC | IoU | MAE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| HED (fully) | 0.86 | 0.72 | 0.07 | ||||||
| RCF (fully) | 0.88 | 0.74 | 0.06 | ||||||
| U-Net (fully) | 0.87 | 0.85 | 0.06 | ||||||
| Label ratio lr | 5% | 20% | 50% | 5% | 20% | 50% | 5% | 20% | 50% |
| HED | 0.49 | 0.70 | 0.77 | 0.34 | 0.60 | 0.68 | 0.08 | 0.07 | 0.07 |
| RCF | 0.66 | 0.74 | 0.80 | 0.57 | 0.61 | 0.73 | 0.08 | 0.07 | 0.06 |
| U-Net | 0.43 | 0.75 | 0.77 | 0.33 | 0.65 | 0.69 | 0.07 | 0.07 | 0.06 |
| CrackSL-Net | 0.72 | 0.79 | 0.87 | 0.67 | 0.74 | 0.84 | 0.06 | 0.05 | 0.04 |
| Method | IoU (5%) | IoU (20%) | IoU (50%) |
|---|---|---|---|
| CrackSL-Net (baseline) | 0.61 | 0.70 | 0.83 |
| +Fractal dimension | 0.67 | 0.74 | 0.84 |
| Label Ratio | Classifier | Projector | DSC | IoU | MAE |
|---|---|---|---|---|---|
| 5% | x | x | 0.62 | 0.47 | 0.06 |
| √ | x | 0.67 | 0.54 | 0.06 | |
| x | √ | 0.71 | 0.57 | 0.05 | |
| √ | √ | 0.82 | 0.79 | 0.03 | |
| 20% | x | x | 0.69 | 0.59 | 0.05 |
| √ | x | 0.76 | 0.63 | 0.04 | |
| x | √ | 0.79 | 0.64 | 0.04 | |
| √ | √ | 0.86 | 0.83 | 0.03 | |
| 50% | x | x | 0.77 | 0.67 | 0.03 |
| √ | x | 0.85 | 0.76 | 0.03 | |
| x | √ | 0.86 | 0.76 | 0.03 | |
| √ | √ | 0.90 | 0.87 | 0.03 |
| α | β | γ | δ | DSC | IoU | MAE |
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.89 | 0.83 | 0.02 |
| 0.1 | 0.2 | 0.4 | 0.3 | 0.88 | 0.83 | 0.02 |
| 0.2 | 0.1 | 0.3 | 0.4 | 0.89 | 0.84 | 0.02 |
| 0.2 | 0.1 | 0.4 | 0.3 | 0.89 | 0.84 | 0.02 |
| 0.3 | 0.4 | 0.1 | 0.2 | 0.88 | 0.85 | 0.02 |
| 0.3 | 0.4 | 0.2 | 0.1 | 0.89 | 0.85 | 0.02 |
| 0.4 | 0.3 | 0.1 | 0.2 | 0.89 | 0.86 | 0.02 |
| 0.4 | 0.3 | 0.2 | 0.1 | 0.89 | 0.84 | 0.02 |
| 0.2 | 0.2 | 0.3 | 0.3 | 0.89 | 0.87 | 0.02 |
| 0.3 | 0.3 | 0.2 | 0.2 | 0.89 | 0.87 | 0.02 |
| 0.25 | 0.25 | 0.25 | 0.25 | 0.90 | 0.89 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Zhong, L.; Zhang, D.; Li, Q. Pavement Crack Detection Using Fractal Dimension and Semi-Supervised Learning. Fractal Fract. 2024, 8, 468. https://doi.org/10.3390/fractalfract8080468
Guo W, Zhong L, Zhang D, Li Q. Pavement Crack Detection Using Fractal Dimension and Semi-Supervised Learning. Fractal and Fractional. 2024; 8(8):468. https://doi.org/10.3390/fractalfract8080468
Chicago/Turabian StyleGuo, Wenhao, Leiyang Zhong, Dejin Zhang, and Qingquan Li. 2024. "Pavement Crack Detection Using Fractal Dimension and Semi-Supervised Learning" Fractal and Fractional 8, no. 8: 468. https://doi.org/10.3390/fractalfract8080468
APA StyleGuo, W., Zhong, L., Zhang, D., & Li, Q. (2024). Pavement Crack Detection Using Fractal Dimension and Semi-Supervised Learning. Fractal and Fractional, 8(8), 468. https://doi.org/10.3390/fractalfract8080468








