Analysis of Truncated M-Fractional Mathematical and Physical (2+1)-Dimensional Nonlinear Kadomtsev–Petviashvili-Modified Equal-Width Model
Abstract
1. Introduction
2. Description of Strategies
2.1. Function Method
2.2. Modified Extended Tanh Function Method
- Case 1: if :
3. Model Description and Mathematical Analysis
4. Exact Wave Solutions
4.1. By Function Method
- Set 1:
4.2. Application to the Modified Extended Function Method
- Set 1:
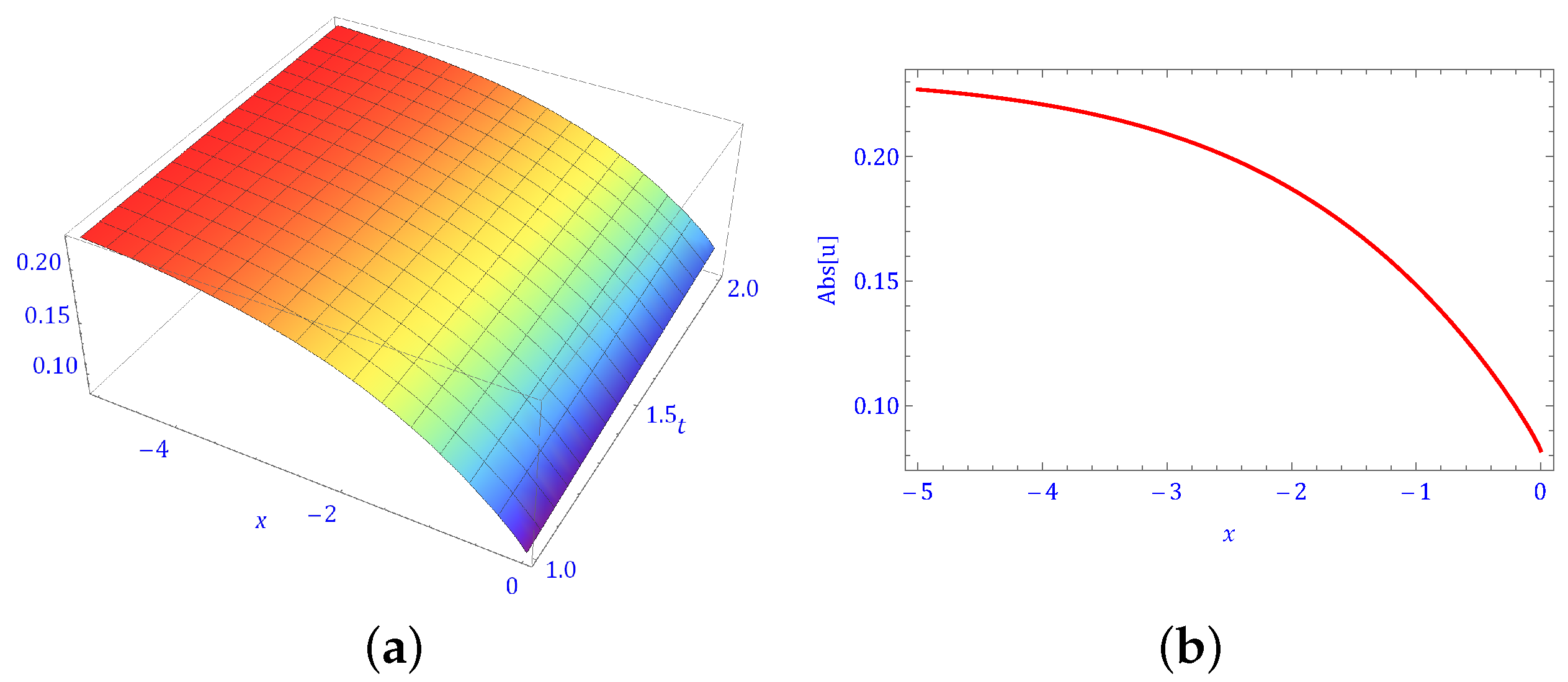
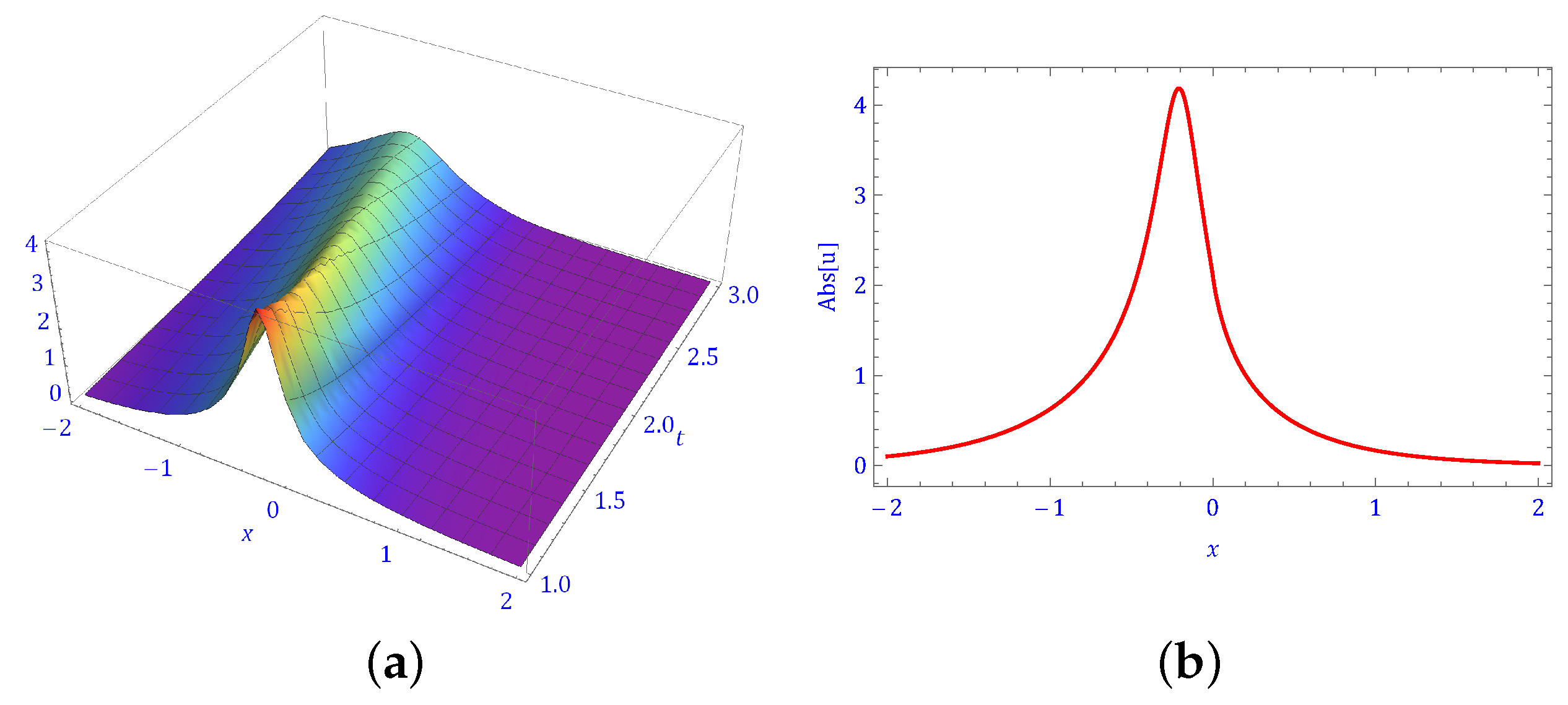
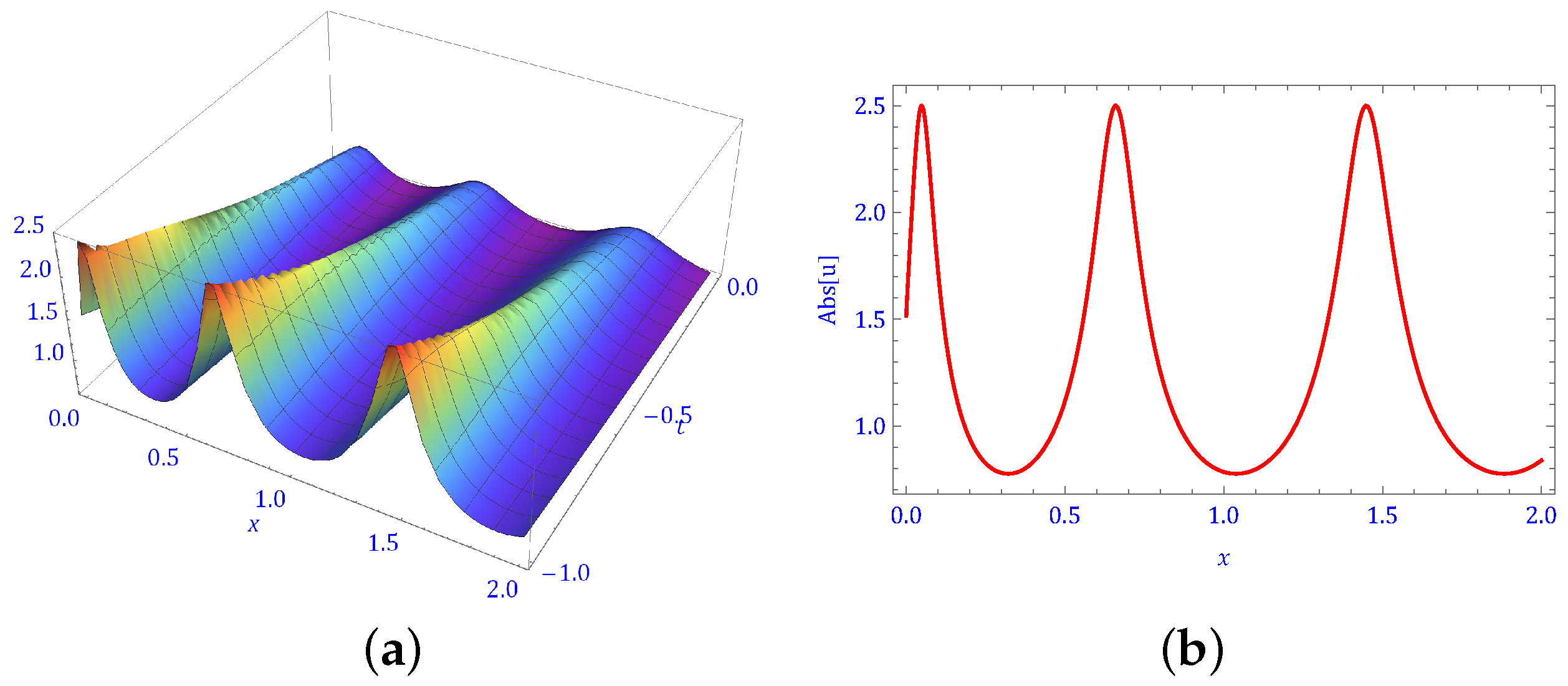
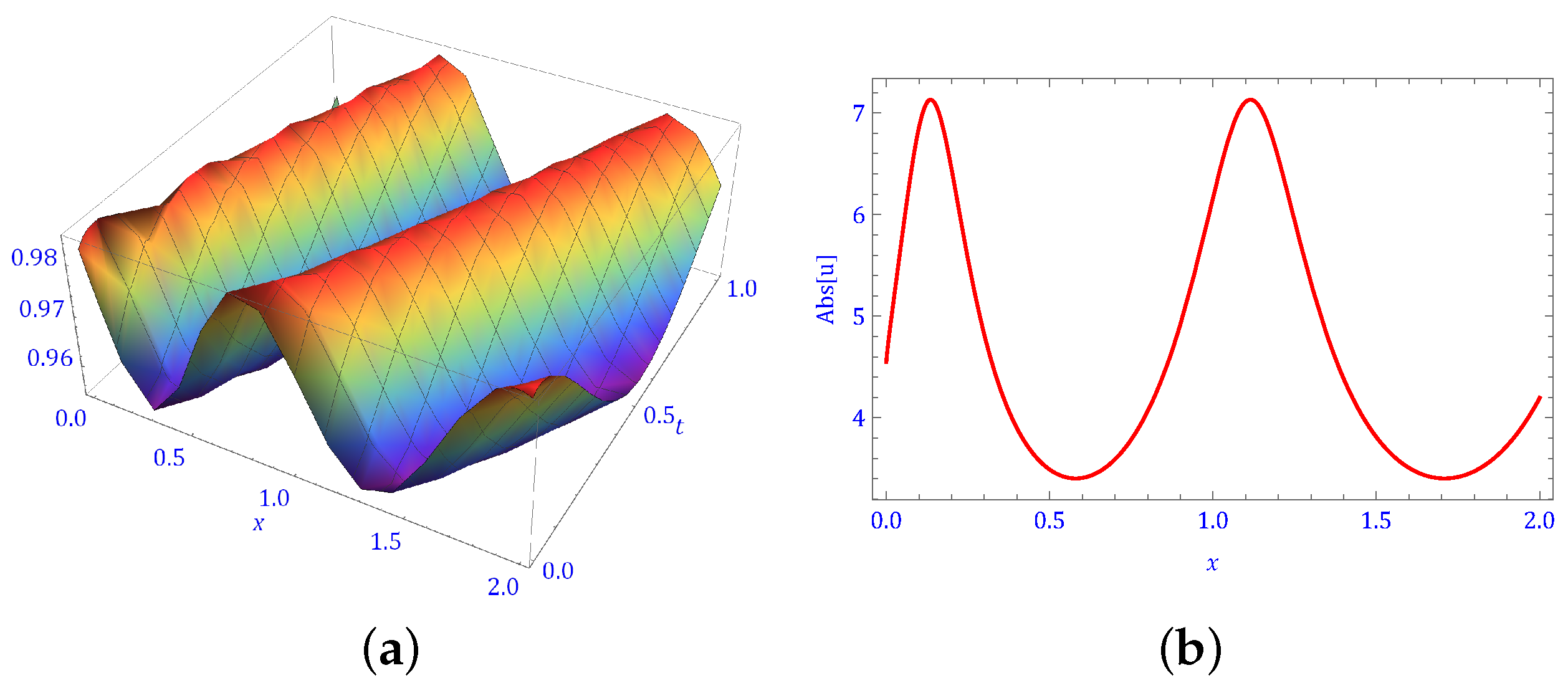
5. Physical Behavior of Solutions
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seadawy, A.R.; Ali, A.; Bekir, A. Exact wave solutions of new generalized Bogoyavlensky–Konopelchenko model in fluid mechanics. Mod. Phys. Lett. B 2024, 38, 2450262. [Google Scholar] [CrossRef]
- Kai, Y.; Yin, Z. Linear structure and soliton molecules of Sharma-Tasso-Olver-Burgers equation. Phys. Lett. A 2022, 452, 128430. [Google Scholar] [CrossRef]
- Durur, H. Exact Solutions of the Oskolkov Equation in Fluid Dynamics. Afyon Kocatepe Üniversitesi Fen Ve Mühendislik Bilimleri Dergisi 2023, 23, 355–361. [Google Scholar] [CrossRef]
- Zhou, Q.; Pan, A.; Mirhosseini-Alizamini, S.M.; Mirzazadeh, M.; Liu, W.; Biswas, A. Group analysis and exact soliton solutions to a new (3+1)-dimensional generalized Kadomtsev-Petviashvili equation in fluid mechanics. Acta Phys. Pol. A 2018, 134, 564–569. [Google Scholar] [CrossRef]
- Ullah, M.S.; Abdeljabbar, A.; Roshid, H.-O.; Ali, M.Z. Application of the unified method to solve the Biswas–Arshed model. Results Phys. 2022, 42, 105946. [Google Scholar] [CrossRef]
- Aydemir, T. Application of the generalized unified method to solve (2+1)-dimensional Kundu–Mukherjee–Naskar equation. Opt. Quantum Electron. 2023, 55, 534. [Google Scholar] [CrossRef]
- Nikan, O.; Avazzadeh, Z.; Rasoulizadeh, M.N. Soliton wave solutions of nonlinear mathematical models in elastic rods and bistable surfaces. Eng. Anal. Bound. Elem. 2022, 143, 14–27. [Google Scholar] [CrossRef]
- Kai, Y.; Ji, J.; Yin, Z. Study of the generalization of regularized long-wave equation. Nonlinear Dyn. 2022, 107, 2745–2752. [Google Scholar] [CrossRef]
- Ma, W.-X.; Huang, Y.; Wang, F.; Zhang, Y.; Ding, L. Binary Darboux transformation of vector nonlocal reverse-space nonlinear Schrödinger equations. Int. J. Geom. Methods Mod. Phys. 2024, 2450182. [Google Scholar] [CrossRef]
- Yang, J.Y.; Ma, W.X. Four-component Liouville integrable models and their bi-Hamiltonian formulations. Rom. J. Phys. 2024, 69, 101. [Google Scholar] [CrossRef]
- Arnous, A.H.; Hashemi, M.S.; Nisar, K.S.; Shakeel, M.; Ahmad, J.; Ahmad, I.; Jan, R.; Ali, A.; Kapoor, M.; Shah, N.A. Investigating solitary wave solutions with enhanced algebraic method for new extended Sakovich equations in fluid dynamics. Results Phys. 2024, 57, 107369. [Google Scholar] [CrossRef]
- Islam, S.M.R. Bifurcation analysis and exact wave solutions of the nano-ionic currents equation: Via two analytical techniques. Results Phys. 2024, 58, 107536. [Google Scholar] [CrossRef]
- Zhu, C.; Al-Dossari, M.; Rezapour, S.; Shateyi, S. On the exact soliton solutions and different wave structures to the modified Schrödinger’s equation. Results Phys. 2023, 54, 107037. [Google Scholar] [CrossRef]
- Zhu, C.; Abdallah, S.A.O.; Rezapour, S.; Shateyi, S. On new diverse variety analytical optical soliton solutions to the perturbed nonlinear Schrödinger equation. Results Phys. 2023, 54, 107046. [Google Scholar] [CrossRef]
- Tala-Tebue, E.; Rezazadeh, H.; Djoufack, Z.I.; Eslam, M.; Kenfack-Jiotsa, A.; Bekir, A. Optical solutions of cold bosonic atoms in a zig-zag optical lattice. Opt. Quantum Electron. 2021, 53, 1–13. [Google Scholar] [CrossRef]
- Raheel, M.; Zafar, A.; Tala-Tebue, E. Optical solitons to time-fractional Sasa-Satsuma higher-order non-linear Schrödinger equation via three analytical techniques. Opt. Quantum Electron. 2023, 55, 307. [Google Scholar] [CrossRef]
- Zafar, A.; Ali, K.K.; Raheel, M.; Nisar, K.S.; Bekir, A. Abundant M-fractional optical solitons to the pertubed Gerdjikov–Ivanov equation treating the mathematical nonlinear optics. Opt. Quantum Electron. 2022, 54, 25. [Google Scholar] [CrossRef]
- Hussein, H.H.; Ahmed, H.M.; Alexan, W. Analytical soliton solutions for cubic-quartic perturbations of the Lakshmanan-Porsezian-Daniel equation using the modified extended tanh function method. Ain Shams Eng. J. 2024, 15, 102513. [Google Scholar] [CrossRef]
- Akbulut, A.; Taşcan, F. Application of conservation theorem and modified extended tanh-function method to (1+1)-dimensional nonlinear coupled Klein–Gordon–Zakharov equation. Chaos Solitons Fractals 2017, 104, 33–40. [Google Scholar] [CrossRef]
- Islam, M.T.; Akter, M.A.; Gómez-Aguilar, J.F.; Akbar, M.A.; Torres-Jiménez, J. A novel study of the nonlinear Kadomtsev–Petviashvili-modified equal width equation describing the behavior of solitons. Opt. Quantum Electron. 2022, 54, 725. [Google Scholar] [CrossRef]
- Islam, M.T.; Akter, M.A.; Ryehan, S.; Gómez-Aguilar, J.F.; Akbar, M.A. A variety of solitons on the oceans exposed by the Kadomtsev Petviashvili-modified equal width equation adopting different techniques. J. Ocean Eng. Sci. 2022; in press. [Google Scholar]
- Ali, A.T.; Hassan, E.R. General expa-function method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 451–459. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A.G. Generalized kudryashov method and general expa function method for solving a high order nonlinear schrödinger equation. J. Space Explor. 2017, 6, 1–26. [Google Scholar]
- Hosseini, K.; Ayati, Z.; Ansari, R. New exact solutions of the Tzitzéica-type equations in non-linear optics using the expa function method. J. Mod. Opt. 2018, 65, 847–851. [Google Scholar] [CrossRef]
- Zafar, A. The expa function method and the conformable time-fractional KdV equations. Nonlinear Eng. 2019, 8, 728–732. [Google Scholar] [CrossRef]
- Ma, W.-X.; Fuchssteiner, B. Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. Int. J. Non-Linear Mech. 1996, 31, 329–338. [Google Scholar] [CrossRef]
- Sulaiman, T.A.; Yel, G.; Bulut, H. M-fractional solitons and periodic wave solutions to the Hirota- Maccari system. Mod. Phys. Lett. B 2019, 33, 1950052. [Google Scholar] [CrossRef]
- Sousa, J.V.D.C.; de Oliveira, E.C. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int. J. Anal. Appl. 2018, 16, 83–96. [Google Scholar]
- Wazwaz, A.M. The tanh method and the sine–cosine method for solving the KP-MEW equation. Int. J. Comput. Math. 2005, 82, 235–246. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alomair, M.A.; Junjua, M.-u.-D. Analysis of Truncated M-Fractional Mathematical and Physical (2+1)-Dimensional Nonlinear Kadomtsev–Petviashvili-Modified Equal-Width Model. Fractal Fract. 2024, 8, 442. https://doi.org/10.3390/fractalfract8080442
Alomair MA, Junjua M-u-D. Analysis of Truncated M-Fractional Mathematical and Physical (2+1)-Dimensional Nonlinear Kadomtsev–Petviashvili-Modified Equal-Width Model. Fractal and Fractional. 2024; 8(8):442. https://doi.org/10.3390/fractalfract8080442
Chicago/Turabian StyleAlomair, Mohammed Ahmed, and Moin-ud-Din Junjua. 2024. "Analysis of Truncated M-Fractional Mathematical and Physical (2+1)-Dimensional Nonlinear Kadomtsev–Petviashvili-Modified Equal-Width Model" Fractal and Fractional 8, no. 8: 442. https://doi.org/10.3390/fractalfract8080442
APA StyleAlomair, M. A., & Junjua, M.-u.-D. (2024). Analysis of Truncated M-Fractional Mathematical and Physical (2+1)-Dimensional Nonlinear Kadomtsev–Petviashvili-Modified Equal-Width Model. Fractal and Fractional, 8(8), 442. https://doi.org/10.3390/fractalfract8080442






