Morphological Features of Mathematical and Real-World Fractals: A Survey
Abstract
1. Introduction
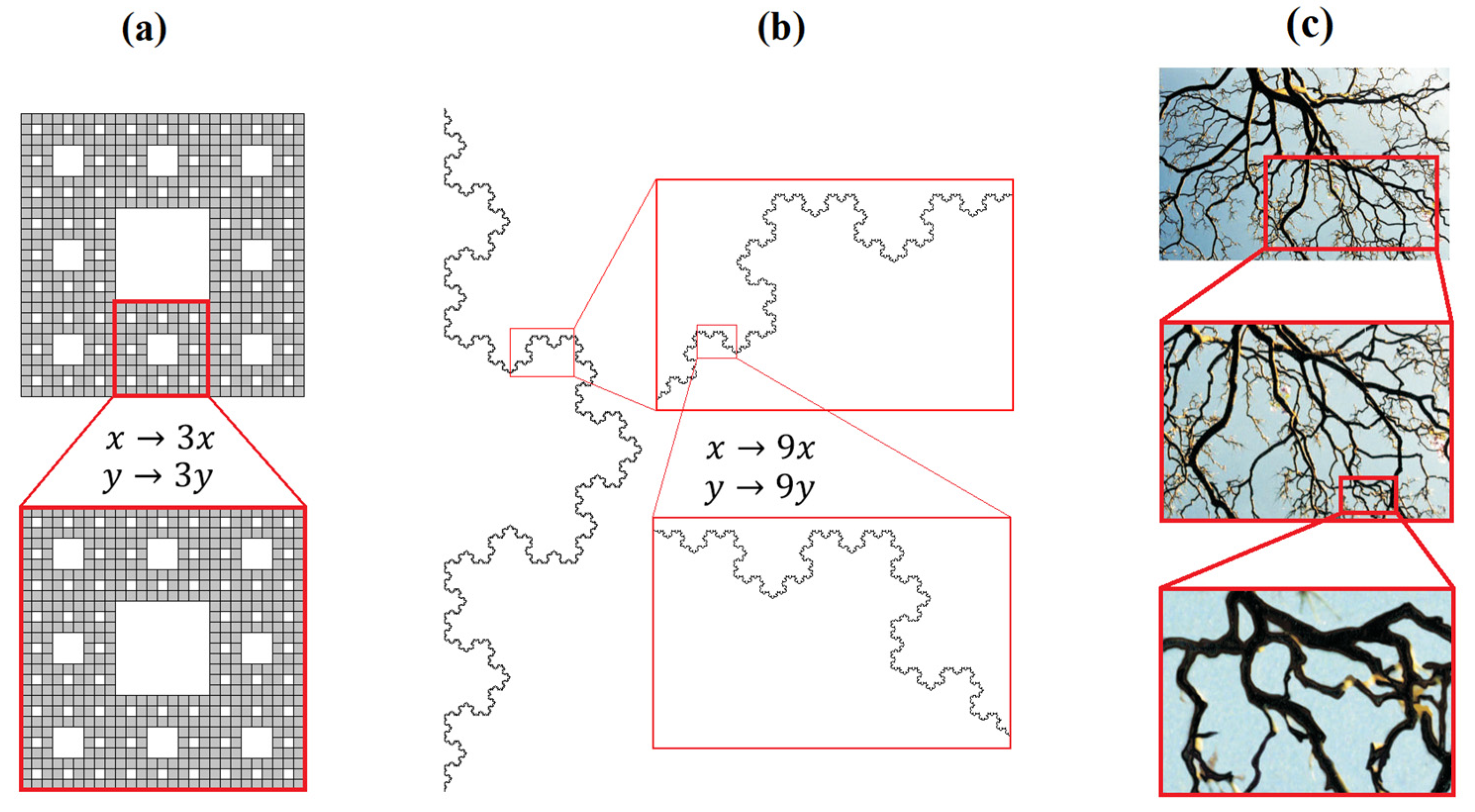
2. Scale and Conformal Invariance of Mathematical and Real-World Fractals
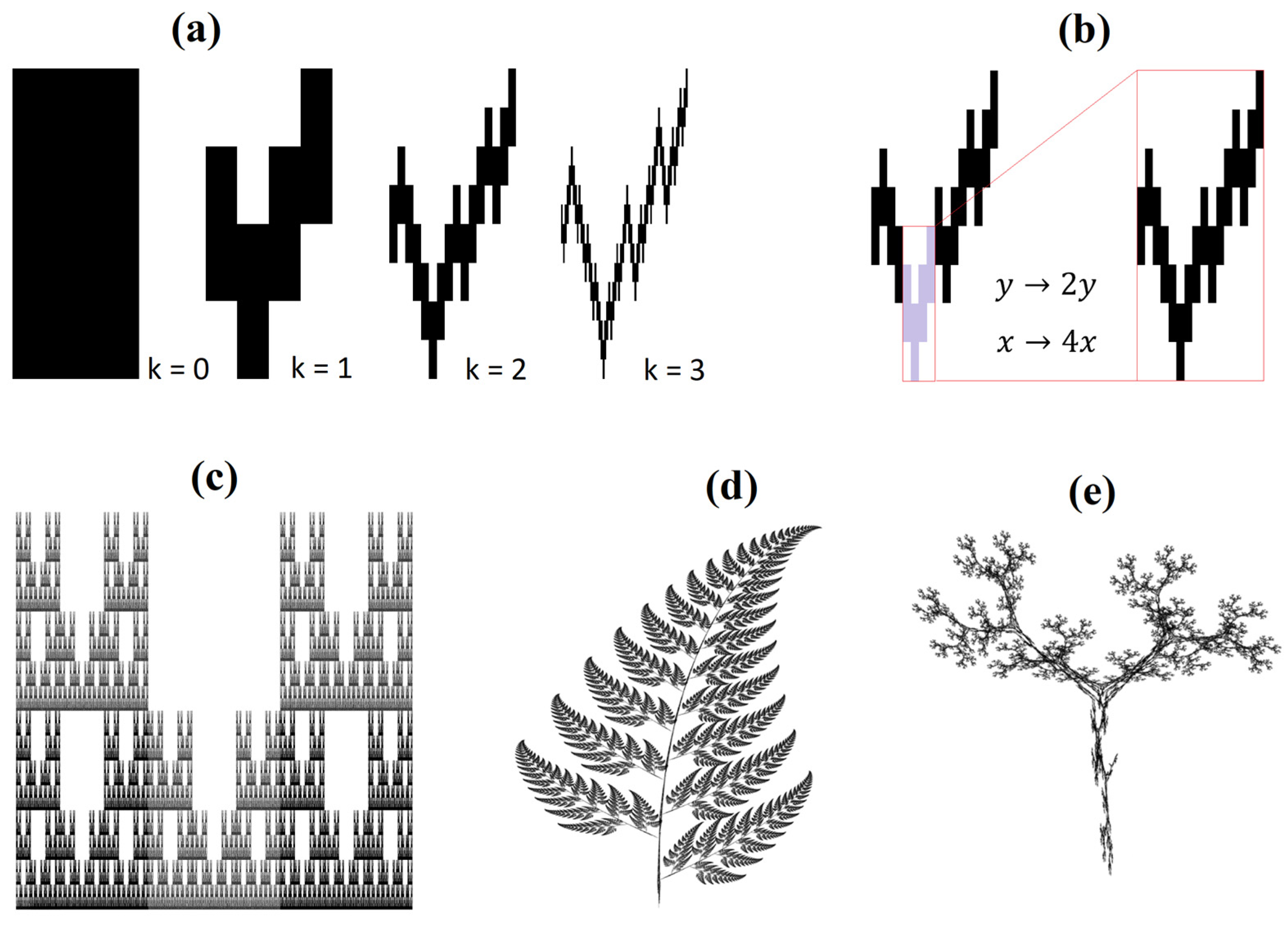
3. Fractal Non-Uniformity and Multifractality
4. Fractal Inhomogeneity and Lacunarity
5. Fractal Anisotropy and Succolarity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freemann: New York, NY, USA, 1982. [Google Scholar]
- Stanley, H.E. Application of fractal concepts to polymer statistics and to anomalous transport in randomly porous media. J. Stat. Phys. 1984, 36, 843–860. [Google Scholar] [CrossRef]
- Havlin, S.; Buldyrev, S.; Goldberger, A.; Mantegna, R.N.; Ossadnik, S.M.; Peng, C.K.; Simons, M.; Stanley, H.E. Fractals in biology and medicine. Chaos Solitons Fractals 1995, 6, 172–201. [Google Scholar] [CrossRef]
- Cherepanov, G.P.; Balankin, A.S.; Ivanova, V.S. Fractal fracture mechanics—A review. Eng. Fract. Mech. 1995, 51, 997–1033. [Google Scholar] [CrossRef]
- Husain, A.; Nanda, M.N.; Chowdary, M.S.; Sajid, M. Fractals: An Eclectic Survey, Part-II. Fractal Fract. 2022, 6, 379. [Google Scholar] [CrossRef]
- Gouyet, J.-F. Physics and Fractal Structures; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 2002, 51, 187–292. [Google Scholar] [CrossRef]
- Balankin, A.S. Physics of fracture and mechanics of self-affine cracks. Eng. Fract. Mech. 1997, 57, 135–203. [Google Scholar] [CrossRef]
- Nicolás-Carlock, J.R.; Carrillo-Estrada, J.L.; Dossetti, V. Fractality à la carte: A general particle aggregation model. Sci. Rep. 2016, 6, 19505. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractal geometry: What is it, and what does it do? Proc. R. Soc. Lond. A 1989, 423, 3–16. [Google Scholar] [CrossRef]
- Husain, A.; Nanda, M.N.; Chowdary, M.S.; Sajid, M. Fractals: An Eclectic Survey, Part-I. Fractal Fract. 2022, 6, 89. [Google Scholar] [CrossRef]
- Balankin, A.S. Fractional space approach to studies of physical phenomena on fractals and in confined low-dimensional systems. Chaos Solitons Fractals 2020, 132, 109572. [Google Scholar] [CrossRef]
- Nakayama, T.; Yakubo, K.; Orbach, R.L. Dynamical properties of fractal networks: Scaling, numerical simulations, and physical realizations. Rev. Mod. Phys. 1994, 66, 381–443. [Google Scholar] [CrossRef]
- Balankin, A.S.; Patiño, J.; Patiño, M. Inherent features of fractal sets and key attributes of fractal models. Fractals 2022, 30, 2250082. [Google Scholar] [CrossRef]
- Patiño-Ortiz, J.; Patiño-Ortiz, M.; Martínez-Cruz, M.A.; Balankin, A.S. A Brief Survey of Paradigmatic Fractals from a Topological Perspective. Fractal Fract. 2023, 7, 597. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications; Springer: New York, NY, USA, 2013. [Google Scholar]
- Radhakrishnan, P.; Daya-Sagar, B.S.; Lian, T.L. Estimation of fractal dimension through morphological decomposition. Chaos Solitons Fractals 2004, 21, 563–572. [Google Scholar] [CrossRef]
- Rout, R.K.; Choudhury, P.P.; Maity, S.P.; Daya-Sagar, B.S.; Hassan, S.S. Fractal and mathematical morphology in intricate comparison between tertiary protein structures. Comp. Meth. Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 192–203. [Google Scholar] [CrossRef]
- Flores-Ortega, A.C.; Nicolás-Carlock, J.R.; Carrillo-Estrada, J.L. Network efficiency of spatial systems with fractal morphology: A geometric graphs approach. Sci. Rep. 2023, 13, 18706. [Google Scholar] [CrossRef]
- Nakayama, Y. Scale invariance vs conformal invariance. Phys. Rep. 2015, 569, 1–93. [Google Scholar] [CrossRef]
- Edgar, G. Measure, Topology, and Fractal Geometry; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kombrink, S. Renewal theorems for processes with dependent inter arrival times. Adv. Appl. Prob. 2018, 50, 1193–1216. [Google Scholar] [CrossRef]
- Banaji, A.; Fraser, J.M. Assouad type dimensions of infinitely generated self-conformal sets. Nonlinearity 2024, 37, 045004. [Google Scholar] [CrossRef]
- Hutchinson, J.E. Fractals and self-similarity. Indiana Univ. Math. J. 1981, 30, 713–747. [Google Scholar] [CrossRef]
- Kiinkenberg, B. Review of Methods Used to Determine the Fractal Dimension of Linear Features. Math. Geol. 1994, 26, 23–46. [Google Scholar] [CrossRef]
- Mandelbrot, B. Self-Affine Fractals and the Fractal Dimension. Phys. Scr. 1985, 32, 257–260. [Google Scholar] [CrossRef]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 3rd ed.; John Wiley & Sons, Ltd.: West Sussex, UK, 2014. [Google Scholar]
- Luukkainen, J. Assouad dimension: Antifractal metrization, porous sets, and homogeneous measures. J. Korean Math. Soc. 1998, 35, 23–76. [Google Scholar]
- Gehring, F.W.; Väisälä, J. Hausdorff dimension and quasiconformal mappings. J. Lond. Math. Soc. 1973, 2–6, 504–512. [Google Scholar] [CrossRef]
- Pansu, P. Dimension conforme et sphère à l’infini des variétés à courbure négative. Ann. Acad. Sci. Fenn. Ser. A 1989, 14, 177–212. [Google Scholar] [CrossRef]
- DiMarco, C.A. Fractal curves and rugs of prescribed conformal dimension. Topol. Appl. 2018, 248, 117–127. [Google Scholar] [CrossRef]
- Heinonen, J.; Koskela, P. Quasiconformal maps in metric spaces with controlled geometry. Acta Math. 1998, 181, 1–61. [Google Scholar] [CrossRef]
- Malcai, O.; Lidar, D.A.; Biham, O.; Avnir, D. Scaling range and cutoffs in empirical fractals. Phys. Rev. E 1997, 56, 2817–2828. [Google Scholar] [CrossRef]
- Balankin, A.S.; Rangel, A.H.; Pérez, G.G.; Martinez, F.G.; Chavez, H.S.; Martinez-Gonzalez, C.L. Fractal features of a crumpling network in randomly folded thin matter and mechanics of sheet crushing. Phys. Rev. E 2013, 87, 052806. [Google Scholar] [CrossRef]
- Glenny, R.W.; Krueger, M.; Bauer, C.; Beichel, R.R. The fractal geometry of bronchial trees differs by strain in mice. J. Appl. Physiol. 2020, 128, 362–367. [Google Scholar] [CrossRef]
- Berntson, G.M.; Stoll, P. Correcting for finite spatial scales of self–similarity when calculating fractal dimensions of real–world structures. Proc. R. Soc. Lond. B 1997, 264, 1531–1537. [Google Scholar] [CrossRef]
- Bouda, M.; Caplan, J.S.; Saiers, J.E. Box-Counting Dimension Revisited: Presenting an Efficient Method of Minimizing Quantization Error and an Assessment of the Self-Similarity of Structural Root Systems. Front. Plant Sci. 2016, 7, 149. [Google Scholar] [CrossRef]
- Xia, Y.; Cai, J.; Perfect, E.; Wei, W.; Zhang, Q.; Meng, Q. Fractal dimension, lacunarity and succolarity analyses on CT images of reservoir rocks for permeability prediction. J. Hydrol. 2019, 579, 124198. [Google Scholar] [CrossRef]
- Panigrahy, C.; Seal, A.; Mahato, N.K.; Bhattacharjee, D. Differential box counting methods for estimating fractal dimension of gray-scale images: A survey. Chaos Solitons Fractals 2019, 126, 178–202. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Wang, J.; Li, R.; Liu, X.; Zhang, J. Problems of the Grid Size Selection in Differential Box-Counting (DBC) Methods and an Improvement Strategy. Entropy 2022, 24, 977. [Google Scholar] [CrossRef]
- Gazit, Y.; Baish, J.W.; Safabakhsh, N.; Leunig, M.; Baxter, L.T.; Jain, R.K. Fractal Characteristics of Tumor Vascular Architecture During Tumor Growth and Regression. Microcirculation 1997, 4, 395–402. [Google Scholar] [CrossRef]
- Cheeseman, A.K.; Vrscay, E.R. Estimating the Fractal Dimensions of Vascular Networks and Other Branching Structures: Some Words of Caution. Mathematics 2022, 10, 839. [Google Scholar] [CrossRef]
- Rak, R.; Rak, E. Multifractality of Complex Networks Is Also Due to Geometry: A Geometric Sandbox Algorithm. Entropy 2023, 25, 1324. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hou, L.; Chen, Y. Fractal Analysis of Fuel Nozzle Surface Morphology Based on the 3D-Sandbox Method. Micromachines 2023, 14, 904. [Google Scholar] [CrossRef] [PubMed]
- Zhao, F.X.; Liu, J.L.; Zhou, Y. Sandbox edge-based algorithm for multifractal analysis of complex networks. Chaos, Solitons Fractals 2023, 173, 113719. [Google Scholar] [CrossRef]
- Mandeibrot, B.B.; Passoia, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Gorsich, D.J.; Tolle, C.R.; Karlsen, R.E.; Gerhart, G.R. Wavelet and fractal analysis of ground-vehicle images. Proc. SPIE Wavelet Appl. Signal Image Process. 1996, 2825, 109–119. [Google Scholar] [CrossRef]
- Ahammer, H. Higuchi Dimension of Digital Images. PLoS ONE 2011, 6, e24796. [Google Scholar] [CrossRef] [PubMed]
- Babadagli, T.; Develi, K. On the application of methods used to calculate the fractal dimension of fracture surfaces. Fractals 2001, 9, 105–128. [Google Scholar] [CrossRef]
- Balankin, A.; López, T.; Alexander-Katz, R.; Córdova, A.; Susarrey, O.; Montiel, R. Phosphate Alumina Process by Sol−Gel: Textural and Fractal Properties. Langmuir 2003, 19, 3628–3634. [Google Scholar] [CrossRef]
- Oleschko, K.; Korvin, G.; Figueroa, B.; Vuelvas, M.A.; Balankin, A.S.; Flores, L.; Carreón, D. Fractal radar scattering from soil. Phys. Rev. E 2003, 67, 041403. [Google Scholar] [CrossRef] [PubMed]
- López, T.; Rojas, F.; Alexander-Katz, R.; Galindo, F.; Balankin, A.S.; Buljan, A. Porosity, structural and fractal study of sol–gel TiO2–CeO2 mixed oxides. J. Solid State Chem. 2004, 177, 1873–1885. [Google Scholar] [CrossRef]
- López, T.; Patiño-Ortiz, M.; Balankin, A.S.; González, R.D. Fractal Analysis of Tissue Biocompatible Neuroreservoir. Appl. Mech. Mat. 2009, 15, 121–126. [Google Scholar] [CrossRef]
- Du, J.; Zhai, C.M.; Wang, Q.P. Recognition of plant leaf image based on fractal dimension features. Neurocomputing 2013, 116, 150–156. [Google Scholar] [CrossRef]
- Wang, R.; Singh, A.K.; Kolan, S.R.; Tsotsas, E. Investigation of the Relationship between the 2D and 3D Box-Counting Fractal Properties and Power Law Fractal Properties of Aggregates. Fractal Fract. 2022, 6, 728. [Google Scholar] [CrossRef]
- Hastings, H.M.; Sugihara, G. Fractals: A User’s Guide for the Natural Sciences; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Hobbs, B.E.; Ord, A.; Blenkinsop, T. The spatial distributions of mineralization. J. Struct. Geol. 2022, 156, 104529. [Google Scholar] [CrossRef]
- Ciccotti, M.; Mulargia, F. Pernicious effect of physical cutoffs in fractal analysis. Phys. Rev. E 2002, 65, 037201. [Google Scholar] [CrossRef]
- Sakhr, J.; Nieminen, J.M. Local box-counting dimensions of discrete quantum eigenvalue spectra: Analytical connection to quantum spectral statistics. Phys. Rev. E 2018, 97, 030202(R). [Google Scholar] [CrossRef] [PubMed]
- Carpena, P.; Coronado, A.V. Connection of the nearest-neighbor spacing distribution and the local box-counting dimension for discrete sets. Phys. Rev. E 2019, 100, 022205. [Google Scholar] [CrossRef]
- Takayasu, H. Fractals in the Physical Sciences; Manchester University Press: Manchester, NH, USA, 1990. [Google Scholar]
- Catrakis, H.J. Distribution of scales in turbulence. Phys. Rev. E 2000, 62, 564–578. [Google Scholar] [CrossRef]
- Catrakis, H.J. Flow Complexity, Multiscale Flows, and Turbulence. WSEAS Trans. Fluid Mech. 2006, 1, 53–58. [Google Scholar]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Cheng, Q. Multifractality and spatial statistics. Comp. Geosci. 1999, 25, 949–961. [Google Scholar] [CrossRef]
- Balankin, A.S.; Ixotov, A.D.; Novikov, V.U. Multifractal Analysis of Relations between Structural and Mechanical Parameters of Polymer-Matrix Composites. Inorg. Mater. 1999, 35, 1047–1053. [Google Scholar]
- Lopes, L.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef]
- Salat, H.; Murcio, R.; Arcaute, E. Multifractal methodology. Physica A 2017, 473, 467–487. [Google Scholar] [CrossRef]
- Guoxi, C.; Bo, J.; Ming, L.; Fengli, L.; Shaochun, X. Quantitative characterization of fracture structure in coal based on image processing and multifractal theory. Int. J. Coal Geol. 2020, 228, 103566. [Google Scholar] [CrossRef]
- Ju, X.; Jia, Y.; Li, T.; Gao, L.; Gan, M. Morphology and multifractal characteristics of soil pores and their functional implication. Catena 2021, 196, 104822. [Google Scholar] [CrossRef]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552. [Google Scholar] [CrossRef] [PubMed]
- Feagin, R.A. Relationship of second-order lacunarity, Hurst exponent, Brownian motion, and pattern organization. Physica A 2003, 328, 315–321. [Google Scholar] [CrossRef]
- Vernon-Carter, J.; Lobato-Calleros, C.; Escarela-Perez, R.; Rodriguez, E.; Alvarez-Ramirez, J. A suggested generalization for the lacunarity index. Physica A 2009, 388, 4305–4314. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E.; Dunne, W.M.; Odling, N.; Kim, J.W. Lacunarity analysis of fracture networks: Evidence for scale-dependent clustering. J. Struct. Geol. 2010, 32, 444e1449. [Google Scholar] [CrossRef]
- Gould, D.J.; Vadakkan, T.J.; Poché, R.A.; Dickinson, M.E. Multifractal and lacunarity analysis of microvascular morphology and remodeling. Microcirculation 2011, 18, 136–151. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E. Lacunarity analyses of multifractal and natural grayscale patterns. Fractals 2014, 22, 1440003. [Google Scholar] [CrossRef]
- Popovic, N.; Radunovic, M.; Badnjar, J.; Popovic, T. Fractal dimension and lacunarity analysis of retinal microvascular morphology in hypertension and diabetes. Microvasc. Res. 2018, 118, 36–43. [Google Scholar] [CrossRef]
- Palanivel, D.A.; Natarajan, S.; Gopalakrishnan, S.; Jennane, R. Multifractal-based lacunarity analysis of trabecular bone in radiography. Comp. Biolog. Med. 2020, 116, 103559. [Google Scholar] [CrossRef] [PubMed]
- Monjo, R.; Royé, D.; Martin-Vide, J. Meteorological drought lacunarity around the world and its classification. Earth Syst. Sci. Data 2020, 12, 741–752. [Google Scholar] [CrossRef]
- Scott, R.; Kadum, H.; Salmaso, G.; Calaf, M.; Cal, R.B. A lacunarity-based index for spatial heterogeneity. Earth Space Sci. 2022, 9, e2021EA002180. [Google Scholar] [CrossRef]
- de Melo, R.H.C.; Conci, A. Succolarity: Defining a method to calculate this fractal measure. In Proceedings of the 15th International Conference Systems, Signals and Image Processing, IWSSIP 2008, Bratislava, Slovakia, 25–28 June 2008; pp. 291–294. [Google Scholar] [CrossRef]
- de Melo, R.H.C.; Conci, A. How Succolarity could be used as another fractal measure in image analysis. Telecommun. Syst. 2013, 52, 1643–1655. [Google Scholar] [CrossRef]
- Siddiqui, S.; Soldati, M.; Castaldini, D. Appraisal of active deformation from drainage network and faults: Inferences from non-linear analysis. Earth Sci. Inform. 2015, 8, 233–246. [Google Scholar] [CrossRef]
- Metze, K.; Adam, R.; Florindo, J.B. The fractal dimension of chromatin-a potential molecular marker for carcinogenesis, tumor progression and prognosis. Expert Rev. Mol. Diagn. 2019, 19, 299–312. [Google Scholar] [CrossRef]
- Balankin, A.S. A continuum framework for mechanics of fractal materials I: From fractional space to continuum with fractal metric. Eur. Phys. J. B 2015, 88, 90. [Google Scholar] [CrossRef]
- Balankin, A.S. The topological Hausdorff dimension and transport properties of Sierpinski carpets. Phys. Lett. A 2017, 381, 2801–2808. [Google Scholar] [CrossRef]
- Cruz, M.-Á.M.; Ortiz, J.P.; Ortiz, M.P.; Balankin, A.S. Percolation on Fractal Networks: A Survey. Fractal Fract. 2023, 7, 231. [Google Scholar] [CrossRef]
- Balankin, A.S.; Ramírez-Joachin, J.; Gonzalez-Lopez, G.; Gutíerrez-Hernandez, S. Formation factors for a class of deterministic models of pre-fractal pore-fracture networks. Chaos Solitons Fractals 2022, 162, 112452. [Google Scholar] [CrossRef]
- Farrah, T.E.; Dhillon, B.; Keane, P.A.; Webb, D.J.; Dhaun, N. The eye, the kidney, and cardiovascular disease: Old concepts, better tools, and new horizons. Kidney Int. 2020, 98, 323–342. [Google Scholar] [CrossRef]
- Wang, J.; Shao, W.; Kim, J. Combining MF-DFA and LSSVM for retina images classification. Biomed. Signal Process. Control 2020, 60, 101943. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, J.; Bian, M.; He, Q.; Shen, Y.; Lan, Y.; Huang, D. Retinal Imaging Techniques Based on Machine Learning Models in Recognition and Prediction of Mild Cognitive Impairment. Neuropsychiatr. Dis. Treat. 2021, 17, 3267–3281. [Google Scholar] [CrossRef]
- Lakshminarayanan, S.Y.V. Fractal dimension and retinal pathology: A meta-analysis. Appl. Sci. 2021, 11, 2376. [Google Scholar] [CrossRef]
- Lyu, X.; Jajal, P.; Tahir, M.Z.; Zhang, S. Fractal dimension of retinal vasculature as an image quality metric for automated fundus image analysis systems. Sci. Rep. 2022, 12, 11868. [Google Scholar] [CrossRef]
- Yi, S.; Wei, Y.; Zhang, G.; Wang, T.; She, F.; Yang, X. Segmentation of retinal vessels based on MRANet. Heliyon 2023, 9, e12361. [Google Scholar] [CrossRef]
- Chan, Y.K.; Cheng, C.Y.; Sabanayagam, C. Eyes as the windows into cardiovascular disease in the era of big data. Taiwan J. Ophthalmol. 2023, 13, 151–167. [Google Scholar] [CrossRef]
- Kiselev, V.G.; Hahn, K.R.; Auer, D.P. Is the brain cortex a fractal? NeuroImage 2003, 20, 1765–1774. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, J.Z.; Dean, D.; Sahgal, V.; Yue, G.H. A three-dimensional fractal analysis method for quantifying white matter structure in human brain. J. Neurosci. Meth. 2006, 150, 242–253. [Google Scholar] [CrossRef]
- de Miras, J.R.; Martínez-Lledó, G.; Orwig, W.; Sepulcre, J. A MATLAB tool for computing the spherical harmonic fractal dimension of the cerebral cortex. Comp. Phys. Comm. 2020, 254, 107381. [Google Scholar] [CrossRef]
- Grosu, G.F.; Hopp, A.V.; Moca, V.V.; Bârzan, H.; Ciuparu, A.; Ercsey-Ravasz, M.; Winkel, M.; Linde, H.; Muresan, R.C. The fractal brain: Scale-invariance in structure and dynamics. Cereb. Cortex 2023, 33, 4574–4605. [Google Scholar] [CrossRef] [PubMed]





| Pre-Fractal | |||||||
|---|---|---|---|---|---|---|---|
| Sierpinski carpet after six iteration steps | 1.893 | 1.797 | 0 | - | 1.03 | 1 | |
| Menger sponge after six iteration steps | 2.727 | 2.262 | 0 | - | 5.05 | 1 | |
| Phosphate alumina gel | 1.84 ± 0.02 | 1.4 ± 0.1 | 0 | - | 1.2 | 0 | |
| Balls folded from randomly crumpled paper sheets | 2.66 ± 0.03 | 2 | 0.00 ± 0.02 | - | 4.8 | 1.0 ± 0.1 | |
| Retinal vessel network images | Normal | 1.697 ± 0.003 | 1 | 0.065 ± 0.007 | 0.96 ± 0.02 | 2.7 | 1.3 ± 0.3 |
| Hypertension | 1.41 ± 0.01 | 1 | 0.067 ± 0.007 | 0.92 ± 0.02 | 12.1 | 1.4 ± 0.3 | |
| Glaucoma | 1.39 ± 0.02 | 1 | 0.07 ± 0.01 | 0.89 ± 0.03 | 13.3 | 1.4 ± 0.3 | |
| Human brains (tomography) | 2.69 ± 0.07 | - | 0.05 ± 0.01 | 0.87 ± 0.03 | 3.0 | 1.5 ± 0.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patiño-Ortiz, M.; Patiño-Ortiz, J.; Martínez-Cruz, M.Á.; Esquivel-Patiño, F.R.; Balankin, A.S. Morphological Features of Mathematical and Real-World Fractals: A Survey. Fractal Fract. 2024, 8, 440. https://doi.org/10.3390/fractalfract8080440
Patiño-Ortiz M, Patiño-Ortiz J, Martínez-Cruz MÁ, Esquivel-Patiño FR, Balankin AS. Morphological Features of Mathematical and Real-World Fractals: A Survey. Fractal and Fractional. 2024; 8(8):440. https://doi.org/10.3390/fractalfract8080440
Chicago/Turabian StylePatiño-Ortiz, Miguel, Julián Patiño-Ortiz, Miguel Ángel Martínez-Cruz, Fernando René Esquivel-Patiño, and Alexander S. Balankin. 2024. "Morphological Features of Mathematical and Real-World Fractals: A Survey" Fractal and Fractional 8, no. 8: 440. https://doi.org/10.3390/fractalfract8080440
APA StylePatiño-Ortiz, M., Patiño-Ortiz, J., Martínez-Cruz, M. Á., Esquivel-Patiño, F. R., & Balankin, A. S. (2024). Morphological Features of Mathematical and Real-World Fractals: A Survey. Fractal and Fractional, 8(8), 440. https://doi.org/10.3390/fractalfract8080440









