Abstract
This paper aims to examine an approach that studies many Euler–Maclaurin-type inequalities for various function classes applying Riemann–Liouville fractional integrals. Afterwards, our results are provided by using special cases of obtained theorems and examples. Moreover, several Euler–Maclaurin-type inequalities are presented for bounded functions by fractional integrals. Some fractional Euler–Maclaurin-type inequalities are established for Lipschitzian functions. Finally, several Euler–Maclaurin-type inequalities are constructed by fractional integrals of bounded variation.
MSC:
26D07; 26D10; 26D15
1. Introduction
Inequality theory is well known and still a fascinating field of research with a wide range of applications in several areas of mathematics. In mathematical analysis, convex functions are significant in the study of inequalities due to their specific geometric and analytical properties. Afterwards, mathematicians have been interested in fractional calculus due to its fundamental properties and its applications.
In [1], Dragomir proved an estimate of the remainder for Simpson’s quadratic formula for functions of bounded variation and gave some applications for special means. Budak et al. [2] presented some variations of Simpson-type inequalities using generalized fractional integrals in the context of differentiable convex functions. For additional information on Simpson-type inequalities and other features associated with Riemann–Liouville fractional integrals, readers can see [3,4,5] and its references.
In the literature, evaluations for three-step quadratic kernels are frequently referred to as Newton-type results, because the three-point Newton–Cotes quadrature is a rule of Simpson’s second rule. In recent years, a number of mathematicians have focused on Newton-type inequalities. For example, in [6], Erden et al. established some Newton-type integral inequalities for functions whose first derivative is arithmetically–harmonically convex in absolute value at a given power. Moreover, in [7], Sitthiwirattham et al. offered some Newton-type inequalities for Riemann–Liouville fractional integrals by using convex functions and functions of bounded variation. Please refer to [8,9,10] and its references for more details on the Newton-type inequality, which includes convex differentiable functions.
Dedić et al. [11] constructed a set of inequalities using the Euler–Maclaurin-type inequalities, and the results were used to produce specific error estimates in the case of the Maclaurin quadrature rules. In [12], the results were applied to provide some error estimates for the Simpson
quadrature rules. In paper [13], several Euler–Maclaurin-type inequalities were considered for the case of differentiable convex functions. Moreover, in paper [14], several Euler–Maclaurin-type inequalities were established using the Riemann–Liouville fractional integrals. The reader is referred to [15,16,17,18] and the references therein for further information on such types of inequalities.
The purpose of this paper is to use Riemann–Liouville fractional integrals to obtain Euler–Maclaurin-type inequalities for the different function classes. This paper is organized according to the following plan: In Section 3, an integral equality is proved that is essential in order to establish the main findings. In Section 4, using the Riemann–Liouville fractional integrals, some Euler–Maclaurin-type inequalities are constructed for differentiable convex functions. In Section 5, we give several Euler–Maclaurin-type inequalities for bounded functions by fractional integrals. In Section 6, some fractional Euler–Maclaurin-type inequalities will be proved for Lipschitzian functions. Moreover, in Section 7, the Euler–Maclaurin-type inequalities are constructed by fractional integrals of bounded variation. Furthermore, in Section 8, we provide several graphical examples in order to demonstrate the accuracy of the newly established inequalities. Finally, in Section 9, the summary and concluding remarks are noted.
2. Preliminaries
The Riemann–Liouville integrals
and
of order
with
are given by
and
respectively [19,20]. Here,
belongs to
, and
denotes the Gamma function, which is defined as
The fractional integral coincides with the classical integral for the case of
The formula for Simpson’s quadrature, commonly referred as Simpson’s
rule, is as follows:
The most popular Newton–Cotes quadrature using a three-point Simpson-type inequality is as follows:
Theorem 1.
Let
denote a four times differentiable and continuous function on
, and let
Then, the following inequality holds:
The Newton–Cotes quadrature formula, frequently referred to as Simpson’s second formula (also known as Simpson’s
rule; see [18]), is defined as follows:
The Simpson
rule, a classical closed-type quadrature rule based on the Simpson
inequality, approximates this.
Theorem 2.
If
is a four times differentiable and continuous function on
and
then one has the inequality
The Maclaurin rule, which is derived from the Maclaurin formula (see [18]), is equivalent to the corresponding dual Simpson’s
formula:
The Maclaurin rule, which is derived from the Maclaurin inequality, is equivalent to the corresponding dual Simpson’s
formula:
Theorem 3.
Let
be a four times differentiable and continuous function on
, and let
Then, the following inequality holds:
3. A Crucial Equality
In this section, we express integral equality in order to demonstrate the main results of the study.
Lemma 1.
If
is an absolutely continuous function
such that
, then the equality
is valid. Here,
Proof.
If we first use the integration by parts, then one can obtain
In a similar manner, we have
Combining (1) and (2) allows us to easily obtain
If we use the change of the variable
and
for
, then the equality (3) can be rewritten as follows
Finally, if we multiply both sides of (4) by
, then we conclude the proof of Lemma 1. □
4. Convex Functions: Euler–Maclaurin-Type Inequalities with Fractional Integrals
In this section, we obtain several Euler–Maclaurin-type inequalities for differentiable convex functions by using the Riemann–Liouville fractional integrals.
Theorem 4.
Suppose that Lemma 1 holds, and the function
is convex on the interval
. Then, one can prove the following fractional Euler–Maclaurin-type inequality:
where
and
Proof.
By taking into account the absolute value of Lemma 1, one may directly obtain
Since
is convex, it yields
which completes the proof of Theorem 1. □
Remark 1.
If we assign
in Theorem 4, then we can obtain the following Euler–Maclaurin-type inequality:
which is given in (Corollary 1, [13]).
Theorem 5.
Let us consider the assumptions in Lemma 1, and the function
,
is convex on
. Then, the following Euler–Maclaurin-type inequality holds:
Here,
.
Proof.
If we apply Hölder’s inequality to (6), then we obtain
Taking advantage of the convexity of
, we can easily obtain
This ends the proof of Theorem 5. □
Corollary 1.
If we select
in Theorem 5, then the following inequality holds:
Theorem 6.
Assume that the assumptions of Lemma 1 are satisfied, and the function
,
is convex on
Then, we obtain the following Euler–Maclaurin-type inequality:
Here,
and
are specified in Theorem 4, and
Proof.
When we apply (6) to the power mean inequality, we have
By using the convexity of
, it follows that
This finishes the proof of Theorem 6. □
Remark 2.
If we choose
in Theorem 6, then we obtain the following Euler–Maclaurin-type inequality:
which is established in (Corollary 3, [13]).
5. Bounded Functions: Euler–Maclaurin-Type Inequalities with Fractional Integrals
In this section, we consider some Euler–Maclaurin-type inequalities for bounded functions by fractional integrals.
Theorem 7.
Note that the conditions of Lemma 1 hold. If there exists
so that
for
then we have
Proof.
By using the Lemma 1, we obtain
Let us take the absolute value of (10). Then, it follows that
It is known that
for
Then, we readily obtain
With the aid of the (11) and (12), we have
□
Corollary 2.
If we consider
in Theorem 7, then the following inequality holds:
Corollary 3.
Under the assumption of Theorem 7, if there exist
such that
for all
then we have
Corollary 4.
For
in Corollary 3, the following inequality holds:
6. Lipschitzian Functions: Euler–Maclaurin-Type Inequalities with Fractional Integrals
In this section, we prove some fractional Euler–Maclaurin-type inequalities for Lipschitzian functions.
Theorem 8.
Consider that the assumptions of Lemma 1 are valid. If
is a L-Lipschitzian function on
then the following inequality holds:
where
and
Proof.
By using Lemma 1, and since
is the L-Lipschitzian function, we easily have
□
Corollary 5.
Note that
in Theorem 8. Then, the following Euler–Maclaurin-type inequality holds:
7. Functions of Bounded Variation: Euler–Maclaurin-Type Inequalities via Fractional Integrals
In this section, we establish some Euler–Maclaurin-type inequalities by fractional integrals of bounded variation.
Theorem 9.
If
is a function of bounded variation on
then we obtain
where
denotes the total variation of
on
Proof.
Define the function
as
With the help of integrating by parts, we have
Namely, we have
It is known that if
are such that g is continuous on
and
is of bounded variation on
, then
exists, and
By using (13), it follows that
This finishes the proof of Theorem 9. □
Corollary 6.
Let us consider
in Theorem 9. Then, the following inequality holds:
8. Examples of Main Results
Example 1.
Let us consider that a function
is defined by
with
. Then, the left-hand side of (5) coincides with
The right-hand side of (5) becomes
Consequently, we have
One can see the correctness of the inequalities (15) in Figure 1.
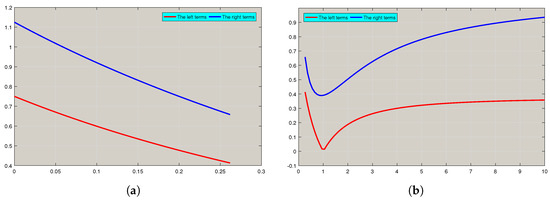
Example 2.
Note that function
is presented by
. From Theorem 5 with
and
, the left-hand side of (7) reduces to equality (14), and the right-hand side of (7) is equal to
Consequently, we have the inequality
One can see the correctness of the inequality (16) in Figure 2.
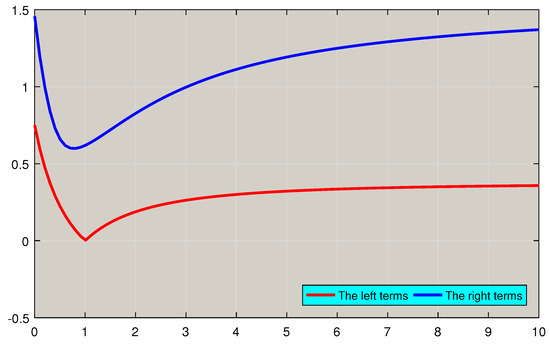
Figure 2.
In Example 2, depending on
, MATLAB has been used to compute and plot the graph of both sides of (7).
Example 3.
A function
is given by
. From Theorem 6, with
and
, the left-hand side of (8) becomes equality (14), and the right-hand side of (8) coincides with
Finally, we have the inequality
One can see the correctness of the inequalities (17) in Figure 3.
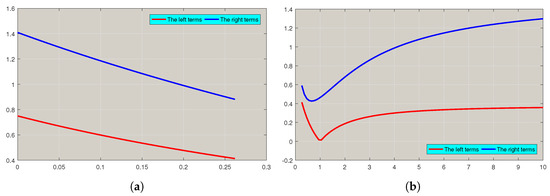
Figure 3.
In Example 3, using MATLAB software, it is clear that the left-hand side of (8) constantly stays below the right-hand side. (a) The specified values of
from 0 to
. (b) The specified values of
from
to 10.
Example 4.
Consider that a function
is presented by
. From Theorem 7, with
and
, the left-hand side of (9) coincides with equality (14), and the right-hand side of (9) is
One can see the correctness of the inequalities (18) in Figure 4.
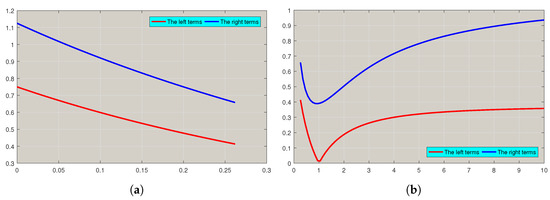
Figure 4.
Example 4 shows that the left side of (9) consistently remains lower than the right side when evaluated with MATLAB software. (a) The specified values of
from 0 to
. (b) The specified values of
from
to 10.
9. Concluding Remarks and Future Works
In this paper, we proved some Euler–Maclaurin-type inequalities for various function classes by using Riemann–Liouville fractional integrals. First of all, we gave an integral equality that is necessary in order to prove the main findings of the paper. Subsequently, several Euler–Maclaurin-type inequalities were investigated for differentiable convex functions by using the Riemann–Liouville fractional integrals. In addition to this, we gave some Euler–Maclaurin-type for bounded functions by fractional integrals. Moreover, some fractional Euler–Maclaurin-type inequalities were established for Lipschitzian functions. Furthermore, some Euler–Maclaurin-type inequalities were proved by fractional integrals of bounded variation. Finally, we gave several examples using graphs in order to show that our main result is correct.
In future papers, the ideas and strategies for our results about Euler–Maclaurin-type inequalities by Riemann–Liouville fractional integrals may open new avenues for further research in this field. Improvements or generalizations of our results can be investigated by using different kinds of convex function classes or other types of fractional integral operators. In addition, one can obtain some Euler–Maclaurin-type inequalities for various function classes with the help of the quantum calculus.
Author Contributions
Conceptualization, F.H. and H.B.; investigation, M.G. and H.B.; methodology, F.H.; validation, M.G. and F.H.; visualization, H.B. and F.H.; writing—original draft, M.G. and F.H.; writing—review and editing, M.G. and H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this paper, as no datasets were generated or analyzed during the current study.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Dragomir, S.S. On Simpson’s quadrature formula for mappings of bounded variation and applications. Tamkang J. Math. 1999, 30, 53–58. [Google Scholar] [CrossRef]
- Budak, H.; Hezenci, F.; Kara, H. On parametrized inequalities of Ostrowski and Simpson type for convex functions via generalized fractional integral. Math. Methods Appl. Sci. 2021, 44, 12522–12536. [Google Scholar] [CrossRef]
- Ali, M.A. On Simpson’s and Newton’s type inequalities in multiplicative fractional calculus. Filomat 2023, 37, 10133–10144. [Google Scholar]
- Moumen, A.; Boulares, H.; Meftah, B.; Shafqat, R.; Alraqad, T.; Ali, E.E.; Khaled, Z. Multiplicatively Simpson type inequalities via fractional integral. Symmetry 2023, 15, 460. [Google Scholar] [CrossRef]
- Sarikaya, M.Z. On the some generalization of inequalities associated with Bullen, Simpson, midpoint and trapezoid type. Acta Univ. Apulensis Math. Inform. 2023, 73, 33–52. [Google Scholar]
- Erden, S.; Iftikhar, S.; Kumam, P.; Awan, M.U. Some Newton’s like inequalities with applications. Rev. Real Acad. Cienc. Exactas Fis. Nat. Ser. Mat. 2020, 114, 195. [Google Scholar] [CrossRef]
- Sitthiwirattham, T.; Nonlaopon, K.; Ali, M.A.; Budak, H. Riemann-Liouville fractional Newton’s type inequalities for differentiable convex functions. Fractal Fract. 2022, 6, 175. [Google Scholar] [CrossRef]
- Gao, S.; Shi, W. On new inequalities of Newton’s type for functions whose second derivatives absolute values are convex. Int. J. Pure Appl. Math. 2012, 74, 33–41. [Google Scholar]
- Iftikhar, S.; Kumam, P.; Erden, S. Newton’s-type integral inequalities via local fractional integrals. Fractals 2020, 28, 2050037. [Google Scholar] [CrossRef]
- Noor, M.A.; Noor, K.I.; Iftikhar, S. Newton inequalities for p-harmonic convex functions. Honam Math. J. 2018, 40, 239–250. [Google Scholar]
- Dedić, L.J.; Matić, M.; Pečarić, J. Euler-Maclaurin formulae. Math. Inequal. Appl. 2003, 6, 247–275. [Google Scholar] [CrossRef]
- Dedić, L.J.; Matić, M.; Pečarić, J.; Vukelic, A. On Euler-Simpson 3/8 formulae. Nonlinear Stud. 2011, 18, 1–26. [Google Scholar]
- Hezenci, F.; Budak, H. Maclaurin-type inequalities for Riemann-Liouville fractional integrals. Ann. Univ. Mariae Curie-Sklodowska Sect. A Math. 2022, 76, 15–32. [Google Scholar] [CrossRef]
- Hezenci, F. Fractional Maclaurin-type inequalities for twice-differentiable functions. Rocky Mt. J. Math. 2023, in press. [Google Scholar]
- Franjic, I.; Pečarić, J.; Perić, I.; Vukelić, A. Euler Integral Identity, Quadrature Formulae and Error Estimations; Element: Zagreb, Croatia, 2011. [Google Scholar]
- Pečarić, J.E.; Proschan, F.; Tong, Y.L. Convex Functions, Partial Orderings and Statistical Applications; Academic Press: Boston, MA, USA, 1992. [Google Scholar]
- Meftah, B. Maclaurin type inequalities for multiplicatively convex functions. Proc. Amer. Math. Soc. 2023, 151, 2115–2125. [Google Scholar] [CrossRef]
- Davis, P.J.; Rabinowitz, P. Methods of Numerical Integration; Academic Press: New York, NY, USA; San Francisco, CA, USA; London, UK, 1975. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order; Springer: Vienna, Austria, 1997. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).