Robust Speed Control of Permanent Magnet Synchronous Motor Drive System Using Sliding-Mode Disturbance Observer-Based Variable-Gain Fractional-Order Super-Twisting Sliding-Mode Control
Abstract
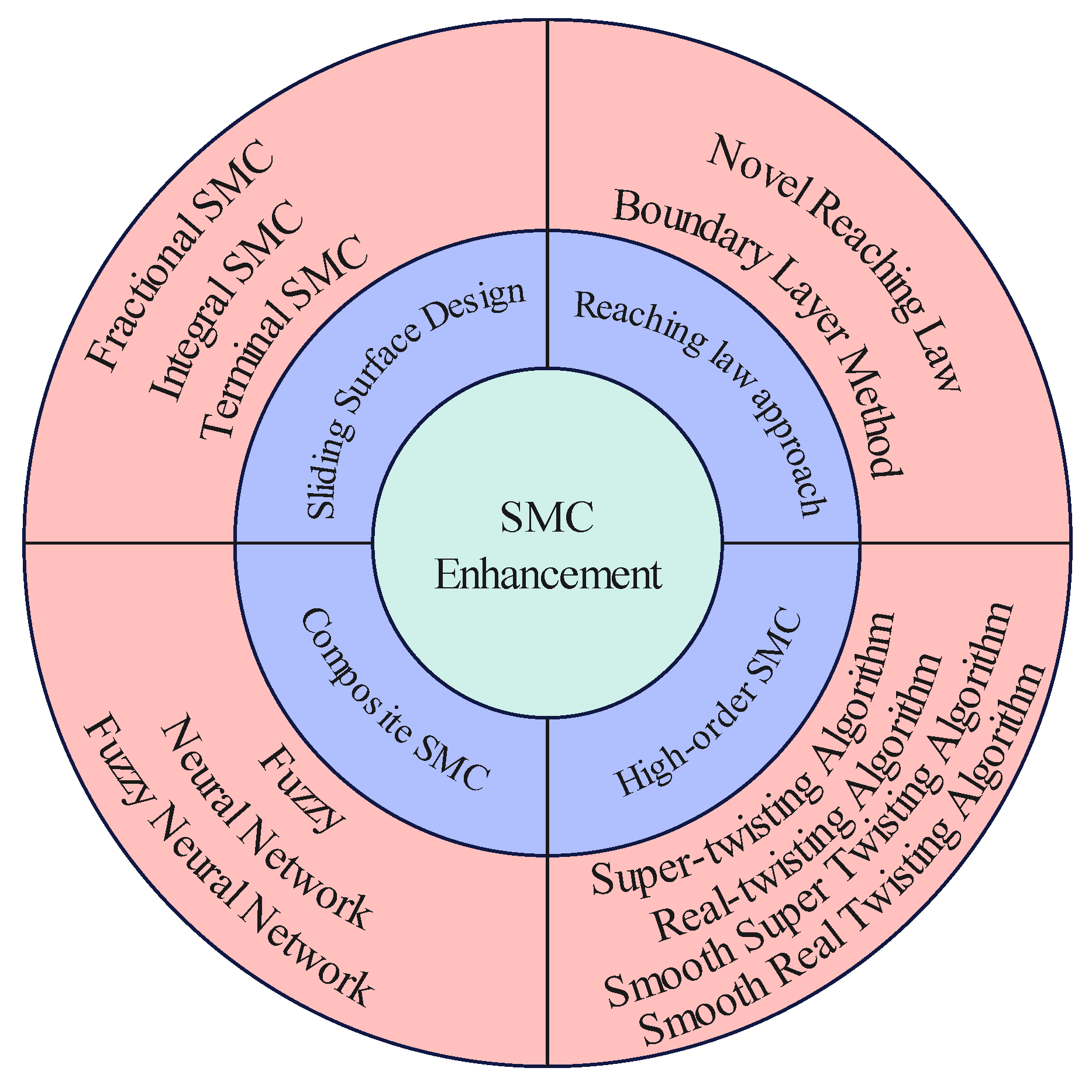
1. Introduction
- Responsively track the reference signal while minimizing steady-state error, overshoots, and settling times.
- Demonstrate robust performance in the presence of uncertain disturbances.
- Possess a relatively straightforward design process.
- 1.
- A unique FOSS is formulated and disseminated. Including a specific term accelerates convergence to the sliding manifold, enabling the controller to demonstrate improved performance without additional tunable parameters.
- 2.
- Introducing a new variable-gain super-twisting sliding-mode control law enables the system state to swiftly approach the sliding manifold, regardless of the initial position. Additionally, the proposed reaching law effectively mitigates high-frequency chattering, which is an undesirable phenomenon in SMC.
- 3.
- Proposing a sliding-mode disturbance observer (SMDO) to enhance the disturbance rejection capabilities of the VGFOSTSMC method. The estimated system disturbance is used for the feedforward of the speed controller.
- 4.
- Developing a new sliding-mode speed controller rooted in the advancements above; this controller integrates an adaptive disturbance estimator/observer to offset the outputs of the enhanced sliding-mode-based speed controller. The method ensures finite-time convergence and exhibits higher precision, stronger robustness, and reduced chattering compared to conventional SMC.
- 5.
- The study showcases the effectiveness of the proposed VGFOSTSMC method in regulating PMSM speed through simulations and experimental results.
2. Preliminaries
3. Mathematical Model of PMSM
- 1.
- The hysteresis and eddy current losses generated by the iron core of the PMSM are not considered.
- 2.
- The three-phase windings of the PMSM are assumed to be perfectly symmetrical.
- 3.
- The conductivity of the PMSM is assumed to be zero, and the rotor lacks damping windings.
- 4.
- The electromotive force (EMF) induced in the stator is considered a pure sine wave during PMSM operation.
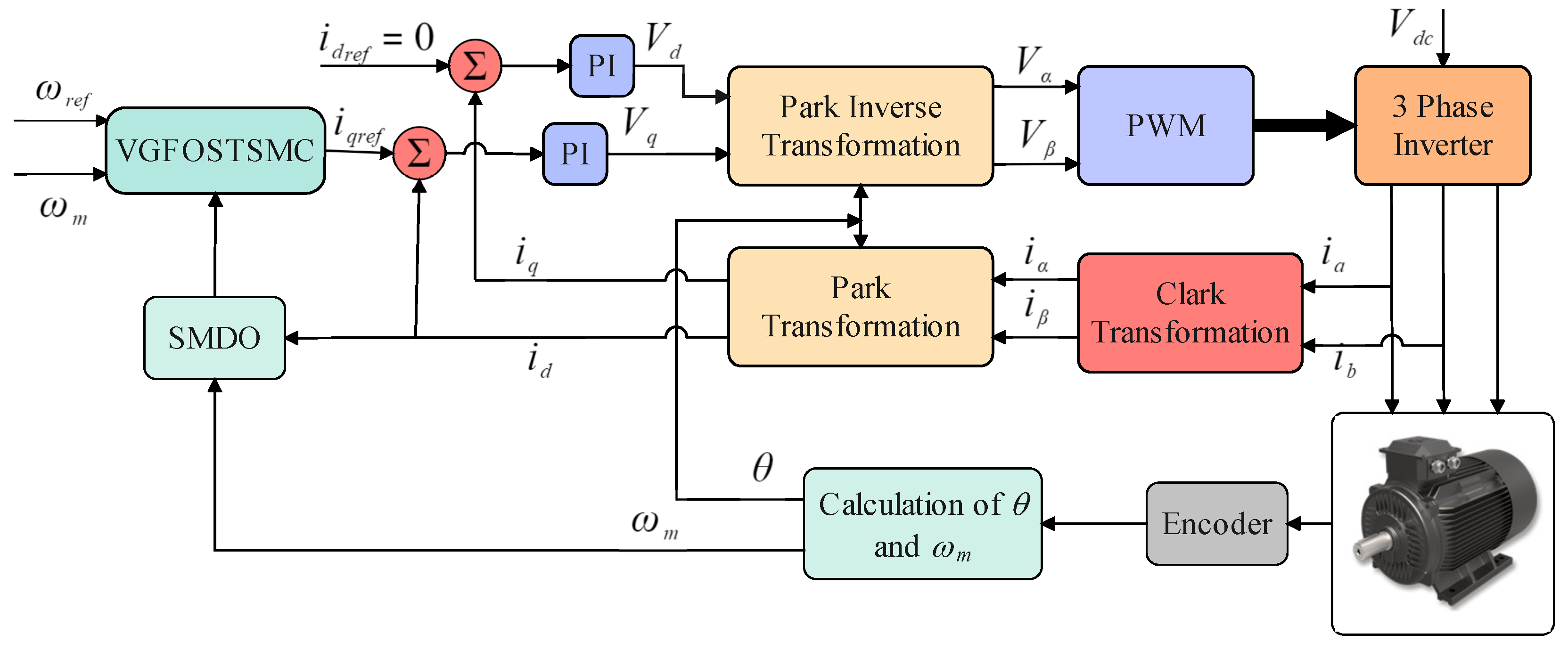
4. PMSM Speed Controller Design
4.1. Variable-Gain Super-Twisting SMC Design
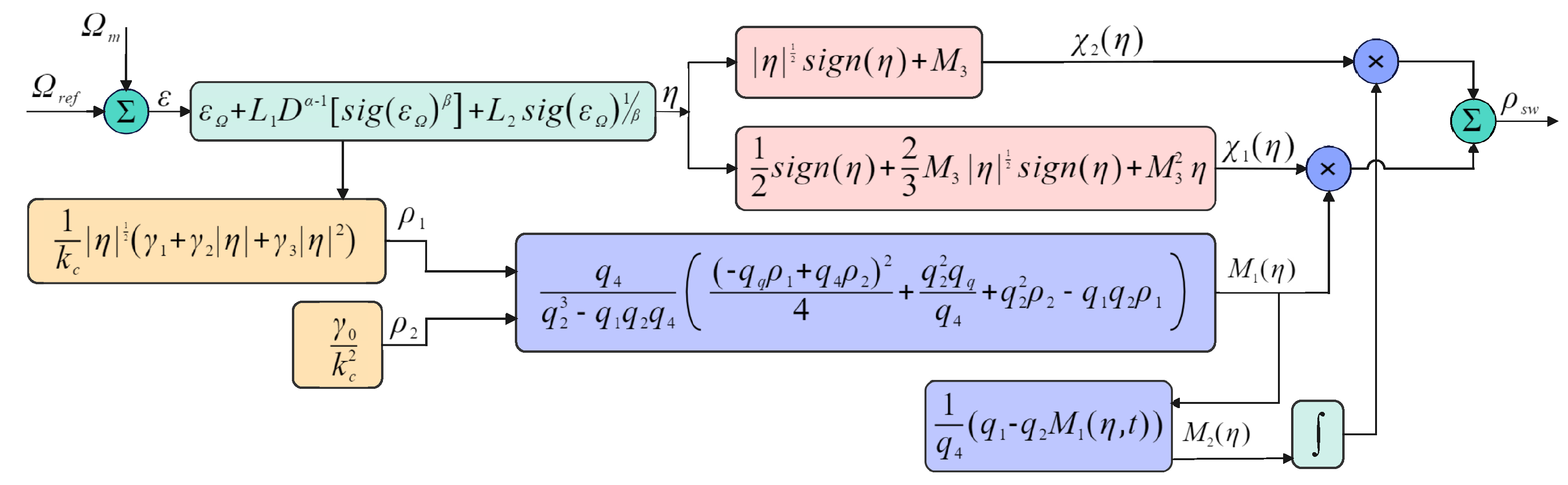
4.2. Fractional-Order Variable-Gain Super-Twisting SMC Design
4.3. Stability Analysis of VGFOSTSMC
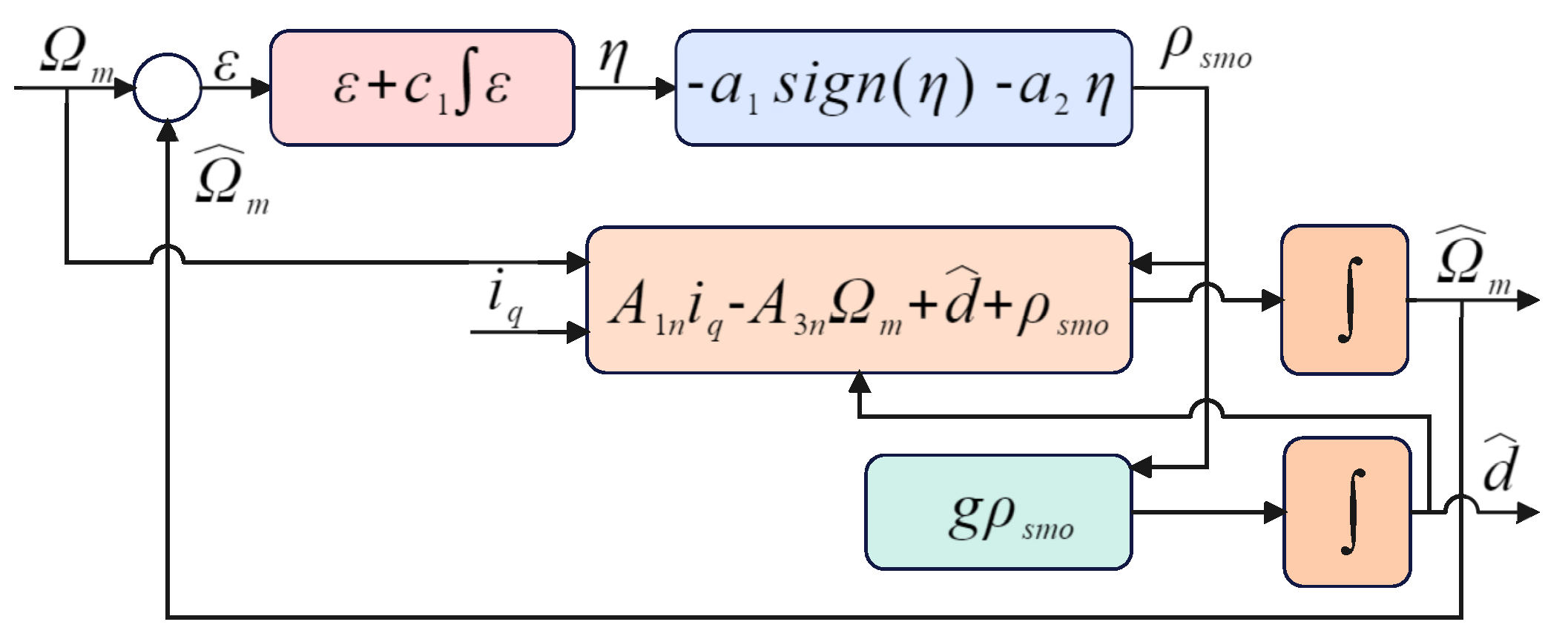
4.4. Sliding-Mode Disturbance Observer Design
5. Results and Discussion
- 1.
- PI Controller.
- 2.
- CSMC:
- 3.
- Super-twisting sliding-mode control (STSMC) [27]:
- 4.
- Proposed VGFOSTSMC: + ,
5.1. Simulation Verification
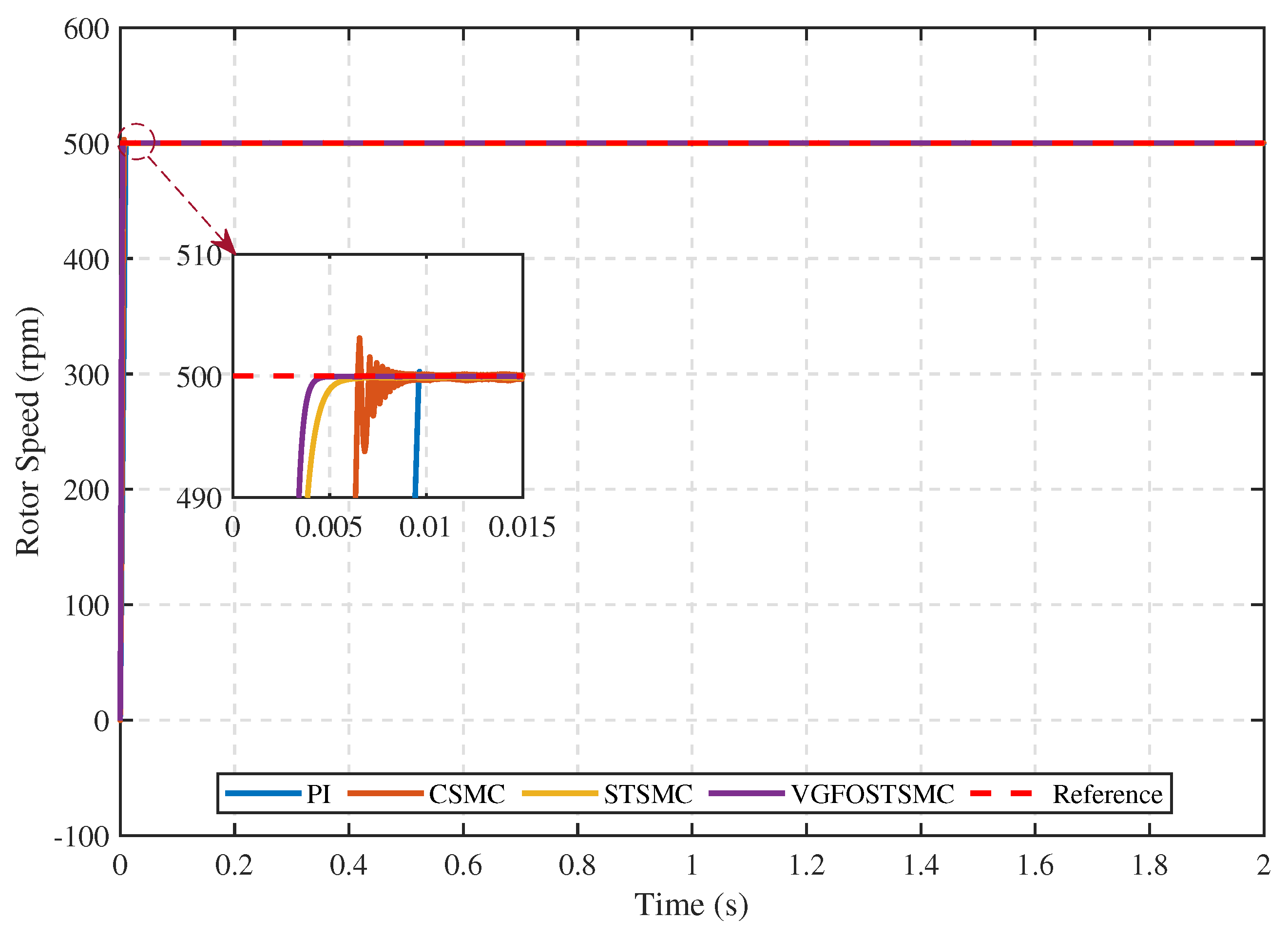
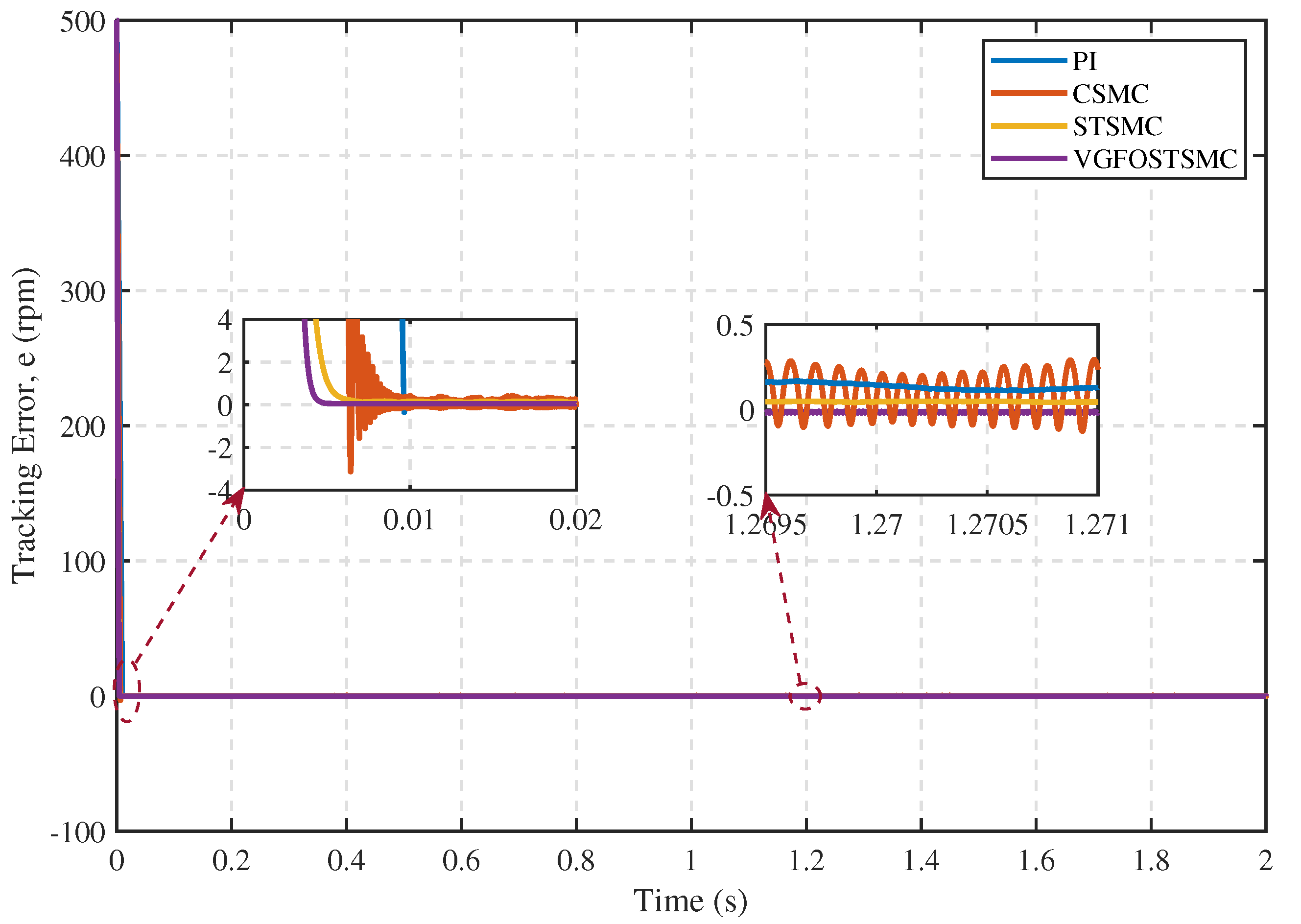
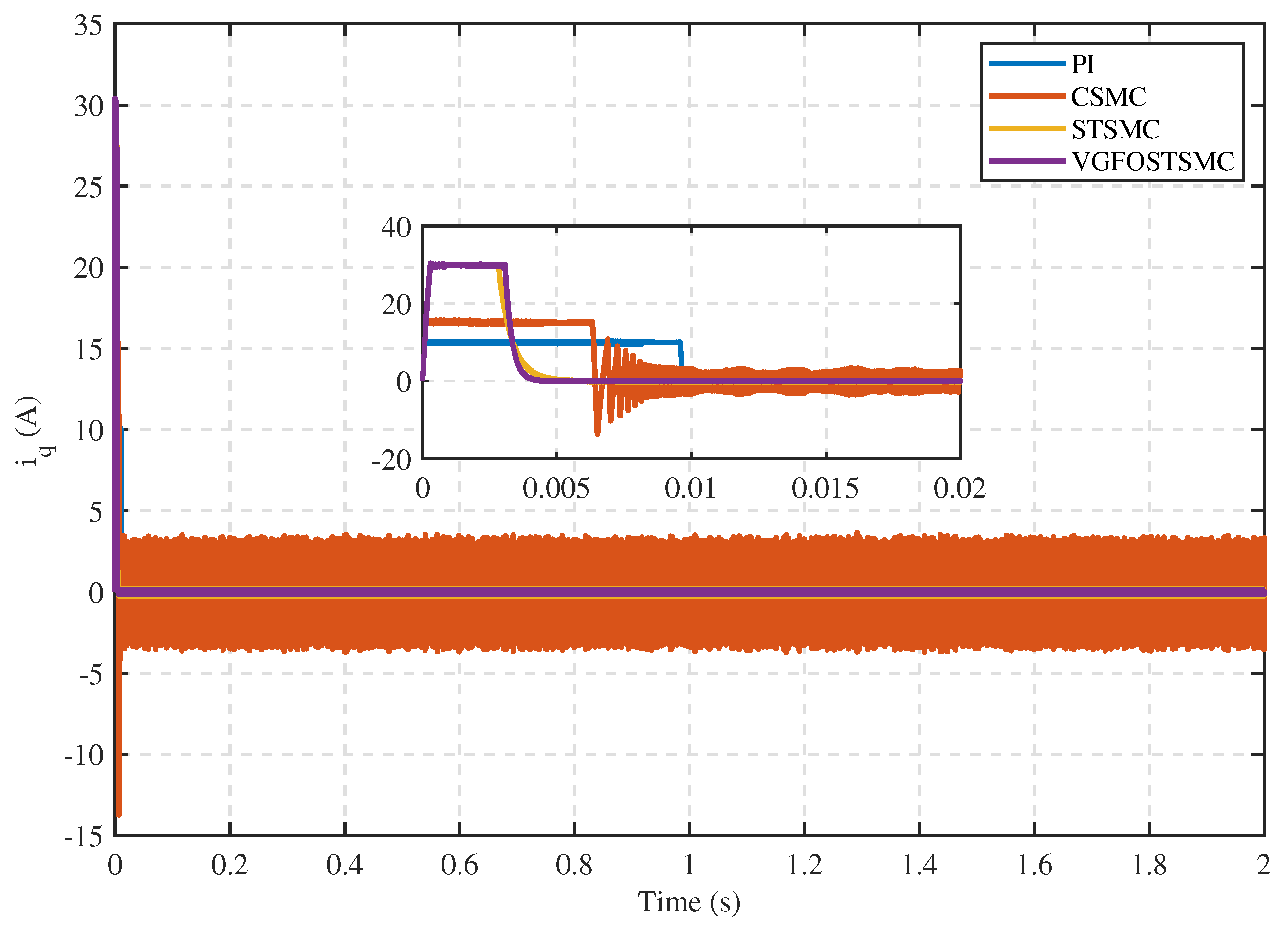
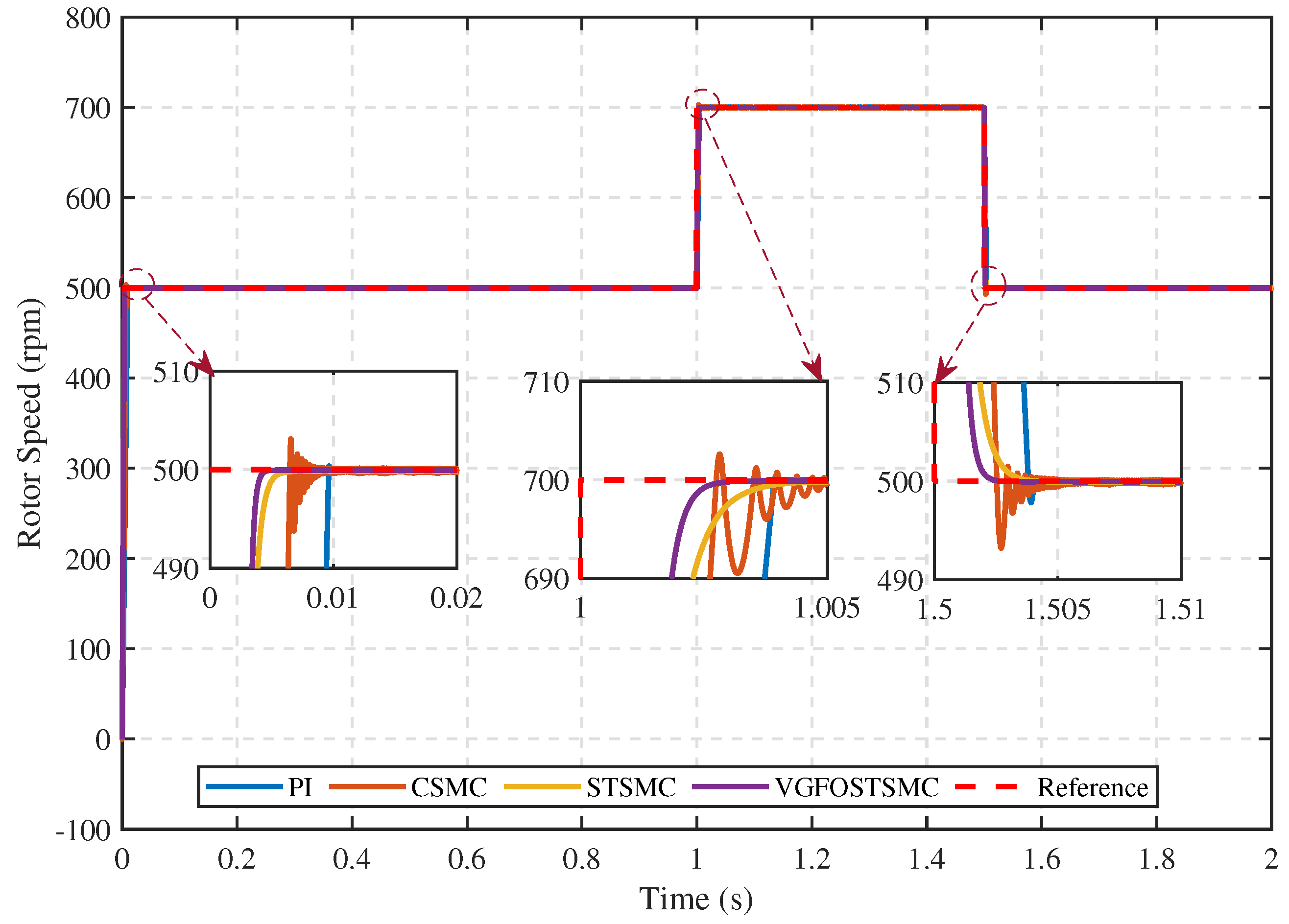
5.1.1. Comparative Performance Analysis of the Proposed Controller with Alternative Control Techniques
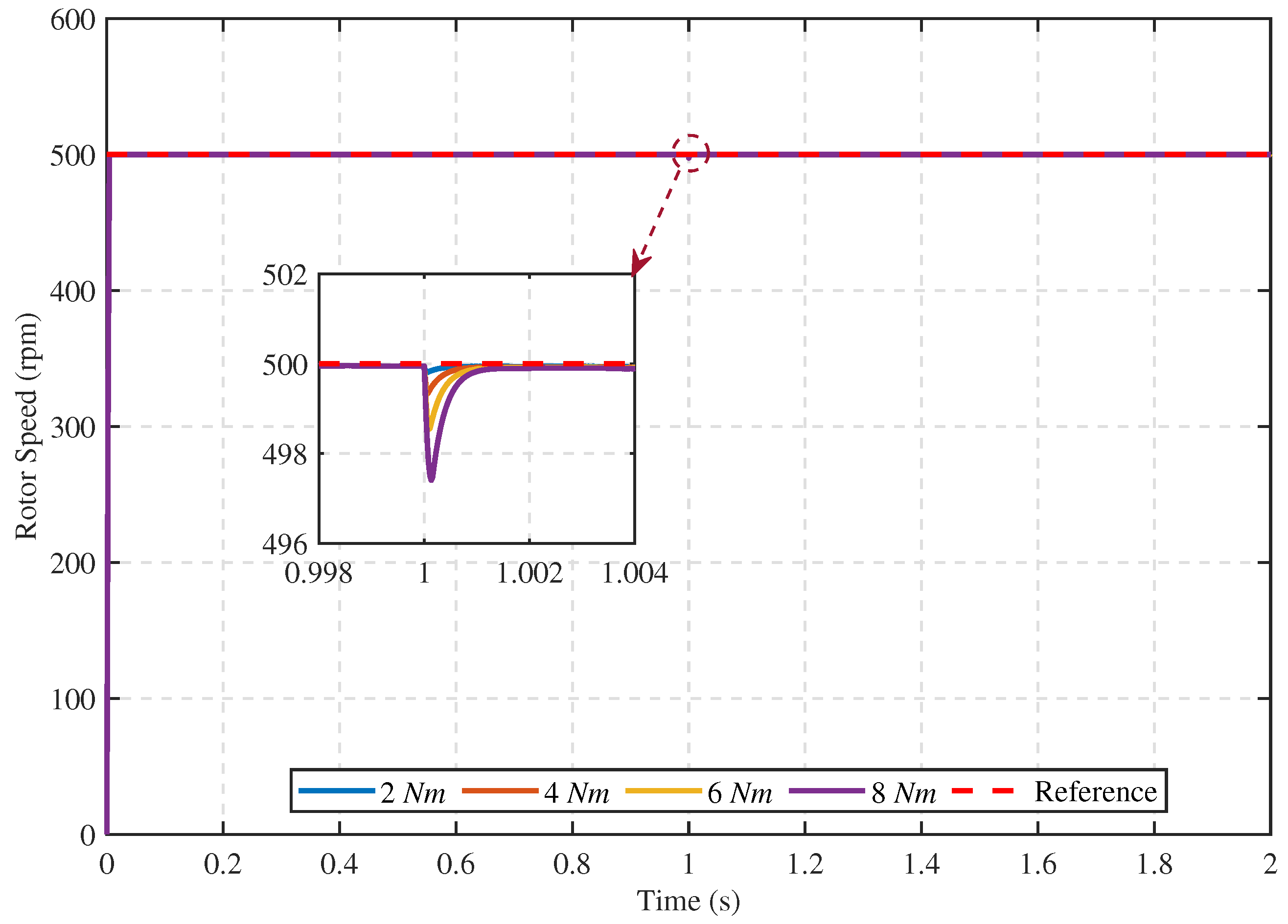
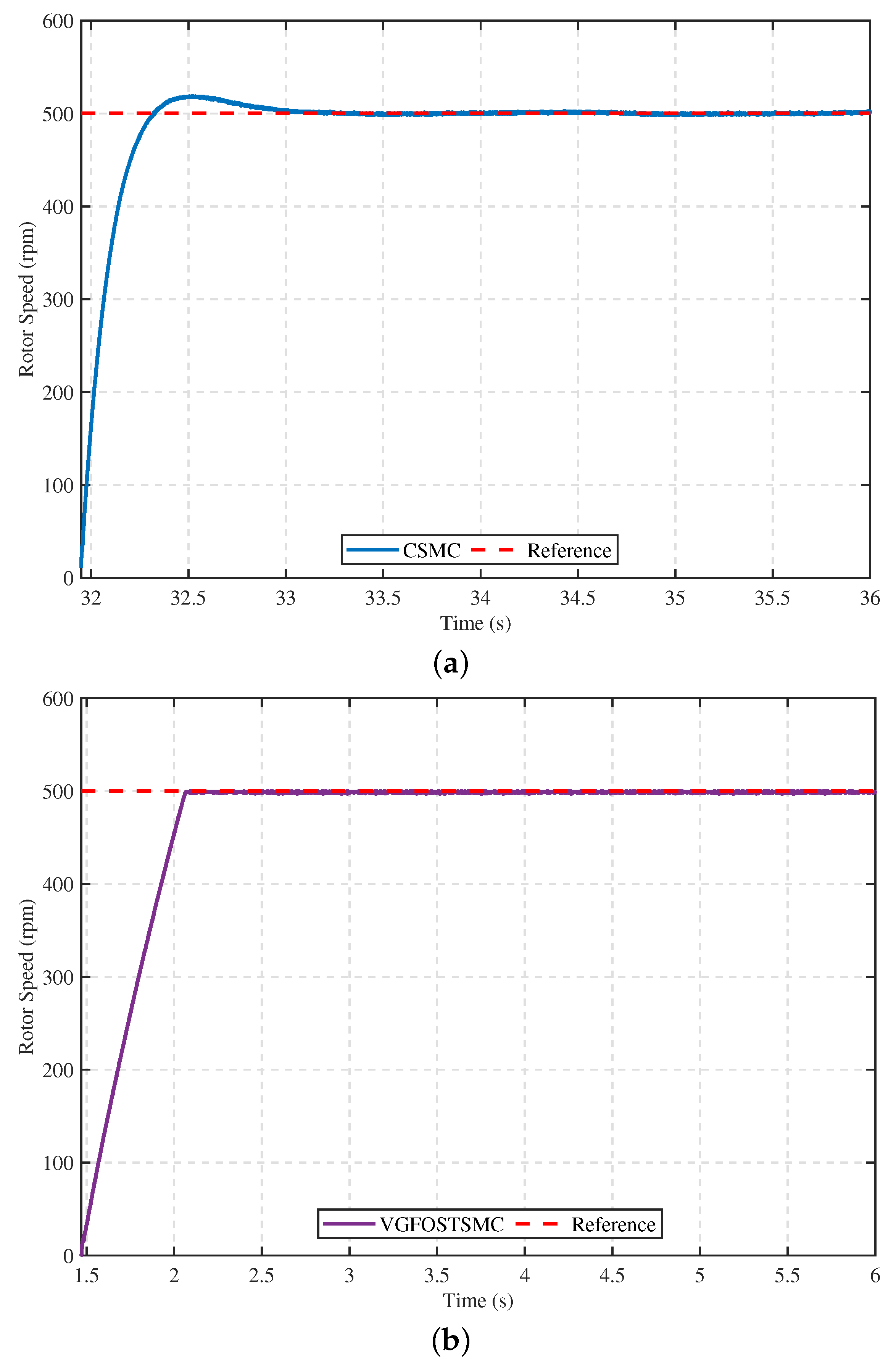
- Case 1:
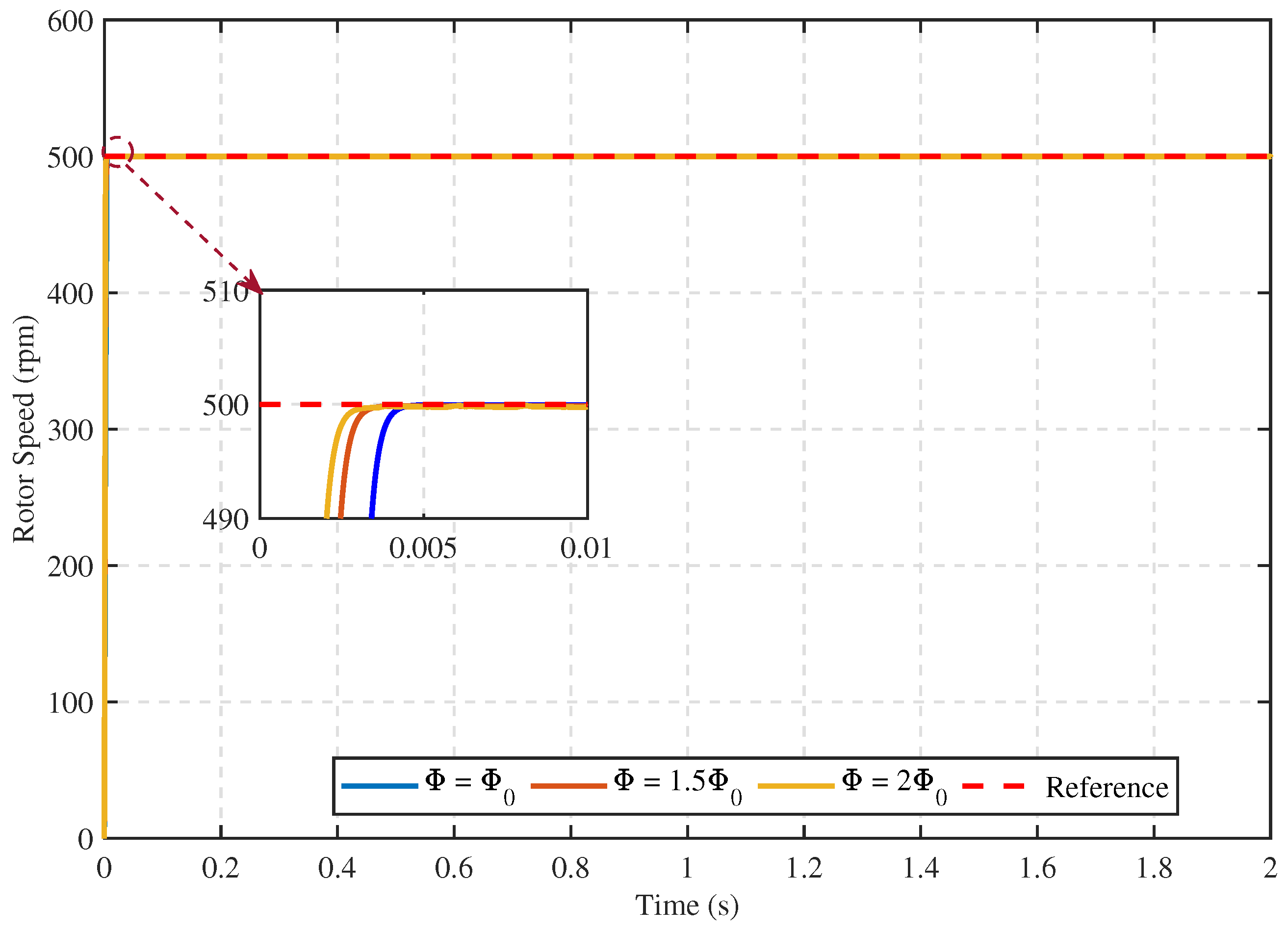
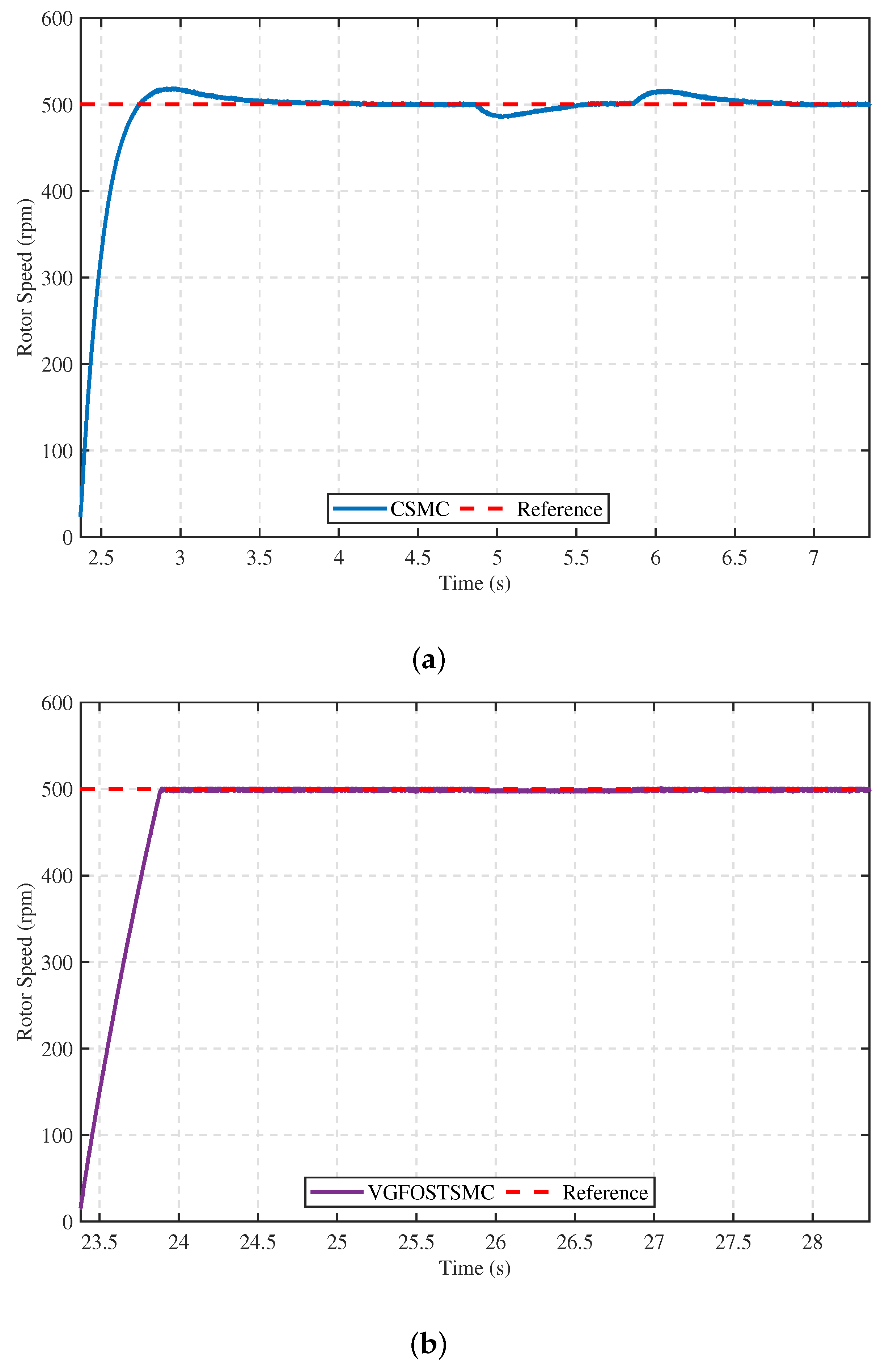
- Case 2:
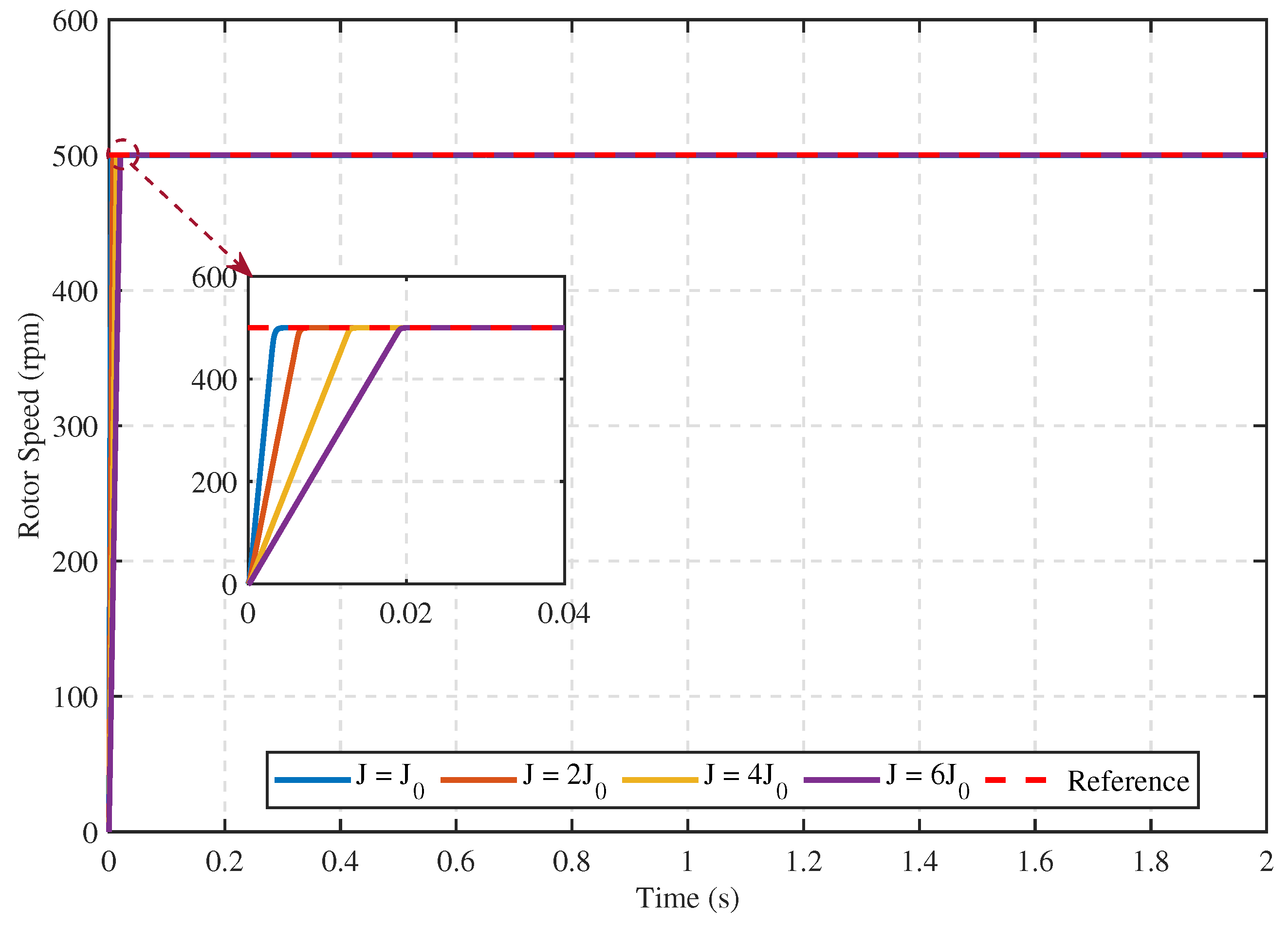
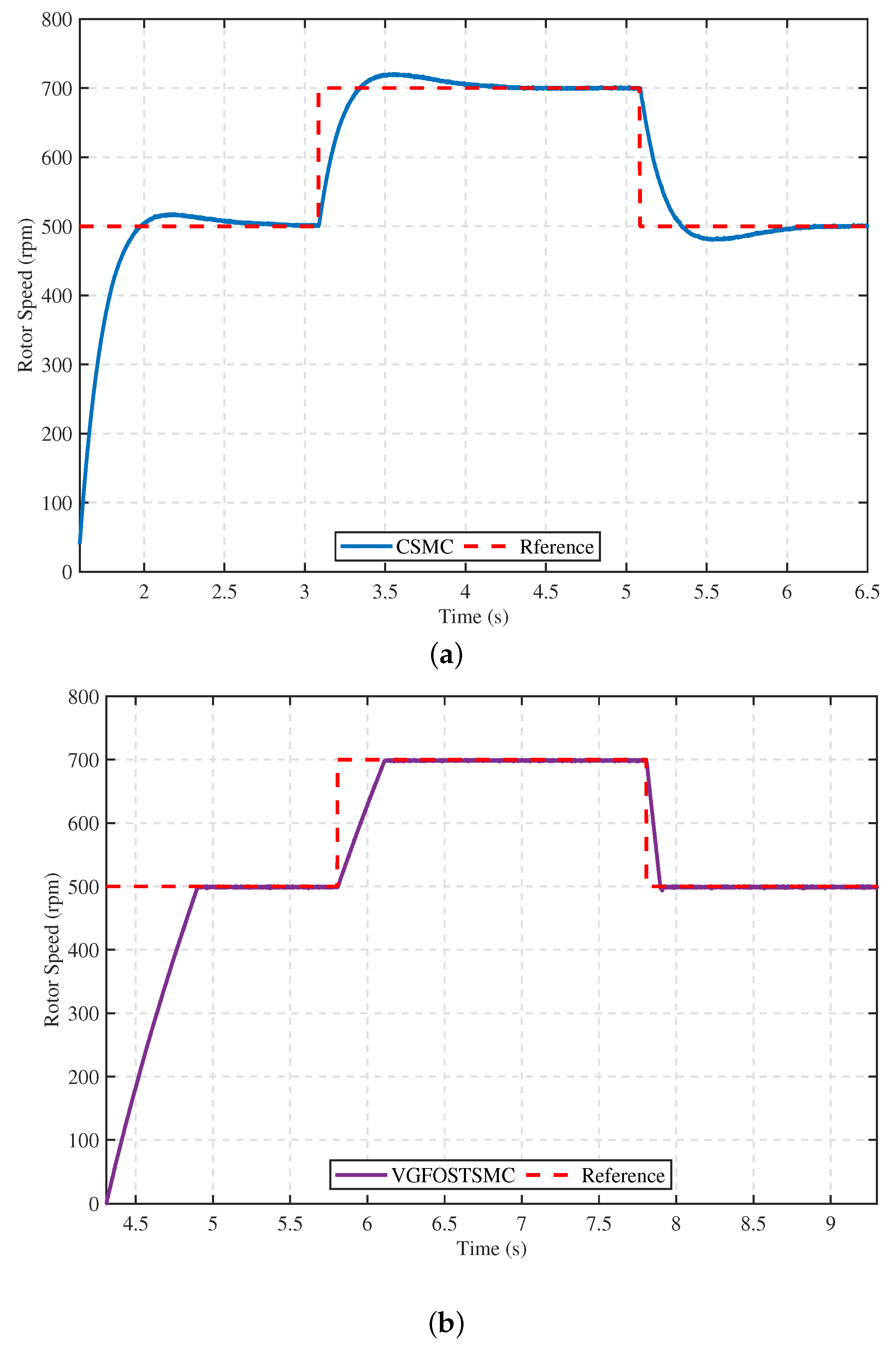
- Case 3:
- Case 4:
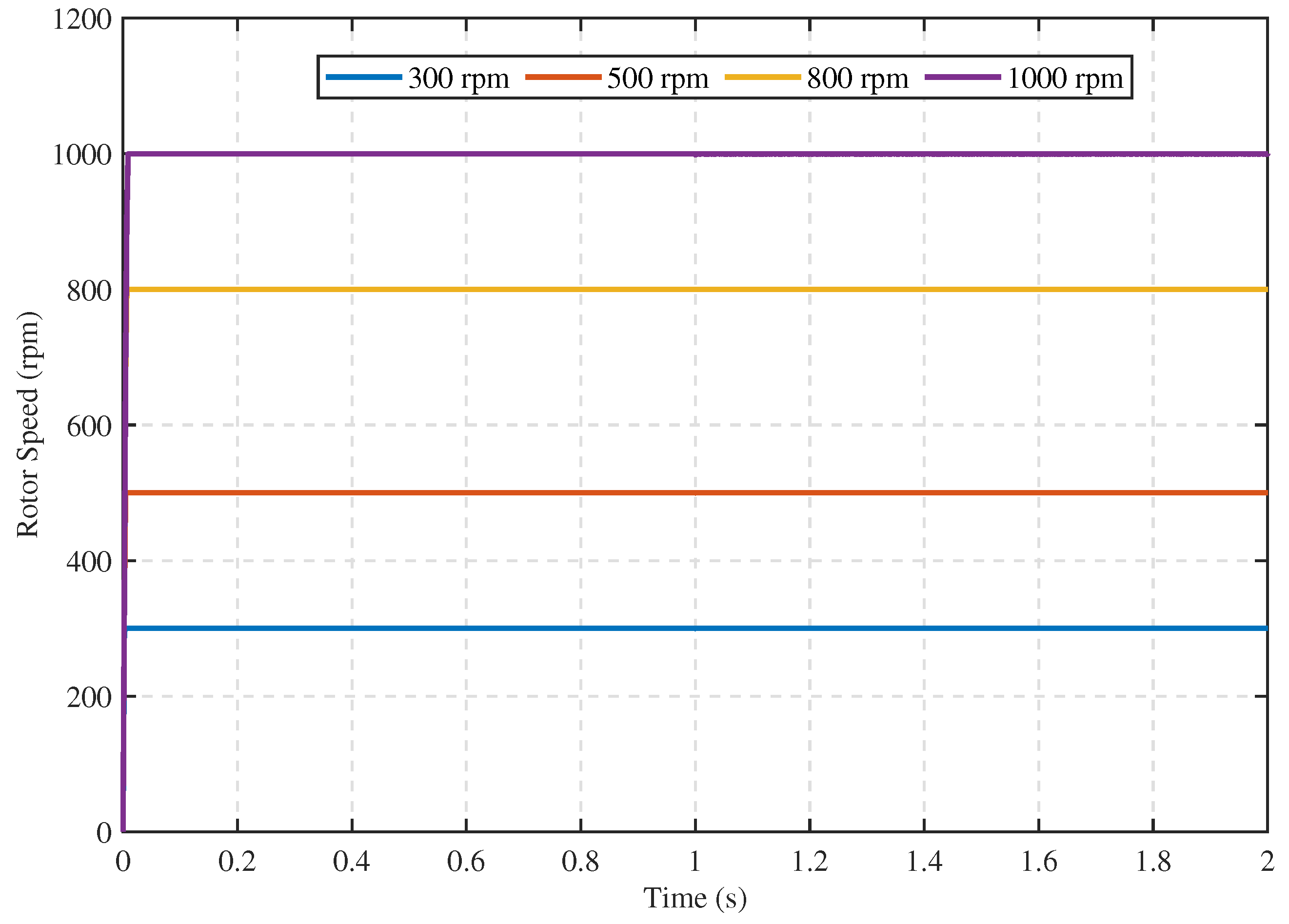
5.1.2. Comparative Performance of the Proposed Speed Controller under Different Conditions
5.2. Experimental Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vlachou, V.I.; Sakkas, G.K.; Xintaropoulos, F.P.; Pechlivanidou, M.S.C.; Kefalas, T.D.; Tsili, M.A.; Kladas, A.G. Overview on Permanent Magnet Motor Trends and Developments. Energies 2024, 17, 538. [Google Scholar] [CrossRef]
- Majout, B.; Bossoufi, B.; Karim, M.; Skruch, P.; Mobayen, S.; El Mourabit, Y.; Laggoun, Z.E.Z. Artificial neural network-based direct power control to enhance the performance of a PMSG-wind energy conversion system under real wind speed and parameter uncertainties: An experimental validation. Energy Rep. 2024, 11, 4356–4378. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, G.; Jing, R.; Bi, G.; Xiang, R.; Wang, G.; Xu, D. Nonlinear active disturbance rejection control strategy for permanent magnet synchronous motor drives. IEEE Trans. Energy Convers. 2022, 37, 2119–2129. [Google Scholar] [CrossRef]
- Zheng, Y.; Cao, Z.; Wang, S.; Man, Z.; Chuei, R. Extreme learning machine-based field-oriented feedback linearization speed control of permanent magnetic synchronous motors. Neural Comput. Appl. 2022, 34, 5267–5282. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, J.; Liu, W.; Lee, C.H. A linear control approach to design digital speed control system for PMSMs. IEEE Trans. Power Electron. 2022, 37, 8596–8610. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C. Model predictive control for open winding PMSM considering dead-zone effect. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 874–885. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, X.; Hu, Q.; Li, Z.; Jiang, Z.; Yu, Y.; Chen, Z. A modified deadbeat predictive current control for improving dynamic performance of PMSM. IEEE Trans. Power Electron. 2022, 37, 14173–14185. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. Active-disturbance-rejection-based sliding-mode current control for permanent-magnet synchronous motors. IEEE Trans. Power Electron. 2020, 36, 751–760. [Google Scholar] [CrossRef]
- Dai, C.; Guo, T.; Yang, J.; Li, S. A disturbance observer-based current-constrained controller for speed regulation of PMSM systems subject to unmatched disturbances. IEEE Trans. Ind. Electron. 2020, 68, 767–775. [Google Scholar] [CrossRef]
- Senhaji, A.; Abdelouhab, M.; Attar, A.; Bouchnaif, J. Backstepping control of a permanent magnet synchronous motor. Mater. Today Proc. 2023, 72, 3730–3737. [Google Scholar] [CrossRef]
- Regaya, C.B.; Farhani, F.; Zaafouri, A.; Chaari, A. A novel adaptive control method for induction motor based on Backstepping approach using dSpace DS 1104 control board. Mech. Syst. Signal Process. 2018, 100, 466–481. [Google Scholar] [CrossRef]
- Ullah, S.; Mehmood, A.; Khan, Q.; Rehman, S.; Iqbal, J. Robust integral sliding mode control design for stability enhancement of under-actuated quadcopter. Int. J. Control Autom. Syst. 2020, 18, 1671–1678. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, Q.; Zaidi, M.M.; Hua, L.G. Neuro-adaptive non-singular terminal sliding mode control for distributed fixed-time synchronization of higher-order uncertain multi-agent nonlinear systems. Inf. Sci. 2024, 659, 120087. [Google Scholar] [CrossRef]
- Sreejeth, M.; Singh, M. Improved ANFIS based MRAC observer for sensorless control of PMSM. J. Intell. Fuzzy Syst. 2022, 42, 1061–1073. [Google Scholar]
- Ullah, S.; Khan, Q.; Mehmood, A. Neuro-adaptive fixed-time non-singular fast terminal sliding mode control design for a class of under-actuated nonlinear systems. Int. J. Control 2023, 96, 1529–1542. [Google Scholar] [CrossRef]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust speed control of PMSM using sliding mode control (SMC)—A review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Bouguenna, I.F.; Tahour, A.; Kennel, R.; Abdelrahem, M. Multiple-vector model predictive control with fuzzy logic for PMSM electric drive systems. Energies 2021, 14, 1727. [Google Scholar] [CrossRef]
- He, H.; Gao, J.; Wang, Q.; Wang, J.; Zhai, H. Improved Sliding Mode Observer for the Sensorless Control of Permanent Magnet Synchronous Motor. J. Electr. Eng. Technol. 2024, 1–13. [Google Scholar] [CrossRef]
- Regaya, C.B.; Farhani, F.; Zaafouri, A.; Chaari, A. An adaptive sliding-mode speed observer for induction motor under backstepping control. ICIC Express Lett. 2017, 11, 763–771. [Google Scholar]
- Mishra, R.N.; Mohanty, K.B. Development and implementation of induction motor drive using sliding-mode based simplified neuro-fuzzy control. Eng. Appl. Artif. Intell. 2020, 91, 103593. [Google Scholar] [CrossRef]
- Zhang, W.; Kong, J. A novel fast and chattering-free speed control method for PMSM motor drive based on sliding mode control. Int. J. Dyn. Control 2024, 1–7. [Google Scholar] [CrossRef]
- Guo, J. The load frequency control by adaptive high order sliding mode control strategy. IEEE Access 2022, 10, 25392–25399. [Google Scholar] [CrossRef]
- Liu, Y.C.; Laghrouche, S.; Depernet, D.; Djerdir, A.; Cirrincione, M. Disturbance-observer-based complementary sliding-mode speed control for PMSM drives: A super-twisting sliding-mode observer-based approach. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 5416–5428. [Google Scholar] [CrossRef]
- Marcos-Andrade, D.; Beltran-Carbajal, F.; Rivas-Cambero, I.; Yañez-Badillo, H.; Favela-Contreras, A.; Rosas-Caro, J.C. Sliding Mode Speed Control in Synchronous Motors for Agriculture Machinery: A Chattering Suppression Approach. Agriculture 2024, 14, 737. [Google Scholar] [CrossRef]
- Hernandez-Gonzalez, M.; Alanis, A.; Rios, J.; Hernadez-Vargas, E. Exponential sliding mode controller for tracking trajectory of nonlinear systems. Trans. Inst. Meas. Control 2024, 46, 1058–1068. [Google Scholar] [CrossRef]
- Ge, Y.; Yang, L.; Ma, X. Adaptive sliding mode control based on a combined state/disturbance observer for the disturbance rejection control of PMSM. Electr. Eng. 2020, 102, 1863–1879. [Google Scholar] [CrossRef]
- Hu, M.; Ahn, H.; Chung, Y.; You, K. Speed Regulation for PMSM with Super-Twisting Sliding-Mode Controller via Disturbance Observer. Mathematics 2023, 11, 1618. [Google Scholar] [CrossRef]
- Karami-Mollaee, A.; Barambones, O. Higher Order Sliding Mode Control of MIMO Induction Motors: A New Adaptive Approach. Mathematics 2023, 11, 4558. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, J.; Huang, L. Model-free predictive current control of PMSM drives based on extended state observer using ultralocal model. IEEE Trans. Ind. Electron. 2020, 68, 993–1003. [Google Scholar] [CrossRef]
- El-Sousy, F.F.; Amin, M.M.; Soliman, A.S.; Mohammed, O.A. Optimal Adaptive Ultra-Local Model-Free Control Based-Extended State Observer for PMSM Driven Single-Axis Servo Mechanism System. IEEE Trans. Ind. Appl. 2024, 1–8. [Google Scholar] [CrossRef]
- Long, Y.; Wang, Y.M.; Yao, C.; Song, E.Z.; Dong, Q. Adaptive Second-order Sliding Mode Control of Electrical Throttles Based on Online Zero-crossing Checking. Int. J. Control Autom. Syst. 2024, 22, 489–502. [Google Scholar] [CrossRef]
- Levant, A. Sliding order and sliding accuracy in sliding mode control. Int. J. Control 1993, 58, 1247–1263. [Google Scholar] [CrossRef]
- Levant, A. Homogeneity approach to high-order sliding mode design. Automatica 2005, 41, 823–830. [Google Scholar] [CrossRef]
- Gonzalez, T.; Moreno, J.A.; Fridman, L. Variable gain super-twisting sliding mode control. IEEE Trans. Autom. Control 2011, 57, 2100–2105. [Google Scholar] [CrossRef]
- Kürkçü, B.; Kasnakoğlu, C.; Efe, M.Ö. Disturbance/uncertainty estimator based integral sliding-mode control. IEEE Trans. Autom. Control 2018, 63, 3940–3947. [Google Scholar] [CrossRef]
- Eray, O.; Tokat, S. The design of a fractional-order sliding mode controller with a time-varying sliding surface. Trans. Inst. Meas. Control 2020, 42, 3196–3215. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Zaihidee, F.M.; Mekhilef, S.; Mubin, M. Application of fractional order sliding mode control for speed control of permanent magnet synchronous motor. IEEE Access 2019, 7, 101765–101774. [Google Scholar] [CrossRef]
- Xu, S.; Sun, G.; Ma, Z.; Li, X. Fractional-order fuzzy sliding mode control for the deployment of tethered satellite system under input saturation. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 747–756. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Yan, F.; Zhu, K.; Chen, B. Adaptive super-twisting fractional-order nonsingular terminal sliding mode control of cable-driven manipulators. ISA Trans. 2019, 86, 163–180. [Google Scholar] [CrossRef]
- Daftardar-Gejji, V. Fractional Calculus and Fractional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Dávila, A.; Moreno, J.A.; Fridman, L. Variable gains super-twisting algorithm: A Lyapunov based design. In Proceedings of the 2010 American Control Conference, Baltimore, MD, USA, 30 June–2 July 2010; pp. 968–973. [Google Scholar]
- Utkin, V.I. Sliding Modes in Optimization and Control Problems; Springer: New York, NY, USA, 1992. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.V.; Polyakov, A. Road Map for Sliding Mode Control Design; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Utkin, V.; Poznyak, A.; Orlov, Y.; Polyakov, A. Conventional and high order sliding mode control. J. Frankl. Inst. 2020, 357, 10244–10261. [Google Scholar] [CrossRef]
- Boeren, F.; Bareja, A.; Kok, T.; Oomen, T. Frequency-domain ILC approach for repeating and varying tasks: With application to semiconductor bonding equipment. IEEE/ASME Trans. Mechatron. 2016, 21, 2716–2727. [Google Scholar] [CrossRef]
- Zheng, M.; Wang, C.; Sun, L.; Tomizuka, M. Design of arbitrary-order robust iterative learning control based on robust control theory. Mechatronics 2017, 47, 67–76. [Google Scholar] [CrossRef]

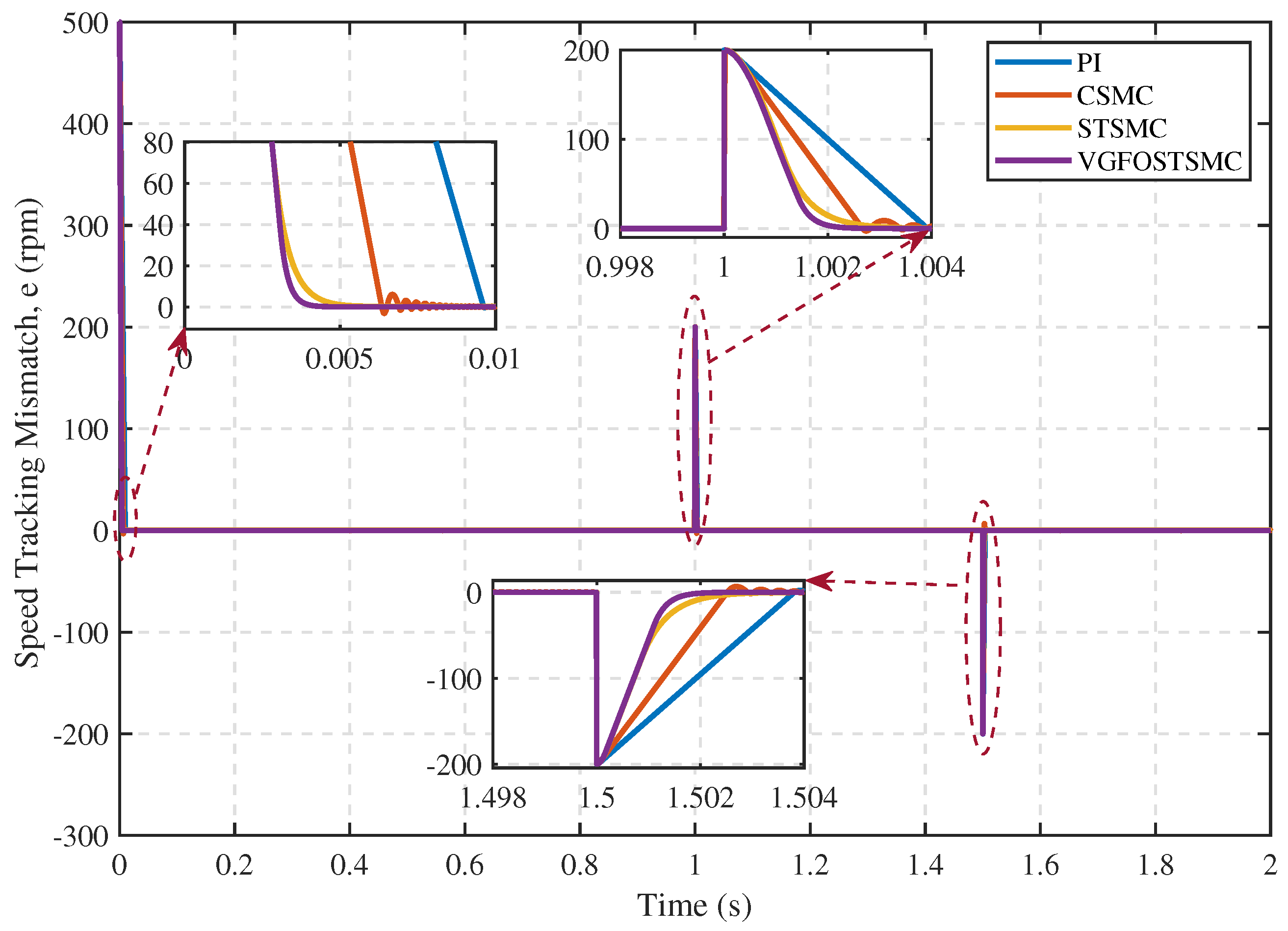
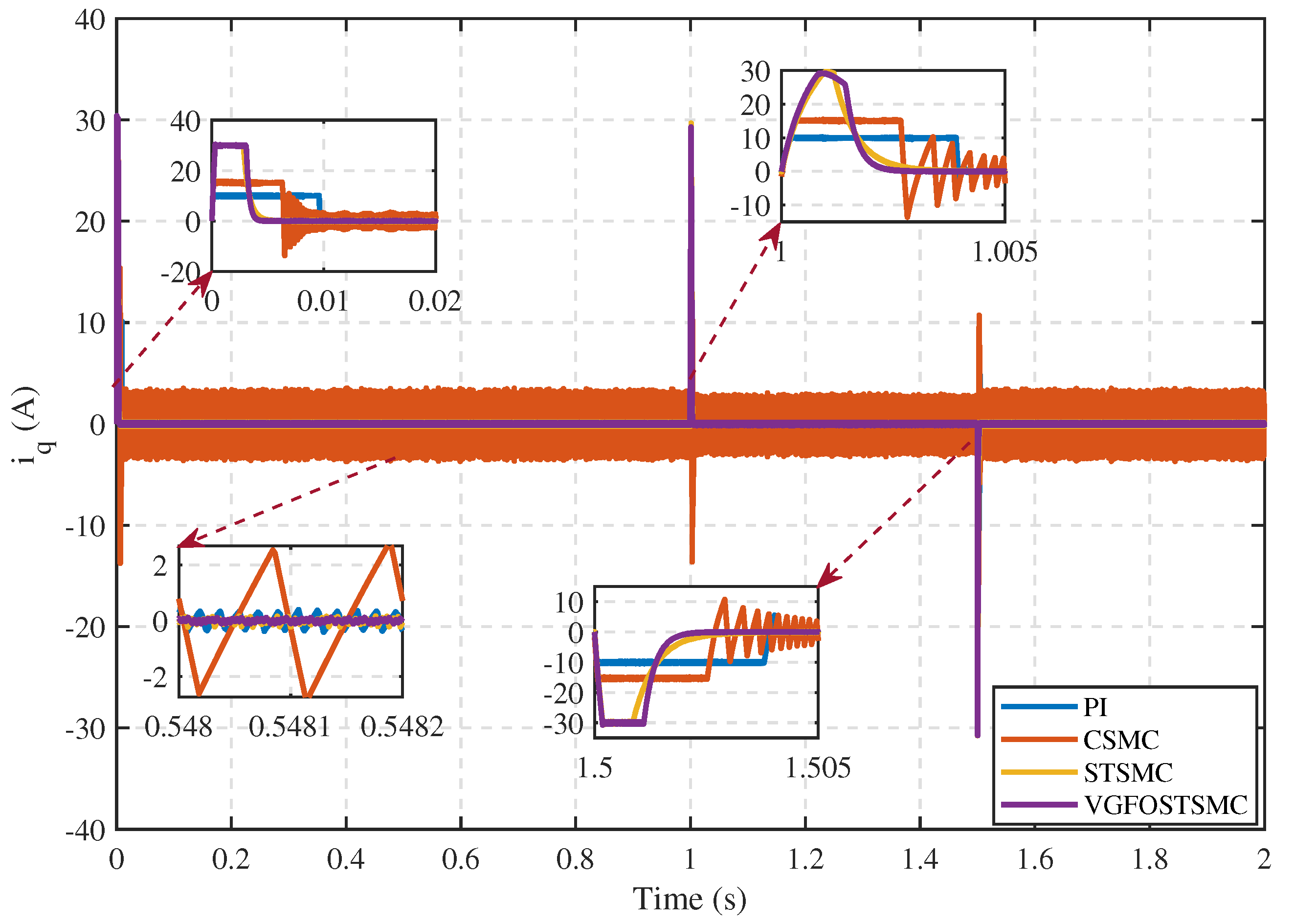
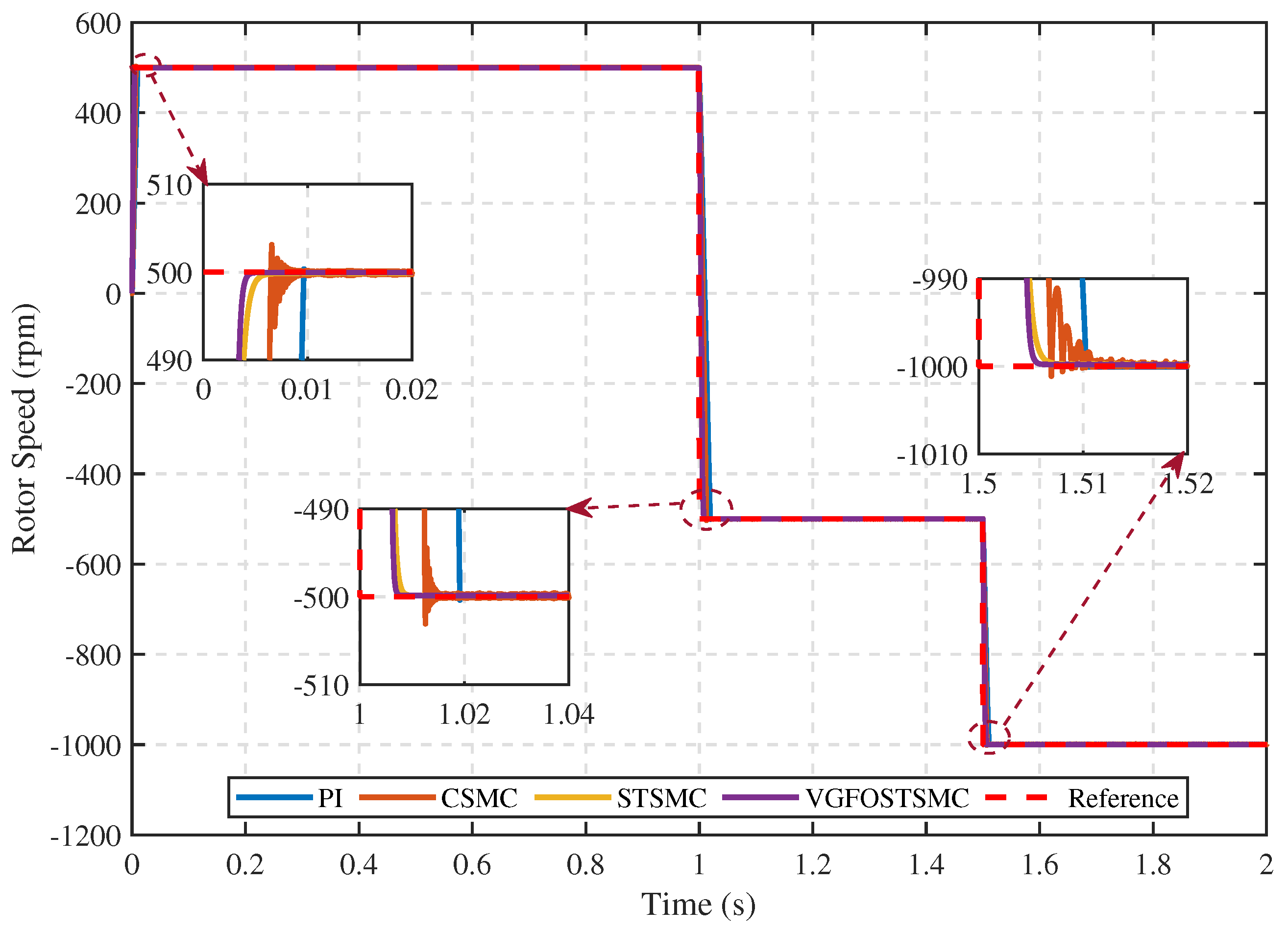
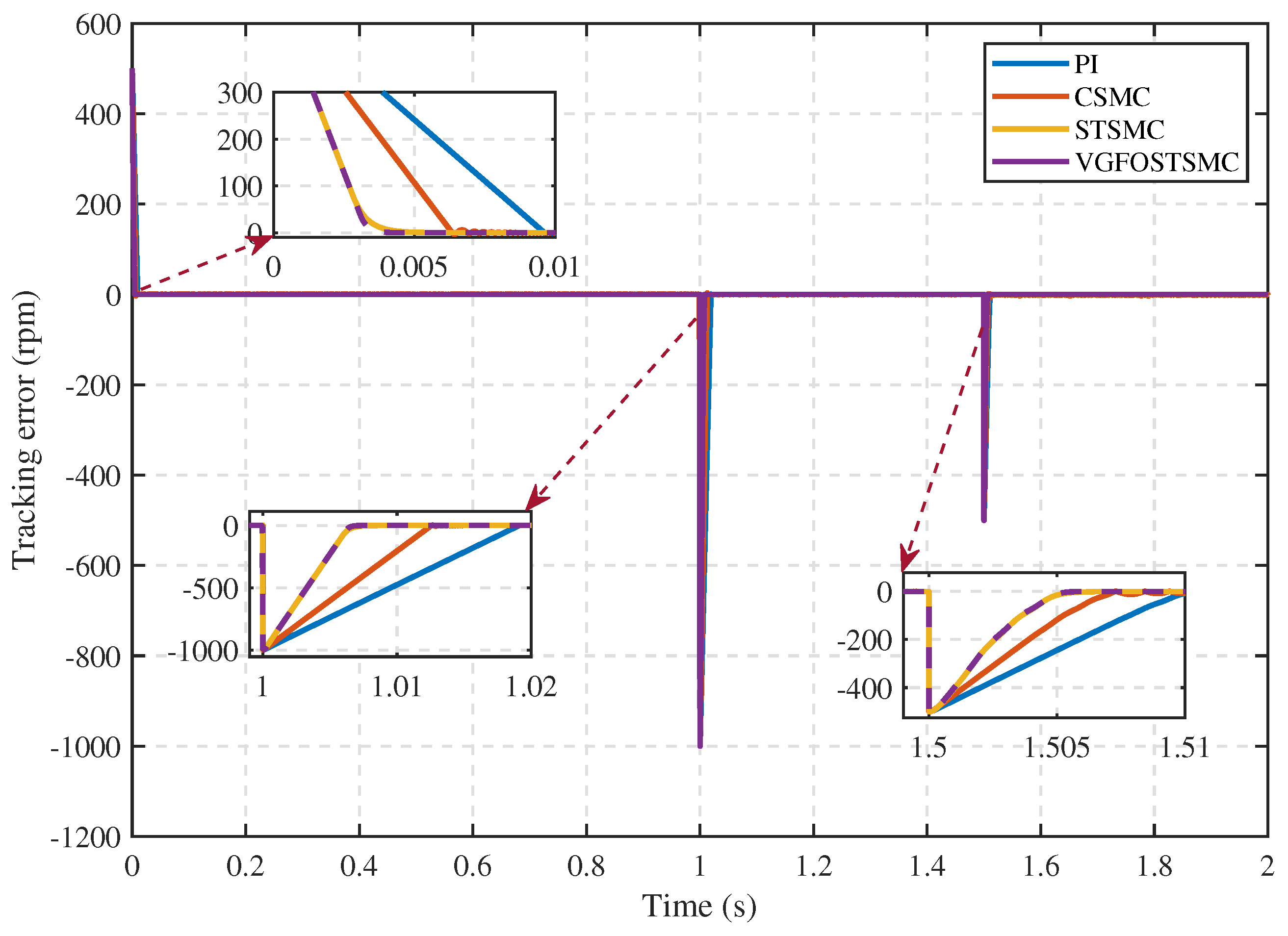

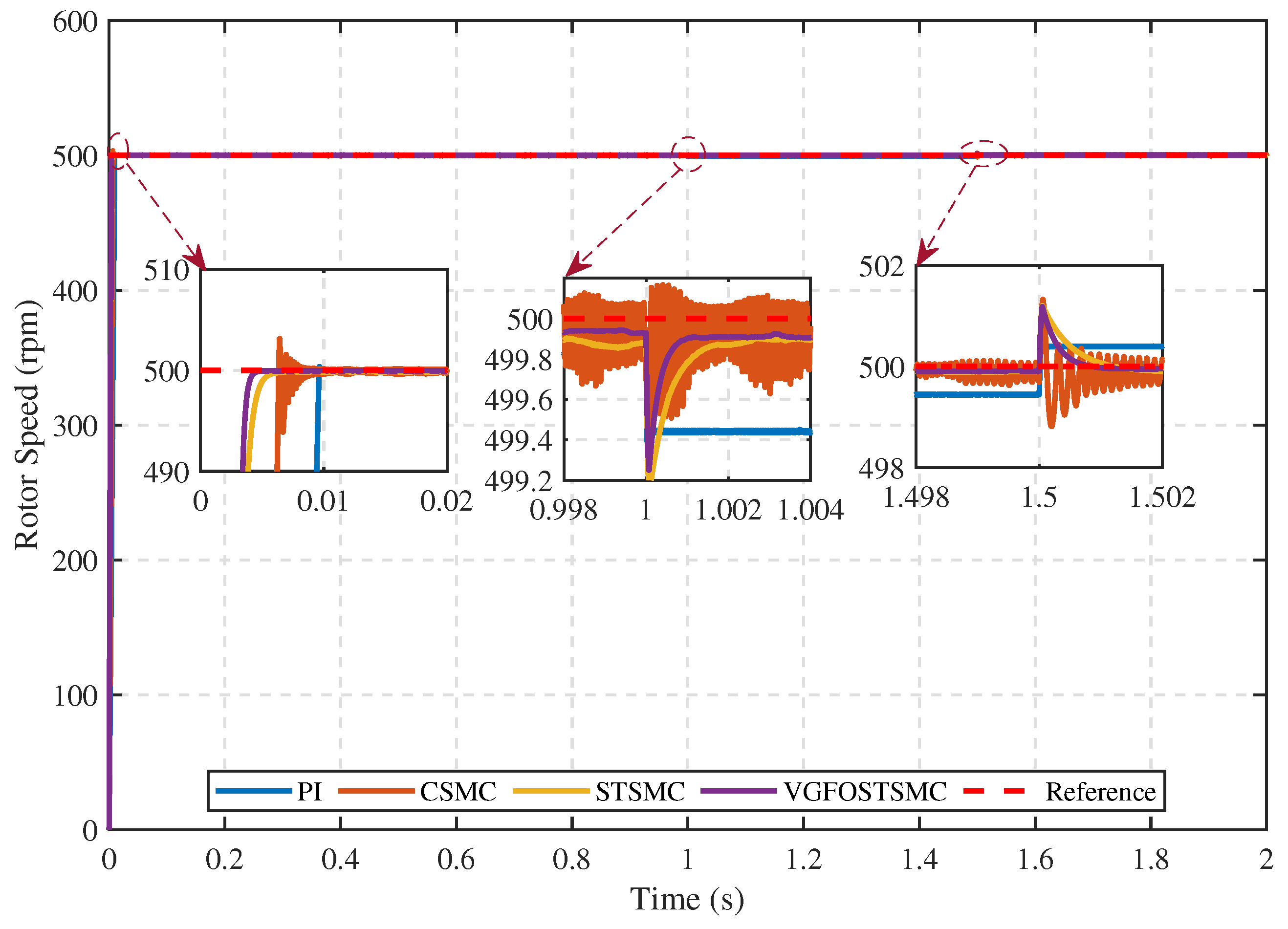
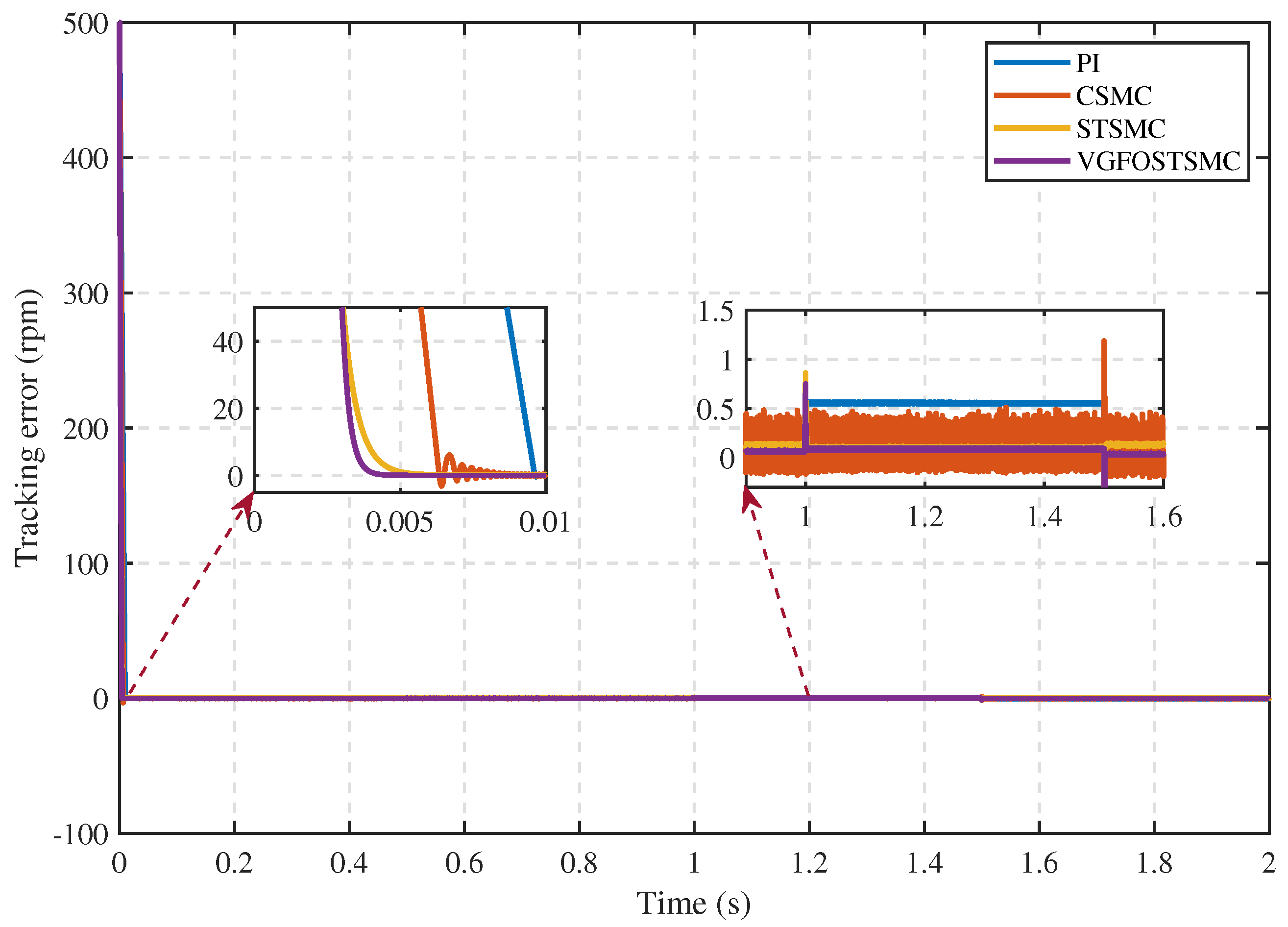
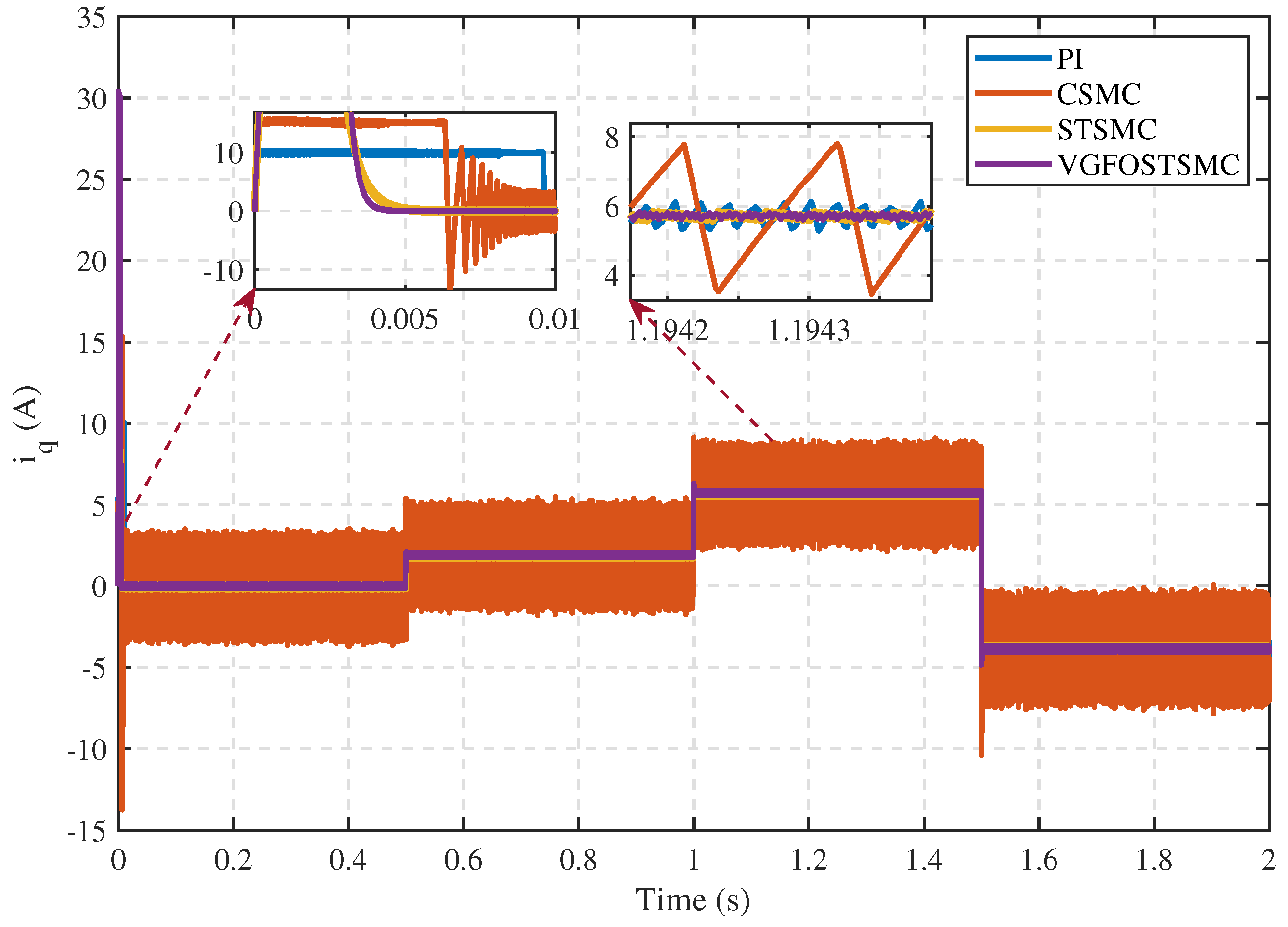
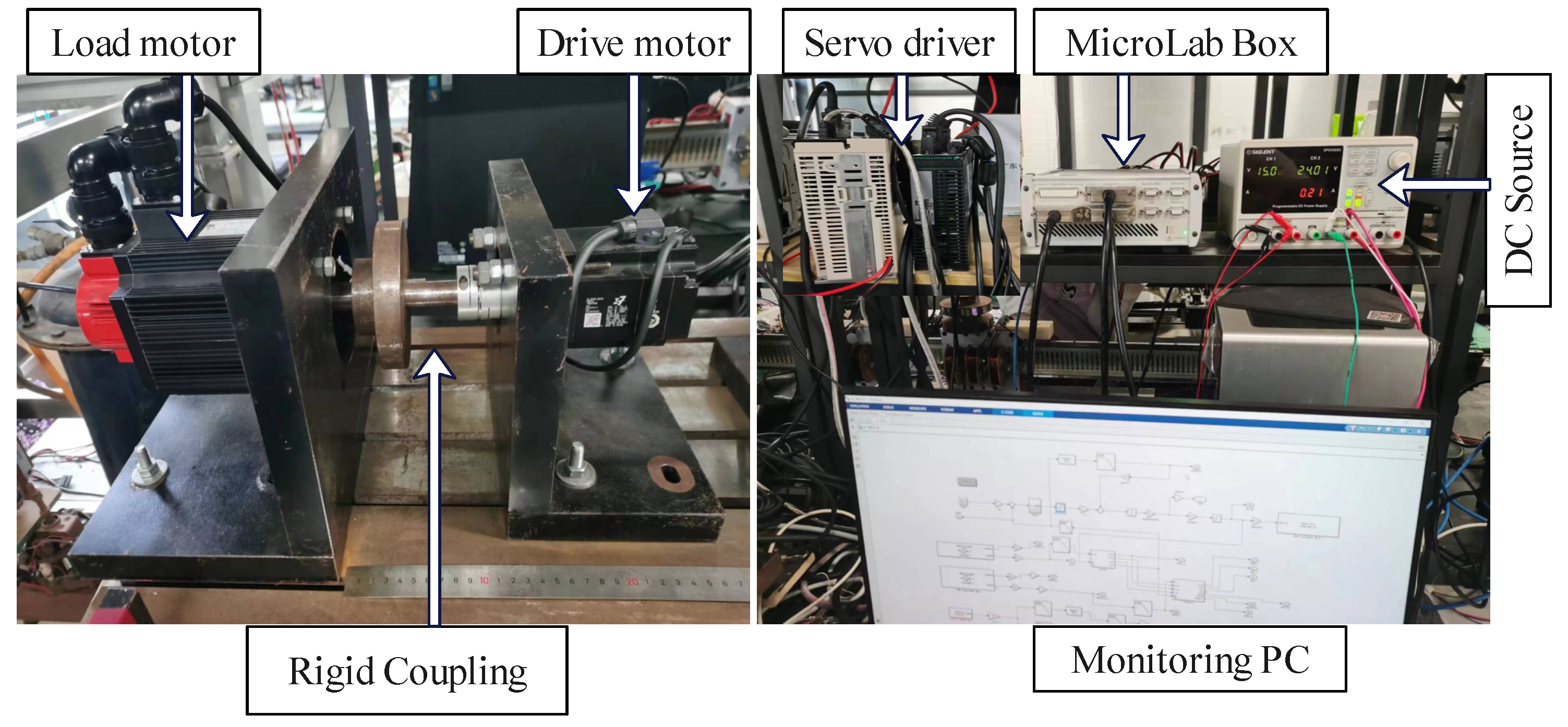
| Parameter | Symbol | Value |
|---|---|---|
| Flux | 0.181 Wb | |
| System inertia | J | 0.00079 kgm2 |
| Number of pole pairs | 3 | |
| Viscous friction coefficient | B | 0.00001 Nms/rad |
| dq-axis inductances | , | 11.58 mH |
| Stator resistance | 3.45 | |
| Rated speed | 3001 rpm | |
| Rated power | P | 1.21 kW |
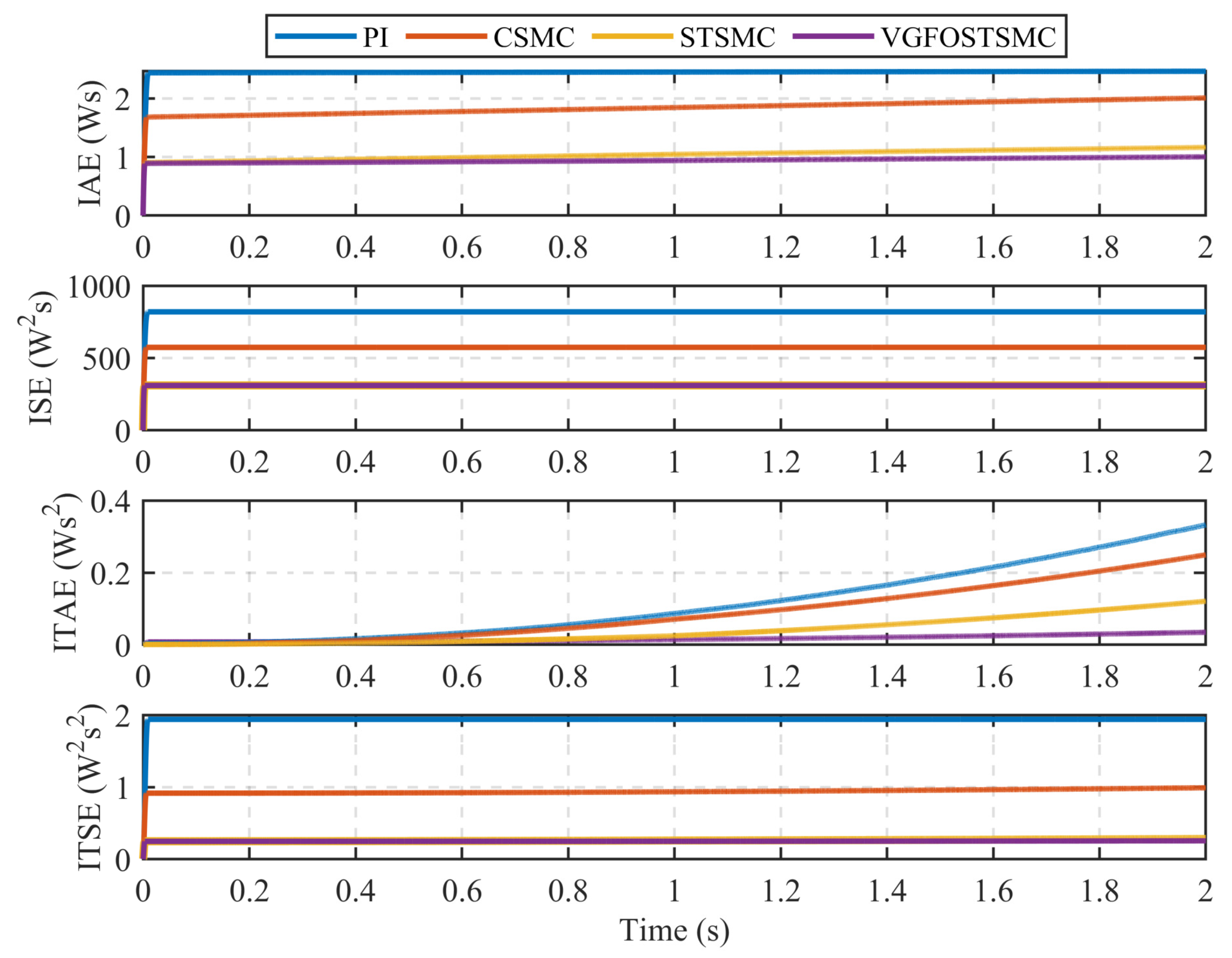
| Index | PI | CSMC | STSMC | VGFOSTSMC |
|---|---|---|---|---|
| ISE | 819.5 | 548.5 | 310.6 | 310.1 |
| IAE | 2.464 | 1.948 | 1.164 | 1.002 |
| ITSE | 1.94 | 0.9211 | 0.2809 | 0.2553 |
| ITAE | 0.03458 | 0.3291 | 0.2494 | 0.1207 |
| Specifications | PI | CSMC | STSMC | VGFOSTSMC |
|---|---|---|---|---|
| Steady-state error | 0.0102 | 0.1983 | 0.1143 | 0.0614 |
| Maximum overshoot [%] | 0.0693 | 0.6666 | 0.0054 | 0.0041 |
| Settling time (s) | 0.0094 | 0.0062 | 0.0038 | 0.0034 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, A.; Pan, J.; Ullah, S.; Zhang, Z. Robust Speed Control of Permanent Magnet Synchronous Motor Drive System Using Sliding-Mode Disturbance Observer-Based Variable-Gain Fractional-Order Super-Twisting Sliding-Mode Control. Fractal Fract. 2024, 8, 368. https://doi.org/10.3390/fractalfract8070368
Ullah A, Pan J, Ullah S, Zhang Z. Robust Speed Control of Permanent Magnet Synchronous Motor Drive System Using Sliding-Mode Disturbance Observer-Based Variable-Gain Fractional-Order Super-Twisting Sliding-Mode Control. Fractal and Fractional. 2024; 8(7):368. https://doi.org/10.3390/fractalfract8070368
Chicago/Turabian StyleUllah, Ameen, Jianfei Pan, Safeer Ullah, and Zhang Zhang. 2024. "Robust Speed Control of Permanent Magnet Synchronous Motor Drive System Using Sliding-Mode Disturbance Observer-Based Variable-Gain Fractional-Order Super-Twisting Sliding-Mode Control" Fractal and Fractional 8, no. 7: 368. https://doi.org/10.3390/fractalfract8070368
APA StyleUllah, A., Pan, J., Ullah, S., & Zhang, Z. (2024). Robust Speed Control of Permanent Magnet Synchronous Motor Drive System Using Sliding-Mode Disturbance Observer-Based Variable-Gain Fractional-Order Super-Twisting Sliding-Mode Control. Fractal and Fractional, 8(7), 368. https://doi.org/10.3390/fractalfract8070368









