Fractional-Order Modeling and Nonlinear Dynamic Analysis of Forward Converter
Abstract
1. Introduction
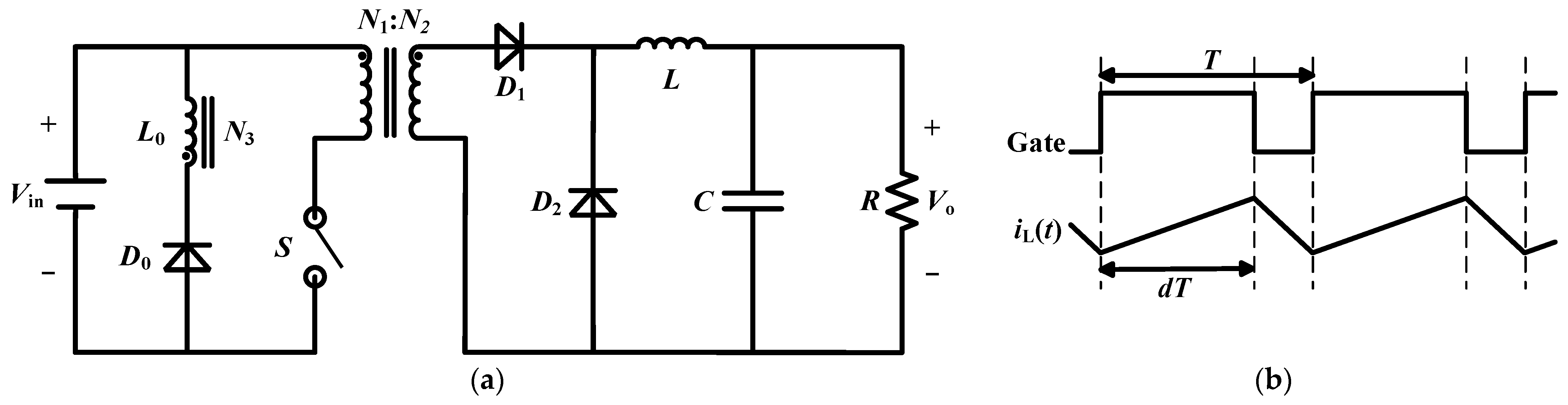
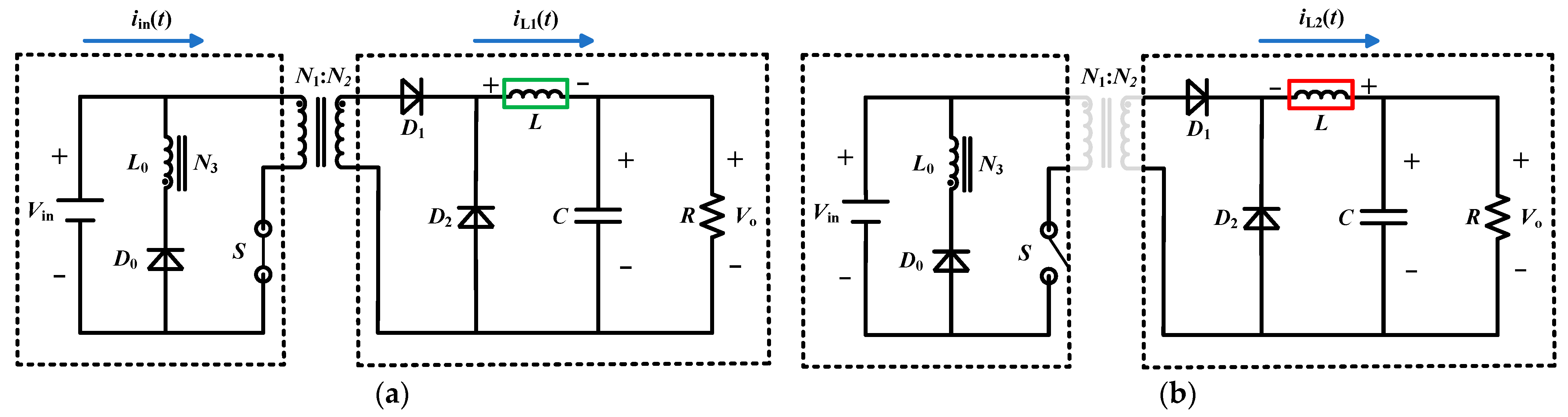
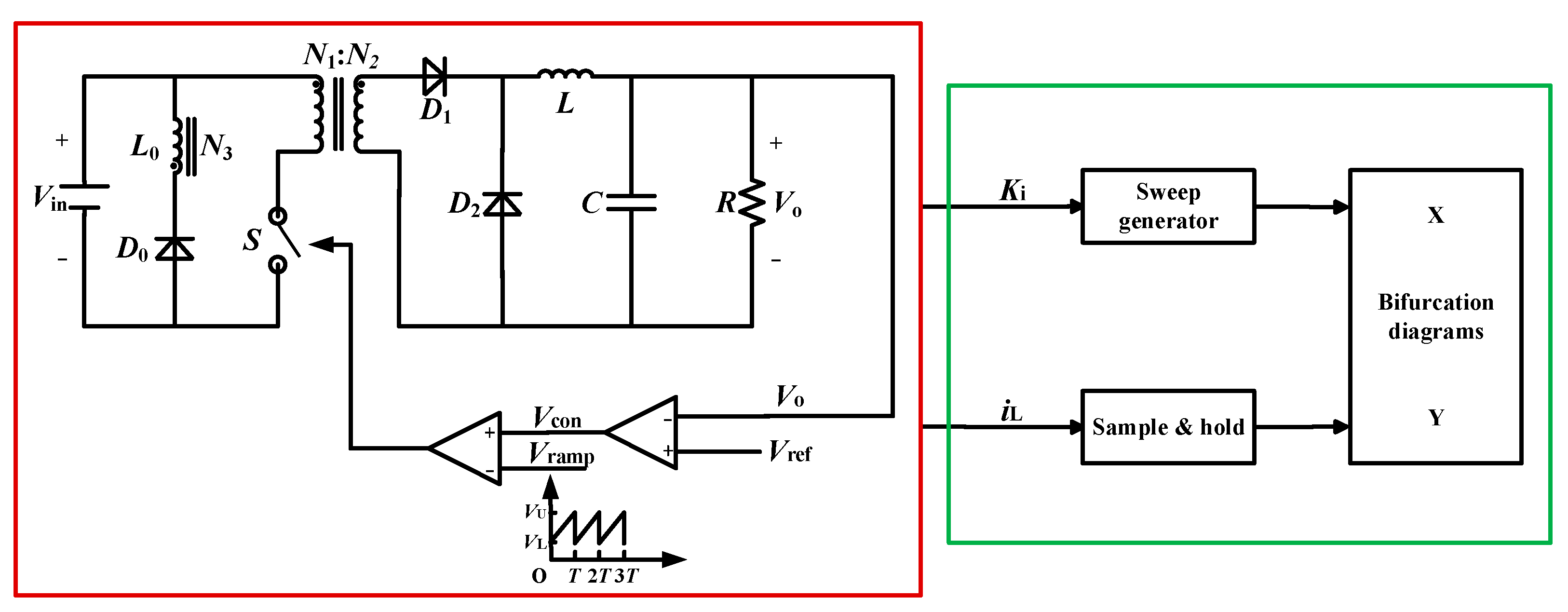
2. Fractional-Order Modeling of Forward Converter
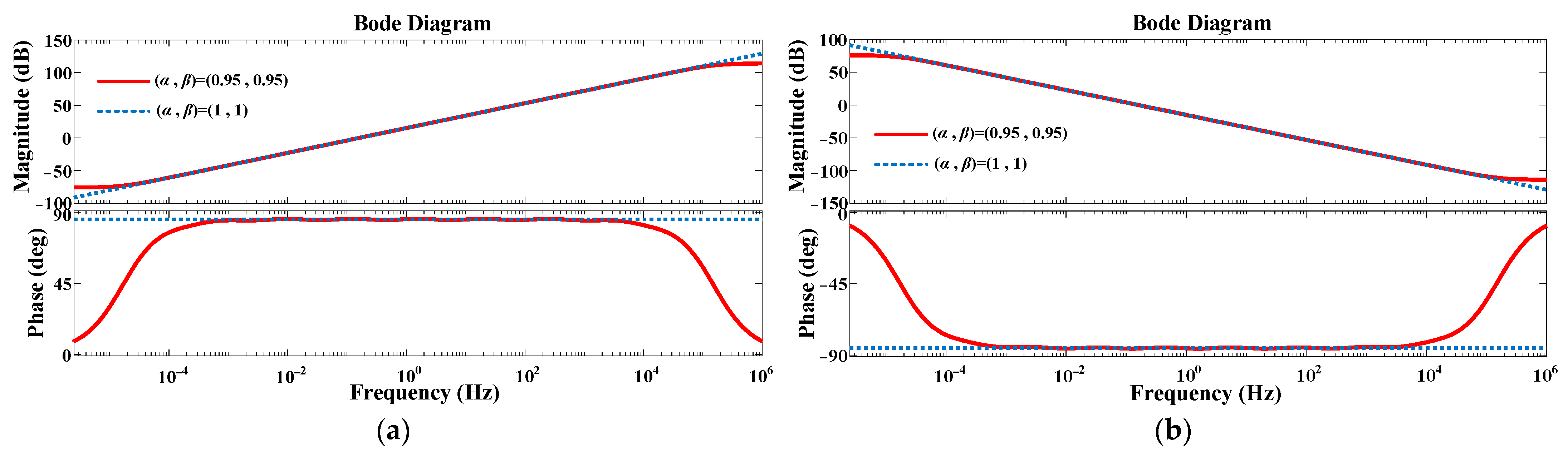
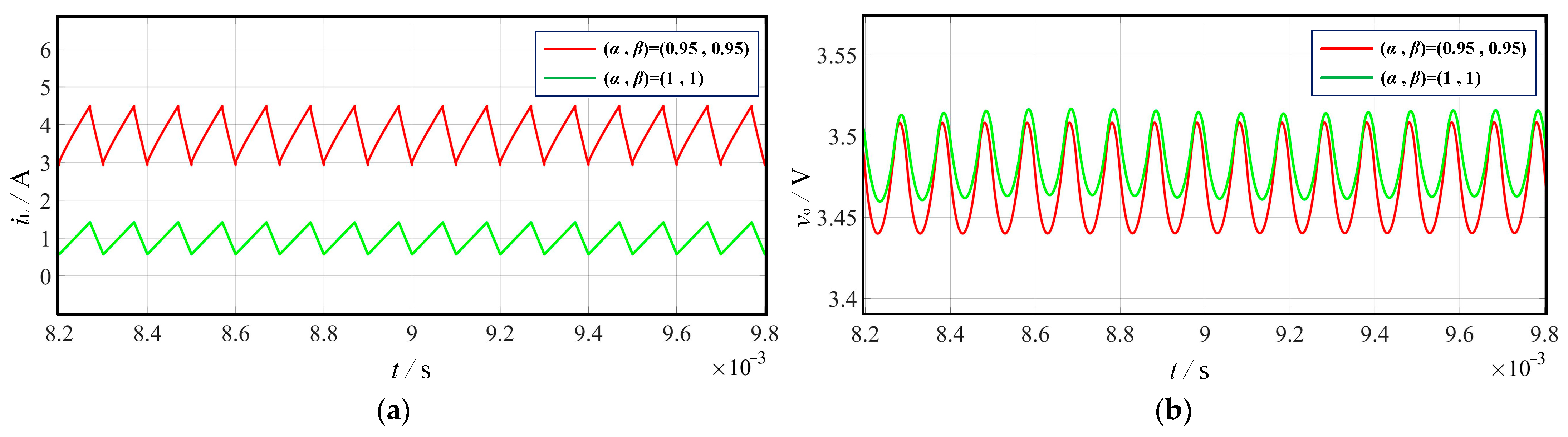
3. Simulation Results
4. Nonlinear Dynamic Analysis
4.1. Low-Frequency Oscillation Phenomena
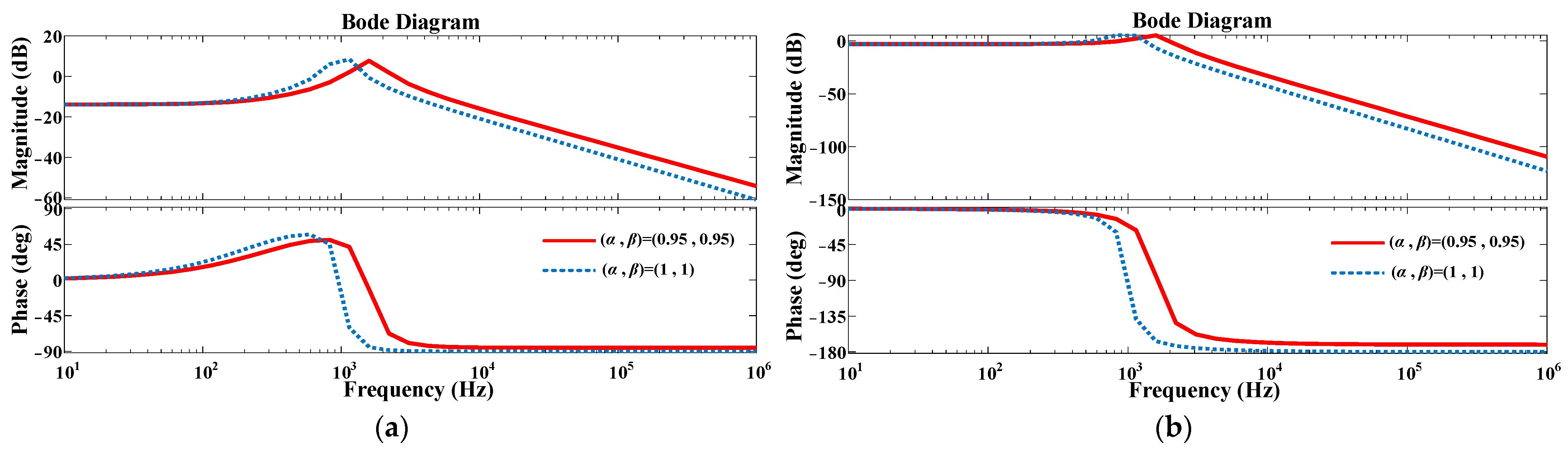
4.1.1. Low-Frequency Oscillation Phenomena in Fractional-Order Forward Converter
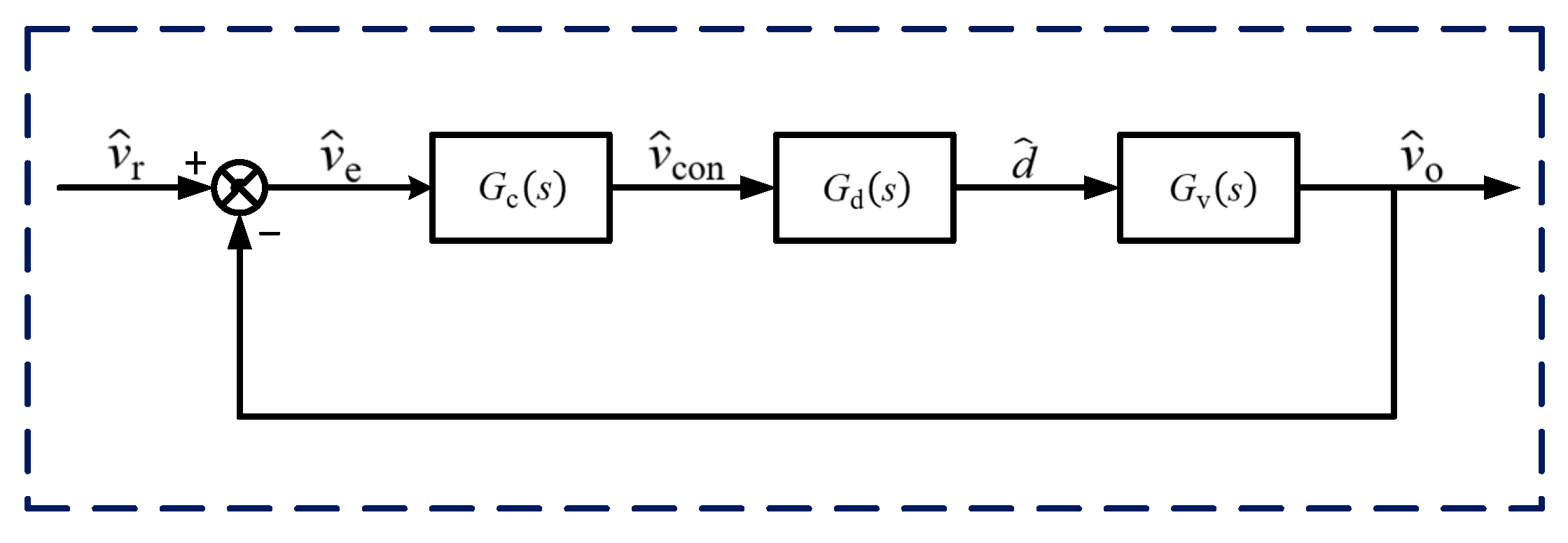
4.1.2. Predicting the Low-Frequency Oscillation Characteristics of the Fractional-Order Forward Converter
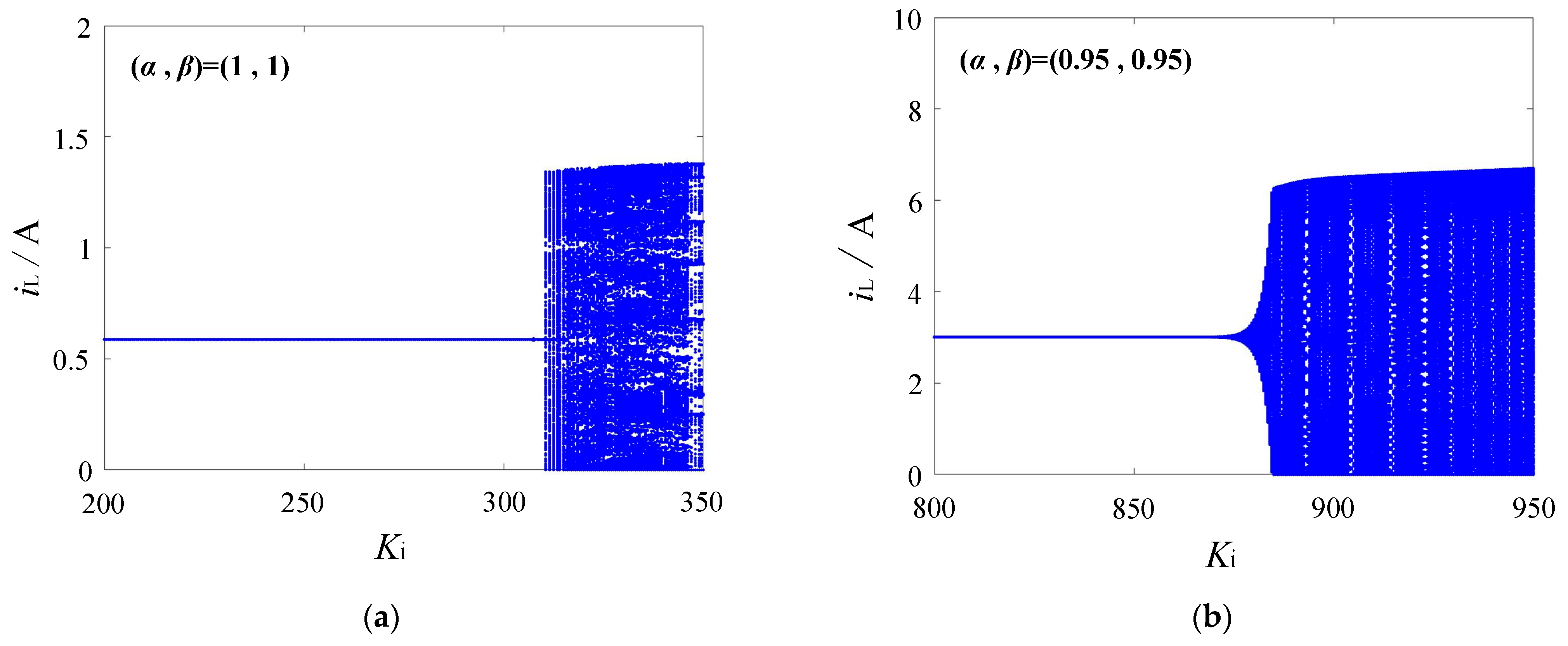
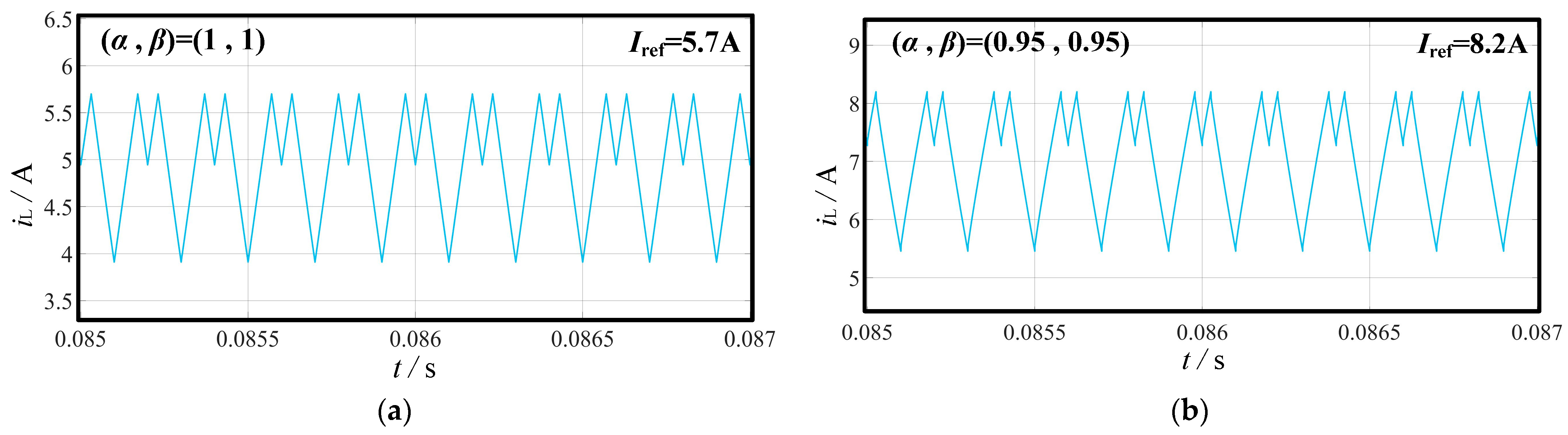
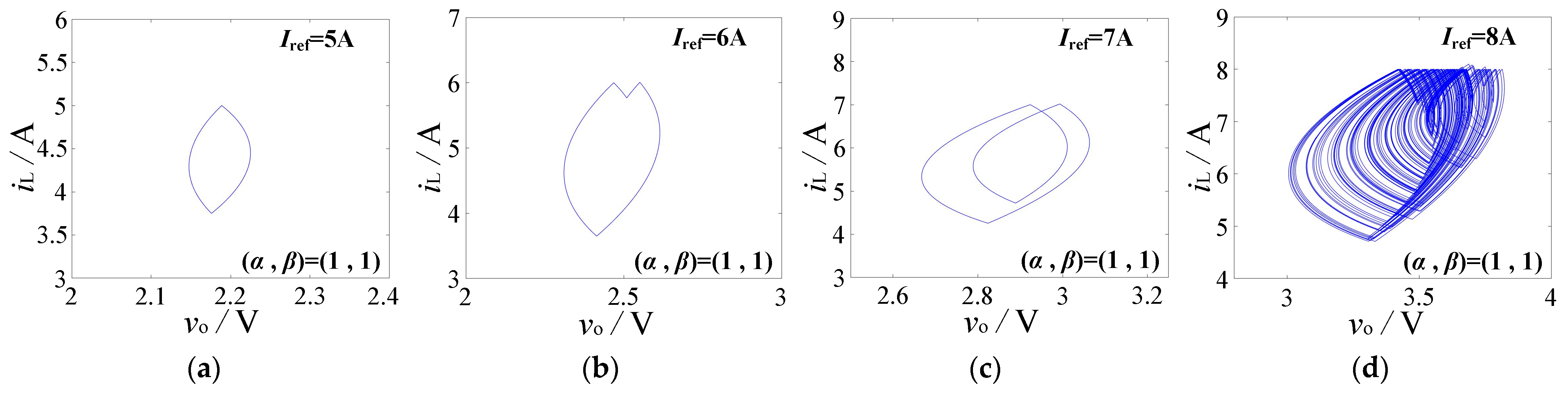
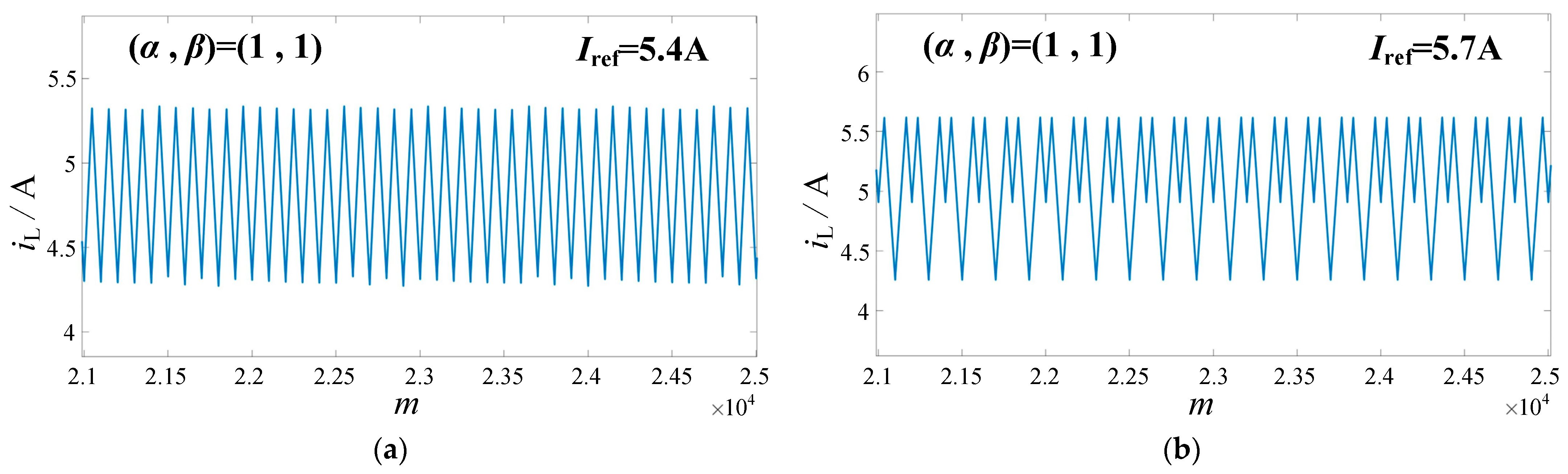
4.2. Period-Doubling Bifurcation
4.2.1. The Period-Doubling Bifurcation in Fractional-Order Forward Converter
4.2.2. Prediction of the Period-Doubling Bifurcation Boundary for Fractional-Order Forward Converter
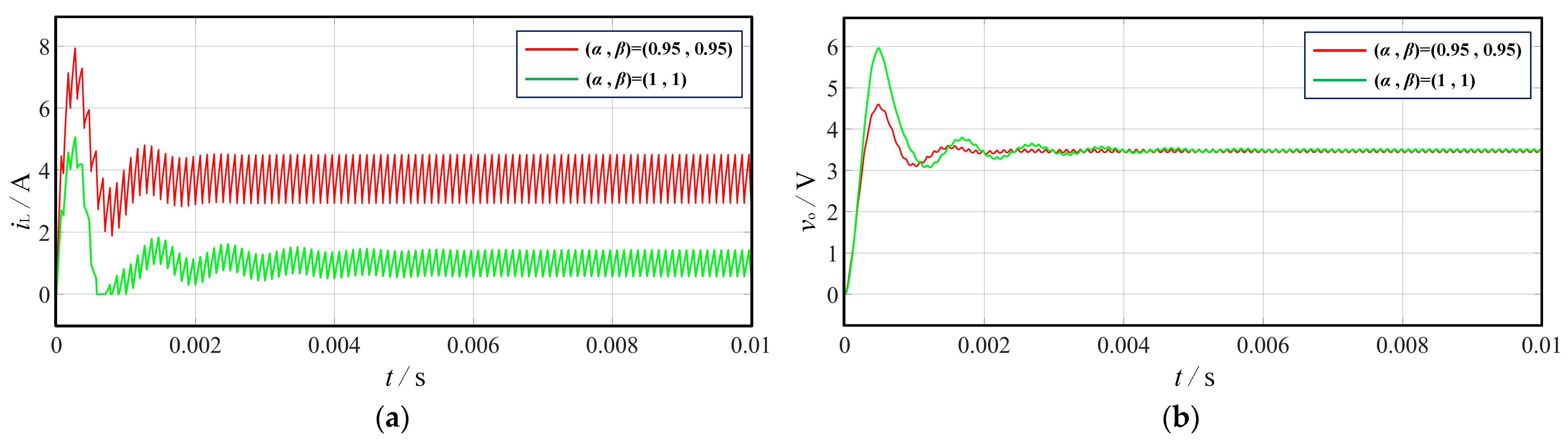
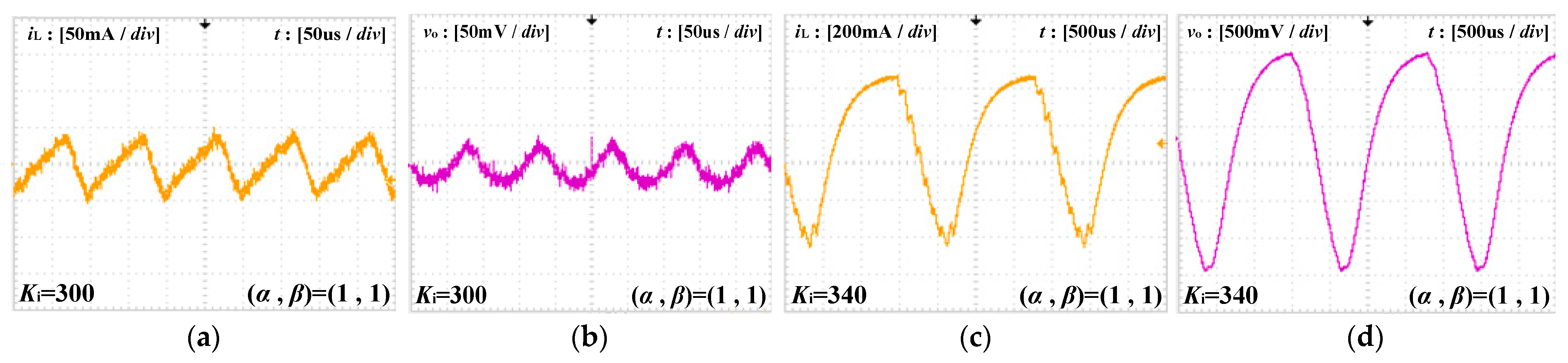
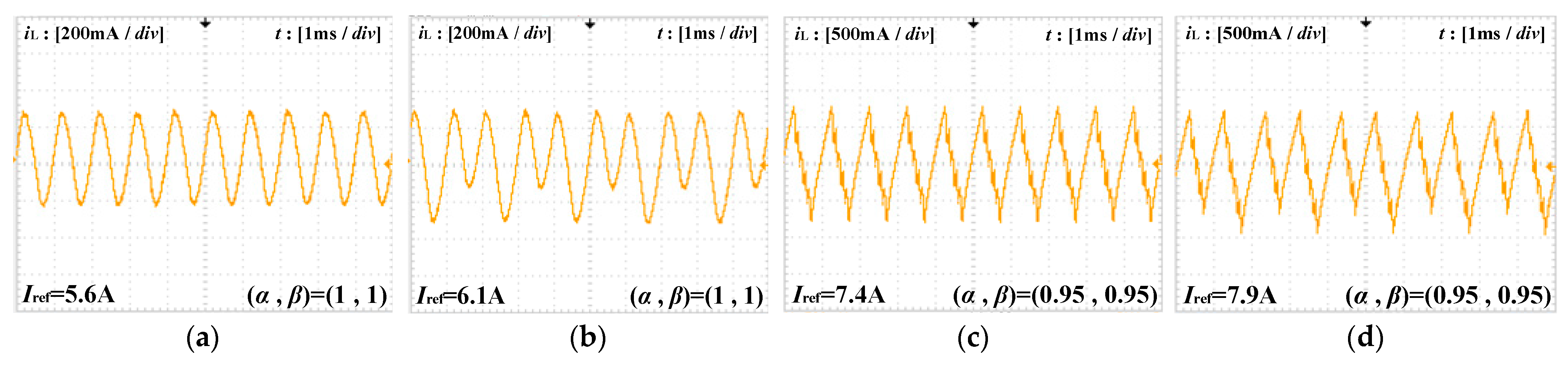
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Probl. Eng. 2014, 2014, 1–6. [Google Scholar] [CrossRef]
- Petráš, I. A note on the fractional-order Chua’s system. Chaos Solitons Fractals 2008, 38, 140–147. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Electr. Insul. 1994, 1, 826–839. [Google Scholar] [CrossRef]
- Westerlund, S. Dead matter has memory! Phys. Scr. 1991, 43, 174–179. [Google Scholar] [CrossRef]
- Jesus, I.S.; Tenreiro Machado, J.A. Development of fractional order capacitors based on electrolyte processes. Nonlinear Dyn. 2009, 56, 45–55. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, B. High-power fractional-order capacitor with 1<α<2 based on power converter. IEEE Trans. Ind. Electron. 2018, 65, 3157–3164. [Google Scholar]
- Wang, F.Q.; Ma, X.K. Fractional order buck–boost converter in CCM: Modelling, analysis and simulations. Int. J. Electron. 2014, 101, 1671–1682. [Google Scholar] [CrossRef]
- Sharma, M.; Rajpurohit, B.S.; Agnihotri, S.; Rathore, A.K. Development of fractional order modeling of voltage source converters. IEEE Access 2020, 8, 131750–131759. [Google Scholar] [CrossRef]
- Laugesen, J.L.; Mosekilde, E.; Zhusubaliyev, Z.T. Bifurcation structure of the -type period-doubling transition. Phys. D Nonlinear Phenom. 2012, 241, 488–496. [Google Scholar] [CrossRef]
- Xie, F.; Yang, R.; Zhang, B. Bifurcation and border collision analysis of voltage-mode-controlled Flyback converter based on total ampere-turns. IEEE Trans. Circuits Syst. I Regul. Pap. 2011, 58, 2269–2280. [Google Scholar] [CrossRef]
- Liu, J.; Xu, H. Nonlinear dynamic research of Buck converter based on multiscale entropy. In Proceedings of the 2015 Fifth International Conference on Instrumentation and Measurement, Computer, Communication and Control (IMCCC) 2015, Qinhuangdao, China, 18–20 September 2015; pp. 1042–1045. [Google Scholar]
- Aroudi, A.E.; Debbat, M.; Martinez-Salamero, L. Poincaré maps modeling and local orbital stability analysis of discontinuous piecewise affine periodically driven systems. Nonlinear Dyn. 2007, 50, 431–445. [Google Scholar] [CrossRef]
- Rodriguez-Amenedo, J.L.; Gomez, S.A. Damping low-frequency oscillations in power systems using grid-forming converters. IEEE Access 2021, 9, 158984–158997. [Google Scholar] [CrossRef]
- He, G.T.; Luo, M.K. Dynamic behavior of fractional order Duffing chaotic system and its synchronization via singly active control. Appl. Math. Mech. 2012, 33, 567–582. [Google Scholar] [CrossRef]
- Xie, L.; Liu, Z.; Zhang, B. A modeling and analysis method for CCM Ffractional order buck-boost converter by using R–L fractional definition. J. Electr. Eng. Technol. 2020, 15, 1651–1661. [Google Scholar] [CrossRef]
- Wang, F.Q.; Ma, X.K. Fractional order modeling and simulation analysis of boost converter in continuous conduction mode operation. Acta Phys. 2011, 60, 070506. [Google Scholar] [CrossRef]
- Tan, C.; Liang, Z.S. Modeling and simulation analysis of fractional-order boost converter in pseudo-continuous conduction mode. Acta Phys. 2014, 63, 070502. [Google Scholar]
- Kianpoor, N.; Yousefi, M.; Bayati, N.; Hajizadeh, A.; Soltani, M. Fractional order modelling of dc-dc boost converters. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 864–869. [Google Scholar]
- Chen, X.; Chen, Y.; Zhang, B.; Qiu, D. A modeling and analysis method for fractional-order dc–dc converters. IEEE Trans. Power Electron. 2017, 32, 7034–7044. [Google Scholar] [CrossRef]
- Fang, S.; Wang, X. Modeling and analysis method of fractional-order buck–boost converter. Int. J. Circuit Theory Appl. 2020, 48, 1493–1510. [Google Scholar] [CrossRef]
- El Aroudi, A.; Debbat, M.; Giral, R.; Olivar, G.; Benadero, L.; Toribio, E. Bifurcations in dc–dc switching converters: Review of methods and applications. Int. J. Bifurc. Chaos 2005, 15, 1549–1578. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Garefalo, F.; Glielmo, L.; Vasca, F. Switchings, bifurcations, and chaos in dc/dc converters. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1998, 45, 133–141. [Google Scholar] [CrossRef]
- Luo, Z.; Xie, F.; Zhang, B.; Qiu, D. Quantifying the nonlinear dynamic behavior of the dc-dc converter via permutation entropy. Energies 2018, 11, 2747. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, A.; Zhang, S.; Wang, Z.; Cang, S. Dynamical analysis and circuit implementation of a dc/dc single-stage boost converter with memristance load. Nonlinear Dyn. 2018, 93, 1741–1755. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Q.; Yang, N.; Jia, R.; Liu, C. Dynamical analysis of a fractional-order boost converter with fractional-order memristive load. Int. J. Bifurc. Chaos 2022, 32, 2250032. [Google Scholar] [CrossRef]
- Jia, Z.; Liu, C. Fractional-order modeling and simulation of magnetic coupled boost converter in continuous conduction mode. Int. J. Bifurc. Chaos 2018, 28, 1850061. [Google Scholar] [CrossRef]
- Li, Z.; Chen, D.; Zhu, J.; Liu, Y. Nonlinear dynamics of fractional order Duffing system. Chaos Solitons Fractals 2015, 81, 111–116. [Google Scholar] [CrossRef]
- Yang, C.; Xie, F.; Chen, Y.; Xiao, W.; Zhang, B. Modeling and Analysis of the Fractional-order flyback converter in continuous conduction mode by Caputo fractional calculus. Electronics 2020, 9, 1544. [Google Scholar] [CrossRef]
- Uchaikin, V.V.; Cahoy, D.O.; Sibatov, R.T. Fractional processes: From Poisson to branching one. Int. J. Bifurc. Chaos 2008, 18, 2717–2725. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Yang, N.N.; Liu, C.X.; Wu, C.J. Modeling and dynamics analysis of the fractional-order Buck-Boost converter in continuous conduction mode. Chin. Phys. B 2012, 21, 080503. [Google Scholar] [CrossRef]
- Dwari, S.; Jayawant, S.; Beechner, T.; Miller, S.K.; Mathew, A.; Chen, M.; Riehl, J.; Sun, J. Dynamics characterization of coupled-inductor boost dc-dc converters. In Proceedings of the 2006 IEEE Workshops on Computers in Power Electronics, Troy, NY, USA, 16–19 July 2006; pp. 264–269. [Google Scholar]
- Charef, A.; Sun, H.H.; Tsao, Y.Y.; Onaral, B. Fractal system as represented by singularity function. IEEE Trans. Autom. Control 1992, 37, 1465–1470. [Google Scholar] [CrossRef]
- Valsa, J.; Vlach, J. RC models of a constant phase element. Int. J. Circuit Theory Appl. 2013, 41, 59–67. [Google Scholar] [CrossRef]

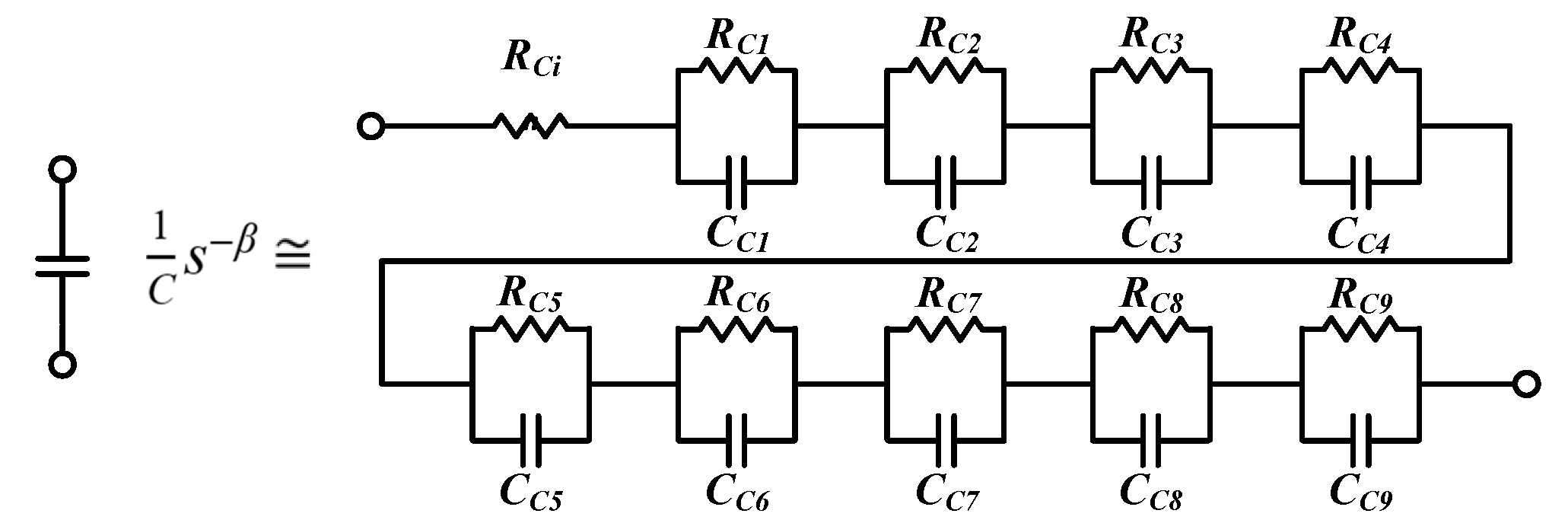







| α/β | 0.95 | 0.95 | ||
|---|---|---|---|---|
| i | RLi (Ω) | LLi (mH) | RCi (Ω) | CCi (mF) |
| in | 0.00000002 | / | 0.000000000399 | / |
| 1 | 61.875 | 0.06588 | 0.000000000504 | 0.952 |
| 2 | 0.7125 | 0.00981 | 0.00000000614 | 1.021 |
| 3 | 0.05875 | 0.01038 | 0.0000000704 | 1.176 |
| 4 | 0.00513 | 0.01175 | 0.000000804 | 1.296 |
| 5 | 0.00045 | 0.01338 | 0.00000902 | 1.492 |
| 6 | 0.00004 | 0.01513 | 0.000104 | 1.694 |
| 7 | 0.0000035 | 0.01725 | 0.00116 | 1.924 |
| 8 | 0.0000003 | 0.01951 | 0.0142 | 2.041 |
| 9 | 0.000000025 | 0.02063 | 1.24 | 0.304 |
| Parameter | Symbol | (α, β) = (1, 1) | (α, β) = (0.95, 0.95) |
|---|---|---|---|
| Maximum of inductor current | iL_max | 1.121 A | 4.204 A |
| Minimum of inductor current | iL_min | 0.274 A | 2.641 A |
| Maximum of output voltage | vo_max | 3.517 V | 3.511 V |
| Minimum of output voltage | vo_min | 3.464 V | 3.443 V |
| (α, β) | Setting Time (ms) | Overshoot (%) | Peak Time (ms) | Peak Voltage (V) |
|---|---|---|---|---|
| (1, 1) | 5.834 | 80.91 | 0.4841 | 6.241 |
| (0.95, 0.95) | 1.541 | 36.31 | 0.4811 | 4.702 |
| (α, β) = (1, 1) | (α, β) = (0.95, 0.95) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ki | A(fg) (dB) | φ(fc) (°) | fc(Hz) | State | Ki | A(fg) (dB) | φ(fc) (°) | fc (Hz) | State |
| 280 | 0.98 | 7.21 | 6251 | stable | 845 | 0.33 | 4.61 | 10,009 | stable |
| 290 | 0.68 | 4.93 | 6290 | stable | 855 | 0.24 | 3.63 | 10,080 | stable |
| 300 | 0.38 | 2.81 | 6331 | stable | 865 | 0.13 | 2.25 | 10,130 | stable |
| 310 | 0.11 | 1.24 | 6370 | stable | 875 | 0.05 | 0.74 | 10,195 | stable |
| 320 | −0.23 | −1.25 | 6408 | unstable | 885 | −0.07 | −1.12 | 10,260 | unstable |
| Variable | Signification | Value |
|---|---|---|
| Vin | Input voltage | 10 V/5 V |
| f | Switching frequency | 10 kHz |
| L | Inductance | 0.125 mH |
| C | Capacitance | 200 μF |
| R | Load resistance | 3.5 Ω/1 Ω |
| n | Transformer ratio | 1 |
| α | Inductor order | 0.95/1 |
| β | Capacitor order | 0.95/1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, Z. Fractional-Order Modeling and Nonlinear Dynamic Analysis of Forward Converter. Fractal Fract. 2024, 8, 362. https://doi.org/10.3390/fractalfract8060362
Wang X, Zhang Z. Fractional-Order Modeling and Nonlinear Dynamic Analysis of Forward Converter. Fractal and Fractional. 2024; 8(6):362. https://doi.org/10.3390/fractalfract8060362
Chicago/Turabian StyleWang, Xiaogang, and Zetian Zhang. 2024. "Fractional-Order Modeling and Nonlinear Dynamic Analysis of Forward Converter" Fractal and Fractional 8, no. 6: 362. https://doi.org/10.3390/fractalfract8060362
APA StyleWang, X., & Zhang, Z. (2024). Fractional-Order Modeling and Nonlinear Dynamic Analysis of Forward Converter. Fractal and Fractional, 8(6), 362. https://doi.org/10.3390/fractalfract8060362







