Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques
Abstract
1. Introduction
2. Review of Time-Fractional Derivative
- ;
- ;
- ;
- ;
- .
3. Methodology
The Sardar Subequation Approach
4. Method Workflow
The -Expansion Approach
5. Method Roadmap
5.1. Application
5.2. For the Sardar Subequation Method
5.3. For the Method
5.4. For Trigonometric Solutions
5.5. For Hyperbolic Solutions
5.6. For Rational Solutions
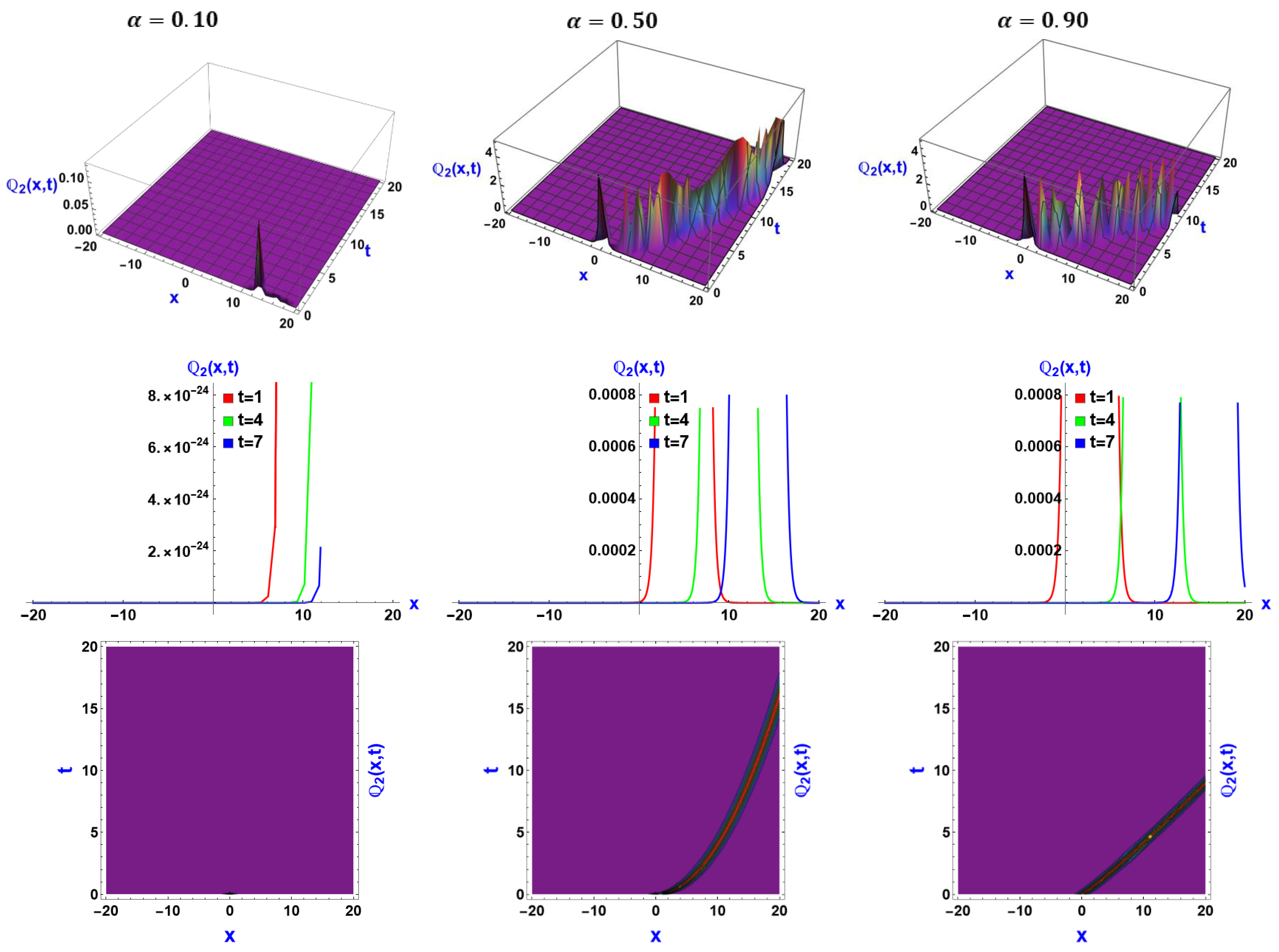
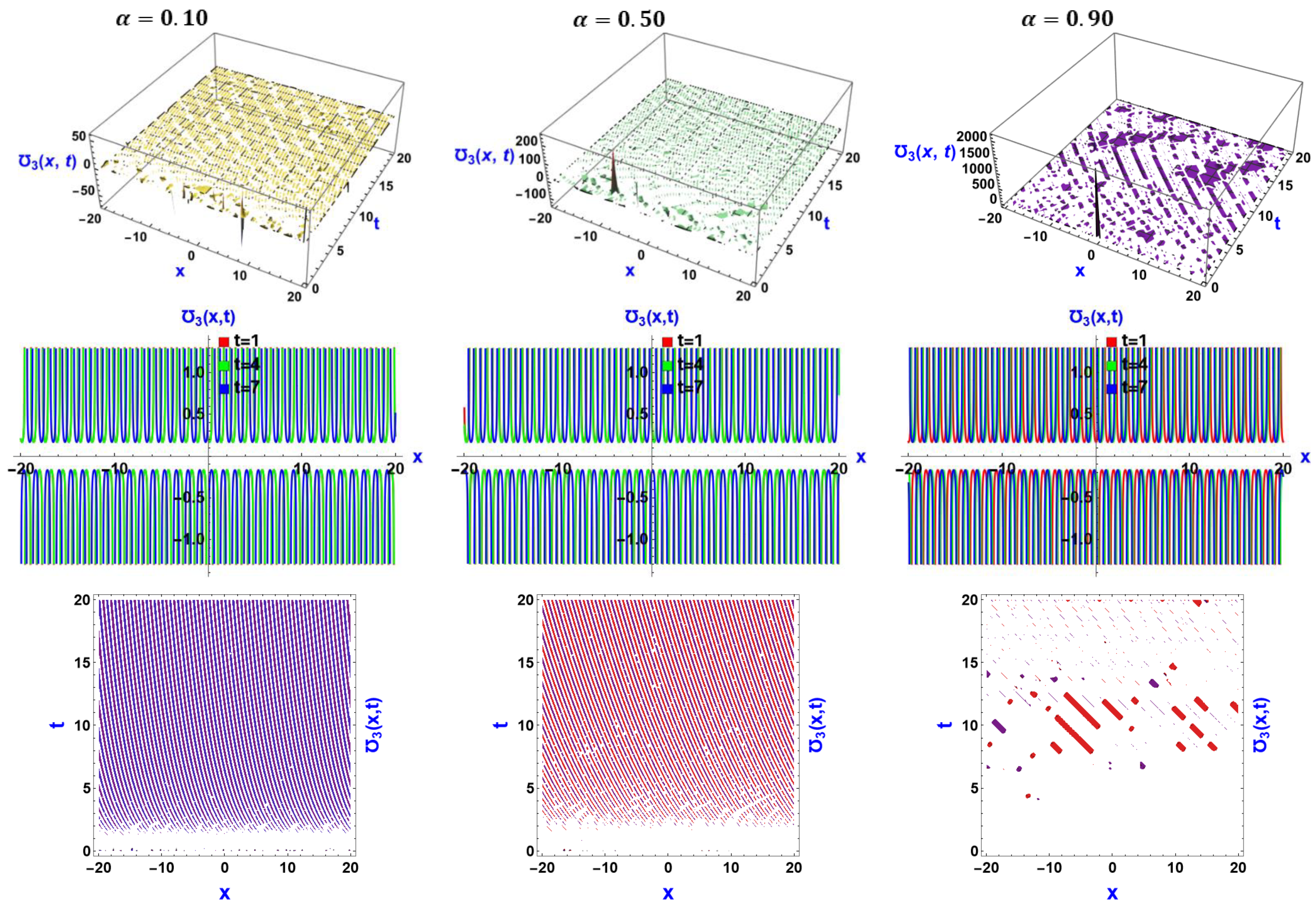
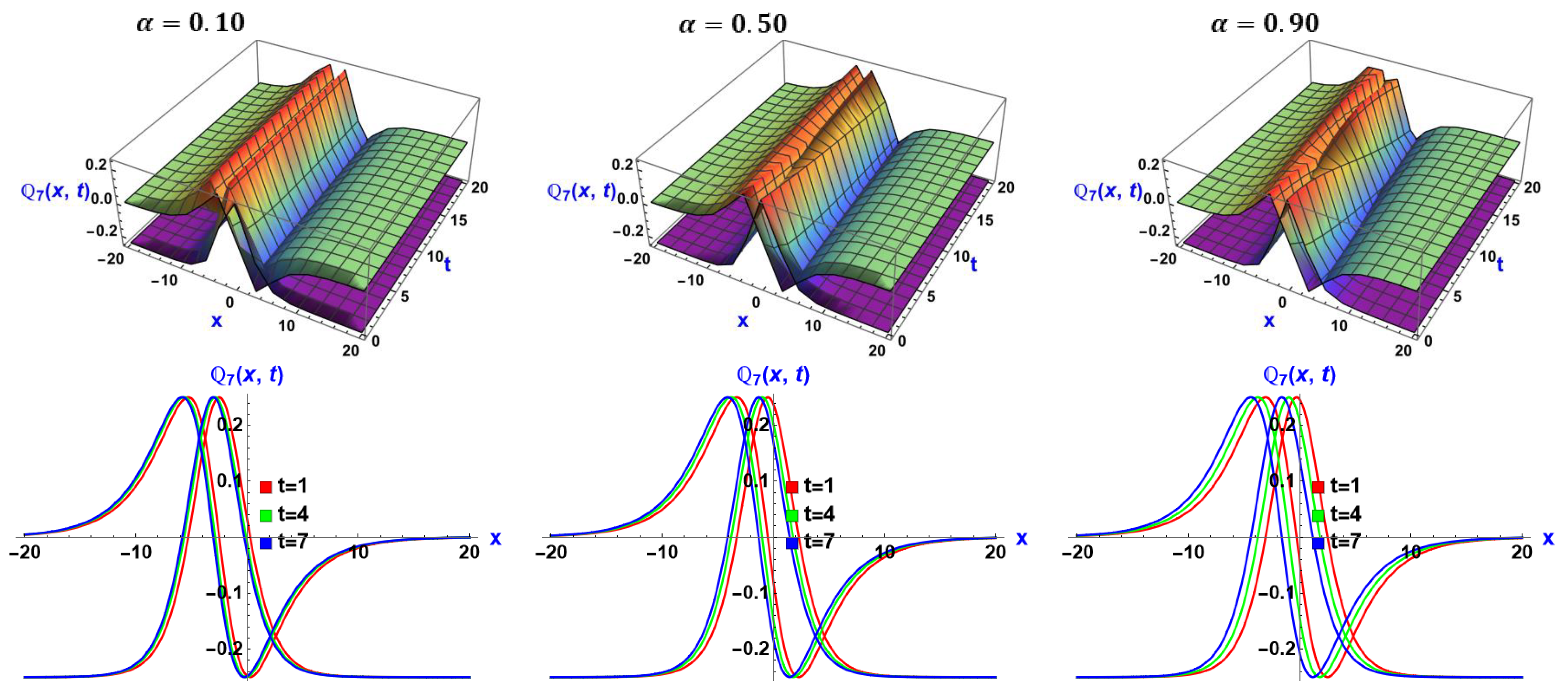
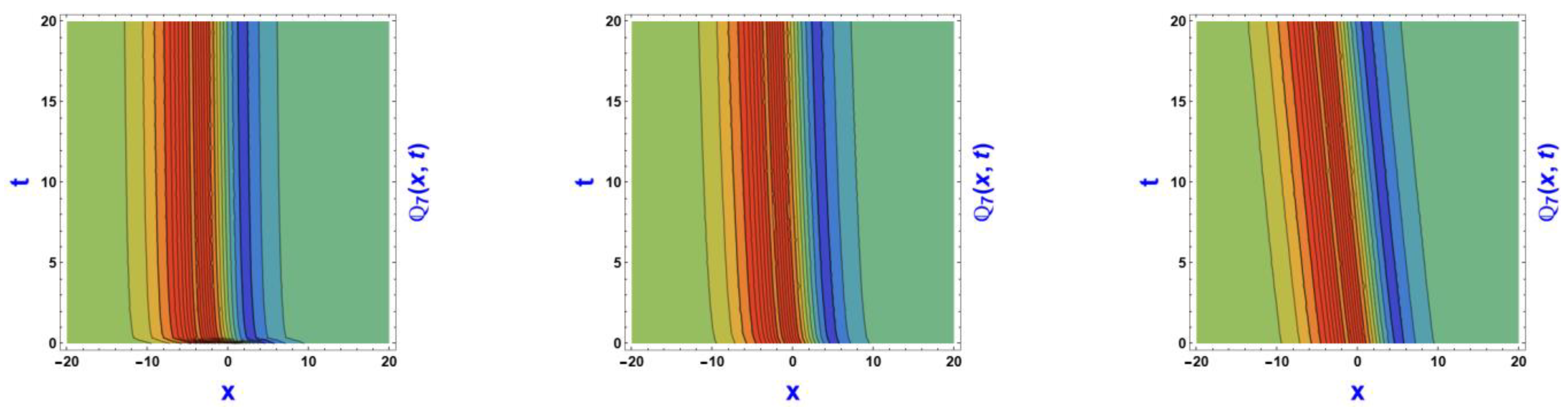
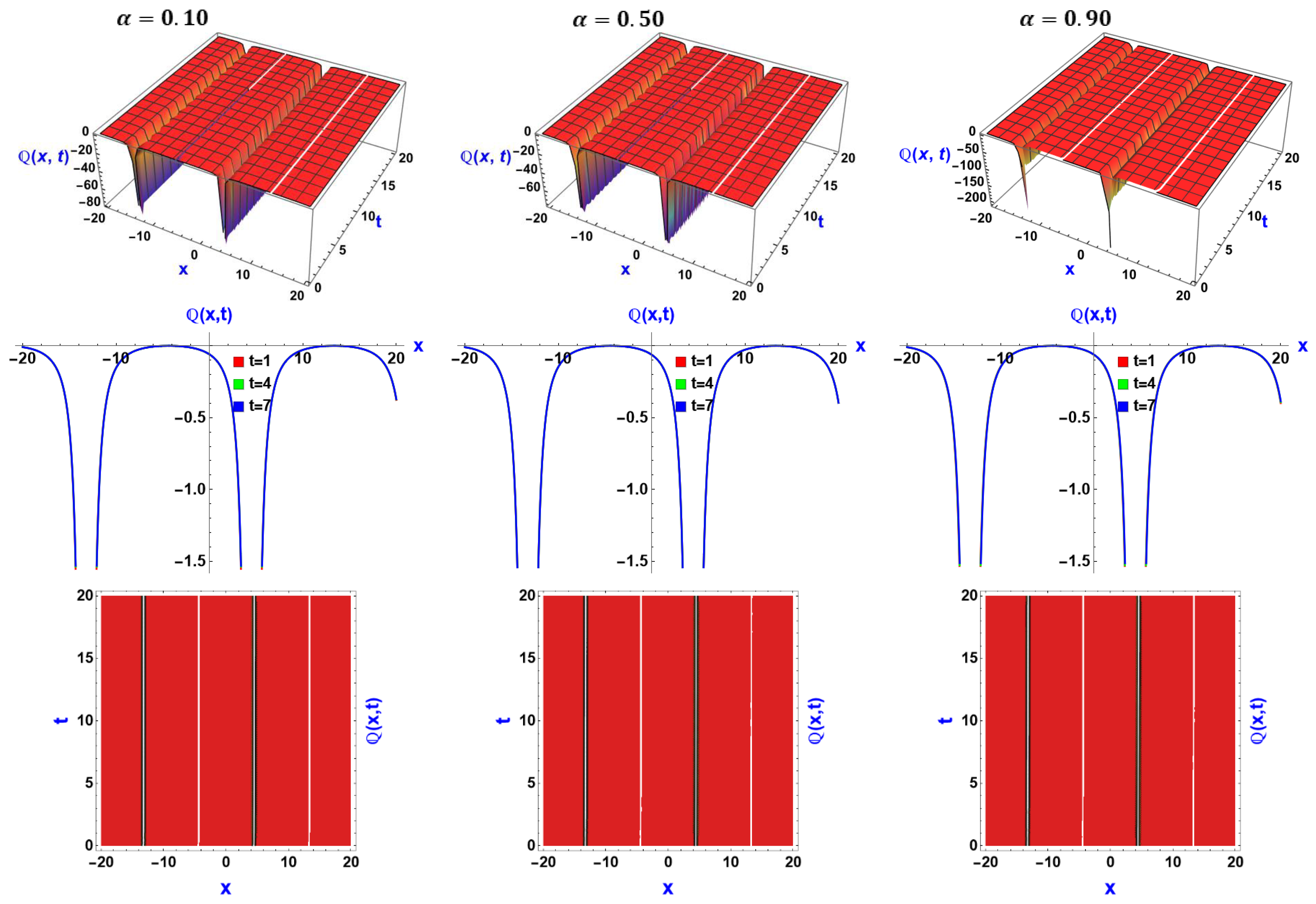
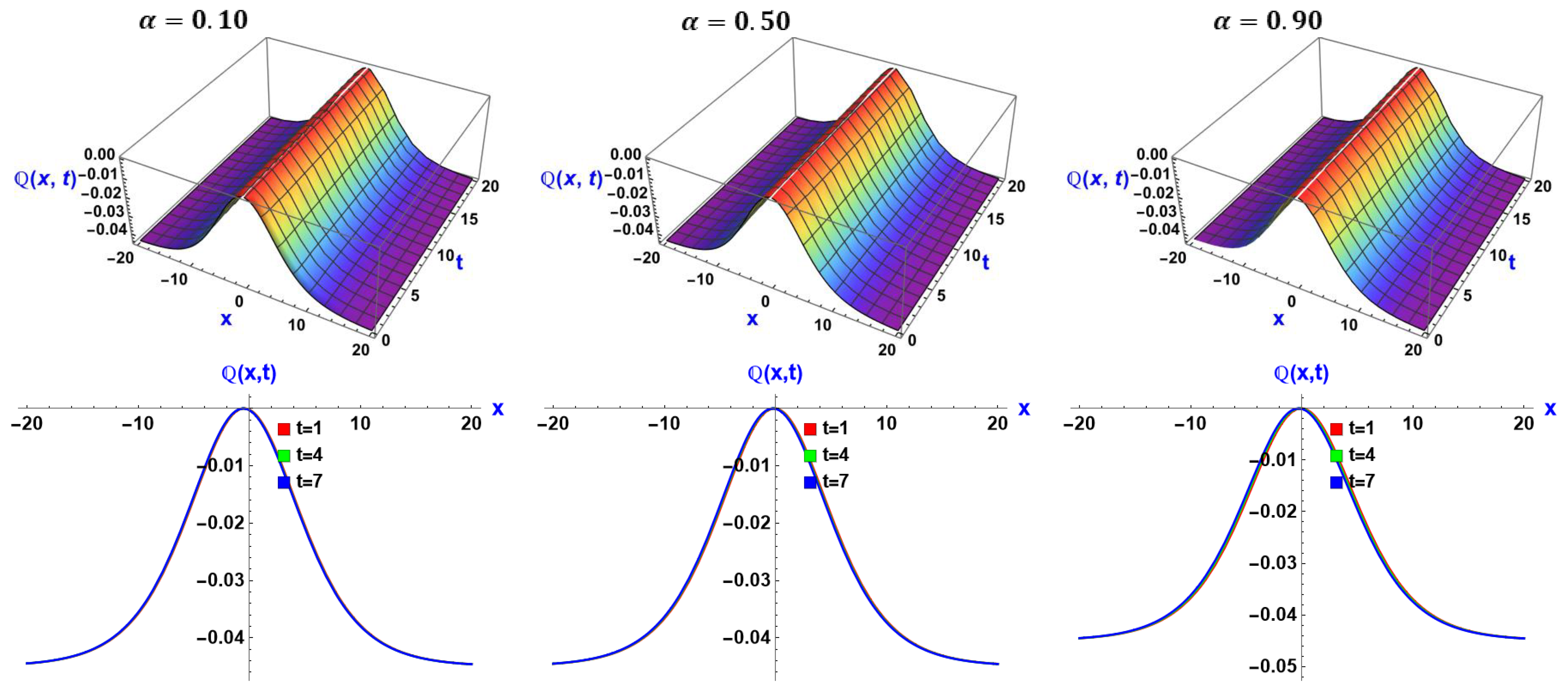
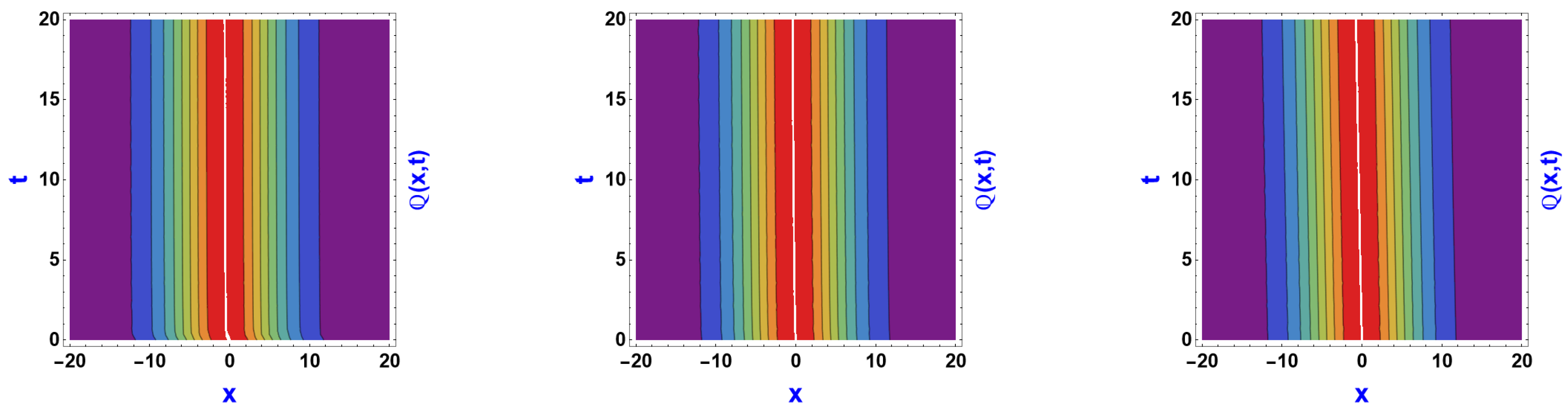
6. Visual Representation of the Exact Solutions
Discussions of the Graphs
7. Comparison
7.1. Uniformities
- i.
- Both studies center on the conformal time-fractional DSW equations, a crucial nonlinear complex model employed to analyze wave dynamics, particularly phenomena such as soliton propagation and interactions;
- ii.
- Both studies seek to derive exact solutions through analytical methods.
7.2. Variation and Uniqueness
- i.
- Reference [6] employed the modified extended tanh method (one variable) to derive exact solutions, whereas this study utilizes two efficient methods: the Sardar subequation method (one variable) and the -expansion technique (two variables);
- ii.
- While they only obtained multiple singular and bell-shaped solitons, this study includes a wider variety, such as kink, dark, multi-dark, bell-shaped, bright, multiple singular, and singular solitons;
- iii.
- This study presents a more diverse range of graphical representations, including 2D, 3D, and contour plots of exact solutions, whereas [6] utilized only 3D and density diagrams.
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
- Case I:
- For trigonometric solution:
- Case II:
- For hyperbolic solution:
- Case III:For rational solution:
References
- Khater, M.M.A. Soliton Propagation under Diffusive and Nonlinear Effects in Physical Systems; (1+1)–Dimensional MNW Integrable Equation. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2023, 480, 128945. [Google Scholar] [CrossRef]
- Chahlaoui, Y.; Ali, A.; Ahmad, J.; Hussain, R.; Javed, S. Dynamical Behavior of Optical Soliton Solutions, Time Series and Sensitivity Analysis to the Schrödinger Model with Eta Fractional Derivative. Opt. Quantum Electron. 2024, 56, 704. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Wang, H. Some Analytical Soliton Solutions of the Nonlinear Evolution Equations. J. Ocean Eng. Sci. 2022, 1–9. [Google Scholar] [CrossRef]
- Hossain, M.N.; Alsharif, F.; Miah, M.M.; Kanan, M. Abundant New Optical Soliton Solutions to the Biswas—Milovic Equation with Sensitivity Analysis for Optimization. Mathematics 2024, 12, 1585. [Google Scholar] [CrossRef]
- Noor, S.; Alshehry, A.S.; Dutt, H.M.; Nazir, R.; Khan, A.; Shah, R. Investigating the Dynamics of Time-Fractional Drinfeld–Sokolov–Wilson System through Analytical Solutions. Symmetry 2023, 15, 703. [Google Scholar] [CrossRef]
- Bashar, M.H.; Mawa, H.Z.; Biswas, A.; Rahman, M.M.; Roshid, M.M.; Islam, J. The Modified Extended Tanh Technique Ruled to Exploration of Soliton Solutions and Fractional Effects to the Time Fractional Couple Drinfel’d–Sokolov–Wilson Equation. Heliyon 2023, 9, e15662. [Google Scholar] [CrossRef]
- Ali, A.; Ahmad, J.; Javed, S. Exploring the Dynamic Nature of Soliton Solutions to the Fractional Coupled Nonlinear Schrödinger Model with Their Sensitivity Analysis. Opt. Quantum Electron. 2023, 55, 810. [Google Scholar] [CrossRef]
- Baleanu, D.; Agarwal, R.P. Fractional Calculus in the Sky. Adv. Differ. Equ. 2021, 2021, 117. [Google Scholar] [CrossRef]
- Shahzad, M.U.; Rehman, H.U.; Awan, A.U.; Zafar, Z.; Hassan, A.M.; Iqbal, I. Analysis of the Exact Solutions of Nonlinear Coupled Drinfeld–Sokolov–Wilson Equation through Φ^6-Model Expansion Method. Results Phys. 2023, 52, 106771. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Y.; Wei, L.; Guan, B. Exact Solutions to Fractional Drinfel’d–Sokolov–Wilson Equations. Chin. J. Phys. 2018, 56, 708–720. [Google Scholar] [CrossRef]
- Shakeel, M.; AlQahtani, S.A.; Rehman, M.J.U.; Kudra, G.; Awrejcewicz, J.; Alawwad, A.M.; A.Alotaibi, A.; Safran, M. Construction of Diverse Water Wave Structures for Coupled Nonlinear Fractional Drinfel’d-Sokolov-Wilson Model with Beta Derivative and Its Modulus Instability. Sci. Rep. 2023, 13, 17528. [Google Scholar] [CrossRef] [PubMed]
- Kawser, M.A.; Ali Akbar, M.; Khan, M.A.; Ghazwan, H.A. Exact Soliton Solutions and the Signifcance of Time-dependent Coefcients in the Boussinesq Equation: Theory and Application in Mathematical Physics. Sci. Rep. 2024, 14, 762. [Google Scholar] [CrossRef] [PubMed]
- Borhan, J.R.M.; Ganie, A.H.; Miah, M.M.; Iqbal, M.A.; Seadawy, A.R.; Mishra, N.K. A Highly Effective Analytical Approach to Innovate the Novel Closed Form Soliton Solutions of the Kadomtsev–Petviashivili Equations with Applications. Opt. Quantum Electron. 2024, 56, 938. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Miah, M.M.; Rasid, M.M.; Alshehri, H.M.; Osman, M.S. An Investigation of Two Integro-Differential KP Hierarchy Equations to Find out Closed Form Solitons in Mathematical Physics. Arab J. Basic Appl. Sci. 2023, 30, 535–545. [Google Scholar] [CrossRef]
- Ma, W.X. N-Soliton Solutions and the Hirota Conditions in (1 + 1)-Dimensions. Int. J. Nonlinear Sci. Numer. Simul. 2022, 23, 123–133. [Google Scholar] [CrossRef]
- Yomba, E. The General Projective Riccati Equations Method and Exact Solutions for a Class of Nonlinear Partial Differential Equations. Chin. J. Phys. 2005, 43, 991–1003. [Google Scholar]
- Jafari, H.; Kadkhoda, N.; Baleanu, D. Fractional Lie Group Method of the Time-Fractional Boussinesq Equation. Nonlinear Dyn. 2015, 81, 1569–1574. [Google Scholar] [CrossRef]
- Zafar, A.; Raheel, M.; Ali, K.K.; Razzaq, W. On Optical Soliton Solutions of New Hamiltonian Amplitude Equation via Jacobi Elliptic Functions. Eur. Phys. J. Plus 2020, 135, 674. [Google Scholar] [CrossRef]
- Khan, M.A.U.; Akram, G.; Sadaf, M. Dynamics of Novel Exact Soliton Solutions of Concatenation Model Using Efective Techniques. Opt. Quantum Electron. 2024, 56, 385. [Google Scholar] [CrossRef]
- Babajanov, B.; Abdikarimov, F. The Application of the Functional Variable Method for Solving the Loaded Non-Linear Evaluation Equations. Front. Appl. Math. Stat. 2022, 8, 912674. [Google Scholar] [CrossRef]
- Ma, W.X.; Zhu, Z. Solving the (3 + 1)-Dimensional Generalized KP and BKP Equations by the Multiple Exp-Function Algorithm. Appl. Math. Comput. 2012, 218, 11871–11879. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Arafat, S.M.Y.; Wang, H. Abundant Closed-Form Wave Solutions to the Simplified Modified Camassa-Holm Equation. J. Ocean Eng. Sci. 2023, 8, 238–245. [Google Scholar] [CrossRef]
- Fan, E. Extended Tanh-Function Method and Its Applications to Nonlinear Equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Nofal, T.A. Simple Equation Method for Nonlinear Partial Differential Equations and Its Applications. J. Egypt. Math. Soc. 2016, 24, 204–209. [Google Scholar] [CrossRef]
- Kumar, A.; Pankaj, R.D. Tanh–Coth Scheme for Traveling Wave Solutions for Nonlinear Wave Interaction Model. J. Egypt. Math. Soc. 2015, 23, 282–285. [Google Scholar] [CrossRef]
- Habib, M.A.; Ali, H.M.S.; Miah, M.M.; Akbar, M.A. The Generalized Kudryashov Method for New Closed Form Traveling Wave Solutions to Some NLEEs. AIMS Math. 2019, 4, 896–909. [Google Scholar] [CrossRef]
- Fokas, A.S.; Lenells, J. The Unified Method: I. Nonlinearizable Problems on the Half-Line. J. Phys. A Math. Theor. 2012, 45, 195201. [Google Scholar] [CrossRef]
- Santillana, M.; Dawson, C. A Numerical Approach to Study the Properties of Solutions of the Diffusive Wave Approximation of the Shallow Water Equations. Comput. Geosci. 2010, 14, 31–53. [Google Scholar] [CrossRef]
- Ren, B.; Lou, Z.M.; Liang, Z.F.; Tang, X.Y. Nonlocal Symmetry and Explicit Solutions for Drinfel’d-Sokolov-Wilson System. Eur. Phys. J. Plus 2016, 131, 441. [Google Scholar] [CrossRef]
- Zhao, X.Q.; Zhi, H.Y. An Improved F-Expansion Method and Its Application to Coupled Drinfel’d-Sokolov-Wilson Equation. Commun. Theor. Phys. 2008, 50, 309–314. [Google Scholar] [CrossRef]
- Sahoo, S.; Ray, S.S. New Double-Periodic Solutions of Fractional Drinfeld–Sokolov–Wilson Equation in Shallow Water Waves. Nonlinear Dyn. 2017, 88, 1869–1882. [Google Scholar] [CrossRef]
- Inc, M. On Numerical Doubly Periodic Wave Solutions of the Coupled Drinfel’d-Sokolov-Wilson Equation by the Decomposition Method. Appl. Math. Comput. 2006, 172, 421–430. [Google Scholar] [CrossRef]
- Rehman, H.U.; Habib, A.; Ali, K.; Awan, A.U. Study of Langmuir Waves for Zakharov Equation Using Sardar Sub-Equation Method. Int. J. Nonlinear Anal. Appl. 2023, 14, 9–18. [Google Scholar]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New Exact Solutions of (3+1)-Dimensional Modified KdV-Zakharov-Kuznetsov Equation by Sardar-Subequation Method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New Solitary Wave Solutions for Variants of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony Equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Rehman, H.U.; Iqbal, I.; Subhi Aiadi, S.; Mlaiki, N.; Saleem, M.S. Soliton Solutions of Klein–Fock–Gordon Equation Using Sardar Subequation Method. Mathematics 2022, 10, 3377. [Google Scholar] [CrossRef]
- Ibrahim, S.; Ashir, A.M.; Sabawi, Y.A.; Baleanu, D. Realization of Optical Solitons from Nonlinear Schrödinger Equation Using Modified Sardar Sub-Equation Technique. Opt. Quantum Electron. 2023, 55, 617. [Google Scholar] [CrossRef]
- Cinar, M.; Secer, A.; Ozisik, M.; Bayram, M. Derivation of Optical Solitons of Dimensionless Fokas-Lenells Equation with Perturbation Term Using Sardar Sub-Equation Method. Opt. Quantum Electron. 2022, 54, 402. [Google Scholar] [CrossRef]
- Sadaf, M.; Arshed, S.; Ghazala Akram, I. Exact Soliton and Solitary Wave Solutions to the Fokas System Using Two Variables (G′/G,1/G)-Expansion Technique and Generalized Projective Riccati Equation Method. Opt.-Int. J. Light Electron Opt. 2022, 268, 169713. [Google Scholar] [CrossRef]
- Vivas-Cortez, M.; Akram, G.; Sadaf, M.; Arshed, S.; Rehan, K.; Farooq, K. Traveling Wave Behavior of New (2+1)-Dimensional Combined KdV–MKdV Equation. Results Phys. 2023, 45, 106244. [Google Scholar] [CrossRef]
- Miah, M.M.; Ali, H.M.S.; Akbar, M.A.; Wazwaz, A.M. Some Applications of the (G’/G, 1/G)-Expansion Method to Find New Exact Solutions of NLEEs. Eur. Phys. J. Plus 2017, 132, 252. [Google Scholar] [CrossRef]
- Sirisubtawee, S.; Koonprasert, S.; Sungnul, S. Some Applications of the (G’/G, 1/G)-Expansion Method for Finding Exact Traveling Wave Solutions of Nonlinear Fractional Evolution Equations. Symmetry 2019, 11, 952. [Google Scholar] [CrossRef]
- Rasid, M.M.; Miah, M.M.; Ganie, A.H.; Alshehri, H.M.; Osman, M.S.; Ma, W.X. Further Advanced Investigation of the Complex Hirota-Dynamical Model to Extract Soliton Solutions. Mod. Phys. Lett. B 2023, 38, 2450074. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Duraihem, F.Z.; Rehman, S. Stability, Modulation Instability, and Analytical Study of the Confirmable Time Fractional Westervelt Equation and the Wazwaz Kaur Boussinesq Equation. Opt. Quantum Electron. 2024, 56, 948. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Hamid, A.; Osman, G.M.S. Discovering New Abundant Optical Solutions for the Resonant Nonlinear Schrödinger Equation Using an Analytical Technique. Opt. Quantum Electron. 2024, 56, 847. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A New Definition of Fractional Derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Conformable Fractional Calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hossain, M.N.; Miah, M.M.; Alosaimi, M.; Alsharif, F.; Kanan, M. Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques. Fractal Fract. 2024, 8, 352. https://doi.org/10.3390/fractalfract8060352
Hossain MN, Miah MM, Alosaimi M, Alsharif F, Kanan M. Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques. Fractal and Fractional. 2024; 8(6):352. https://doi.org/10.3390/fractalfract8060352
Chicago/Turabian StyleHossain, Md Nur, M. Mamun Miah, Moataz Alosaimi, Faisal Alsharif, and Mohammad Kanan. 2024. "Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques" Fractal and Fractional 8, no. 6: 352. https://doi.org/10.3390/fractalfract8060352
APA StyleHossain, M. N., Miah, M. M., Alosaimi, M., Alsharif, F., & Kanan, M. (2024). Exploring Novel Soliton Solutions to the Time-Fractional Coupled Drinfel’d–Sokolov–Wilson Equation in Industrial Engineering Using Two Efficient Techniques. Fractal and Fractional, 8(6), 352. https://doi.org/10.3390/fractalfract8060352





