Abstract
An essential mathematical structure that demonstrates the nonlinear short-wave movement across the ferromagnetic materials having zero conductivity in an exterior region is known as the fractional stochastic Kraenkel–Manna–Merle system. In this article, we extract abundant wave structure closed-form soliton solutions to the fractional stochastic Kraenkel–Manna–Merle system with some important analyses, such as bifurcation analysis, chaotic behaviors, sensitivity, and modulation instability. This fractional system renders a substantial impact on signal transmission, information systems, control theory, condensed matter physics, dynamics of chemical reactions, optical fiber communication, electromagnetism, image analysis, species coexistence, speech recognition, financial market behavior, etc. The Sardar sub-equation approach was implemented to generate several genuine innovative closed-form soliton solutions. Additionally, phase portraiture of bifurcation analysis, chaotic behaviors, sensitivity, and modulation instability were employed to monitor the qualitative characteristics of the dynamical system. A certain number of the accumulated outcomes were graphed, including singular shape, kink-shaped, soliton-shaped, and dark kink-shaped soliton in terms of 3D and contour plots to better understand the physical mechanisms of fractional system. The results show that the proposed methodology with analysis in comparison with the other methods is very structured, simple, and extremely successful in analyzing the behavior of nonlinear evolution equations in the field of fractional PDEs. Assessments from this study can be utilized to provide theoretical advice for improving the fidelity and efficiency of soliton dissemination.
1. Introduction
Most of the procedures on the planet have many nonlinear phenomena and oscillating parameters. Nonlinear partial differential equations (NLPDEs) have been utilized to define real-world natural problems. Fractional calculus is a branch of mathematical analysis that generalizes the concepts of differentiation and integration to non-integer orders. The roots of fractional calculus can be traced back to the work of mathematicians like Leibniz, Euler, and Laplace. However, the modern development of fractional calculus gained momentum in the 19th century with the works of Liouville, Riemann, and others. There are various definitions of fractional derivatives and integrals, such as Riemann–Liouville, Grünwald–Letnikov, Caputo, conformable fractional derivative, and others, each with its own properties and applications [1,2,3]. Fractional calculus has found applications in numerous fields, including physics, engineering, signal processing, control theory, signal transmission, chemical kinematics, finance, biology, viscoelastic materials and complex fluids, anomalous diffusion phenomena, electromagnetic, nano-technology, flat wave propagation, caustic wave in crystals, digital communication, optical fibers, and more. A subclass of fractional partial differential equations known as stochastic fractional partial differential equations (SFPDEs) is a strong mathematical foundation with a wide range of potential uses in scientific and technical disciplines. The outcomes of these SFPDEs provide additional understanding of the physical challenge by illuminating the evolution features of real-life complications. A new avenue for research into systems that seem wave-like in nature is opened up by the notion of soliton. For deeper consideration of nonlinear occurrence and realistic challenges, it is essential to discover closed-form soliton solutions of SFPDEs. According to the quick advancements in nonlinear sciences, a variety of simple and efficient approaches have been developed to obtain closed-form soliton solutions to NLPDEs, including the Hirota method [4,5], the Bernoulli sub-equation method [6,7], the F-expansion method [8], the (/)-expansion method [9], the simple equation method [10], the modified auxiliary equation method [11,12], the two variable (/, 1/)-expansion method [13,14,15,16], the Lie symmetric analysis [17], the polynomial complete discriminant system [18], the tanh-coth scheme [19], the Conservation laws method [20], the generalized exponential rational function approach [21,22], the binary bell polynomials method [23], the mapping method [24], the Shehu transform scheme [25], the sine–Gordon expansion [26], the Cole–Hopf transformation method [27,28], the Fan sub-equation technique [29], the unified method [30], the Khater method [31], the r + mEDAM method [32], the spectral Tau method [33], the -expansion procedure [34,35,36,37,38], the sub-equation method [39], the collocation method [40], the finite element method [41], and the generalized -expansion method [42], and there may be enough others. In an earlier investigation, [13] pursued the two expansion algorithms to identify the rational, trigonometric, and hyperbolic solitary wave solutions for the fractional-order Hirota–Satsuma-coupled KdV system, which is highly beneficial for the field of analysis. Numerous features of this system have been studied in these investigations; in addition, multiple uses rely on it as well. A few years ago, Chen et al. [43] examined the periodic travelling waves of the modified KdV equation and rogue waves on the periodic background by implementing an algebraic method. Very recently, in [44], wave patterns were established for the discontinuous initial value problem to the generalized Gerdjikov–Ivanov equation by operating Whitham modulation. Lately, Iqbal et al. [38] applied the -expansion procedure most recently to analyze the fractional order (4 + 1)-dimensional Fokas equation and the fractional order (2 + 1)-dimensional breaking soliton equation to calculate the closed-form solutions that are better suited for nonlinear science. One of the most recently invented methods established in this area is the Sardar sub-equation procedure. The majority of fractional NLPDEs can be solved quickly and easily with this innovative approach, which is regarded as one of the most contemporary and comprehensive approaches in this field. A few years back, Rezazadeh et al. [45] produced some novel exact solutions to the (3 + 1)-dimensional Wazwaz–Benjamin–Bona–Mahony equations by effectively applying the Sardar sub-equation procedure. Employing the proposed method, ref. [46] quite recently achieved the soliton solutions of the M-truncated paraxial wave equation. Scholars have proven the usefulness of the suggested method and expressed an attraction to understanding this nonlinear phenomenon scientifically. Very recently, Yasin et al. [47], discover the closed-form solutions of the (3 + 1)-dimensional modified KdV–Zakharov–Kuznetsov equation with the aid of the suggested technique. The Kraenkel–Manna–Merle system (KMMS) refers to a specific nonlinear dynamical system proposed by Kraenkel, Manna, and Merle [48]. The fractional stochastic Kraenkel–Manna–Merle system (FSKMMS) is a mathematical model that combines elements of fractional calculus, stochastic processes, and nonlinear dynamics. The FSKMMS likely incorporates nonlinear dynamics to capture the intricate interactions between different components or variables within the system. It also represents an interdisciplinary approach to understanding the dynamics of systems with memory effects, randomness, and nonlinear interactions. It is commonly recognized that the electromagnetic wave propagation problem in ordered magnetic materials, particularly in a ferromagnetic medium, becomes extremely nonlinear. The FSKMMS demonstrates exactly how nonlinear short waves spread in an external domain across ferromagnetic materials that have zero conductivity. Over the past few decades, there have been a lot of fascinating studies on ferromagnetic materials because of the enormous advancements in information technology to address the requirement for massive data as well as high-density storage. Gaining more insight into the unique properties of micro- and super-microstructures in nanoscale ferrous metals is indispensable. Typically, it is exceptionally challenging for FSKMMS to retrieve closed-form soliton solutions. Our recommended strategy can be used to solve most of the fractional NLPDEs, including FSKMMS, quickly and effectively without abandoning its generality. The FSKMMS has not yet been inspected using the aforementioned approach, to the best of our collective understanding. Considering the foregoing arguments, the intention of the present study was to implement the Sardar sub-equation strategy to determine the closed-form soliton solutions of the FSKMMS including the damping effect . Utilizing the above-mentioned approach, certain innovative solutions to trigonometric, exponential, and rational functions have already been established, which are novel in the research. Andrew Kay invented nonlinear systems in 1952. Analysis of phase profiles of bifurcation, sensitivity, stability, and modulation instability is being used in nonlinear physical models more and more in recent decades [49,50,51,52,53]. In dynamical systems theory, bifurcation analysis, which includes phase portraiture, is a method for examining how a system’s behavior varies with changes in parameters. This framework provides a useful mathematical basis for examining physical events in relation to classical mechanics. The relative significance of various inputs or factors in causing the variability of model results is revealed by sensitivity analysis. Using the Runge–Kutta method, we performed a thorough sensitivity analysis of the dynamical system. A basic idea in many domains of signal processing, control, and systems engineering is stability analysis. It is frequently associated with identifying the behavior of dynamic systems in the natural world, which can be mechanical, electrical, or chemical. Here, we analyzed the dynamical system’s stability. This also addresses the investigated system’s modulation instability analysis, which had not been reported before for that system. Scientists will find enormous utility in the solutions along with the several analysis provided, as they provide vital insights into pertinent physical phenomena. Meanwhile, we display the acquired figures to demonstrate the numerous diverse wave natures, which are highly beneficial for learning deeper about fractional NLDPEs.
This research’s succeeding segments are organized as follows: Section 2 incorporates an extensive description and analysis of the preferred procedure alongside amenities. The inflictions of the elected technique are explored in Section 3. Diverse analyses are examined in Section 4. Section 5 conveys a visual depiction together with a rationalization of the findings. The conclusions are laid out in Section 6.
2. Standard Process of the Methodology and Amenities
2.1. Brownian Motion
The Brownian motion has a stochastic process and accomplishes the subsequent specification:
- ;
- is continuous for ;
- is independent for ;
- Anormal distribution is exhibited by with mean as well as variance .
2.2. Fractional Derivative and Its Feature
A fractional derivative is a generalization of the concept of a derivative to non-integer orders. While the traditional derivative represents the rate of change of a function with respect to a variable, fractional derivatives extend this notion to allow for non-integer orders of differentiation. Researchers have been exploring multiple versions of fractional derivatives over the years. Contributions by Riesz, Marchaud, Kober, Riemann–Liouville, Erdelyi, Hadamard, Grunwald–Letnikov, and Caputo have become the most recognized. A new fractional derivative categorized as the conformable derivative was just recently discovered by Mohammed et al. [24]. The concept of the conformable derivative seems natural and covers most of the requirements of the classical integral derivative, such as the vanishing derivatives for constant functions, the mean value theorem, the Rolle’s theorem, the chain rule, the power rule, linearity, and the quotient and product rules. It has advantages for modeling a wide range of real-world phenomena, as differential equations with conformable derivatives are easier to solve numerically than those with Riemann–Liouville or Caputo fractional derivatives.
Now, for , the conformable derivative of is expressed as follows:
If we take into consideration that are differentiable and δ-differentiable functions, then the conformable derivative preserves each of the following features:
- ;
- ;
- ;
- ;
- .
Here, and stand for constants.
2.3. Methodology
This segment includes a description of the suggested method’s step-by-step workflow, which was established to produce innovative traveling wave solutions for noteworthy NLPDEs in fractional form. Say an address of a nonspecific fractional NLPDEs involving self-governing variables with is accomplished:
Wherever is an unexplained function, a polynomial in and its fractional derivative are represented by . The succeeding phases in the foregoing advance:
Phase 1: Think about a fresh variable that is the combination of all the self-regulating variables as well as :
in which stands for nonzero constants. Operating Equation (3), we may make Equation (2) into an ordinary differential equation (ODE):
At this point, symbolizes a polynomial of together with its several ordinary derivatives with the aid of the self-regulating variable .
Phase 2: The arrangement shown below is able to build the solution of Equation (4):
The homogeneous balancing principle may have been used for determining . However, the coefficients are easily calculated by solving a set of algebraic equations resulting from suggested approach. Moreover, maintains the subsequent ODE:
where remain real constants. After resolving Equation (6), we discover the following subsequent possible outcomes:
Scenario 1: When and ,
herein, .
Scenario 2: When and ,
here, .
Scenario 3: When and ,
in which .
Scenario 4: When and ,
in which .
Phase 3: The polynomial of is now easily obtained by applying Equation (5) in Equation (4) together with Equation (6), and the algebraic equations for might be generated by adjusting the coefficient to zero. Upon completion all of these algebraic calculations, we quickly discover the necessary solutions to the provided fractional NLPDEs by exchanging the values of .
3. Application of the Method
This component focuses on how the Sardar sub-equation approach has been implemented to generate the newer, broadly applicable closed-form traveling wave solutions for fractional NLPDEs. The fractional stochastic Kraenkel–Manna–Merle system refers to an exclusive nonlinear dynamical system suggested by Kraenkel, Manna, and Merle. Soon after, this structure underwent extensive investigation in relation to information systems, signal processing, control systems, condensed matter physics, climate system modeling, optical fiber communication, chaotic systems, electromagnetism, signal processing, fluid dynamics, porous media, coastal engineering, epidemiology, microelectronics, biological systems, financial markets, chemical reactions, and ecological systems. It is an adaptable tool for modeling and analyzing a wide range of systems in science, engineering, finance, and other fields because of its multifaceted character and capacity to accurately represents challenging phenomena. So, the fractional stochastic Kraenkel–Manna–Merle system is represented here [24,32]:
where endures the magnetization, and the external magnetic fields symbolized by are associated to ferrite; characterizes the conformal derivative operator ; corresponds to the damping coefficient, the noise intensity denoted by ; and symbolizes Brownian motion. After exploiting the value for together with in the aforementioned equation, we discover the following equation:
The above description incorporates short-wave nonlinear propagation in zero conductivity saturated in ferromagnetic material. Equation (8) exhibits Lax pairings and becomes integrable when damping is abolished ( = 0).
To determine the wave equation of the fractional stochastic Kraenkel–Manna–Merle system, we assume the damping effect along with the provided following wave transformation:
where are real functions, and and are nonzero constants. The following is noted:
where the Ito correction term is represented by . Applying Equation (9) in Equation (7) together with Equation (10), we determine the following:
Evaluating expectations for each side of the above Equation (11), we develop the following:
Here, is situated for normal standard distribution along side , with the aid of these concepts Equation (12) altered as given below:
If we integrate once to the second member of the Equation (13), we attain the following:
where means integrating constant. Utilizing Equation (14) to the first member of Equation (13), we obtain the following:
Here, the homogeneous balance process supplies us . So, the Equation (5) can be written as given below:
After a successful calculation, we obtain the value of constants :
In concern to the constants directly above, the soliton solutions are as follows:
Scenario-1: When and ,
At the moment of employing the modification in Equation (9) to Equation (17) on or after (20), linking and operates the solutions of Equation (7).
where represents the noise intensity, and and are nonzero constants.
Scenario-2: When and ,
In a similar fashion, using the change in Equation (9) to Equation (25) on or after Equation (28), relating and , we can carry out the solutions of Equation (7).
Scenario 3: When and ,
In a similar fashion, we can determine from the Equation (33) to Equation (35) along with Equation (14), which was omitted for avoiding complication of calculation. Now, applying the conversion in Equation (9) to all the and , we can drive the solutions of Equation (7).
Scenario 4: When and ,
Likewise, can be found from the Equation (40) through Equation (42) together with Equation (14), which was left out in order to simplify the computation. Here, we can use the modification in Equation (9) to all the and to construct the solutions of Equation (7).
4. Diverse Analyses Concerning to the Fractional Equation
Bifurcation analysis, chaotic behaviors, sensitivity, and modulation instability analysis for the Equation (15) are explored in detail in the following paragraphs.
4.1. Bifurcation Analysis
Bifurcation analysis, comprising phase portraits, is a technique used in dynamical systems theory to study how the behavior of a system changes as parameters are varied. In essence, it examines the points at which a system undergoes qualitative changes in its behavior. It has applications across various fields, including physics, biology, chemistry, economics, and engineering. It also helps understand phenomena such as phase transitions, population dynamics, chemical reactions, and electronic circuits. Firstly, we generate a dynamical system from Equation (15) by means of the Galilean transformation. This dynamical system offers an effective mathematical foundation for analyzing physical phenomena within the context of classical mechanics.
where . Now, the Hamiltonian function for the Equation (43) might be represented by
here, is situated for Hamiltonian constant. We have the following dynamical system:
to calculate the equilibrium points of Equation (43). The equilibrium points of the above dynamical system are . The Jacobian of the system in Equation (43) is as follows:
Planar dynamical systems theory reveals the following to us:
- The equilibrium position represents a saddle point, when ;
- The equilibrium position denotes a center point, when ;
- The equilibrium position signifies a cuspid point, when .
The content that follows is a list of possible outcomes that can be obtained through modifying the relevant parameters.
- Instance 1: and .
Considering the particular values for the parameters , we observed that the equilibrium position represents a saddle point, which is exhibited in Figure 1a.
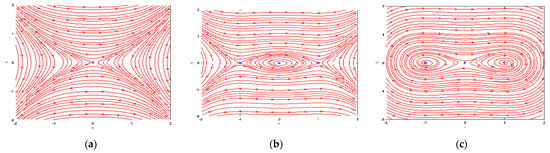
Figure 1.
Bifurcation analysis of the proposed system with different state for and along with several values of the parameters: for (a) , (b), , and (c) .
- Instance 2: and .
By selecting the fixed value of the parameters , we detect that the equilibrium position stands for a center point, and equilibrium position together with stand for saddle points, which is displayed in Figure 1b.
- Instance 3: and .
After choosing the definite value of the parameters , we notice that the equilibrium position represents a saddle point, and equilibrium position together with represent center points, which is shown in Figure 1c.
4.2. Chaotic Nature of the Dynamic System
In chaotic systems, small variations in input can lead to drastically different outcomes in which nonlinear dynamics clarifies ostensibly arbitrary behavior in these systems. To explore the chaotic nature, we augment a perturbed term in the planar dynamical systems that yields us the subsequent dynamical system:
where and stand for the amplitude and frequency of the dynamical system in Equation (44). The impact of the perturbed term on the dynamic structure stated above is analyzed in the subsequent figures. In this instance, we identify the chaotic nature of the recommended dynamical system and illustrate the phase portraits of this system for several values of the parameters: in Figure 2a, ; Figure 2b, ; Figure 2c, ; Figure 3a, ; Figure 3b, ; Figure 3c, ; Figure 4a, ; Figure 4b, ; and Figure 4c, . Upon examining the provided figures, we observe highly complex and attractive behaviors. We detect the ringlet dynamics in Figure 2a,b and Figure 4a,c, besides those in Figure 2c and Figure 4b; we also see the complex dynamics. In a similar way, one can observe the periodic nature in Figure 3a as well as Figure 3b together with Figure 3c, which show the surprising periodic nature. This improved conception of the system’s sensitivity to fluctuations in parameters aid us in accomplishing the complex interactions among the frequency , the perturbation term, as well the dynamics of the system. The inference from this analysis allows us to launch a strong and progressive mathematical structure.
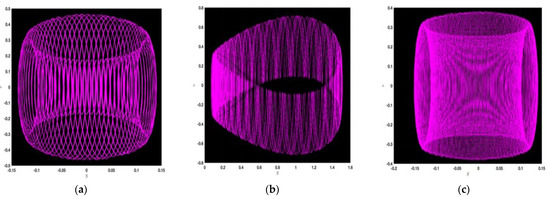
Figure 2.
Chaotic nature of the dynamical system for the values (a) , (b) , and (c) .

Figure 3.
Chaotic nature of the dynamical system for arbitrary values (a) , (b) , and (c) .

Figure 4.
Chaotic nature of the dynamical system for the values, (a) , (b) , and (c) .
4.3. Sensitivity Analysis of the Dynamic System
Sensitivity analysis offers insights into the comparative importance of different inputs or parameters in driving the changeability of model aftereffects. It is a precious tool for understanding the behavior of complex systems, advancing model accuracy, and making informed decisions in the face of ambiguity. Sensitivity analysis is extensively used in several fields, together with engineering, finance, environmental science, epidemiology, and policy analysis. To examine the sensitivity of the dynamical system described by Equation (43), we utilize the widely recognized and effective Runge–Kutta technique. Now, the Runge–Kutta technique is utilized to solve the following dynamical system to observe its sensitivity:
Here, we pick the value of the parameters like . The system’s beginning conditions are provided by the following:
Figure 5 illustrates the outcomes that this competent plan manufactures. The dynamics of class are demonstrated by blue curves, and dynamics of class are displayed with orange curves. A close examination of the figures reveals that even minor modifications to the initial setting result in substantial modifications in the system’s behavior.
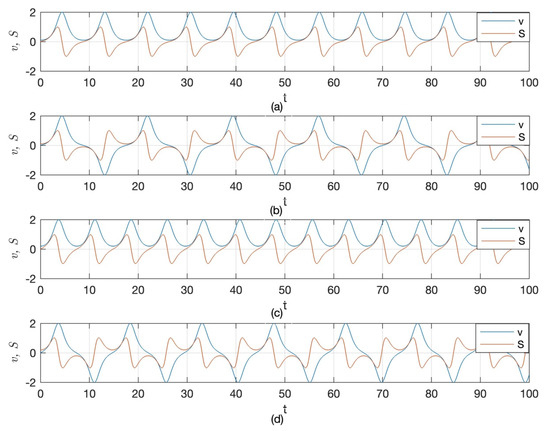
Figure 5.
Sensitivity analysis of the proposed system with several initial conditions along with the parameters values : (a) and , (b) and , (c) and , (d) and .
4.4. Modulation Instability
Modulation instability is an elementary phenomenon detected in nonlinear systems, remarkably in optics and fluid dynamics. It illustrates the unconstrained growth of perturbations or fluctuations in a system, running to the creation of patterns or structures. In optics, modulation instability arises when a beam of light interacts with a nonlinear medium, such as assured optical fibers or photonic devices. In fluid dynamics, modulation instability can demonstrate as the spontaneous generation of patterns or waves in fluid flows, such as the development of ripples on the surface of water or the occurrence of turbulence in a flow. Modulation instability has various applications, including the generation of optical frequency combs, which are used in telecommunications, spectroscopy, optical coherence tomography, nonlinear imaging, optical signal processing, wavelength conversion, and pulse shaping. It remains to be a lively area of research in modern physics and contemporary engineering.
In this part, we identify the traveling wave modulation instability of Equation (8). Consider the disturbed solution specified by the following:
in which the constants and aim for a steady flow attitude for Equation (8). Operating Equation (46) to Equation (8) and at the same time linearizing in and yields the following:
Differentiating the second equation of Equation (47), one can obtain . Now, apply this value in the first equation of Equation (47):
Assume the solution of the system in Equation (48):
where stands for the waveform quantity, and represents the frequency. Perform Equation (49) to Equation (48):
Equation (50):
From Equation (51), the following is obtained:
For the value of and , the right-hand side of Equation (52) gives us the negative value, which shows that any combination of the soliton solutions demonstrates a decaying pattern. Finally, Equation (52) confirms that any arrangement of the outcomes appears to decay. This reveals a stable dispersion of the model.
5. Graphical Explanation of Closed-Form Solutions
Graphs afford an adaptable framework for modeling complex relationships along with resolving a wide range of difficulties in modern science and beyond. They are exercised to represent complex information in a clear, concise, and easily understandable manner. Also, they play a decisive role in data analysis, decision making based on data-driven insights, and communication across various domains, including business, science, education, and public policy. Numerous researchers have studied the FSKMMS with the aid of several techniques. However, the mechanical features of the FSKMMS in saturated ferromagnetic materials, a specific kind of the fractional NLPDEs, are presented here in this unique analysis by applying a novel procedure, the Sardar sub-equation approach. For the FSKMMS, we reveal the traveling wave along with soliton profile in 3D and contour forms with appropriate constant values. The mechanisms associated with the complex nonlinear physical phenomenon are competently described by the offered solutions. The most intriguing features of FSKMMS, which accounts for the many wonders of fractional nonlinear science, are better understood by researchers. This segment contains the visual depiction of the revealed closed-form soliton solutions to the stated previous equations. At first, we place the solution of Equation (21) in two formats, namely 3D with and contour with we obtain a singular shape soliton, which arise exposed in Figure 6 for the parameters , and . Afterward, we depict the solution of Equation (22) as well in two different compositions: 3D using and contour using , and we obtain the soliton shape disclosed in Figure 7 alongside the parameters , and . The kink-shaped soliton solution presented in Equation (29) is given in Figure 8, in which the formats include 3D within and contour within we count the parameters , and . Furthermore, Figure 9 describes the singular soliton solution of Equation (30), wherein we employ 3D with and contour with , and the parameters bear , and . Subsequently, we show the solution of Equation (31) as well in two different compositions, namely 3D with and contour with we thus obtain the kink-shaped soliton that is revealed in Figure 10 along with the parameters , and . The dark kink-shaped soliton solution stated in Equation (32) is given in Figure 11, which uses 3D within and contour within , incorporating the parameters and .
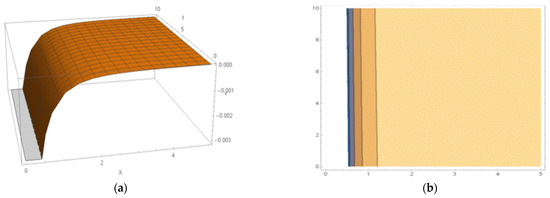
Figure 6.
Singular shape soliton offered by Equation (21): (a) 3D structure and (b) the contour shape.
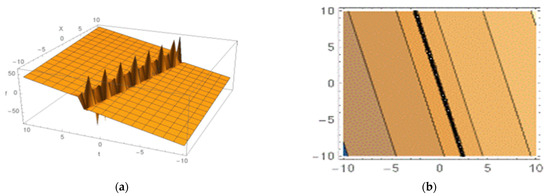
Figure 7.
Soliton shape yielded by Equation (22): (a) 3D structure and (b) the contour shape.
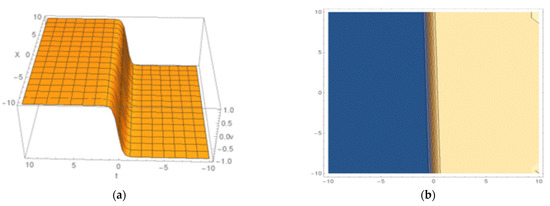
Figure 8.
Kink-shaped soliton of Equation (29): (a) 3D structure and (b) the contour shape.
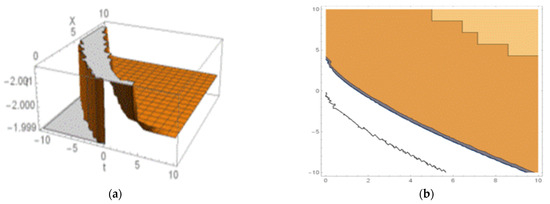
Figure 9.
Singular soliton obtained from Equation (30): (a) 3D structure and (b) the contour shape.
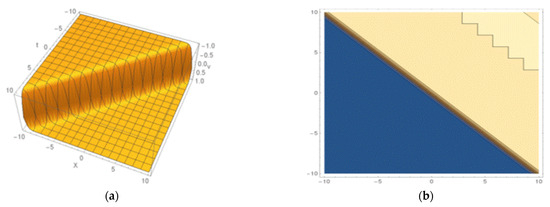
Figure 10.
Kink-shaped soliton found by Equation (31): (a) 3D structure and (b) the contour shape.
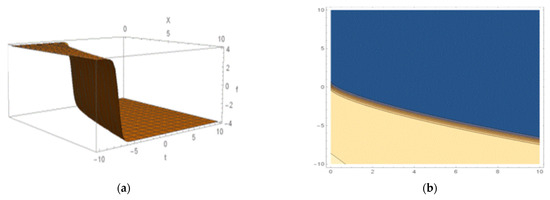
Figure 11.
Dark kink-shaped soliton obtained through Equation (32): (a) 3D structure and (b) the contour shape.
The links between various types of solitons and their propagation trends, interactions, and the consequence of noise on them are illustrated in the 3D and contour shape of the concluded solutions containing various values for the parameters. The effectiveness of the Sardar sub-equation method in organizing complex nonlinear systems was proven by this visual study, which also highlights the significance of our findings. This graphic representation further emphasizes the important contributions made by the Sardar sub-equation technique for analyzing complex nonlinear occurrences and advancing our understanding of soliton behavior in the context of FSKMMS, which has not been recognized in the past literature.
6. Conclusions
The recommended model in this research is expected to be extremely beneficial in comprehending significant physical occurrences in signal transmission, biophysics, mechanical and electrical engineering, materials sciences, plasma physics, chaotic systems, ocean waves, fluid dynamics, porous media, optical fiber communication, electromagnetism, magneto-acoustic waves in plasma, epidemiology, photonics, and other fields. Electromagnetic wave propagation in ordered magnetic materials, particularly in a ferromagnetic medium, is essential to achieve faster and greater density storage fields. The present investigation revives analytical solutions for the FSKMMS in ferromagnetic materials. A potent and innovative methodology, the Sardar sub-equation technique, was performed to produce closed-form soliton solutions of the suggested model in different forms of functions. In contemporary science, engineering, finance, and other fields, the innovative closed-form solutions, which might be applied to define magnetic fields in ferromagnets with zero conductivity, offered in this research work could be highly useful. To explore the nature of what was discovered, we completed phase portraiture of bifurcation analysis, chaotic behaviors, sensitivity, and modulation instability analysis. By using these analytical processes, we were able to verify that the system under investigation has a saddle point as well as a center point in its equilibrium position, sensitivity, and modulation instability and maintains a stable dispersion. The precise impact of each parameter on soliton interactions was thoroughly examined. An incredible wave shape associated with singular shape, soliton-shaped, kink-shaped, and dark kink-shaped soliton was generated by the fantastic physical features of the gathered solutions. We performed extensive research about the closed-form soliton solutions as well as their visualization in contour and 3D diagrams. The framework has marvelous potential for further development. Additionally, it is readily apparent that the advised strategy is simple to implement for gaining newer soliton solutions that have not been accomplished before. As a result, the suggested approach is genuine and adaptive for overcoming an extensive range of diverse fractional NLPDEs that have risen in the fields of mathematical physics as well as contemporary engineering technology.
Author Contributions
Conceptualization, J.R.M.B., F.A., and M.K.; methodology, J.R.M.B., M.M.M., and F.A.; software, M.M.M.; validation, J.R.M.B. and M.K.; investigation, F.A., M.M.M., and M.K.; writing—original draft, J.R.M.B. and F.A.; writing—review and editing, M.M.M. and M.K.; supervision, M.M.M. and M.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
I hereby declare that this manuscript is the result of my independent creation under the reviewers’ comments. Except for the quoted contents, this manuscript does not contain any research achievements that have been published or written by other individuals or groups.
Data Availability Statement
All data generated or analyzed during this study are included in this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Varol, D. Solitary and Periodic Wave Solutions of the Space-Time Fractional Extended Kawahara Equation. Fractal Fract. 2023, 7, 539. [Google Scholar] [CrossRef]
- Gebril, E.; El-Azad, M.S.; Sameeh, M. Chebyshev collocation method for fractional Newell-Whitehead-Segel equation. Alex. Eng. J. 2024, 87, 39–46. [Google Scholar] [CrossRef]
- Guswanto, B.H.; Suroto; Istikaanah, N. Multi-order fractional nonlinear evolution equations system. Partial Differ. Equ. Appl. Math. 2024, 9, 100620. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Q.; Biswas, A.; Liu, W. Phase-shift controlling of three solitons in dispersion-decreasing fibers. Nonlinear Dyn. 2019, 98, 395–401. [Google Scholar] [CrossRef]
- Ma, W.X. Solitons by means of Hirota bilinear forms. Partial Differ. Equ. Appl. Math. 2022, 5, 100220. [Google Scholar] [CrossRef]
- Ali, K.K.; Yilmazer, R.; Baskonus, H.M.; Bult, H. Modulation instability analysis and analytical solutions to the system of equations for the ion sound and Langmuir waves. Phys. Scr. 2020, 95, 065602. [Google Scholar] [CrossRef]
- Dusunceli, F.; Celik, E.; Askin, M.; Bulut, H. New exact solutions for the doubly dispersive equation using improved Bernoulli sub-equation method. Indian J. Phys. 2021, 95, 309–314. [Google Scholar] [CrossRef]
- Ozkan, E.M. New Exact Solutions of Some Important Nonlinear Fractional Partial Differential Equations with Beta Derivative. Fractal Fract. 2022, 6, 173. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Alyoubi, A.F.; Aloufi, R.G. New analytical solutions for two physical applications by the modified / expansion method. AIP Conf. Proc. 2022, 2472, 020001. [Google Scholar]
- Jordanov, I.P. Simple equations method applied to the equations of nonlinear Schrödinger kind. AIP Conf. Proc. 2022, 2459, 030016. [Google Scholar]
- Akram, G.; Sadaf, M.; Khan, M.A.U. Soliton solutions of Lakshmanan-Porsezian-Daniel model using modified auxiliary equation method with parabolic and anti-cubic law of nonlinearities. Opt.-Int. J. Light Electron Opt. 2022, 252, 168372. [Google Scholar] [CrossRef]
- Akram, G.; Zainab, I.; Sadaf, M.; Bucur, A. Solitons, one line rogue wave and breather wave solutions of a new extended KP-equation. Results Phys. 2023, 55, 107147. [Google Scholar] [CrossRef]
- Ali, H.M.S.; Habib, M.A.; Miah, M.M.; Miah, M.M.; Akbar, M.A. Diverse solitary wave solutions of fractional order Hirota-Satsuma coupled KdV system using two expansion methods. Alex. Eng. J. 2023, 66, 1001–1014. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Baleanu, D.; Miah, M.M.; Ali, H.M.S.; Alshehri, H.M.; Osman, M.S. New soliton solutions of the mZK equation and the Gerdjikov-Ivanov equation by employing the double (/, 1/)-expansion method. Results Phys. 2023, 47, 106391. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Duraihem, F.Z.; Rehman, S. Stability, modulation instability, and analytical study of the confirmable time fractional Westervelt equation and the Wazwaz Kaur Boussinesq equation. Opt. Quantum Electron. 2024, 56, 948. [Google Scholar] [CrossRef]
- Hossain, M.N.; Miah, M.M.; Ganie, A.H.; Osman, M.; Ma, W.X. Discovering new abundant optical solutions for the resonant nonlinear Schrödinger equation using an analytical technique. Opt. Quantum Electron. 2024, 56, 847. [Google Scholar] [CrossRef]
- Hussain, A.; Kara, A.H.; Zaman, F.D. An invariance analysis of the Vakhnenko-Parkes equation. Chaos Solitons Fractals 2023, 171, 113423. [Google Scholar] [CrossRef]
- Li, S. Nonlinear chirped optical solitons of the perturbation Fokas-Lenells equation in optical fibers. Opt.-Int. J. Light Electron Opt. 2023, 276, 170627. [Google Scholar] [CrossRef]
- Alam, B.E.; Javid, A. Optical dual-waves to a new dual-mode extension of a third order dispersive nonlinear Schrödinger’s equation. Phys. Lett. A 2023, 480, 128954. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Nifontov, D.R. Some specific optical wave solutions and combined other solitons to the advanced (3+1)-dimensional Schrödinger equation in nonlinear optical fibersy. Chaos Solitons Fractals 2023, 175, 114076. [Google Scholar] [CrossRef]
- Kumar, S.; Hamid, I.; Abdou, M.A. Some specific optical wave solutions and combined other solitons to the advanced (3+1)-dimensional Schrödinger equation in nonlinear optical fibers. Opt. Quantum Electron. 2023, 55, 728. [Google Scholar] [CrossRef]
- Niwas, M.; Kumar, S. New plenteous soliton solutions and other form solutions for a generalized dispersive long-wave system employing two methodological approaches. Opt. Quantum Electron. 2023, 55, 630. [Google Scholar] [CrossRef]
- Singh, S.; Ray, S.S. Newly exploring the Lax pair, bilinear form, bilinear Backlund transformation through binary Bell polynomials, and analytic solutions for the (2+1)-dimensional generalized Hirota-Satsuma-Ito equation. Phys. Fluids 2023, 34, 087134. [Google Scholar] [CrossRef]
- Mohammed, W.W.; El-Morshedy, M.; Cesarano, C.; Al-Askar, F.M. Soliton solutions of fractional stochastic Kraenkel-Manna-Merle equations in ferromagnetic materials. Fractal Fract. 2023, 7, 328. [Google Scholar] [CrossRef]
- Liaqat, M.I.; Khan, A.; Alqudah, M.A.; Abdeljawad, T. Adapted homotopy perturbation method with Shehu transform for solving conformable fractional nonlinear partial differential equations. Fractals 2023, 31, 2340027. [Google Scholar] [CrossRef]
- Du, H.; Yang, X.; Chen, Z. A new method of solving the best approximate solution for a nonlinear fractional equation. Int. J. Comput. Math. 2023, 100, 1702–1718. [Google Scholar] [CrossRef]
- Kumar, S.; Mohan, B. A novel analysis of Cole-Hopf transformations in different dimensions, solitons, and rogue wave for a (2+1)-dimensional shallow water wave equation of ion-acoustic waves in plasmas. Phys. Fluids 2023, 35, 127128. [Google Scholar] [CrossRef]
- Rong, F.; Li, Q.; Shi, B.; Chai, Z. A lattics Boltzmann model based on Cole-Hopf transformation for N-dimensional coupled Burgers’ equations. Comput. Math. Appl. 2023, 134, 101–111. [Google Scholar] [CrossRef]
- Ashraf, R.; Hussain, S.; Ashraf, F.; Akgul, A.; El Din, S.M. The extended Fan’s sub-equation method and its application to nonlinear Schrodinger equation with saturable nonlinearity. Results Phys. 2023, 52, 106755. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, S. Dynamic nature of analytical soliton solutions of the (1+1)-dimensional Mikhailov-Novikov-Wang equation using the unified approach. Int. J. Math. Comput. Eng. 2023, 1, 217–228. [Google Scholar] [CrossRef]
- Mahmood, A.; Abbas, M.; Akram, G.; Sadaf, M.; Riaz, M.B.; Abdeljawad, T. Solitary wave solution of (2+1)-dimensional Chaffee–Infante equation using the modified Khater method. Results Phys. 2023, 48, 106416. [Google Scholar] [CrossRef]
- Yasmin, H.; Alshehry, A.S.; Ganie, A.H.; Shafee, A.; Shah, R. Noise effect on soliton phenomena in fractional stochastic Kraenkel-Manna-Merle system arising in ferromagnetic materials. Sci. Rep. 2024, 14, 1810. [Google Scholar] [CrossRef] [PubMed]
- Youssri, Y.H.; Zaky, M.A.; Hafez, R.M. Romanovski-Jacobi spectral schemes for higher-order differential equations. Appl. Numer. Math. 2024, 198, 148–159. [Google Scholar] [CrossRef]
- Tripathy, A.; Sahoo, S. A novel analytical method for solving (2+1)-dimensional extended Calogero-Bogoyavlenskii-Schiff equation in plasma physics. J. Ocean Eng. Sci. 2021, 6, 405–409. [Google Scholar] [CrossRef]
- Khalid, S.; Ahmad, S.; Ullah, A.; Ahmad, H.; Saifullah, S.; Nofal, T.A. New wave solutions of the (2+1)-dimensional generalized Hirota-Satsuma-Ito equation using a novel expansion method. Results Phys. 2023, 50, 106450. [Google Scholar] [CrossRef]
- Mia, R.; Miah, M.M.; Osman, M.S. A new implementation for finding of analytical solutions in nonlinear PDEs. Heliyon 2023, 9, e15690. [Google Scholar] [CrossRef] [PubMed]
- Khalid, S.; Ullah, A.; Ahmad, S.; Akg, A.; Yusuf, A.; Sulaiman, T.A. Some novel analytic solutions of a new extended (2+1)-dimensional Boussinesq equation using a novel method. J. Ocean. Eng. Sci. 2022, in press. [Google Scholar]
- Iqbal, M.A.; Miah, M.M.; Ali, H.M.S.T.; Shahen, N.H.M.; Deifalla, A. New applications of the fractional derivative to extract abundant soliton solutions of the fractional order PDEs in mathematics physics. Partial Differ. Equ. Appl. Math. 2024, 9, 100597. [Google Scholar] [CrossRef]
- Senol, M.; Akinyemi, L.; Nkansah, H.; Adel, W. New solutions for four novel generalized nonlinear fractional fifth-order equations. J. Ocean Eng. Sci. 2024, 9, 59–65. [Google Scholar]
- Zeid, S.S.; Alipour, M. A collocation method using generalized Laguerre polynomials for solving nonlinear optimal control problems governed by integro-differential equations. J. Comput. Appl. Math. 2024, 436, 115410. [Google Scholar] [CrossRef]
- Prathumwan, D.; Chaiya, I.; Trachoo, K. Three-dimensional simulation of the lumbar spine under lumbar spinal stenosis with different sizes of spinal canal. Partial Differ. Equ. Appl. Math. 2024, 9, 100614. [Google Scholar] [CrossRef]
- Borhan, J.R.M.; Ganie, A.H.; Miah, M.M.; Iqbal, M.A.; Seadawy, A.R.; Mishra, N.K. A highly effective analytical approach to innovate the novel closed form soliton solutions of the Kadomtsev-Petviashivili equations with applications. Opt. Quantum Electron. 2024, 56, 938. [Google Scholar] [CrossRef]
- Chen, J.; Pelinovsky, D.E. Periodic Travelling Waves of the Modified KdV Equation and Rogue Waves on the Periodic Background. J. Nonlinear Sci. 2019, 29, 2797–2843. [Google Scholar] [CrossRef]
- Liu, Y.; Zeng, S. Discontinuous initial value and Whitham modulation for the generalized Gerdjikov-Ivanov equation. Wave Motion 2024, 127, 103276. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Inc, M.; Baleanu, D. New solitary wave solutions for variants of (3+1)-Dimensional Wazwaz-Benjamin-Bona-Mahony equations. Front. Phys. 2020, 8, 332. [Google Scholar] [CrossRef]
- Rasool, T.; Hussain, R.; Al Sharif, M.A.; Mahmoud, W.; Osman, M.S. A variety of optical soliton solutions for the M-truncated Paraxial wave equation using Sardar-subequation technique. Opt. Quantum Electron. 2023, 55, 396. [Google Scholar] [CrossRef]
- Yasin, S.; Khan, A.; Ahmad, S.; Osman, M.S. New exact solutions of (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation by Sardar-subequation method. Opt. Quantum Electron. 2024, 56, 90. [Google Scholar] [CrossRef]
- Kraenkel, R.A.; Manna, M.A.; Merle, V. Nonlinear short-wave propagation in ferrites. Phys. Rev. E 2000, 61, 976–979. [Google Scholar] [CrossRef]
- Hussain, Z.; Rehman, Z.U.; Abbas, T.; Smida, K.; Le, Q.H.; Abdelmalek, Z.; Tlili, I. Analysis of bifurcation and chaos in the traveling wave solution in optical fibers using the Radhakrishnan–Kundu–Lakshmanan equation. Results Phys. 2023, 55, 107145. [Google Scholar] [CrossRef]
- Biswas, A.; Bagchi, B.K.; Yildirim, Y.; Khan, S.; Asiri, A. Quasimonochromatic dynamical system and optical soliton cooling with triple-power law of self-phase modulation. Phys. Lett. A 2023, 480, 128985. [Google Scholar] [CrossRef]
- Shehzad, K.; Seadawy, A.R.; Wang, J.; Arshad, M. Multi peak solitons and breather types wave solutions of unstable NLSEs with stability and applications in optics. Opt. Quantum Electron. 2023, 55, 7. [Google Scholar] [CrossRef]
- Yang, Z. Voltammetry for quantitative determination of trace mercury ions in water via acetylene black modified carbon paste electrode. Alex. Eng. J. 2024, 87, 107–113. [Google Scholar] [CrossRef]
- Li, Z.; Hu, H. Chaotic pattern, bifurcation, sensitivity and traveling wave solution of the coupled Kundu-Mukherjee-Naskar equation. Results Phys. 2023, 48, 106441. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).