Abstract
The epidemic norovirus causes vomiting and diarrhea and is a highly contagious infection. The disease is affecting human lives in terms of deaths and medical expenses. This study examines the governing dynamics of norovirus by incorporating Lévy noise into a stochastic (susceptible, infected, recovered, water contamination, and food contamination) model. The existence of a non-negative solution and its uniqueness are proved after model formulation. Subsequently, the threshold parameter is calculated, and this number is used to explore the conditions under which disease tends to exist in the population. Likewise, additional conditions are derived that ensure the elimination of the disease from the community. It is proved that the norovirus is extinct whenever the threshold parameter is less than one and it persists for
. The work assumes two working examples to numerically explain the theoretical findings. Simulations of the study are visually presented, and comparisons are made. The results of this study suggest a robust approach for handling complex biological and epidemic phenomena.
Keywords:
norovirus epidemic model; environmental perturbations; threshold; extinction; persistence in mean MSC:
15B51; 26A18; 37H05
1. Introduction
The norovirus (NoV) is a highly contagious viral infection that results in vomiting and diarrhea. The disease equally infects every individual in the population, irrespective of their age and sex. It is observed that the epidemic norovirus spreads in the population (i) when direct contact has been made with an infected person, (ii) by consuming contaminated water and food, and (iii) by touching dirty objects and then taking the hands in the mouth [1]. Common symptoms of the disease include nausea, diarrhea, stomach pain, and vomiting. Washing hands at regular intervals reduces the risk of becoming infected, and other known control strategies are isolation, cleaning fruits and vegetables with water, etc. If the control strategies are not strictly followed, the disease may transfer very easily and quickly within the population. The existing literature and fact sheets suggest that NoV is one of the responsible viruses for transmitting foodborne infections [2,3].
Viral gastroenteritis is an intestine infection caused by numerous viruses. Food does not directly cause viral gastroenteritis; however, the following three foods are considered responsible for the occasional cases of the disease [4]:
- A1:
- During the process of marketing, the molluscan shellfish may become infected with the virus.
- A2:
- The fresh food items may acquire the virus during manufacturing/harvesting and packaging.
- A3:
- The ready-to-eat food items may be contaminated in the preparation stage.
The packed items of food are usually considered to be the main source of NoV spread, and they acquire the virus through food workers during food preparation and packing. The degree to which food workers contribute to contamination depends on several factors, including their health and hygiene practices, the stage of their clinical infections, the effectiveness of their efforts to inactivate or remove the virus, and their characteristics. Hands that have been contaminated and, to a lesser extent, surfaces that have been polluted are important places for viruses to survive and spread [5].
The disease that follows due to the transmission of NoV might be caused by a variety of circumstances. The seasonality effect is the most prominent one, and over 50% of infections took place during the winter period [6]. The seasonal differences in the spread of norovirus are due to both environmental conditions and human behavior. As per studies [7,8], norovirus has the tendency to spread more quickly at lower temperatures, and the transmission rate can be further increased with heavy rainfall. There may be other community elements that impact how severe the epidemic of norovirus is. Although this disease can infect anyone at any age under certain circumstances, children five years of age and under are more likely to have the infection [9]. The findings of serological research suggest that the disease is most likely to be a childhood disease. A higher risk of serious complications and death exists for the elderly and those with compromised immune systems [10,11]. Because of this, even though the illness usually subsides on its own in healthy people, it can have disastrous effects on high-risk groups. If not properly treated, the disease may persist for longer and potentially lead to an endemic situation [11,12,13,14].
To comprehend the dynamic pattern and control strategies of infectious diseases, it is highly recommended to utilize the techniques of mathematical modeling [15,16,17,18]. Such models produce a connection between reality and the future or past prediction of the disease while using the available data. Numerous norovirus models—from single outbreak analysis to population level—have revealed plenty of illness patterns. Environmental variations are always critical in biological systems as well as in physical phenomena. The dynamics of norovirus transmission are significantly impacted by these environmental variables [19]. Because interpersonal relationships and other aspects of the population are unexpected, the course and spread of epidemics are also uncertain. Therefore, the pattern of the disease could be highly disturbed by the unpredictability of the surroundings. Water and food are major components of the NoV infection and are subject to environmental changes and person-to-person contact; therefore, modeling NoV with tools that account for such aspects of the disease is strongly suggested.
The literature on dynamical systems is extensive, and the underlying systems have been represented using a variety of methodologies such as deterministic and stochastic, fractional, and fractal–fractional approaches [19,20,21]. Numerous deterministic systems were expanded through the use of fractional calculus and various fractional derivative definitions. The deterministic model assumes only integer ordered derivatives of the state variables, whereas the fractional models are free in selection and can take any positive real number as an order. Modeling with stochastic differential equations (SDEs) is far more realistic than the deterministic modeling modeled either through ODEs or fractional derivatives [20,21]. The usage of SDEs for experimentally evaluating a genuine scenario results in a different output each time. To obtain a better understanding, it is necessary to simulate the model millions of times, with the average results recommended. Like fractional models, stochastic models can be tested for dynamical properties such as the uniqueness and existence of positive solutions, optimality, stability, and simulations. Deterministic systems can be easily transformed into stochastic models by including noise, and these noises play a significant role in explaining real systems. Among all known noises, Lévy noise is one of the most severe disruptions because it functions as a threshold parameter by drifting the velocity. In particular, incorporating this noise into epidemic models yields solid data and explains previously unknown insights regarding the disease’s dynamics. Specifically, Lévy noise has numerous advantages over Gaussian noise. Gaussian noise is extensively utilized in mathematical modeling; nonetheless, this causes uncertainty in the modeling [22,23,24]. Because jumps are incorporated, which diffuses the problem of Lévy noise, the model beats the extended Lévy model in terms of neuron efficiency development. Thus, based on the current research, we may conclude that Lévy noise is particularly advantageous for epidemic problems where the stability of the system fluctuates with time [25,26,27].
This work extends the previous models on the transmission mechanism of NoV by accounting for environmental variations through Lévy noises in the stochastic system. The work focuses on the forecasting of the long-run behavior of the disease and on the inclusion of contamination through both food and water. The whole population, including people and germs, is stratified into five categories. These classes comprise susceptible people (), infected individuals (), and recovered/removed individuals (). There are also two bacterial compartments:
indicates the density of bacteria contamination in water, whereas indicates the density of NoV bacteria in food. The state variables and parameters of the disease are related to each other according to the characteristics of the NoV. The detailed assumption and model formulation are explained in the subsequent section.
The remaining sections of this paper are organized as follows: In Section 2, the NoV model is established with specific assumptions regarding the system, and the role of Lévy noise is explained. Section 3.1 presents some fundamental definitions and lemmas on stochastic modeling. Section 3.2 assesses the certainty and positivity of the suggested model solution. Section 3.3 examines the behavior of the stochastic model solution near the disease-free state of the ODE model and presents the extinction theory of the disease. The work was extended by analyzing the long-run behavior of the stochastic curves in the vicinity of the endemic fixed point of the ODE model. Section 3.4 explains the persistence of the infection. Section 4 simulates both stochastic and deterministic systems and provides graphical demonstrations to validate the theoretical conclusions. Finally, we conclude our work by discussing the study’s findings, summarizing them, and suggesting future research directions.
2. Model Formulation
Norovirus is a highly contagious virus that can cause gastroenteritis, an inflammation of the stomach and intestines. Modeling the spread of an infectious disease like norovirus can be done using compartmental models. As we know, the incidence rate of infectious diseases plays a key role in the investigation of mathematical epidemiology. Recently, Din [28] constructed a mathematical problem using the approach of a stochastic version of the Nov epidemic model. Motivated by the above discussion, we take the following epidemic model with general incidence and obtain the below equations to represent the dynamics of the NoV:
In the above equations, the notation for stands for the environmental noises, which are in fact the known Brownian motions satisfying the condition . The associated intensity with each is denoted with , a positive real number. The description of other parameters of the model is well explained in Table 1.

Table 1.
The description of parameters.
Besides the above-mentioned properties of the Lévy noise, it can also be useful when the noise-scaled drift velocity falls within a certain range of the threshold values. The use of both non-local and local Lipschitz conditions implies that integrating Lévy noise might improve the shared information or bit count in a variety of feedback-related epidemic scenarios that follow a given, random, stochastic differential equation. According to the sources [24,25,26], Lévy noise has advantages over typical Gaussian noise in mathematical models of epidemics, but at the same time, it also adds more mathematical complexity to the problem under consideration. Jump-diffusion Lévy noise outperforms the conventional Lévy model by precisely describing the development of a neuron’s membrane potential. As a result, Lévy noise improves the stability of time-varying recurrent neural networks. By applying Lévy noise to the system (1), the model will take the form of the system of Ito’s stochastic differential Equations [29]:
In the above system, we may incorporate the fractal–fractional derivative as it has the unique capability to model the complex and intricate patterns of the underlying system. Traditional fractional calculus has already been shown to be useful in explaining complicated behaviors; however, introducing fractal aspects improves it even more by accounting for the intrinsic fractal aspects seen in chaotic dynamics. This novel technique improves the accuracy of chaotic system modeling and allows for a more in-depth study of their underlying structures and dynamics. In the sequel, the inclusion of the fractal–fractional derivative will add complexity to the analysis, perhaps making it difficult to implement and analyze chaotic dynamical systems. These methodologies associated with these concepts could have a substantial influence on the viability of real-world applications as well as the computer resources needed for simulations. Furthermore, the suggested fractal–fractional derivative may be parameter-sensitive. Given its complications, this study will concentrate primarily on conventional derivatives, leaving the investigation of fractal–fractional derivatives to future research.
For the sake of simplicity in calculation and model analysis, let us define
The notation refers to the compensated Poisson random measure, which is defined as . The notation stands for the left limit. All other parameters have the same meaning. In this context, is the Poisson random measure, and is its intensity measure. Further, the function v is defined on a measurable subset having the properties and and . Additionally, v is defined for the measurable subset of with and for and .
By using system (2) as a base for analysis, we investigate answers to the below questions:
- Q1:
- Can the dynamics pattern of the NoV be affected by the Lévy noises?
- Q2:
- Does contaminated water play a role in spreading the NoV?
- Q3:
- Does contaminated food play a role in spreading the NoV?
- Q4:
- What conditions are needed for the existence of NoV throughout infection?
- Q5:
- What condition must be met in order for the infection to subside in the population?
3. Stochastic Analysis
3.1. Basic Concept
Throughout this section, we will establish some basic definitions and Lemmas in the stochastic sense. The notation used below is consistent with that provided in reference [22] and will be used in the rest of the manuscript.
Lemma 1.
To simplify our analysis, we will use two fundamental assumptions provided below and labeled as and . These assumptions are essential for proving the existence and uniqueness of a global positive solution of the model (2) [24,25,26].
- (H1).
- such thatwith , wherewhere denotes the compensated random measure.
- (H2).
- for where C is a positive constant.
Lemma 2.
If for system (2), is a solution with initial conditions , then a.s.,
Moreover, if , then
Then, the solutions of model (2) have the following properties:
Proof.
Since the proofs for the Lemma are extremely close to those of Lemmas and [30], respectively, we opt to ignore them in this context. □
The following definitions for the mean persistence are worth recalling and are outlined in [22,23].
Definition 1
[24,25]. For model (2) to have the property of durability or persistence, the following condition must be met
Parallel to the above condition, the following Lemmas employed in [21,22] must hold for the NoV persistence.
Lemma 3
(Strong Law) [24,26]. For a continuous real process , the property of the local martingale exists if it vanishes at and
Lemma 4.
Suppose and ∋ , a.s. If ∀
Then
Here, λ and represent positive and non-negative real numbers, respectively.
3.2. Positive Global Solution of the Model
As system (2) physiologically depicts the problem of population dynamics, it requires a positive, global, and bounded solution. In this section, we will investigate the system’s well-posedness described by Equations (2) by analyzing these properties. For convenience, we will use two common assumptions, and , as explained in Lemma 1. These assumptions are crucial for demonstrating the uniqueness and existence of a positive global solution to the model (2).
Theorem 1.
There is a unique solution of system (2) on for any initial value , and the solution will remain in with probability one, namely, for all almost surely.
Proof.
The condition ensures that the drift and diffusion are locally Lipschitz, resulting in a time t during which the proposed problem has a locally unique solution within the interval . Here, represents the explosion time; for further information, readers are referred to references [22,23]. It must be demonstrated that is sufficient to prove that the solution is global. To demonstrate this, assume a sufficiently large positive real integer such that each solution of the model is contained within the interval . Finally, for , allow
where . Throughout this work, we denote the inf of an empty set by . By definition, grows as . Assuming has a limit of , it is nearly certain that . In other words, it is required to show that a.s. If this assumption is untrue, then there would be constants and an in such that
So, for a natural number , the following holds
To prove the remaining part of the theorem, let us define the function:
In the above relation, the operator is defined from to and is given by
Assume that , then by selecting which shows . Further, Equation (11) guarantees the inequality , thus
The remainder of the proof roughly follows from the proof of Theorem 2.1 of reference [22]. As a result, we shall omit it here, bringing the theorem’s proof to completion. □
3.3. Extinction of the Disease
In this section, we offer supportive conditions for the extinction of the NoV in the population. Particularly, our emphasis is on the long-term behavior of the model solution. Our method begins with introducing the threshold number for the model and then providing the theorem for the extinction of the disease. The threshold number regarding the stochastic model is given by the expression
Theorem 2.
Let
be the solution of stochastic system (2) with initial value . If , then such a system’s solution will have the following properties:
In other words, the above implies the extinction of the NoV in the community with unit probability.
Proof.
After integrating the model (2), the following equations may be easily derived:
Using Itô’s formula, the second equation in the model (2) becomes:
Further, for are the martingale functions (locally continuous) and vanishes for . By letting and using Lemma (2), we have
With a similar approach, one can easily prove and .
For , relation (26) yields
Consequently, Equation (28) guarantees
Similarly, we can obtain
Finally
completes the proof of the theorem. □
3.4. Persistence of the Disease
This section will examine the long-term survival of the NoV in the community. To be more specific, we will investigate the conditions on the parameters that assure disease persistence, which is required before establishing an effective control program. We will start by studying the concept of average persistence described in [22,23].
Theorem 3.
The system (2) is said to be persistent in the mean if:
where , and it assures the existence of the disease at all times t within the population.
Let us define
Proof.
Let us suppose
where , , , and are real numbers to be calculated.
Let , and
For the sake of simplicity, let
By using these s, we have
Substituting Equation (40) into Equation (36), then integrating both side of the stochastic NoV epidemic model (2), we obtain
where
.
By virtue of strong law presented in Lemma 3, we obtain
From Equation (41), we have
4. Numerical Simulations and Discussion
The validation of theoretical results via simulations, an integral part of epidemic modeling, and forecasting the future behavior of the disease under various circumstances are presented in this section. To create a strategy for a numerically solving system (2), we employed the conventional numerical approach established in [31]. To successfully implement the algorithm, we took
, where and . To describe the time period , we considered the constant step size . Further, for and , and , where stands for the Gaussian noises having the distributions . In addition, , defined as , follows a Poisson distribution with intensity v when considering with . As a result, the Milstein algorithm for obtaining the numerical solution of the model (2) takes the following form:
In addition to the aforementioned technique, one can use an alternate numerical method, such as the positive preserving truncated Euler–Maruyama (PPTEM) method [32], to obtain numerical solutions to the model. Several writers have employed PPTEM approaches to address complicated physical phenomena (e.g., ref. [33] and references mentioned therein). In this particular case, the reasons for selecting this specific method include its simplicity and efficacy in controlling Lévy jumps.
We need certain parameter values for the model (2) to numerically validate the theoretical results. Two sets of parameter values, which are presented in Table 2, were used while simulating the model. These sets also contain the initial populations of humans and microorganisms. For every combination of parameters, the model was simulated for the time interval
, and each aspect was studied with detailed graphical illustrations.

Table 2.
The value of the parameters of model (2).
4.1. Numerical Simulations of the Extinction
In the preceding sections, we have investigated conditions under which the disease is extinct in the population and the condition that ensures the survival of the disease in the long term. Based on the condition of , we proved Theorem 2. The theorem biologically explains the elimination of the NoV from the population with unit probability whenever the required conditions are met. The disease will be eliminated from the community irrespective of the fact that the initial size of the infection is very high. To verify these facts numerically, we simulated the model based on Example 1 and present visual representations in Figure 1. One can easily notice that the curves generated by the stochastic system gradually approach the infection-free state of the associated deterministic system.
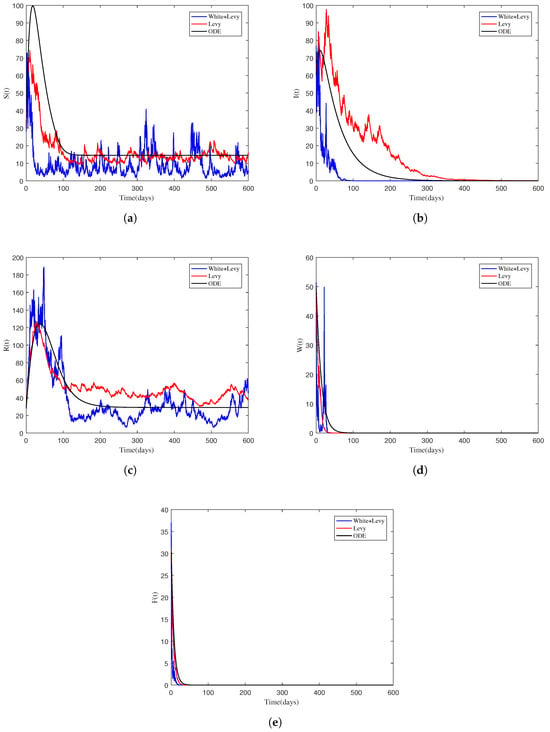
Figure 1.
Sample solution profiles of stochastic model (2) along with the solution of the associated deterministic system explaining extinction of the NoV. (a) Susceptible individuals. (b) Infected individuals. (c) Recovered individuals. (d) Bacteria contaminated NoV through water. (e) Bacteria contaminated NoV through food.
Example 1.
In this example, values of the parameter are assumed from Table 2 Test 1. By using these values of the parameter, the threshold parameter was calculated, which is surely less than unity. Thus, the premise of Theorem 2 holds true, and hence the conclusion must follow. In other words, each component of the solution to the model will satisfy the following expressions:
and
These inequalities represent the extinction of the infection within the population, and numerically Figure 1 verifies these conclusions. Consequently, the analytical findings showing extinction have been validated and can be deemed reliable.
4.2. Numerical Simulations of the Persistence
Likewise in this part, we attempt to quantify the persistence of NoV in the population. Theoretically, Theorem 3 explains the mean presence of infection throughout the population at all times. The theorem states that if the hypothesis is correct, the conclusion follows. To demonstrate the numerical verification of the theorem, we have considered data from Table 2 Test 2, and it was found that . Both the stochastic and deterministic models were simulated with these data, and the findings are presented in Figure 2. The figure depicts that the norovirus tends to exist in the population as long as the threshold exceeds the value of one. Thus, in such cases, the stakeholders must look for a control program to control the infection.
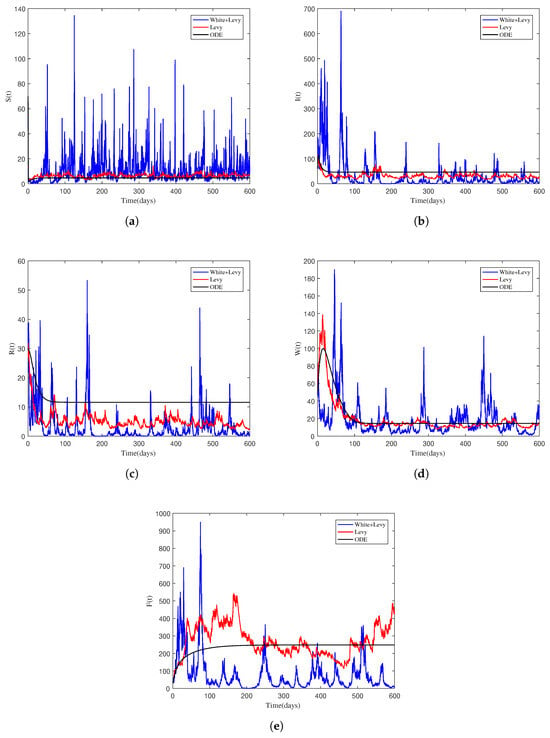
Figure 2.
Sample solution profiles of the stochastic model (2) along with the solution of the associated deterministic system explaining the persistence of the NoV. (a) Susceptible individuals. (b) Infected individuals. (c) Recovered individuals. (d) Bacteria contaminated NoV through water. (e) Bacteria contaminated NoV through food.
Example 2.
To numerically validate the findings of Theorem 3 related to the persistence of the disease, we have assumed values of the parameters from Table 2 Test 2. Based on the studied data, we found that the value of is greater than one. Further study indicated that the parameters in this example satisfy the assumptions specified in Theorem 3. The model was simulated using these settings, and the results are visualized in Figure 2. The graph indicates that the infection will survive within the population, in which case the model will have a uniform stationary distribution.
4.3. The Impact of , , and on the Infected Individual
To show the effect of , , and on the dynamic pattern of the NoV (specifically on the infected compartments), we considered values of the parameters in Table 2 Test 3. The dynamic behavior of the infected classes , and as well as the mean-relative infections are displayed in Figure 3 and Figure 4 and were obtained from simulating the stochastic system. Reducing the levels of , , and accelerates disease extinction in the relevant populations. To promote disease extinction, it is required to lower the values of these parameters. Furthermore, the simulations show that including nonlinear stochastic noises is critical for a better understanding of the disease dynamics.
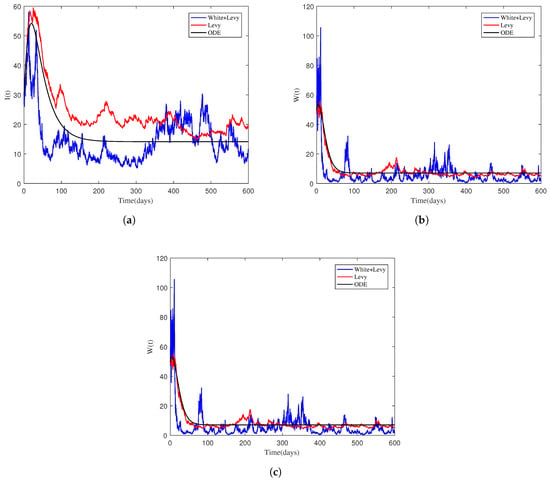
Figure 3.
Sample trajectories for the compartments , , and obtained from simulating both the deterministic and stochastic models with variations in the transmission coefficients. (a) . (b) . (c) .
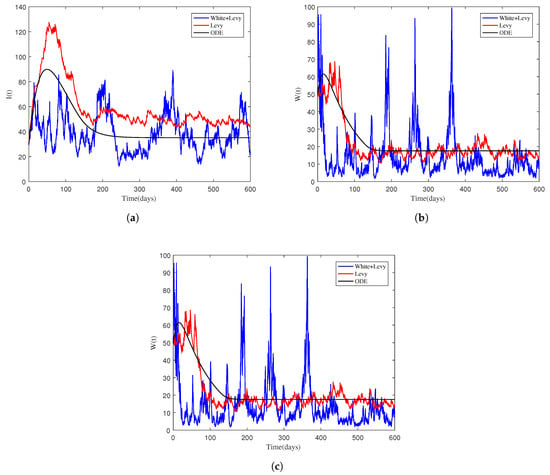
Figure 4.
The impact of the transmission coefficients on the dynamics of the compartments , , and obtained from simulating both the deterministic and stochastic models. (a)
. (b)
. (c) .
5. Concluding Remarks and Future Research Directions
Norovirus is a highly infectious disease causing vomiting and diarrhea and affects humanity both in terms of deaths and health expenditure. In this manuscript, we investigated the dynamics of norovirus via the inclusion of Lévy noise in stochastic modeling. After the formulation of a stochastic model, we studied the existence and uniqueness of a global solution of the model. We calculated the threshold number and the number was used in investigating the long-term behavior of the norovirus. The results show that when another threshold parameter exceeds one, the norovirus survives in the community. However, for the reproductive number (in a stochastic sense) less than one, the disease tends toward extinction. Furthermore, the paper uses simulated examples to demonstrate the real-world implications of these findings, providing important insights into norovirus transmission dynamics. We employed the usual Milstein technique to numerically verify the stability-based analytical conclusions. It has been found that the disease can only be eliminated if the values of all of the transmission coefficients are reduced significantly. Overall, this study adds to our understanding of complicated biological and epidemiological events, providing a solid foundation for studying and managing infectious diseases.
The research findings further recommend that the dynamic pattern of norovirus increases through contaminated water and food compared with human-to-human NoV transmission. Further, it was noted that to considerably reduce the risk, all three components must be simultaneously addressed. The authors plan to incorporate other disease-related characteristics into the model in the future, such as age and the temporal dynamics of the disease.
Author Contributions
Methodology, Y.S. and P.L.; Software, A.D.; Investigation, data curation, Y.S. and P.L.; Writing—original draft, Y.S., P.L., and A.D.; Writing—review & editing, A.D.; Project administration, Y.S. and P.L.; Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
Research on Key parameters of structure design of petal vortex shaft torsional section (No. JG523001), Development of Optimization Algorithm for 3D Data of Light Field (No. 3630019001), Hunan Provincial Educational Foundation of China (Grant No. 23B0569), and Hunan Provincial Natural Science Foundation of China (2024JJ7162), and the National Natural Science Foundation of China (No. 11901114).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare that there are no conflicts of interest.
References
- Koopmans, M.; Duizer, E. Foodborne viruses: An emerging problem. Int. J. Food Microbiol. 2004, 90, 23–41. [Google Scholar] [CrossRef] [PubMed]
- Widdowson, M.A.; Sulka, A.; Bulens, S.N.; Beard, R.S.; Chaves, S.S.; Hammond, R.; Salehi, E.D.P.; Swanson, E.; Totaro, J.; Woron, R.; et al. Norovirus and foodborne disease, United States, 1991–2000. Emerg. Infect. 2005, 11, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Mead, P.S.; Slutsker, L.; Dietz, V.; McCaig, F.; Bresee, J.S.; Shapiro, C. Food-related illness and death in the United States. Emerg. Infect. Dis. 1999, 5, 607–625. [Google Scholar] [CrossRef]
- Amirhossein, M.; Jaykus, L. Quantitative exposure model for the transmission of norovirus in retail food preparation. Int. J. Food Microbiol. 2009, 133, 38–47. [Google Scholar]
- Bean, N.H.; Goulding, J.S.; Daniels, M.T.; Angulo, F.J. Surveillance for foodborne disease outbreaks—United States, 1988–1992. J. Food Prot. 1997, 60, 1265–1286. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.M.; Lopman, B.A.; Lévy, K. A systematic review and meta-analysis of the global seasonality of norovirus. PLoS ONE 2013, 8, e75922. [Google Scholar] [CrossRef] [PubMed]
- Marshall, J.A.; Bruggink, L.D. The dynamics of norovirus outbreak epidemics: Recent insights. Int. J. Environ. Res. Public Health 2011, 8, 1141–1149. [Google Scholar] [CrossRef]
- Rohayem, J. Norovirus seasonality and the potential impact of climate change. Clin. Microbiol. Infect. 2009, 15, 524–527. [Google Scholar] [CrossRef]
- Carmona-Vicente, N.; Fernández-Jiménez, M.; Ribes, J.M.; Téllez-Castillo, C.J.; Khodayar-Pardo, P.; Rodríguez-Diaz, J.; Buesa, J. Norovirus infections and seroprevalence of genotype GII. 4-specific antibodiesin a Spanish population. J. Med. Virol. 2015, 87, 675–682. [Google Scholar] [CrossRef]
- Honma, S.; Nakata, S.; Numata, K.; Kogawa, K.; Yamashita, T.; Oseto, M.; Jiang, X.; Chiba, S. Epidemiological study of prevalence of genogroup II human calicivirus (Mexico virus) infections in Japan and Southeast Asia as determined by enzyme-linked immunosorbent assays. J. Clin. Microbiol. 1998, 36, 2481–2484. [Google Scholar] [CrossRef]
- Simmons, K.; Gambhir, M.; Leon, J.; Lopman, B. Duration of immunity to norovirus gastroenteritis. Emerg. Infect. Dis. 2013, 19, 1260–1267. [Google Scholar] [CrossRef] [PubMed]
- Hall, A.J.; Lopman, B.A.; Payne, D.C.; Patel, M.M.; Gastañaduy, P.A.; Vinjé, J.; Parashar, U.D. Norovirus disease in the United States. Emerg. Infect. Dis. 2013, 19, 1198–1205. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.-C.; Wang, Y.-H.; Wu, C.-Y.; Hung, C.-H.; Jiang, D.D.-S.; Wu, F.-T. A norovirus outbreak in a nursing home: Norovirus shedding time associated with age. J. Clin. Virol. 2013, 56, 96–101. [Google Scholar] [CrossRef] [PubMed]
- Murata, T.; Katsushima, N.; Mizuta, K.; Muraki, Y.; Hongo, S.; Matsuzaki, Y. Prolonged norovirus shedding in infants 6 months of age with gastroenteritis. Pediatr. Infect. Dis. J. 2007, 26, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, K.F.; Khan, Z.U. Numerical analysis of fractional order drinking mathematical model. J. Math. Tech. Model. 2024, 1, 11–24. [Google Scholar]
- Ali, K.W.; Zarin, R.; Zeb, A.; Khan, Y.; Khan, A. Navigating food allergy dynamics via a novel fractional mathematical model for antacid-induced allergies. J. Math. Tech. Model. 2024, 1, 25–51. [Google Scholar]
- Yassine, S.; Khan, A.; Tilioua, M. New method to investigate the impact of independent quadratic stable Poisson jumps on the dynamics of a disease under vaccination strategy. Fractal Fract. 2023, 7, 226. [Google Scholar]
- He, Y.; Wang, Z. Stability analysis and optimal control of a fractional cholera epidemic model. Fractal Fract. 2022, 6, 157. [Google Scholar] [CrossRef]
- Cui, T.; Liu, P.; Din, A. Fractal–fractional and stochastic analysis of norovirus transmission epidemic model with vaccination effects. Sci. Rep. 2021, 11, 24360. [Google Scholar] [CrossRef]
- Shah, S.M.A.; Tahir, H.; Khan, A.; Arshad, A. Stochastic Model on the Transmission of Worms in Wireless Sensor Network. J. Math. Tech. Model. 2024, 1, 75–88. [Google Scholar]
- Ain, Q.T. Nonlinear stochastic cholera epidemic model under the influence of noise. J. Math. Tech. Model. 2024, 1, 52–74. [Google Scholar]
- El Fatini, M.; Sekkak, I. Lévy noise impact on a stochastic delayed epidemic model with Crowly–Martin incidence and crowding effect. Physica A 2020, 541, 123315. [Google Scholar] [CrossRef]
- Dong, Y.; Lin, T. Dynamics of a stochastic rumor propagation model incorporating media coverage and driven by Lévy noise. Chin. Phys. B 2021, 30, 080201. [Google Scholar] [CrossRef]
- Berrhazi, B.-e.; Fatini, M.E.; Garrido, T.C.; Pettersson, R. A stochastic SIRI epidemic model with Lévy noise. Discret. Contin. Dyn. Syst.-Ser. B 2018, 23, 3645–3661. [Google Scholar] [CrossRef]
- Din, A.; Li, Y. Lévy noise impact on a stochastic hepatitis B epidemic model under real statistical data and its fractal–fractional Atangana–Baleanu order model. Phys. Scr. 2021, 96, 124008. [Google Scholar] [CrossRef]
- Guarcello, C.; Valenti, D.; Carollo, A.; Spagnolo, B. Effects of Lévy noise on the dynamics of sine-Gordon solitons in long Josephson junctions. J. Stat. Mech. 2016, 2016, 054012. [Google Scholar] [CrossRef]
- Caraballo, T.; Fatini, M.E.; Khalifi, M.E.; Rathinasamy, A. Analysis of a stochastic coronavirus (COVID-19) Lévy jump model with protective measures. Stoch. Anal. Appl. 2023, 41, 45–59. [Google Scholar] [CrossRef]
- Din, A. Optimal control theory of a novel stochastic human norovirus model and vaccine development. Int. J. Mod. Phys. B 2022, 36, 2250238. [Google Scholar] [CrossRef]
- Gikhman, I.I.; Skorokhod, A.V.; Gikhman, I.I.; Skorokhod, A.V. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Zhang, X.-B.; Wang, X.-D.; Huo, H.-F. Extinction and stationary distribution of a stochastic SIRS epidemic model with standard incidence rate and partial immunity. Phys. A Stat. Mech. Its Appl. 2019, 531, 121548. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, L.; Qiu, Z. Dynamics of a stochastic cholera epidemic model with Lévy process. Physica A 2022, 595, 127069. [Google Scholar] [CrossRef]
- Ain, Q.T.; Din, A.; Qiang, X.; Kou, Z. Dynamics for a Nonlinear Stochastic Cholera Epidemic Model under Lévy Noise. Fractal Fract. 2024, 8, 293. [Google Scholar] [CrossRef]
- Mao, X.; Wei, F.; Wiriyakraikul, T. Positivity preserving truncated Euler-Maruyama method for stochastic Lotka-Volterra competition model. J. Comput. Appl. Math. 2021, 394, 113566. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).