Command Filter-Based Adaptive Neural Control for Nonstrict-Feedback Nonlinear Systems with Prescribed Performance
Abstract
1. Introduction
- (1)
- This paper focuses on a class of NSFNSs, which are more general than SFNSs reported in [3,4] and the traditional NSFNSs proposed in [25,28]. And thus, the developed control scheme has wider applicability. Moreover, for the nonstrict-feedback structure, differently from the variable separation method with the requirement that the system function is less than or equal to a strictly increasing function in [22,23], the property of the Gaussian basis function is utilized without any restriction on the unknown functions.
- (2)
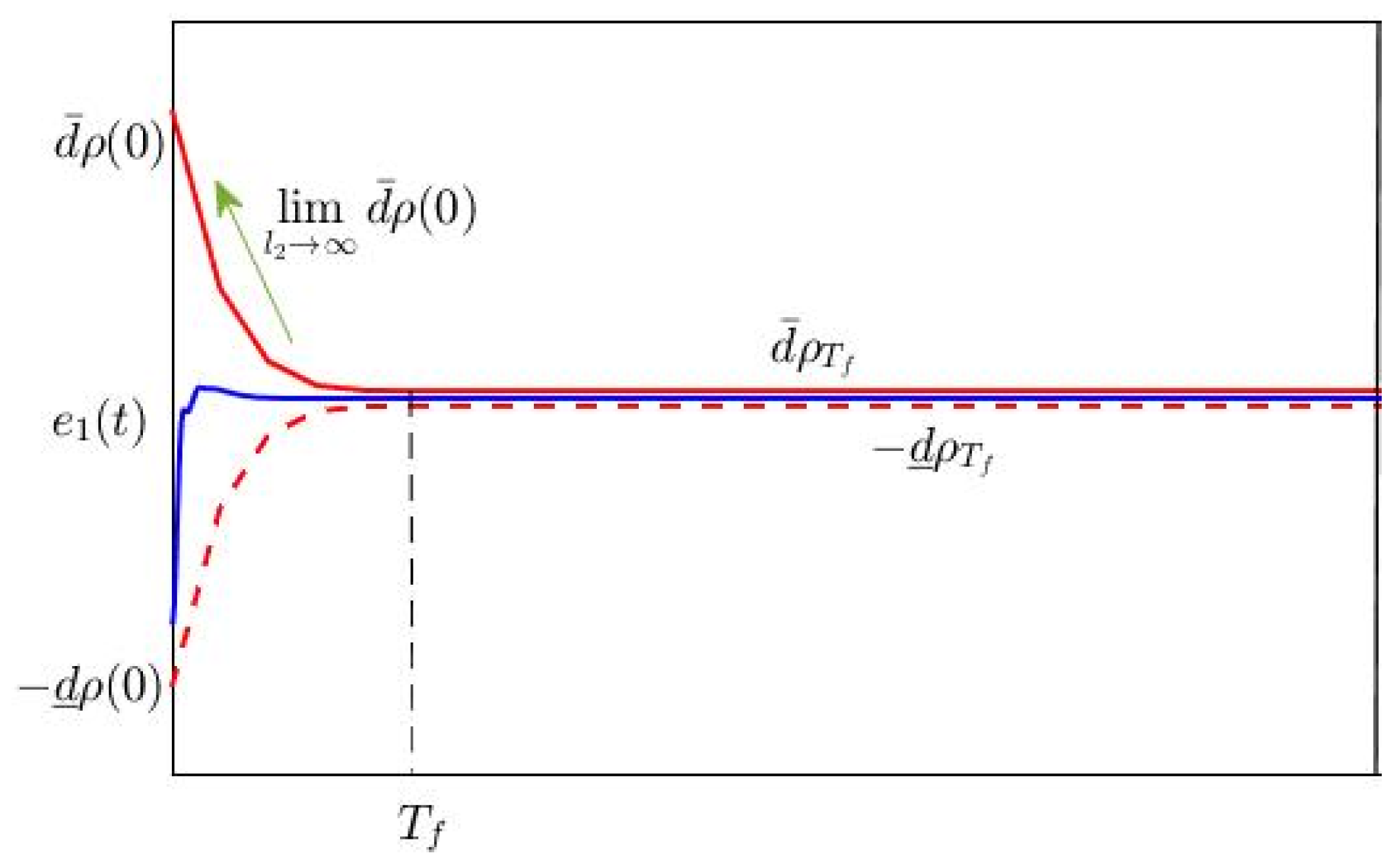
- A novel FTPF with fixed-time boundedness is proposed for the first time. Compared with the existing PPC in [29,31,38] where the accurate has to be known in advance, the limitation is removed in this paper. Moreover, differently from the performance functions reported in [32,34] where the asymptotic convergence of the TE is warranted, the FTPF is developed, and the fixed-time prescribed performance of the TE is guaranteed. That is, the transient and steady-state performance of TE is guaranteed within a fixed time, and the convergence time can be designed according to the actual system requirements.
- (3)
- The proposed fixed-time PPC control strategy solves the EOC problem while eliminating the effects of filtering errors. In contrast to the traditional Backstepping technique with the restriction that the n-th derivatives of the reference signal are continuous [3,4], this paper tackles the EOC problem and relaxes the assumption where only the reference signal and its first-order derivative are continuous. Although the control strategies designed based on the DSC method [5,6,7] also deal with the EOC problem, these strategies ignore the influence of filtering errors and do not consider the PPC of the TE.
2. Problem Description and Preliminaries
2.1. Problem Formulation
2.2. Radial Basis Function Neural Networks
2.3. Performance Function
3. Adaptive NN Controller Design
4. Stability Analysis
- (1)
- the closed-loop system is SGUUB;
- (2)
- the fixed-time prescribed performance of the TE is guaranteed, i.e., Ineq. (3) holds.
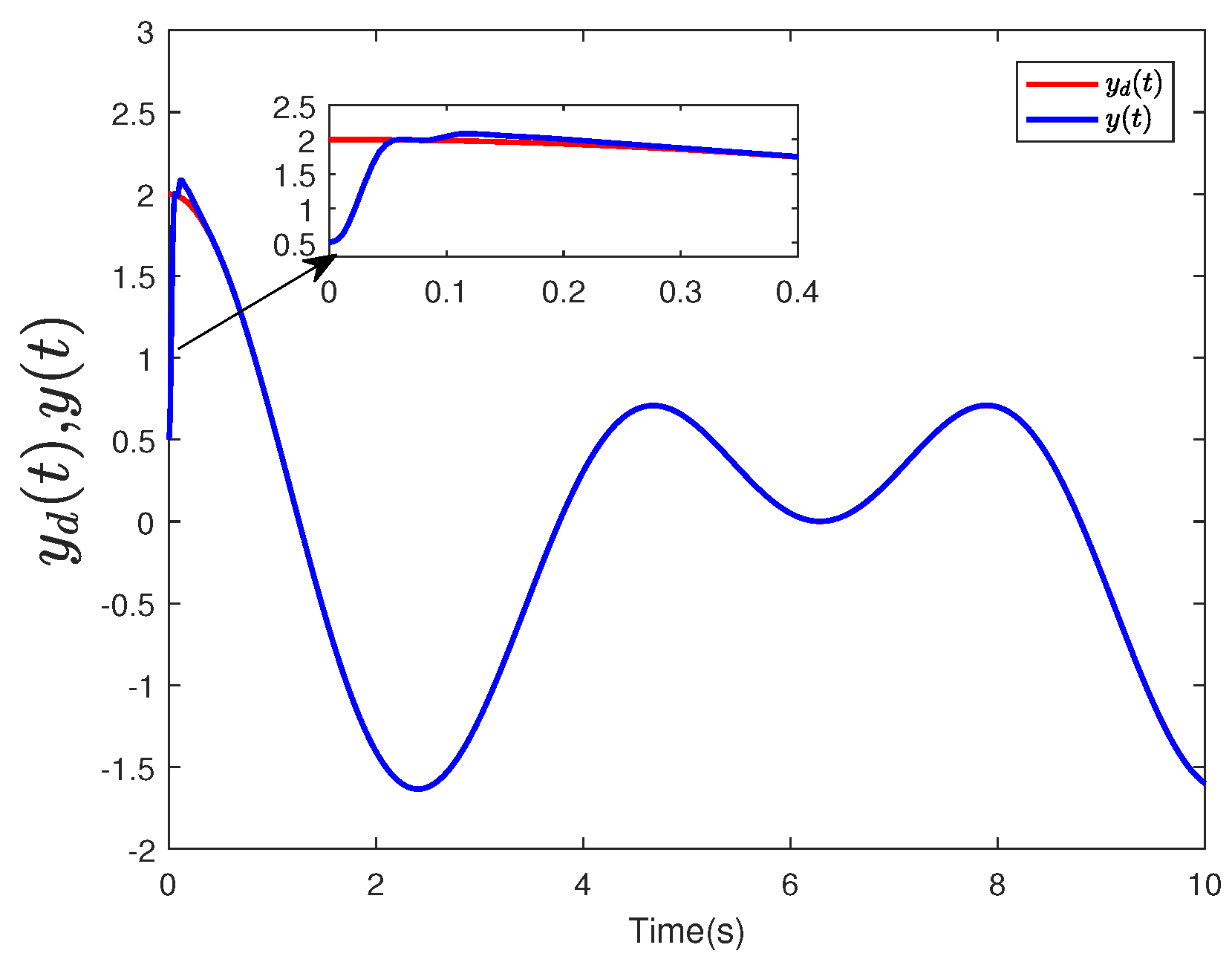
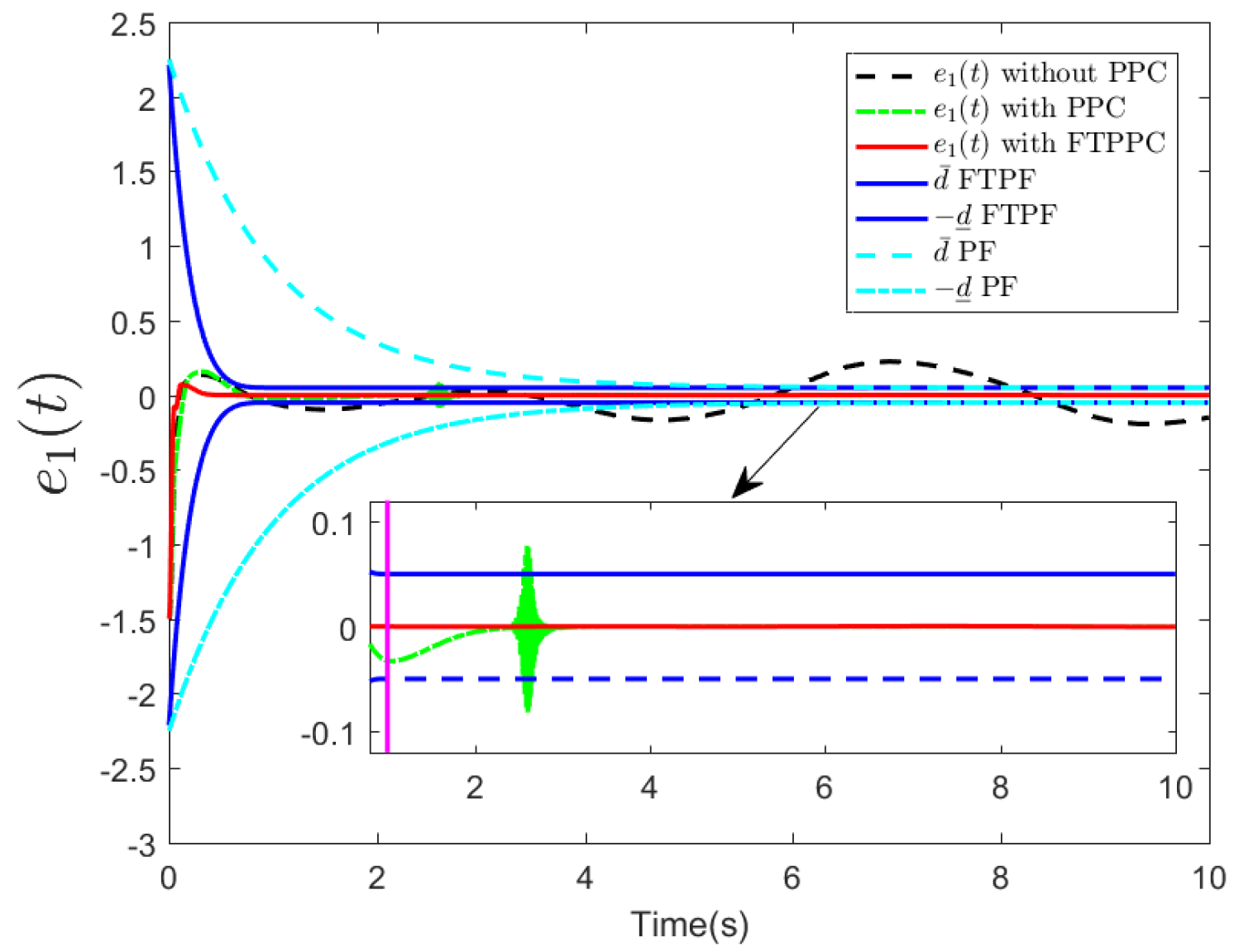
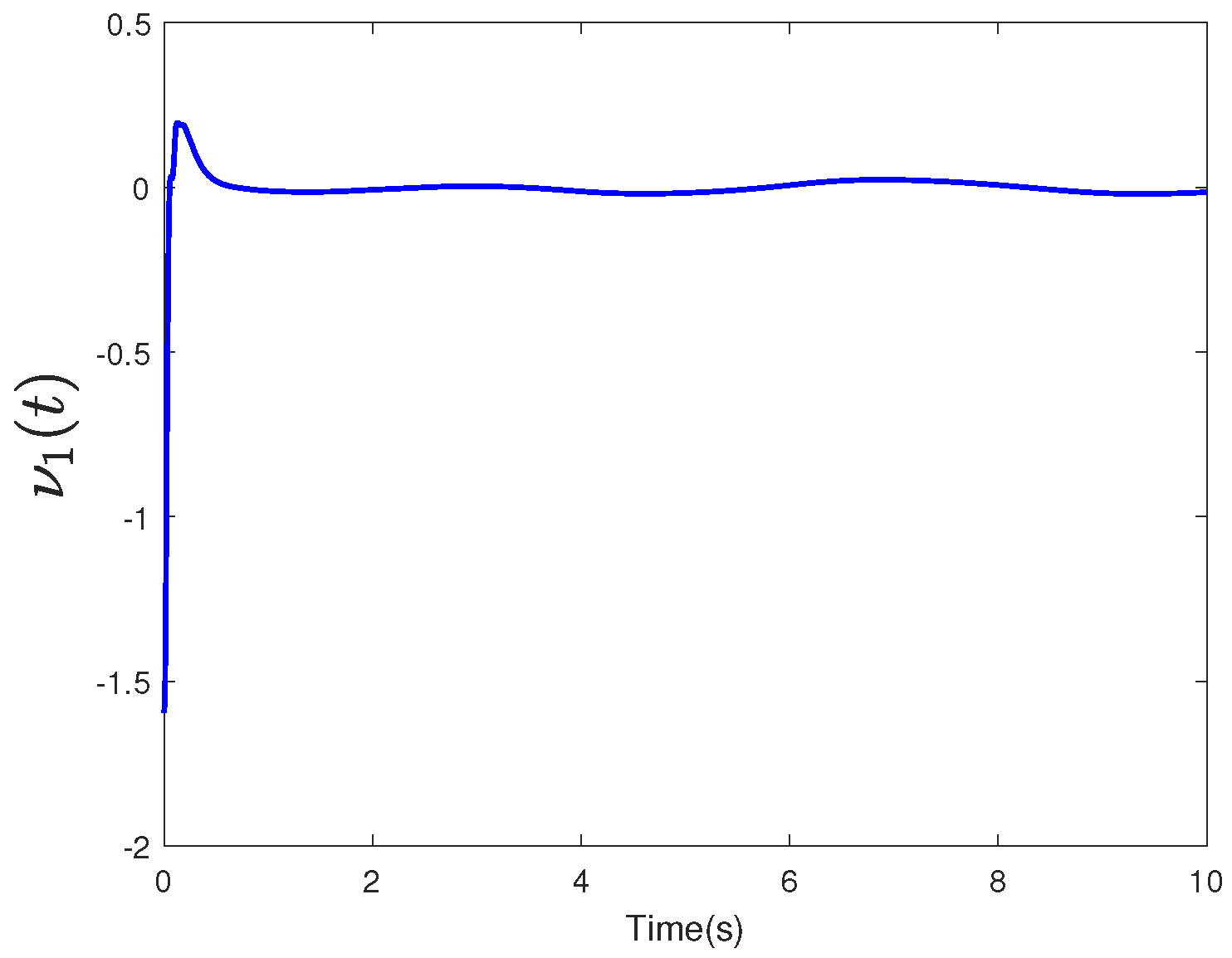
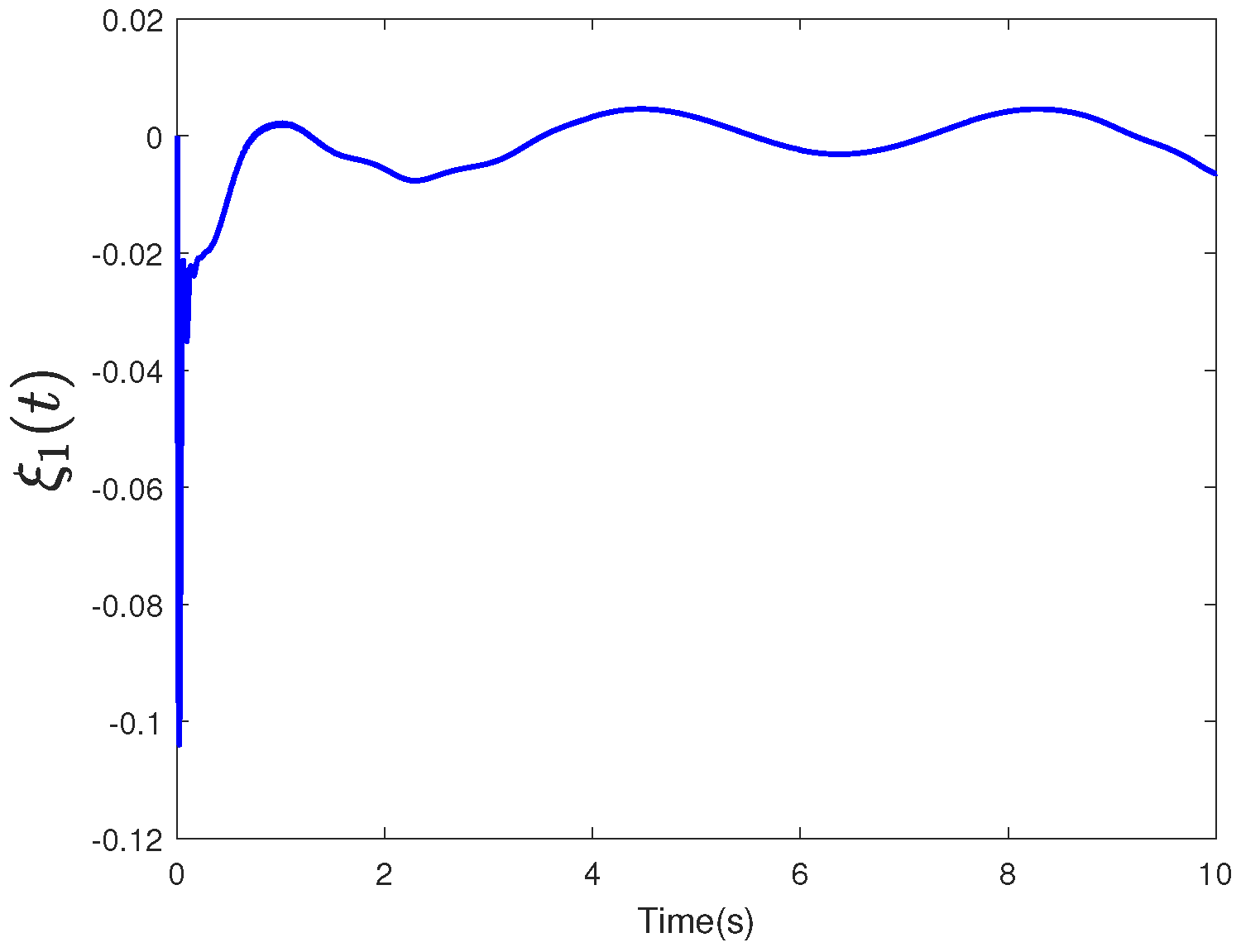
5. Simulation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bechlioulis, C.P.; Doulgeri, Z.; Rovithakis, G.A. Neuro-adaptive force/position control with prescribed performance and guaranteed contact maintenance. IEEE Trans. Neural Netw. 2010, 21, 1857–1868. [Google Scholar] [CrossRef] [PubMed]
- Kostarigka, A.K.; Doulgeri, Z.; Rovithakis, G.A. Prescribed performance tracking for flexible joint robots with unknown dynamics and variable elasticity. Automatica 2013, 49, 1137–1147. [Google Scholar] [CrossRef]
- Zong, G.; Sun, H.; Nguang, S.K. Decentralized adaptive neuro-output feedback saturated control for INS and its application to AUV. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5492–5501. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Wen, C.; Wang, W.; Yang, F. Adaptive backstepping control of nonlinear uncertain systems with quantized states. IEEE Trans. Autom. Control 2019, 64, 4756–4763. [Google Scholar] [CrossRef]
- Swaroop, D.; Hedrick, J.K.; Yip, P.P.; Gerdes, J.C. Dynamic surface control for a class of nonlinear systems. IEEE Trans. Autom. Control 2000, 45, 1893–1899. [Google Scholar] [CrossRef]
- Wang, C.; Li, W.; Liang, M. Event-Triggered Adaptive Fuzzy Control for Strict-Feedback Nonlinear FOSs Subjected to Finite-Time Full-State Constraints. Fractal Fract. 2024, 8, 160. [Google Scholar] [CrossRef]
- Si, W.; Dong, X. Adaptive neural DSC for nonlinear switched systems with prescribed performance and input saturation. IEEE/CAA J. Autom. Sin. 2017, 99, 1–9. [Google Scholar] [CrossRef]
- Farrell, J.A.; Polycarpou, M.; Sharma, M.; Dong, W. Command Filtered Backstepping. IEEE Trans. Autom. Control 2009, 54, 1391–1395. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A.; Polycarpou, M.M.; Djapic, V.; Sharma, M. Command Filtered Adaptive Backstepping. IEEE Trans. Control Syst. Technol. 2012, 20, 566–580. [Google Scholar] [CrossRef]
- Fu, C.; Wang, Q.G.; Yu, J.; Lin, C. Neural Network-Based Finite-Time Command Filtering Control for Switched Nonlinear Systems with Backlash-Like Hysteresis. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 3268–3273. [Google Scholar] [CrossRef]
- Song, S.; Song, X.; Tejado, I. Disturbance Observer-Based Event-Triggered Adaptive Command Filtered Backstepping Control for Fractional-Order Nonlinear Systems and Its Application. Fractal Fract. 2023, 7, 810. [Google Scholar] [CrossRef]
- Ma, R.; Chen, J.; Lv, C.; Yang, Z.; Hu, X. Backstepping Control with a Fractional-Order Command Filter and Disturbance Observer for Unmanned Surface Vehicles. Fractal Fract. 2024, 8, 23. [Google Scholar] [CrossRef]
- Liu, H.; Lu, G.; Zhong, Y. Robust LQR Attitude Control of a 3-DOF Laboratory Helicopter for Aggressive Maneuvers. IEEE Trans. Ind. Electron. 2013, 60, 4627–4636. [Google Scholar] [CrossRef]
- Wang, S.; Na, J.; Chen, Q. Adaptive predefined performance sliding mode control of motor driving systems with disturbances. IEEE Trans. Energy Convers. 2020, 36, 1931–1939. [Google Scholar] [CrossRef]
- Shang, Y.; Li, X.; Qian, H.; Wu, S.; Pan, Q.; Huang, L.; Jiao, Z. A novel electro hydrostatic actuator system with energy recovery module for more electric aircraft. IEEE Trans. Ind. Electron. 2019, 67, 2991–2999. [Google Scholar] [CrossRef]
- Ge, S.S.; Zhang, J. Neural-network control of nonaffine nonlinear system with zero dynamics by state and output feedback. IEEE Trans. Neural Netw. 2003, 14, 900–918. [Google Scholar] [CrossRef] [PubMed]
- Liang, H.; Liu, G.; Zhang, H.; Huang, T. Neural-Network-Based Event-Triggered Adaptive Control of Nonaffine Nonlinear Multiagent Systems with Dynamic Uncertainties. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 2239–2250. [Google Scholar] [CrossRef] [PubMed]
- Meng, W.; Yang, Q.; Jagannathan, S.; Sun, Y. Adaptive neural control of high-order uncertain nonaffine systems: A transformation to affine systems approach. Automatica 2014, 50, 1473–1480. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.; Yin, Z. Adaptive neural network control of an uncertain robot with full-state constraints. IEEE Trans. Cybern. 2015, 46, 620–629. [Google Scholar] [CrossRef]
- Peng, L.; Xun, L.; Han, Y.; Zhang, S.; Liu, J. Extra—Atmospheric Aircraft Control System Design Based on Loop Shaping Method. In Proceedings of the 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Xuzhou, China, 21–24 July 2018. [Google Scholar]
- Li, Y.; Tong, S. Command-Filtered-Based Fuzzy Adaptive Control Design for MIMO-Switched Nonstrict-Feedback Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2017, 25, 668–681. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Lin, C. Observer-Based Adaptive Neural Network Control for Nonlinear Systems in Nonstrict-Feedback Form. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 89–98. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Liu, X.; Liu, K.; Karimi, H.R. Approximation-Based Adaptive Fuzzy Tracking Control for a Class of Nonstrict-Feedback Stochastic Nonlinear Time-Delay Systems. IEEE Trans. Fuzzy Syst. 2015, 23, 1746–1760. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.P.; Ge, S.S.; Lin, C. Adaptive Fuzzy Control of a Class of Nonlinear Systems by Fuzzy Approximation Approach. IEEE Trans. Fuzzy Syst. 2012, 20, 1012–1021. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q. Adaptive Fuzzy Finite-Time Control for Nonstrict-Feedback Nonlinear Systems. IEEE Trans. Cybern. 2022, 52, 10420–10429. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Yang, X. Adaptive neural control for non-strict-feedback nonlinear systems with input delay. Inf. Sci. 2020, 514, 605–616. [Google Scholar] [CrossRef]
- Wang, H.; Xu, K.; Qiu, J. Event-Triggered Adaptive Fuzzy Fixed-Time Tracking Control for a Class of Nonstrict-Feedback Nonlinear Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3058–3068. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, L.Y. Adaptive tracking control for constrained nonlinear nonstrict-feedback switched stochastic systems with unknown control directions. Appl. Math. Comput. 2024, 473. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Robust Adaptive Control of Feedback Linearizable MIMO Nonlinear Systems with Prescribed Performance. IEEE Trans. Autom. Control 2008, 53, 2090–2099. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems. Automatica 2009, 45, 532–538. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Bu, X.; Zhao, J.; Na, J.; Gao, H. Optimal Tracking Control for Autonomous Vehicle with Prescribed Performance via Adaptive Dynamic Programming. IEEE Trans. Intell. Transp. Syst. 2024, 1–13. [Google Scholar] [CrossRef]
- Bu, X.; Wu, X.; Zhu, F.; Huang, J.; Ma, Z.; Zhang, R. Novel prescribed performance neural control of a flexible air-breathing hypersonic vehicle with unknown initial errors. ISA Trans. 2015, 59, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Zhang, C.L. Adaptive Fault-Tolerant Control with Global Prescribed Performance of Strict-Feedback Systems. IEEE Trans. Syst. Man Cybern. Syst. 2024. [Google Scholar] [CrossRef]
- Song, X.; Sun, P.; Song, S.; Stojanovic, V. Saturated-threshold event-triggered adaptive global prescribed performance control for nonlinear Markov jumping systems and application to a chemical reactor model. Expert Syst. Appl. 2024, 249, 123490. [Google Scholar] [CrossRef]
- Liu, Y.; Yao, D.; Li, H.; Lu, R. Distributed Cooperative Compound Tracking Control for a Platoon of Vehicles with Adaptive NN. IEEE Trans. Cybern. 2021, 52, 7039–7048. [Google Scholar] [CrossRef]
- Ren, Y.; Geng, Y.; Cao, Q.; Wu, F. Finite-time prescribed performance control for approaching non-cooperative target’s feature surface. Nonlinear Dyn. 2024, 112, 9179–9193. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y. Global adaptive output-feedback tracking with prescribed performance for uncertain nonlinear systems. Sci. China Inf. Sci. 2024, 67, 152201. [Google Scholar] [CrossRef]
- Ma, C.; Dong, D. Finite-Time Prescribed Performance Time-Varying Formation Control for Second-Order Multi-Agent Systems with Non-Strict Feedback Based on a Neural Network Observer. IEEE-CAA J. Autom. Sin. 2024, 11, 1039–1050. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Rovithakis, G.A. A low-complexity global approximation-free control scheme with prescribed performance for unknown pure feedback systems. Automatica 2014, 50, 1217–1226. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems; Patience Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Ge, S.S.; Hang, C.C.; Lee, T.H.; Zhang, T. Stable Adaptive Neural Network Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Sun, Y.; Chen, B.; Lin, C.; Wang, H.; Zhou, S. Adaptive neural control for a class of stochastic nonlinear systems by backstepping approach. Inf. Sci. 2016, 369, 748–764. [Google Scholar] [CrossRef]


| Initial conditions | 0.5 | Parameters | Value | |
| 1 | 1 | |||
| 0 | 200 | |||
| 0 | 10 | |||
| Node number | q | 9 | 20 | |
| Performance function | 1 | 0.05 | ||
| 1 | 0.05 | |||
| Command filter parameters | 100 | 1 | ||
| 0.5 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Li, J.; Ge, S.; Liang, X.; Han, T. Command Filter-Based Adaptive Neural Control for Nonstrict-Feedback Nonlinear Systems with Prescribed Performance. Fractal Fract. 2024, 8, 339. https://doi.org/10.3390/fractalfract8060339
Yang X, Li J, Ge S, Liang X, Han T. Command Filter-Based Adaptive Neural Control for Nonstrict-Feedback Nonlinear Systems with Prescribed Performance. Fractal and Fractional. 2024; 8(6):339. https://doi.org/10.3390/fractalfract8060339
Chicago/Turabian StyleYang, Xiaoli, Jing Li, Shuzhi (Sam) Ge, Xiaoling Liang, and Tao Han. 2024. "Command Filter-Based Adaptive Neural Control for Nonstrict-Feedback Nonlinear Systems with Prescribed Performance" Fractal and Fractional 8, no. 6: 339. https://doi.org/10.3390/fractalfract8060339
APA StyleYang, X., Li, J., Ge, S., Liang, X., & Han, T. (2024). Command Filter-Based Adaptive Neural Control for Nonstrict-Feedback Nonlinear Systems with Prescribed Performance. Fractal and Fractional, 8(6), 339. https://doi.org/10.3390/fractalfract8060339






