An Approximation Method for Fractional-Order Models Using Quadratic Systems and Equilibrium Optimizer
Abstract
1. Introduction
- This study is the first to use a curve fitting method in the time domain using a quadratic standard model structure and EO optimizer. The proposed method allows us to achieve integer approximations with a lower order model and smaller margin of error. Thus, using the proposed method, classical control theory computations, such as State-Space form, Root-Locus and Routh-Hurwitz analysis, can be easily implemented.
- Using the proposed direct method, an integer-order approximate transfer function is achieved with a maximum of five orders. Additionally, lower-order approximation is obtained compared to operator-based methods.
- It has been shown that the proposed method is more accurate than operator-based methods in terms of frequency and time response performances.
- These are applicable to closed-loop fractional-order systems.
2. Equilibrium Optimizer Algorithm
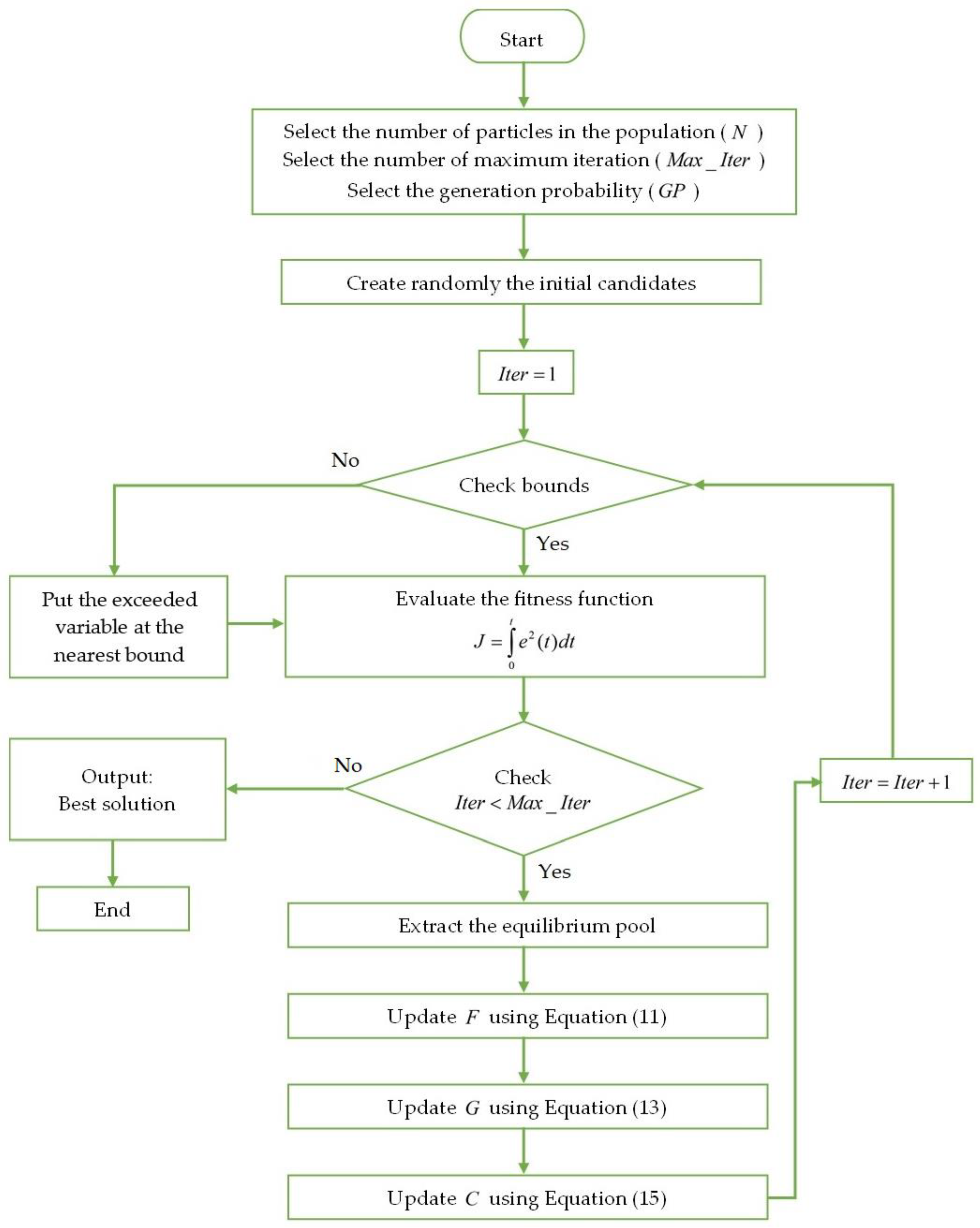
3. The Methodology of the Proposed Direct Integer-Order Approximation Method
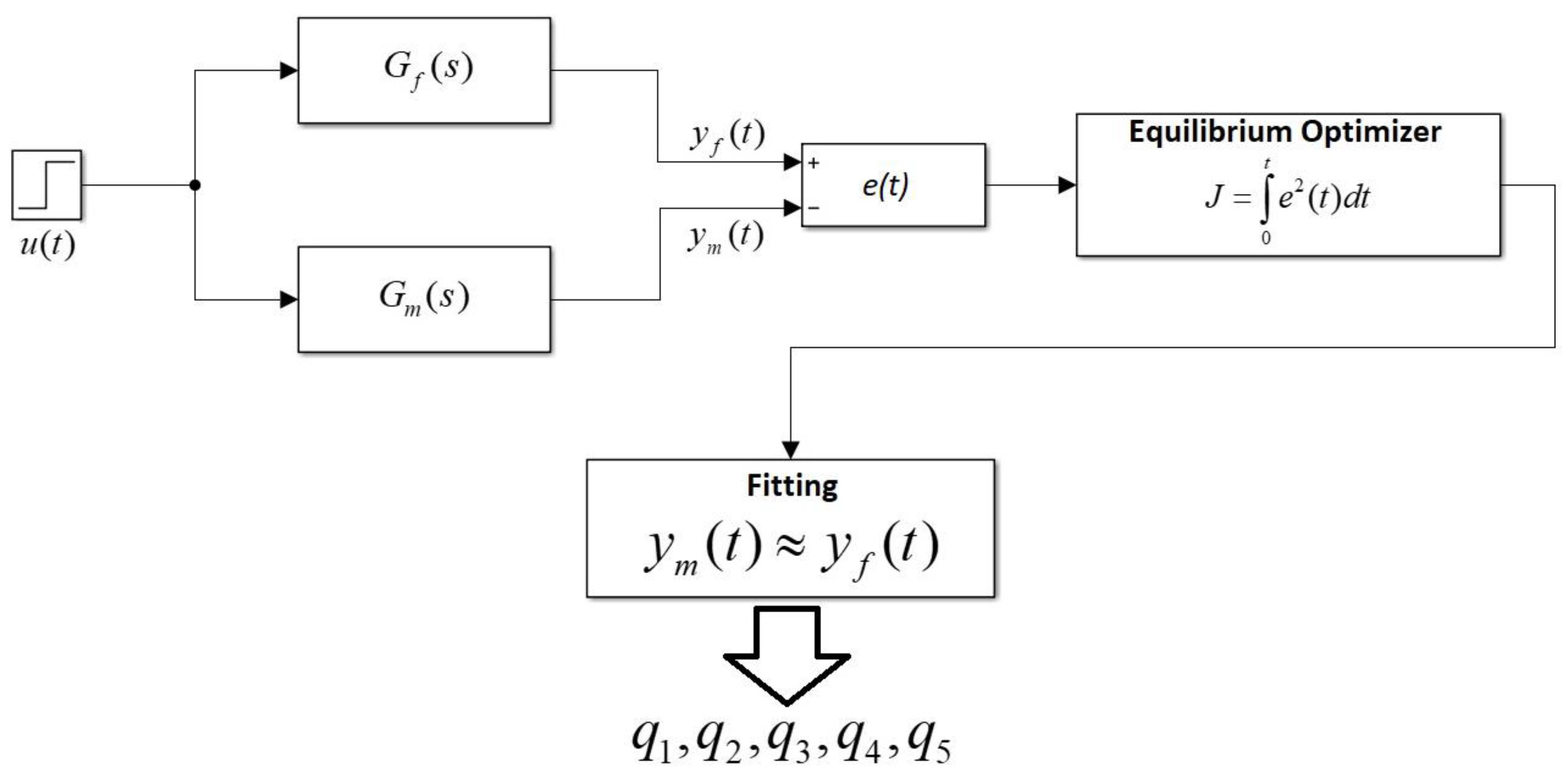
3.1. Block Scheme for Curve Fitting Computation with the EO
3.2. Determination of the Proposed Model-Transfer-Function Parameters
- The Integral of Error (IE) is defined as:
- The Mean Square Error (MSE) is defined as:
- The Integral Squared Error (ISE) is defined as:
- The Integral Absolute Error (IAE) is defined as:
- The Integral of the Square of the Time-Weighted Error (ITSE) is defined as:
- The Integral of the Absolute of the Time-Weighted Error (ITAE) is defined as:
4. Numerical Examples
4.1. Examining the Proposed Method in Various Transfer Function Forms
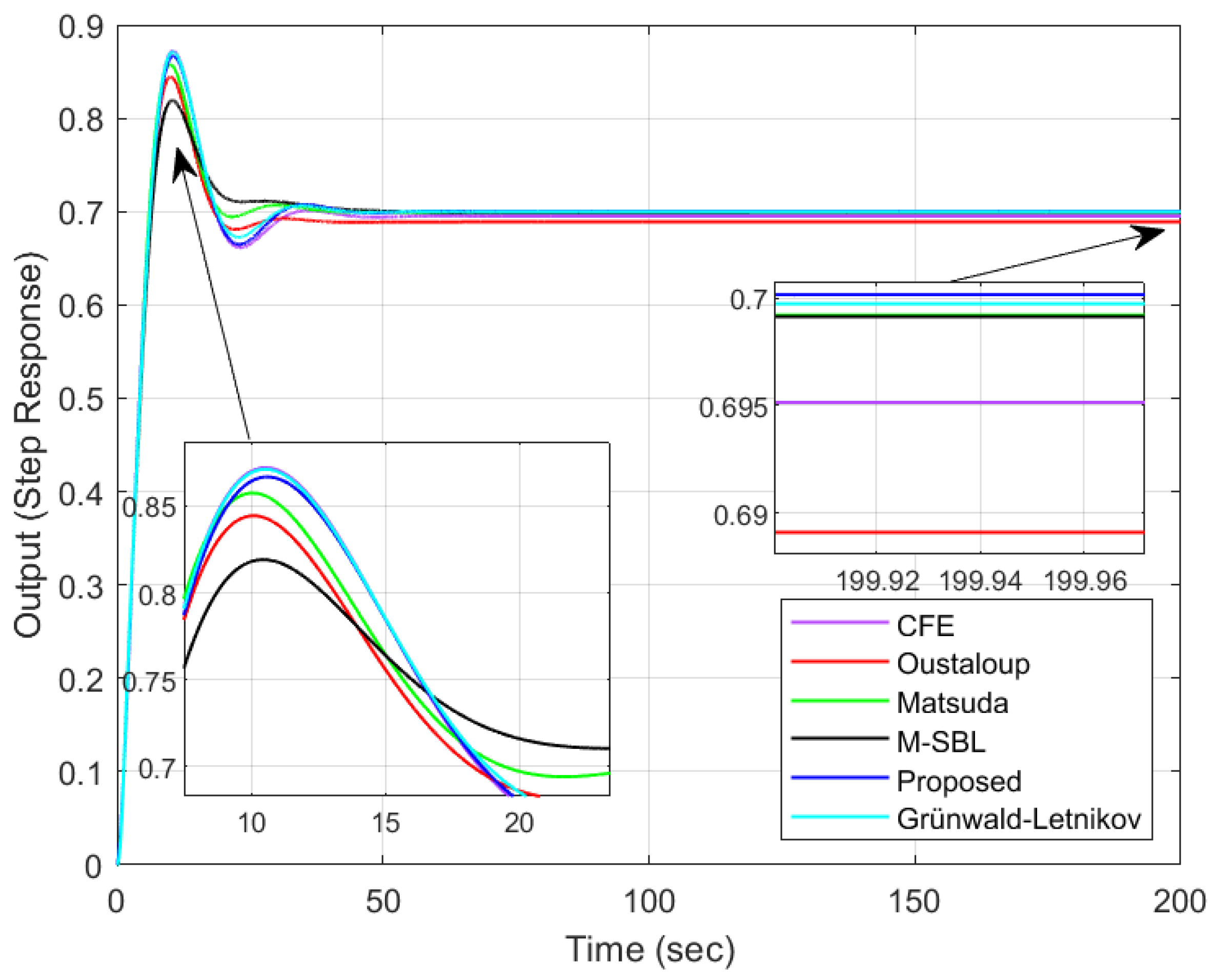
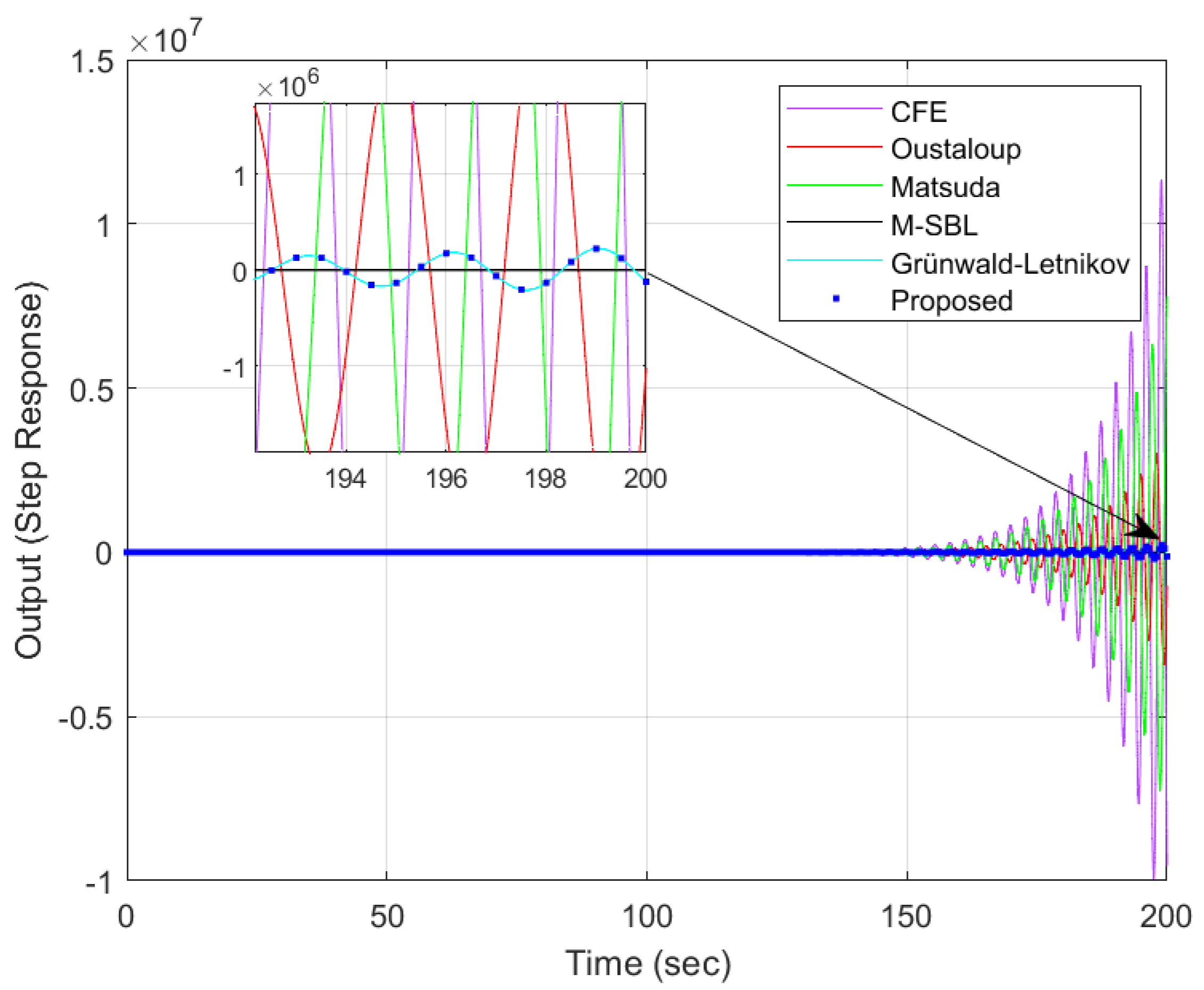
4.2. Comparison with Direct Approximation Methods in the Literature
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls: Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Yu, W.; Luo, Y.; Pi, Y. Fractional order modeling and control for permanent magnet synchronous motor velocity servo system. Mechatronics 2013, 23, 813–820. [Google Scholar] [CrossRef]
- Das, S. Functional Fractional Calculus for System Identification and Controls; Springer-Verlag: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Zhao, K. Existence, stability and simulation of a class of nonlinear fractional Langevin equations involving nonsingular Mittag–Leffler kernel. Fractal Fract. 2022, 6, 469. [Google Scholar] [CrossRef]
- Rendón, J.E.; Mejía, C.E. Fractional order modeling of a nonlinear electromechanical system. Enfoque UTE 2018, 9, 45–56. [Google Scholar]
- Hartley, T.T.; Lorenzo, C.F. Dynamics and control of initialized fractional-order systems. Nonlinear Dyn. 2002, 29, 201–233. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Inc.: Redding, CT, USA, 2006; Volume 2. [Google Scholar]
- Zhang, T.; Xiong, L. Periodic motion for impulsive fractional functional differential equations with piecewise Caputo derivative. Appl. Math. Lett. 2020, 101, 106072. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y. Exponential Euler scheme of multi-delay Caputo–Fabrizio fractional-order differential equations. Appl. Math. Lett. 2022, 124, 107709. [Google Scholar] [CrossRef]
- Rauh, A. Exponential Enclosures for the Verified Simulation of Fractional-Order Differential Equations. Fractal Fract. 2022, 6, 567. [Google Scholar] [CrossRef]
- Chen, Y.; Petras, I.; Vinagre, B. A list of Laplace and Inverse Laplace Transforms Related to Fractional Order Calculus. 2001, pp. 1–3. Available online: http://ivopetras.tripod.com/foc_laplace.pdf (accessed on 6 January 2023).
- Iqbal, A.; Shekh, R.R. A comprehensive study on different approximation methods of Fractional order system. Int. Res. J. Eng. Technol. IRJET 2016, 3, 1848–1863. [Google Scholar]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: Fractional-order modeling and control toolbox for MATLAB. In Proceedings of the 2011 18th International Conference on Mixed Design of Integrated Circuits and Systems (MIXDES), Gliwice, Poland, 16–18 June 2011; pp. 684–689. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Polubny, I. Fractional-order systems and PIλDμ controller. IEEE Trans. Autom. Control. 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Atherton, D.P.; Tan, N.; Yüce, A. Methods for computing the time response of fractional-order systems. IET Control. Theory Appl. 2014, 9, 817–830. [Google Scholar] [CrossRef]
- Vinagre, B.; Podlubny, I.; Hernandez, A.; Feliu, V. Some approximations of fractional order operators used in control theory and applications. Fract. Calc. Appl. Anal. 2000, 3, 231–248. [Google Scholar]
- Krishna, B. Studies on fractional order differentiators and integrators: A survey. Signal Process. 2011, 91, 386–426. [Google Scholar] [CrossRef]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F.M. Frequency-band complex noninteger differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Carlson, G.; Halijak, C. Approximation of fractional capacitors (1/s)^(1/n) by a regular Newton process. IEEE Trans. Circuit Theory 1964, 11, 210–213. [Google Scholar] [CrossRef]
- Matsuda, K.; Fujii, H. H~ Optimized Wave-Absorbing Control: Analytical and Experimental Results. J. Guid. Control. Dyn. 1993, 16, 1146. [Google Scholar] [CrossRef]
- Charef, A.; Sun, H.; Tsao, Y.; Onaral, B. Fractal system as represented by singularity function. IEEE Trans. Autom. Control. 1992, 37, 1465–1470. [Google Scholar] [CrossRef]
- Khanra, M.; Pal, J.; Biswas, K. Rational approximation of fractional operator—A comparative study. In Proceedings of the 2010 International Conference on Power, Control and Embedded Systems, Allahabad, India, 29 November–1 December 2010; pp. 1–5. [Google Scholar]
- Deniz, F.N.; Alagoz, B.B.; Tan, N.; Atherton, D.P. An integer order approximation method based on stability boundary locus for fractional order derivative/integrator operators. ISA Trans. 2016, 62, 154–163. [Google Scholar] [CrossRef]
- Yüce, A.; Tan, N. A New Integer Order Approximation Table for Fractional Order Derivative Operators. In Proceedings of the IFAC 2017 World Congress, Toulouse, France, 9–14 July 2017; pp. 9736–9741. [Google Scholar]
- Shrivastava, N.; Varshney, P. Frequency band implementation of non-integer order functions. In Proceedings of the 5th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 22–23 February 2018; pp. 852–857. [Google Scholar]
- Deniz, F.N.; Alagoz, B.B.; Tan, N.; Koseoglu, M. Revisiting four approximation methods for fractional order transfer function implementations: Stability preservation, time and frequency response matching analyses. Annu. Rev. Control. 2020, 49, 239–257. [Google Scholar] [CrossRef]
- Casagrande, D.; Krajewski, W.; Viaro, U. The Integer–Order Approximation of Fractional–Order Systems in the Loewner Framework. IFAC-PapersOnLine 2019, 52, 43–48. [Google Scholar] [CrossRef]
- Krajewski, W.; Viaro, U. A method for the integer-order approximation of fractional-order systems. J. Frankl. Inst. 2014, 351, 555–564. [Google Scholar] [CrossRef]
- Mansouri, R.; Bettayeb, M.; Djennoune, S. Optimal reduced-order approximation of fractional dynamical systems. In Proceedings of the AIP Conference Proceedings, Annaba, Algeria, 30 June–2 July 2008; pp. 127–132. [Google Scholar]
- Rachid, M.; Maamar, B.; Said, D. Comparison between two approximation methods of state space fractional systems. Signal Process. 2011, 91, 461–469. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. Rational approximations in the simulation and implementation of fractional-order dynamics: A descriptor system approach. Automatica 2010, 46, 94–100. [Google Scholar] [CrossRef]
- Mihaly, V.; Şuşcă, M.; Dulf, E.H.; Dobra, P. Approximating the Fractional-Order Element for the Robust Control Framework. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 1151–1157. [Google Scholar]
- Mouhou, A.; Badri, A. Low Integer-Order Approximation of Fractional-Order Systems Using Grey Wolf Optimizer-Based Cuckoo Search Algorithm. Circuits Syst. Signal Process. 2022, 41, 1869–1894. [Google Scholar] [CrossRef]
- Maiti, D.; Konar, A. Approximation of a fractional order system by an integer order model using particle swarm optimization technique. arXiv 2008, arXiv:0811.0077. [Google Scholar]
- Soloklo, H.N.; Bigdeli, N. Direct approximation of fractional order systems as a reduced integer/fractional-order model by genetic algorithm. Sādhanā 2020, 45, 277. [Google Scholar] [CrossRef]
- Mahata, S.; Saha, S.; Kar, R.; Mandal, D. Optimal integer-order rational approximation of α and α + β fractional-order generalised analogue filters. IET Signal Process. 2019, 13, 516–527. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Nazaroff, W.W.; Alvarez-Cohen, L. Environmental Engineering Science; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Dogruer, T. Design of I-PD Controller Based Modified Smith Predictor for Processes with Inverse Response and Time Delay Using Equilibrium Optimizer. IEEE Access 2023, 11, 14636–14646. [Google Scholar] [CrossRef]
- Haidekker, M.A. Linear Feedback Controls: The Essentials; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Sundaram, S. ECE 380: Control systems. In Course Notes; Department of Electrical and Computer Engineering, University of Waterloo: Waterloo, ON, Canada, 2013; Available online: https://engineering.purdue.edu/~sundara2/misc/ece380_notes.pdf (accessed on 10 January 2023).
- Graham, D.; Lathrop, R.C. The synthesis of” optimum” transient response: Criteria and standard forms. Trans. Am. Inst. Electr. Eng. Part II Appl. Ind. 1953, 72, 273–288. [Google Scholar] [CrossRef]
- Atherton, D.; Boz, A. Using standard forms for controller design. In Proceedings of the UKACC International Conference on Control’98 (Conf. Publ. No. 455), Swansea, UK, 1–4 September 1998; pp. 1066–1071. [Google Scholar]
- Joseph, S.B.; Dada, E.G.; Abidemi, A.; Oyewola, D.O.; Khammas, B.M. Metaheuristic algorithms for PID controller parameters tuning: Review, approaches and open problems. Heliyon 2022, e09399. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.; Atherton, D.P. Linear Feedback Control: Analysis and Design with MATLAB; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007. [Google Scholar]
- Wang, C.-H.; Chen, C.-Y. Finding the integer order systems for fractional order systems via fractional operational matrices. In Proceedings of the 2012 9th IEEE International Conference on Networking, Sensing and Control, Beijing, China, 11–14 April 2012; pp. 267–270. [Google Scholar]
- Senol, B.; Yeroglu, C. Filter approximation and model reduction comparison for fractional order systems. In Proceedings of the ICFDA’14 International Conference on Fractional Differentiation and Its Applications 2014, Catania, Italy, 23–25 June 2014; pp. 1–6. [Google Scholar]
- Verma, S.K.; Nagar, S.K. Approximation and order reduction of fractional order SISO system. In Proceedings of the 2016 IEEE Annual India Conference (INDICON), Bangalore, India, 16–18 December 2016; pp. 1–6. [Google Scholar]

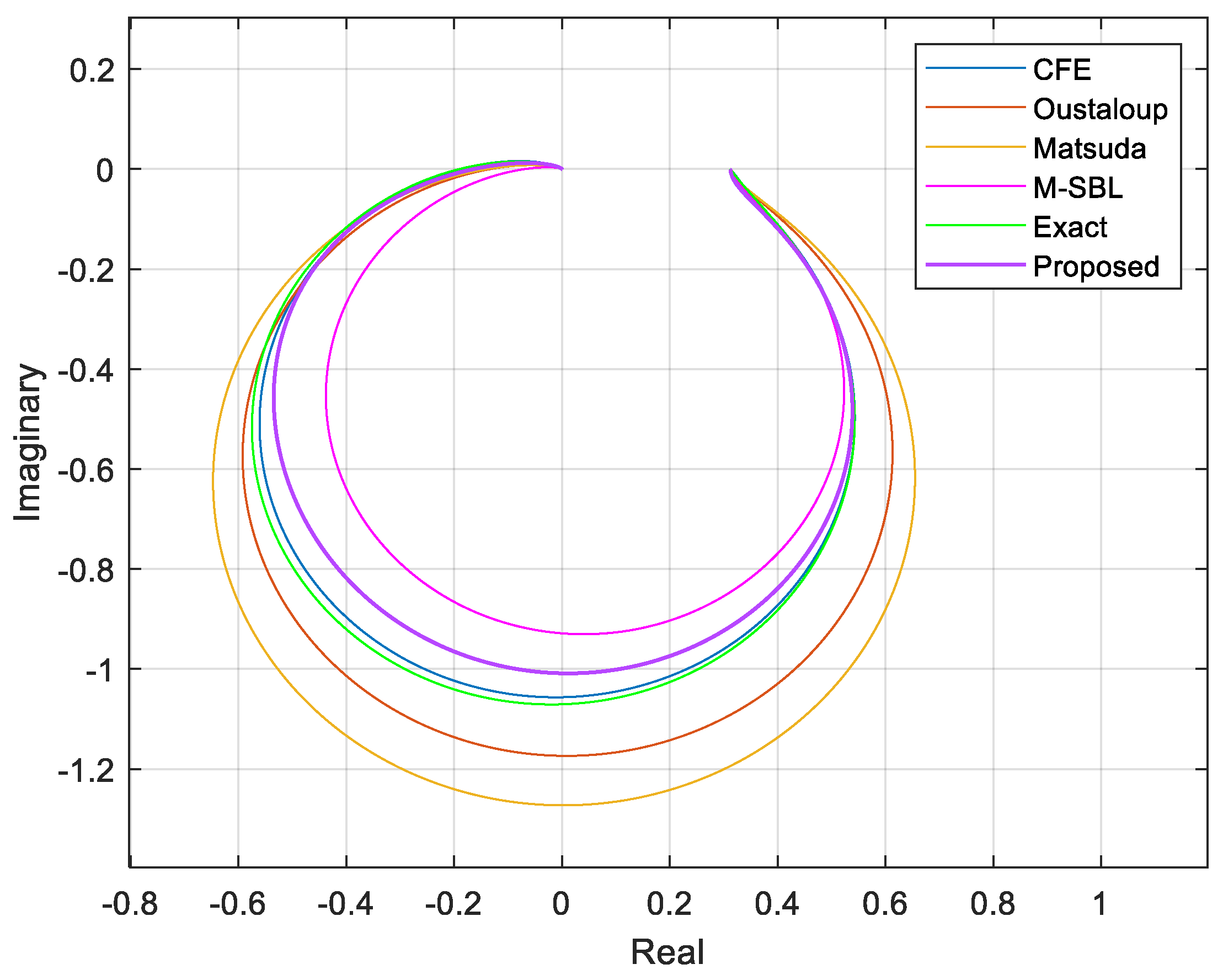
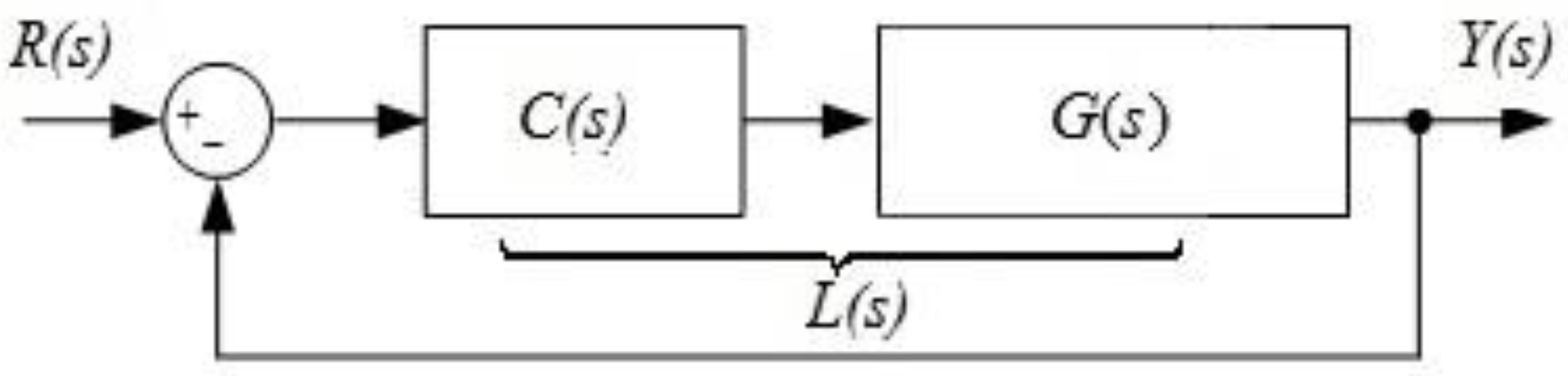



| Method | Order of Approximation | MSE (10−5) |
|---|---|---|
| CFE | 22 | 2.5229 |
| 28 | 0.7592 | |
| 34 | 0.2811 | |
| Oustaloup | 22 | 13.9400 |
| 34 | 11.5180 | |
| 48 | 11.6350 | |
| Matsuda | 22 | 3.5524 |
| 28 | 0.6710 | |
| 34 | 0.0852 | |
| M-SBL | 22 | 13.5050 |
| 28 | 0.4819 | |
| 34 | 0.2716 | |
| Proposed | 4 | 0.3864 |
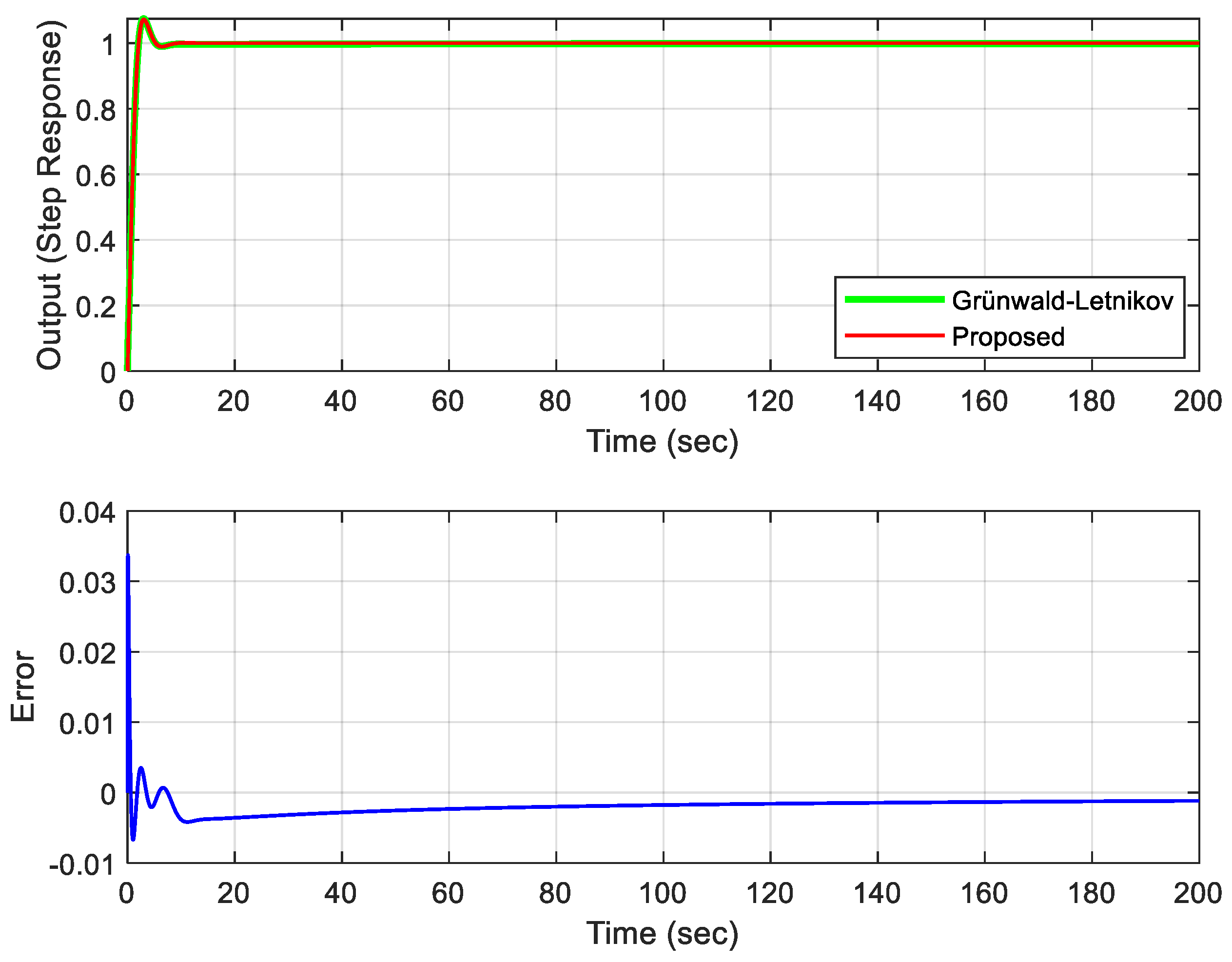
| Methods | Rise Time (s) | Settling Time (5%) (s) | Peak Time (s) | Peak Value | Overshoot (%) | Steady State Error |
|---|---|---|---|---|---|---|
| GL Method | 4.4106 | 16.9845 | 10.5200 | 0.8711 | 24.4432 | 0 |
| 4.4276 | 23.3043 | 10.6000 | 0.8667 | 23.8176 | 0 | |
| GCFE(s) | 4.4009 | 25.0050 | 10.5300 | 0.8720 | 24.5749 | 0.0048 |
| GOus(s) | 4.3822 | 15.9932 | 10.0800 | 0.8444 | 20.6241 | 0.0110 |
| 4.3098 | 16.4427 | 10.0400 | 0.8575 | 22.4929 | 0.0008 | |
| 4.5750 | 17.2698 | 10.4400 | 0.8191 | 17.0191 | 0.0006 |
| Methods | Order of Approximation | Gain Margin (dB) | Phase Margin (Degree) | Critical Point |
|---|---|---|---|---|
| CFE | 8 | 14.533 | 68.9600 | −0.1877 |
| Oustaloup | 8 | 17.489 | 58.3900 | −0.1337 |
| Matsuda | 8 | 17.100 | 51.9000 | −0.1398 |
| M-SBL | 8 | 23.200 | None | −0.0693 |
| Proposed | 5 | 15.713 | 99.4540 | −0.1641 |
| Exact | - | 14.406 | 109.8400 | −0.1904 |
| Methods | Rise Time (s) | Settling Time (5%) (s) | Peak Time (s) | Peak Value | Overshoot (%) | Steady State Error |
|---|---|---|---|---|---|---|
| GL Method | 1.0630 | 21.9606 | 2.8400 | 1.5658 | 56.5764 | 0 |
| GProposed (s) | 1.0719 | 24.0946 | 2.8500 | 1.5799 | 57.9923 | 0 |
| 0.9951 | 26.6459 | 2.8400 | 1.6332 | 63.3222 | 0.0258 | |
| GBlock_Pulse1(s) | 1.1777 | 31.8859 | 3.1100 | 1.5282 | 52.8180 | 0.0458 |
| 0.8756 | 21.1973 | 2.7300 | 1.6351 | 63.5147 | 0.0293 | |
| GBT(s) | 0.8883 | 32.3321 | 2.8000 | 1.7945 | 79.4513 | 0.0007 |
| 0.8388 | 29.6601 | 2.8800 | 1.6662 | 66.6186 | 0.0007 | |
| GHNA(s) | 0.8679 | 32.1206 | 2.8400 | 1.8865 | 88.6464 | 0.0007 |
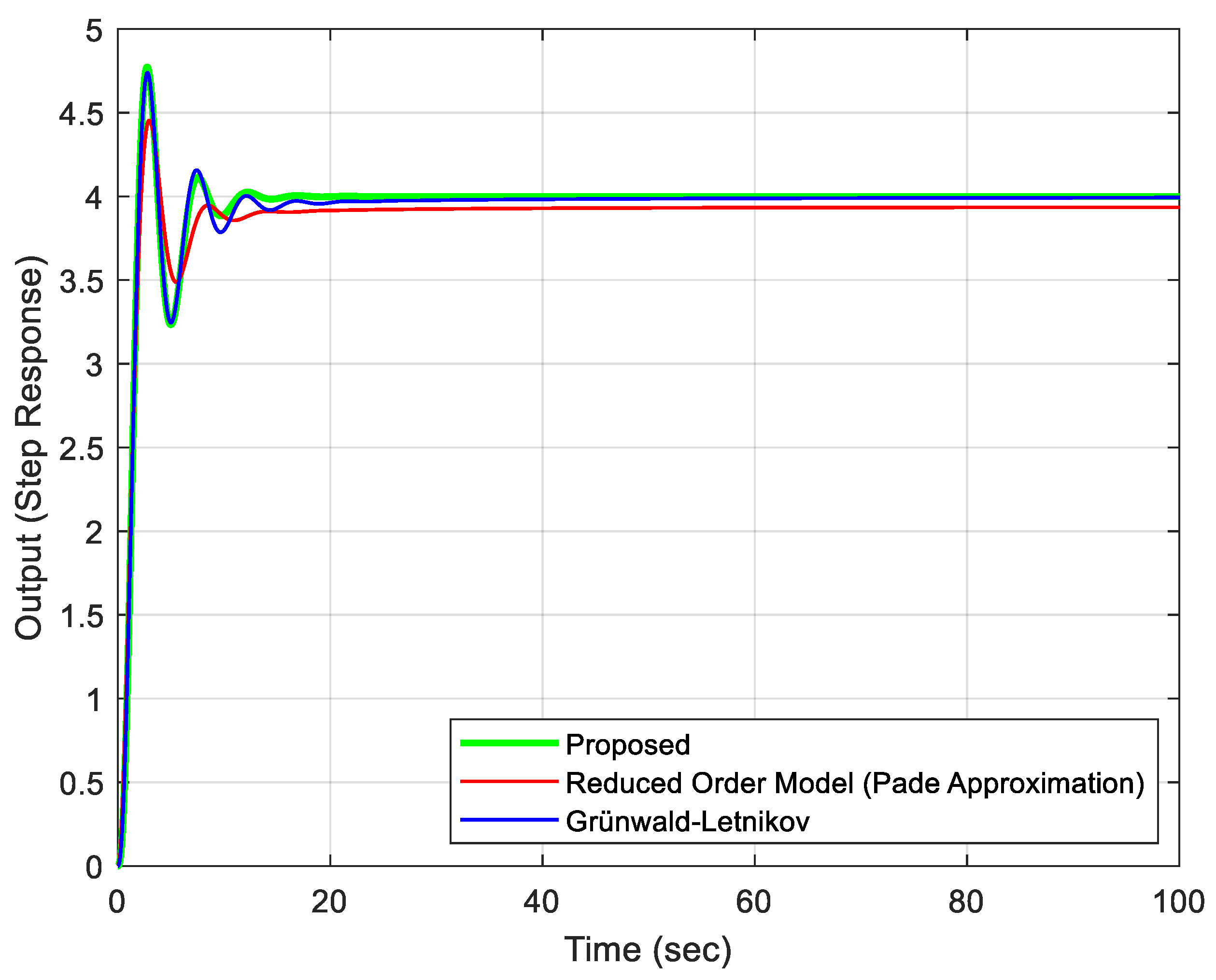
| Methods | Rise Time (s) | Settling Time (5%) (s) | Peak Time (s) | Peak Value | Overshoot (%) | Steady State Error |
|---|---|---|---|---|---|---|
| GL Method | 1.2786 | 10.0216 | 2.7800 | 4.7386 | 18.4639 | 0 |
| 1.2342 | 6.3591 | 2.7500 | 4.7723 | 19.3085 | 0 | |
| 1.4545 | 7.1269 | 2.9600 | 4.4537 | 11.3415 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yüce, A. An Approximation Method for Fractional-Order Models Using Quadratic Systems and Equilibrium Optimizer. Fractal Fract. 2023, 7, 460. https://doi.org/10.3390/fractalfract7060460
Yüce A. An Approximation Method for Fractional-Order Models Using Quadratic Systems and Equilibrium Optimizer. Fractal and Fractional. 2023; 7(6):460. https://doi.org/10.3390/fractalfract7060460
Chicago/Turabian StyleYüce, Ali. 2023. "An Approximation Method for Fractional-Order Models Using Quadratic Systems and Equilibrium Optimizer" Fractal and Fractional 7, no. 6: 460. https://doi.org/10.3390/fractalfract7060460
APA StyleYüce, A. (2023). An Approximation Method for Fractional-Order Models Using Quadratic Systems and Equilibrium Optimizer. Fractal and Fractional, 7(6), 460. https://doi.org/10.3390/fractalfract7060460










