1. Introduction
Neural networks can simulate the thinking process of the human brain and have important application value in the field of artificial intelligence [
1]. With the rise of intelligent computing, various interdisciplinary fields such as machine learning, control theory, computer science, and system stability require neural networks as important research tools [
2,
3,
4,
5,
6,
7,
8,
9]. Memristors, as the fourth basic circuit component, have a monumental memory function similar to the neuronal protrusions in the human brain [
10]. They can be stored and calculated in a cross-array form, with fast computing speed and low energy consumption when processing analog signals. The research results have shown that using memristors to replace neuronal protrusions can establish various memristive neural networks with parallel computing capabilities [
11]. Therefore, memristive neural networks (MNNs), as a special type of state-dependent network model, naturally receive much attention from scientific research personnel [
12,
13,
14].
Due to the nonlinear nature of memristor-based neural networks, MNNs are often rich in dynamic states, such as equilibrium points, periodic solutions, traveling wave solutions, synchronization, and chaos. Applying integer-order differential integral operators to model the network dynamic behaviors, memristor-based neural networks have been widely studied [
15]. In particular, synchronization, as an important stable state in neural networks, can be achieved through internal coupling or external force input [
16]. For instance, utilizing external non-delayed and delayed impulse effects, the authors in [
17] deliberated the global synchronization task of stochastic MNNs with Wiener distribution and coupling delays. Based on the differential inclusions, Li et al. [
18] paid attention to the synchronization within a settling time for master-slave MNNs involving nonlinear driving functions and variable system delays using adaptive feedback schemes. In [
19], the authors solved the fixed-time driver-response synchronization challenge of MNNs including complex-valued parameters. In [
20], Alsaedi et al. deliberated the complete synchronization of fuzzy MNNs with external perturbation by using fuzzy rules and adaptive rules. In [
21], Fu et al. dealt with the weak projective synchronization task for Takagi-Sugeno fuzzy MNNs with parameter mismatch based on Liapunov-Krasovsky functions and variable parameter formulas.
The synchronization research results of MNNs mentioned above mainly focused on mathematical modeling based on integer-order calculus operators. Fractional calculus, as a promotional version of integer order differentiation and integration, adds a degree of freedom parameter, and more importantly, includes all the communication from the initial moment to the current one [
22]. Therefore, it has special memory and heritability, which can characterize various phenomena and processes that cannot be described by integer calculus [
23]. As a simple example, in neural cell tissues, the application of fractional calculus can break the inherent complexity of a single molecular membrane, thereby comprehensively understanding the memory capability and behavior of biological systems. Researchers replaced ordinary capacitors with fractional capacitors and established the fractional-order memristive neural network model, which can better characterize the function and behavior of neurons. In [
24], using the nature of the proportional derivative, a class of generalized Caputo and Riemann-Liouville fractional derivatives including exponential kernels was studied. In [
25], utilizing stability theory and immovable point techniques, the solution of proportional Liouville-Caputo fractional stochastic equations was discussed. By introducing the Riemann-Liouville fractional derivative, Gu et al. [
26] established fractional-order MNNs with unsuspected parameters, and further implemented parameter adaptive discrimination and identification. With the help of the Caputo fractional derivative, Chen et al. [
27] constructed fractional-order Caputo MNNs and analyzed the global stability conditions of the system in detail. Li et al. [
28] studied the nonlocal anti-synchronization challenge for fractional-order neural networks involving mixed variable delays utilizing state information feedback. Yang et al. [
29] deliberated the complete synchronization for fractional-order delayed MNNs with unidentified parameters by feedback control schemes. More synchronization results, such as robust synchronization [
30] and pinning multi-synchronization [
31] for fractional-order MNNs were investigated based on fractional-order Lyapunov function methods.
In particular, two complex systems are known to achieve projective synchronization if the corresponding state variables of master neural networks and slave neural networks reach identical dynamical behavior under certain scaling factors [
32]. Projection synchronization can be regarded as a generalized class of synchronization modes since it can be converted into synchronization modes such as complete synchronization and anti-synchronization by adjusting the projection scaling factor. Note that projection synchronization can be relied upon for faster communication with its scaling properties [
33]. Consequently, it has important theoretical and practical significance to investigate the projection synchronization of fractional-order neural networks. Latterly, researchers used different control strategies to solve the projective synchronization goal for fractional-order MNNs, and many worthwhile works have been achieved [
34,
35,
36,
37,
38,
39,
40]. For instance, in [
34], Velmurugan et al. dealt with the hybrid projection synchronization of fractional-order MNNs with delays based on a simple state feedback control scheme. Gu et al. [
35] discussed the projection synchronization of fractional-order delayed MNNs by applying open-loop control and continuous feedback control. Considering the sliding mode control and adaptive control techniques, researchers in [
36] investigated the passive projective synchronization of uncertain MNNs and derived the stability conditions for error systems. In [
37,
38], the projection synchronization and the modified projection synchronization of fractional-order MNNs in finite time were explored based on feedback control methods. Ding et al. [
40] were concerned about the complex projection synchronization for fractional-order complex-valued MNNs utilizing hybrid feedback controllers.
As everyone knows, the scale factor in projection synchronization as a key parameter increases the safety of signal transmission between the drive and response systems. However, as mentioned above in the literature [
34,
35,
36,
37,
38,
39,
40], the projected scale factors between fractional-order master-slave networks are generally constant matrices or fixed diagonal forms. If the scale factor is adjusted to be a time-varying function matrix including multiple variable elements, it undoubtedly increases the communication security letter. Until now, no works have considered projective synchronization with scaling factors of time-varying function matrices for FOUMNNs by mixed impulsive feedback control. This is also the main motivation of this study. The main reasons include three points. First, scaling factors that vary with time
t are more complex to predict than constant matrices or fixed diagonal forms. Second, the delays or uncertainties caused by limited information processing speed or external disturbances can make the dynamic behaviors of the system more complex and disrupt the stability of nonlinear systems. Third, the primary objective of this study is to develop a broader projection synchronization model and to overcome the previously mentioned difficulties with a new mixed impulsive feedback control technique. This requires us to establish a more generalized impulse comparison theorem first.
Motivated by what has been considered above, this article deliberates the TFMPS of Caputo FOUMNNs with multiple delays. The worthwhile contributions of this study include three aspects. First, we extend the traditional projective scaling factor to a time-dependent function matrix and define a generalized synchronization mode, i.e., TFMPS. This synchronization mode can degenerate into matrix projective synchronization (PS) [
41], modified PS [
38], and anti-synchronization under specific restrictive requirements. The adjustability of fractional orders and the time-varying unpredictability of elements in function matrices can improve the safety of secret communication, providing better application prospects for communication encryption systems. Second, an important impulsive comparison theorem that considers delays and time-varying coefficients is provided as an analytical tool. In addition to the memristive neural network model considered in this article, the comparison theorem can be applied to more neural networks, such as pantograph neural networks or Cohen-Grossberg neural networks. Finally, different from the feedback control or sliding mode control schemes in [
34,
35,
36,
37,
38,
39,
40], novel mixed impulsive feedback control schemes, including open-loop feedback control and impulsive sampling control, have been designed to achieve the TFMPS in FOUMNNs. Both the state information in the time-delayed interval and the sampling information at the impulse moments are comprehensively utilized in our controller. Theoretical analysis and numerical experiments show that the derived synchronization conditions rely on impulsive strengths, feedback strengths, uncertain boundaries, and fractional order.
2. Theoretical Foundation and Model Establishment
In this section, some fundamental knowledge closely related to this study is first reviewed. Then, an important impulsive comparison theorem involving various delays is given, and drive-response network models concerning the Caputo derivative are established.
Definition 1 ([
34]).
Fractional integral for an integral function is given aswhere , , and . Definition 2 ([
34]).
η-order Caputo derivative for a function is given bywhere , and . Especially, when , ; when , the fractional derivative can convert to the one-order derivative. Consider fractional-order uncertain memristive neural networks involving multiple delays as below:
where
and
is a positive parameter signifying the decay rate coefficient.
denotes the
jth transmission delay satisfying
.
represents the bounded control input.
stands for the state vector at point
t.
and
mean nonlinear activation functions at points
t and
, respectively.
and
express the uncertain deviation of
and
, which satisfying
and
. The initial conditions of memristive system (3) are
.
and
represent the connection weights, where
and
describe the memductances of resistors
and
.
displays the resistor between
and
.
displays the resistor between
and
.
represents the voltage of the capacitor. Considering the distinctions of the memristor and the nature of current-voltage,
and
satisfy two constraints as follows:
where
,
or
,
or
, and the switching jumps
.
and
are scalars regarding memristances.
By manipulating the differential inclusion theory, uncertain memristive dynamical networks (3) are reformulated as
where
,
,
,
,
,
,
then, there exist functions
,
, for
, such that
Based on neural networks (3), one can obtain the corresponding response networks as below:
where
is the mixed impulsive feedback controller. The initial conditions of response memristive networks (8) are
.
and
represent the connection weights and can be defined by
where
, and the switching jumps
.
and
are constants. Then, memristive networks (8) can be rewritten by
where
Similarly, there exist
,
,
, such that
To establish the error system between memristive neural networks (3) and (8), the definition of the error vector is first given by
where
,
,
,
and
represents a variable and bounded projective matrix. Applying Caputo derivatives for component function
, and combining deduced networks (7) and (10), we can obtain the fractional derivative of the error function below.
Based on the above error system, a mixed impulsive feedback controller including three items is designed as below:
where
are feedback control strengths and
shows the impulsive control strength.
represents the Dirac delta function. Combining error system (12) and mixed impulsive controller (
13), one can obtain
where
and
.
Remark 1. The mixed control schemes in equation (13) comprise three significant parts. and represent the open loop and feedback controllers, while considering historical status information in time-delayed intervals. denotes the impulsive sampling controller, which plays a motivating role at the impulse instants. Compared to the memoryless continuous feedback input, we comprehensively utilize the state information in the time-delayed interval and the sampling information at the impulse moments, making it easier to quickly obtain good synchronization results. Assumption 1. For the nonlinear mappings and , there are nonnegative scalars and satisfyingfor . Assumption 2. All elements in projective scaling matrix are continuously differentiable, and each row of the matrix has at least one non-zero element.
Definition 3. Master system (3) and slave system (8) can accomplish the TFMPS, if the error vector conforms to .
Remark 2. By selecting predigested forms of projection matrix , we can obtain different projection synchronization modes as below:
(1) Choosing matrix , the TFMPS could degenerate into the matrix PS [41]. (2) Choosing matrix , the TFMPS could degenerate into the modified PS [38]. (3) Choosing matrix , the TFMPS could degenerate into the anti-synchronization [42]. (4) Choosing matrix , the TFMPS could degenerate into the complete synchronization [29]. The synchronization mode in this article can be seen as a generalized form of the aforementioned synchronization modes, as the elements of the projection matrix in this study can be time-varying functions rather than constants or diagonal forms. Lemma 1 ([
43]).
Consider a fractional multi-delayed system as below:where , , , and . Assuming the eigenvalues of multi-delayed Equation (16) meet the constraint and the equation does not have pure imaginary solutions for ∀, one can attain that the zero solution of (16) can be globally asymptotically stable. Lemma 2 ([
7]).
Suppose that , is differentiable. If one can find a point satisfying and for , then . Lemma 3 ([
44]).
Assume that is a differentiable function, we have Lemma 4 ([
45]).
The following matrix inequality is equivalent to condition or condition as below:where and . Lemma 5. Let nonnegative functions and satisfyingandwhere , , and . and are continuous and nonnegative real-valued functions. Then for yields for . Proof. Confirm this conclusion using the mathematical induction method. First, we shall validate that
,
. Evidently,
means
if
denotes any constant. Assume the result
for
is wrong. Considering that
for
and the continuity of
and
in
, there exists
satisfying
where
represents any constant. By utilizing Lemma 2, one can obtain
From another perspective, it derives from (
19)–(
21) that
which contradicts with (
22). Consequently, by using the reduction to absurdity, we can acquire
Let
, one obtains
for
. Suppose there exists
satisfying
,
, then we obtain
for
and
. Note that
is continuous on
, utilizing the analogous stages as the proof of
in
, we can derive
for
. Accordingly, mathematical induction indicates that the comparison principle is correct. □
Remark 3. MNNs constructed by integer-order calculus operators have been extensively investigated and many meaningful synchronization results have been obtained in [16,17,18,19,20,21]. However, the comparison theorem and impulsive control schemes for neural networks with integer differential operators cannot be directly applied to fractional-order neural networks since fractional-order memristive systems possess special memory and hereditary properties. Therefore, synchronization of fractional-order delayed MNNs with uncertainties using impulse feedback control remains a challenging problem since the fractional-order impulse comparison theorem with delays is rare. Remark 4. To overcome the influence of delays on network stability, some kinds of literature have established useful fractional-order time-delay comparison theorems for continuous systems, such as [15,23,43]. Different from these results, the fractional-order time-delay comparison theorem established in this paper considers impulse effects and time-varying coefficients. Consequently, the comparison theorem contemplated in this paper is not only applicable to continuous network models but also can be used for discontinuous impulse networks. 3. Synchronization Analysis Results
Before giving the principal theorem and corollary in this article, we first bring in a significant matrix symbol. Denote
, then the second impulsive expression in (
14) can be simply rewritten as
for
.
Theorem 1. Under Assumptions 1–2 and mixed impulsive feedback controller (13), the global TFMPS between memristive neural networks (3) and (8) can be achieved, if there exist suitable parameters , and , such thatwhere , and . Proof. Consider an auxiliary function as below:
When
, calculating the Caputo derivative of
and applying Lemma 3 yields that
According to Assumption 1, one can obtain
Utilizing the inequality
, one can obtain
Substituting inequalities (29)–(
31) into (26), we have
Note that , .
Take
, then one can obtain
where
Based on condition (i) of Theorem 1, we have
It follows from Lemma 4 and inequality (33) that
Combining the mathematical expression of
and inequality (
34), when
, we have
where
. From inequalities (33) and (36), one has
Contemplate a Caputo fractional-order differential system as below:
where
is continuous in the interval
and it owns identical starting values with
. Taking into consideration the condition
and utilizing Lemma 5, we acquire
Applying the Laplace transform tool for differential system (
38) gives that
Combining transformed expression (40) and Lemma 1, we can derive
where characteristic polynomial
. Next, contemplate the approach of the proof by contradiction to illustrate that the equation
has no pure imaginary solutions. Suppose a pure imaginary number
, where
. If
, choose
; otherwise, choose
. Substituting
into
and utilizing the well-known Euler formula, we can obtain
Note that the equal of two complex numbers is equivalent to the corresponding equal of the real part and imaginary part separately. Separating real and imaginary parts in (
42) gives
Squaring the above two equations first and then adding them together yields
Note the following trigonometric equality
Substituting equation (45) into equation (
44), we have
Considering a two-order polynomial function
. One can obtain
, since
,
,
. Moreover,
represents a two-order polynomial function with a strictly monotonically increasing interval
, we can obtain
. Hence,
, which shows equation (
46) has no solution, namely, we cannot find a pure imaginary solution that meets the mathematical Equation
. In addition, when
, one can gain
. Based on Lemma 1, the zero solution of system (
38) is asymptotically stable and
. According to inequality (
39) and the Sandwich theorem, one can derive that
, and the time-varying function matrix projection synchronization of memristive systems can be achieved. □
Remark 5. The feedback control part mainly utilizes the current error information and assists the delayed error information as a supplement. To accelerate the synchronization efficiency of the driver network and the response network, selecting the relatively large adjustable parameter and the relatively small parameter can ensure that the condition in Theorem 1 is more easily met. To minimize control costs, we generally choose the minimum that satisfies condition (ii).
Remark 6. Different from continuous feedback control, mixed impulse feedback control considered in this paper is a discontinuous control strategy with the merit of high transmission security. If we replace the mixed impulse control with pure impulse control, the parameter in condition (ii) of Theorem 1 may become negative. Since is positive, this will make condition (ii) not hold. Accordingly, the feedback parts of our controller are indispensable.
Remark 7. The impulsive control part and condition (i) in Theorem 1 ensure that condition in (37) is satisfied. This lays the important foundation for utilizing the proposed comparison theorem and Laplace transforms to complete the stability analysis of error systems. Especially, with time-varying uncertainties
and
, memristive neural networks (3) with the Caputo derivative can be simplified as
Correspondingly, response memristive neural networks are simplified by
Construct the external control input
as
Employing the similar proof approach in Theorem 1, one can acquire the following Corollary.
Corollary 1. Under Assumptions 1 and 2 and mixed impulsive feedback controller (49), the global TFMPS between memristive neural networks (47) and (48) can be achieved, if there exist suitable parameters and , such thatwhere , and . Remark 8. Based on the system environment and control requirements, when the impulsive strength satisfies and , impulsive intervals are not tightly constrained by time delays.
4. Illustrative Experiments
In this section, we will present simulation experiments with different dimensions to verify the applicability of Theorem 1.
Example 1. Take the following two-dimensional fractional-order delayed memristive networks with bounded uncertainties as the drive system.where, , , , , −, , and . According to drive neural networks (
50), the response neural networks can be given as
where
and other network parameters have the same values as system (
50). Based on the synchronization Definition and Assumption 2, choosing the time-varying projective scaling matrix as
, then one can obtain the error functions of TFMPS as
and
.
To achieve the TFMPS between Caputo FOUMNNs (
50) and (
51), feedback control strengths
and
in (
13) can be selected as
,
. The impulsive control strength and impulsive intervals can be chosen as
and
, respectively. The Lipschitz constants are set as
, which shows that Assumption 1 is valid. Let parameter
, and then simple calculation shows that
,
,
,
, and
. Thereupon, the calculation results indicate that all parameters above meet the conditions of Theorem 1.
The initial values of memristive network systems (
50) and (
51) are generated randomly in the interval
. By utilizing prediction-correction methods with Matlab software, the state trajectories and error functions for (
50) and (
51) are displayed in
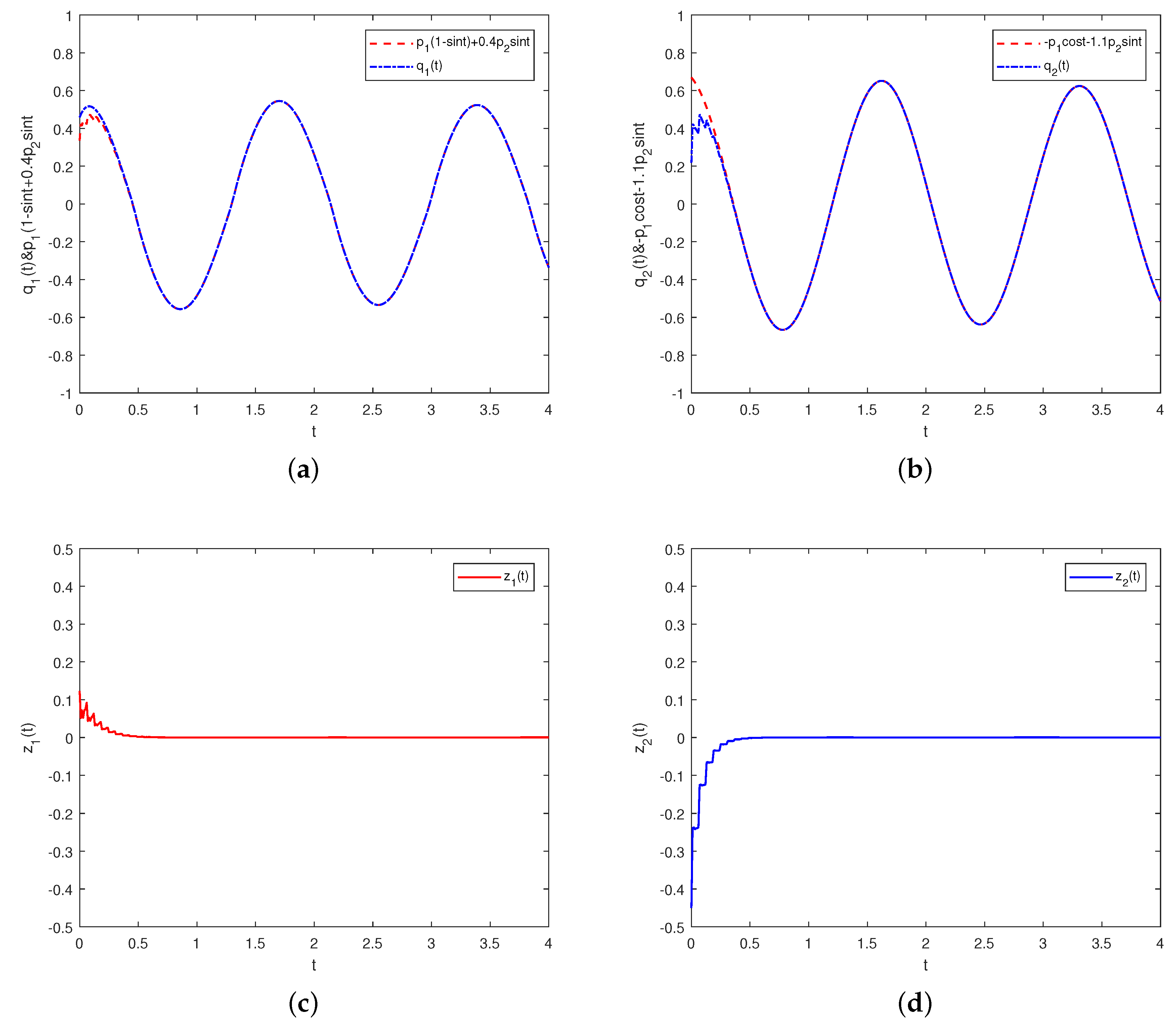
Figure 1. As one can see in
Figure 1a,b, under the influence of scale factors, the red and blue curves in the controlled drive-response networks gradually overlap. Moreover, as shown in
Figure 1c,d, the two error curves of different dimensions gradually approach zero, indicating the effectiveness of the control scheme utilized in this study. To further observe the effect of the feedback control intensity
on the synchronization speed, we enhance the control intensity as
and keep the remaining control intensities unchanged. Comparing
Figure 1 and
Figure 2, one can easily observe that a larger non-delay feedback control intensity
can improve synchronization speed. Therefore, for the synchronization speed requirements of actual systems, we can flexibly choose the control intensity.
Remark 9. Considering that the fractional-order system in this article has multiple time delays, a modified prediction-correction algorithm called Adams–Bashforth–Moulton [46] is used to solve the fractional-order equations in numerical simulations based on the Matlab software. The algorithm consists of two main steps: Adams-Bashforth prediction and Adams-Moulton correction. The product trapezoidal product rule is applied to the corrector part and the product rectangular rule is used to assess the predictor part. Therefore, the whole numerical method is easily implemented by applying these two rules, and detailed algorithm steps can be seen in [46]. Example 2. As the drive system, a three-dimensional fractional-order delayed memristive network with uncertainties is denoted aswhere, , , , , , , , and . According to drive neural networks (
52), the response neural networks can be given as
where
and other network parameters have the same values as system (
52). Based on Definition 3 and Assumption 2, choosing the time-varying projective scaling matrix as
, then one can obtain the error functions of TFMPS as
,
, and
.
To achieve the TFMPS between Caputo FOUMNNs (
52) and (
53), feedback control strengths
and
in (
13) can be selected as
,
. The impulsive control strength and impulsive intervals can be chosen as
and
, respectively. The Lipschitz constants are set as
, and one can verify that Assumption 1 is valid. Chose parameter
, and then simple calculation shows that
,
,
,
,
, and
. Consequently, the calculation results indicate that all parameters meet the requirements of Theorem 1.
The initial values of memristive network systems (
52) and (
53) are generated randomly in the interval
. By utilizing Matlab software, the state trajectories and error functions for systems (
52) and (
53) are shown in
Figure 3. As one can see in
Figure 3a–c, under the influence of scale factors, the red, blue, and pink curves representing state trajectories in the controlled drive-response memristive systems gradually overlap with time evolution. Furthermore, as shown in
Figure 3d,f, three colored error curves of different dimensions gradually approach zero, indicating the correctness of the obtained theorem and the effectiveness of the mixed control scheme proposed in this article.
Remark 10. Our control techniques and synchronization results are still effective when uncertainty factors are not considered, as shown in Corollary 1. Under this case, our network model degenerates into [30,31,32]. Therefore, the results of this article are more generalized than existing results [30,31,32]. Remark 11. The derived results in our theorem and corollary are also applicable for parameter , i.e., the mixed impulsive feedback control method is still suitable for the corresponding integer-order memristor-based systems, such as [18,20].