Author Contributions
Conceptualization, M.H.A. and A.M.S.; Methodology, M.H.A., A.M.S., G.M. and A.A.E.-F.; Software, M.H.A., A.M.S. and A.A.E.-F.; Validation, M.H.A., S.Z.A., A.S.A. and A.M.S.; Formal analysis, M.H.A., A.M.S., G.M. and A.A.E.-F.; Resources, A.S.A.; Data curation, S.Z.A. and G.M.; Writing—original draft, M.H.A., S.Z.A., A.M.S. and A.A.E.-F.; Writing—review & editing, A.S.A., A.M.S., G.M. and A.A.E.-F.; Visualization, A.S.A.; Supervision, S.Z.A.; Project administration, M.H.A.; Funding acquisition, M.H.A. All authors have read and agreed to the published version of the manuscript.
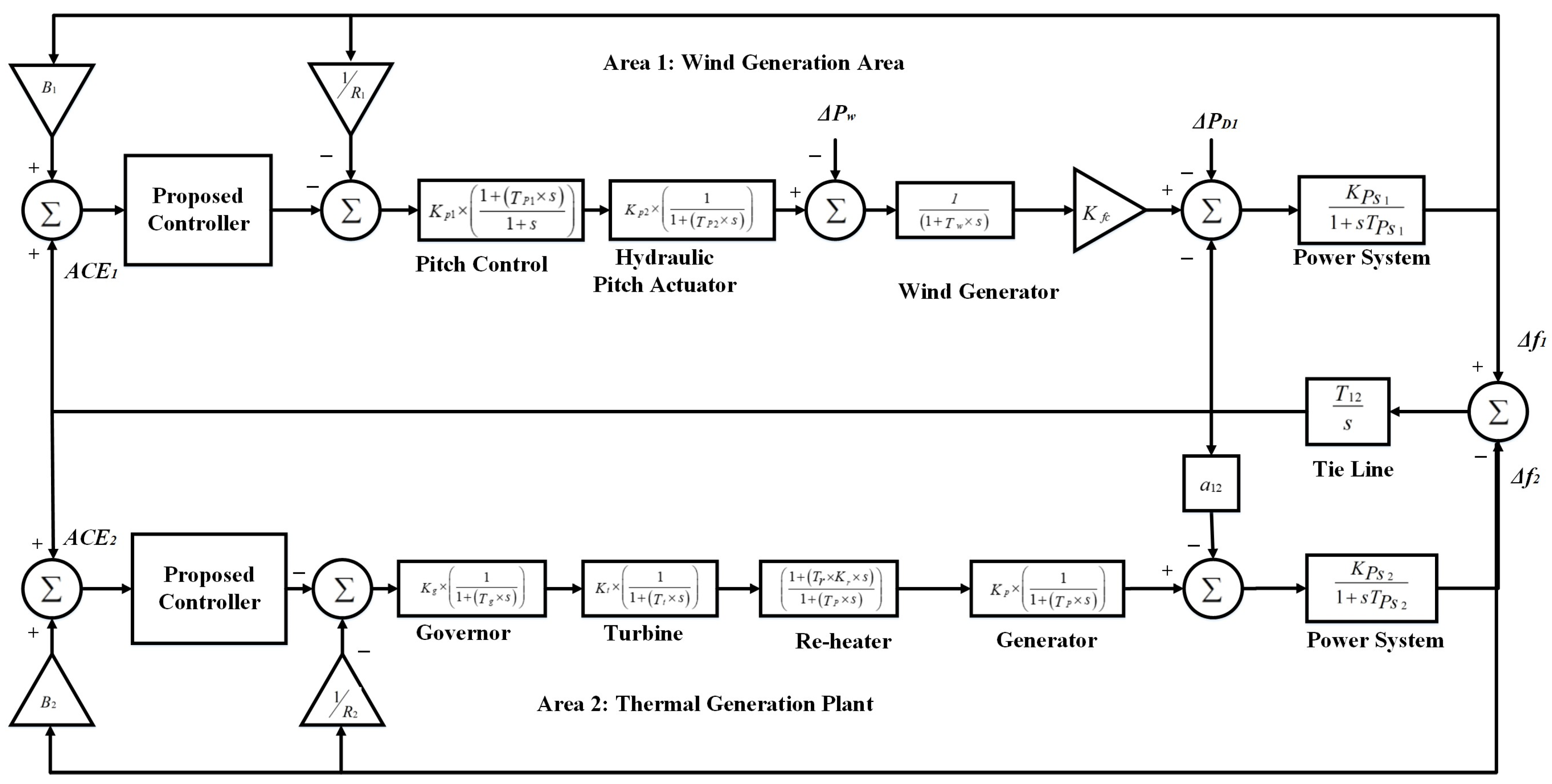
Figure 1.
Power system model.
Figure 1.
Power system model.
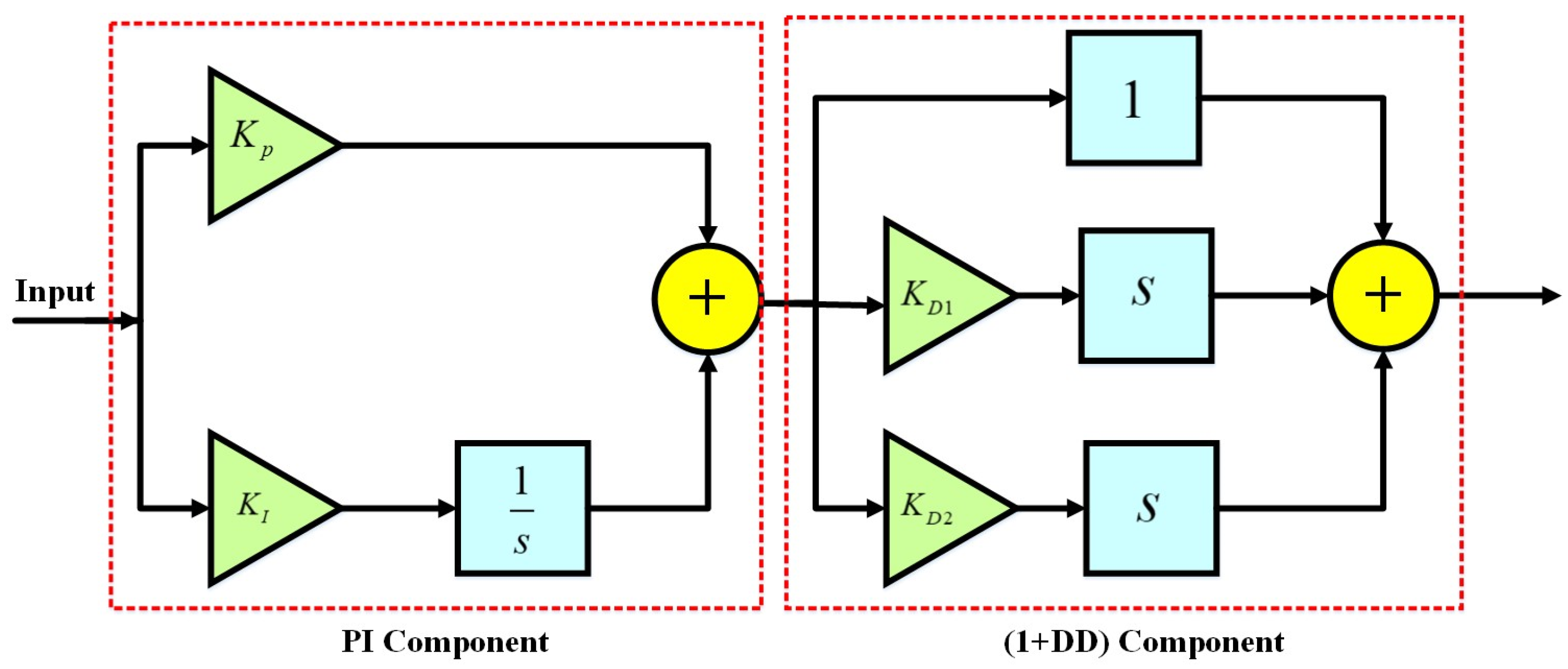
Figure 2.
Proposed controller of PI–(1+DD) [
29].
Figure 2.
Proposed controller of PI–(1+DD) [
29].
Figure 3.
Flowchart of the proposed EKO.
Figure 3.
Flowchart of the proposed EKO.
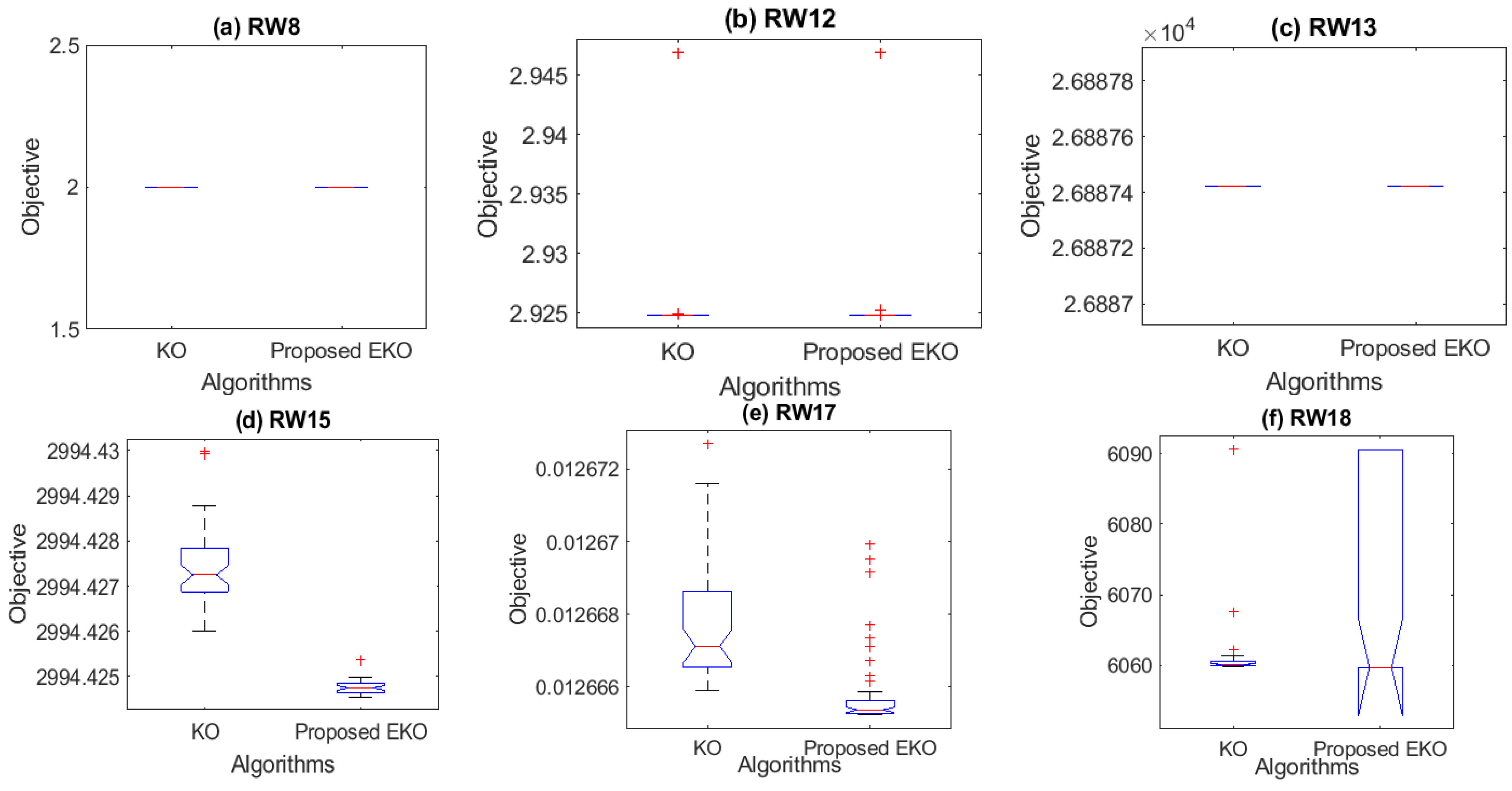
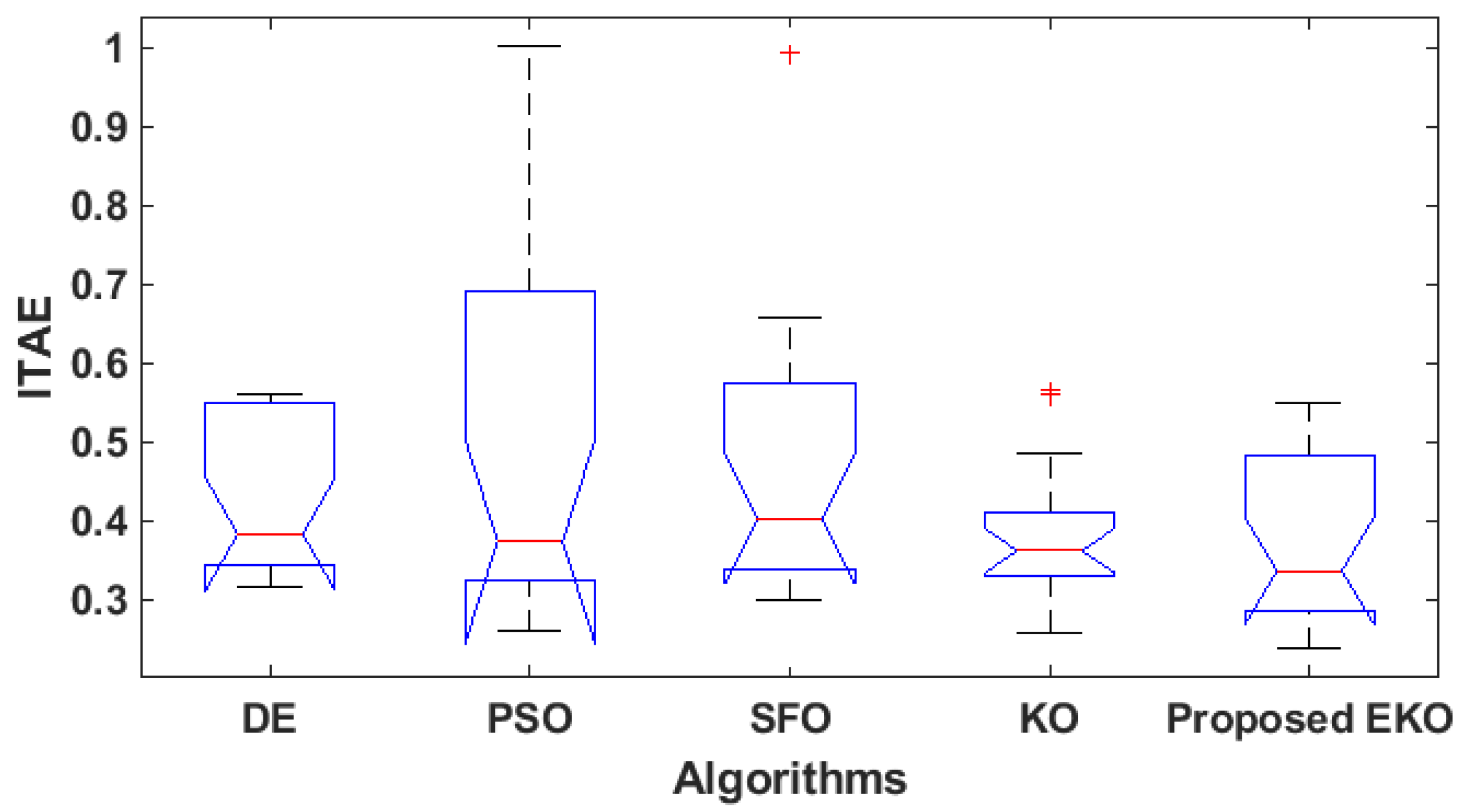
Figure 4.
Boxplots of the proposed EKO and KO for RW engineering problems.
Figure 4.
Boxplots of the proposed EKO and KO for RW engineering problems.
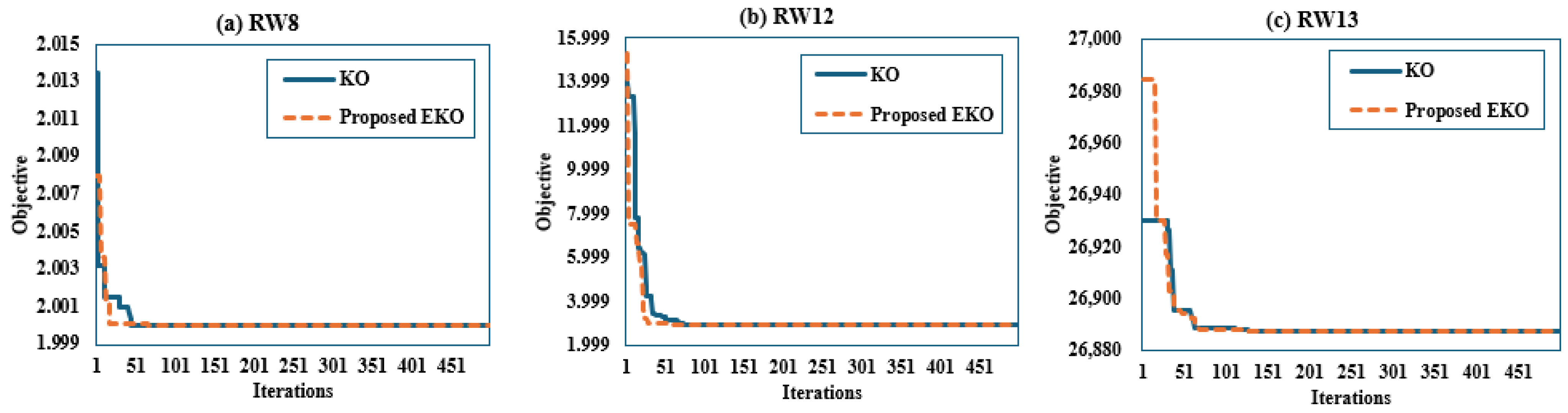
Figure 5.
Convergence curves of the proposed EKO and KO for RW engineering problems.
Figure 5.
Convergence curves of the proposed EKO and KO for RW engineering problems.
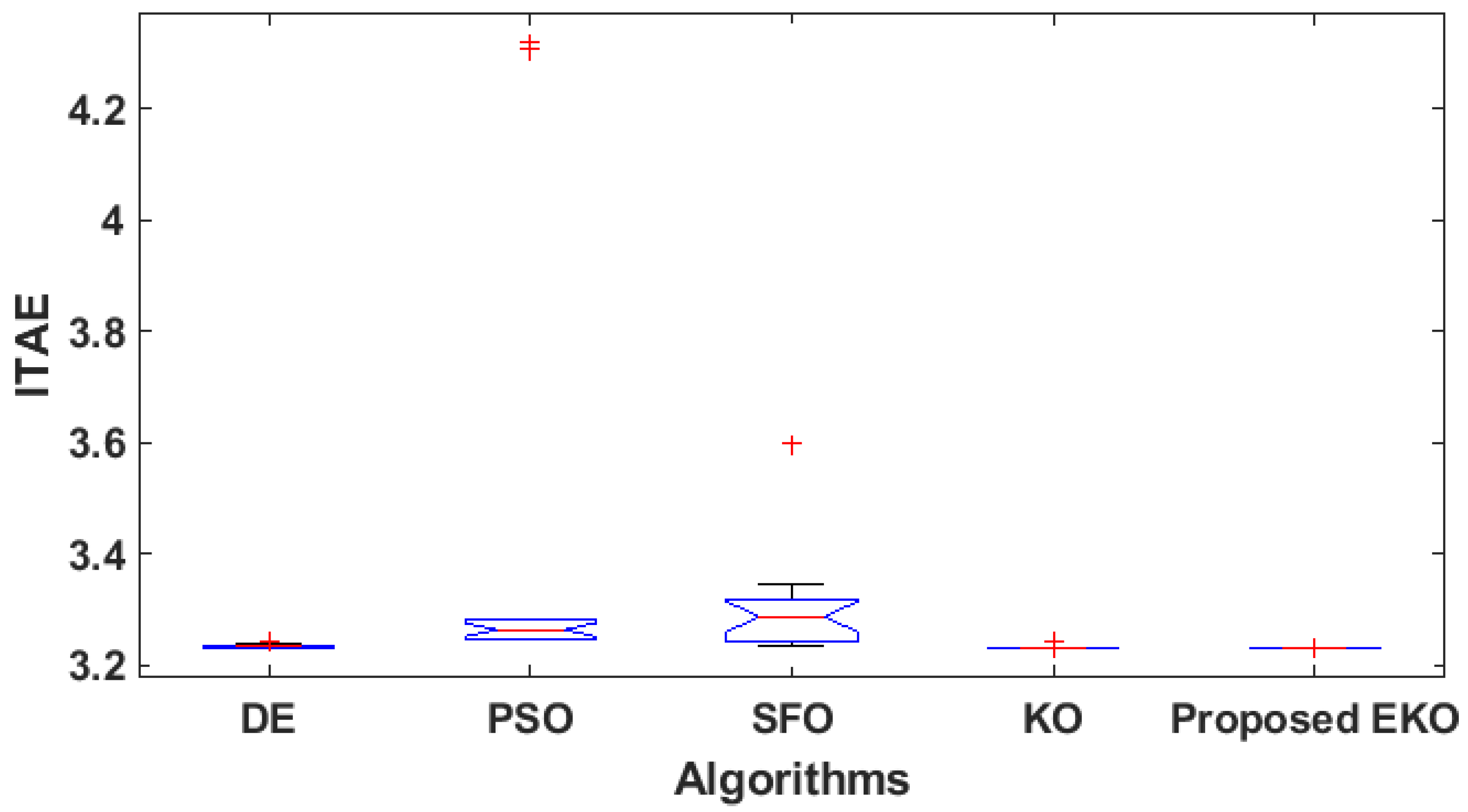
Figure 6.
Boxplots of the DE, PSO, SFO, KO, and proposed EKO for Case 1.
Figure 6.
Boxplots of the DE, PSO, SFO, KO, and proposed EKO for Case 1.
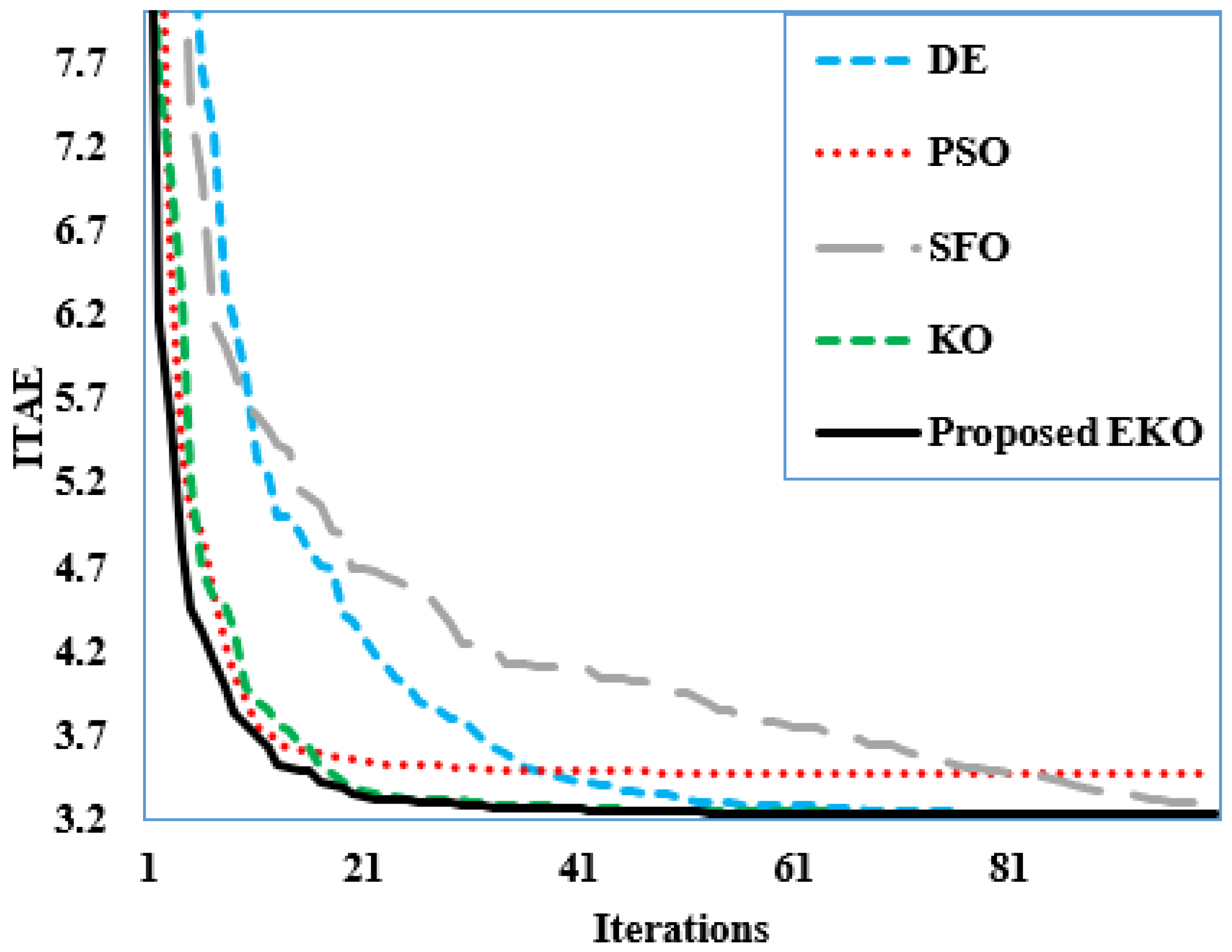
Figure 7.
Average converging characteristics of DE, PSO, SFO, KO, and proposed EKO for Case 1.
Figure 7.
Average converging characteristics of DE, PSO, SFO, KO, and proposed EKO for Case 1.
Figure 8.
Boxplots of the DE, PSO, SFO, KO, and proposed EKO for Case 2.
Figure 8.
Boxplots of the DE, PSO, SFO, KO, and proposed EKO for Case 2.
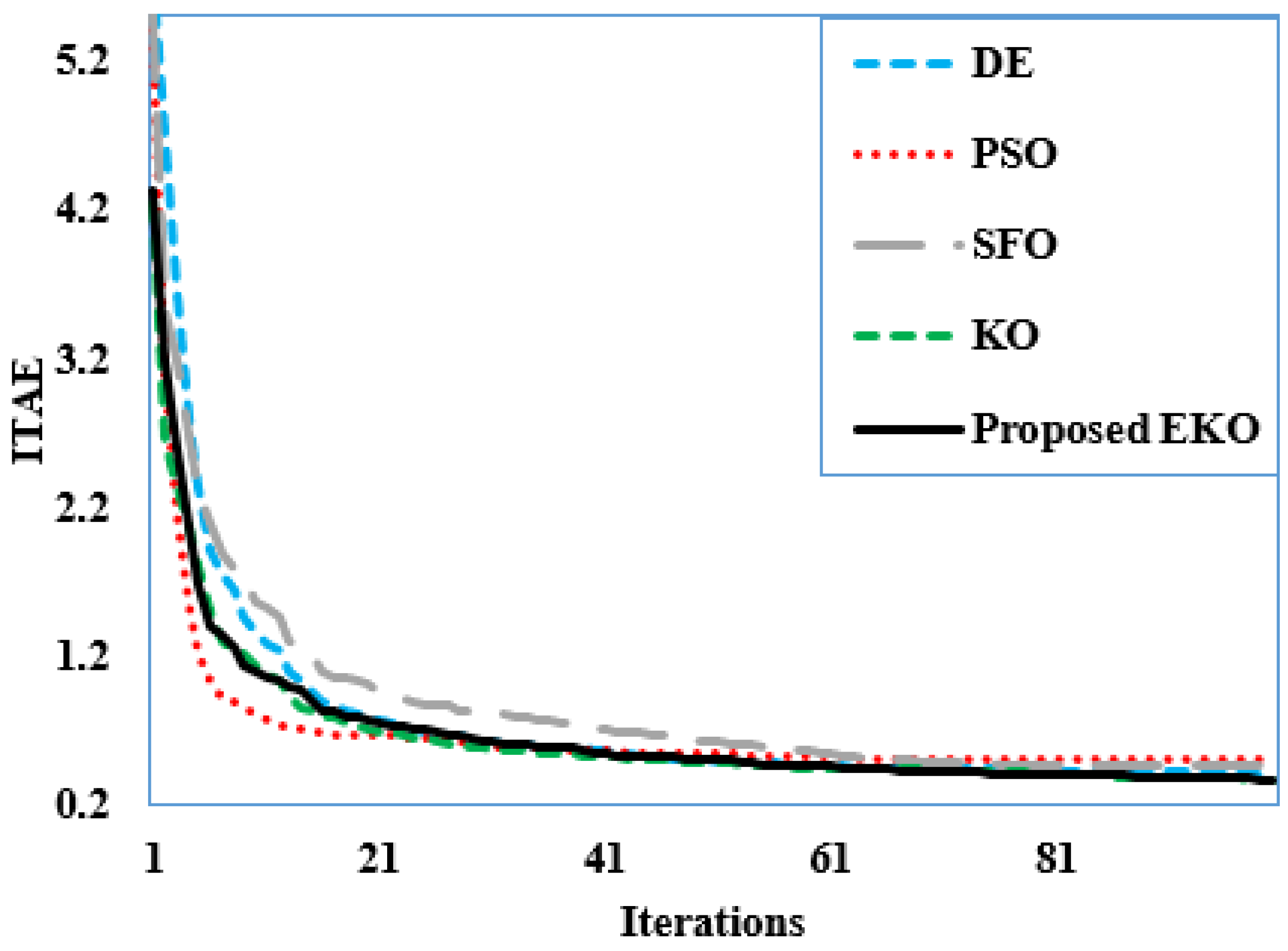
Figure 9.
Average converging characteristics of the DE, PSO, SFO, KO, and proposed EKO for Case 2.
Figure 9.
Average converging characteristics of the DE, PSO, SFO, KO, and proposed EKO for Case 2.
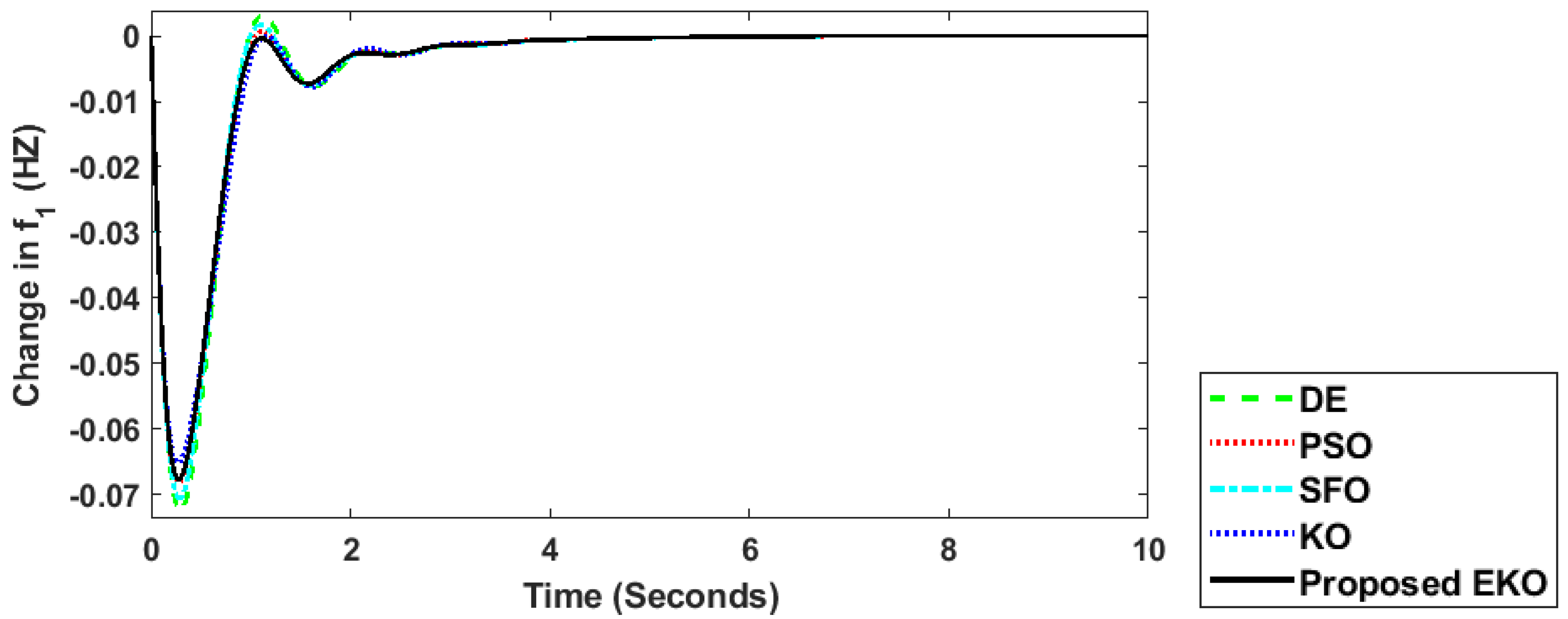
Figure 10.
Change in frequency (Area 1) regarding the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 2.
Figure 10.
Change in frequency (Area 1) regarding the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 2.
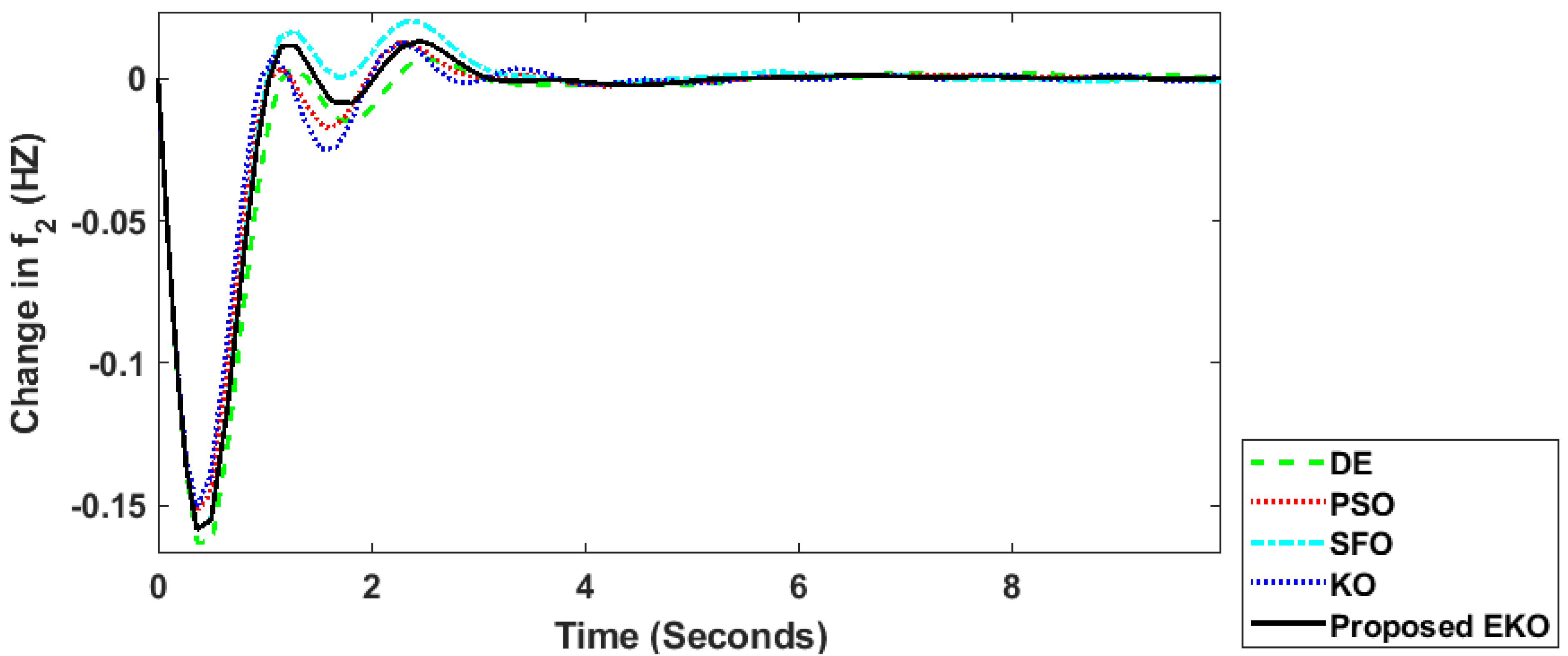
Figure 11.
Change in frequency (Area 2) regarding the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 2.
Figure 11.
Change in frequency (Area 2) regarding the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 2.
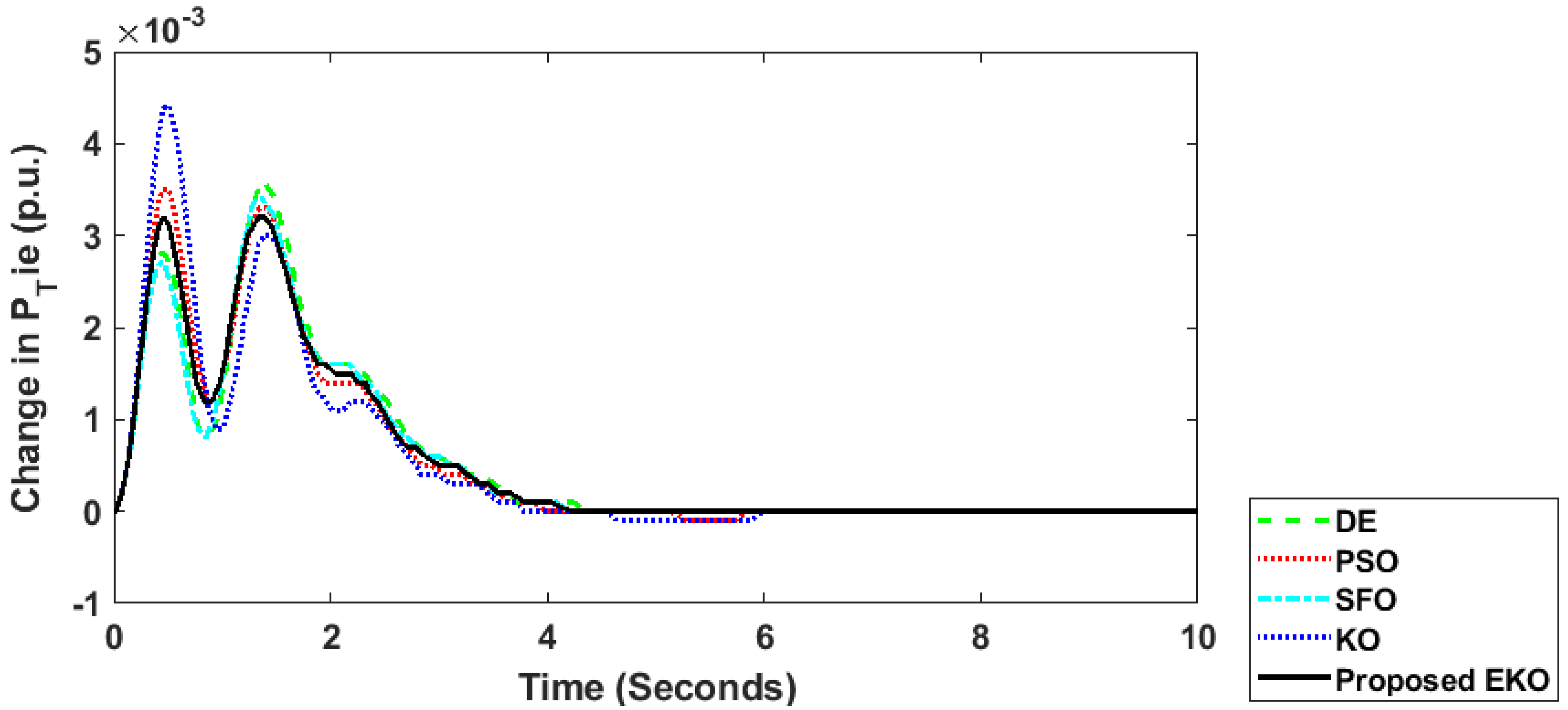
Figure 12.
Change in transfer power between areas regarding the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 2.
Figure 12.
Change in transfer power between areas regarding the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 2.
Figure 13.
Boxplots of the DE, PSO, SFO, KO and proposed EKO algorithms for Case 3.
Figure 13.
Boxplots of the DE, PSO, SFO, KO and proposed EKO algorithms for Case 3.
Figure 14.
Converging characteristics of the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 3.
Figure 14.
Converging characteristics of the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 3.
Figure 15.
Change in frequency (Area 1) regarding the DE, PSO, SFO, KO and proposed EKO algorithms for Case 3.
Figure 15.
Change in frequency (Area 1) regarding the DE, PSO, SFO, KO and proposed EKO algorithms for Case 3.
Figure 16.
Change in frequency (Area 2) regarding the DE, PSO, SFO, KO, and proposed EKO for Case 3.
Figure 16.
Change in frequency (Area 2) regarding the DE, PSO, SFO, KO, and proposed EKO for Case 3.
Figure 17.
Change in transfer power between areas regarding the DE, PSO, SFO, KO, and proposed EKO for Case 3.
Figure 17.
Change in transfer power between areas regarding the DE, PSO, SFO, KO, and proposed EKO for Case 3.
Table 1.
Summary of existing state-of-the-art compared to the presented work considering a two-area system.
Table 1.
Summary of existing state-of-the-art compared to the presented work considering a two-area system.
| Ref. | Year | Controller | Tuning the Controller Parameters: Algorithm | RES Integration |
|---|
| [8] | 2019 | PI | Restricted population extreme optimizer considering a four-area system | Not considered |
| [11] | 2019 | TID | Salp Swarm Algorithm | Not specified |
| [7] | 2023 | I, PI, PID | Hit-and-trial | Not Considered |
| [18] | 2023 | Cascaded PD-PI | Enhanced version of slime mold optimizer | Not Considered |
| [19] | 2023 | PID | Antlion algorithm with experimental validation via electronics environment | Not Considered |
| [10] | 2020 | I | Electro-search optimizer | Solar power |
| [20] | 2021 | PI | Moth flame optimizer | Wind power plant |
| [21] | 2022 | Model Predictive Control | PSO | DFIG wind systems |
| [22] | 2022 | Cascaded PDn-PI | Coyote optimizer | Solar and wind power integrated |
| [23] | 2023 | A backpropagation-trained neural network-PI | PSO is utilized to adjust the neuron weights of the neural network to optimize the PI controller | Wind power generation |
| [16] | 2023 | PID | Hybrid sparrow optimization and bald eagle algorithm | Multiple sources including wind |
| [24] | 2024 | Fuzzy Logic Self-Tuning PID | Genetic algorithm | Wind, biomass, and photovoltaic power plants |
| Proposed Study | | PI–(1+DD) | EKO | Wind |
Table 2.
Statistical metrics for the RW engineering benchmarks under study.
Table 2.
Statistical metrics for the RW engineering benchmarks under study.
| Engineering Design Problem | Items | WSO | DBO | MFO | LWSO | FOX | KO | Proposed EKO |
|---|
| RW8 | Min. | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Av. | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Med. | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Max. | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| STd | 2.88 × 10−16 | 2.44 × 10−16 | 2.28 × 10−16 | 2.44 × 10−16 | 7.1 × 10−8 | 4.432 × 10−12 | 1.337184 × 10−12 |
| Rank | 4 | 1 | 1 | 1 | 7 | 6 | 5 |
| RW12 | Min. | 2.924831 | 2.924831 | 2.924831 | 2.924831 | 2.924831 | 2.924832232 | 2.924830555 |
| Av. | 2.924831 | 3.378957 | 2.96061 | 2.940521 | 2.946508 | 2.92529553 | 2.927494414 |
| Med. | 2.924831 | 3.081732 | 2.946961 | 2.924831 | 2.925031 | 2.946961824 | 2.946961113 |
| Max. | 2.924831 | 4.074353 | 3.081732 | 3.081732 | 3.082564 | 2.924844916 | 2.924830584 |
| STd | 1.43 × 10−7 | 0.481632 | 0.053133 | 0.048293 | 0.047529 | 0.003126717 | 0.00726176 |
| Rank | 1 | 7 | 6 | 4 | 5 | 2 | 3 |
| RW13 | Min. | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 |
| Av. | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 27,135.01 | 26,887.42 | 26,887.42 |
| Med. | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 |
| Max. | 26,887.42 | 26,887.42 | 26,887.42 | 26,887.42 | 28,368.22 | 26,887.42 | 26,887.42 |
| STd | 8.52 × 10−5 | 1.12 × 10−11 | 1.12 × 10−11 | 2.05 × 10−6 | 473.4105 | 1.74905 × 10−7 | 9.35193 × 10−9 |
| Rank | 6 | 1 | 1 | 5 | 7 | 4 | 3 |
| RW15 | Min. | 2994.648 | 2994.424 | 2994.424 | 2994.429 | 2995.595 | 2994.426015 | 2994.424539 |
| Av. | 6 × 1014 | 6 × 1014 | 2998.352 | 5 × 1013 | 6.5 × 1014 | 2994.427404 | 2994.424768 |
| Med. | 1 × 1015 | 1 × 1015 | 2994.424 | 2994.439 | 1 × 1015 | 2994.429985 | 2994.425372 |
| Max. | 1 × 1015 | 1 × 1015 | 3033.702 | 1 × 1015 | 1 × 1015 | 2994.427249 | 2994.424751 |
| STd | 5.03 × 1014 | 5.03 × 1014 | 12.08925 | 2.24 × 1014 | 4.89 × 1014 | 0.000867638 | 0.000154279 |
| Rank | 5 | 6 | 3 | 4 | 7 | 2 | 1 |
| RW17 | Min. | 0.012665 | 0.012666 | 0.012674 | 0.012665 | 0.012677 | 0.01266588 | 0.012665241 |
| Av. | 0.012665 | 0.012742 | 0.012827 | 0.012665 | 5 × 1013 | 0.01266772 | 0.012665815 |
| Med. | 0.012665 | 0.012719 | 0.012719 | 0.012665 | 0.012781 | 0.012672708 | 0.01266995 |
| Max. | 0.012665 | 0.012928 | 0.014283 | 0.012665 | 1 × 1015 | 0.012667121 | 0.012665365 |
| STd | 1.69 × 10−8 | 7.56 × 10−5 | 0.000356 | 8.3 × 10−13 | 2.24 × 1014 | 1.61767 × 10−6 | 1.10174 × 10−6 |
| Rank | 2 | 6 | 6 | 1 | 7 | 1 | 3 |
| RW18 | Min. | 6247.675 | 6247.673 | 6247.673 | 6247.72 | 6359.528 | 6059.74963 | 6059.714355 |
| Av. | 6247.681 | 6544.502 | 6283.05 | 6247.934 | 39,927.73 | 6061.052218 | 6073.212954 |
| Med. | 6247.681 | 6382.985 | 6247.673 | 6247.853 | 15,046.06 | 6090.661389 | 6090.532868 |
| Max. | 6247.688 | 7319.001 | 6436.743 | 6248.808 | 239,304.1 | 6060.129709 | 6059.726443 |
| STd | 0.003228 | 400.6724 | 63.7404 | 0.236775 | 65,645.18 | 4.432071131 | 15.38116002 |
| Rank | 3 | 6 | 5 | 4 | 7 | 2 | 1 |
| RW19 | Min. | 1.670218 | 1.670218 | 1.670218 | 1.670218 | 1.67593 | 1.670251358 | 1.670217856 |
| Av. | 1.670218 | 1.700254 | 1.670219 | 1.670218 | 1.756922 | 1.670303479 | 1.670218426 |
| Med. | 1.670218 | 1.670218 | 1.670218 | 1.670218 | 1.722726 | 1.670434518 | 1.670219985 |
| Max. | 1.670218 | 1.816712 | 1.670239 | 1.670218 | 1.994586 | 1.670301692 | 1.670218296 |
| STd | 6.2 × 10−8 | 0.055884 | 4.83 × 10−6 | 5.61 × 10−8 | 0.080852 | 3.12104 × 10−5 | 4.87676 × 10−7 |
| Rank | 2 | 6 | 4 | 1 | 7 | 5 | 3 |
| RW20 | Min. | 263.8958 | 263.8958 | 263.8958 | 263.8958 | 263.8958 | 263.8958434 | 263.8958434 |
| Av. | 263.8958 | 263.8958 | 263.8985 | 263.8958 | 263.8959 | 263.8958434 | 263.8958434 |
| Med. | 263.8958 | 263.8958 | 263.8967 | 263.8958 | 263.8959 | 263.8958434 | 263.8958434 |
| Max. | 263.8958 | 263.8961 | 263.9237 | 263.8958 | 263.8962 | 263.8958434 | 263.8958434 |
| STd | 4.29 × 10−12 | 4.76 × 10−5 | 0.006081 | 1.3 × 10−14 | 7.87 × 10−5 | 8.72047 × 10−10 | 1.58449 × 10−11 |
| Rank | 2 | 5 | 7 | 1 | 6 | 4 | 3 |
| RW21 | Min. | 0.235242 | 0.235242 | 0.235242 | 0.235242 | 0.235242 | 0.235242458 | 0.235242458 |
| Av. | 0.235242 | 0.235242 | 0.235242 | 0.235242 | 0.235243 | 0.235242458 | 0.235242458 |
| Med. | 0.235242 | 0.235242 | 0.235242 | 0.235242 | 0.235243 | 0.235242459 | 0.235242458 |
| Max. | 0.235242 | 0.235242 | 0.235242 | 0.235242 | 0.235243 | 0.235242458 | 0.235242458 |
| STd | 5.94 × 10−9 | 1.14 × 10−16 | 1.14 × 10−16 | 1.87 × 10−11 | 9.23 × 10−8 | 1.8999 × 10−10 | 6.82535 × 10−13 |
| Rank | 6 | 1 | 1 | 4 | 7 | 5 | 3 |
| RW28 | Min. | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 |
| Av. | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 |
| Med. | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 |
| Max. | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 | 5599.448 |
| STd | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Rank | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| RW29 | Min. | 2,964,895 | 2,964,895 | 2,964,897 | 2,964,895 | 2,989,723 | 2,964,895.455 | 2,964,895.417 |
| Av. | 2,964,895 | 3,011,451 | 2,965,099 | 2,964,895 | 3,086,914 | 2,964,895.914 | 2,964,895.417 |
| Med. | 2,964,895 | 2,964,897 | 2,964,99 | 2,964,895 | 3,096,913 | 2,964,897.792 | 2,964,895.418 |
| Max. | 2,964,895 | 3,147,942 | 2,966,063 | 2,964,895 | 3,104,538 | 2,964,895.788 | 2,964,895.417 |
| STd | 9.68 × 10−5 | 74,628.94 | 302.1104 | 1.85 × 10−5 | 29,668.78 | 0.419557334 | 0.000130887 |
| Rank | 4 | 6 | 5 | 3 | 7 | 2 | 1 |
| RW31 | Min. | 3.89 × 10−20 | 0 | 0 | 5.46 × 10−19 | 3.38 × 10−19 | 2.57685 × 10−16 | 0 |
| Av. | 3.91 × 10−16 | 0 | 0 | 8.34 × 10−17 | 4.3 × 10−17 | 1.57017 × 10−12 | 7.96262 × 10−20 |
| Med. | 7.25 × 10−17 | 0 | 0 | 1.44 × 10−17 | 6.21 × 10−18 | 1.61363 × 10−11 | 3.9813 × 10−18 |
| Max. | 1.95 × 10−15 | 0 | 0 | 4.52 × 10−16 | 3.28 × 10−16 | 3.14661 × 10−13 | 6.93335 × 10−33 |
| STd | 5.92 × 10−16 | 0 | 0 | 1.33 × 10−16 | 8.09 × 10−17 | 3.14661 × 10−12 | 5.63041 × 10−19 |
| Rank | 6 | 1 | 1 | 5 | 4 | 7 | 3 |
| RW32 | Min. | 2.6393 | 2.6393 | 2.6393 | 2.6393 | 2.6393 | 2.6393 | 2.6393 |
| Av. | 2.6393 | 2.6393 | 2.6393 | 2.6393 | 2.6541 | 2.6393 | 2.6393 |
| Med. | 2.6393 | 2.6393 | 2.6393 | 2.6393 | 2.6939 | 2.6393 | 2.6393 |
| Max. | 2.6393 | 2.6393 | 2.6393 | 2.6393 | 2.6513 | 2.6393 | 2.6393 |
| STd | 0.001059 | 3.73 × 10−12 | 3.73 × 10−12 | 0.002432 | 0.415896 | 1.79439 × 10−15 | 1.79439 × 10−15 |
| Rank | 5 | 3 | 7 | 6 | 5 | 1 | 1 |
| Ranks summation | 47 | 50 | 48 | 40 | 77 | 42 | 31 |
| Average rank | 3.615385 | 3.846154 | 3.692308 | 3.076923 | 5.923077 | 3.230769 | 2.384615 |
| Regarding improvement % | 34.043% | 38.000% | 35.417% | 22.500% | 59.740% | 26.190% | - |
| Final ranking | 4 | 6 | 5 | 2 | 7 | 3 | 1 |
Table 3.
Optimized gains using DE, PSO, SFO, KO, and EKO for Case 1.
Table 3.
Optimized gains using DE, PSO, SFO, KO, and EKO for Case 1.
| Parameters | DE | PSO | SFO | KO | Proposed EKO |
|---|
| Area 1 | KP | 0.090109 | 0.072778354 | 0.098906 | 0.091053 | 0.090498113 |
| KI | 0.280171 | 0.283155395 | 0.276407 | 0.281548 | 0.281895243 |
| Area 2 | KP | 0.081499 | 0 | 0.10512 | 0.08444 | 0.087513508 |
| KI | 0.457284 | 0.441958801 | 0.462502 | 0.454033 | 0.455743125 |
| ITAE | 3.232596 | 3.247192601 | 3.234732 | 3.232469 | 3.232379096 |
| Regarding improvement % | 0.0067% | 0.4562% | 0.0727% | 0.0028% | - |
Table 4.
Statistical metrics for DE, PSO, SFO, KO, and proposed EKO for Case 1.
Table 4.
Statistical metrics for DE, PSO, SFO, KO, and proposed EKO for Case 1.
| | DE | PSO | SFO | KO | Proposes EKO |
|---|
| Min | 0.315377 | 0.259712 | 0.298104 | 0.257969 | 0.238278 |
| Average | 0.420843 | 0.508383 | 0.469785 | 0.37775 | 0.374211 |
| Median | 0.382479 | 0.373369 | 0.401883 | 0.36156 | 0.335956 |
| Max | 0.560605 | 1.001491 | 0.995069 | 0.566848 | 0.549338 |
| STd | 0.093496 | 0.26523 | 0.173228 | 0.084127 | 0.111095 |
Table 5.
Optimized gains using DE, PSO, SFO, KO, and EKO for Case 2.
Table 5.
Optimized gains using DE, PSO, SFO, KO, and EKO for Case 2.
| Parameters | DE | PSO | SFO | KO | Proposed EKO |
|---|
| Area 1 | KP | 1.438757 | 1.900453 | 1.586249 | 2.219521 | 1.983181 |
| KI | 1.215012 | 1.603468 | 2.200458 | 1.685726 | 1.633524 |
| KD1 | 2.140379 | 2.45894 | 2.261332 | 2.61141 | 2.103699 |
| KD2 | 3.649792 | 4 | 3.888985 | 3.786046 | 3.976172 |
| Area 2 | KP | 0.396676 | 0.45051 | 0.173962 | 0.609858 | 0.403955 |
| KI | 2.106416 | 2.558977 | 2.817782 | 2.503367 | 2.461233 |
| KD1 | 0.503803 | 0.658649 | 0.678034 | 0.67905 | 0.570483 |
| KD2 | 3.841419 | 4 | 3.602219 | 3.76936 | 3.889637 |
| ITAE | 0.315377 | 0.259712 | 0.298104 | 0.257969 | 0.238278 |
| Regarding improvement % | 24.4466% | 8.2530% | 20.0688% | 7.6331% | - |
Table 6.
Statistical metrics for DE, PSO, SFO, KO, and proposed EKO for Case 2.
Table 6.
Statistical metrics for DE, PSO, SFO, KO, and proposed EKO for Case 2.
| | DE | PSO | SFO | KO | Proposes EKO |
|---|
| Min | 0.315377 | 0.259712 | 0.298104 | 0.257969 | 0.238278 |
| Average | 0.420843 | 0.508383 | 0.469785 | 0.37775 | 0.374211 |
| Median | 0.382479 | 0.373369 | 0.401883 | 0.36156 | 0.335956 |
| Max | 0.560605 | 1.001491 | 0.995069 | 0.566848 | 0.549338 |
| STd | 0.093496 | 0.26523 | 0.173228 | 0.084127 | 0.111095 |
Table 7.
Optimized gains using DE, PSO, SFO, KO and EKO for Case 3.
Table 7.
Optimized gains using DE, PSO, SFO, KO and EKO for Case 3.
| Parameters | DE | PSO | SFO | KO | Proposed EKO |
|---|
| Area 1 | KP | 2.799941 | 4 | 2.580767 | 3.682332 | 3.524932 |
| KI | 3.851379 | 4 | 3.898463 | 3.925627 | 4 |
| KD1 | −2.14108 | −3.38925 | −1.08412 | 0.139779 | 0.847833 |
| KD2 | 2.939685 | 4 | 1.983451 | 0.582093 | −0.14473 |
| Area 2 | KP | 1.444046 | 1.645876 | 1.884726 | 1.740169 | 1.66395 |
| KI | 3.894251 | 4 | 3.989225 | 4 | 4 |
| KD1 | −0.72786 | −3.61616 | −0.16341 | 2.626995 | 3.982741 |
| KD2 | 1.166057 | 4 | 0.514835 | −2.28613 | −3.58183 |
| ITAE | 0.071969 | 0.068583 | 0.069858 | 0.069735 | 0.068234 |
| Regarding improvement % | 5.1902% | 0.5095% | 2.3251% | 2.1530% | - |
Table 8.
Statistical metrics for the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 3.
Table 8.
Statistical metrics for the DE, PSO, SFO, KO, and proposed EKO algorithms for Case 3.
| | DE | PSO | SFO | KO | Proposes EKO |
|---|
| Min | 0.071969 | 0.068583 | 0.069858 | 0.069735 | 0.068234 |
| Average | 0.111844 | 0.331536 | 0.111255 | 0.080092 | 0.070255 |
| Median | 0.09293 | 0.270314 | 0.08282 | 0.077899 | 0.0696 |
| Max | 0.193783 | 1.100891 | 0.652739 | 0.108116 | 0.074528 |
| STd | 0.040317 | 0.329608 | 0.127764 | 0.008283 | 0.001992 |