A New Fractional Discrete Memristive Map with Variable Order and Hidden Dynamics
Abstract
1. Introduction
2. The Fractional Discrete Memristive-Based Duffing Map
2.1. Preliminaries
2.2. Model Description
2.3. Analysis of Equilibrium Point
3. Dynamical Analysis
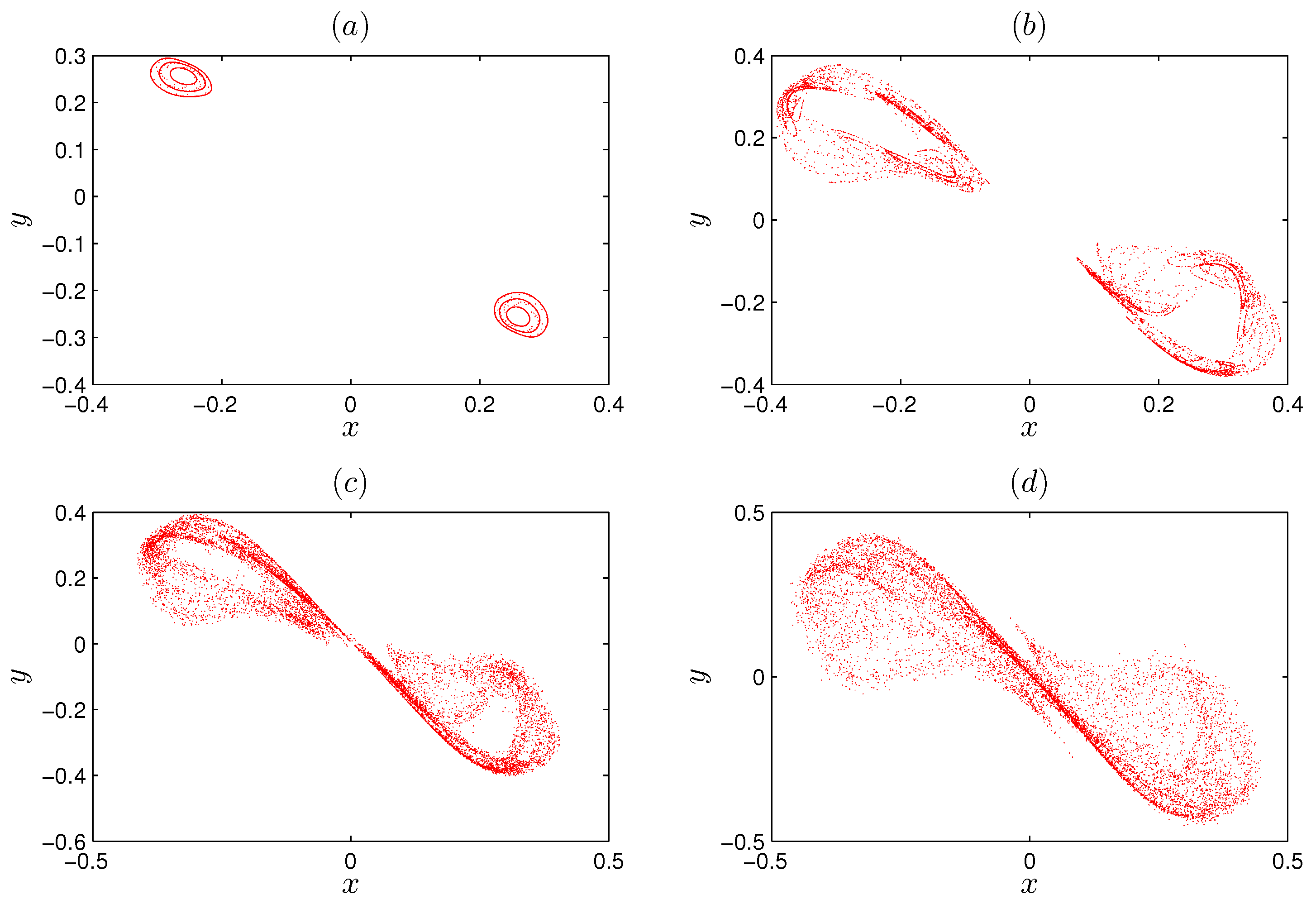
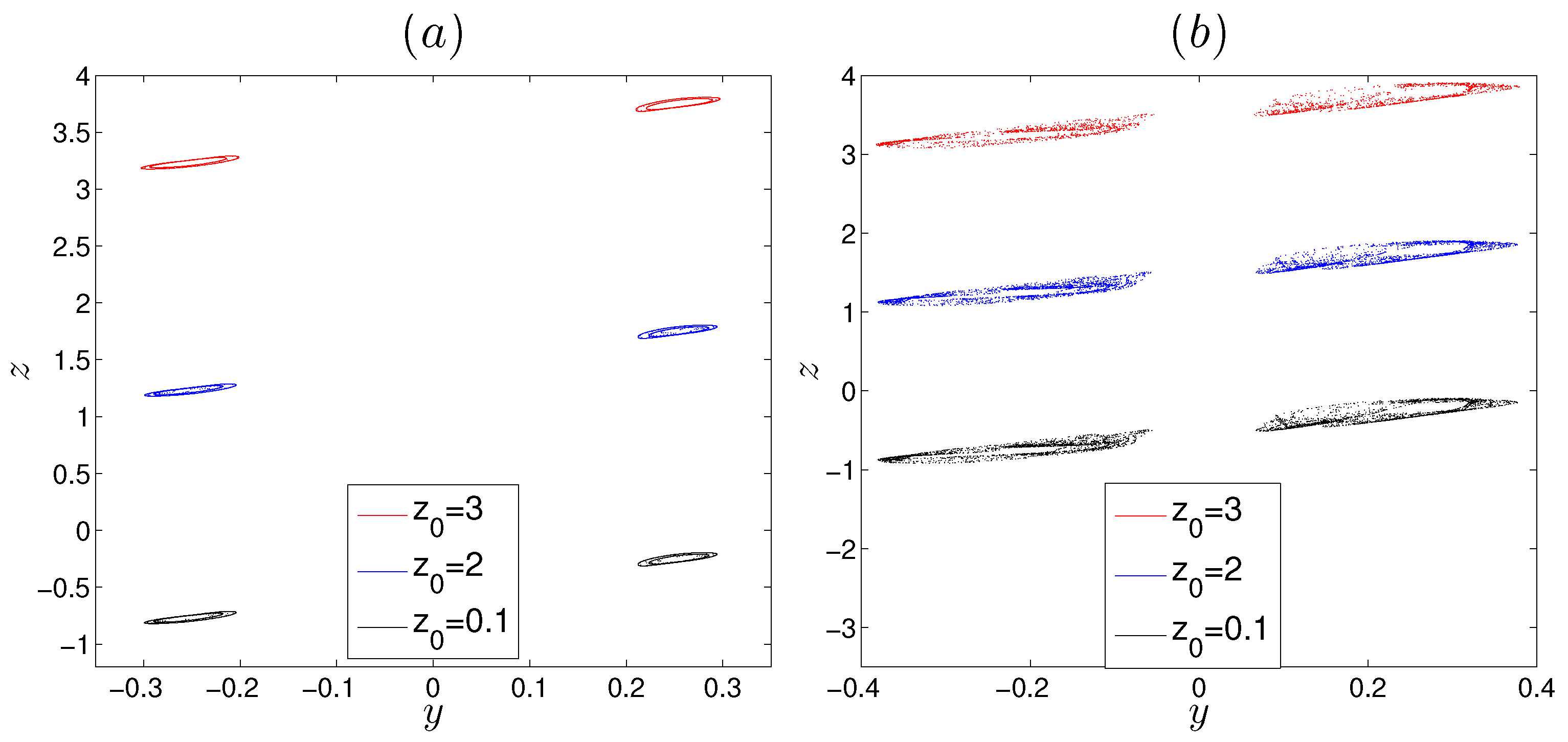
3.1. Coexisting Multiple Hidden Attractors
3.2. The Invariance Property
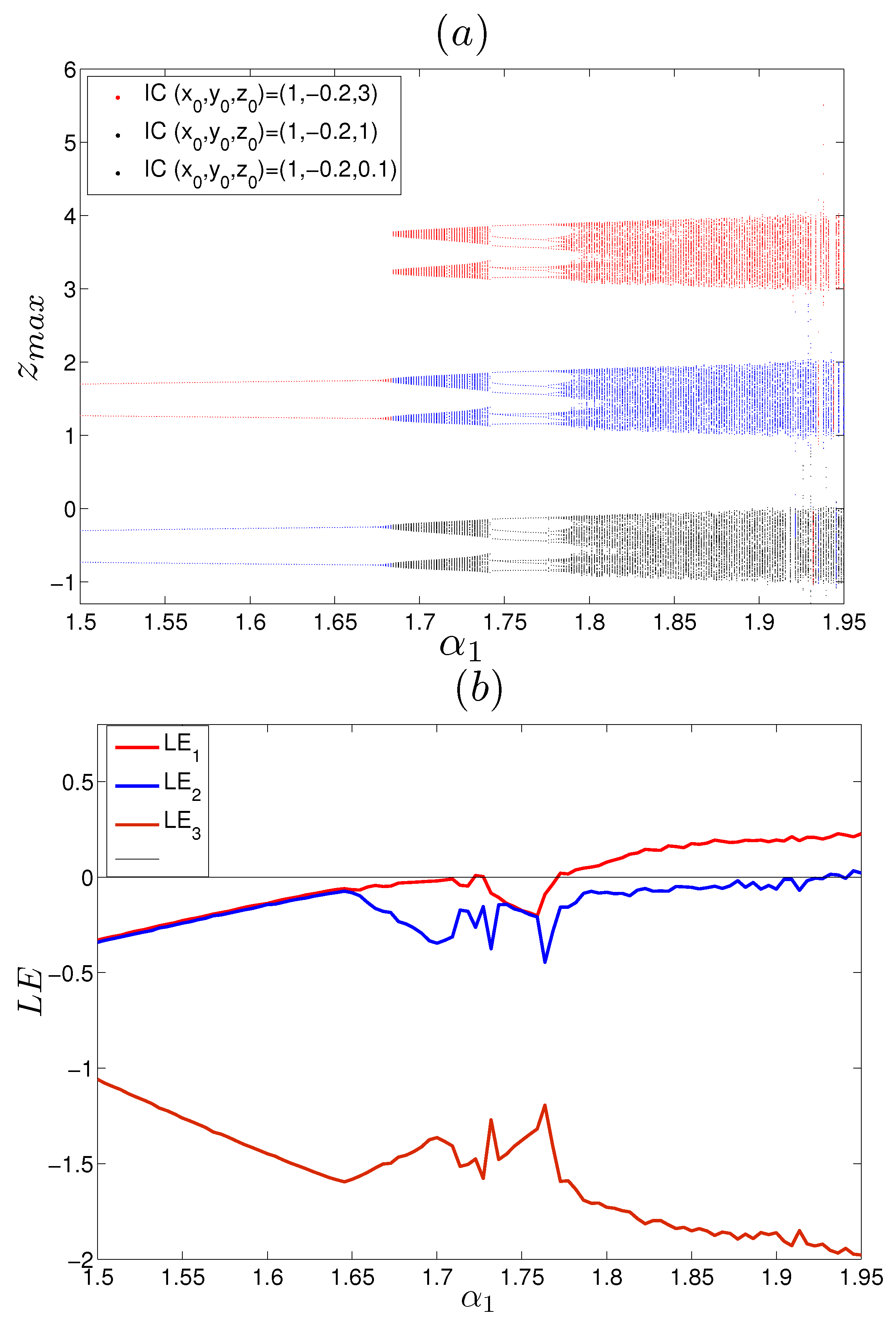
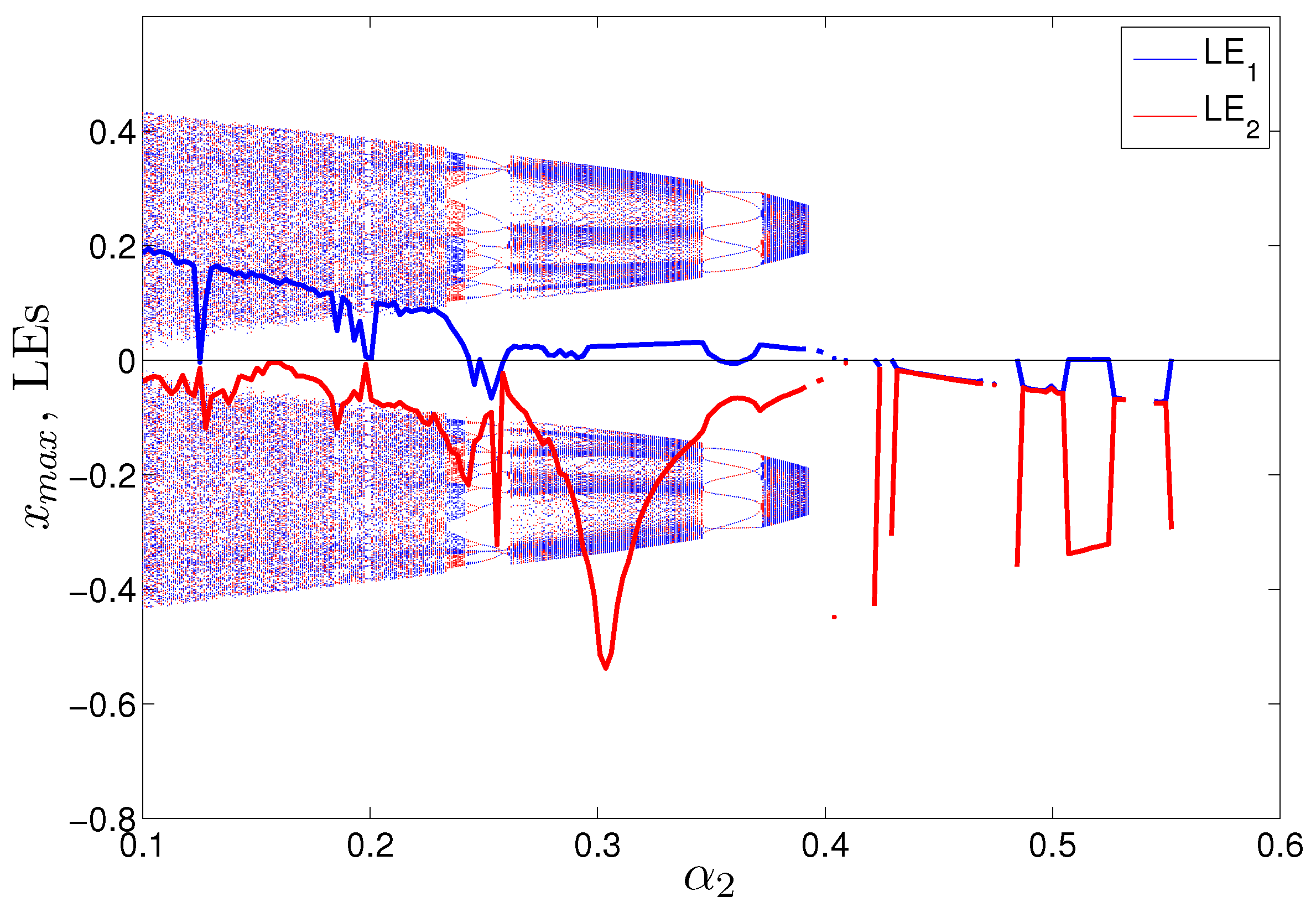
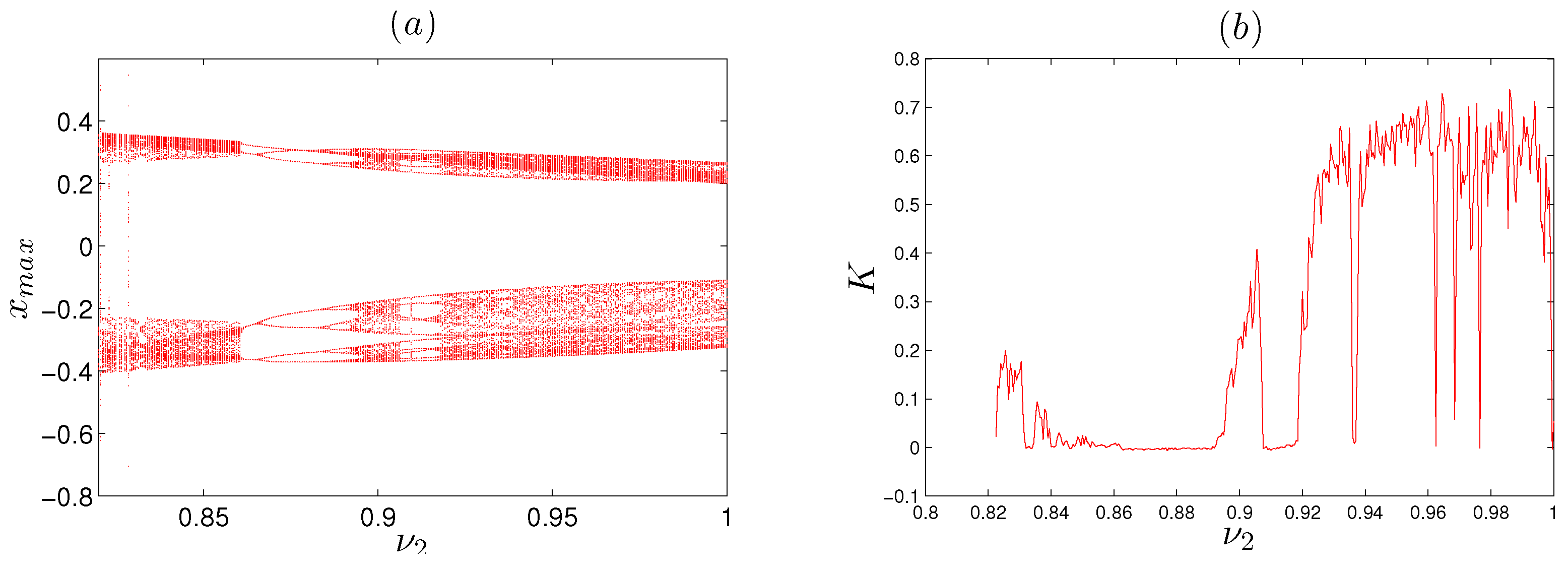
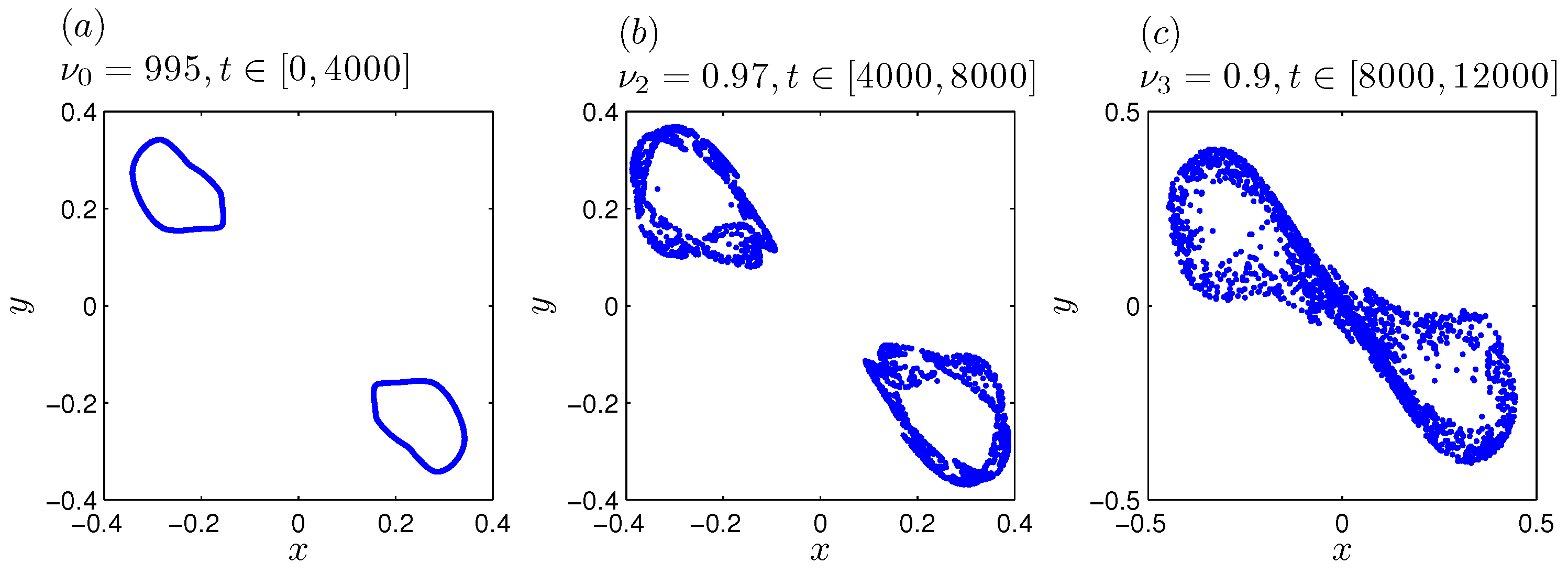
3.3. Effect of the Fractional Variable Order
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Diaz, J.B.; Olser, T.J. Differences of fractional order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Wu, G.C.; Baleanu, D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dyn. 2015, 80, 1697–1703. [Google Scholar] [CrossRef]
- Wang, L.; Sun, K.; Peng, Y.; He, S. Chaos and complexity in a fractional-order higher-dimensional multicavity chaotic map. Chaos Solitons Fractals 2020, 131, 109488. [Google Scholar] [CrossRef]
- Shukla, M.K.; Sharma, B.B. Investigation of chaos in fractional order generalized hyperchaotic Hénon map. Int. J. Elec. Comm. 2017, 78, 265–273. [Google Scholar] [CrossRef]
- Wu, G.C.; Deng, Z.G.; Baleanu, D.; Zneg, D.Q. New variable-order fractional chaotic systems for fast image encryption. Chaos 2019, 29, 083103. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.B.; Ouannas, A.; Horani, M.A.; Grassi, G. The Discrete Fractional Variable-Order Tinkerbell Map: Chaos, 0–1 Test, and Entropy. Mathematics 2022, 10, 3173. [Google Scholar] [CrossRef]
- Bao, B.C.; Li, H.; Wu, H.; Zhang, X.; Chen, M. Hyperchaos in a second order discrete memristor-based map model. Electron. Lett. 2020, 56, 769–770. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Momani, S.; Almatroud, O.A.; Al-Sawalha, M.M.; Boulaaras, S.M.; Pham, V.T. Special Fractional-Order Map and Its Realization. Mathematics 2022, 10, 4474. [Google Scholar] [CrossRef]
- He, S.; Zhan, D.; Wang, H.; Sun, K.; Peng, Y. Discrete memristive and Discrete Memristive Systems. Entropy 2022, 24, 786. [Google Scholar] [CrossRef] [PubMed]
- Chua, L. memristive-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Pham, V.T.; Thoai, V.P.; Ouannas, A.; Grassi, G.; Momani, S. From Lozi map to fractional memristive Lozi map. Eur. Phys. J. Spec. Top. 2023, 232, 2385–2393. [Google Scholar] [CrossRef]
- Shatnawi, M.T.; Khennaoui, A.A.; Ouannas, A.; Grassi, G.; Radogna, A.V.; Bataihah, A.; Batiha, I.M. A Multistability Discrete memristive and Its Application to Discrete-Time FitzHugh–Nagumo Model. Electronics 2023, 12, 2929. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D.; Jarad, F.; Agarwal, R.P. Fractional sums and differences with binomial coefficients. Discret. Dyn. Nat. Soc. 2013, 2013, 104173. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Li, H.; Bao, M.C.B. Discrete memristive hyperchaotic maps. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 4534–4544. [Google Scholar] [CrossRef]
- Li, K.; Cao, J.; He, J.M. Hidden hyperchaotic attractors in a new 4D fractional order system and its synchronization. Chaos 2020, 30, 033129. [Google Scholar] [CrossRef] [PubMed]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in deterministic systems. Proc. Math. Phys. Eng. Sci. 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Ouannas, A.; Khennaoui, A.A.; Momani, S.; Pahm, V.T. The discrete fractional duffing system: Chaos, 0–1 test, C0 complexity, entropy, and control. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 083131. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almatroud, O.A.; Khennaoui, A.-A.; Ouannas, A.; Alshammari, S.; Albosaily, S. A New Fractional Discrete Memristive Map with Variable Order and Hidden Dynamics. Fractal Fract. 2024, 8, 322. https://doi.org/10.3390/fractalfract8060322
Almatroud OA, Khennaoui A-A, Ouannas A, Alshammari S, Albosaily S. A New Fractional Discrete Memristive Map with Variable Order and Hidden Dynamics. Fractal and Fractional. 2024; 8(6):322. https://doi.org/10.3390/fractalfract8060322
Chicago/Turabian StyleAlmatroud, Othman Abdullah, Amina-Aicha Khennaoui, Adel Ouannas, Saleh Alshammari, and Sahar Albosaily. 2024. "A New Fractional Discrete Memristive Map with Variable Order and Hidden Dynamics" Fractal and Fractional 8, no. 6: 322. https://doi.org/10.3390/fractalfract8060322
APA StyleAlmatroud, O. A., Khennaoui, A.-A., Ouannas, A., Alshammari, S., & Albosaily, S. (2024). A New Fractional Discrete Memristive Map with Variable Order and Hidden Dynamics. Fractal and Fractional, 8(6), 322. https://doi.org/10.3390/fractalfract8060322






