Analyzing a Dynamical System with Harmonic Mean Incidence Rate Using Volterra–Lyapunov Matrices and Fractal-Fractional Operators
Abstract
1. Introduction
2. Foundational Concepts
2.1. Foundational Concept for V-L Matrix Theory
2.2. Foundational Concept of Fractional Calculus
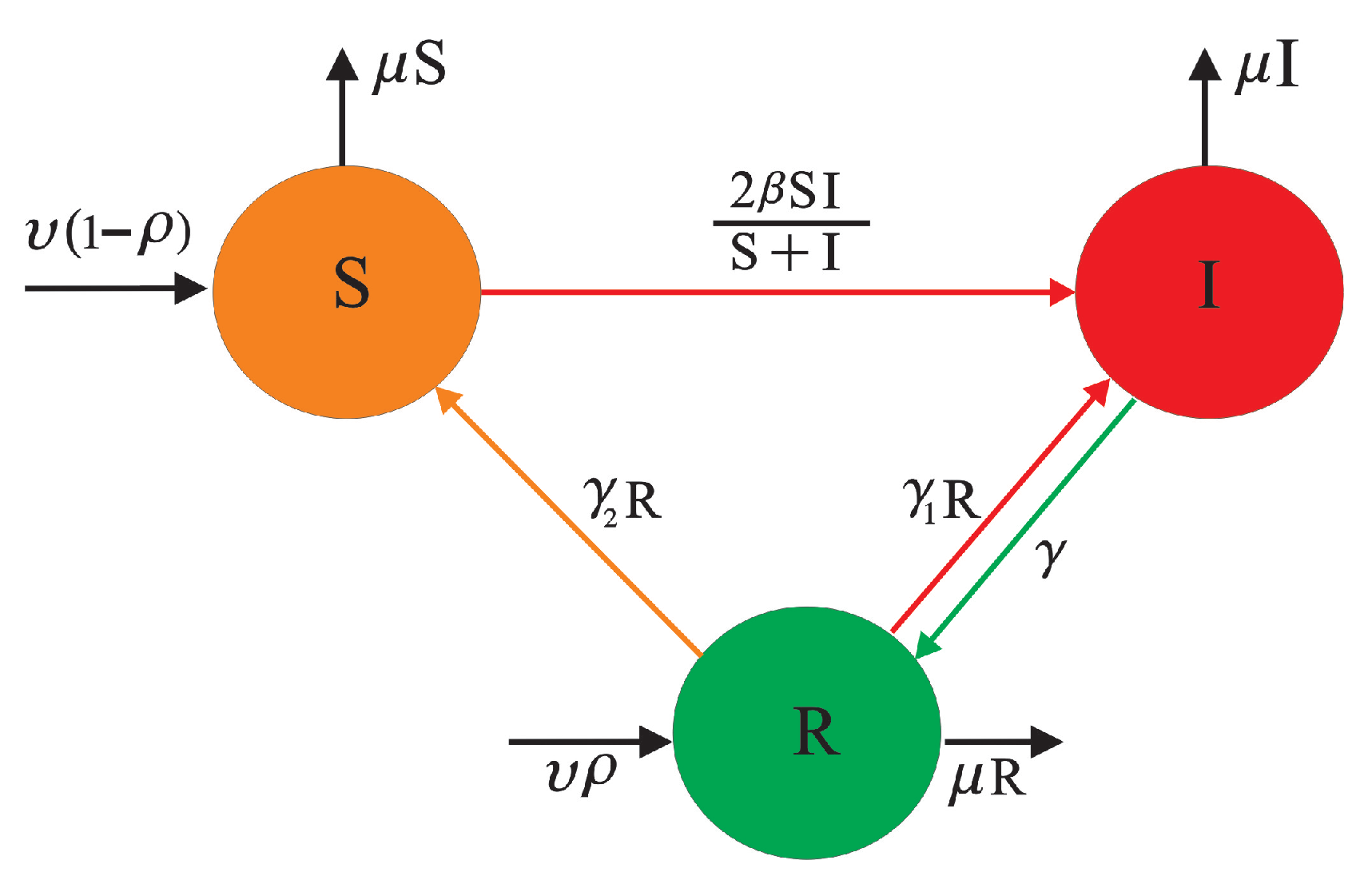
3. Model Building Process
3.1. Introduction to Equilibrium Points
3.2. Disease-Free Equilibrium (DFE)
3.3. Endemic Equilibrium (EE)
3.4. Fundamental Number
3.5. Sensitivity Analysis
3.6. Local Stability of DFE and EE
3.7. Global Stability of DFE at
Global Stability Analysis of EE at
- (i)
- ;
- (ii)
- ;
- (iii)
- .
- (i)
- (ii)
- (iii)
4. Fractal-Fractional Model Formulation and Methodology
5. Stability Analysis
6. Scheme for Numerical Results
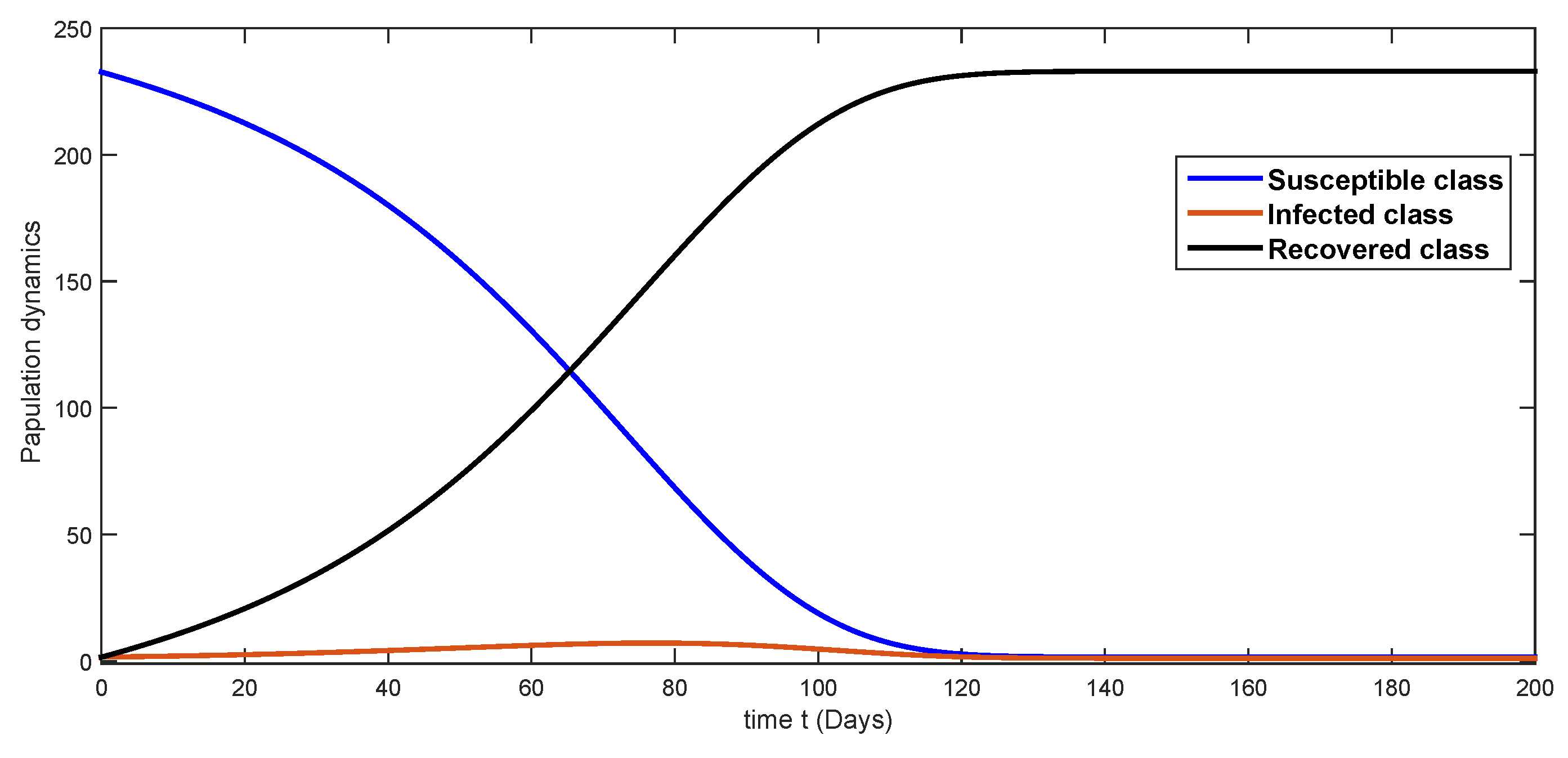
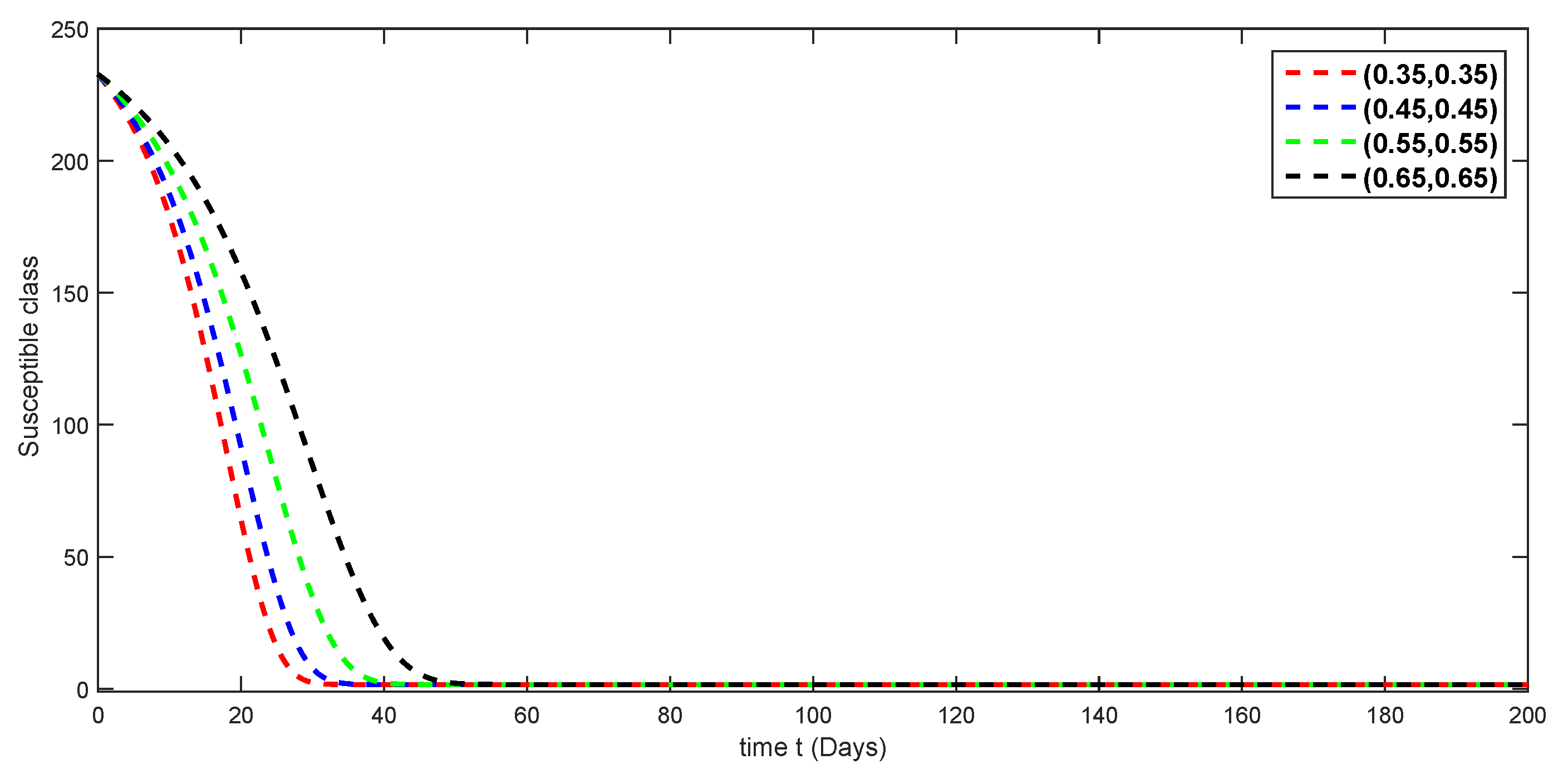
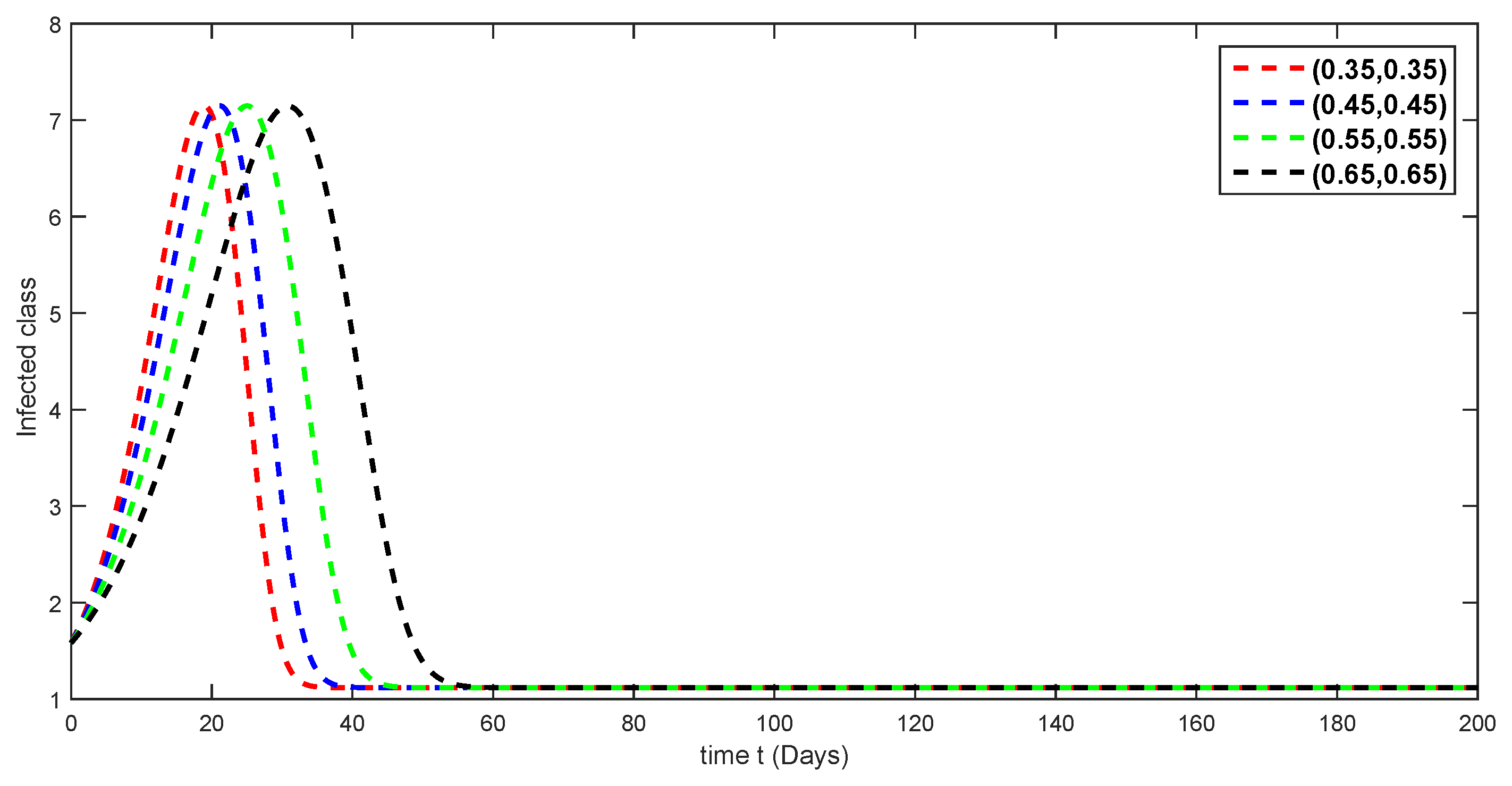
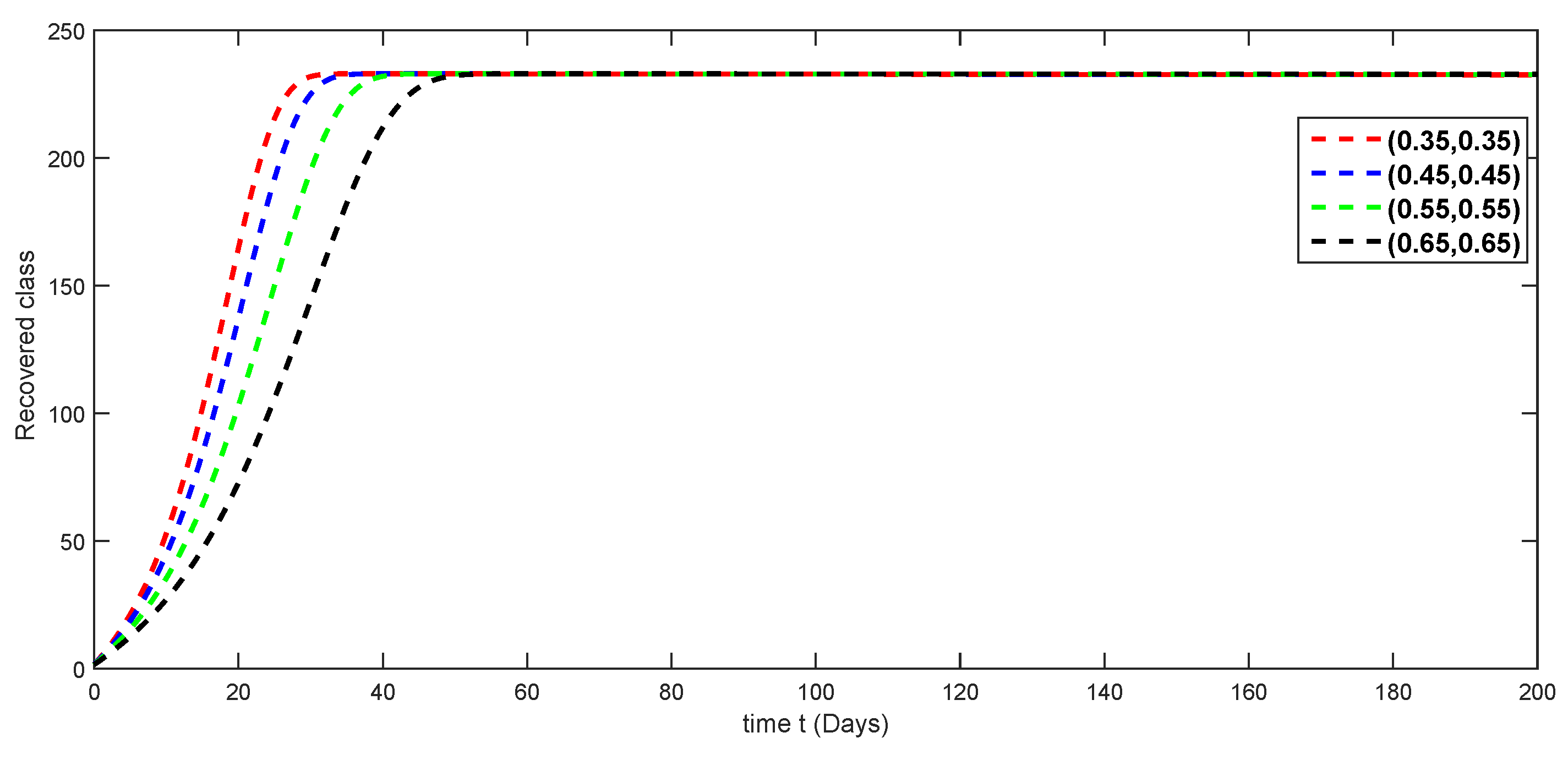
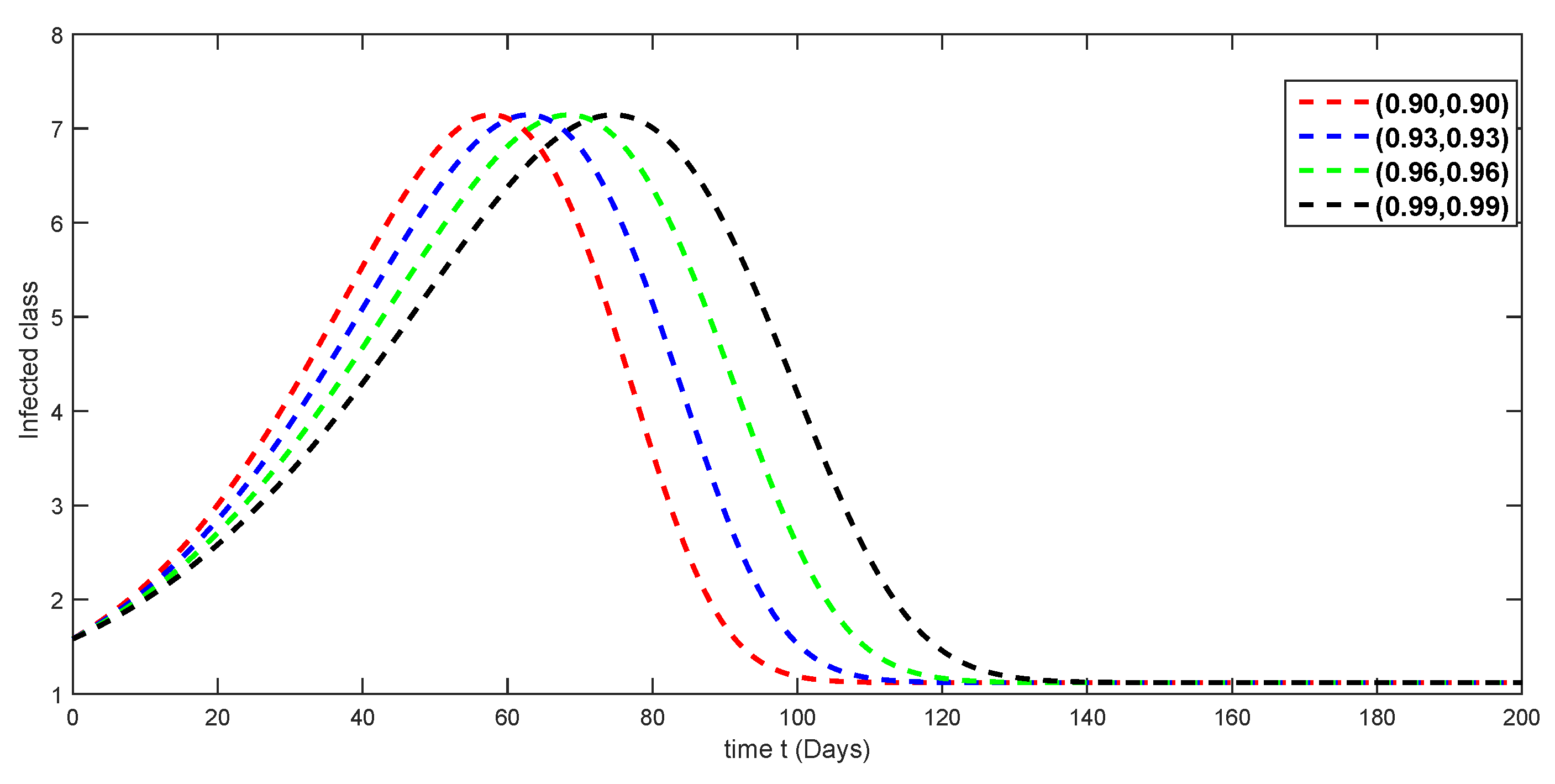
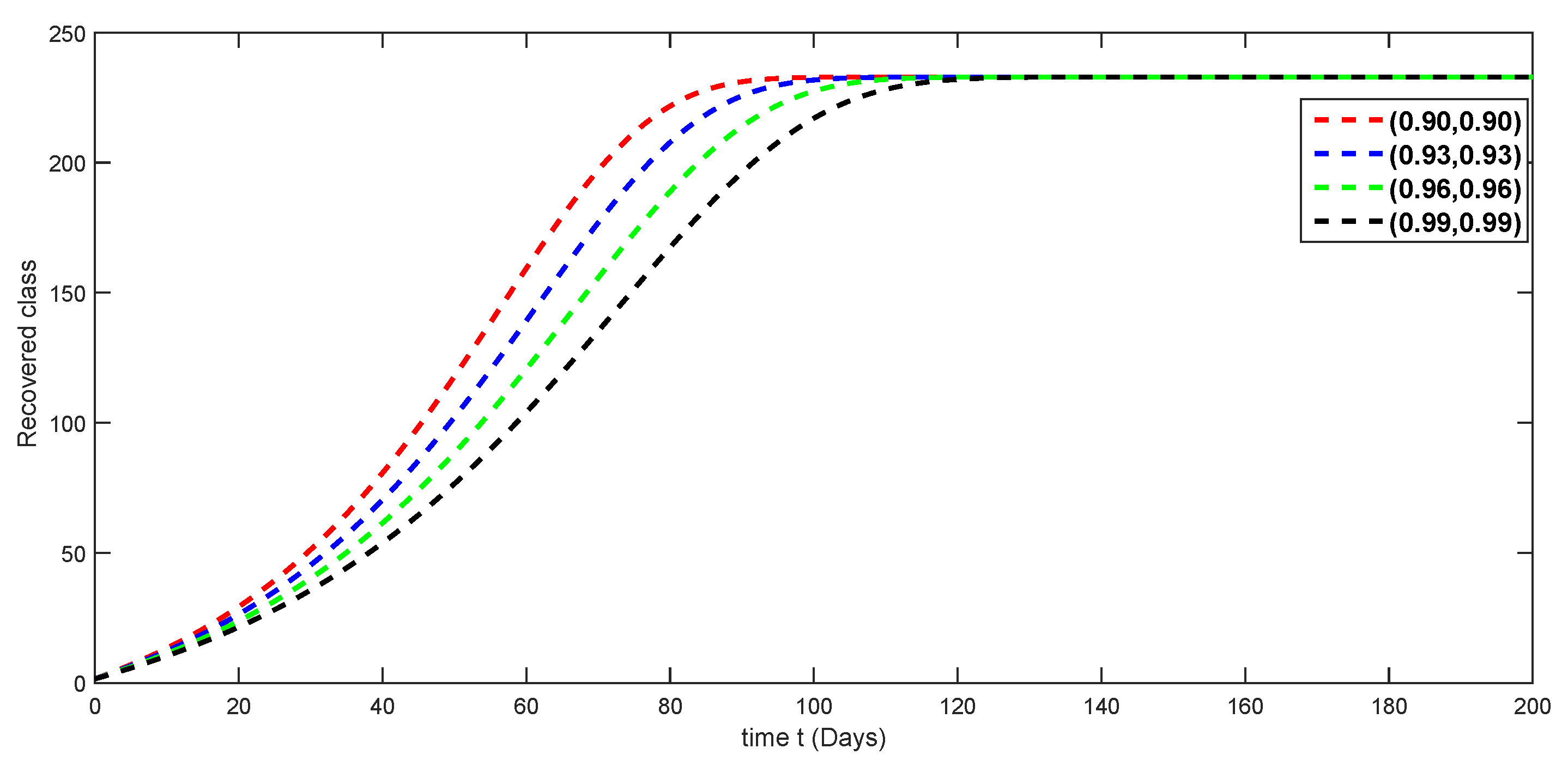
7. Numerical Simulations and Discussion
Some Discussion and Potential Limitations of Our Assumptions and Tools
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roccetti, M. Drawing a parallel between the trend of confirmed COVID-19 deaths in the winters of 2022/2023 and 2023/2024 in Italy, with a prediction. Math. Biosci. Eng. 2024, 21, 3742–3754. [Google Scholar] [CrossRef] [PubMed]
- Mohamadou, Y.; Halidou, A.; Kapen, P.T. A review of mathematical modeling, artificial intelligence and datasets used in the study, prediction and management of COVID-19. Appl. Intell. 2020, 50, 3913–3925. [Google Scholar] [CrossRef] [PubMed]
- Margenov, S.; Popivanov, N.; Ugrinova, I.; Hristov, T. Mathematical Modeling and Short-Term Forecasting of the COVID-19 Epidemic in Bulgaria: SEIRS Model with Vaccination. Mathematics 2022, 10, 2570. [Google Scholar] [CrossRef]
- Vytla, V.; Ramakuri, S.K.; Peddi, A.; Srinivas, K.K.; Ragav, N.N. Mathematical models for predicting COVID-19 pandemic: A review. J. Phys. Conf. Ser. 2021, 1797, 012009. [Google Scholar] [CrossRef]
- Starshinova, A.; Osipov, N.; Dovgalyk, I.; Kulpina, A.; Belyaeva, E.; Kudlay, D. COVID-19 and Tuberculosis: Mathematical Modeling of Infection Spread Taking into Account Reduced Screening. Diagnostics 2024, 14, 698. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Liu, J.B.; Li, H. Global dynamics of an SIQR model with vaccination and elimination hybrid strategies. Mathematics 2018, 6, 328. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Pal, A.K.; Kumari, S.; Roy, P. Dynamics of an SEIR epidemic model with nonlinear incidence and treatment rates. Nonlinear Dyn. 2019, 96, 2351–2368. [Google Scholar] [CrossRef]
- Mwasa, A.; Tchuenche, J.M. Mathematical analysis of a cholera model with public health interventions. Biosystems 2011, 105, 190–200. [Google Scholar] [CrossRef]
- Wang, L.; Xu, R. Global stability of an SEIR epidemic model with vaccination. Int. J. Biomath. 2016, 9, 1650082. [Google Scholar] [CrossRef]
- Bentaleb, D.; Amine, S. Lyapunov function and global stability for a two-strain SEIR model with bilinear and non-monotone incidence. Int. J. Biomath. 2019, 12, 1950021. [Google Scholar] [CrossRef]
- Chen, X.; Cao, J.; Park, J.H.; Qiu, J. Stability analysis and estimation of domain of attraction for the endemic equilibrium of an SEIQ epidemic model. Nonlinear Dyn. 2017, 87, 975–985. [Google Scholar] [CrossRef]
- Baba, I.A.; Hincal, E. Global stability analysis of two-strain epidemic model with bilinear and non-monotone incidence rates. Eur. Phys. J. Plus 2017, 132, 208. [Google Scholar] [CrossRef]
- Geng, Y.; Xu, J. Stability preserving NSFD scheme for a multi-group SVIR epidemic model. Math. Methods Appl. Sci. 2017, 40, 4917–4927. [Google Scholar] [CrossRef]
- McCluskey, C.C. Global stability for an SIR epidemic model with delay and nonlinear incidence. Nonlinear Anal. Real World Appl. 2010, 11, 3106–3109. [Google Scholar] [CrossRef]
- Arfan, M.; Shah, K.; Ullah, A. Fractal-fractional mathematical model of four species comprising of prey-predation. Phys. Scr. 2021, 96, 124053. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Xie, W.C.; Xu, W.; Xu, Y. Global stability and persistence of HIV models with switching parameters and pulse control. Math. Comput. Simul. 2016, 123, 53–67. [Google Scholar] [CrossRef]
- Hu, Z.; Ma, W.; Ruan, S. Analysis of SIR epidemic models with nonlinear incidence rate and treatment. Math. Biosci. 2012, 238, 12–20. [Google Scholar] [CrossRef] [PubMed]
- Misra, A.K.; Sharma, A.; Shukla, J.B. Stability analysis and optimal control of an epidemic model with awareness programs by media. Biosystems 2015, 138, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Thieme, H.R. Global stability of the endemic equilibrium in infinite dimension: Lyapunov functions and positive operators. J. Diff. Equ. 2011, 250, 3772–3801. [Google Scholar] [CrossRef]
- Naik, P.A.; Farman, M.; Zehra, A.; Nisar, K.S.; Hincal, E. Analysis and modeling with fractal-fractional operator for an epidemic model with reference to COVID-19 modeling. Partial Differ. Equ. Appl. Math. 2024, 10, 100663. [Google Scholar] [CrossRef]
- Shah, K.; Sarwar, M.; Abdeljawad, T. On mathematical model of infectious disease by using fractals fractional analysis. Discret. Contin. Dyn. Syst.—S 2024. [Google Scholar] [CrossRef]
- Kubra, K.T.; Ali, R.; Alqahtani, R.T.; Gulshan, S.; Iqbal, Z. Analysis and comparative study of a deterministic mathematical model of SARS-COV-2 with fractal-fractional operators: A case study. Sci. Rep. 2024, 14, 6431. [Google Scholar] [CrossRef] [PubMed]
- Farman, M.; Akgül, A.; Hashemi, M.S.; Guran, L.; Bucur, A. Fractal fractional order operators in computational techniques for mathematical models in epidemiology. Comput. Model. Eng. Sci. 2024, 138, 1385–1402. [Google Scholar] [CrossRef]
- Fowler, A.C. Mathematical Models in the Applied Sciences; Cambridge University Press: Cambridge, UK, 1997; Volume 17. [Google Scholar]
- West, B.J. Fractal physiology and the fractional calculus: A perspective. Front. Physiol. 2010, 1, 1886. [Google Scholar] [CrossRef] [PubMed]
- Baishya, C.; Achar, S.J.; Veeresha, P. An Application of the Caputo Fractional Domain in the Analysis of a COVID-19 Mathematical Model. Contemp. Math. 2024, 5, 255–283. [Google Scholar] [CrossRef]
- Gao, W.; Veeresha, P.; Cattani, C.; Baishya, C.; Baskonus, H.M. Modified predictor-corrector method for the numerical solution of a fractional-order SIR model with 2019-nCoV. Fractal Fract. 2022, 6, 92. [Google Scholar] [CrossRef]
- Achar, S.J.; Baishya, C.; Veeresha, P.; Akinyemi, L. Dynamics of fractional model of biological pest control in tea plants with Beddington-DeAngelis functional response. Fractal Fract. 2021, 6, 1. [Google Scholar] [CrossRef]
- Jan, R.; Khan, A.; Boulaaras, S.; Ahmed Zubair, S. Dynamical behaviour and chaotic phenomena of HIV infection through fractional calculus. Discret. Dyn. Nat. Soc. 2022, 2022, 5937420. [Google Scholar] [CrossRef]
- Tang, T.Q.; Jan, R.; Bonyah, E.; Shah, Z.; Alzahrani, E. Qualitative analysis of the transmission dynamics of dengue with the effect of memory, reinfection, and vaccination. Comput. Math. Methods Med. 2022, 2022, 7893570. [Google Scholar] [CrossRef] [PubMed]
- Jan, R.; Boulaaras, S.; Shah, S.A.A. Fractional-calculus analysis of human immunodeficiency virus and CD4+ T-cells with control interventions. Commun. Theor. Phys. 2022, 74, 105001. [Google Scholar] [CrossRef]
- Jan, A.; Boulaaras, S.; Abdullah, F.A.; Jan, R. Dynamical analysis, infections in plants, and preventive policies utilizing the theory of fractional calculus. Eur. Phys. J. Spec. Top. 2023, 232, 2497–2512. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Alzahrani, E.; Jan, R.; Alreshidi, N.A. Chaotic phenomena and oscillations in dynamical behaviour of financial system via fractional calculus. Complexity 2022, 2022, 8113760. [Google Scholar] [CrossRef]
- Jan, R.; Boulaaras, S.; Alyobi, S.; Jawad, M. Transmission dynamics of Hand-Foot-Mouth Disease with partial immunity through non-integer derivative. Int. J. Biomath. 2023, 16, 2250115. [Google Scholar] [CrossRef]
- Jan, R.; Khan, H.; Kumam, P.; Tchier, F.; Shah, R.; Jebreen, H.B. The investigation of the fractional-view dynamics of Helmholtz equations within Caputo operator. Comput. Mater. Contin. 2021, 68, 3185–3201. [Google Scholar] [CrossRef]
- Jan, R.; Razak, N.N.A.; Boulaaras, S.; Rehman, Z.U.; Bahramand, S. Mathematical analysis of the transmission dynamics of viral infection with effective control policies via fractional derivative. Nonlinear Eng. 2023, 12, 20220342. [Google Scholar] [CrossRef]
- Jódar, L.; Villanueva, R.J.; Arenas, A.J.; González, G.C. Nonstandard numerical methods for a mathematical model for influenza disease. Math. Comput. Simul. 2008, 79, 622–633. [Google Scholar] [CrossRef]
- Khan, A.; Abdeljawad, T.; Alqudah, M.A. Neural networking study of worms in a wireless sensor model in the sense of fractal fractional. AIMS Math. 2023, 8, 26406–26424. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T. On complex fractal-fractional order mathematical modeling of CO2 emanations from energy sector. Phys. Scr. 2023, 99, 015226. [Google Scholar] [CrossRef]
- Shafiullah; Shah, K.; Sarwar, M.; Abdeljawad, T. On theoretical and numerical analysis of fractal–fractional non-linear hybrid differential equations. Nonlinear Eng. 2024, 13, 20220372. [Google Scholar] [CrossRef]
- Shah, K.; Arfan, M.; Mahariq, I.; Ahmadian, A.; Salahshour, S.; Ferrara, M. Fractal-fractional mathematical model addressing the situation of corona virus in Pakistan. Results Phys. 2020, 19, 103560. [Google Scholar] [CrossRef]
- Khan, Z.A.; Shah, K.; Abdalla, B.; Abdeljawad, T. A numerical study of complex dynamics of a chemostat model under fractal-fractional derivative. Fractals 2023, 31, 2340181. [Google Scholar] [CrossRef]
- Strichartz, R.S. Analysis on fractals. Not. AMS 1999, 46, 1199–1208. [Google Scholar]
- Dietz, K. The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med Res. 1993, 2, 23–41. [Google Scholar] [CrossRef] [PubMed]
- Chien, F.; Shateyi, S. Volterra-Lyapunov stability analysis of the solutions of babesiosis disease model. Symmetry 2021, 13, 1272. [Google Scholar] [CrossRef]
- Zahedi, M.S.; Kargar, N.S. The Volterra-Lyapunov matrix theory for global stability analysis of a model of HIV/AIDS. Int. J. Biomath. 2017, 10, 1750002. [Google Scholar] [CrossRef]
- Shao, P.; Shateyi, S. Stability Analysis of SEIRS Epidemic Model with Nonlinear Incidence Rate Function. Mathematics 2021, 9, 2644. [Google Scholar] [CrossRef]
- Masoumnezhad, M.; Rajabi, M.; Chapnevis, A.; Dorofeev, A.; Shateyi, S.; Kargar, N.S.; Nik, H.S. An approach for the global stability of mathematical model of an infectious disease. Symmetry 2020, 12, 1778. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Partial Differ. Equ. 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Ahmad, S.; Shah, K.; Abdeljawad, T.; Abdalla, B. On the Approximation of Fractal-Fractional Differential Equations Using Numerical Inverse Laplace Transform Methods. Comput. Model. Eng. Sci. 2023, 135, 2743. [Google Scholar]
- Ali, Z.; Rabiei, F.; Shah, K.; Khodadadi, T. Fractal-fractional order dynamical behavior of an HIV/AIDS epidemic mathematical model. Eur. Phys. J. Plus 2021, 136, 36. [Google Scholar] [CrossRef]
- Khan, Z.A.; Rahman, M.U.; Shah, K. Study of a fractal-fractional smoking models with relapse and harmonic mean type incidence rate. J. Funct. Spaces 2021, 2021, 6344079. [Google Scholar] [CrossRef]
- Abdel-Gawad, H.I.; Baleanu, D.; Abdel-Gawad, A.H. Unification of the different fractional time derivatives: An application to the epidemic-antivirus dynamical system in computer networks. Chaos Solitons Fractals 2021, 142, 110416. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Özdemir, N.; Uçar, S.; Iskender Eroglu, B.B. Dynamical analysis of fractional order model for computer virus propagation with kill signals. Int. J. Nonlinear Sci. Numer. Simul. 2020, 21, 239–247. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J. New aspects of fractional epidemiological model for computer viruses with Mittag-Leffler law. In Mathematical Modelling in Health, Social and Applied Sciences; Springer: Singapore, 2020; pp. 283–301. [Google Scholar]
- Maji, C.; Al Basir, F.; Mukherjee, D.; Ravichandran, C.; Nisar, K. COVID-19 propagation and the usefulness of awareness-based control measures: A mathematical model with delay. AIMs Math. 2022, 7, 12091–12105. [Google Scholar] [CrossRef]
- Perko, L. Differential Equations and Dynamical Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 7. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Yusuf, T.T. On global stability of disease-free equilibrium in epidemiological models. Eur. J. Math. Stat. 2021, 2, 37–42. [Google Scholar] [CrossRef]
- Johnson, M.L.; Faunt, L.M. Parameter estimation by least-squares methods, In Methods in Enzymology; Academic Press: New York, NY, USA, 1992; Volume 210, pp. 1–37. [Google Scholar]
- Worldometer. Available online: https://www.worldometers.info/coronavirus/country/pakistan/ (accessed on 12 March 2024).




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riaz, M.; Alqarni, F.A.; Aldwoah, K.; Birkea, F.M.O.; Hleili, M. Analyzing a Dynamical System with Harmonic Mean Incidence Rate Using Volterra–Lyapunov Matrices and Fractal-Fractional Operators. Fractal Fract. 2024, 8, 321. https://doi.org/10.3390/fractalfract8060321
Riaz M, Alqarni FA, Aldwoah K, Birkea FMO, Hleili M. Analyzing a Dynamical System with Harmonic Mean Incidence Rate Using Volterra–Lyapunov Matrices and Fractal-Fractional Operators. Fractal and Fractional. 2024; 8(6):321. https://doi.org/10.3390/fractalfract8060321
Chicago/Turabian StyleRiaz, Muhammad, Faez A. Alqarni, Khaled Aldwoah, Fathea M. Osman Birkea, and Manel Hleili. 2024. "Analyzing a Dynamical System with Harmonic Mean Incidence Rate Using Volterra–Lyapunov Matrices and Fractal-Fractional Operators" Fractal and Fractional 8, no. 6: 321. https://doi.org/10.3390/fractalfract8060321
APA StyleRiaz, M., Alqarni, F. A., Aldwoah, K., Birkea, F. M. O., & Hleili, M. (2024). Analyzing a Dynamical System with Harmonic Mean Incidence Rate Using Volterra–Lyapunov Matrices and Fractal-Fractional Operators. Fractal and Fractional, 8(6), 321. https://doi.org/10.3390/fractalfract8060321







