Exponential H∞ Output Control for Switching Fuzzy Systems via Event-Triggered Mechanism and Logarithmic Quantization
Abstract
1. Introduction
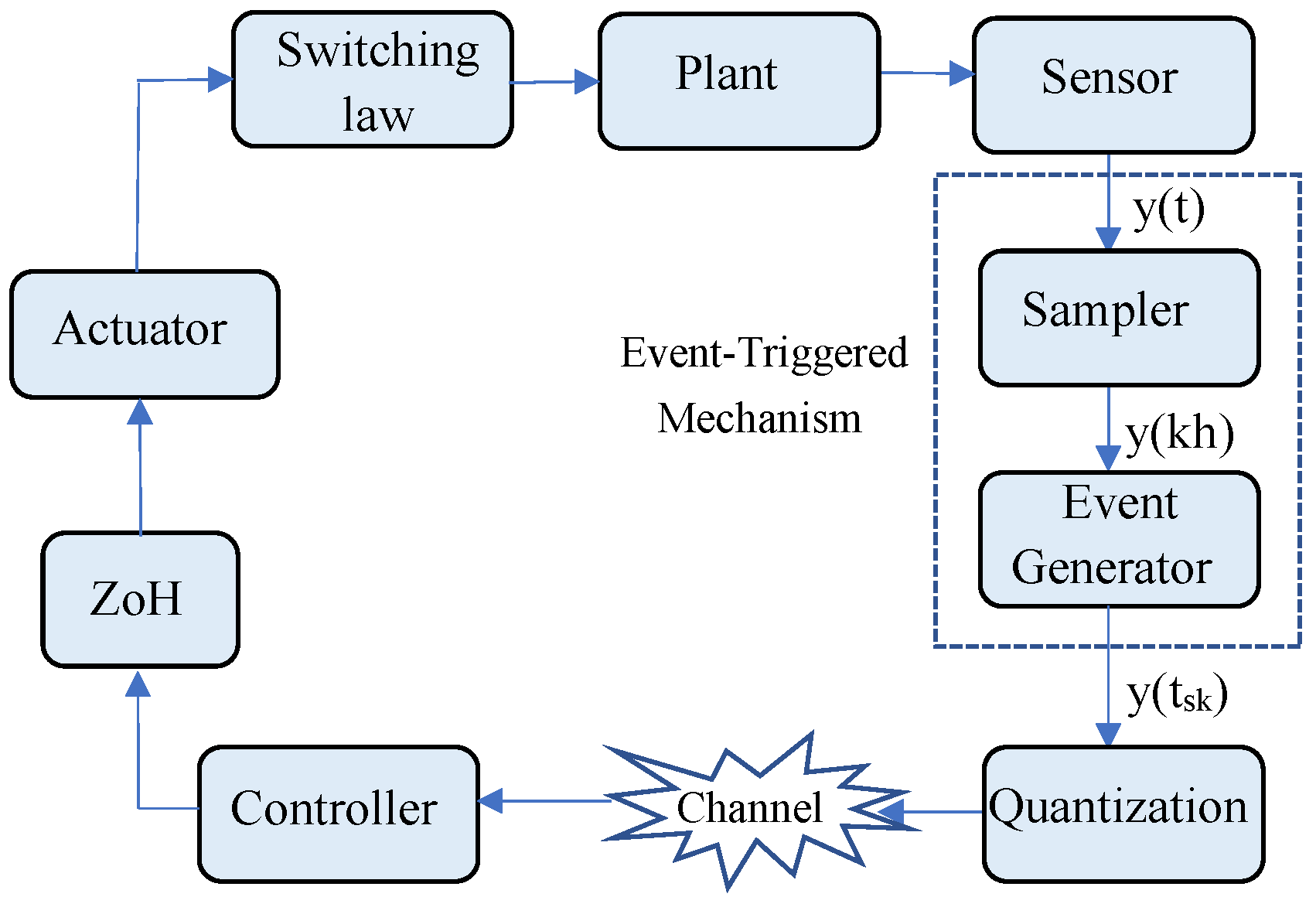
2. Problem Statement and Preliminaries
- Region Rule j: If is , then
- Local Plant Rule i: If is and … is , thenwhere ; is a classical set, which means that the system, over interval , only belongs to a certain Region j. That is, the switching subsystem j is active over . Regions j are the mutually disjoint regions. The union of all regions forms the universe of discourse; each Region j corresponds to each switching subsystem j. All switching subsystems constitute a switching system; region rules describe how the system switches, and local plant rules describe the fuzzy plant rule under each switching subsystem; ; and are premise variables and the membership functions, respectively; represents the state of system; represents the network measurement; represents the estimated signal; represents the nonlinear activation function; represents the noise input; represents the initial function on . , , , , , , , and are constant matrices; represents delay, the condition and hold, where and are constant scalars; the switching instant satisfies , .
- Controller Region Rule : If is , then
- Controller Local Plant Rule : If is and … is , thenwhere and are the controller gain and logarithmic quantizer, respectively. The latter satisfiesand
3. Main Results
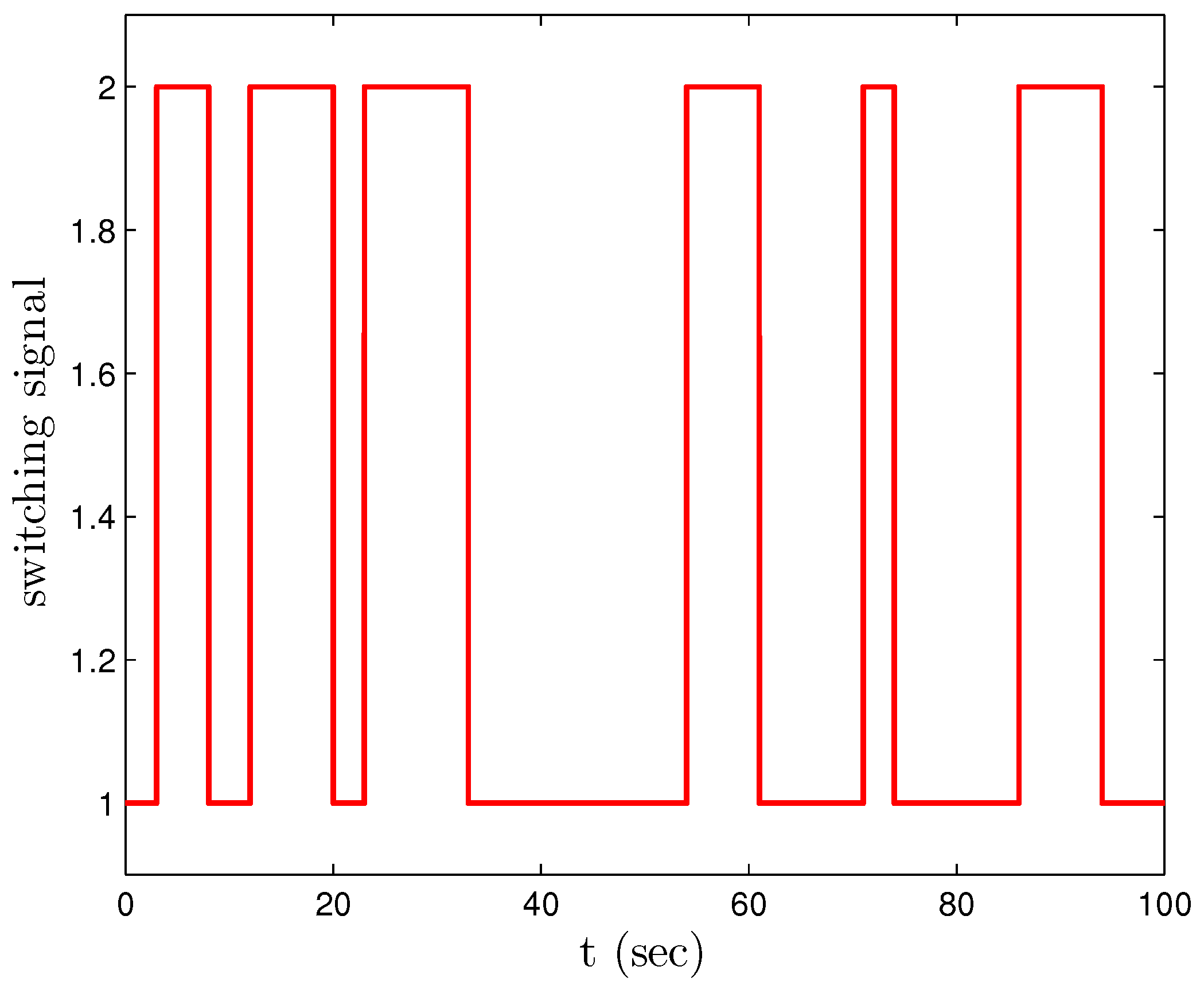
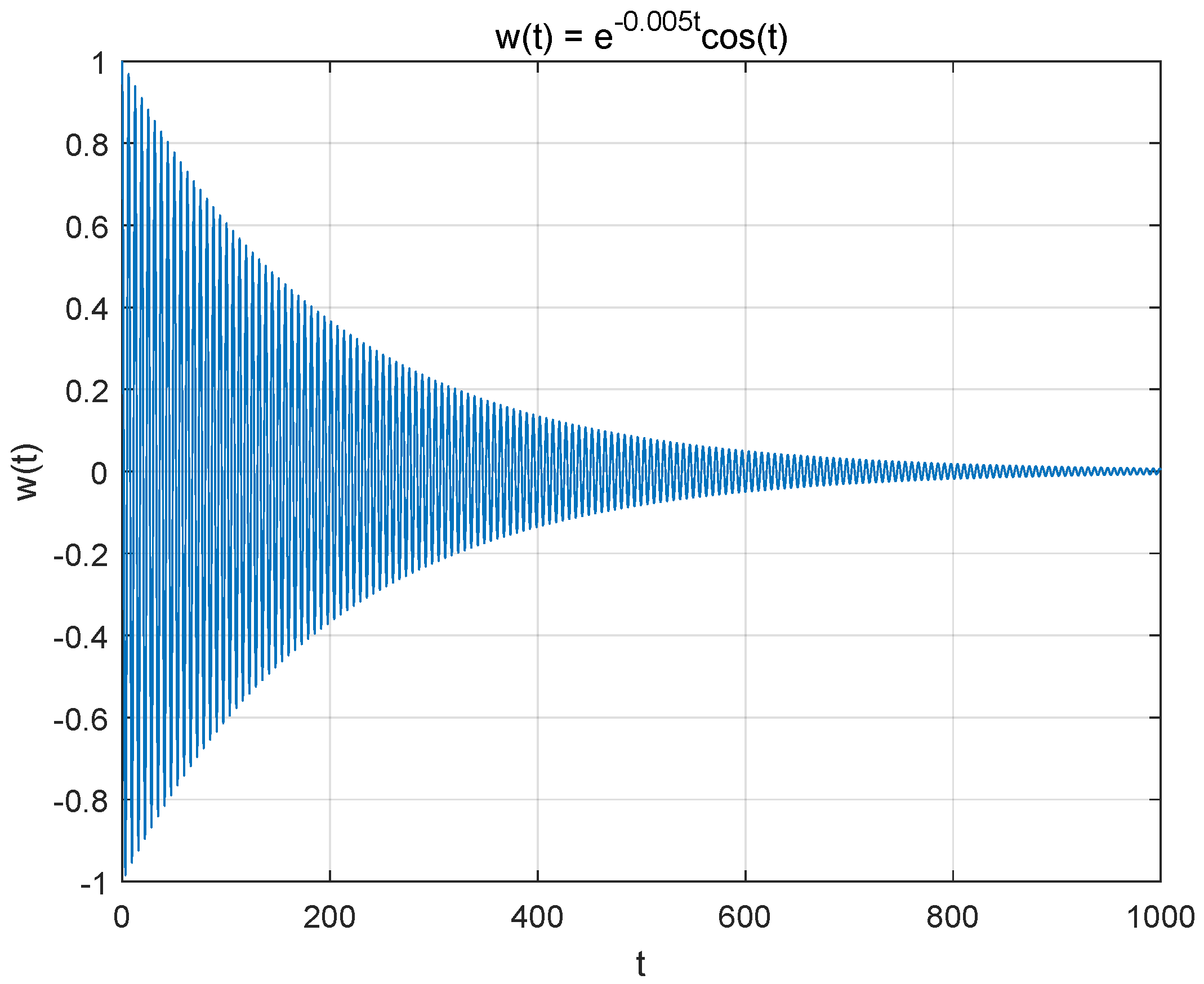
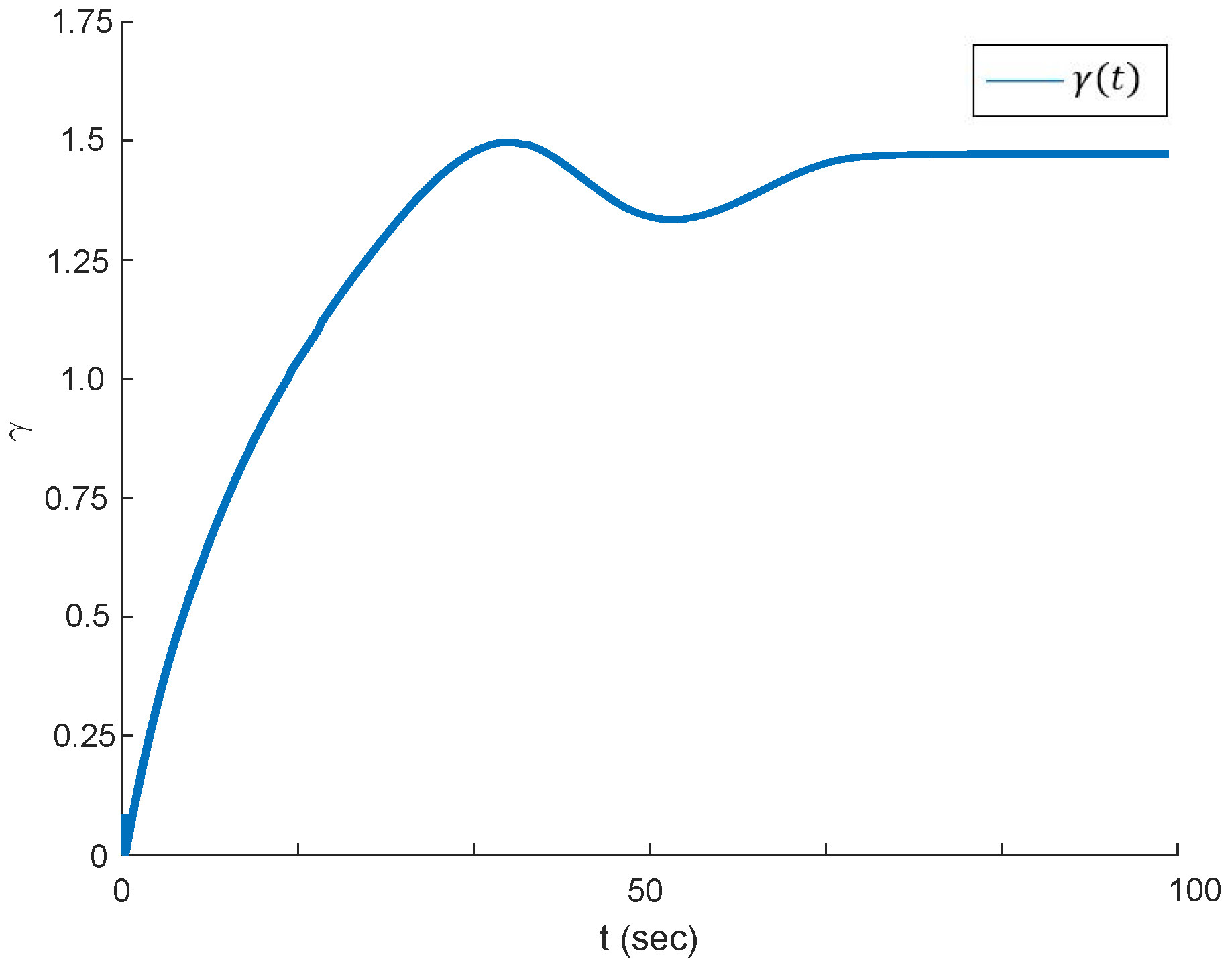
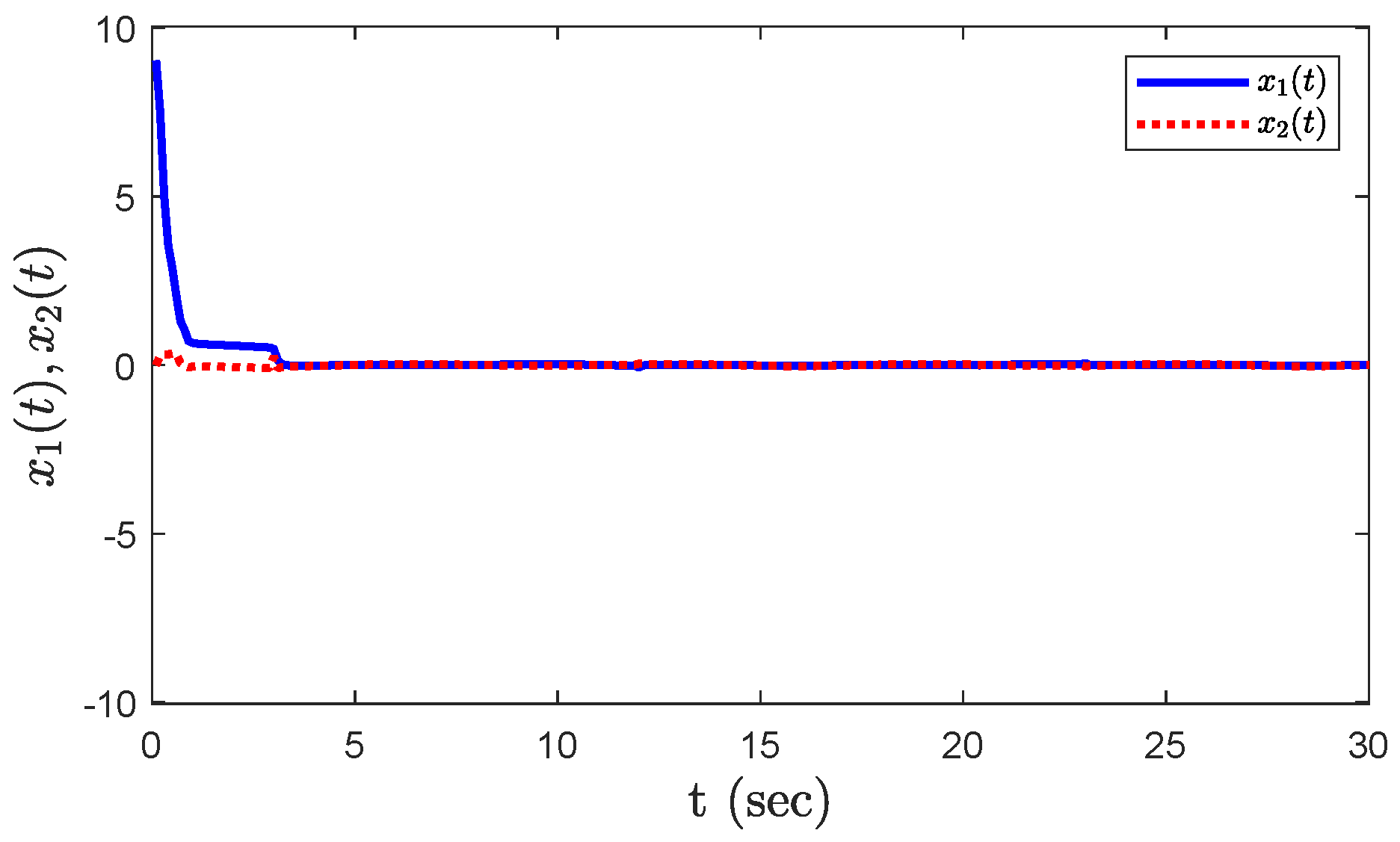
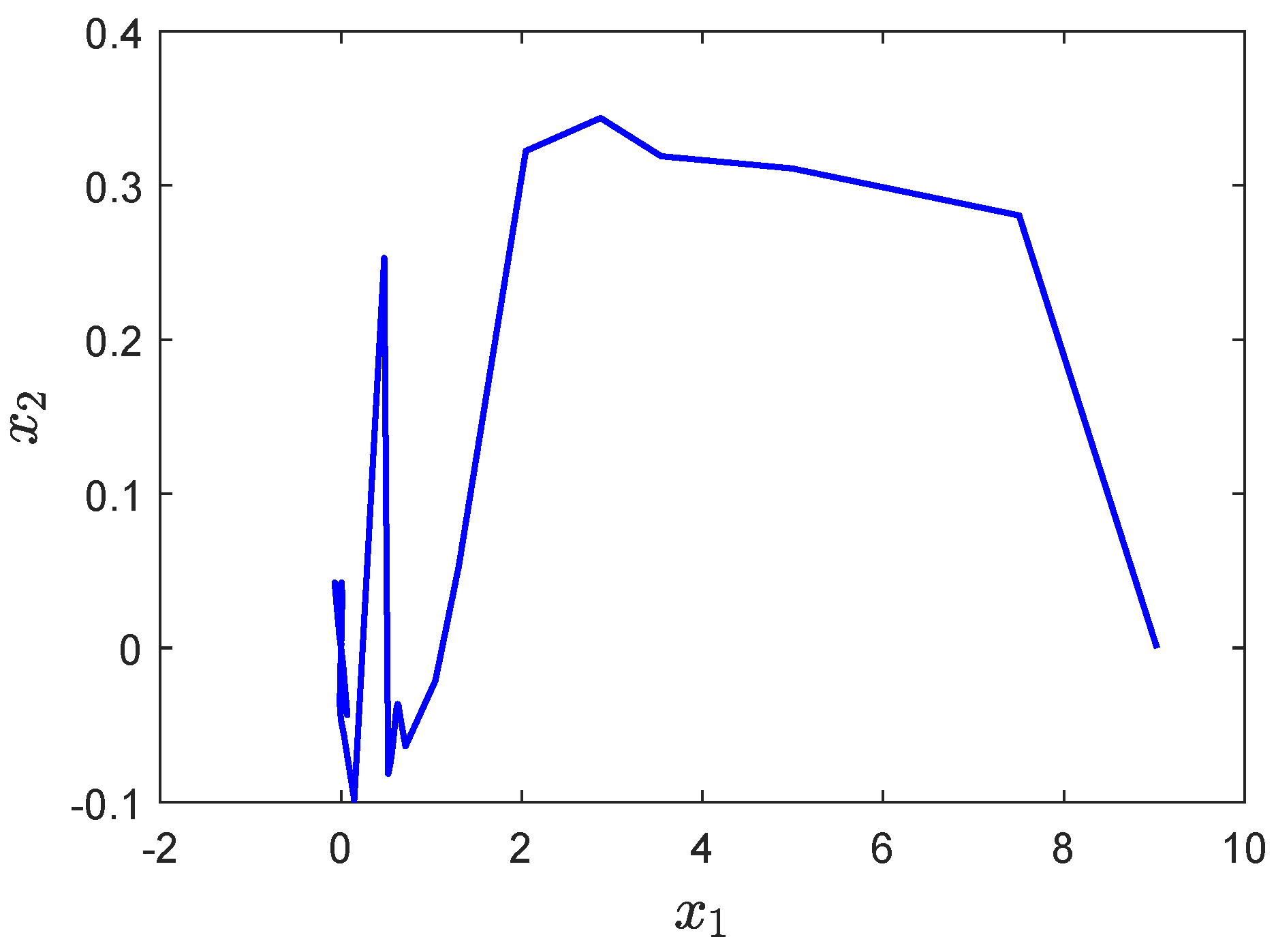
4. Examples
- Subsystem 1:
- Subsystem 2:
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tanaka, K.; Iwasaki, M.; Wang, H. Stabilization of switching fuzzy systems. Asian Fuzzy Syst. Symp. 2000. [Google Scholar]
- Kim, S.; Campbell, S.A.; Liu, X.Z. Stability of a class of linear switching systems with time delay. IEEE Trans. Circuits Syst. I 2006, 53, 384–393. [Google Scholar]
- Su, Y.F.; Huang, J. Stability of a class of linear switching systems with applications to two consensus problems. IEEE Trans. Autom. Control 2012, 57, 1420–1430. [Google Scholar] [CrossRef]
- Savkin, A.; Evans, R. Hybrid Dynamical Systems, Controller and Sensor Switching Problems; Birkhaser: Boston, MA, USA, 2002. [Google Scholar]
- Sun, Z.; Ge, S. Switched Linear Systems: Control and Design; Springer: London, UK, 2005. [Google Scholar]
- Yan, S.; Sun, Z. Study on separation principles for T-S fuzzy system with switching controller and switching observer. Neurocomputing 2010, 73, 2431–2438. [Google Scholar] [CrossRef]
- Mao, Y.; Zhang, H.; Xu, S. Exponential stability and asynchronous stabilization of a class of switched nonlinear system via T-S fuzzy model. IEEE Trans. Fuzzy Syst. 2014, 22, 817–828. [Google Scholar] [CrossRef]
- Ren, J.; Wu, C. External stability and H∞ control of switching systems with delay and impulse. Adv. Differ. Equ. 2020, 652, 1–20. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, S.; Du, B. Asynchronous nonfragile mixed H∞ and L2 − L∞ control of switched fuzzy systems with multiple state impulsive jumps. IEEE Trans. Fuzzy Syst. 2023, 31, 1966–1980. [Google Scholar] [CrossRef]
- Ye, H.; Michel, A.; Hou, L. Stability analysis of systems with impulse effects. IEEE Trans. Fuzzy Syst. 1998, 43, 1719–1723. [Google Scholar] [CrossRef]
- Fu, M.; Xie, L. The sector bound approach to quantized feedback control. IEEE Trans. Autom. Control 2005, 50, 1698–1711. [Google Scholar]
- He, Y.; Wang, Y.; Li, X. Quadratic stabilization for linear time-delay systems with a logarithmic quantizer. Neurocomputing 2016, 173, 1995–2000. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y.; Wang, W. Sampled-data-based dissipative control of T-S fuzzy systems. Appl. Math. Model. 2019, 65, 415–427. [Google Scholar] [CrossRef]
- Liu, J.L.; Wei, L.L.; Xie, X.P.; Tian, E.G.; Fei, S.M. Quantized stabilization for T-S fuzzy systems with hybrid-triggered mechanism and stochastic cyber-attacks. IEEE Trans. Fuzzy Syst. 2018, 26, 3820–3834. [Google Scholar] [CrossRef]
- Xiao, J.; Zhong, S.; Wen, S. Unified analysis on the global dissipativity and stability of fractional-order multidimension-valued memristive neural networks with time delay. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 5656–5665. [Google Scholar] [CrossRef]
- Xiao, J.; Guo, X.; Li, Y.; Wen, S.; Shi, K.; Tang, Y. Extended analysis on the global Mittag–Leffler synchronization problem for fractional-order octonion-valued BAM neural networks. Neural Netw. 2022, 154, 491–507. [Google Scholar] [CrossRef] [PubMed]
- Fei, Z.; Guan, C.; Zhao, X. Event-triggered dynamic output feedback control for switched systems with frequent asynchronism. IEEE Trans. Autom. Control 2020, 65, 3120–3127. [Google Scholar] [CrossRef]
- Gao, H.; Shi, K.; Zhang, H. A novel event-triggered strategy for networked switched control systems. J. Frankl. Inst. 2021, 358, 251–267. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, X.; Wen, C.; Wang, W. Estimation of sampling period for stochastic nonlinear sampled-data systems with emulated controllers. IEEE Trans. Autom. Control 2017, 62, 4713–4718. [Google Scholar] [CrossRef]
- Li, T.; Fu, J. Event-triggered control of switched linear systems. J. Frankl. Inst. 2017, 354, 6451–6462. [Google Scholar] [CrossRef]
- Li, T.; Fu, J.; Deng, F.; Chai, T. Stabilization of switched linear neutral systems: An event-triggered sampling control scheme. IEEE Trans. Autom. Control 2018, 63, 3537–3544. [Google Scholar] [CrossRef]
- Ali, M.; Saravanan, S.; Cao, J. Finite-time boundedness, L2-gain analysis and control of Markovian jump switched neural networks with additive time-varying delays. Nonlinear Anal. Hybrid Syst. 2017, 23, 27–43. [Google Scholar] [CrossRef]
- Wu, L.; Zheng, W. Weighted H∞ model reduction for linear switched systems with time-varying delay. Automatica 2009, 45, 186–193. [Google Scholar] [CrossRef]
- Wang, G.; Xie, R.; Zhang, H.; Yu, G.; Dang, C. Robust Exponential H∞ filtering for discrete-time switched fuzzy systems with time-varying delay. Circuits Syst. Signal Process. 2016, 35, 117–138. [Google Scholar] [CrossRef]
- Hespanha, J.; Morse, A. Stability of Switched Systems with Average Dwell-Time; Technical Report; University of Southern California: Los Angeles, CA, USA, 1999. [Google Scholar]
- Liu, X.; Yuan, S. Reduced-order fault detection filter design for switched nonlinear systems with time delay. Nonlinear Dyn. 2012, 67, 601–617. [Google Scholar] [CrossRef]
- Wu, C.; Liu, X. External stability of switching control systems. Syst. Control Lett. 2017, 106, 24–31. [Google Scholar] [CrossRef]
- Zheng, Q.; Xu, S.; Zhang, Z. Nonfragile quantized H∞ filtering for discrete-time switched T–S fuzzy systems with local nonlinear models. IEEE Trans. Fuzzy Syst. 2021, 29, 1507–1517. [Google Scholar] [CrossRef]
- Zhao, N.; Shi, P.; Xing, W.; Chambers, J. Observer-based event-triggered approach for stochastic networked control systems under denial of service attacks. IEEE Trans. Control Netw Syst. 2021, 8, 158–167. [Google Scholar] [CrossRef]
- Ren, J.; Liu, X.; Zhu, H.; Zhong, S.; Wu, C. Exponential H∞ synchronization of switching fuzzy systems with time-varying delay and impulses. Fuzzy Sets Syst. 2019, 365, 116–139. [Google Scholar] [CrossRef]
- Liu, X.; Wu, C. Fault-tolerant synchronization for nonlinear switching systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 2017, 23, 91–110. [Google Scholar] [CrossRef]
- Wu, L.; Feng, Z.; Zheng, W. Exponential stability analysis for delayed neural networks with switching Parameters: Average dwell time approach. IEEE Trans. Neural Netw. 2010, 21, 1396–1407. [Google Scholar]
- Tanaka, K.; Iwasaki, M.; Wang, H. Switching control of an R/C hovercraft: Stabilization and smooth switching. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2001, 31, 853–863. [Google Scholar] [CrossRef]
- Nair, G.; Evans, R. Exponential stabilisability of finite-dimensional linear systems with limited data rates. Automatica 2003, 39, 585–593. [Google Scholar] [CrossRef]
- Sahai, A. The necessity and sufficiency of anytime capacity for control over a noisy communication link. In Proceedings of the 2004 43rd IEEE Conference on Decision and Control (CDC), Nassau, Bahamas, 14–17 December 2004. [Google Scholar]

| ETM | ADT | MMDT | Switching Law | Logarithmic Quantizers | Frequent Switching | Normal L2 Norm Constraint | |
|---|---|---|---|---|---|---|---|
| [21] | Yes | Yes | No | No | No | No | - |
| [17] | Yes | Yes | No | No | No | No | - |
| [18] | Yes | Yes | No | No | No | No | - |
| [28] | No | Yes | No | No | Yes | - | No |
| [29] | Yes | Yes | No | No | No | - | No |
| [30] | No | No | Yes | No | No | - | Yes |
| Our method | Yes | Yes | No | Yes | Yes | Yes | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, J.; Zhao, C.; Xiao, J.; Luo, R.; He, N. Exponential H∞ Output Control for Switching Fuzzy Systems via Event-Triggered Mechanism and Logarithmic Quantization. Fractal Fract. 2024, 8, 290. https://doi.org/10.3390/fractalfract8050290
Ren J, Zhao C, Xiao J, Luo R, He N. Exponential H∞ Output Control for Switching Fuzzy Systems via Event-Triggered Mechanism and Logarithmic Quantization. Fractal and Fractional. 2024; 8(5):290. https://doi.org/10.3390/fractalfract8050290
Chicago/Turabian StyleRen, Jiaojiao, Can Zhao, Jianying Xiao, Renfu Luo, and Nanrong He. 2024. "Exponential H∞ Output Control for Switching Fuzzy Systems via Event-Triggered Mechanism and Logarithmic Quantization" Fractal and Fractional 8, no. 5: 290. https://doi.org/10.3390/fractalfract8050290
APA StyleRen, J., Zhao, C., Xiao, J., Luo, R., & He, N. (2024). Exponential H∞ Output Control for Switching Fuzzy Systems via Event-Triggered Mechanism and Logarithmic Quantization. Fractal and Fractional, 8(5), 290. https://doi.org/10.3390/fractalfract8050290







