Quasi-Projective Synchronization of Discrete-Time Fractional-Order Complex-Valued BAM Fuzzy Neural Networks via Quantized Control

Abstract

In this paper, we ponder a kind of discrete-time fractional-order complex-valued fuzzy BAM neural network. Firstly, in order to guarantee the quasi-projective synchronization of the considered networks, an original quantitative control strategy is designed. Next, by virtue of the relevant definitions and properties of the Mittag-Leffler function, we propose a novel discrete-time fractional-order Halanay inequality, which is more efficient for disposing of the discrete-time fractional-order models with time delays. Then, based on the new lemma, fractional-order h-difference theory, and comparison principle, we obtain some easy-to-verify synchronization criteria in terms of algebraic inequalities. Finally, numerical simulations are provided to check the accuracy of the proposed theoretical results.

1. Introduction

Artificial neural networks are mathematical models used to distribute parallel information processing by imitating behavioral characteristics of biological neural networks. Due to their associative memory functions, powerful fault tolerance, and optimized computing functions, neural networks (NNs) have been widely applied in many fields involving image recognition, signal processing, fault diagnosis, as well as biological mathematics [1,2,3,4]. In real-life applications, many adverse factors may influence the dynamic behaviors of NNs. For example, time delays [5], due to the limited switching speed of the amplifier, often lead to oscillation and instability phenomena in NNs. Another example is the existence of uncertain factors, such as parameter uncertainty and random disturbance, which make the dynamic behaviors of NNs more complicated and increase the research difficulty of NNs. To better study these NNs with the above elements, in 1996, Pecora and Carroll first proposed fuzzy NNs [6], which led to further research on NNs.

Based on the special memory advantage and heritability of fractional calculus, fractional differential equations have become useful tools to accurately describe varieties of practical complex problems. As we all know, the origin of fractional calculus is a problem statement, which was posed in 1695 by a correspondence between the German mathematician Leibniz and the French mathematician L’Hopital. The Riemann derivative [7] and Caputo derivative [8] are two common types of fractional-order derivatives. The Caputo derivative is sought-after by a lot of scholars because it has the same initial condition as the integer-order one. Moreover, it can also efficaciously reflect the physical facts of models. Through the unremitting efforts of researchers, some relevant results of fractional calculus were successively put forward [9,10], providing strong support for in-depth discussions of fractional-order systems. Later, scholars utilized inequality techniques, differential inclusion theory, the M-matrix, and other methods to explore the dynamical behaviors of fractional-order NNs. Some excellent results were obtained, such as dissipativity and contractivity [11], existence and uniqueness [12], stabilization [13], and synchronization [14].

The dynamical behaviors of chaotic systems that achieve consistent behaviors over time are referred to as synchronization. Since similar clustering behaviors exist in nature, this has sparked curiosity among researchers about synchronization problems. With a deepening understanding of synchronization, various synchronization types have been raised triumphantly, such as quasi-synchronization [15], finite-time synchronization [16], Mittag-Leffler synchronization [17], and so on. In the above discussion, quasi-synchronization is diffusely praised because of its relatively broad conditions. A quasi-projective synchronization is a special form of quasi-synchronization owing to the existence of its projection factor, which can accelerate the communication speed. Therefore, quasi-projective synchronization is sought after by academics and numerous excellent conclusions have been published in different journals [18,19]. Meanwhile, scholars have found that the synchronization of chaotic systems cannot be achieved without any affection from external forces. This discovery led to the development of various control strategies to meet different synchronization requirements, such as pinning control [20], linear control [21], intermittent control [22], etc. Concurrently, some undesirable phenomena, such as the waste of resources and the associated increase in costs, have emerged in the process of signal transmission due to the limited capacity and bandwidth of the communication channel. In response, some effective quantized controllers have been proposed in [23,24].

The associative memory function of NNs is divided into auto-associative memory and hetero-associative memory; Hopfield NNs represent auto-associative memory. A BAM NN (BAMNN) is a continuous improvement of the Hopfield NN, which was first proposed by Kosko in 1987 [25]. One advantage of BAMNN is its ability to associate complete patterns stored in memory with incomplete patterns. This improvement has attracted many academics to research BAMNNs in full swing, significantly accelerating their development [26,27]. Note that the above discussions are based on the continuous-time framework. With the development of science and technology, we discovered that it is not precise enough to use continuous-time models to solve real problems, because the analysis and processing of some problems need to be completed after discretization [28,29,30]. Therefore, it is time to incorporate discrete-time correlation theory into NNs. Over time, many excellent discrete-time conclusions have been drawn [31,32,33]. In [33], the authors discussed synchronization issues for a class of discrete-time fractional-order complex-valued NNs.

Based on the above discussion, it is evident that there is still relatively limited research on complete synchronization in discrete-time fractional-order BAMNNs, let alone quasi-projective synchronization; this motivated us to conduct research. To make our model more general and valuable, we consider the quasi-projective synchronization of a class of discrete-time fractional-order complex-valued fuzzy BAMNNs (DFCFBAMNNs). The main highlights of this paper are as follows: (1) Compared with models in [26,27,28,30,31,32], our model is more general as it integrates fuzzy logic, fractional difference operators, and plurality into BAMNNs. (2) In order to better deal with the time-delay term of the considered networks, a new lemma is brought forward that can avoid the use of inequality scaling or the design of a special controller. (3) To chase the target of synchronization, a novel quantized controller is designed. (4) Simple and easy-to-verify synchronization criteria are given.

The rest of this paper is arranged as follows. In Section 2, the model description and some preparatory knowledge are given. Effective criteria for quasi-projective synchronization in DFCFBAMNNs are presented in Section 3. In Section 4, numerical simulations are provided to illustrate the availability of theoretical results. A succinct discussion is presented in Section 5.

Notations:${ }_0^C{\nabla }_h^{\alpha }$ denotes the Caputo h-discrete fractional difference with order $\alpha (0<\alpha <1)$, then ${\mathbb{R}}^{+}$, $\mathbb{R}$, $\mathbb{C}$, and ${\mathbb{C}}^n$ denote the set of positive real numbers, real numbers, complex numbers, and n-dimensional complex vectors. $z_i(t)=z_i^R(t)+z_i^I(t)\mathfrak{i}$, $\mathfrak{i}=\sqrt{-1}$, $\overline{z_i(t)}$ denotes the conjugate of $z_i(t)$, $|z_i(t)|={\left(z_i(t)\overline{z_i(t)}\right)}^{\frac{1}{2}}$ stands for the module of $z_i(t)$, $z(t)={\left(z_1(t),z_2(t),\cdots ,z_n(t)\right)}^T\in {\mathbb{C}}^n$, ${\parallel z(t)\parallel }_2={\left({\displaystyle \sum _{i=1}^{\mathcal{N}}}{z}_i(t)\overline{z_i(t)}\right)}^{\frac{1}{2}}$ denotes the two-norm of $z(t)$, $\left[d\right]$ denotes the great integer less than d, ${(h\mathbb{N})}_b=\{x|x=b,b+h,b+2h,\cdots \}$, ${(h\mathbb{N})}_b^c=\{x|x=b,b+h,b+2h,\cdots ,c,\}$, where $c-b=kh$.

2. Preparatory Knowledge and Model Description

In this part, we recall common definitions, lemmas, assumptions, and other conditions that will be used later, and a new lemma is proved to establish the quasi-projective synchronization criteria of DFCFBAMNNs.

Definition 1

([29]). The backing difference $\varsigma (t)$ on ${(h\mathbb{N})}_0$ is defined as

$${\nabla }_h\varsigma (t)=\frac{\varsigma (t)-\varsigma (t-h)}{h}.$$

Definition 2

([29]). The α-th order h-rising function is defined by the following:

$${\gamma }_h^{\overline{\alpha }}=h^{\alpha }\frac{\mathrm{\Gamma }(\frac{\gamma }{h}+\alpha )}{\mathrm{\Gamma }(\frac{\gamma }{h})},$$

where $h>0$, $0_h^{\overline{\alpha }}=0$.

Definition 3

([29]). The α-th order fractional h-monomial ${\widehat{H}}_{\alpha }(t,0)$ is written as follows:

$${\widehat{H}}_{\alpha }(t,0)=\frac{t_h^{\overline{\alpha }}}{\mathrm{\Gamma }(\alpha +1)}=h^{\alpha }\frac{\mathrm{\Gamma }(\frac{t}{h}+\alpha )}{\mathrm{\Gamma }(\frac{t}{h})\mathrm{\Gamma }(\alpha +1)}.$$

Definition 4

([5]). Let $\varsigma (t):{(h\mathbb{N})}_0\mapsto \mathbb{R}$ and $\alpha >0$. The α-th order h-sum with a basing point of 0 is given by

$${ }_0^C{\nabla }_h^{-\alpha }\varsigma (t)={\int }_0^t{\widehat{H}}_{\alpha -1}(t,\xi (s))\varsigma (s){\nabla }_{h}s,t\in {(h\mathbb{N})}_h,$$

by convention ${ }_0^C{\nabla }_h^{-\alpha }\varsigma (0)=0$ and $\xi (s)=s-h$.

Definition 5

([5]). The Caputo nabla fractional difference of $\varsigma (t)\in {(h\mathbb{N})}_0$ and $n-1<\alpha <n$ of $\alpha (\alpha \in {\mathbb{R}}^{+})$ is expressed as

$${ }_0^C{\nabla }_h^{\alpha }\varsigma (t)={ }_0{\nabla }_h^{-(n-\alpha )}{\nabla }_h^n\varsigma (t),t\in {(h\mathbb{N})}_{nh},$$

when $0<\alpha <1$, and we have the following:

$${ }_0^C{\nabla }_h^{\alpha }\varsigma (t)={ }_0{\nabla }_h^{-(1-\alpha )}{\nabla }_h\varsigma (t),t\in {(h\mathbb{N})}_h.$$

Definition 6

([29]). The discrete Mittag-Leffler function is stated as follows:

$$E_{\alpha ,b}^h(c,t)=\sum _{k=0}^{\infty }{c}^k\frac{t_h^{\overline{k\alpha +b}}}{\mathrm{\Gamma }(\alpha k+b+1)}.$$

For $b=0$, we have the following:

$$E_{\alpha ,0}^h(c,t)=E_{\alpha ,0}^h(c,t)=\sum _{k=0}^{\infty }{c}^k\frac{t_h^{\overline{k\alpha }}}{\mathrm{\Gamma }(\alpha k+1)},$$

in which $0<\alpha <1$, $b\in \mathbb{R}$ and $|c|<h^{-\alpha }$.

Lemma 1

([30]). For the arbitrary two complex numbers, υ, ν, and arbitrary real number $\iota >0$, we obtain the following:

$$\overline{\upsilon }\nu +\upsilon \overline{\nu }\le \iota \upsilon \overline{\upsilon }+\frac{1}{\iota }\nu \overline{\nu }.$$

Lemma 2

([34]). Let $0<\sigma <h^{-\alpha }$, the $E_{\alpha ,0}^h(-\sigma ,t)$ is monotonically non-increasing and $0<E_{\alpha ,0}^h(-\sigma ,t)\le 1$ for $t\in {(h\mathbb{N})}_0$.

Lemma 3

([5]). For $|\sigma |<h^{-\alpha }$, $0<\alpha <1$, we have the following:

$${ }_0^C{\nabla }_h^{\alpha }{E}_{\alpha ,0}^h(-\sigma ,t)=-\sigma E_{\alpha ,0}^h(-\sigma ,t),t\in {(h\mathbb{N})}_h.$$

Lemma 4.

Let $x(t):{(h\mathbb{N})}_0⟶{\mathbb{R}}^{+}$ be a function meeting

$${ }_0^C{\nabla }_h^{\alpha }x(t)\le -bx(t)+\sum _{i=1}^{n}cx(t-{\tau }_i(t)),t\in {(h\mathbb{N})}_h,$$

(1)

where $0<b$, $c<h^{-\alpha }$, $nc<b$ and $0\le {\tau }_i(t)\le \tau$, then we obtain the following:

$$x(t)\le k{E}_{-\alpha ,0}^h(-\acute{\sigma },t),k>0,0<\acute{\sigma }<h^{-\alpha }.$$

Proof. 

We consider a continuously differentiable function of $\sigma$, as follows:

$$H(\sigma )=\sigma +\sum _{i=1}^n\frac{c{E}_{\alpha ,0}^h(-\sigma ,t-{\tau }_i(t))}{E_{\alpha ,0}^h(-\sigma ,t)}-b,$$

and according to Lemma 2 and Definition 6, we have the following:

$$H(0)=\sum _{i=1}^n\frac{c{E}_{\alpha ,0}^h(0,t-{\tau }_i(t))}{E_{\alpha ,0}^h(0,t)}-b=nc-b<0,$$

and

$$H(b)=b+\sum _{i=1}^n\frac{c{E}_{\alpha ,0}^h(-b,t-{\tau }_i(t))}{E_{\alpha ,0}^h(-b,t)}-b=\sum _{i=1}^n\frac{c{E}_{\alpha ,0}^h(-b,t-{\tau }_i(t))}{E_{\alpha ,0}^h(-b,t)}>0.$$

According to the zero-point existence theorem of continuous functions, there is a $\acute{\sigma }\in (0,b)$, and $H(\acute{\sigma })=\acute{\sigma }+\frac{c{\displaystyle \sum _{i=1}^n}{E}_{\alpha ,0}^h(-\acute{\sigma },t-{\tau }_i(t))}{E_{\alpha ,0}^h(-\acute{\sigma },t)}-b=0$, i.e.,

$$-\acute{\sigma }{E}_{\alpha ,0}^h(-\acute{\sigma },t)=c\sum _{i=1}^n{E}_{\alpha ,0}^h(-\acute{\sigma },t-{\tau }_i(t)))-b{E}_{\alpha ,0}^h(-\acute{\sigma },t).$$

(2)

Let us consider the comparison system of (1) as follows:

$${ }_0^C{\nabla }_h^{\alpha }\mu (t)=-b\mu (t)+\sum _{i=1}^{n}c\mu (t-{\tau }_i(t)),t\in {(h\mathbb{N})}_h,$$

(3)

it has the same initial value as (1). Using Lemma 3 and (2), we obtain the following equation:

$${ }_0^C{\nabla }_h^a{E}_{\alpha ,0}^h(-\acute{\sigma },t)=-\acute{\sigma }{E}_{\alpha ,0}^h(-\acute{\sigma },t)=-b{E}_{\alpha ,0}^h(-\acute{\sigma },t)+\sum _{i=1}^{n}c{E}_{\alpha ,0}^h(-\acute{\sigma },t-{\tau }_i(t)),$$

it is not hard to see that $E_{\alpha ,0}^h(-\acute{\sigma },t)$ is the solution of (3), in view of the fractional comparison principle, we obtain

$$x(t)\le k{E}_{\alpha ,0}^h(-\acute{\sigma },t),t\in {(h\mathbb{N})}_h.$$

□

Corollary 1.

Let $x(t):{(h\mathbb{N})}_0⟶{\mathbb{R}}^{+}$ be a function satisfying

$${ }_0^C{\nabla }_h^{\alpha }x(t)\le a-bx(t)+\sum _{i=1}^{n}cx(t-{\tau }_i(t)),t\in {(h\mathbb{N})}_h,$$

(4)

where $0<a$, $0<b$, $c<h^{-\alpha }$, $nc<b$ and $0\le {\tau }_i(t)\le \tau$, then we obtain the following:

$$x(t)\le k{E}_{-\alpha ,0}^h(-\acute{\sigma },t)+\frac{a}{b-c},k>0,0<\acute{\sigma }<h^{-\alpha }.$$

(5)

Proof. 

The upper formula hints that

$${ }_0^C{\nabla }_h^{\alpha }\left(x(t)-\frac{a}{b-c}\right)\le -b\left(x(t)-\frac{a}{b-c}\right)+\sum _{i=1}^{n}c\left(x(t-{\tau }_i(t))-\frac{a}{b-c}\right),$$

then according to Lemma 4, we obtain the following: $x(t)-\frac{a}{b-c}\le k{E}_{-\alpha ,0}^h(-\acute{\sigma },t),$ i.e.,

$$x(t)\le k{E}_{-\alpha ,0}^h(-\acute{\sigma },t)+\frac{a}{b-c},t\in {(h\mathbb{N})}_h.$$

□

Remark 1.

In [14], the authors successfully extended the Halanay inequality to the continuous-time fractional-order case, which is a huge improvement for solving continuous-time fractional-order NNs with time delays. On this basis, this paper further popularizes the Halanay inequality to discrete-time fractional-order situations, which is of great significance to research on discrete-time fractional-order NNs with time delays.

Consider a general DFCFBAMNN as follows:

$$\left\{\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{\alpha }{x}_i(t)}\hfill & =\hfill & -a_i{x}_i(t)+{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}{f}_l(y_l(t))+{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}{f}_l(y_l(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}{f}_l(y_l(t-\tau (t)))+I_i,t\in {(h\mathbb{N})}_h,\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{\alpha }{y}_l(t)}\hfill & =\hfill & -{\delta }_l{y}_l(t)+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\beta }_{li}{g}_i(x_i(t))+{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigwedge }}}{\gamma }_{li}{g}_i(x_i(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigvee }}}{\theta }_{li}{g}_i(x_i(t-\tau (t)))+I_l,t\in {(h\mathbb{N})}_h,\hfill \end{array}\right.$$

(6)

with the following initial condition:

$$\left\{\begin{array}{ccc}{\displaystyle x_i(p)}\hfill & =\hfill & {\mathrm{\Phi }}_i(p),p\in {(h\mathbb{N})}_{-\tau }^0,i\in \mathcal{N},\hfill \\ {\displaystyle y_l(p)}\hfill & =\hfill & {\mathrm{\Psi }}_l(p),p\in {(h\mathbb{N})}_{-\tau }^0,l\in \mathcal{M},\hfill \end{array}\right.$$

here, $a_i,{\delta }_l\in {\mathbb{R}}^{+}$ denote the neuron’s self-inhibition rates, $x(t)={(x_1(t),x_2(t)\cdots x_n(t))}^T$ denotes the i-th state variable vector in the X-layer; similarly, $y(t)={(y_1(t),y_2(t)\cdots y_m(t))}^T$ represents the l-th state variable vector in the Y-layer; $b_{il}$ and ${\beta }_{li}$ stand for the synaptic connection strengths without delay; ⋁ and ⋀ denote fuzzy OR and fuzzy AND operations; $c_{il}$ and ${\gamma }_{li}$ denote elements of the fuzzy feedback MIN template; similarly, $d_{il}$ and ${\theta }_{li}$ denote fuzzy feedback MAX templates; $I_i,I_l\in \mathbb{R}$ denote external inputs of the X-layer and Y-layer; $f_l(·),g_i(·):\mathbb{C}\to \mathbb{C}$ denote the activation functions, $\tau (t)$ denotes the time delay and contents $0\le \tau (t)\le \tau$.

Definition 7

([35]). For the arbitrary appropriate cone $\mathsf{\Im }\subseteq {\mathbb{R}}^n$, the partial relation acquired by ℑ in ${\mathbb{R}}^n$ is stipulated as follows:

$$(1)ϵ⪰\epsilon \iff ϵ-\epsilon \in \mathsf{\Im },$$

$$(2)ϵ\succ \epsilon \iff ϵ-\epsilon \in \mathrm{int}\mathit{\Im },$$

where the interior of ℑ is represented by $\mathrm{int}$ ℑ.

Remark 2.

For arbitrary ϵ, $\epsilon \in \mathbb{C}$, $ϵ={ϵ}_1+{ϵ}_2\mathfrak{i},\epsilon ={\epsilon }_1+{\epsilon }_2\mathfrak{i}$, $ϵ-\epsilon ={ϵ}_1-{\epsilon }_1+({ϵ}_2-{\epsilon }_2)\mathfrak{i}$. The magnitude on different relationships of ϵ and ε can be determined according to the following rules: (1) If ${ϵ}_1>(<){\epsilon }_1$, ${ϵ}_2\ne {\epsilon }_2$, then $ϵ\succ (\prec )\epsilon$; (2) if ${ϵ}_1>(<){\epsilon }_1$, ${ϵ}_2={\epsilon }_2$ or ${ϵ}_1={\epsilon }_1$, ${ϵ}_2>(<){\epsilon }_2$, then $ϵ⪰(⪯)\epsilon$; (3) if ${ϵ}_1={\epsilon }_1$, and ${ϵ}_2={\epsilon }_2$, then $ϵ=\epsilon$.

Remark 3.

In DFCFBAMNN (6), fuzzy AND operator and fuzzy OR operator can be understood as follows:

$$\underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}{c}_{il}{f}_l(y_l(t))=\underset{1\le l\le \mathcal{M}}{min}\left\{c_{il}{f}_l(y_l(t))\right\},$$

$$\underset{l=1}{\overset{\mathcal{M}}{\bigvee }}{d}_{il}{f}_l(y_l(t))=\underset{1\le l\le \mathcal{M}}{max}\left\{d_{il}{f}_l(y_l(t))\right\}.$$

Assumption 1.

For arbitrary $\mu ,\nu \in \mathbb{C}$, there exist real numbers ${\iota }_l,{\mathsf{ȷ}}_i>0$, such that

$$|f_l(\mu )-f_l(v)|\le {\iota }_l|\mu -v|,$$

$$|g_i(\mu )-g_i(v)|\le {\mathsf{ȷ}}_i|\mu -v|.$$

Assumption 2.

For arbitrary $f_l(·),g_i(·):\mathbb{C}\to \mathbb{C}$ and $I_i(·),I_l(·)$, there exist real numbers ${\wp }_{f_l},{\wp }_{g_i},l_{f_i},l_{g_l}\in \mathbb{R}$ satisfying

$$|f_l(·)|<{\wp }_{f_l},|g_i(·)|<{\wp }_{g_i},$$

$$|I_i(·)|<l_{f_i},|I_l(·)|<l_{g_l}.$$

Remark 4.

Assumption 1 is the Lipschitz condition, which is a prerequisite for the existence and uniqueness of solutions to fractional-order neural networks. Assumption 2 is given for the needs of the theoretical results. In the future, we will explore quasi-projective synchronization criteria with low conservatism, weakening or removing Assumption 2.

The controlled DFCFBAMNN is given as follows:

$$\left\{\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{\alpha }{\breve{x}}_i(t)}\hfill & =\hfill & -a_i{\breve{x}}_i(t)+{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}{f}_l({\breve{y}}_l(t))+{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}{f}_l({\breve{y}}_l(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}{f}_l({\breve{y}}_l(t-\tau (t)))+I_i+u_i(t),t\in {(h\mathbb{N})}_h,\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{\alpha }{\breve{y}}_l(t)}\hfill & =\hfill & -{\delta }_l{\breve{y}}_l(t)+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\beta }_{li}{g}_i({\breve{x}}_i(t))+{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigwedge }}}{\gamma }_{li}{g}_i({\breve{x}}_i(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigvee }}}{\theta }_{li}{g}_i({\breve{x}}_i(t-\tau (t)))+I_l+u_l(t),t\in {(h\mathbb{N})}_h,\hfill \end{array}\right.$$

(7)

with the initial condition:

$$\left\{\begin{array}{ccc}{\displaystyle {\breve{x}}_i(p)}\hfill & =\hfill & {\breve{\mathrm{\Phi }}}_i(p),p\in {(h\mathbb{N})}_{-\tau }^0,i\in \mathcal{N},\hfill \\ {\displaystyle {\breve{y}}_l(p)}\hfill & =\hfill & {\breve{\mathrm{\Psi }}}_l(p),p\in {(h\mathbb{N})}_{-\tau }^0,l\in \mathcal{M}.\hfill \end{array}\right.$$

Definition 8

([19]). DFCFBAMNNs (6) and (7) can achieve quasi-projective synchronization, if there exist r and a small error bound $\eta >0$ satisfying

$$\underset{t\to \infty }{lim}\left(||\breve{x}(t)-{rx(t)||}_2+||\breve{y}(t)-ry(t){||}_2\right)\le \eta ,$$

$r\in \mathbb{C}$ is projective coefficient. When $r=1$, DFCFBAMNNs (6) and (7) can achieve quasi-synchronization, we can define the error signals of (6) and (7) as follows:

$${\psi }_i(t)={\breve{x}}_i(t)-r{x}_i(t),{\phi }_l(t)={\breve{y}}_l(t)-r{y}_l(t).$$

(8)

By counting the Caputo difference of (8), we have the following:

$$\left\{\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{\alpha }{\psi }_i(t)}\hfill & =\hfill & -a_i{\psi }_i(t)+(1-r)I_i(t)+u_{i1}(t)\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}\left(f_l({\check{y}}_l(t))-f_l(r{y}_l(t))\right)+{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}\left(f_l(r{y}_l(t))-r{f}_l(y_l(t))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right),t\in {(h\mathbb{N})}_h,\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{\alpha }{\phi }_l(t)}\hfill & =\hfill & -{\delta }_l{\phi }_l(t)+(1-r)I_l(t)+u_{l2}(t)\hfill \\ \hfill & \hfill & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\beta }_{li}\left(g_i({\check{x}}_i(t))-g_i(r{x}_i(t))\right)+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\beta }_{li}\left(g_i(r{x}_i(t))+r{g}_i(x_i(t))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigwedge }}}{\gamma }_{li}\left(g_i({\check{x}}_i(t-\tau (t)))-g_i(r{x}_i(t-\tau (t)))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigwedge }}}{\gamma }_{li}\left(g_i(r{x}_i(t-\tau (t)))+r{g}_i(x_i(t-\tau (t)))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigvee }}}{\theta }_{li}\left(g_i({\check{x}}_i(t-\tau (t)))-g_i(r{x}_i(t-\tau (t)))\right)\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{\mathcal{N}}{\bigvee }}}{\theta }_{li}\left(g_i(r{x}_i(t-\tau (t)))+r{g}_i(x_{i}t-\tau (t)))\right),t\in {(h\mathbb{N})}_h,\hfill \end{array}\right.$$

(9)

with initial value

$$\left\{\begin{array}{ccc}{\displaystyle {\psi }_i(p)}\hfill & =\hfill & {\mathrm{\Phi }}_i(p)-r{\breve{\mathrm{\Phi }}}_i(p),p\in {(h\mathbb{N})}_{-\tau }^0,i\in \mathcal{N},\hfill \\ {\displaystyle {\phi }_l(p)}\hfill & =\hfill & {\mathrm{\Psi }}_l(p)-r{\breve{\mathrm{\Psi }}}_l(p),p\in {(h\mathbb{N})}_{-\tau }^0,l\in \mathcal{M}.\hfill \end{array}\right.$$

We designed a quantized state feedback controller, as follows:

$$\left\{\begin{array}{c}{\displaystyle u_{i1}(t)=-p_i\left(\mathsf{\ell }\left({\psi }_i^R(t)\right)+\mathfrak{i}\mathsf{\ell }\left({\psi }_i^I(t)\right)\right),}\hfill \\ {\displaystyle u_{l2}(t)=-q_l\left(\mathsf{\ell }\left({\phi }_i^R(t)\right)+\mathfrak{i}\mathsf{\ell }\left({\phi }_i^I(t)\right)\right),}\hfill \end{array}\right.$$

(10)

where $p_i,q_l$ are positive control gains, $\mathsf{\ell }(·):\mathrm{R}\to F$, $F=\{\pm s_i:s_i={\zeta }^i{s}_0,i=0,\pm 1,\pm 2\cdots \}$ $\bigcup \left\{0\right\}$ with $s_0>0$, the quantizer $\mathsf{\ell }(·)$ can be described as follows:

$$\mathsf{\ell }(ϵ)=\left\{\begin{array}{cc}{s}_i,\hfill & \mathrm{i}\mathrm{f}\frac{1}{1+\mathrm{\Pi }}{s}_i<ϵ<\frac{1}{1-\mathrm{\Pi }}{s}_i,\hfill \\ 0,\hfill & \mathrm{i}\mathrm{f}ϵ=0,\hfill \\ -\mathsf{\ell }(-ϵ),\hfill & \mathrm{i}\mathrm{f}ϵ<0,\hfill \end{array}\right.$$

in which $0<\zeta <1$ stands for the density of the quantizer, and $\mathrm{\Pi }=\frac{1-\zeta }{1+\zeta }$ denotes the parameter of the quantizer, $s_i$ represents the level of the quantizer. There exists a Filippov solution $\widehat{\xi }\in [-\mathrm{\Pi },\mathrm{\Pi })$ such that $\mathsf{\ell }(ϵ)=(1+\widehat{\xi })ϵ$. To put it simply, we have the following abbreviation: $\varphi (t)={\left({\psi }_1(t),{\psi }_2(t)\cdots ,{\psi }_n(t),{\phi }_1(t),{\phi }_2(t)\cdots ,{\phi }_m(t)\right)}^T.$

3. Main Results

In this part, we receive some standards for DFCFBAMNNs (6) and (7) to achieve quasi-projective synchronization based on the discrete-time fractional-order Halanay inequality.

For the sake of convenience, we introduce notations as follows:

$$\lambda =\mathcal{M}{\mathsf{\Im }}_1+{\mathsf{\Im }}_2+{\mathsf{\Im }}_3+{\mathsf{\Im }}_5+{\mathsf{\Im }}_6+{\mathsf{\Im }}_7{l}_{f_i}^2,$$

$$\breve{\lambda }=\mathcal{M}{\breve{\mathsf{\Im }}}_1+{\breve{\mathsf{\Im }}}_2+{\breve{\mathsf{\Im }}}_3+{\breve{\mathsf{\Im }}}_5+{\breve{\mathsf{\Im }}}_6+{\breve{\mathsf{\Im }}}_7{l}_{g_l}^2.$$

Theorem 1.

Under Assumptions 1 and 2, DFCFBAMNNs (6) and (7) realize quasi-projective synchronization if

$$0<\mathrm{{\rm Y}},\mathrm{\Theta }<h^{-a},$$

(11)

$$\mathrm{\Theta }-\mathrm{{\rm Y}}<0,$$

(12)

in which $\mathrm{{\rm Y}}=min\left\{{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right\},\mathrm{\Theta }=max\left\{\widetilde{{\mathrm{\Omega }}_1},\widetilde{{\mathrm{\Omega }}_2}\right\}$, ${\mathrm{\Omega }}_1=2a_i+2p_i(1-\mathrm{\Pi })-{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4|b_{il}{|}^2-\lambda -\frac{1}{{\breve{\mathsf{\Im }}}_1}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|{\beta }_{li}|}^2{\mathsf{ȷ}}_i^2$, ${\mathrm{\Omega }}_2=2{\delta }_l+2q_l(1-\mathrm{\Pi })-{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\breve{\mathsf{\Im }}}_4|{\beta }_{li}{|}^2-\breve{\lambda }-\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{|b_{il}|}^2{\iota }_l^2$, $\widetilde{{\mathrm{\Omega }}_1}={\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{ȷ}}_i^2\times (\frac{1}{{\breve{\mathsf{\Im }}}_2}|{\gamma }_{li}{|}^2+\frac{1}{{\breve{\mathsf{\Im }}}_3}|{\theta }_{li}{|}^2)$, $\widetilde{{\mathrm{\Omega }}_2}={\displaystyle \sum _{i=1}^{\mathcal{N}}}{\iota }_l^2(\frac{1}{{\mathsf{\Im }}_2}|c_{il}{|}^2+\frac{1}{{\mathsf{\Im }}_3}|d_{il}{|}^2).$

Proof. 

The constructed Lyapunov function

$$V(t)=\sum _{i=1}^{\mathcal{N}}{\psi }_i(t)\overline{{\psi }_i(t)}+\sum _{l=1}^{\mathcal{M}}{\phi }_l(t)\overline{{\phi }_l(t)}.$$

(13)

Calculating the Caputo difference of $V(t)$ derives the following:

$$\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{\alpha }V(t)}& =& {\displaystyle { }_0^C{\nabla }_h^{\alpha }\left(\sum _{i=1}^{\mathcal{N}}{\psi }_i(t)\overline{{\psi }_i(t)}+\sum _{l=1}^{\mathcal{M}}{\phi }_l(t)\overline{{\phi }_l(t)}\right)}\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}\left(\overline{{\psi }_i(t)}{ }_0^C{\nabla }_h^{\alpha }{\psi }_i(t)+{\psi }_i(t){ }_0^C{\nabla }_h^{\alpha }\overline{{\psi }_i(t)}\right)}\hfill \\ & & {\displaystyle +\sum _{l=1}^{\mathcal{M}}\left(\overline{{\phi }_l(t)}{ }_0^C{\nabla }_h^{\alpha }{\phi }_l(t)+{\phi }_l(t){ }_0^C{\nabla }_h^{\alpha }\overline{{\phi }_l(t)}\right).}\hfill \end{array}$$

(14)

It follows from (9) that

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}\left(\overline{{\psi }_i(t)}{ }_0^C{\nabla }_h^{\alpha }{\psi }_i(t)+{\psi }_i{(t)}_0^C{\nabla }_h^{\alpha }\overline{{\psi }_i(t)}\right)\hfill \\ & =& {\displaystyle {\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}\{-a_i{\psi }_i(t)+u_{i1}(t)+{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}\left(f_l({\check{y}}_l(t))-f_l(r{y}_l(t))\right)}\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}\left(f_l(r{y}_l(t))-r{f}_l(y_l(t))\right)+(1-r)I_i(t)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\}\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t)\{-a_i\overline{{\psi }_i(t)}+\overline{u_{i1}(t)}+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\overline{b_{il}}\left(\overline{f_l({\check{y}}_l(t))}-\overline{f_l(r{y}_l(t))}\right)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}\overline{c_{il}}\left(\overline{f_l({\check{y}}_l(t-\tau (t)))}-\overline{f_l(r{y}_l(t-\tau (t)))}\right)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}\overline{d_{il}}\left(\overline{f_l({\check{y}}_l(t-\tau (t)))}-\overline{f_l(r{y}_l(t-\tau (t)))}\right)\hfill \\ & & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}\overline{b_{il}}\left(\overline{f_l(r{y}_l(t))}+\overline{r}\overline{f_l(y_l(t))}\right)+(1-\overline{r})I_i(t)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}\overline{c_{il}}\left(\overline{f_l(r{y}_l(t-\tau (t)))}-\overline{r}\overline{f_l(y_l(t-\tau (t)))}\right)\hfill \\ & & +{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}\overline{d_{il}}\left(\overline{f_l(r{y}_l(t-\tau (t)))}-\overline{r}\overline{f_l(y_l(t-\tau (t)))}\right)\}.\hfill \end{array}$$

(15)

According to Lemma 1 and Assumption 1, we have the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}\overline{{\psi }_i(t)}{b}_{il}\left(f_l({\check{y}}_l(t))-f_l(r{y}_l(t))\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\psi }_i(t)\overline{b_{il}}\left(\overline{f_l({\check{y}}_l(t))}-\overline{f_l(r{y}_l(t))}\right)\hfill \\ & \le & \mathcal{M}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_1{\psi }_i(t)\overline{{\psi }_i(t)}+\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{b}_{il}\overline{b_{il}}\left(f_l({\check{y}}_l(t))-f_l(r{y}_l(t))\right)\hfill \\ & & \times \left(\overline{f_l({\check{y}}_l(t))}-\overline{f_l(r{y}_l(t))}\right)\hfill \\ & \le & \mathcal{M}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_1{\psi }_i(t)\overline{{\psi }_i(t)}+\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|b_{il}|}^2{\iota }_l^2{\phi }_l(t)\overline{{\phi }_l(t)},\hfill \end{array}$$

(16)

and

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t){\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}\overline{c_{il}}\left(\overline{f_l({\check{y}}_l(t-\tau (t)))}-\overline{f_l(r{y}_l(t-\tau (t)))}\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}\overline{d_{il}}\left(\overline{f_l({\check{y}}_l(t-\tau (t)))}-\overline{f_l(r{y}_l(t-\tau (t)))}\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_2{\psi }_i(t)\overline{{\psi }_i(t)}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_3{\psi }_i(t)\overline{{\psi }_i(t)}\hfill \\ & & +\frac{1}{{\mathsf{\Im }}_2}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{c}_{il}\overline{c_{il}}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ & & \times \left(\overline{f_l({\check{y}}_l(t-\tau (t)))}-\overline{f_l(r{y}_l(t-\tau (t)))}\right)\hfill \\ & & +\frac{1}{{\mathsf{\Im }}_3}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{d}_{il}\overline{d_{il}}\left(f_l({\check{y}}_l(t-\tau (t)))-f_l(r{y}_l(t-\tau (t)))\right)\hfill \\ & & \times \left(\overline{f_l({\check{y}}_l(t-\tau (t)))}-\overline{f_l(r{y}_l(t-\tau (t)))}\right)\hfill \\ & \le & ({\mathsf{\Im }}_2+{\mathsf{\Im }}_3){\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t)\overline{{\psi }_i(t)}\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\iota }_l^2(\frac{1}{{\mathsf{\Im }}_2}|c_{il}{|}^2+\frac{1}{{\mathsf{\Im }}_3}|d_{il}{|}^2)\overline{{\phi }_l(t-\tau (t))}{\phi }_l(t-\tau (t)).\hfill \end{array}$$

(17)

According to Assumption 2 and Lemma 1, we obtain the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}\overline{{\psi }_i(t)}{b}_{il}\left(f_l(r{y}_l(t))-r{f}_l(y_l(t))\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\psi }_i(t)\overline{b_{il}}\left(\overline{f_l(r{y}_l(t))}-\overline{r}\overline{f_l(y_l(t)})\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4\overline{b_{il}}{b}_{il}\overline{{\psi }_i(t)}{\psi }_i(t)\hfill \\ & & +\frac{\mathcal{N}}{{\mathsf{\Im }}_4}{\displaystyle \sum _{l=1}^{\mathcal{M}}}\left(f_l(r{y}_l(t))-r{f}_l(y_l(t))\right)\left(\overline{f_l(r{y}_l(t))}-\overline{r}\overline{f_l(y_l(t))}\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4\overline{b_{il}}{b}_{il}\overline{{\psi }_i(t)}{\psi }_i(t)\hfill \\ & & +\frac{\mathcal{N}}{{\mathsf{\Im }}_4}{\displaystyle \sum _{l=1}^{\mathcal{M}}}(f_l(r{y}_l(t))\overline{f_l(r{y}_l(t))}+f_l(r{y}_l(t))\overline{r}\overline{f_l(y_l(t))}\hfill \\ & & +r{f}_l(y_l(t))\overline{f_l(r{y}_l(t))}+r\overline{r}{f}_l(y_l(t))\overline{f_l(y_l(t))})\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4{|b_{il}|}^2\overline{{\psi }_i(t)}{\psi }_i(t)\hfill \\ & & +\frac{2\mathcal{N}}{{\mathsf{\Im }}_4}{\displaystyle \sum _{l=1}^{\mathcal{M}}}\left(f_l(r{y}_l(t))\overline{f_l(r{y}_l(t))}+r\overline{r}{f}_l(y_l(t))\overline{f_l(y_l(t)}\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4|b_{il}{|}^2\overline{{\psi }_i(t)}{\psi }_i(t)+\frac{2\mathcal{N}}{{\mathsf{\Im }}_4}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{(1-|r|}^2){\wp }_{f_l}^2.\hfill \end{array}$$

(18)

In the light of Lemma 1, we obtain the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}{c}_{il}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t){\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigwedge }}}\overline{c_{il}}\left(\overline{f_l(r{y}_l(t-\tau (t)))}-\overline{r}\overline{f_l(y_l(t-\tau (t))})\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}{\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}{d}_{il}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t){\displaystyle \underset{l=1}{\overset{\mathcal{M}}{\bigvee }}}\overline{d_{il}}\left(\overline{f_l(r{y}_l(t-\tau (t)))}-\overline{r}\overline{f_l(y_l(t-\tau (t))})\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_5{\psi }_i(t)\overline{{\psi }_i(t)}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_6{\psi }_i(t)\overline{{\psi }_i(t)}\hfill \\ & & +\frac{1}{{\mathsf{\Im }}_5}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{c}_{il}\overline{c_{il}}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\hfill \\ & & \times \left(\overline{f_l(r{y}_l(t-\tau (t)))}-\overline{r}\overline{f_l(y_l(t-\tau (t))})\right)\hfill \\ & & +\frac{1}{{\mathsf{\Im }}_6}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{d}_{il}\overline{d_{il}}\left(f_l(r{y}_l(t-\tau (t)))-r{f}_l(y_l(t-\tau (t)))\right)\hfill \\ & & \times \left(\overline{f_l(r{y}_l(t-\tau (t)))}-\overline{r}\overline{f_l(y_l(t-\tau (t))})\right)\hfill \\ & \le & ({\mathsf{\Im }}_5+{\mathsf{\Im }}_6){\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t)\overline{{\psi }_i(t)}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}(\frac{2}{{\mathsf{\Im }}_5}|c_{il}{|}^2+\frac{2}{{\mathsf{\Im }}_6}|d_{il}{|}^2)(1-{|r|}^2){\wp }_{f_l}^2.\hfill \end{array}$$

(19)

Due to the boundedness of the external input function and Lemma 1, we obtain the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}\overline{{\psi }_i(t)}(1-r)I_i+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t)(1-\overline{r})I_i\hfill \\ & \le & {\displaystyle {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_7\overline{{\psi }_i(t)}{\psi }_i(t)I_i^2+\frac{\mathcal{N}}{{\mathsf{\Im }}_7}(1-r)(1-\overline{r})}\hfill \\ & \le & {\displaystyle {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{\Im }}_7\overline{{\psi }_i(t)}{\psi }_i(t)l_{f_i}^2+\frac{\mathcal{N}}{{\mathsf{\Im }}_7}(1-r)(1-\overline{r}).}\hfill \end{array}$$

(20)

According to (10), we obtain the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}\left(\overline{{\psi }_i(t)}{u}_{i1}(t))+{\psi }_i(t)\overline{u_{i1}(t))}\right)\hfill \\ & =& {\displaystyle \sum _{i=1}^{\mathcal{N}}}-p_i\{\left({\psi }_i^R(t)-\mathfrak{i}{\psi }_i^I(t)\right)\left(\mathsf{\ell }\left({\psi }_i^R(t)\right)+\mathfrak{i}\mathsf{\ell }\left({\psi }_i^I(t)\right)\right)\hfill \\ & & +\left({\psi }_i^R(t)+\mathfrak{i}{\psi }_i^I(t)\right)\left(\mathsf{\ell }\left({\psi }_i^R(t)\right)-\mathfrak{i}\mathsf{\ell }\left({\psi }_i^I(t)\right)\right)\}\hfill \\ & =& -2{\displaystyle \sum _{i=1}^{\mathcal{N}}}{p}_i\left({\psi }_i^R(t)\mathsf{\ell }\left({\psi }_i^R(t)\right)+{\psi }_i^I(t)\mathsf{\ell }\left({\psi }_i^I(t)\right)\right)\hfill \\ & =& -2{\displaystyle \sum _{i=1}^{\mathcal{N}}}{p}_i\left\{(1-\mathrm{\Pi }){\left({\psi }_i^R(t)\right)}^2+(1-\mathrm{\Pi }){\left({\psi }_i^I(t)\right)}^2\right\}\hfill \\ & =& -2{\displaystyle \sum _{i=1}^{\mathcal{N}}}{p}_i(1-\mathrm{\Pi }){\psi }_i(t)\overline{{\psi }_i(t)}.\hfill \end{array}$$

(21)

By integrating the above inequalities, we obtain the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{i=1}^{\mathcal{N}}}\left(\overline{{\psi }_i(t)}{ }_0^C{\nabla }_h^{\alpha }{\psi }_i(t)+{\psi }_i{(t)}_0^C{\nabla }_h^{\alpha }\overline{{\psi }_i(t)}\right)\hfill \\ & \le & {\displaystyle \sum _{i=1}^{\mathcal{N}}}(\mathcal{M}{\mathsf{\Im }}_1+{\mathsf{\Im }}_2+{\mathsf{\Im }}_3+{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4{|b_{il}|}^2+{\mathsf{\Im }}_5+{\mathsf{\Im }}_6+{\mathsf{\Im }}_7{l}_{f_i}^2\hfill \\ & & -2a_i-2p_i(1-\mathrm{\Pi })){\psi }_i(t)\overline{{\psi }_i(t)}+\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|b_{il}|}^2{\iota }_l^2{\phi }_l(t)\overline{{\phi }_l(t)}\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\iota }_l^2(\frac{1}{{\mathsf{\Im }}_2}|c_{il}{|}^2+\frac{1}{{\mathsf{\Im }}_3}|d_{il}{|}^2){\phi }_l(t-\tau (t))\overline{{\phi }_l(t-\tau (t))}\hfill \\ & & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}(\frac{2\mathcal{N}}{{\mathsf{\Im }}_4}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_5}|c_{il}{|}^2+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_6}|d_{il}{|}^2)(1-{|r|}^2){\wp }_{f_l}^2+\frac{\mathcal{N}}{{\mathsf{\Im }}_7}(1-r)(1-\overline{r})\hfill \\ & =& {\displaystyle \sum _{i=1}^{\mathcal{N}}}\left({\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4{|b_{il}|}^2+\lambda -2a_i-2p_i(1-\mathrm{\Pi })\right){\psi }_i(t)\overline{{\psi }_i(t)}\hfill \\ & & +\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|b_{il}|}^2{\iota }_l^2{\phi }_l(t)\overline{{\phi }_l(t)}\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\iota }_l^2(\frac{1}{{\mathsf{\Im }}_2}|c_{il}{|}^2+\frac{1}{{\mathsf{\Im }}_3}|d_{il}{|}^2){\phi }_l(t-\tau (t))\overline{{\phi }_l(t-\tau (t))}\hfill \\ & & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}(\frac{2\mathcal{N}}{{\mathsf{\Im }}_4}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_5}|c_{il}{|}^2+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_6}|d_{il}{|}^2)(1-{|r|}^2){\wp }_{f_l}^2+\frac{\mathcal{N}}{{\mathsf{\Im }}_7}(1-r)(1-\overline{r}).\hfill \end{array}$$

(22)

By methods like (15)–(21), we obtain the following:

$$\begin{array}{ccc}& & {\displaystyle \sum _{l=1}^{\mathcal{M}}}\left(\overline{{\phi }_l(t)}{ }_0^C{\nabla }_h^{\alpha }{\phi }_l(t)+{\phi }_l{(t)}_0^C{\nabla }_h^{\alpha }\overline{{\phi }_l(t)}\right)\hfill \\ & \le & {\displaystyle \sum _{l=1}^{\mathcal{M}}}(\mathcal{N}{\breve{\mathsf{\Im }}}_1+{\breve{\mathsf{\Im }}}_2+{\breve{\mathsf{\Im }}}_3+{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\breve{\mathsf{\Im }}}_4{|{\beta }_{li}|}^2+{\breve{\mathsf{\Im }}}_5+{\breve{\mathsf{\Im }}}_6+{\breve{\mathsf{\Im }}}_7{l}_{g_l}^2\hfill \\ & & -2{\delta }_l-2q_l(1-\mathrm{\Pi })){\phi }_l(t)\overline{{\phi }_l(t)}+\frac{1}{{\breve{\mathsf{\Im }}}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|{\beta }_{li}|}^2{\mathsf{ȷ}}_i^2{\psi }_i(t)\overline{{\psi }_i(t)}\hfill \\ & & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{ȷ}}_i^2(\frac{1}{{\breve{\mathsf{\Im }}}_2}|{\gamma }_{li}{|}^2+\frac{1}{{\breve{\mathsf{\Im }}}_3}|{\theta }_{li}{|}^2){\psi }_i(t-\tau (t))\overline{{\psi }_i(t-\tau (t))}\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}(\frac{2\mathcal{M}}{{\breve{\mathsf{\Im }}}_4}+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{{\breve{\mathsf{\Im }}}_5}|{\gamma }_{li}{|}^2+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{{\breve{\mathsf{\Im }}}_6}|{\theta }_{li}{|}^2)(1-{|r|}^2){\wp }_{g_i}^2+\frac{\mathcal{M}}{{\breve{\mathsf{\Im }}}_7}(1-r)(1-\overline{r})\hfill \\ & =& {\displaystyle \sum _{l=1}^{\mathcal{M}}}\left({\displaystyle \sum _{i=1}^{\mathcal{N}}}{\breve{\mathsf{\Im }}}_4{|{\beta }_{li}|}^2+\breve{\lambda }-2{\delta }_l-2q_l(1-\mathrm{\Pi })\right){\phi }_l(t)\overline{{\phi }_l(t)}\hfill \\ & & +\frac{1}{{\breve{\mathsf{\Im }}}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|{\beta }_{li}|}^2{\mathsf{ȷ}}_i^2{\psi }_i(t)\overline{{\psi }_i(t)}\hfill \\ & & +{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{ȷ}}_i^2(\frac{1}{{\breve{\mathsf{\Im }}}_2}|{\gamma }_{li}{|}^2+\frac{1}{{\breve{\mathsf{\Im }}}_3}|{\theta }_{li}{|}^2){\psi }_i(t-\tau (t))\overline{{\psi }_i(t-\tau (t))}\hfill \\ & & +{\displaystyle \sum _{i=1}^{\mathcal{N}}}(\frac{2\mathcal{M}}{{\breve{\mathsf{\Im }}}_4}+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{{\breve{\mathsf{\Im }}}_5}|{\gamma }_{li}{|}^2+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{{\breve{\mathsf{\Im }}}_6}|{\theta }_{li}{|}^2)(1-{|r|}^2){\wp }_{g_i}^2+\frac{\mathcal{M}}{{\breve{\mathsf{\Im }}}_7}(1-r)(1-\overline{r}).\hfill \end{array}$$

(23)

By combining inequalities (22) and (23), we obtain the following:

$$\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{\alpha }V(t)}& =& {\displaystyle \sum _{i=1}^{\mathcal{N}}}{\psi }_i(t)\overline{{\psi }_i(t)}+{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\phi }_l(t)\overline{{\phi }_l(t)}\hfill \\ & \le & {\displaystyle -{\displaystyle \sum _{i=1}^{\mathcal{N}}}\left(2a_i+2p_i(1-\mathrm{\Pi })-{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4|b_{il}{|}^2-\lambda -\frac{1}{\breve{{\mathsf{\Im }}_1}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|{\beta }_{li}|}^2{\mathsf{ȷ}}_i^2\right){\psi }_i(t)\overline{{\psi }_i(t)}}\hfill \\ & & {\displaystyle -{\displaystyle \sum _{l=1}^{\mathcal{M}}}\left(2{\delta }_l+2q_l(1-\mathrm{\Pi })-{\displaystyle \sum _{i=1}^{\mathcal{N}}}\breve{{\mathsf{\Im }}_4}|{\beta }_{li}{|}^2-\breve{\lambda }-\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{|b_{il}|}^2{\iota }_l^2\right){\phi }_l(t)\overline{{\phi }_l(t)}}\hfill \\ & & {\displaystyle +{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\mathsf{ȷ}}_i^2(\frac{1}{\breve{{\mathsf{\Im }}_2}}|{\gamma }_{li}{|}^2+\frac{1}{\breve{{\mathsf{\Im }}_3}}|{\theta }_{li}{|}^2){\psi }_i(t-\tau (t))\overline{{\psi }_i(t-\tau (t))}}\hfill \\ & & {\displaystyle +{\displaystyle \sum _{i=1}^{\mathcal{N}}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\iota }_l^2(\frac{1}{{\mathsf{\Im }}_2}|c_{il}{|}^2+\frac{1}{{\mathsf{\Im }}_3}|d_{il}{|}^2){\phi }_l(t-\tau (t))\overline{{\phi }_l(t-\tau (t))}}\hfill \\ & & {\displaystyle +{\displaystyle \sum _{l=1}^{\mathcal{M}}}(\frac{2\mathcal{N}}{{\mathsf{\Im }}_4}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_5}|c_{il}{|}^2+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_6}|d_{il}{|}^2)(1-{|r|}^2){\wp }_{f_l}^2}\hfill \\ & & {\displaystyle +{\displaystyle \sum _{i=1}^{\mathcal{N}}}(\frac{2\mathcal{M}}{\breve{{\mathsf{\Im }}_4}}+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{\breve{{\mathsf{\Im }}_5}}|{\gamma }_{li}{|}^2+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{\breve{{\mathsf{\Im }}_6}}|{\theta }_{li}{|}^2)(1-{|r|}^2){\wp }_{g_i}^2}\hfill \\ & & {\displaystyle +\frac{\mathcal{N}}{{\mathsf{\Im }}_7}(1-r)(1-\overline{r})+\frac{\mathcal{M}}{\breve{{\mathsf{\Im }}_7}}(1-r)(1-\overline{r})}\hfill \\ & =& {\displaystyle -\mathrm{{\rm Y}}V(t)+\mathrm{\Theta }V(t-\tau (t))+\iota ,}\hfill \end{array}$$

(24)

where $\mathrm{{\rm Y}}=min\left\{{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right\}$ and $\mathrm{\Theta }=max\left\{\widetilde{{\mathrm{\Omega }}_1},\widetilde{{\mathrm{\Omega }}_2}\right\},\iota ={\displaystyle \sum _{l=1}^{\mathcal{M}}}(\frac{2\mathcal{N}}{{\mathsf{\Im }}_4}+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_5}|c_{il}{|}^2+{\displaystyle \sum _{i=1}^{\mathcal{N}}}\frac{2}{{\mathsf{\Im }}_6}|d_{il}{|}^2{)\times (1-|r|}^2){\wp }_{f_l}^2+{\displaystyle \sum _{i=1}^{\mathcal{N}}}(\frac{2\mathcal{M}}{{\breve{\mathsf{\Im }}}_4}+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{{\breve{\mathsf{\Im }}}_5}|{\gamma }_{li}{|}^2+{\displaystyle \sum _{l=1}^{\mathcal{M}}}\frac{2}{{\breve{\mathsf{\Im }}}_6}|{\theta }_{li}{|}^2)(1-{|r|}^2){\wp }_{g_i}^2+\frac{\mathcal{N}}{{\mathsf{\Im }}_7}(1-r)(1-\overline{r})+\frac{\mathcal{M}}{{\breve{\mathsf{\Im }}}_7}(1-r)(1-\overline{r}).$

According to Corollary 1, we have the following:

$$V(t)\le \widehat{k}{E}_{-\alpha ,0}^h(-\widehat{\sigma },t)+\frac{\iota }{\mathrm{{\rm Y}}-\mathrm{\Theta }},t\in {(h\mathbb{N})}_0,$$

where $\widehat{k}>0$, $0<\widehat{\sigma }<h^{-\alpha }$ are constants and

$$\underset{t\to \infty }{lim}{(||\psi (t)||}_2+{||\phi (t)||}_2)\le {\left(\frac{2\iota }{\mathrm{{\rm Y}}-\mathrm{\Theta }}\right)}^{\frac{1}{2}}.$$

Hence, DFCFBAMNNs (6) and (7) can reach quasi-projective synchronization.

If fuzzy logic is not considered in this paper, then DFCFBAMNNs (6) and (7) degenerate to the following:

$$\left\{\begin{array}{c}{\displaystyle { }_0^C{\nabla }_h^{\alpha }{x}_i(t)=-a_i{x}_i(t)+\sum _{l=1}^{\mathcal{M}}{b}_{il}{f}_l(y_l(t))+\sum _{l=1}^{\mathcal{M}}{\rho }_{il}{f}_l(y_l(t-\tau (t)))+I_i,t\in {(h\mathbb{N})}_h,}\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{\alpha }{y}_l(t)=-{\delta }_l{y}_l(t)+\sum _{i=1}^{\mathcal{N}}{\beta }_{li}{g}_i(x_i(t))+\sum _{i=1}^{\mathcal{N}}{\varrho }_{li}{g}_i(x_i(t-\tau (t)))+I_l,t\in {(h\mathbb{N})}_h,}\hfill \end{array}\right.$$

(25)

and

$$\left\{\begin{array}{c}{\displaystyle { }_0^C{\nabla }_h^{\alpha }{\breve{x}}_i(t)=-a_i{\breve{x}}_i(t)+\sum _{l=1}^{\mathcal{M}}{b}_{il}{f}_l({\breve{y}}_l(t))+\sum _{l=1}^{\mathcal{M}}{\rho }_{il}{f}_l({\breve{y}}_l(t-\tau (t)))+I_i+u_{i1}(t),t\in {(h\mathbb{N})}_h,}\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{\alpha }{\breve{y}}_l(t)=-{\delta }_l{\breve{y}}_l(t)+\sum _{i=1}^{\mathcal{N}}{\beta }_{li}{g}_i({\breve{x}}_i(t))+\sum _{i=1}^{\mathcal{N}}{\varrho }_{li}{g}_i({\breve{x}}_i(t-\tau (t)))+I_l+u_{l2}(t),t\in {(h\mathbb{N})}_h.}\hfill \end{array}\right.$$

(26)

Similar to the proof method of Theorem 1, we obtain Corollary 2. □

Corollary 2.

Under Assumptions 1 and 2, DFCFBAMNNs (25) and (26) achieve quasi-projective synchronization if

$$0<\widetilde{\mathrm{{\rm Y}}},\tilde{\mathrm{\Theta }}<h^{-\alpha },$$

(27)

$$\tilde{\mathrm{\Theta }}-\widetilde{\mathrm{{\rm Y}}}<0,$$

(28)

where $\widetilde{\mathrm{{\rm Y}}}=min\left\{{\mathrm{\Omega }}_3,{\mathrm{\Omega }}_4\right\}$, $\tilde{\mathrm{\Theta }}=max\left\{\widetilde{{\mathrm{\Omega }}_3},\widetilde{{\mathrm{\Omega }}_4}\right\}$, ${\mathrm{\Omega }}_3=2a_i+2p_i(1-\mathrm{\Pi })-\frac{\mathcal{M}}{{\breve{\mathsf{\Im }}}_8}{\mathsf{ȷ}}_i^2-{\displaystyle \sum _{l=1}^{\mathcal{M}}}({\mathsf{\Im }}_8|b_{il}{|}^2+{\mathsf{\Im }}_9|{\rho }_{il}{|}^2),$${\mathrm{\Omega }}_4=2{\delta }_l+2q_l(1-\mathrm{\Pi })-\frac{\mathcal{N}}{{\mathsf{\Im }}_8}{\iota }_l^2-{\displaystyle \sum _{i=1}^{\mathcal{N}}}({\breve{\mathsf{\Im }}}_8|{\beta }_{li}{|}^2+{\breve{\mathsf{\Im }}}_9|{\varrho }_{li}{|}^2)$, $\widetilde{{\mathrm{\Omega }}_3}=\frac{\mathcal{M}}{{\breve{\mathsf{\Im }}}_9}{\mathsf{ȷ}}_i^2,\widetilde{{\mathrm{\Omega }}_4}=\frac{\mathcal{N}}{{\mathsf{\Im }}_9}{\iota }_l^2.$

Remark 5.

Compared with the linear controllers in [19,26,30], the controller in this paper quantifies the signal before it is transmitted, which not only reduces the cost but also decreases the waste of resources in practical applications. At the same time, compared with the hybrid controller composed of the open loop control and adaptive feedback control proposed in [32], the quantitative control in this paper is easy to operate, so the controller in this paper is more practical.

Remark 6.

In fact, due to the associative memory characteristics of BAMNNs, they hold high research value. However, there are still relatively few articles related to synchronization research of BAMNNs within the discrete-time fractional-order framework. Compared to continuous-time models [20,26,27], this paper studies the synchronization problem of BAMNNs under the discrete-time fractional-order framework. Therefore, the models in this paper are more applicable and flexible.

Remark 7.

Compared with the real decomposition approach used in [4,15,17], the direct plurality approach is adopted herein, which not only reduces the computational complexity but also makes our results more compact and natural.

4. Numerical Simulations

In this section, numerical simulation results are provided to demonstrate the applicability of Theorem 1. We consider a 4-dimensional DFCFBAMNN, and the drive system is given as follows:

$$\left\{\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{0.9}{x}_i(t)}\hfill & =\hfill & -a_i{x}_i(t)+{\displaystyle \sum _{l=1}^2}{b}_{il}{f}_l(y_l(t))+{\displaystyle \underset{l=1}{\overset{2}{\bigwedge }}}{c}_{il}{f}_l(y_l(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{2}{\bigvee }}}{d}_{il}{f}_l(y_l(t-\tau (t)))+I_i,t\in {(h\mathbb{N})}_h,\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{0.9}{y}_l(t)}\hfill & =\hfill & -{\delta }_l{y}_l(t)+{\displaystyle \sum _{i=1}^2}{\beta }_{li}{g}_i(x_i(t))+{\displaystyle \underset{i=1}{\overset{2}{\bigwedge }}}{\gamma }_{li}{g}_i(x_i(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{2}{\bigvee }}}{\theta }_{li}{g}_i(x_i(t-\tau (t)))+I_l,t\in {(h\mathbb{N})}_h,\hfill \end{array}\right.$$

(29)

where activation functions $f_1(p)=f_2(p)=g_1(p)=g_2(p)=\frac{1}{2}tanh(p)$, $\tau (t)=0.25+[25sin(10t)]\ast h$, $h=0.01$, $\alpha =0.9$, $I_i=I_l=0$ for $i,l=1,2,$${\mathsf{\Im }}_k=\breve{{\mathsf{\Im }}_k}=\frac{1}{4}$ for $k=1,2,\cdots ,9$, and other parameters are chosen as follows:

$A={(a_{il})}_{2\times 2}=\left(\begin{array}{cc}0.15& 0\\ 0& 0.13\end{array}\right)$, $\delta ={({\delta }_{li})}_{2\times 2}=\left(\begin{array}{cc}0.25& 0\\ 0& 0.16\end{array}\right)$,

$B={(b_{il})}_{2\times 2}=\left(\begin{array}{cc}-0.1652-0.1001\mathfrak{i}& -0.2048-0.1010\mathfrak{i}\\ -0.1780-0.1448\mathfrak{i}& -0.1924-0.0114\mathfrak{i}\end{array}\right)$,

$\beta ={({\beta }_{li})}_{2\times 2}=\left(\begin{array}{cc}-0.0918+0.0000\mathfrak{i}& -0.2792-0.0000\mathfrak{i}\\ -0.2293+0.0000\mathfrak{i}& -0.0908+0.0000\mathfrak{i}\end{array}\right)$,

$C={(c_{il})}_{2\times 2}=\left(\begin{array}{cc}-0.0950-0.0010\mathfrak{i}& -0.000-0.0000\mathfrak{i}\\ -0.2778-0.0151\mathfrak{i}& 0.0000+0.0090\mathfrak{i}\end{array}\right)$,

$\gamma ={({\gamma }_{li})}_{2\times 2}=\left(\begin{array}{cc}-0.3310+0.0000\mathfrak{i}& -0.0020+0.0000\mathfrak{i}\\ -0.1569+0.0000\mathfrak{i}& -0.000+0.1288\mathfrak{i}\end{array}\right)$,

$D={(d_{il})}_{2\times 2}=\left(\begin{array}{cc}-0.1952-0.1101\mathfrak{i}& -0.0080+0.0000\mathfrak{i}\\ -0.1528-0.0905\mathfrak{i}& -0.0000+0.0000\mathfrak{i}\end{array}\right)$,

$\theta ={({\theta }_{li})}_{2\times 2}=\left(\begin{array}{cc}-0.1627+0.0000\mathfrak{i}& -0.0980+0.0000\mathfrak{i}\\ -0.2116+0.0000\mathfrak{i}& 0.0000+0.0098\mathfrak{i}\end{array}\right)$, the initial values of (29) are $\mathrm{\Phi }(p)={[-0.7448+0.8282\mathfrak{i},0.0659-0.2778\mathfrak{i}]}^T$, $\mathrm{\Psi }(p)={[-0.001-0.0010\mathfrak{i},-0.0010\mathfrak{i}]}^T$ for $p\in {(0.01\mathbb{N})}_{-0.5}^0$. Figure 1 shows the time evolutions of the real and imaginary parts of the X-layer and Y-layer neurons of DFCFBAMNN (29), respectively. Figure 2 shows phase trajectories of the X-layer and Y-layer neurons $x_1(t),x_2(t)$, and $y_1(t),y_2(t)$ of DFCFBAMNN (29).

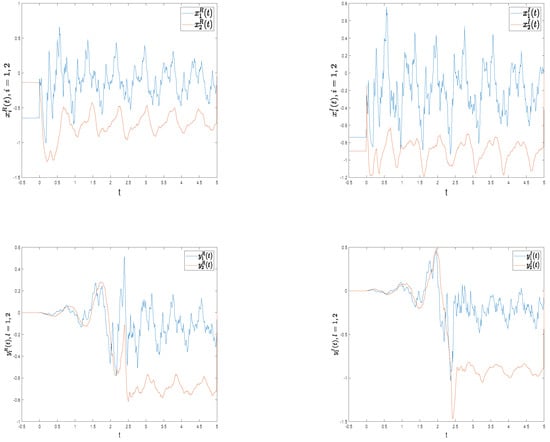
Figure 1. Trajectories of the X-layer and Y-layer neurons of DFCFBAMNN (29).

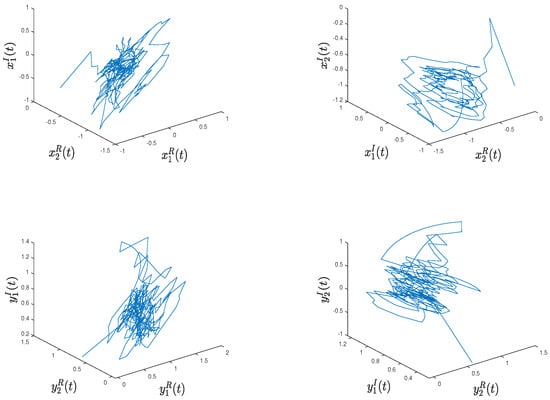
Figure 2. Phase portraits of the X-layer and Y-layer neurons of DFCFBAMNN (29).

The corresponding response system is given as follows:

$$\left\{\begin{array}{ccc}{\displaystyle { }_0^C{\nabla }_h^{0.9}{\breve{x}}_i(t)}\hfill & =\hfill & -a_i{\breve{x}}_i(t)+{\displaystyle \sum _{l=1}^2}{b}_{il}{f}_l({\breve{y}}_l(t))+{\displaystyle \underset{l=1}{\overset{2}{\bigwedge }}}{c}_{il}{f}_l({\breve{y}}_l(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{l=1}{\overset{2}{\bigvee }}}{d}_{il}{f}_l({\breve{y}}_l(t-\tau (t)))+I_i+u_i(t),t\in {(h\mathbb{N})}_h,\hfill \\ {\displaystyle { }_0^C{\nabla }_h^{0.9}{\breve{y}}_l(t)}\hfill & =\hfill & -{\delta }_l{\breve{y}}_l(t)+{\displaystyle \sum _{i=1}^2}{\beta }_{li}{g}_i({\breve{x}}_i(t))+{\displaystyle \underset{i=1}{\overset{2}{\bigwedge }}}{\gamma }_{li}{g}_i({\breve{x}}_i(t-\tau (t)))\hfill \\ \hfill & \hfill & +{\displaystyle \underset{i=1}{\overset{2}{\bigvee }}}{\theta }_{li}{g}_i({\breve{x}}_i(t-\tau (t)))+I_l+u_l(t),t\in {(h\mathbb{N})}_h,\hfill \end{array}\right.$$

(30)

the parameters are the same as (29) and the initial values of (30) are $\breve{\mathrm{\Phi }}(p)={[-0.2428+0.8221\mathfrak{i},0.5675-0.7618\mathfrak{i}]}^T$, $\breve{\mathrm{\Psi }}(p)={[-0.0010,0.020\mathfrak{i}]}^T$ for $p\in {(0.01\mathbb{N})}_{-0.5}^0$. Figure 3 reveals the time track of errors of DFCFBAMNNs (29) and (30) without the controller.

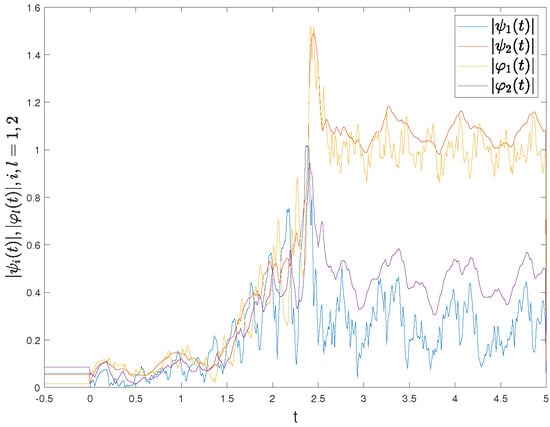
Figure 3. State trajectories of error modules $|{\psi }_1(t)|$, $|{\psi }_2(t)|$, ${\phi }_1(t)|$ and $|{\phi }_2(t)|$ without the controller.

We set projective coefficients $r_1=r_2=0.06-0.01i$ and devise a comfortable quantized controller as follows:

$$\left\{\begin{array}{c}{\displaystyle u_{i1}(t)=-p_i\left(\mathsf{\ell }\left({\psi }_i^R(t)\right)+\mathfrak{i}\mathsf{\ell }\left({\psi }_i^I(t)\right)\right),}\hfill \\ {\displaystyle u_{l2}(t)=-q_l\left(\mathsf{\ell }\left({\phi }_i^R(t)\right)+\mathfrak{i}\mathsf{\ell }\left({\phi }_i^I(t)\right)\right).}\hfill \end{array}\right.$$

(31)

We choose $p_1=p_2=q_1=q_2=0.6$, ${\zeta }^i=0.9^i,s_0=1.3$. By a simple calculation, we can attain the following: ${\iota }_1={\iota }_2={\mathsf{ȷ}}_1={\mathsf{ȷ}}_2=0.5$, and ${\wp }_{f_1}={\wp }_{f_2}={\wp }_{g_1}={\wp }_{g_2}=1.6$, $l_{f_1}=l_{f_2}=l_{g_1}=l_{g_2}=0$, ${\mathrm{\Omega }}_1=2a_i+2p_i(1-\mathrm{\Pi })-{\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{\Im }}_4|b_{il}{|}^2-\lambda -\frac{1}{\breve{{\mathsf{\Im }}_1}}{\displaystyle \sum _{l=1}^{\mathcal{M}}}{|{\beta }_{li}|}^2{\mathsf{ȷ}}_i^2\approx 0.0535+0.1882=0.2417$, ${\mathrm{\Omega }}_2=2{\delta }_l+2q_l(1-\mathrm{\Pi })-{\displaystyle \sum _{i=1}^{\mathcal{N}}}\breve{{\mathsf{\Im }}_4}|{\beta }_{li}{|}^2-\breve{\lambda }-\frac{1}{{\mathsf{\Im }}_1}{\displaystyle \sum _{i=1}^{\mathcal{N}}}{|b_{il}|}^2{\iota }_l^2\approx 0.5452+0.0523=0.5975$, $\widetilde{{\mathrm{\Omega }}_1}={\displaystyle \sum _{l=1}^{\mathcal{M}}}{\mathsf{ȷ}}_i^2(\frac{1}{\breve{{\mathsf{\Im }}_2}}|{\gamma }_{li}{|}^2+\frac{1}{\breve{{\mathsf{\Im }}_3}}|{\theta }_{li}{|}^2)\approx 0.1456+0.0860=0.2316$, $\widetilde{{\mathrm{\Omega }}_2}={\displaystyle \sum _{i=1}^{\mathcal{N}}}{\iota }_l^2(\frac{1}{{\mathsf{\Im }}_2}|c_{il}{|}^2+\frac{1}{{\mathsf{\Im }}_3}|d_{il}{|}^2)\approx 0.0593+0.109=0.1683$. $\mathrm{\Pi }=\frac{1-\zeta }{1+\zeta }=\frac{1-0.9}{1+0.9}=\frac{1}{19}$, and $h^{-\alpha }\approx 63$. In combination with (11) and (12), the $\mathrm{{\rm Y}}=min\left\{{\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\right\}=0.2417,\mathrm{\Theta }=max\left\{\widetilde{{\mathrm{\Omega }}_1},\widetilde{{\mathrm{\Omega }}_2}\right\}=0.2316.$ By a simple count, we obtain $\mathrm{\Theta }-\mathrm{{\rm Y}}=-0.0101<0$, which fulfills Theorem 1. Therefore, we can conclude that DFCFBAMNNs (29) and (30) attain quasi-projective synchronization, as portrayed in Figure 4. We can see from Figure 4 that the curves fluctuate in a certain range. Figure 5 shows a variation diagram of the quantization controller.

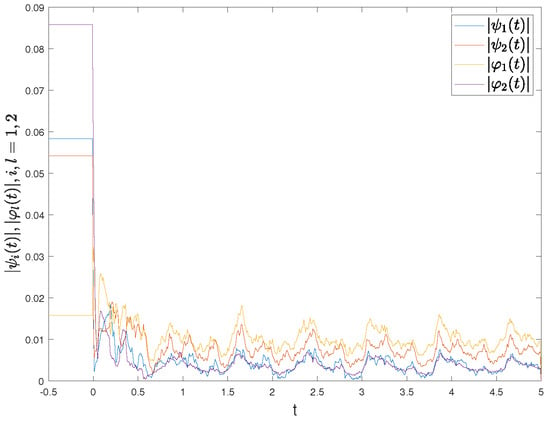
Figure 4. State trajectories of error modules of $|{\psi }_1(t)|$, $|{\psi }_2(t)|$, ${\phi }_1(t)|$ and $|{\phi }_2(t)|$ under the controller (31).

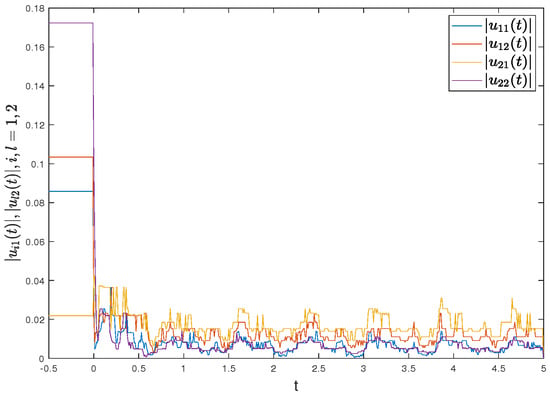
Figure 5. State evolutions of the quantization controller (31).

5. Conclusions

In this paper, we consider quasi-projective synchronization for a class of DFCFBAMNNs with time delays. In order to better deal with time delays, we propose a new lemma that expands the Halanay inequality to a discrete-time fractional-order case. Compared with the linear controller in [19,26,30], this paper devises a more practical quantitative controller. Based on the proposed lemma and related properties of complex-valued functions, some original criteria are obtained to fulfill quasi-projective synchronization. Finally, numerical simulations are given to verify the validity of the theoretical results.