New Generalized Jacobi Polynomial Galerkin Operational Matrices of Derivatives: An Algorithm for Solving Boundary Value Problems

Abstract

In this study, we present a novel approach for the numerical solution of high-order ODEs and MTVOFDEs with BCs. Our method leverages a class of GSJPs that possess the crucial property of satisfying the given BCs. By establishing OMs for both the ODs and VOFDs of the GSJPs, we integrate them into the SCM, enabling efficient and accurate numerical computations. An error analysis and convergence study are conducted to validate the efficacy of the proposed algorithm. We demonstrate the applicability and accuracy of our method through eight numerical examples. Comparative analyses with prior research highlight the improved accuracy and efficiency achieved by our approach. The recommended approach exhibits excellent agreement between approximate and precise results in tables and graphs, demonstrating its high accuracy. This research contributes to the advancement of numerical methods for ODEs and MTVOFDEs with BCs, providing a reliable and efficient tool for solving complex BVPs with exceptional accuracy.

1. Introduction

BVPs involving high order ODEs and MTVOFDEs arise in various areas of science and engineering, such as visco-elastic materials [1,2,3], economics [4], continuum and statistical mechanics [5], solid mechanics [6], and dynamics of interfaces between soft-nanoparticles and rough substrates [7]; for more applications of differential equations, see the monograph by Gregus [8]. These problems often pose significant challenges due to their complex nature and the presence of BCs that must be satisfied. Therefore, the development of efficient and accurate numerical methods for solving such BVPs is of great importance.

There are many approximation approaches in the literature that use orthogonal polynomials and non-orthogonal polynomials to obtain numerical solutions for different types of differential equations [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29]. In this paper, we present a novel approach for the numerical solution of high-order ODEs and MTVOFDEs with BCs in the following forms:

$${\mathfrak{X}}^{\left(n\right)}\left(\mathfrak{Z}\right)=\mathfrak{F}(\mathfrak{Z},\mathfrak{X}\left(\mathfrak{Z}\right),{\mathfrak{X}}^{\left(1\right)}\left(\mathfrak{Z}\right),\dots ,{\mathfrak{X}}^{(n-1)}\left(\mathfrak{Z}\right)),\mathfrak{Z}\in [0,\mathcal{L}],n=1,2,3,\dots ,$$

(1)

or

$${\mathcal{D}}^{\nu \left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)=\mathfrak{F}(\mathfrak{Z},\mathfrak{X}\left(\mathfrak{Z}\right),{\mathcal{D}}^{{\nu }_1\left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right),{\mathcal{D}}^{{\nu }_2\left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right),\dots ,{\mathcal{D}}^{{\nu }_m\left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)),0<\mathfrak{Z}\le \mathcal{L},$$

(2)

with each one of these two models subject to the following BCs:

$${\mathfrak{X}}^{\left(i\right)}\left(0\right)={\alpha }_i,{\mathfrak{X}}^{\left(j\right)}\left(\mathcal{L}\right)={\beta }_j,i=0,1,\dots ,n_1,j=0,1,\dots ,n_2,n_1+n_2+2=n,$$

(3)

where n is the smallest positive integer number such that $0\le {\nu }_1\left(\mathfrak{Z}\right)<{\nu }_2\left(\mathfrak{Z}\right)<\cdots <{\nu }_m\left(\mathfrak{Z}\right)<\nu \left(\mathfrak{Z}\right)\le n$ holds for all $\mathfrak{Z}\in [0,\mathcal{L}]$ and where ${\mathcal{D}}^{\nu \left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)$, ${\mathcal{D}}^{{\nu }_i\left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)$$(i=1,2,\dots ,m)$ are the VOFDs defined in the Caputo sense, $\mathfrak{F}$ is a continuous function, and ${\alpha }_i(i=0,1,\dots ,n_1),{\beta }_j(j=0,1,\dots ,n_2)$ are constants.

The establishment of OMs for ODs and VOFDs for GSJP is crucial to our technique. These OMs enable us to efficiently compute the derivatives of the GSJPs, which are then incorporated into the SCM. The SCM is a powerful numerical technique that approximates the solution by expanding it in a series of basis functions and collocating the governing equation at specific points within the domain. By integrating these innovative techniques, we effectively bridge a gap in the existing literature, offering a reliable and efficient numerical tool for addressing complex BVPs while advancing our understanding of systems characterized by variable-order fractional dynamics. Our method provides a significant contribution by precisely solving the mentioned high-order ODEs (1) and MTVOFDEs (2) with BCs (3).

It can be said that the integration of these techniques is a dependable and efficient tool for tackling these specific classes of equations, enabling accurate representations of the solutions and precise enforcement of the BCs. This level of specificity enhances the clarity of our research targets, ensuring that readers comprehend the problem domain we aim to address. Additionally, employing these techniques enables us to effectively handle the varying fractional orders, providing a powerful tool for the numerical solution of complex BVPs. For example, in [19] the author discussed using the proposed techniques to obtain the numerical solution of multi-term variable-order time-fractional diffusion-wave equations. This capability opens up new avenues for studying real-world phenomena that exhibit variable-order fractional dynamics. To ensure the reliability and effectiveness of our proposed algorithm, we conduct an error analysis and convergence study. These analyses provide theoretical guarantees for the accuracy and convergence properties of our method. Additionally, we present a set of seven numerical examples to demonstrate the applicability and accuracy of our approach. The numerical results obtained using our method exhibit a high degree of agreement between the approximate solutions and the exact solutions. We present these results in the form of tables and graphs, illustrating the accuracy and reliability of our approach in solving complex BVPs. By introducing this novel numerical approach for high-order ODEs and MTVOFDEs with BCs, we obtain a reliable and efficient tool for solving the challenging BVPs encountered in various scientific and engineering applications. The accuracy and effectiveness of our method make it a valuable asset for researchers and practitioners seeking accurate numerical solutions for complex BVPs.

This paper’s structure is as follows. In Section 2, we cover the essential notions and principles of VOFC. Section 3 delves into the essential characteristics of shifted JPs and GSJPs. We explore their properties and significance in the context of our study. In Section 4, we focus on the development of novel OMs tailored specifically for GSJP ODs and VOFDs. These newly constructed OMs are crucial for solving the problem described by Equations (1) and (2) subject to the BCs outlined in Equation (3). Section 5 delves into the application of the newly developed OMs within the framework of the SCM to solve the aforementioned problems. In Section 6, we present a comprehensive analysis of the error estimate. To showcase the effectiveness and practicality of the proposed method, we provide eight numerical examples in Section 7. These examples serve to validate our method and enable comparisons with alternative approaches. We conclude our analysis with a summary of key results and important conclusions in Section 8. We discuss the contributions and implications of our research, highlighting the advantages and potential applications of the proposed method in solving problems involving ODEs and VOFDEs with BCs.

2. Basic Definition of Caputo VOFDs

This section introduces the tools needed to construct the suggested approach and enable us to address the given problems.

Definition 1

([30,31,32,33]). The Caputo VOFDs for $h\left(\mathfrak{Z}\right)$ are defined as follows:

$${\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}h\left(\mathfrak{Z}\right)={\displaystyle \frac{1}{\Gamma (\mathfrak{N}-\mu (\mathfrak{Z}\left)\right)}}\underset{0}{\overset{\mathfrak{Z}}{\int }}{(\mathfrak{Z}-\tau )}^{\mathfrak{N}-\mu \left(\mathfrak{Z}\right)-1}{h}^{\left(\mathfrak{N}\right)}\left(\tau \right)d\tau ,n-1<\mu \left(\mathfrak{Z}\right)\le \mathfrak{N},\mathfrak{Z}>0.$$

(4)

When $\mu \left(\mathfrak{Z}\right)=\alpha$, Definition 1 provides the Caputo fractional derivative (FD) of order $\alpha$. Further, ${\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}$ has the following characteristics:

$$\begin{gathered} \begin{array}{cc}\hfill {\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}({\lambda }_1{h}_1\left(\mathfrak{Z}\right)+{\lambda }_2{h}_2\left(\mathfrak{Z}\right))& ={\lambda }_1{\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}{h}_1\left(\mathfrak{Z}\right)+{\lambda }_2{\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}{h}_2\left(\mathfrak{Z}\right),\hfill \end{array} \\ \begin{array}{cc}\hfill {\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}h\left(\mathfrak{Z}\right)& ={\displaystyle \frac{d^{\mathfrak{N}}h\left(\mathfrak{Z}\right)}{d{\mathfrak{Z}}^{\mathfrak{N}}}},\mu \left(\mathfrak{Z}\right)=\mathfrak{N},\mathfrak{N}\in \mathbb{N}.\hfill \end{array} \end{gathered}$$

(5)

Furthermore, Equation (4) provides us with the following [30,31]:

$$\begin{gathered} \begin{array}{cc}\hfill {\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}\left(\mathfrak{C}\right)& =0,(\mathfrak{C}\mathrm{is}\mathrm{a}\mathrm{const}.),\hfill \end{array} \\ \begin{array}{cc}\hfill {\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}{\mathfrak{Z}}^k& =\left\{\begin{array}{cc}0,\hfill & k=0,1,\dots ,\lceil \mu \left(\mathfrak{Z}\right)\rceil -1,\hfill \\ {\displaystyle \frac{\Gamma (k+1)}{\Gamma (k+1-\mu (\mathfrak{Z}\left)\right)}}{\mathfrak{Z}}^{k-\mu \left(\mathfrak{Z}\right)},\hfill & k\ge \lceil \mu \left(\mathfrak{Z}\right)\rceil .\hfill \end{array}\right.\hfill \end{array} \end{gathered}$$

(6)

3. A Brief Description of JPs and GSJPs

The primary goal of this section is to introduce the essential aspects of JPs and their derived forms.

3.1. A Summary of the Shifted JPs

Orthogonal JPs, ${\mathcal{V}}_n^{(\mathfrak{a},\mathfrak{b})}\left(x\right),\mathfrak{a},\mathfrak{b}>-1$, satisfy [34]

$${\int }_{-1}^1{w}^{\mathfrak{a},\mathfrak{b}}\left(x\right){\mathcal{V}}_n^{(\mathfrak{a},\mathfrak{b})}\left(x\right){\mathcal{V}}_m^{(\mathfrak{a},\mathfrak{b})}\left(x\right)dx=\left\{\begin{array}{cc}0,\hfill & m\ne n,\hfill \\ h_n^{(\mathfrak{a},\mathfrak{b})},\hfill & m=n,\hfill \end{array}\right.$$

where $w^{\mathfrak{a},\mathfrak{b}}\left(x\right)={(1-x)}^{\mathfrak{a}}{(1+x)}^{\mathfrak{b}}$ and $h_n^{(\mathfrak{a},\mathfrak{b})}={\displaystyle \frac{2^{\lambda }\Gamma (n+\mathfrak{a}+1)\Gamma (n+\mathfrak{b}+1)}{n!(2n+\lambda )\Gamma (n+\lambda )}},\lambda =\mathfrak{a}+\mathfrak{b}+1.$

The shifted JPs, denoted as ${\mathcal{V}}_{\mathcal{L},n}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathcal{V}}_n^{(\mathfrak{a},\mathfrak{b})}(2\mathfrak{Z}/\mathcal{L}-1)$, are in accordance with

$${\int }_0^{\mathcal{L}}{w}_{\mathcal{L}}^{\mathfrak{a},\mathfrak{b}}\left(\mathfrak{Z}\right){\mathcal{V}}_{\mathcal{L},n}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right){\mathcal{V}}_{\mathcal{L},m}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)d\mathfrak{Z}=\left\{\begin{array}{cc}0,\hfill & m\ne n,\hfill \\ {\left(\frac{\mathcal{L}}{2}\right)}^{\lambda }{h}_n^{(\mathfrak{a},\mathfrak{b})},\hfill & m=n,\hfill \end{array}\right.$$

where $w_{\mathcal{L}}^{\mathfrak{a},\mathfrak{b}}\left(\mathfrak{Z}\right)={(\mathcal{L}-\mathfrak{Z})}^{\mathfrak{a}}{\mathfrak{Z}}^{\mathfrak{b}}$.

The fundamental expansions that will be used in this paper are [35] (Section 11.3.4):

• The power form representation of ${\mathcal{V}}_{\mathcal{L},n}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$ is as follows:

  $${\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=\sum _{k=0}^i{c}_k^{\left(i\right)}{\mathfrak{Z}}^k=\sum _{k=0}^i{\overline{c}}_k^{\left(i\right)}{(\mathcal{L}-\mathfrak{Z})}^k,$$

  (7)

  where

  $$c_k^{\left(i\right)}=\frac{{(-1)}^{i-k}\Gamma (i+\mathfrak{b}+1)\Gamma (i+k+\lambda )}{{\mathcal{L}}^{k}k!(i-k)!\Gamma (k+\mathfrak{b}+1)\Gamma (i+\lambda )}\mathrm{and}{\overline{c}}_k^{\left(i\right)}=\frac{{(-1)}^k{(\mathfrak{a}+1)}_i{(\lambda +i)}_k}{{\mathcal{L}}^{k}k!(i-k)!{(\mathfrak{a}+1)}_k}.$$

  (8)
• The forms of ${\mathfrak{Z}}^k$ and ${(\mathcal{L}-\mathfrak{Z})}^k$ in regard to ${\mathcal{V}}_{\mathcal{L},r}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$ are

  $${\mathfrak{Z}}^k=\sum _{r=0}^k{b}_r^{\left(k\right)}{\mathcal{V}}_{\mathcal{L},r}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),and{(\mathcal{L}-\mathfrak{Z})}^k=\sum _{r=0}^k{\overline{b}}_r^{\left(k\right)}{\mathcal{V}}_{\mathcal{L},r}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),$$

  (9)

  where

  $$b_r^{\left(k\right)}=\frac{{\mathcal{L}}^{k}k!(\lambda +2r)\Gamma (k+\mathfrak{b}+1)\Gamma (r+\lambda )}{(k-r)!\Gamma (r+\mathfrak{b}+1)\Gamma (k+r+\lambda +1)}and{\overline{b}}_r^{\left(k\right)}=\frac{(2j+\lambda ){\mathcal{L}}^k{(-k)}_j{(\lambda +1)}_{j-1}{(\mathfrak{a}+1)}_k}{{(\mathfrak{a}+1)}_j{(\lambda +1)}_k{(k+\lambda +1)}_j}.$$

  (10)

3.2. Offering GSJPs

In this part, it is important to discuss the polynomials ${\left\{{\varphi }_{p,q,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\right\}}_{j\ge 0}$, defined as follows:

$${\varphi }_{p,q,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^p{(\mathcal{L}-\mathfrak{Z})}^q{\mathcal{V}}_{\mathcal{L},j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),p,q=0,1,2,\dots .$$

(11)

These are required to meet the homogenous form of the BCs (3) for a suitable choice of $p,q$. Subsequently, they satisfy

$${\int }_0^{\mathcal{L}}\frac{w_{\mathcal{L}}^{\mathfrak{a},\mathfrak{b}}\left(\mathfrak{Z}\right)}{{\mathfrak{Z}}^{2p}{(\mathcal{L}-\mathfrak{Z})}^{2q}}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right){\varphi }_{p,q,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)d\mathfrak{Z}=\left\{\begin{array}{cc}0,\hfill & i\ne j,\hfill \\ {\left(\frac{\mathcal{L}}{2}\right)}^{\lambda }{h}_i^{(\mathfrak{a},\mathfrak{b})},\hfill & i=j.\hfill \end{array}\right.$$

(12)

4. Two OMs for Ods and VOFDs of ${\mathit{\varphi }}_{\mathit{p}\mathbf{,}\mathit{q}\mathbf{,}\mathit{j}}^{\mathbf{(}\mathfrak{a}\mathbf{,}\mathfrak{b}\mathbf{)}}\mathbf{\left(}\mathfrak{Z}\mathbf{\right)}$

In this section, we present two OMs for Ods and VOFDs of ${\varphi }_{p,q,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$. To do this, we start with Theorem 1 and Lemma 1, which enable us to prove Theorem 2.

Theorem 1

([9]). The first derivative of ${\varphi }_{p,0,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),i\ge 0$, can be written in the form

$$\mathcal{D}{\varphi }_{p,0,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=\sum _{j=0}^{i-1}{\theta }_{i,j}^{\mathfrak{a},\mathfrak{b}}\left(p\right){\varphi }_{p,0,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{ϵ}_{p,i}\left(\mathfrak{Z}\right),$$

(13)

where ${ϵ}_{p,i}\left(\mathfrak{Z}\right)={\displaystyle \frac{1}{i!}}{(-1)}^{i}p{(\mathfrak{b}+1)}_i{\mathfrak{Z}}^{p-1}$ and

$${\theta }_{i,j}^{\mathfrak{a},\mathfrak{b}}\left(p\right)=C_{i,j}^{\mathfrak{a},\mathfrak{b}}\sum _{r=0}^{i-j-1}\frac{{(-1)}^r(r+p+j+1){(j+i+\lambda +1)}_r}{r!(r+j+1)(r+j+\mathfrak{b}+1)(i-j-r-1)!\Gamma (r+2j+\lambda +1)},$$

(14)

where

$$C_{i,j}^{\mathfrak{a},\mathfrak{b}}=\frac{{(-1)}^{i+j-1}(\lambda +i){(\mathfrak{b}+1)}_i(\lambda +2j)\Gamma (j+\lambda ){(i+\lambda +1)}_j}{\ell {(\mathfrak{b}+1)}_j}.$$

Lemma 1.

The polynomials ${\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),i\ge 0,$ have the following expression:

$${\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=(\mathfrak{Z}-\mathcal{L})\sum _{j=0}^{i-1}{{\rm Y}}_{i,j}^{\mathfrak{a},\mathfrak{b}}{\mathcal{V}}_{\mathcal{L},j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathcal{L}\right),$$

(15)

where

$${{\rm Y}}_{i,j}^{\mathfrak{a},\mathfrak{b}}=\frac{\Gamma (i+\mathfrak{a}+1)\Gamma (j+\lambda )\Gamma (i+j+\lambda +1)}{\mathcal{L}(j+1)\Gamma (i-j)\Gamma (j+\mathfrak{a}+2)\Gamma (i+\lambda )\Gamma (2j+\lambda )}{}_{4}F_3\left(\begin{array}{c}1-i+j,1+j,j+\mathfrak{a}+1,i+j+\lambda +1\hfill \\ 2+j,\mathfrak{a}+j+2,2j+\lambda +1\hfill \end{array};1\right).$$

(16)

Proof. 

We have

$${\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=(\mathfrak{Z}-\mathcal{L})\left(\frac{{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)-{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathcal{L}\right)}{\mathfrak{Z}-\mathcal{L}}\right)+{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathcal{L}\right).$$

(17)

In view of (7) and (9), we obtain

$$\frac{{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)-{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathcal{L}\right)}{\mathfrak{Z}-\mathcal{L}}=-\sum _{k=0}^{i-1}{\overline{c}}_{k+1}^{\left(i\right)}{(\mathcal{L}-\mathfrak{Z})}^k=-\sum _{k=0}^{i-1}{\overline{c}}_{k+1}^{\left(i\right)}\left(\sum _{r=0}^k{\overline{b}}_r^{\left(k\right)}{\mathcal{V}}_{\mathcal{L},r}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\right),$$

(18)

consequently,

$$\frac{{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)-{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathcal{L}\right)}{\mathfrak{Z}-\mathcal{L}}=-\sum _{j=0}^{i-1}\left(\sum _{r=0}^{i-j-1}{\overline{c}}_{r+j+1}^{\left(i\right)}{\overline{b}}_j^{(r+j)}\right){\mathcal{V}}_{\mathcal{L},j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=-\sum _{j=0}^{i-1}{{\rm Y}}_{i,j}^{\mathfrak{a},\mathfrak{b}}{\mathcal{V}}_{\mathcal{L},j}^{(\mathfrak{a},\mathfrak{b})},$$

(19)

where ${{\rm Y}}_{i,j}^{\mathfrak{a},\mathfrak{b}}$ has the form from (16). Substitution of (19) into (17) leads to (15). □

Theorem 2.

$\mathcal{D}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),i\ge 0$, can be expressed as follows:

$$\mathcal{D}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=\sum _{j=0}^{i-1}{\Omega }_{i,j}^{p,q}{\varphi }_{p,q,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{\vartheta }_{p,q,i}\left(\mathfrak{Z}\right),$$

(20)

where ${\vartheta }_{p,q,i}\left(\mathfrak{Z}\right)={\displaystyle \frac{p}{i!}}{(-1)}^i{(\mathfrak{b}+1)}_i{\mathfrak{Z}}^{p-1}{(\mathcal{L}-\mathfrak{Z})}^q-{\displaystyle \frac{q}{i!}}{(\mathfrak{a}+1)}_i{(\mathcal{L}-\mathfrak{Z})}^{q-1}{\mathfrak{Z}}^p$ and

$${\Omega }_{i,j}^{p,q}={\theta }_{i,j}^{\mathfrak{a},\mathfrak{b}}\left(p\right)+q{{\rm Y}}_{i,j}^{\mathfrak{a},\mathfrak{b}}.$$

(21)

Proof. 

In view of (11), the first derivative of ${\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$ takes the following form:

$$\mathcal{D}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={(\mathcal{L}-\mathfrak{Z})}^q\mathcal{D}\left({\mathfrak{Z}}^p{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\right)-q{(\mathcal{L}-\mathfrak{Z})}^{q-1}{\mathfrak{Z}}^p{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right).$$

(22)

Using Lemma 1 and Theorem 1 leads to (22), which takes the form from (20). □

Now, we have reached one of the main desired results in this section, which is the OM of the ods of

$${\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={[{\varphi }_{p,q,0}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),{\varphi }_{p,q,1}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),\dots ,{\varphi }_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)]}^T.$$

(23)

Corollary 1 shows this outcome, which directly follows from Theorem 2.

Corollary 1.

$$\frac{d^m{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)}{d{\mathfrak{Z}}^m}=G_{p,q}^m{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{\mathit{\eta }}_{p,q,\mathcal{N}}^{\left(m\right)}\left(\mathfrak{Z}\right)$$

(24)

with

$${\mathit{\eta }}_{p,q,\mathcal{N}}^{\left(m\right)}\left(\mathfrak{Z}\right)=\sum _{k=0}^{m-1}{G}_{p,q}^k{\mathbf{\vartheta }}_{p,q,\mathcal{N}}^{(m-k-1)}\left(\mathfrak{Z}\right),$$

where ${\mathbf{\vartheta }}_{p,q,\mathcal{N}}\left(\mathfrak{Z}\right)={\left[{\vartheta }_{p,q,0}\left(\mathfrak{Z}\right),{\vartheta }_{p,q,1}\left(\mathfrak{Z}\right),\cdots ,{\vartheta }_{p,q,\mathcal{N}}\left(\mathfrak{Z}\right)\right]}^{T}and{G}_{p,q}={\left(g_{i,j}(p,q)\right)}_{0\le i,j\le \mathcal{N}}$

$$g_{i,j}(p,q)=\left\{\begin{array}{cc}{\Omega }_{i,j}^{p,q},\hfill & i>j,\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

The OM of the VOFDs of ${\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$ is the second primary desired result, which is provided in Theorem 4. To achieve this, we need to consider the following theorem:

Theorem 3

([9]). ${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,0,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),i\ge 0$ has the following expression:

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,0,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}\sum _{j=0}^i{\Theta }_{i,j}^{(p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right){\varphi }_{p,0,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),$$

(25)

which leads to

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}{\mathbf{D}}_{p,0}^{\left(\upsilon \right(\mathfrak{Z}\left)\right)}{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),$$

(26)

where ${\mathbf{D}}_{p,0}^{\left(\upsilon \right(\mathfrak{Z}\left)\right)}=\left(d_{i,j}^{(p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right)\right)$ is a matrix of order $(\mathcal{N}+1)\times (\mathcal{N}+1)$ with elements defined as follows:

$$d_{i,j}^{(p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right)=\left\{\begin{array}{cc}{\Theta }_{i,j}^{(p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right),\hfill & i\ge j,\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

(27)

and

$${\Theta }_{i,j}^{(p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right)=\frac{{(-1)}^{i-j}(p+j)!\Gamma (i+\mathfrak{b}+1)\Gamma (j+\lambda )\Gamma (i+j+\lambda )}{(i-j)!\Gamma (j+\mathfrak{b}+1)\Gamma (2j+\lambda )\Gamma (i+\lambda )\Gamma (p+j-\upsilon (\mathfrak{Z})+1)}\times {}_{3}F_2\left(\begin{array}{c}j-i,p+j+1,i+j+\lambda \hfill \\ 2j+\lambda +1,p+j-\upsilon \left(\mathfrak{Z}\right)+1\hfill \end{array};1\right).$$

(28)

Theorem 4.

${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),i\ge 0$ has the following expression:

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}\sum _{j=0}^i{\Lambda }_{i,j}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z}){\varphi }_{p,0,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$$

(29)

and consequently,

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}{\mathbf{D}}_{p,q}^{\left(\upsilon \right(\mathfrak{Z}\left)\right)}\left(\mathfrak{Z}\right){\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),$$

(30)

where ${\mathbf{D}}_{p,q}^{\left(\upsilon \right(\mathfrak{Z}\left)\right)}\left(\mathfrak{Z}\right)=\left(d_{i,j}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z})\right)$ is a matrix of order $(\mathcal{N}+1)\times (\mathcal{N}+1)$ with elements defined as follows:

$$d_{i,j}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z})=\left\{\begin{array}{cc}{\Lambda }_{i,j}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z}),\hfill & i\ge j,\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

(31)

and

$${\Lambda }_{i,j}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z})=\sum _{k=0}^q{(-1)}^k\left(\genfrac{}{}{0pt}{}{q}{k}\right){\mathcal{L}}^{q-k}{\Theta }_{i,j}^{(k+p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right){\mathfrak{Z}}^k.$$

(32)

Proof. 

We have

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)=\sum _{k=0}^q{(-1)}^k\left(\genfrac{}{}{0pt}{}{q}{k}\right){\mathcal{L}}^{q-k}{\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}\left({\mathfrak{Z}}^{k+p}{\mathcal{V}}_{\mathcal{L},i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\right).$$

(33)

Applying Theorem 3, we obtain

$$\begin{array}{cc}\hfill {\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)& =\sum _{k=0}^q{(-1)}^k\left(\genfrac{}{}{0pt}{}{q}{k}\right){\mathcal{L}}^{q-k}\left({\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}\sum _{j=0}^i{\Theta }_{i,j}^{(k+p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right)\left({\mathfrak{Z}}^{k+p}{\mathcal{V}}_{\mathcal{L},j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\right)\right),\hfill \\ & ={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}\sum _{j=0}^i\left(\sum _{k=0}^q{(-1)}^k\left(\genfrac{}{}{0pt}{}{q}{k}\right){\mathcal{L}}^{q-k}{\Theta }_{i,j}^{(k+p,0)}\left(\upsilon \left(\mathfrak{Z}\right)\right){\mathfrak{Z}}^k\right){\varphi }_{p,0,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),\hfill \\ & ={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}\sum _{j=0}^i{\Lambda }_{i,j}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z}){\varphi }_{p,0,j}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right);\hfill \end{array}$$

(34)

then,

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\varphi }_{p,q,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}\left([{\Lambda }_{i,0}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z}),{\Lambda }_{i,1}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z}),\dots ,{\Lambda }_{i,i}^{(p,q)}(\upsilon \left(\mathfrak{Z}\right),\mathfrak{Z}),0,\dots ,0]{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\right)$$

(35)

and (30) is obtained. □

5. Numerical Handling for the DEs (1) and (2) Subject to BCs (3)

In this part, we use the computed OMs to find numerical solutions for (1) and (2) subject to (3).

5.1. Homogeneous BCs

Suppose that

$${\mathfrak{X}}^{\left(i\right)}\left(0\right)=0,{\mathfrak{X}}^{\left(j\right)}\left(\mathcal{L}\right)=0,i=0,1,\dots ,n_1,j=0,1,\dots ,n_2,n_1+n_2+2=n,$$

(36)

$p=n_1+1$, and $q=n_1+1$; then, the following approximations can be considered:

$${\displaystyle \mathfrak{X}\left(\mathfrak{Z}\right)\simeq {\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\sum _{i=0}^{\mathcal{N}}{a}_i{\varphi }_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)={\mathcal{A}}^T{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)}$$

(37)

and

$${\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)\simeq {\mathcal{D}}^{\upsilon \left(\mathfrak{Z}\right)}{\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\left\{\begin{array}{c}{\mathcal{A}}^T{G}_{p,q}^m{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{a})}\left(\mathfrak{Z}\right)+{\mathit{\eta }}_{p,q,\mathcal{N}}^{\left(m\right)}\left(\mathfrak{Z}\right),\upsilon \left(\mathfrak{Z}\right)=m,m\mathrm{is}\mathrm{an}\mathrm{integer},\hfill \\ \\ {\mathfrak{Z}}^{-\upsilon \left(\mathfrak{Z}\right)}{\mathcal{A}}^T{\mathbf{D}}_{p,q}^{\left(\upsilon \right(\mathfrak{Z}\left)\right)}{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{a})}\left(\mathfrak{Z}\right),\upsilon \left(\mathfrak{Z}\right)\mathrm{is}\mathrm{a}\mathrm{fraction}\mathrm{number}\mathrm{or}\mathrm{function},\hfill \end{array}\right.$$

(38)

where $\mathcal{A}={\left[a_0,a_1,\dots ,a_{\mathcal{N}}\right]}^T.$

To express the residual of Equation (1) in the method suggested, it is possible to use the approximations provided by (37) and (38):

$$\begin{array}{cc}\hfill {\mathfrak{R}}_{p,q,\mathcal{N}}\left(\mathfrak{Z}\right)=& {\mathcal{A}}^T{G}_{p,q}^n{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{\mathit{\eta }}_{p,q,\mathcal{N}}^{\left(n\right)}\left(\mathfrak{Z}\right)\hfill \\ & -\mathfrak{F}(\mathfrak{Z},{\mathcal{A}}^T{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),{\mathcal{A}}^T{G}_{p,q}{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{\mathit{\eta }}_{p,q,\mathcal{N}}^{\left(1\right)}\left(\mathfrak{Z}\right),\dots ,{\mathcal{A}}^T{G}_{p,q}^{n-1}{\mathbf{\Phi }}_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+{\mathit{\eta }}_{p,q,\mathcal{N}}^{(n-1)}\left(\mathfrak{Z}\right)),\hfill \end{array}$$

(39)

while the residual of Equation (2) is in the following form:

$$\begin{array}{cc}\hfill {\widehat{\mathfrak{R}}}_{p,q,\mathcal{N}}\left(\mathfrak{Z}\right)=& {\mathfrak{Z}}^{-\nu \left(\mathfrak{Z}\right)}{\mathcal{A}}^T{\mathbf{D}}_{p,q}^{\left(\nu \right(\mathfrak{Z}\left)\right)}{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\hfill \\ & -\mathfrak{F}(\mathfrak{Z},{\mathcal{A}}^T{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),{\mathfrak{Z}}^{-{\nu }_1\left(\mathfrak{Z}\right)}{\mathcal{A}}^T{\mathbf{D}}_{p,q}^{\left({\nu }_1\left(\mathfrak{Z}\right)\right)}{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),\dots ,{\mathfrak{Z}}^{-{\nu }_m\left(\mathfrak{Z}\right)}{\mathcal{A}}^T{\mathbf{D}}_{p,q}^{\left({\nu }_m\left(\mathfrak{Z}\right)\right)}{\mathbf{\Phi }}_{p,0,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)).\hfill \end{array}$$

(40)

Using the $(\mathcal{N}+1)$ zeros of ${\mathcal{V}}_{\mathcal{L},\mathcal{N}+1}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$ as collocation points, or alternatively, using ${\mathfrak{Z}}_k=\frac{\mathcal{L}(k+1)}{\mathcal{N}+2},0\le k\le \mathcal{N}$, we obtain the system

$${\mathfrak{R}}_{p,q,\mathcal{N}}\left({\mathfrak{Z}}_k\right)=0,0\le k\le \mathcal{N}$$

(41)

in the case of ODE (1) and the system

$${\widehat{\mathfrak{R}}}_{p,q,\mathcal{N}}\left({\mathfrak{Z}}_k\right)=0,0\le k\le \mathcal{N}$$

(42)

in the case of VOFDE (2). We can compute the coefficients $a_k,0\le k\le \mathcal{N},$ by solving (41) or (42) to obtain the approximated solutions of (1) or (2), respectively. This proposed algorithm is referred to as $GSJCOPMM$.

5.2. Nonhomogeneous BCs

It is important to change the nonhomogeneous conditions (3), the ODE (1), and the VOFDE (2) into similar forms with homogeneous conditions in order to make the suggested algorithm work. The following transformation is what makes these changes possible:

$$\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)=\mathfrak{X}\left(\mathfrak{Z}\right)-{\mathfrak{T}}_n\left(\mathfrak{Z}\right),{\mathfrak{T}}_n\left(\mathfrak{Z}\right)=\sum _{j=0}^{n-1}{C}_j{\mathfrak{Z}}^j,$$

(43)

where the coefficients $C_j(j=0,1,\dots ,n-1)$ can be computed by solving the system

$${\mathfrak{T}}_n^{\left(i\right)}\left(0\right)=0,{\mathfrak{T}}_n^{\left(j\right)}\left(\mathcal{L}\right)=0,i=0,1,2,\dots ,n_1,j=0,1,2,\dots ,n_2,n_1+n_2+2=n.$$

(44)

Solving the following amended equations can simplify the current issue:

$${\overline{\mathfrak{X}}}^{\left(n\right)}\left(\mathfrak{Z}\right)=\mathfrak{F}(\mathfrak{Z},\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)+{\mathfrak{T}}_n\left(\mathfrak{Z}\right),{(\overline{\mathfrak{X}}+{\mathfrak{T}}_n\left(\mathfrak{Z}\right))}^{\left(1\right)},\dots ,{(\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)+{\mathfrak{T}}_n\left(\mathfrak{Z}\right))}^{(n-1)}),\mathfrak{Z}\in [0,\mathcal{L}],$$

(45)

and

$$\begin{array}{cc}\hfill {\mathcal{D}}^{\nu \left(\mathfrak{Z}\right)}\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)=\mathfrak{F}(\mathfrak{Z},\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)+{\mathfrak{T}}_n\left(\mathfrak{Z}\right),{\mathcal{D}}^{{\nu }_1\left(\mathfrak{Z}\right)}(\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)+{\mathfrak{T}}_n\left(\mathfrak{Z}\right)),{\mathcal{D}}^{{\nu }_2\left(\mathfrak{Z}\right)}(\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)& +{\mathfrak{T}}_n\left(\mathfrak{Z}\right)),\dots ,{\mathcal{D}}^{{\nu }_m\left(\mathfrak{Z}\right)}(\overline{\mathfrak{X}}\left(\mathfrak{Z}\right)+{\mathfrak{T}}_n\left(\mathfrak{Z}\right))),\mathfrak{Z}\in [0,\mathcal{L}],\hfill \\ \hfill & 0\le {\nu }_1\left(\mathfrak{Z}\right)<{\nu }_2\left(\mathfrak{Z}\right)<\cdots <{\nu }_m\left(\mathfrak{Z}\right)<\nu \left(\mathfrak{Z}\right)\le n,\hfill \end{array}$$

(46)

with the following BCs:

$${\overline{\mathfrak{X}}}^{\left(i\right)}\left(0\right)=0,{\overline{\mathfrak{X}}}^{\left(j\right)}\left(\mathcal{L}\right)=0,i=0,1,2,\dots ,n_1,j=0,1,2,\cdots ,n_2,n_1+n_2+2=n.$$

(47)

Hence,

$${\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)={\overline{\mathfrak{X}}}_{\mathcal{N}}\left(\mathfrak{Z}\right)+{\mathfrak{T}}_n\left(\mathfrak{Z}\right).$$

(48)

6. Convergence and Error Analysis

Here, we look at the suggested method’s convergence and error estimations. To do this, we first need to define the space ${\mathfrak{S}}_{p,q,\mathcal{N}}$ and obtained error ${\mathfrak{e}}_{\mathcal{N}}\left(\mathfrak{Z}\right)$, which are our primary focus:

$${\mathfrak{S}}_{p,q,\mathcal{N}}=Span\{{\varphi }_{p,q,0}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),{\varphi }_{p,q,1}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right),...,{\varphi }_{p,q,\mathcal{N}}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)\},{\mathfrak{e}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\left|\mathfrak{X}\left(\mathfrak{Z}\right)-{\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)\right|.$$

Then,

$$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2={\left({\int }_0^{\mathcal{L}}{\left({\mathfrak{e}}_{\mathcal{N}}\left(\mathfrak{Z}\right)\right)}^{2}d\mathfrak{Z}\right)}^{1/2},{\parallel {\mathfrak{e}}_{\mathcal{N}}\parallel }_{\infty }=\underset{0\le \mathfrak{Z}\le \mathcal{L}}{max}{\mathfrak{e}}_{\mathcal{N}}\left(\mathfrak{Z}\right).$$

(49)

Theorem 5.

Suppose that $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^p{(\mathcal{L}-\mathfrak{Z})}^{q}u\left(\mathfrak{Z}\right)$ and that ${\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)$ is provided by (37), which represents the best possible approximation for $\mathfrak{X}\left(\mathfrak{Z}\right)$ out of ${\mathfrak{S}}_{p,q,\mathcal{N}}$. Then,

$$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }\le \frac{\mathfrak{K}{\mathcal{L}}^{p+q+1}}{2^{\lambda }}{\left(\frac{p}{p+q}\right)}^p{\left(\frac{q}{p+q}\right)}^q{\left(\frac{e\mathcal{L}}{4}\right)}^{\mathcal{N}}{(\mathcal{N}+1)}^{s-\mathcal{N}-1}$$

(50)

and

$$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2\le \frac{\mathfrak{K}{\mathcal{L}}^{p+q+3/2}}{2^{\lambda }}{\left(\frac{p}{p+q}\right)}^p{\left(\frac{q}{p+q}\right)}^q{\left(\frac{e\mathcal{L}}{4}\right)}^{\mathcal{N}}{(\mathcal{N}+1)}^{s-\mathcal{N}-1},$$

(51)

where $s=max\{\mathfrak{a},\mathfrak{b},-1/2\}<\mathcal{N}+1$ and $\mathfrak{K}=\underset{\mathfrak{Z}\in [0,\mathcal{L}]}{max}|{\displaystyle \frac{d^{\mathcal{N}+1}u\left(\eta \right)}{d{\mathfrak{Z}}^{\mathcal{N}+1}}}|,\eta \in [0,\mathcal{L}]$.

Proof. 

The author of [9] (the proof of Theorem 6.1) shows that if $u_{\mathcal{N}}\left(\mathfrak{Z}\right)$ is the interpolating polynomial for $u\left(\mathfrak{Z}\right)$ at the roots of ${\mathcal{V}}_{\mathcal{L},\mathcal{N}+1}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)$, then we obtain

$$\parallel u-u_{\mathcal{N}}{\parallel }_{\infty }\le \frac{\mathfrak{K}\mathcal{L}}{2^{\lambda }}{\left(\frac{e\mathcal{L}}{4}\right)}^{\mathcal{N}}{(\mathcal{N}+1)}^{s-\mathcal{N}-1},\mathcal{N}>s-1.$$

(52)

Now, consider the approximation $\mathfrak{X}\left(\mathfrak{Z}\right)\simeq {\mathcal{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^p{(\mathcal{L}-\mathfrak{Z})}^q{u}_{\mathcal{N}}\left(\mathfrak{Z}\right)$; in this case,

$$\parallel \mathfrak{X}-{\mathcal{X}}_{\mathcal{N}}{\parallel }_{\infty }\le \left(\underset{0\le \mathfrak{Z}\le \mathcal{L}}{max}{\mathfrak{Z}}^p{(\mathcal{L}-\mathfrak{Z})}^q\right){\parallel u-u_{\mathcal{N}}\parallel }_{\infty }.$$

(53)

It is not difficult to show that

$$\underset{0\le \mathfrak{Z}\le \mathcal{L}}{max}{\mathfrak{Z}}^p{(\mathcal{L}-\mathfrak{Z})}^q={\mathcal{L}}^{p+q}{\left(\frac{p}{p+q}\right)}^p{\left(\frac{q}{p+q}\right)}^q,$$

(54)

in which case using (52), (53) and (54) leads to

$$\parallel \mathfrak{X}-{\mathcal{X}}_{\mathcal{N}}{\parallel }_{\infty }\le \frac{\mathfrak{K}{\mathcal{L}}^{p+q+1}}{2^{\lambda }}{\left(\frac{p}{p+q}\right)}^p{\left(\frac{q}{p+q}\right)}^q{\left(\frac{e\mathcal{L}}{4}\right)}^{\mathcal{N}}{(\mathcal{N}+1)}^{s-\mathcal{N}-1}.$$

(55)

Because the approximate solution ${\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)\in {\mathfrak{S}}_{p,q,\mathcal{N}}$ represents the best possible approximation of $\mathfrak{X}\left(\mathfrak{Z}\right)$, we obtain

$$\parallel \mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}}{\parallel }_{\infty }\le {\parallel \mathfrak{X}-h\parallel }_{\infty },\forall h\in {\mathfrak{S}}_{p,q,\mathcal{N}}$$

(56)

and

$$\parallel \mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}}{\parallel }_2\le {\parallel \mathfrak{X}-h\parallel }_2,\forall h\in {\mathfrak{S}}_{p,q,\mathcal{N}}.$$

(57)

Therefore,

$$\parallel \mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}}{\parallel }_{\infty }\le {\parallel \mathfrak{X}-{\mathcal{X}}_{\mathcal{N}}\parallel }_{\infty }\le \frac{\mathfrak{K}{\mathcal{L}}^{p+q+1}}{2^{\lambda }}{\left(\frac{p}{p+q}\right)}^p{\left(\frac{q}{p+q}\right)}^q{\left(\frac{e\mathcal{L}}{4}\right)}^{\mathcal{N}}{(\mathcal{N}+1)}^{s-\mathcal{N}-1}$$

and

$$\begin{array}{cc}\hfill \parallel \mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}}{\parallel }_2\le {\parallel \mathfrak{X}-{\mathcal{X}}_{\mathcal{N}}\parallel }_2& \le {\mathcal{L}}^q{\parallel u-u_{\mathcal{N}}\parallel }_{\infty }{\left({\int }_0^{\mathcal{L}}{\mathfrak{Z}}^{2p}d\mathfrak{Z}\right)}^{1/2}\hfill \\ \hfill & \le \frac{\mathfrak{K}{\mathcal{L}}^{p+q+3/2}}{2^{\lambda }}{\left(\frac{p}{p+q}\right)}^p{\left(\frac{q}{p+q}\right)}^q{\left(\frac{e\mathcal{L}}{4}\right)}^{\mathcal{N}}{(\mathcal{N}+1)}^{s-\mathcal{N}-1}.\hfill \end{array}$$

□

The resulting error converges at a very fast rate, as shown by Corollary 2.

Corollary 2.

For all $\mathcal{N}>s-1$, we have

$$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }=\mathcal{O}\left({\left(0.7\right)}^{-\mathcal{N}}{\mathcal{L}}^{\mathcal{N}}{\mathcal{N}}^{s-\mathcal{N}-1}\right)$$

(58)

and

$$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2=\mathcal{O}\left({\left(0.7\right)}^{-\mathcal{N}}{\mathcal{L}}^{\mathcal{N}}{\mathcal{N}}^{s-\mathcal{N}-1}\right).$$

(59)

The stability of error, or the process of estimating the propagation of the error, is the focus of the subsequent theorem.

Theorem 6.

For any two successive approximations of $\mathfrak{X}\left(\mathfrak{Z}\right)$, we obtain

$$|{\mathfrak{X}}_{\mathcal{N}+1}-{\mathfrak{X}}_{\mathcal{N}}|\lesssim \mathcal{O}\left({\left(0.7\right)}^{-\mathcal{N}}{\mathcal{L}}^{\mathcal{N}}{\mathcal{N}}^{s-\mathcal{N}-1}\right),\mathcal{N}>s-1,$$

(60)

where ≲ means that a generic constant d exists such that $|{\mathfrak{X}}_{\mathcal{N}+1}-{\mathfrak{X}}_{\mathcal{N}}{|\le d(e\mathcal{L}/4)}^{\mathcal{N}}{\mathcal{N}}^{s-\mathcal{N}-1}$.

Proof. 

We have

$$|{\mathfrak{X}}_{\mathcal{N}+1}-{\mathfrak{X}}_{\mathcal{N}}|=|{\mathfrak{X}}_{\mathcal{N}+1}-\mathfrak{X}+\mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}}|\le |\mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}+1}|+|\mathfrak{X}-{\mathfrak{X}}_{\mathcal{N}}|\le \parallel {\mathfrak{e}}_{\mathcal{N}+1}{\parallel }_{\infty }+{\parallel {\mathfrak{e}}_{\mathcal{N}}\parallel }_{\infty }.$$

By considering (58), we can obtain (60). □

7. Numerical Simulations

In the current section, we present numerical simulations of BVPs as expressed in Equations (1) and (2). Both types share a common form of BC (3). In the following examples, we demonstrate the application of $GSJCOPMM$ to solve these BVPs. These numerical simulations provide insights into the behavior of the solutions and the accuracy of the proposed $GSJCOPMM$ algorithm. We aim to showcase the applicability, effectiveness, and efficiency of $GSJCOPMM$ in tackling these challenging BVPs. We provide eight examples to satisfy these aims; $\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$ and $\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$ are presented for evaluation purposes. Additionally, the order of convergence provided by the expression

$$R_{\mathcal{N}}\approx \frac{Log(\parallel {\mathfrak{e}}_{\mathcal{N}+1}{\parallel }_{\infty }/\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty })}{Log(\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }/\parallel {\mathfrak{e}}_{\mathcal{N}-1}{\parallel }_{\infty })},$$

(61)

is discussed.

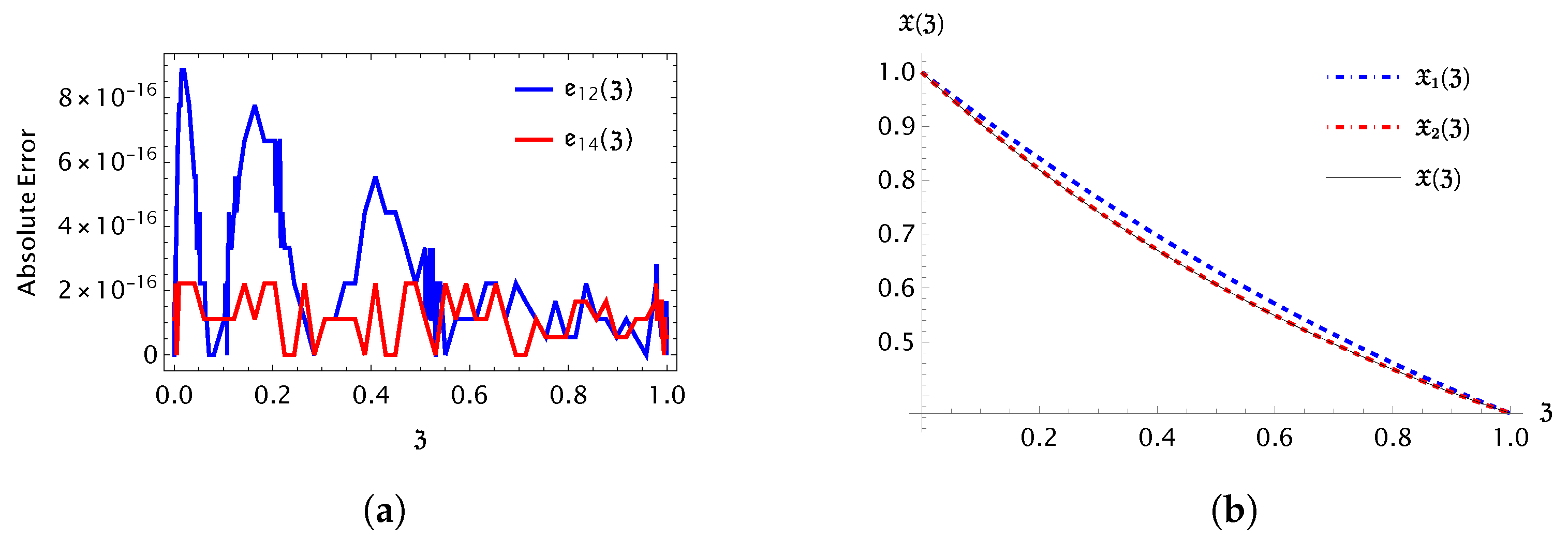
7.1. Numerical Simulations for Handling ODE (1) with BCs (3)

Problem 1.

Consider the differential equation

$$\begin{array}{ll}\hfill & {\mathcal{D}}^5\mathfrak{X}\left(\mathfrak{Z}\right)+{\mathfrak{Z}}^2{\left(\mathcal{D}\mathfrak{X}\left(\mathfrak{Z}\right)\right)}^2+\mathfrak{X}\left(\mathfrak{Z}\right)=g\left(\mathfrak{Z}\right),0\le \mathfrak{Z}\le 1,\\ \hfill & {\mathfrak{X}}^{\left(i\right)}\left(0\right)=0,i=0,1,2,3,\mathfrak{X}\left(1\right)=0,\end{array}\},$$

(62)

where $g\left(\mathfrak{Z}\right)$ is computed such that $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^4(1-\mathfrak{Z})$. Applying the $GSJCOPMM$ algorithm leads to

$${\displaystyle \mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\sum _{i=0}^{\mathcal{N}}{a}_i{\varphi }_{4,1,i}^{(0,0)}\left(\mathfrak{Z}\right),\mathcal{N}=0,1,2,3,4,}$$

where $a_0=1$ and $a_i=0,i\ne 0$.

Problem 2.

Consider the following nonlinear BVP of sixth order [36,37,38]:

$$\begin{array}{ll}\hfill & {\mathcal{D}}^6\mathfrak{X}\left(\mathfrak{Z}\right)=e^{\mathfrak{Z}}{\mathfrak{X}}^2\left(\mathfrak{Z}\right),0\le \mathfrak{Z}\le 1,\\ \hfill & {\mathfrak{X}}^{\left(i\right)}\left(0\right)={(-1)}^i,{\mathfrak{X}}^{\left(i\right)}\left(1\right)={(-1)}^i{e}^{-1},i=0,1,2,\end{array}\},$$

(63)

where $\mathfrak{X}\left(\mathfrak{Z}\right)=e^{-\mathfrak{Z}}$. Applying the $GSJCOPMM$ algorithm leads to

$${\displaystyle {\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\sum _{i=0}^{\mathcal{N}}{a}_i{\varphi }_{3,3,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+\left(-\frac{(7e-19)}{2e}{\mathfrak{Z}}^5-\frac{(46-17e)}{2e}{\mathfrak{Z}}^4-\frac{(11e-29)}{2e}{\mathfrak{Z}}^3+\frac{1}{2}{\mathfrak{Z}}^2-\mathfrak{Z}+1\right),}$$

which provides us with approximated solutions that match the exact solution with a precision of ${10}^{–17}$ at $\mathcal{N}=14$ for various $\mathfrak{a},\mathfrak{b}$ values, as shown in

Table 1. Computed errors in Example 2.

$\mathfrak{a}$	$\mathfrak{b}$	$\mathit{E}\mathit{r}\mathit{r}\mathit{o}\mathit{r}\mathit{s}$	$\mathcal{N}=2$	$\mathcal{N}=4$	$\mathcal{N}=6$	$\mathcal{N}=8$	$\mathcal{N}=12$	$\mathcal{N}=14$
0	0	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.3$\times {10}^{-3}$	1.5$\times {10}^{-6}$	2.9$\times {10}^{-9}$	2.7$\times {10}^{-12}$	1.7$\times {10}^{-15}$	5.5$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.1$\times {10}^{-3}$	1.4$\times {10}^{-6}$	2.5$\times {10}^{-9}$	2.4$\times {10}^{-12}$	1.6$\times {10}^{-15}$	2.4$\times {10}^{-16}$
		$R_{\mathcal{N}}$	1.10	1.12	1.66	1.89	1.92	1.87
1	0	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.4$\times {10}^{-3}$	1.6$\times {10}^{-6}$	1.7$\times {10}^{-9}$	1.9$\times {10}^{-12}$	1.2$\times {10}^{-15}$	4.5$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.1$\times {10}^{-3}$	1.2$\times {10}^{-6}$	1.4$\times {10}^{-9}$	1.0$\times {10}^{-12}$	1.1$\times {10}^{-15}$	2.5$\times {10}^{-16}$
		$R_{\mathcal{N}}$	1.11	1.02	1.46	1.79	1.82	1.75
0	2	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.5$\times {10}^{-3}$	1.4$\times {10}^{-6}$	2.5$\times {10}^{-9}$	1.8$\times {10}^{-12}$	1.4$\times {10}^{-15}$	4.2$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.0$\times {10}^{-3}$	1.3$\times {10}^{-6}$	2.1$\times {10}^{-9}$	1.5$\times {10}^{-12}$	1.2$\times {10}^{-15}$	3.1$\times {10}^{-16}$
		$R_{\mathcal{N}}$	1.08	1.13	1.56	1.79	1.81	1.77
−1/2	1/2	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.2$\times {10}^{-3}$	1.2$\times {10}^{-6}$	2.3$\times {10}^{-9}$	2.4$\times {10}^{-12}$	1.6$\times {10}^{-15}$	7.1$\times {10}^{-17}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.1$\times {10}^{-3}$	1.1$\times {10}^{-6}$	2.1$\times {10}^{-9}$	2.2$\times {10}^{-12}$	1.1$\times {10}^{-15}$	6.2$\times {10}^{-17}$
		$R_{\mathcal{N}}$	1.12	1.23	1.46	1.69	1.71	1.69
1/2	1/2	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	6.1$\times {10}^{-3}$	4.2$\times {10}^{-6}$	3.4$\times {10}^{-9}$	4.5$\times {10}^{-12}$	1.2$\times {10}^{-15}$	8.4$\times {10}^{-17}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	2.5$\times {10}^{-3}$	1.4$\times {10}^{-6}$	1.2$\times {10}^{-9}$	2.7$\times {10}^{-12}$	1.0$\times {10}^{-15}$	7.2$\times {10}^{-17}$
		$R_{\mathcal{N}}$	1.03	1.33	1.62	1.72	1.79	1.71

.

Table 2. A comparison of approaches [36,37,38] and $GSJCOPMM$ for Example 2 using $\mathfrak{a}=\mathfrak{b}=1$.

$\mathfrak{Z}$	$\mathit{G}\mathit{S}\mathit{J}\mathit{C}\mathit{O}\mathit{P}\mathit{M}\mathit{M} (\mathcal{N}=6)$	[38] $(\mathcal{N}=12)$	[36] $(\mathcal{N}=12)$	[37] $(\mathcal{N}=12)$
0.0	0.0	0.0	0.0	0.0
0.1	1.2$\times {10}^{-12}$	4.1$\times {10}^{-12}$	2.3$\times {10}^{-7}$	1.2$\times {10}^{-4}$
0.2	2.0$\times {10}^{-11}$	2.5$\times {10}^{-11}$	1.3$\times {10}^{-6}$	2.3$\times {10}^{-4}$
0.3	5.5$\times {10}^{-12}$	6.3$\times {10}^{-11}$	3.3$\times {10}^{-6}$	3.2$\times {10}^{-4}$
0.4	1.6$\times {10}^{-11}$	1.0$\times {10}^{-10}$	5.2$\times {10}^{-6}$	3.8$\times {10}^{-4}$
0.5	2.7$\times {10}^{-11}$	1.3$\times {10}^{-10}$	6.1$\times {10}^{-6}$	4.0$\times {10}^{-4}$
0.6	1.2$\times {10}^{-11}$	1.3$\times {10}^{-10}$	5.7$\times {10}^{-6}$	3.9$\times {10}^{-4}$
0.7	1.4$\times {10}^{-11}$	1.0$\times {10}^{-10}$	4.0$\times {10}^{-6}$	3.3$\times {10}^{-4}$
0.8	1.5$\times {10}^{-12}$	5.2$\times {10}^{-11}$	1.9$\times {10}^{-6}$	2.4$\times {10}^{-4}$
0.9	1.7$\times {10}^{-12}$	1.0$\times {10}^{-11}$	3.5$\times {10}^{-6}$	1.2$\times {10}^{-4}$
1.0	0.0	2.1$\times {10}^{-17}$	5.0$\times {10}^{-10}$	2.0$\times {10}^{-9}$

presents a comparison between GSJCOPMM and the three methods in [36,37,38]. Figure 1 presents the computed errors and approximate solutions. Based on the given orders of convergence $R_{\mathcal{N}}$, it is apparent see that the convergence rate improves as $\mathcal{N}$ increases; a higher order of convergence means that the error goes down faster.

Problem 3.

Consider the following self-adjoint singularly perturbed singular BVP [39,40]:

$$\begin{array}{ll}\hfill & \epsilon {\mathfrak{X}}^{\left(3\right)}\left(\mathfrak{Z}\right)+{\displaystyle \frac{1}{\mathfrak{Z}}}{\mathfrak{X}}^{\left(2\right)}\left(\mathfrak{Z}\right)+\mathfrak{X}\left(\mathfrak{Z}\right)=3\epsilon \left(sin3\mathfrak{Z}-27\epsilon cos3\mathfrak{Z}-\frac{9}{\mathfrak{Z}}sin3\mathfrak{Z}\right),0\le \mathfrak{Z}\le 1,\\ \hfill & \mathfrak{X}\left(0\right)=0,{\mathfrak{X}}^{\left(1\right)}\left(0\right)=9\epsilon ,\mathfrak{X}\left(1\right)=3\epsilon sin3,\end{array}\}$$

(64)

for which the exact solution is $\mathfrak{X}\left(\mathfrak{Z}\right)=3\epsilon sin3\mathfrak{Z}$. Applying the $GSJCOPMM$ algorithm leads to

$${\displaystyle {\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\sum _{i=0}^{\mathcal{N}}{a}_i{\varphi }_{2,1,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+3\epsilon ((sin3)\mathfrak{Z}-3\mathfrak{Z}+3)\mathfrak{Z}.}$$

Table 3. Computed MAE in Example 3.

$\mathcal{N}$	$\mathfrak{a}$	$\mathfrak{b}$	$\mathit{\epsilon }$	2−4	2−6	2−8	2−10	2−12	2−14	2−16	2−18	2−20
3	0	3		6.9$\times {10}^{-4}$	5.4$\times {10}^{-4}$	4.4$\times {10}^{-4}$	1.1$\times {10}^{-4}$	2.2$\times {10}^{-5}$	6.8$\times {10}^{-6}$	1.7$\times {10}^{-7}$	4.2$\times {10}^{-8}$	1.7$\times {10}^{-8}$
8				7.8$\times {10}^{-10}$	6.3$\times {10}^{-10}$	3.1$\times {10}^{-11}$	7.7$\times {10}^{-12}$	1.9$\times {10}^{-13}$	4.8$\times {10}^{-14}$	1.2$\times {10}^{-14}$	3.0$\times {10}^{-15}$	7.5$\times {10}^{-15}$
10				8.9$\times {10}^{-13}$	1.4$\times {10}^{-14}$	3.0$\times {10}^{-15}$	8.4$\times {10}^{-16}$	2.1$\times {10}^{-16}$	5.3$\times {10}^{-17}$	1.3$\times {10}^{-17}$	2.8$\times {10}^{-18}$	8.0$\times {10}^{-18}$
12				6.5$\times {10}^{-16}$	2.5$\times {10}^{-17}$	2.0$\times {10}^{-17}$	1.8$\times {10}^{-17}$	1.5.0$\times {10}^{-17}$	1.1$\times {10}^{-17}$	5.3$\times {10}^{-18}$	3.0$\times {10}^{-18}$	1.6$\times {10}^{-19}$
3	3	0		6.8$\times {10}^{-4}$	6.2$\times {10}^{-4}$	4.4$\times {10}^{-4}$	1.1$\times {10}^{-4}$	2.2$\times {10}^{-5}$	6.8$\times {10}^{-6}$	1.7$\times {10}^{-7}$	4.2$\times {10}^{-8}$	1.7$\times {10}^{-8}$
8				7.5$\times {10}^{-10}$	6.2$\times {10}^{-10}$	3.3$\times {10}^{-11}$	7.5$\times {10}^{-12}$	2.9$\times {10}^{-13}$	3.8$\times {10}^{-14}$	2.2$\times {10}^{-14}$	3.1$\times {10}^{-15}$	4.5$\times {10}^{-15}$
10				8.7$\times {10}^{-13}$	1.3$\times {10}^{-14}$	3.1$\times {10}^{-15}$	7.7$\times {10}^{-16}$	1.9$\times {10}^{-16}$	4.8$\times {10}^{-17}$	1.2$\times {10}^{-17}$	3.0$\times {10}^{-18}$	7.5$\times {10}^{-19}$
12				6.4$\times {10}^{-16}$	2.3$\times {10}^{-17}$	3.1$\times {10}^{-17}$	1.4$\times {10}^{-17}$	1.1$\times {10}^{-17}$	1.0$\times {10}^{-17}$	5.3$\times {10}^{-18}$	2.8$\times {10}^{-18}$	8.0$\times {10}^{-19}$
3	3.5	0.5		6.5$\times {10}^{-4}$	5.6$\times {10}^{-4}$	5.0$\times {10}^{-4}$	1.2$\times {10}^{-4}$	2.3$\times {10}^{-5}$	6.7$\times {10}^{-6}$	1.8$\times {10}^{-7}$	3.1$\times {10}^{-8}$	2.7$\times {10}^{-8}$
8				7.5$\times {10}^{-10}$	6.1$\times {10}^{-10}$	3.2$\times {10}^{-11}$	7.5$\times {10}^{-12}$	1.8$\times {10}^{-13}$	3.5$\times {10}^{-14}$	1.7$\times {10}^{-14}$	3.1$\times {10}^{-15}$	7.2$\times {10}^{-15}$
10				8.8$\times {10}^{-13}$	2.4$\times {10}^{-14}$	3.3$\times {10}^{-15}$	7.4$\times {10}^{-16}$	2.5$\times {10}^{-16}$	5.5$\times {10}^{-17}$	1.7$\times {10}^{-17}$	1.5$\times {10}^{-18}$	1.2$\times {10}^{-18}$
12				6.0$\times {10}^{-16}$	4.5$\times {10}^{-17}$	4.1$\times {10}^{-17}$	2.8$\times {10}^{-17}$	1.40$\times {10}^{-17}$	1.2$\times {10}^{-17}$	6.3$\times {10}^{-18}$	3.5$\times {10}^{-18}$	2.6$\times {10}^{-19}$
5	6	1		8.1$\times {10}^{-5}$	7.5$\times {10}^{-5}$	7.2$\times {10}^{-5}$	4.1$\times {10}^{-6}$	2.2$\times {10}^{-6}$	6.8$\times {10}^{-7}$	1.7$\times {10}^{-7}$	4.2$\times {10}^{-8}$	1.7$\times {10}^{-8}$
10				7.0$\times {10}^{-11}$	5.3$\times {10}^{-11}$	3.1$\times {10}^{-11}$	7.7$\times {10}^{-12}$	1.9$\times {10}^{-13}$	4.8$\times {10}^{-13}$	1.2$\times {10}^{-14}$	3.0$\times {10}^{-14}$	7.5$\times {10}^{-15}$
12				8.5$\times {10}^{-14}$	6.4$\times {10}^{-14}$	5.1$\times {10}^{-14}$	8.4$\times {10}^{-15}$	2.1$\times {10}^{-16}$	5.3$\times {10}^{-16}$	1.3$\times {10}^{-17}$	2.8$\times {10}^{-17}$	8.0$\times {10}^{-18}$
14				6.6$\times {10}^{-17}$	6.2$\times {10}^{-17}$	5.3$\times {10}^{-17}$	4.1$\times {10}^{-17}$	5.0$\times {10}^{-18}$	4.7$\times {10}^{-18}$	5.3$\times {10}^{-18}$	3.00$\times {10}^{-18}$	1.6$\times {10}^{-19}$

displays the MAE for some values of $\mathfrak{a},\mathfrak{b}$, $\mathcal{N}$, and ε, while

Table 4. Comparison of approaches [39,40] and $GSJCOPMM$ for Example 3 using $\mathfrak{a}=4,\mathfrak{b}=1$.

$\mathcal{N}$	$\mathit{\epsilon }$	2−4	2−6	2−8	2−10	2−12	2−14	2−16	2−18	2−20
12	GSJCOPMM	2.0$\times {10}^{-15}$	4.3$\times {10}^{-16}$	3.9$\times {10}^{-17}$	2.1$\times {10}^{-17}$	1.5$\times {10}^{-17}$	1.3$\times {10}^{-17}$	5.5$\times {10}^{-18}$	3.4$\times {10}^{-18}$	4.1$\times {10}^{-19}$
128	QBSM [39]	2.1$\times {10}^{-7}$	1.7$\times {10}^{-8}$	1.2$\times {10}^{-9}$	7.5$\times {10}^{-11}$	5.2$\times {10}^{-12}$	4.6$\times {10}^{-13}$	6.8$\times {10}^{-14}$	1.5$\times {10}^{-14}$	3.6$\times {10}^{-15}$
128	NCBS [40]	3.5$\times {10}^{-9}$	2.0$\times {10}^{-10}$	5.5$\times {10}^{-12}$	1.5$\times {10}^{-12}$	5.4$\times {10}^{-13}$	1.5$\times {10}^{-13}$	3.7$\times {10}^{-14}$	9.2$\times {10}^{-15}$	2.3$\times {10}^{-15}$

displays a comparison between the $GSJCOPMM$, QBSM [39], and NCBS methods [40]. Figure 2a shows ${\mathfrak{e}}_{12}\left(\mathfrak{Z}\right)$ at $\epsilon =2^{-16},2^{-18}$. In addition, Figure 2b shows the log-errors for various $\mathcal{N}$ and $\epsilon =2^{-4},2^{-8},2^{-16}$. This shows that the solutions are stable and converging.

Problem 4.

For one-dimensional Bratu’s problems [41]

$$\begin{array}{ll}\hfill & {\mathfrak{X}}^{\left(2\right)}\left(\mathfrak{Z}\right)+\lambda e^{\mathfrak{X}\left(\mathfrak{Z}\right)}=0,\lambda \in \mathbb{R},0\le \mathfrak{Z}\le 1,\\ \hfill & \mathfrak{X}\left(0\right)=0,{\mathfrak{X}}^{\left(1\right)}\left(0\right)=0,\end{array}\}$$

(65)

with the exact solution in the form from [42] (Equation 47), we have

$$\mathfrak{X}\left(\mathfrak{Z}\right)=-2ln\left[\frac{cosh\left(\frac{\theta }{2}(\mathfrak{Z}-\frac{1}{2})\right)}{cosh\left(\frac{\theta }{4}\right)}\right],$$

(66)

where θ satisfies $\theta =\sqrt{2\lambda }cosh\left(\frac{\theta }{4}\right)$. Bratu’s problems have either no solution, one solution, or two solutions, respectively, when $\lambda >{\lambda }_c,\lambda ={\lambda }_c,$ or $\lambda <{\lambda }_c,$ where ${\lambda }_c=3.513830719$. The relations between λ and θ for some values of $\lambda <{\lambda }_c$ are provided in [42] (Table 1).

Application of $GSJCOPMM$ leads to the obtained approximated solutions matching the exact solution with a precision of ${10}^{–16}$ at $\mathcal{N}=14$ for various $\mathfrak{a},\mathfrak{b}$ values, as shown in

Table 5. Computed errors in Example 4 when $\lambda =0.5$.

$\mathfrak{a}$	$\mathfrak{b}$	$\mathit{E}\mathit{r}\mathit{r}\mathit{o}\mathit{r}\mathit{s}$	$\mathcal{N}=2$	$\mathcal{N}=4$	$\mathcal{N}=6$	$\mathcal{N}=8$	$\mathcal{N}=12$	$\mathcal{N}=14$
0	0	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.1$\times {10}^{-3}$	1.4$\times {10}^{-6}$	3.0$\times {10}^{-9}$	3.5$\times {10}^{-12}$	2.8$\times {10}^{-15}$	5.9$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.0$\times {10}^{-3}$	1.2$\times {10}^{-6}$	2.4$\times {10}^{-9}$	2.2$\times {10}^{-12}$	1.4$\times {10}^{-15}$	2.1$\times {10}^{-16}$
1	0	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.1$\times {10}^{-3}$	1.5$\times {10}^{-6}$	1.8$\times {10}^{-9}$	1.7$\times {10}^{-12}$	1.3$\times {10}^{-15}$	4.4$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.3$\times {10}^{-3}$	1.1$\times {10}^{-6}$	1.2$\times {10}^{-9}$	1.1$\times {10}^{-12}$	1.2$\times {10}^{-15}$	2.4$\times {10}^{-16}$
0	2	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.4$\times {10}^{-3}$	1.2$\times {10}^{-6}$	2.6$\times {10}^{-9}$	1.7$\times {10}^{-12}$	1.3$\times {10}^{-15}$	4.3$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.1$\times {10}^{-3}$	1.4$\times {10}^{-6}$	2.2$\times {10}^{-9}$	1.6$\times {10}^{-12}$	1.3$\times {10}^{-15}$	3.2$\times {10}^{-17}$
−1/2	1/2	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	1.3$\times {10}^{-3}$	1.1$\times {10}^{-6}$	2.2$\times {10}^{-9}$	2.3$\times {10}^{-12}$	1.4$\times {10}^{-15}$	6.2$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.2$\times {10}^{-3}$	1.0$\times {10}^{-6}$	2.2$\times {10}^{-9}$	2.3$\times {10}^{-12}$	1.3$\times {10}^{-15}$	5.2$\times {10}^{-17}$
1/2	1/2	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	5.9$\times {10}^{-3}$	4.1$\times {10}^{-6}$	3.3$\times {10}^{-9}$	5.5$\times {10}^{-12}$	1.3$\times {10}^{-15}$	7.5$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	2.4$\times {10}^{-3}$	1.5$\times {10}^{-6}$	1.3$\times {10}^{-9}$	2.6$\times {10}^{-12}$	1.1$\times {10}^{-15}$	6.2$\times {10}^{-17}$

. According to Tables 1 and 2 presented in [41],

Table 6. A comparison of approaches [41] and $GSJCOPMM$ for Example 4 $(\lambda =0.5)$ using $\mathfrak{a}=\mathfrak{b}=1$ and $\mathcal{N}=10$.

$\mathfrak{Z}$	$\mathit{G}\mathit{S}\mathit{J}\mathit{C}\mathit{O}\mathit{P}\mathit{M}\mathit{M}$	Scheme (15) $(\mathit{n}=3)$ [41]	Scheme (16)a [41]	Scheme (16)b [41]
0.0	0.0	0.0	0.0	0.0
0.1	1.2$\times {10}^{-17}$	2.2899$\times {10}^{-14}$	3.0786$\times {10}^{-5}$	1.3850$\times {10}^{-7}$
0.2	2.0$\times {10}^{-17}$	1.7382$\times {10}^{-14}$	5.4900$\times {10}^{-5}$	4.1545$\times {10}^{-7}$
0.3	5.5$\times {10}^{-17}$	1.5430$\times {10}^{-14}$	7.2214$\times {10}^{-5}$	7.0764$\times {10}^{-7}$
0.4	1.6$\times {10}^{-16}$	1.3721$\times {10}^{-14}$	8.2639$\times {10}^{-5}$	9.2180$\times {10}^{-7}$
0.5	2.7$\times {10}^{-16}$	1.3222$\times {10}^{-14}$	8.6120$\times {10}^{-5}$	9.9977$\times {10}^{-7}$
0.6	1.2$\times {10}^{-16}$	1.3721$\times {10}^{-14}$	8.2639$\times {10}^{-5}$	9.2180$\times {10}^{-7}$
0.7	1.4$\times {10}^{-17}$	1.5430$\times {10}^{-14}$	7.2214$\times {10}^{-5}$	7.0764$\times {10}^{-7}$
0.8	1.5$\times {10}^{-17}$	1.7382$\times {10}^{-14}$	5.4900$\times {10}^{-5}$	4.1545$\times {10}^{-7}$
0.9	1.7$\times {10}^{-17}$	2.2899$\times {10}^{-14}$	3.0786$\times {10}^{-5}$	1.3850$\times {10}^{-7}$
1.0	0.0	0.0000	0.0000	0.0000
CPU Time	0.61 s	1.63 s	1.59 s	1.69 s

presents a comparison between the absolute errors obtained by the $GSJCOPMM$ method and the three Schemes(15), (16)a, and (16)b in [41] as well as a computational time (CPU time) comparison between $GSJCOPMM$ and the three finite difference Schemes(15), (16)a, and (16)b.

Remark 1.

It is important to note that the comparison of the computational time of the numerical method of $GSJCOPMM$ with the finite difference methods shown in Example 4 shows that $GSJCOPMM$ is faster; however, this result cannot be generalized, as the computational time may vary depending on the problem, the complexity of the equations, and the implementation details.

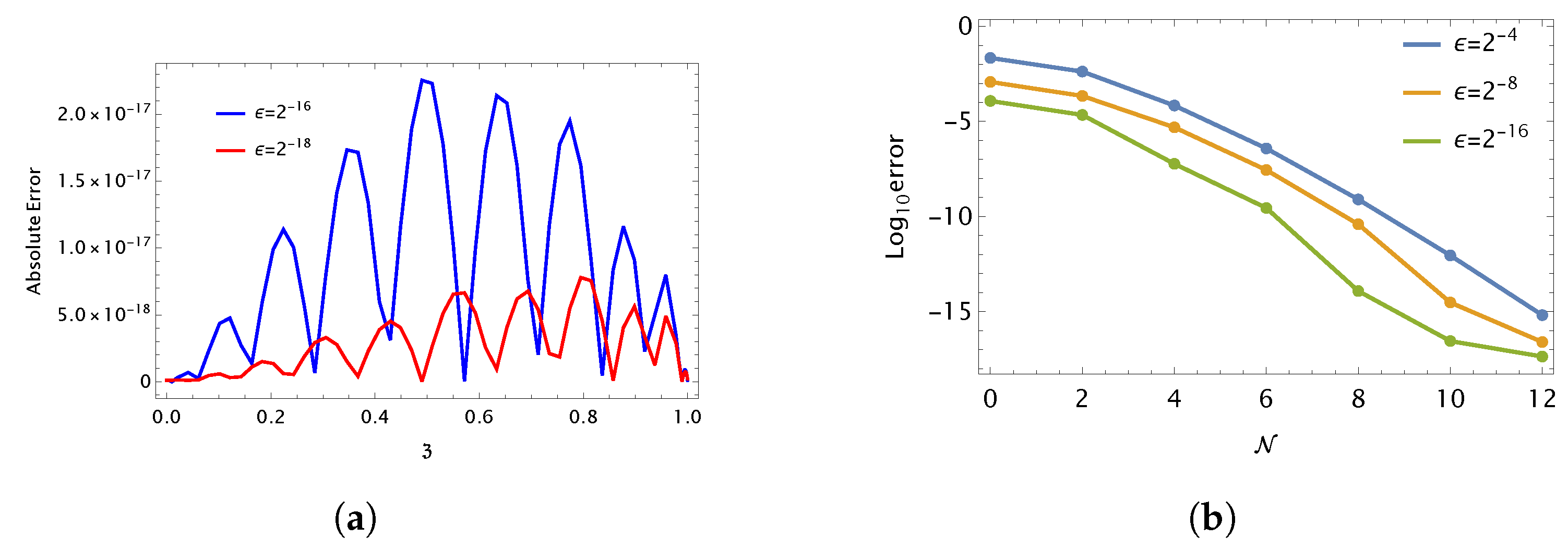
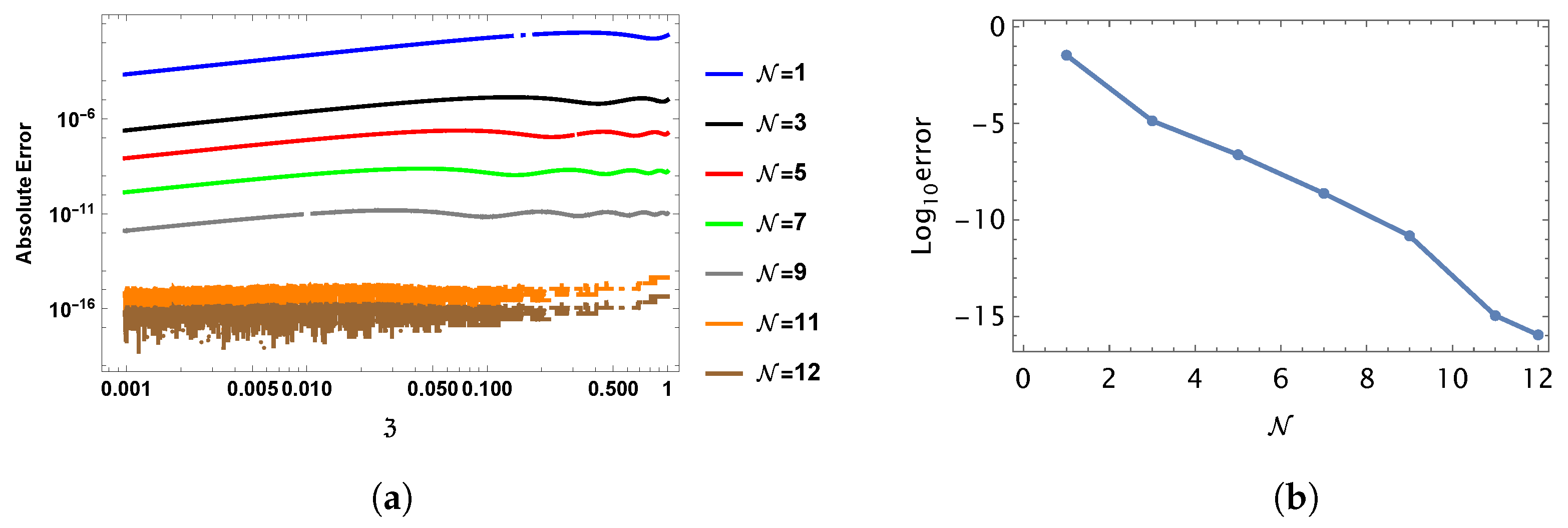
7.2. Numerical Simulations for Handling VOFDE (2) with BCs (3)

Problem 5.

Consider the boundary Bagely–Torvik equation [10,43]

$$\begin{array}{ll}\hfill & {\mathcal{D}}^2\mathfrak{X}\left(\mathfrak{Z}\right)+{\mathcal{D}}^{3/2}\mathfrak{X}\left(\mathfrak{Z}\right)+\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^2+2+4\sqrt{\frac{\mathfrak{Z}}{\pi }},0\le \mathfrak{Z}\le \mathcal{L},\\ \hfill & \mathfrak{X}\left(0\right)=0,\mathfrak{X}\left(\mathcal{L}\right)={\mathcal{L}}^2,\end{array}\}$$

(67)

for which the exact solution is $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^2$. Applying $GSJCOPMM$ leads to

$${\displaystyle \mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\sum _{i=0}^{\mathcal{N}}{a}_i{\varphi }_{1,1,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+\mathcal{L}\mathfrak{Z},\mathcal{N}=0,1,2,\dots ,6,}$$

where $a_0=-1$ and $a_i=0,i\ne 0$.

Remark 2.

It is worth noting that $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{X}}_0\left(\mathfrak{Z}\right),\mathfrak{a},\mathfrak{b}>-1$, while according to the author of [10], at $\mathcal{L}=1$ we obtain $\mathfrak{X}\left(\mathfrak{Z}\right)$ using $\mathcal{N}=2$. Furthermore, the authors of [43] achieved the best error of $3.78\times {10}^{-12}$ at $\mathcal{L}=5$.

Problem 6.

Consider the equation [44,45]:

$$\begin{array}{ll}\hfill & {\mathcal{D}}^{\delta \left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)+cos\left(\mathfrak{Z}\right)\mathcal{D}\mathfrak{X}\left(\mathfrak{Z}\right)+4\mathfrak{X}\left(\mathfrak{Z}\right)+5\mathfrak{X}\left({\mathfrak{Z}}^2\right)={\displaystyle \frac{2{\mathfrak{Z}}^{2-\delta \left(\mathfrak{Z}\right)}}{\Gamma (3-\delta (\mathfrak{Z}\left)\right)}}+5{\mathfrak{Z}}^4+4{\mathfrak{Z}}^2+2tcos\left(\mathfrak{Z}\right),0\le \mathfrak{Z}\le 1,\\ \hfill & \mathfrak{X}\left(0\right)=0,\mathfrak{X}\left(1\right)=1,\end{array}\}$$

(68)

with the exact solution $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^2$, where $\delta \left(\mathfrak{Z}\right)=\frac{1}{4}(sin\left(\mathfrak{Z}\right)+5)$. Applying $GSJCOPMM$ using $\mathcal{N}=0$ yields

$$\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{X}}_0\left(\mathfrak{Z}\right)=-{\varphi }_{1,1,0}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right)+\mathfrak{Z}.$$

Remark 3.

It is worth noting that $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{X}}_0\left(\mathfrak{Z}\right),\mathfrak{a},\mathfrak{b}>-1$, while according to the author of [44]$\mathfrak{X}\left(\mathfrak{Z}\right)$ is obtained using $\mathcal{N}=2$. Furthermore, the authors of [45] achieved the best error of $6.15064\times {10}^{-14}$.

Problem 7.

Consider the nonlinear differential equation

$$\begin{array}{ll}\hfill & {\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)+\mathfrak{Z}\mathfrak{X}\left(\mathfrak{Z}\right)\mathcal{D}\mathfrak{X}\left(\mathfrak{Z}\right)-4{\mathfrak{Z}}^3\mathfrak{X}\left(\mathfrak{Z}\right)={\displaystyle \frac{24{\mathfrak{Z}}^{4-\mu \left(\mathfrak{Z}\right)}}{\Gamma (5-\mu (\mathfrak{Z}\left)\right)}}+4{\mathfrak{Z}}^8-4{\mathfrak{Z}}^7,0\le \mathfrak{Z}\le 1,\\ \hfill & \mathfrak{X}\left(0\right)=0,\mathrm{and}\mathfrak{X}\left(1\right)=1,\end{array}\},$$

(69)

where $\mu \left(\mathfrak{Z}\right)=2\mathfrak{Z}$. The exact solution is $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^4$. Applying $GSJCOPMM$ using $\mathcal{N}=2$ yields

$${\displaystyle \mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{X}}_2\left(\mathfrak{Z}\right)=\sum _{i=0}^2{a}_i{\varphi }_{1,1,i}^{(1,1)}\left(\mathfrak{Z}\right)+\mathfrak{Z},}$$

where $a_0=-\frac{9}{5},a_1=-\frac{1}{2},a_2=-\frac{1}{15}$.

Problem 8.

Consider the nonlinear BVP

$$\begin{array}{ll}\hfill & {\mathcal{D}}^{\mu \left(\mathfrak{Z}\right)}\mathfrak{X}\left(\mathfrak{Z}\right)+sin\left(\mathfrak{Z}\right){\left(\mathfrak{X}\left(\mathfrak{Z}\right)\right)}^2=g\left(\mathfrak{Z}\right),5<\mu \left(\mathfrak{Z}\right)<6,0\le \mathfrak{Z}\le 1,\\ \hfill & {\mathfrak{X}}^{\left(i\right)}\left(0\right)=0,i=0,1,2,3,\mathfrak{X}\left(1\right)=0,{\mathfrak{X}}^{\left(1\right)}\left(1\right)=0,\mu \left(\mathfrak{Z}\right)=5+0.5e^{-\mathfrak{Z}},\end{array}\},$$

(70)

where $g\left(\mathfrak{Z}\right)$ is computed such that $\mathfrak{X}\left(\mathfrak{Z}\right)={\mathfrak{Z}}^4{(1-\mathfrak{Z})}^2{e}^{-\mathfrak{Z}}$. Applying the $GSJCOPMM$ algorithm leads to

$${\displaystyle {\mathfrak{X}}_{\mathcal{N}}\left(\mathfrak{Z}\right)=\sum _{i=0}^{\mathcal{N}}{a}_i{\varphi }_{4,2,i}^{(\mathfrak{a},\mathfrak{b})}\left(\mathfrak{Z}\right).}$$

Table 7. Computed errors in Example 8.

$\mathfrak{a}$	$\mathfrak{b}$	$\mathit{E}\mathit{r}\mathit{r}\mathit{o}\mathit{r}\mathit{s}$	$\mathcal{N}=3$	$\mathcal{N}=5$	$\mathcal{N}=7$	$\mathcal{N}=9$	$\mathcal{N}=11$	$\mathcal{N}=12$
4.5	2.5	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	5.3$\times {10}^{-5}$	7.5$\times {10}^{-7}$	3.9$\times {10}^{-9}$	6.7$\times {10}^{-12}$	5.7$\times {10}^{-15}$	2.5$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	3.1$\times {10}^{-5}$	3.2$\times {10}^{-7}$	3.5$\times {10}^{-9}$	4.6$\times {10}^{-12}$	4.6$\times {10}^{-15}$	1.4$\times {10}^{-16}$
4	3	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	2.6$\times {10}^{-5}$	1.3$\times {10}^{-7}$	1.3$\times {10}^{-9}$	2.6$\times {10}^{-12}$	2.8$\times {10}^{-15}$	7.7$\times {10}^{-17}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	1.1$\times {10}^{-5}$	1.1$\times {10}^{-7}$	1.0$\times {10}^{-9}$	2.1$\times {10}^{-12}$	2.6$\times {10}^{-15}$	6.4$\times {10}^{-17}$
2.5	4.5	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	5.2$\times {10}^{-5}$	7.1$\times {10}^{-7}$	3.5$\times {10}^{-9}$	6.1$\times {10}^{-12}$	7.1$\times {10}^{-15}$	2.2$\times {10}^{-16}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	3.1$\times {10}^{-5}$	3.2$\times {10}^{-7}$	3.4$\times {10}^{-9}$	4.6$\times {10}^{-12}$	4.6$\times {10}^{-15}$	1.4$\times {10}^{-16}$
3	4	$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$	2.3$\times {10}^{-5}$	3.2$\times {10}^{-7}$	1.2$\times {10}^{-9}$	2.5$\times {10}^{-12}$	1.7$\times {10}^{-15}$	7.1$\times {10}^{-17}$
		$\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$	2.2$\times {10}^{-5}$	1.2$\times {10}^{-7}$	1.0$\times {10}^{-9}$	2.2$\times {10}^{-12}$	1.2$\times {10}^{-15}$	2.4$\times {10}^{-17}$

displays the computed errors $\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty }$ and $\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_2$ for some values of $\mathfrak{a},\mathfrak{b}$, and $\mathcal{N}$. The two figures in Figure 3a,b show ${\mathfrak{e}}_{\mathcal{N}}\left(\mathfrak{Z}\right)$ and $Lo{g}_{10}(\parallel {\mathfrak{e}}_{\mathcal{N}}{\parallel }_{\infty })$ for various $\mathcal{N}$, respectively. This shows that the solutions are stable and converging.

8. Conclusions

Our study has introduced a novel and efficient numerical approach for solving problems involving ODEs and VOFDEs associated with BCs. The main achievements of our research can be summarized as follows:

(i)

We have established a solid theoretical foundation by constructing OMs and incorporating them into the SCM. This framework allows for reliable and precise numerical computation of solutions to problems described by the aforementioned ODEs and VOFDEs with BCs.

(ii)

Extensive error analysis and convergence studies have been conducted, providing theoretical guarantees for the effectiveness and reliability of our proposed method, known as GSJCOPMM.

Our research has significant implications, as GSJCOPMM provides several advantages over existing approaches for solving ODEs and VOFDEs with BCs. First, GSJPs ensure that the given BCs are satisfied, resulting in improved numerical solution accuracy. Second, the developed OMs and their implementation within the SCM enable efficient computations, reducing computational costs while maintaining high accuracy. These features make GSJCOPMM particularly well suited for solving complex problems encountered in various scientific and engineering fields.

The potential applications of our proposed method are broad, encompassing a wide range of problems involving ODEs and VOFDEs. Our proposed method has a broad range of potential applications involving PDEs, systems of ODEs and VOFDEs in thhe mathematical modeling of physical systems, heat transfer, boundary layer problems in fluid mechanics, the motion of mass–spring systems, reaction rates, and other phenomena characterized by these models. In conclusion, this research contributes significantly to the advancement of numerical methods for ODEs and VOFDEs with BCs, providing an efficient and accurate approach for solving complex boundary value problems. The establishment of a theoretical foundation together with the demonstrated advantages of GSJCOPMM opens up new avenues for tackling challenging problems in various scientific and engineering domains.