Abstract
The impact of fabric anisotropy, fractal dimension, and breakage on the strength and deformation of granular materials were diminished by uniform-size spherical glass beads. Triaxial drained and undrained tests were performed on glass beads based on a novel method to substitute true triaxial stress paths with conventional triaxial apparatus equivalents with varying intermediate principal stress coefficients (b-values). The result indicates that all specimens manifested a noticeable strain-softening phenomenon. The peak strength decreased with increasing b-value, and the specimens showed more pronounced dilatancy. This pattern is similar to the results of the true triaxial test in current research. Compared to the undrained test, the peak friction angle in the drained test displayed a greater variation with varying b-values, which indicated that the mechanical response of glass beads is sensitive to water. This difference provides experimental evidence for comprehending effective stress in granular materials with constant friction coefficients. The experiments reflect the effect of b-value changes on the p-q stress path, as well as on the peak stress ratio, the state transition stress ratio, and the critical state stress ratio. The specimens exhibited a distinct shear band at different b-values ranging from 0.2 to 0.6, which is different from observations in conventional triaxial tests for granular materials.
1. Introduction
Particle morphology and its fabric determine the mechanical evolution mechanism of granular materials from a microscopic perspective, and the mechanical properties of macroscopic particle aggregates often require the fractal characteristics of particle morphology to reveal their cross-scale relationships. Granular materials play a crucial role and are widely used in road, hydraulic, and civil engineering projects, such as the treatment of foundations and subgrades [1], the control of dynamic and static deformation for rockfill dams [2], the disaster prevention and mitigation of underground buildings [3], and other engineering practices. The three-dimensional mechanical characteristics of granular materials also have significant implications for the safety and reliability of engineering projects. Granular materials are usually aggregates consisting of a large number of discrete particles. The shape, size distribution, and fabric of individual particles significantly influence the macroscopic, three-dimensional mechanical characteristics of granules. The diversity and discreteness of natural particles lead to complex mechanical characteristics [4,5,6], including significant nonlinearity, elastoplasticity, dilatancy, stress-path dependence, anisotropy, etc. Liquification and strain localization are two other phenomena that occur throughout the failure phase, further contributing to the complexity of the mechanical characteristics. Marschi et al. [7] mainly focused on the influence of stress state, path, and particle size distribution on the strength and deformation of granular materials. In recent years, more scholars have focused on low-pressure breakage and its indicators, the natural morphology of microparticles and their fabric characteristics [8,9,10,11,12,13,14,15,16,17,18,19], the effect of breakage on the particle size distribution, macroscopic engineering characteristics, etc. These fields of study are increasing in popularity because they provide a more comprehensive theoretical framework and offer valuable recommendations for the engineering application of granular materials.
To investigate interactions among various factors affecting the macroscopic mechanical characteristics of granular materials, numerous scholars have used various artificial materials made by 3D printing and other methods in experiments and discrete element simulations. To study the strength and deformation of granular materials, some scholars used uncrushable materials to investigate the rolling and slip deformation of granules and established mathematical models to describe the deformation mechanism [20,21,22]. Kong et al. [23] used ellipsoidal and spherical cement particles and steel balls, respectively, in simulations for triaxial tests of rockfill materials to explore strength and deformation under breakage and non-breakage conditions. Their experimental results proved particle breakage is the main reason for the bending of the strength envelopes of natural rockfill materials. Due to the isotropy of spherical glass beads, they can also study the breakage of granular materials. For example, Takei et al. [24] conducted compressive strength and one-dimensional compression tests with four materials, including glass beads and quartz particles, to investigate breakage mechanisms. In addition, with the application of fractal theory in geotechnical engineering, many scholars have paid attention to the effect of fractal dimension on particle breakage and stress–strain relationships [25,26]. Inter-particle friction also essentially influences the mechanical behavior of granular materials, and with this research objective, scholars have investigated the effect of particle friction on the shear behavior of specimens through tests and simulations using glass beads [27,28]. In summary, it is feasible to use artificial particles to study the mechanical characteristics of geotechnical granular materials and to consider different influencing factors such as particle morphologies, size gradation, and breakage. The shortcoming of the current investigation is the relatively limited study of more stress paths, especially the experimental results of the mechanical response under the true triaxial stress state, which cannot adequately characterize the effect of granular fabric anisotropy on practical engineering. Consequently, more scholars are researching the true triaxial mechanical characteristics of granular materials.
Numerous scholars have conducted true triaxial drained tests on different sands to determine the effect of inherent anisotropy on their deformation, strength, and failure, such as Ibsen et al. [29], Rodriguez et al. [30], and Abelev et al. [31]. Additionally, the non-coaxial and anisotropic behavior of spherical glass beads under true three-dimensional stress paths has also been investigated [32,33]. The true triaxial apparatus is essential equipment for experimental studies on the effects of inherent and stress-induced anisotropy, intermediate principal stress coefficients, and true three-dimensional stress paths in granular materials [34,35]. However, the loading device and test operation of the true triaxial apparatus are more complicated and costly, thus greatly affecting the application and popularization of the apparatus. To address this issue, Li et al. [36] proposed a novel method conducted through an equivalent alternative to achieve a true triaxial stress path using conventional triaxial apparatus. This technique keeps the conventional triaxial apparatus while effectively simulating the true triaxial stress path through specific stress loading methods, and it was successfully verified as reasonable and feasible [37]. This method can both simplify the test process and save the test cost, and it can also equivalently obtain true triaxial test results, which provides great convenience for the experimental research on the true three-dimensionality of granular materials.
Based on the novel method of stress path proposed by the authors, this paper uses spherical glass beads of single particle size to weaken the effects of particle gradation, fractal dimension, fabric, and particle breaking on granular mechanical characteristics. Triaxial drained and undrained tests with varying intermediate principal stress coefficients (b-values) are conducted on glass bead specimens using conventional triaxial apparatus. The effects of drained and undrained conditions on granular mechanical characteristics, as well as the strength, deformation, and failure characteristics under a true triaxial stress path, were investigated with relatively constant friction coefficients. Shear band formation under axisymmetric conditions is also explained. The results validated the effectiveness and rationale of the novel method of stress path.
2. Materials and Methods
2.1. Test Materials
In this paper, we employed glass beads produced in Germany for the tests. These beads have an ideal sphere with a diameter of 3 mm, as shown in Figure 1. The main component of these glass beads is silicon dioxide, and they exhibit mechanical characteristics such as light-specific gravity, higher strength, higher sphericity and surface smoothness, higher impact resistance, and crush resistance, among others. They can be regarded as a nearly isotropic, ideal granular material. Their mechanical parameters are shown in Table 1.

Figure 1.
Test materials and specimens: (a) glass beads; (b) specimens.

Table 1.
Mechanical parameters of the glass beads.
2.2. A Novel Method for Stress Paths
The true triaxial apparatus can realize the stress paths under different b-values. Although the conventional triaxial apparatus cannot realize the same stress path directly, we can connect the two-dimensional stress path and the three-dimensional stress path through the generalized stress space, and then use the conventional triaxial apparatus to realize the true three-dimensional stress path. The derivation of the controlling equations in which the stress loading with constant intermediate principal stress coefficients (b) and constant effective mean principal stress (p) is realized is as presented below.
In the true triaxial stress path, we can consider the effective mean principal stress increment (p) and deviatoric stress increment (q) as variables and b as a constant. An equation expressing the p-q relation in terms of the major principal stress increment () and the minor principal stress increment (), along with the constant b, can then be derived in Equation (1).
Similarly, during the conventional triaxial test, we can only control the p-q relation with and . And the relation is derived in Equation (2).
To ensure consistent stress paths in p-q space between true triaxial and conventional triaxial tests, the stress path slope () must be equal. From Equations (1) and (2), we obtain the conventional triaxial slope and the true triaxial slopes, and , and equate them, i.e., . This yields Equation (3).
The proportional relationship for utilizing constant b to control the loading of major and minor principal stresses is found in Equation (3). If a stress path with constant p for different b-values is to be realized with a conventional triaxial apparatus, dp = 0 is required, which can be obtained according to Equation (1).
We can obtain .
Based on Equation (5), we can achieve constant p loading by controlling the major principal stress () increase and the minor principal stress () decrease and different b-value stress paths by controlling the increasing rate of and the decreasing rate of .
2.3. Test Scheme and Procedure
The gradation of granular materials used in practical engineering usually conforms to a fractal distribution. According to the statistical fractal model, the number of granules satisfies Equation (6)
where N is the number of particles, d is the particle size, D is the fractal dimension, and k is a constant.
Equation (6) shows that there is a correspondence between the number of particles and the particle size, and then according to the cubic relationship between the mass and the number of particles, that the following can be obtained:
where is the total mass of the particle aggregate and is the maximum particle size.
In a triaxial test, granular materials are susceptible to sliding, rotation, and particle breakage. Moreover, the complexity of geotechnical particles also influences their strength and deformation characteristics, which increase the difficulty of determining and describing their mechanical behavior. However, in this paper’s test, we consider the limiting value of the fractal dimension of granular material gradation and choose glass beads of uniform size as the test material. The glass beads are uncrushable under low confining pressure, and their ideal spherical shape eliminates particle morphology effects on strength and deformation. Therefore, it can directly reflect the frictional characteristics of an ideal particle aggregate, and we can summarize the mechanical response by comparing the results of the rockfill material triaxial tests. To determine the mechanical characteristics of glass beads under a true three-dimensional stress state, the conventional triaxial apparatus for soil (Figure 2) was employed. According to the novel stress path method, drained and undrained triaxial tests were conducted on glass beads at different b-values. Compared with the test results of true triaxial and conventional triaxial, the test results are in good compliance and have high reliability. The test schemes are shown in Table 2, and the test steps are shown in the flow chart in Figure 3.

Figure 2.
Conventional triaxial apparatus.

Table 2.
Triaxial test scheme.
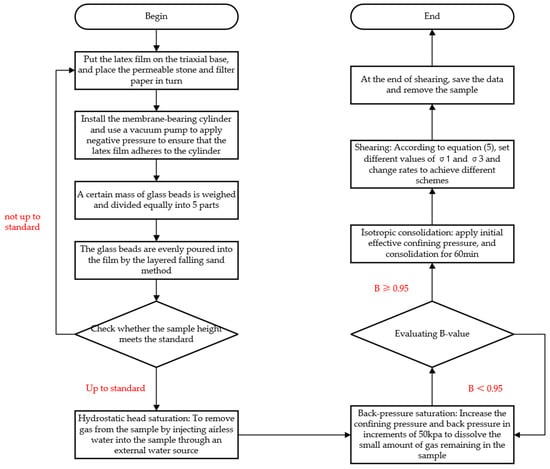
Figure 3.
Test procedure.
3. Results and Discussion
3.1. Strain–Stress Relationship
Figure 4 illustrates the laws of deviatoric stress (q) with axial strain () in both drained and undrained conditions for glass bead specimens with identical densities. The specimens were subjected to two effective mean principal stresses (p) and different b-values. All specimens demonstrate distinct softening characteristics, with the peak generalized shear stress, , decreasing with increasing b-values. This trend is consistent with experimental results documented in existing literature [38]. The results show that the novel stress path method can better determine the true triaxial test characteristics of granular materials, and the true triaxial stress path can be realized by using the conventional triaxial apparatus.
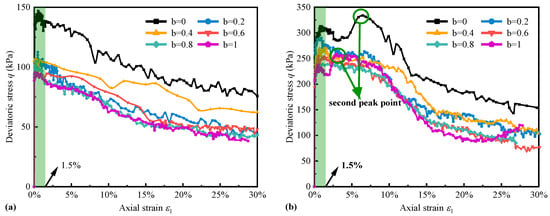
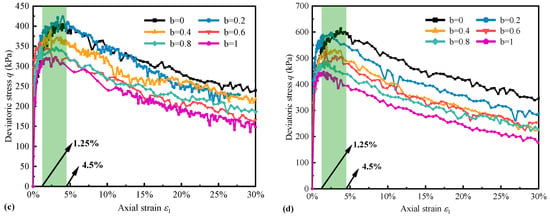
Figure 4.
Stress–strain relationship of glass beads: (a) p = 100 kPa drained; (b) p = 250 kPa drained; (c) p = 100 kPa undrained; (d) p = 250 kPa undrained.
In Figure 4, the regularity of drained and undrained tests is similar, but that of undrained is more obvious and stable than that of drained tests. The q showed excellent regularity, as depicted in Figure 4c,d. For the undrained test, it decreased with an increasing b-value and reached its peak earlier. Similar distinct patterns were observed at different p values. The peak strength of the undrained test is higher than that of the drained test. The reason may be that the fast shear rate and the significant dilatancy of the specimen caused the pore water pressure of the undrained test to rise quickly and not dissipate easily. Additionally, the drained and undrained tests exhibited different strain intervals for peak values. The drained tests peaked within the strain range of 0–1.5%, while the undrained tests exhibited peaks within 1.25–4.5%. It is worth noting that the drained tests show two peak points under p = 250 kPa, particularly at b = 0 and b = 1. This finding indicates that the material may form shear bands under two conditions, which is consistent with the two shear observations in our plane strain tests.
3.2. Dilatancy Characteristics
The relationship between volumetric strain () and axial strains () in drained tests is depicted in Figure 5. These figures indicate the glass bead specimens constantly experienced dilatancy from the beginning, which continued until the reached 30%, and the maximum dilatancy was 6–8%. As the b-values increased, dilatancy progressively increased, and the law was more significant at p = 100 kPa. Additionally, when the axial strain was less than 5%, the rate of volumetric change showed a higher value during the initial shear. This rate gradually decreases as shearing progresses. The main reason is that the arrangement of the particles was relatively dense at the beginning of shearing, and the volumetric change in the specimen was also larger. The volumetric change in the spherical specimen gradually tended to the limit value as the shearing progressed, so the volume change in the specimen gradually slowed down.
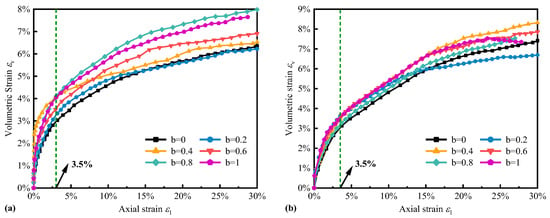
Figure 5.
Relationship between volumetric strain and axial strain under drained conditions. (a) p = 100 kPa; (b) p =250 kPa.
Figure 6 depicts the pore water pressure (u) and axial strain () for the undrained test. In the undrained test, while the specimen’s volumetric remained constant during shearing, the decreased pore water pressure led to an increase in the effective stress, and the specimen tended to dilatancy. As can be seen from Figure 6, the pore water pressure of the specimen gradually decreased with increasing axial strain until it eventually reached a negative value and stabilized. This result may be explained by the fact that the pores of the specimen were originally filled with water, followed by dilatancy during the shearing. This led to enlarged pores between the glass bead particles, and the force of the water on these particles acts as a suction force, resulting in a negative pore pressure. Concerning the influence of b-values, the pore water pressure was at its maximum at b = 0, which indicated that the specimen has the least dilatancy at this point and reached a stabilized magnitude at an axial strain of 6%. In comparison to other b-values, the pore water pressure was lower than that of b = 0, which indicated stronger dilatancy, and the specimens reached a stable value at a lower axial strain of about 3%. Generally, the magnitude of pore water pressure reduction increased with increasing b-values, and the dilatancy became more significant. This pattern was similar to the result of the drained test and the true triaxial test.
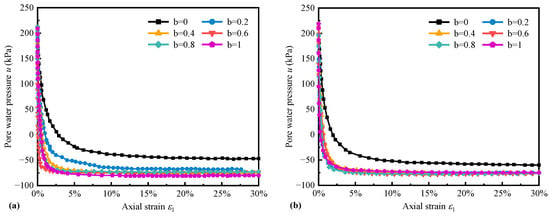
Figure 6.
Relationship between pore water pressure and axial strain under undrained conditions. (a) p = 100 kPa; (b) p = 250 kPa.
The formation of shear bands in the axisymmetric specimens examined in this paper showed a similar pattern to that in true triaxial tests. The deformation of glass bead specimens upon reaching 30% axial strain in both drained and undrained tests at p = 250 kPa is illustrated in Figure 7. As observed in this figure, most of the specimens displayed a “bulging” deformation, and a distinct shear band formation is produced in the b-values range from 0.2 to 0.6. For instance, in the drained test, the shear band inclination was 36.4° at b = 0.2, while in the undrained test, it was measured as 39.1° at b = 0.4 and 40.3° at b = 0.6. Consequently, the specimen’s shear band inclination is below 45°, and the law does not conform with the Coulomb criterion stated in Equation (8). This result is also consistent with the experimental results of Xu et al. [39].

Figure 7.
Shear deformation of glass beads at the axial strain of 30%: (A) drained, (B) undrained.
The internal friction angle (φ) of the glass beads was calculated using Equation (9).
Moreover, the position where the shear band shifts with varying b-values exhibited a particular pattern. When the shear band does not merge, the location of the “bulging” deformation in the specimen is correlated with the b-value. “Bulging” occurred at the upper of the specimen for b = 0, 0.8, and lower for b = 1, while other b-values occurred in the middle of the specimen.
The results of research by scholars such as Hettler et al. [40] and Peric et al. [41] show that shear bands in soils under axisymmetric conditions arise during the strain softening phase and approach the peak point. Figure 8 statistically plots the axial strain corresponding to the peak point of deviatoric stress versus the b-values for both drained and undrained tests at p = 200 kPa. It can be seen that the axial strain corresponding to the peak point of deviatoric stress decreases as the b-value increases, especially in the undrained test, where the b-value has a greater influence. It can be inferred that the b-value also has some influence on the formation of shear bands, and the shear bands will be formed earlier as the b-value increases.
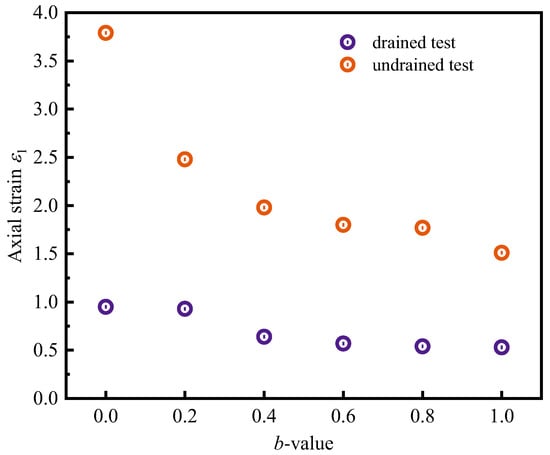
Figure 8.
Distribution of axial strains corresponding to the peak point of deviatoric stresses with the b-values.
3.3. Strength Characteristics
This paper uses a cylindrical specimen to maintain an axisymmetric two-dimensional stress state. The Mohr–Coulomb strength theory is applied to analyze the strength change resulting from variations in the b-values.
We can compare the variation trends between the peak principal stress ratio and the peak friction angle () under the same p using Equation (9). And Figure 9 shows how the and changed with the b-values for specimens under different drained conditions at p = 250 kPa. The data indicates that the strength in the drained tests was higher. Additionally, the strength is more sensitive to changes in the b-value in drained tests. These findings support the credibility of the novel stress path method proposed by the authors for assessing the strength of granular material. The varied from 30° to 31° in the undrained test and from 31° to 35° in the drained tests. Under the drained condition, the and of the sample exhibited a trend of increasing, decreasing, and then increasing again. The increased by 0.5, reaching the maximum value, while at b = 1, the increased by 3.5°. Generally, the and are the largest at the drained condition of b = 1, reaching 34.9° and 3.68, respectively, which are much larger than other b-values. This suggests that, when drained with b = 1, glass beads exhibited the highest compressive performance. The drained test pattern was similar to the true triaxial test, while the difference between drained and undrained conditions indicated that the mechanical response of the glass bead aggregate was very sensitive to water. Meanwhile, this variation offered an experimental foundation for understanding the effective stress in granular materials while keeping friction coefficients constant.
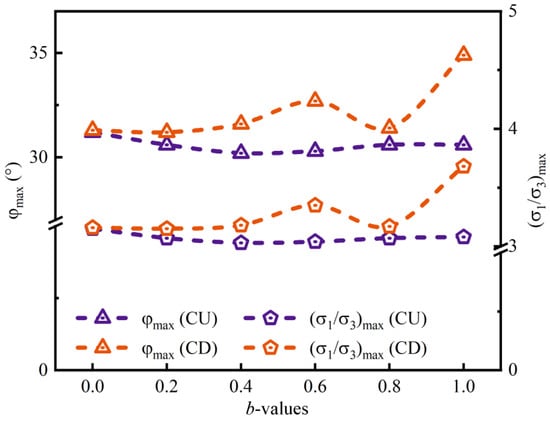
Figure 9.
Distribution of peak friction angle and peak stress ratio.
Figure 10 shows the stress paths of glass beads in the p-q space. All test types were able to represent the impact of b-value variations on the p-q stress paths, peak stress ratio, state transition stress ratio, and critical state stress ratio. During linear stress loading, the stress in drained tests linearly increased along the stress path with various slopes and decreased linearly after reaching the peak. The slope and peak stress reduced proportionally with increasing b-values, and the slope of the critical state line decreased with increases in p. Conversely, under undrained conditions, the stress paths subjected to hydraulic pressure exhibited nonlinear development. At low confining pressure, all the b-value tests were mainly characterized by dilatancy. It was close to a linear increase before reaching the peak; the slope was close and the path was long. After reaching a peak, it also decreased rapidly, near linearly, and then approached a critical state. Under p = 250 kPa, the specimens tended to have negative dilatancy. Additionally, there was an observed state transition from positive dilatancy to negative dilatancy and subsequently to the peak strength line. Following the peak, there was a gradual decline toward a critical state point. The variation of b-values resulted in alterations in state transition, peak, and critical state points.
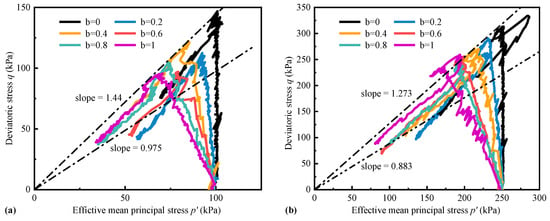
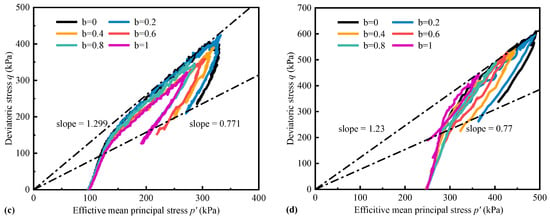
Figure 10.
Effective stress paths measured by conventional triaxial apparatus (): (a) p = 100 kPa drained; (b) p = 250 kPa drained; (c) p = 100 kPa undrained; (d) p = 250 kPa undrained.
Figure 11 gives the effective stress paths calculated by the novel method of this paper when p was 100 kPa and 250 kPa with different b-values. It can be seen that when p was 100 kPa and 250 kPa, respectively, the stress paths under different b-values kept the plumb line perpendicular to the horizontal coordinate axis. This also shows that the novel method in this paper is feasible and controllable and can realize the true triaxial stress paths with constant p under different b-values in the p-q space more accurately by using the conventional triaxial apparatus.
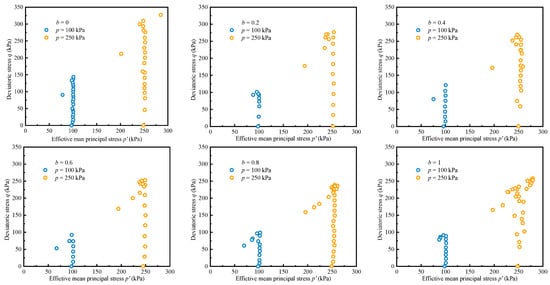
Figure 11.
Effective stress paths were calculated by the novel methods under drained conditions ().
Summarizing, the triaxial test with glass beads provided a more accurate description of the mechanical response of granular materials, such as rockfill material. Remarkably, large-scale true triaxial tests of rockfill materials by Zhou et al. [42] and Zuo et al. [43] indicate that the specimens transition from negative to positive dilatancy as the axial strain increases. In our tests, both drained and undrained triaxial tests commonly displayed positive dilatancy, but the specimens began to show a tendency toward negative dilatancy at higher effective mean principal stress, which was consistent with the results of the existing tests on gradual materials. In this paper, the same particle size was used for the test, which could better determine the limit value of dilatancy. In addition, the dilatancy of granular materials is comprehensively affected by factors such as particle size gradation, morphology, and breakage, but our tests greatly eliminated the influence of these factors, and it is possible to identify the degree and extent of the influence on each element. Finally, the fundamental reason for the stress-path dependence of granular materials was due to the anisotropy of the material and stress. To mitigate the effects of inherent anisotropy, we employed an ideal, single, unbroken isotropic material. The experimental results preliminarily verified the effectiveness of our novel method in achieving the true triaxial stress path equivalently.
4. Conclusions
This study explored the mechanical characteristics of granular materials by using ideally spherical glass beads of uniform size as experimental materials to reduce the effect of the particle gradation fractal dimension. A novel method was applied to explore the material mechanical behavior of nearly isotropic conditions in three-dimensional stress states. With conventional triaxial tests, this approach achieved true triaxial stress paths equivalent. The key findings are as follows:
- (1)
- The specimens exhibited varying degrees of strain softening, dilatancy, and shear band formation phenomena across different b-values under two distinct confining pressures and drained conditions. The initial modulus increased with rising p. Except for b = 0, the initial modulus decreased with increasing b-value, thus verifying the effectiveness of this novel method in illustrating stress paths.
- (2)
- The peak strength of the undrained test was greater than that of the drained test, while the peak strength decreased with increasing b-value. The stress–strain curves of the drained tests showed two notable peaks, particularly at b = 0 and b = 1, and the second peak was significantly higher than the first. Furthermore, the peak friction angle and peak stress ratio of the drained test at p = 250 kPa were higher than those of the undrained test. Under drained conditions, the specimens exhibited the highest compressive performance at b = 1. The disparities between drained and undrained tests indicated an intensified water sensitivity of glass beads.
- (3)
- At an axial strain of 30%, the majority of specimens displayed “bulging” deformations, with the position of this deformation correlated to the b-value. Shear bands were observed at specific b-values, all inclined at angles less than 45°. The application of the novel method generated remarkable shear bands in axisymmetric specimens at b-values ranging from 0.2 to 0.6, which exhibited a substantial deviation from conventional triaxial tests.
Due to the formation of shear zones, the strength of the granular material is reduced. Therefore, the influence of this aspect should be considered in practical projects, and the safety factor appropriately increased to ensure the reliability of the project.
Author Contributions
Conceptualization, X.L. and J.M.; methodology, X.L. and J.M.; software, X.L. and J.M.; validation, L.L.; formal analysis, J.M. and L.L.; investigation, J.M. and L.L.; resources, L.L.; data curation, L.L.; writing—original draft preparation, J.M. and L.L.; writing—review and editing, X.L. and J.M.; visualization, J.M. and L.L.; supervision, X.L.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was founded by the National Natural Science Foundation of China (No. 1216028), the Projects for Leading Talents of Science and Technology Innovation of Ningxia (No. KJT2019001), and the innovation team for multi-scale mechanics and its engineering applications of Ningxia Hui Autonomous Region (2021).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yin, F.J.; Cai, G.Q.; Su, Y.L.; Shan, Y.P.; Li, J. Rate-dependent experimental study on unsaturated coarse-grained soil controlled by matrix suction. Chin. J. Geotech. Eng. 2023, 45, 24–28. [Google Scholar]
- Fu, Z.; Chen, S.; Han, H. Experimental investigations on the residual strain behavior of a rockfill material subjected to dynamic loading. J. Mater. Civ. Eng. 2017, 29, 04016278. [Google Scholar] [CrossRef]
- Chen, B.; Li, Y.Q.; Liu, X.F. Study on Stick-slip Behaviour of Granular Materials in Triaxial Test. J. Disaster Prev. Mitig. Eng. 2023, 43, 568–575. [Google Scholar]
- Liu, J.; Zhou, W.; Ji, X.; Wei, G.; Yuan, S.; Li, X. Dilatancy Analysis of Granular Materials Based on Mesoscopic Topological Evolutions. Chin. J. Mech. 2022, 54, 707–718. [Google Scholar]
- Maosong, H.; Xuefeng, L.; Cangqin, J. A Double Yield Surface Constitutive Model for Sand Based on State-dependent Critical State Theory. Chin. J. Geotech. Eng. 2010, 32, 1764–1771. [Google Scholar]
- Beibing, D.; Juny, Y.; Cuiying, Z. An Experimental Study on the Effect of Inter-particle Friction on Shear Behavior of Granular Materials. Chin. J. Mech. 2013, 45, 375–383. [Google Scholar]
- Marschi, N.D.; Chan, C.K.; Seed, H.B. Evaluation of properties of rockfill materials. ASCE J. Soil Mech. Found. Div. 1972, 98, 95–114. [Google Scholar] [CrossRef]
- Ning, F.; Liu, J.; Kong, X. Critical state and grading evolution of rockfill material under different triaxial compression tests. Int. J. Geomech. 2020, 20, 04019154. [Google Scholar] [CrossRef]
- Marsal, R.J. Large scale testing of rockfill materials. ASCE J. Soil Mech. Found. Div. 1967, 93, 27–43. [Google Scholar] [CrossRef]
- Lee, K.L.; Farhoomand, I. Compressibility and crushing of granular soil in anisotropic triaxial compression. Can. Geotech. J. 1967, 4, 68–86. [Google Scholar] [CrossRef]
- Varadarajan, A.; Sharma, K.G.; Venkatachalam, K. Testing and modeling two rockfill materials. J. Geotech. Geoenviron. Eng. 2003, 129, 206–218. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H. Elastoplastic constitutive model for rockfill materials considering particle breakage. Int. J. Geomech. 2017, 17, 04016041. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Desai, C.S. Effect of intermediate principal-stress ratio on particle breakage of rockfill material. J. Geotech. Geoenviron. Eng. 2016, 142, 06015017. [Google Scholar] [CrossRef]
- Xiao, Y.; Meng, M.; Daouadji, A.; Chen, Q.; Wu, Z.; Jiang, X. Effects of particle size on crushing and deformation behaviors of rockfill materials. Geosci. Front. 2020, 11, 375–388. [Google Scholar] [CrossRef]
- Jia, Y.; Xu, B.; Chi, S.; Xiang, B.; Xiao, D.; Zhou, Y. Particle breakage of rockfill material during triaxial tests under complex stress paths. Int. J. Geomech. 2019, 19, 04019124. [Google Scholar] [CrossRef]
- Guo, X.L.; Hu, H.; Bao, C.G. Experimental Studies of the Effects of Grain Breakage on the Dilatancy and Shear Strength of Rock Fill. Chin. J. Geotech. Eng. 1997, 19, 86–91. [Google Scholar]
- Liu, H.; Qin, H.; Gao, Y.; Zhou, Y. Experimental Study on Particle Breakage of Rockfill and Coarse Aggregates. Rock Soil Mech. 2005, 26, 562–566. [Google Scholar]
- Chi, S.; Jia, Y. Rown’s Stress-dilatancy Model Modified for Energy Dissipation of Particle Breakage. Chin. J. Geotech. Eng. 2005, 27, 31–34. [Google Scholar]
- Liu, E.L.; Tan, Y.L.; Chen, S.S.; Li, G.Y. Investigation on Critical State of Rockfill Materials. J. Hydraul. Eng. 2012, 43, 505–511+519. [Google Scholar]
- Oda, M.; Konishi, J.; Nemat-Nasser, S. Experimental micromechanical evaluation of the strength of granular materials: Effects of particle rolling. Mech. Mater. 1982, 1, 269–283. [Google Scholar] [CrossRef]
- Bésuelle, P.; Desrues, J.; Raynaud, S. Experimental characterization of the localization phenomenon inside a Vosges sandstone in a triaxial cell. Int. J. Rock Mech. Min. Sci. 2000, 37, 1223–1237. [Google Scholar] [CrossRef]
- Cheng, Z.; Ding, H.; Wu, L. Experimental Study on Mechanical Behavior of Granular Material. Chin. J. Geotech. Eng. 2007, 29, 1151–1158. [Google Scholar]
- Kong, D.; Zhang, B.; Sun, X. Triaxial Tests on Particle Breakage Strain of Artificial Rockfill Materials. Chin. J. Geotech. Eng. 2009, 31, 464–469. [Google Scholar]
- Takei, M.; Kusakabe, O.; Hayashi, T. Time-dependent behavior of crushable materials in one-dimensional compression tests. Soils Found. 2001, 41, 97–121. [Google Scholar] [CrossRef]
- Zhao, N.; Zuo, Y.; Wang, Z.; Yu, S. Grading scale method for coarse-grained soils based on fractal theory. Rock Soil Mech. 2016, 37, 3513–3519. [Google Scholar]
- Chen, Z.; Li, G.; Wei, K.; Wu, L.; Zhu, Y. Ultimate state and probability of particle breakage for rockfill materials based on fractal theory. Chin. J. Geotech. Eng. 2021, 43, 1192–1200. [Google Scholar]
- Dai, B.B.; Yang, J.; Zhou, C.Y. Observed effects of interparticle friction and particle size on shear behavior of granular materials. Int. J. Geomech. 2016, 16, 04015011. [Google Scholar] [CrossRef]
- Liu, L. Micromechanics of Granular Assemblies of Elastic-perfectly Plastic Sphered During Qusai-Static Deformation. Chin. J. Geotech. Eng. 2007, 29, 524–530. [Google Scholar]
- Ibsen, L.B.; Prasstrup, U. The Danish rigid boundary true triaxial apparatus for soil testing. Geotech. Test. J. 2002, 25, 254–265. [Google Scholar] [CrossRef]
- Rodriguez, N.M.; Lade, P.V. True triaxial tests on cross-anisotropic deposits of fine Nevada sand. Int. J. Geomech. 2013, 13, 779–793. [Google Scholar] [CrossRef]
- Abelev, A.V.; Lade, P.V. Effects of cross anisotropy on three-dimensional behavior of sand. I: Stress-strain behavior and shear banding. J. Eng. Mech. 2003, 129, 160–166. [Google Scholar] [CrossRef]
- Haruyama, M. Anisotropic deformation-strength characteristics of an assembly of spherical particles under three-dimensional stresses. Soils Found. 1981, 21, 41–55. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Li, X.; Chen, Q. Laboratory Analyses of Noncoaxiality and Anisotropy of Spherical Granular Media under True Triaxial State. Int. J. Geomech. 2023, 23, 04023150. [Google Scholar] [CrossRef]
- Mahmud Sazzad, M.D.; Suzuki, K.; Modaressi-Farahmand-Razavi, A. Macro-micro responses of granular materials under different b values using DEM. Int. J. Geomech. 2012, 12, 220–228. [Google Scholar] [CrossRef]
- Zhou, W.; Xie, T.T.; Ma, G.; Chang, X.L. Stress and Deformation Analysis of Rockfill in True Triaxial Stress Conditions Based on PFC. Rock Soil Mech. 2012, 33, 3006–3012+3080. [Google Scholar]
- Li, X.F.; Ma, Z.G. Method for Achieving Stress or Strain Path in Three-Dimensional Space with Pseudo-Triaxial Apparatus. CN114235571B, 9 May 2023. [Google Scholar]
- Ma, Z.; Li, X. Aeolian Sand Test with True Triaxial Stress Path Achieved by Pseudo-Triaxial Apparatus. Sustainability 2023, 15, 8328. [Google Scholar] [CrossRef]
- Min, Z.; Chengshun, X. True Triaxial Experimental Research on Shear Behaviors of Sand under Different Intermediate Principal Stresses and Different Stress Paths. J. Hydraul. Eng. 2015, 46, 1072–1079. [Google Scholar]
- Xu, W.D.; Li, X.F.; Yang, W.W.; Jia, H.J. Triaxial test on glass beads simulating coarse-grained soil. Res. Cold Arid Reg. 2022, 14, 274–280. [Google Scholar] [CrossRef]
- Hettler, A.; Vardoulakis, I. Behaviour of dry sand tested in a large triaxial apparatus. Geotechnique 1984, 34, 183–197. [Google Scholar] [CrossRef]
- Peric, D.; Runesson, K.; Sture, S. Evaluation of plastic bifurcation for plane strain versus axisymmetry. J. Eng. Mech. 1992, 118, 512–524. [Google Scholar] [CrossRef]
- Zhou, Y.; Pan, J.; Cheng, Z.L. Strength and Dilation of Sandy Gravel Material Based on Large-scale Ture Triaxial Tests. Chin. J. Rock Mech. Eng. 2017, 36, 2818–2825. [Google Scholar]
- Zuo, Y.; Jiang, J.; Pan, J.; Zhao, N.; Zhou, Y. Deformation Characteristics of Coarse Granular Materials in Large-scale True Triaxial Tests. Chin. J. Geotech. Eng. 2019, 41, 37–40. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).