Fractal and Multifractal Analysis of Microscopic Pore Structure of UHPC Matrix Modified with Nano Silica
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Materials
2.2. Sample Preparation Procedures
2.3. Compressive Strength
2.4. Quantitative Characterization of Microstructure
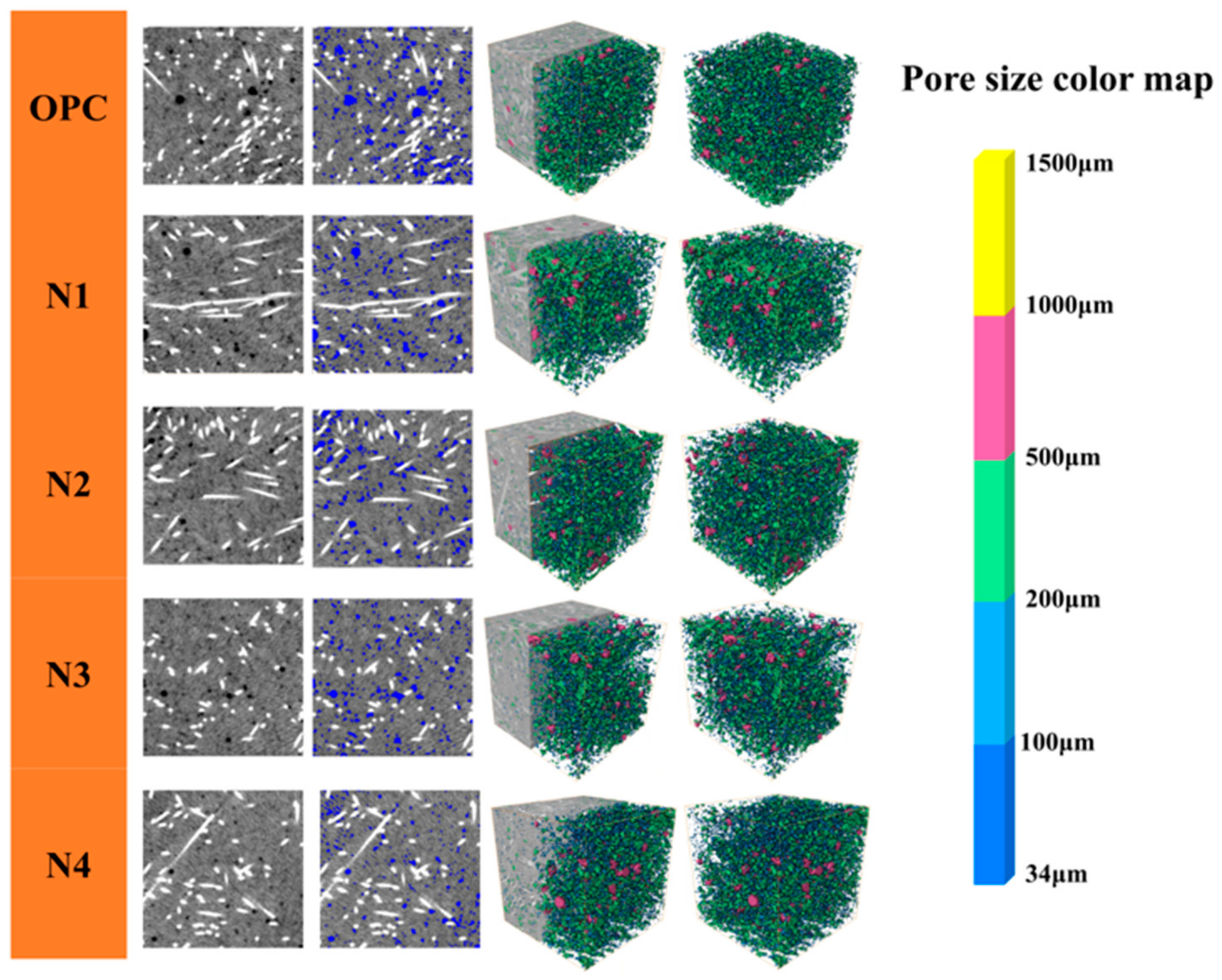
2.4.1. Acquisition and Reconstruction of Microstructure
2.4.2. Fractal Analysis
2.4.3. Multifractal Analysis
3. Results and Discussion
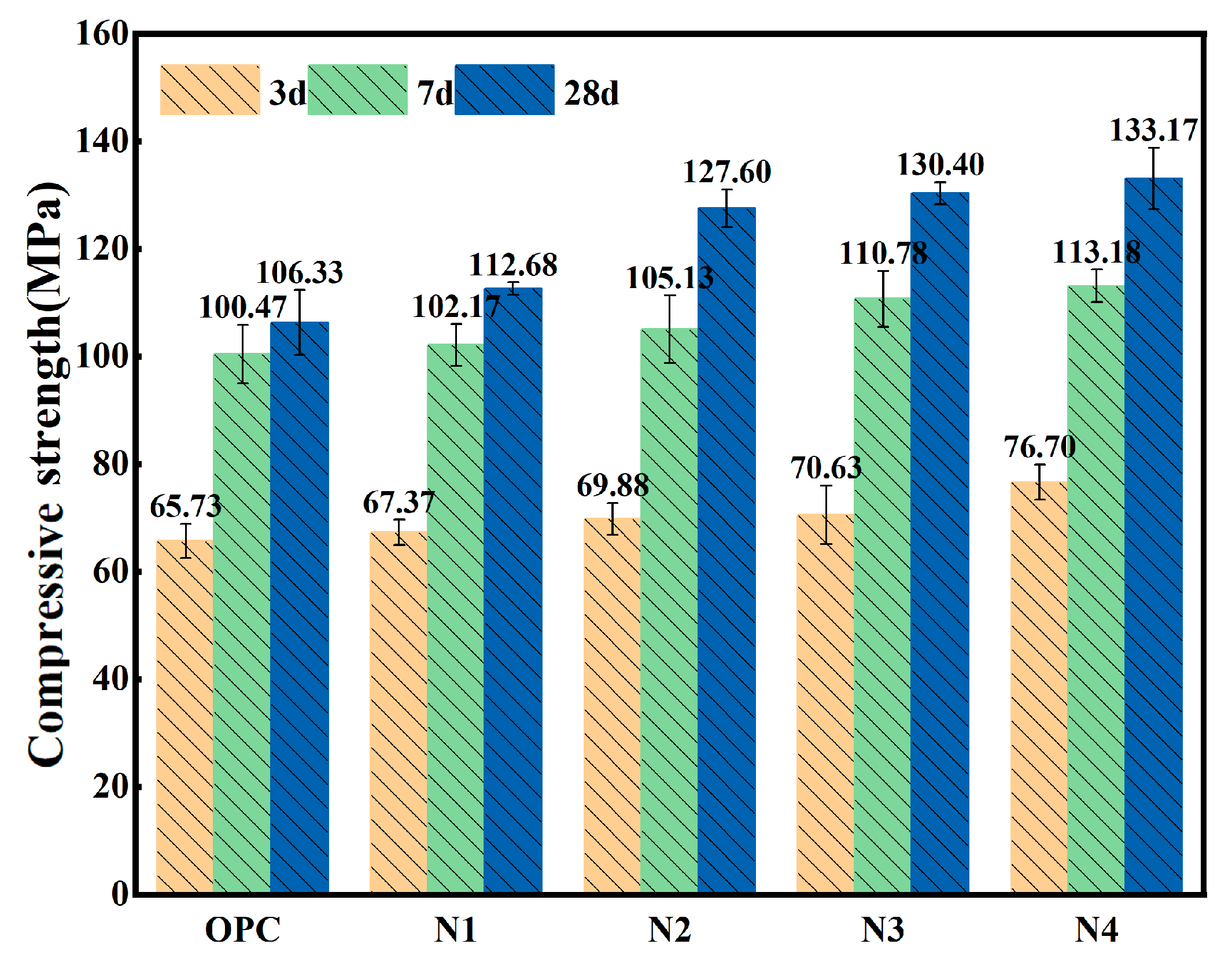
3.1. Compressive Strength
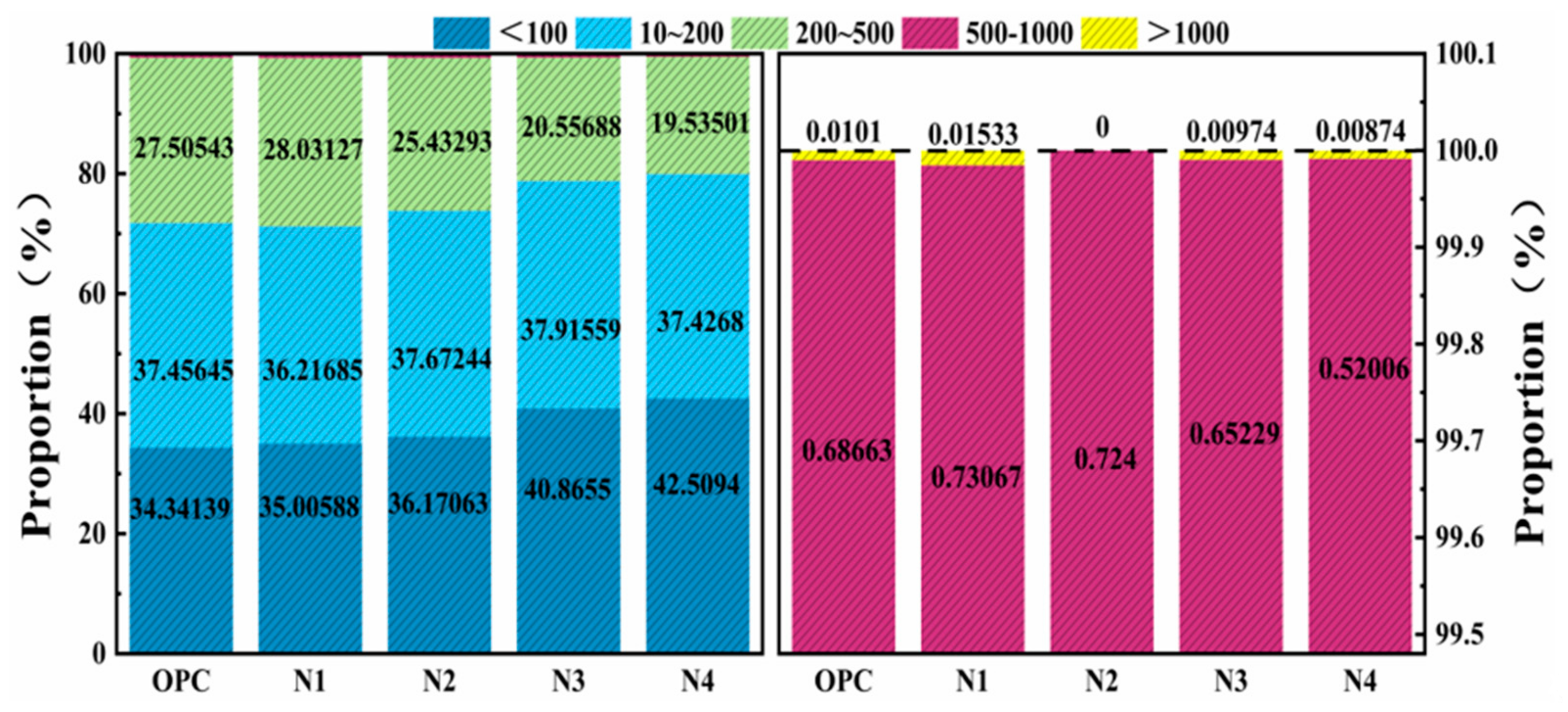
3.2. Pore Size Distribution
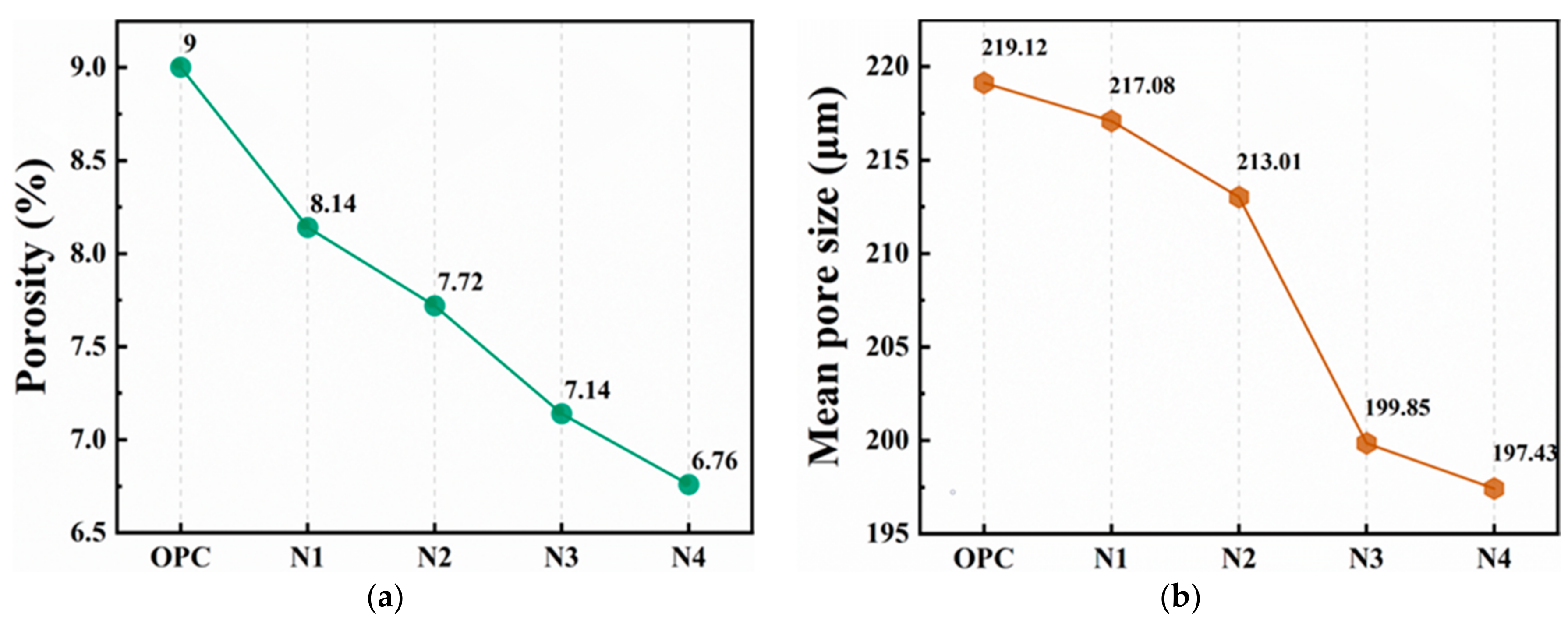
3.3. Porosity and Mean Pore Size
3.4. Fractal and Multifractal
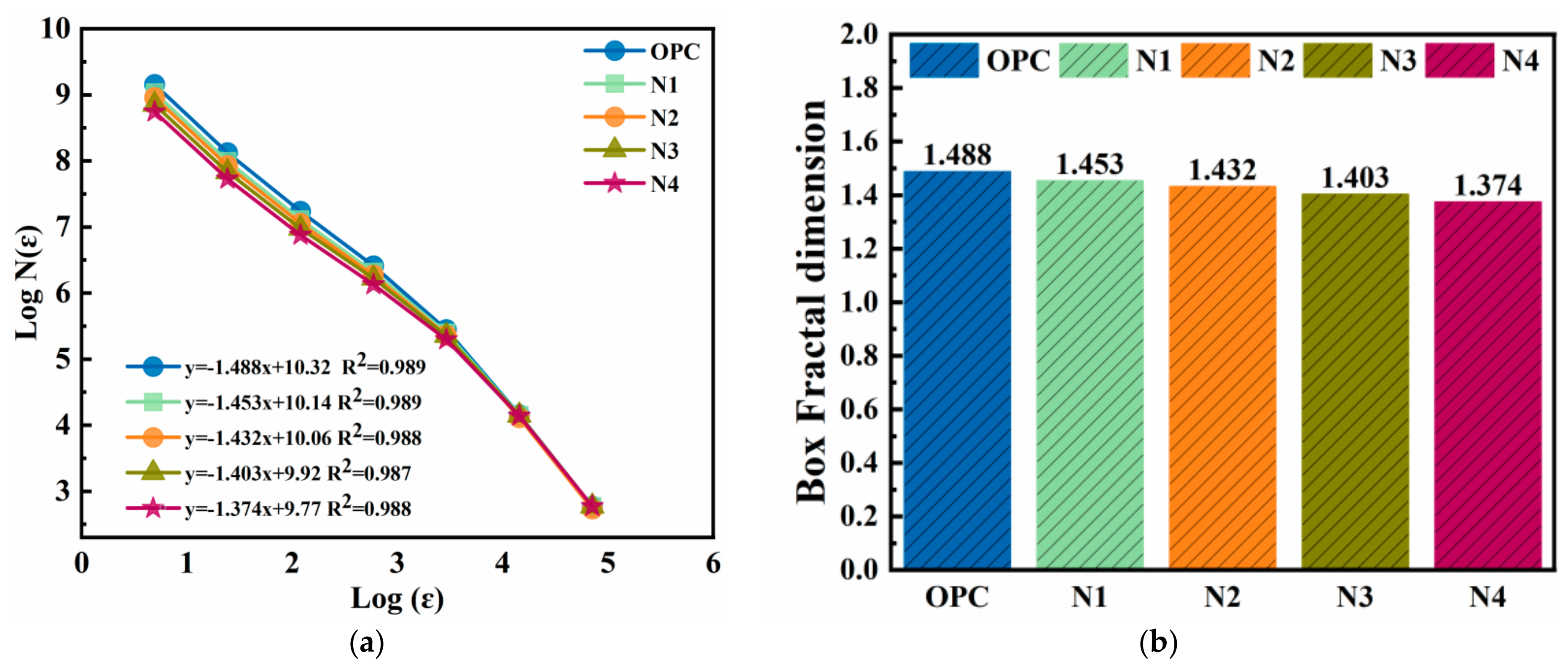
3.4.1. Fractal Dimension
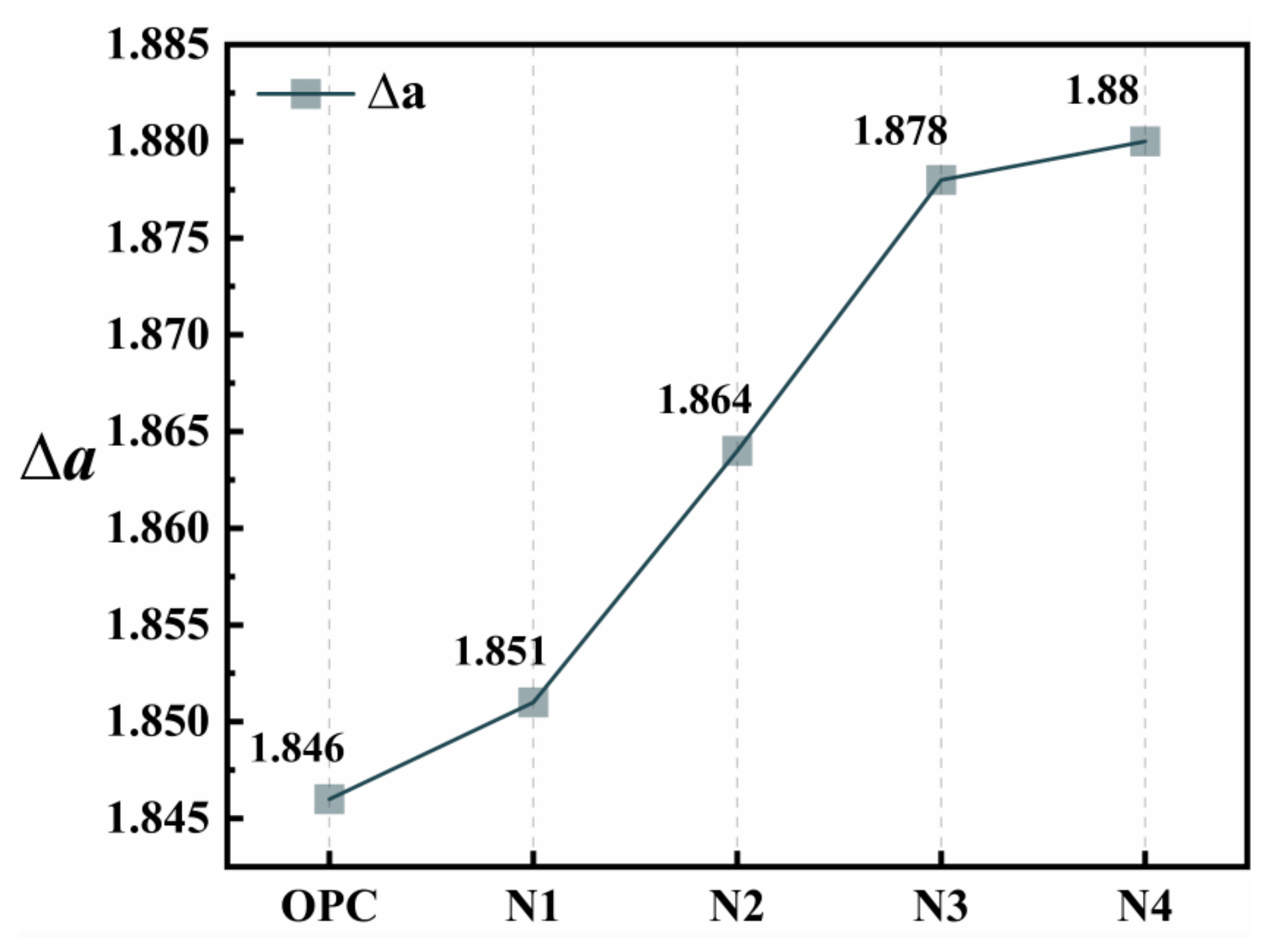
3.4.2. Multifractal
4. Further Discussion
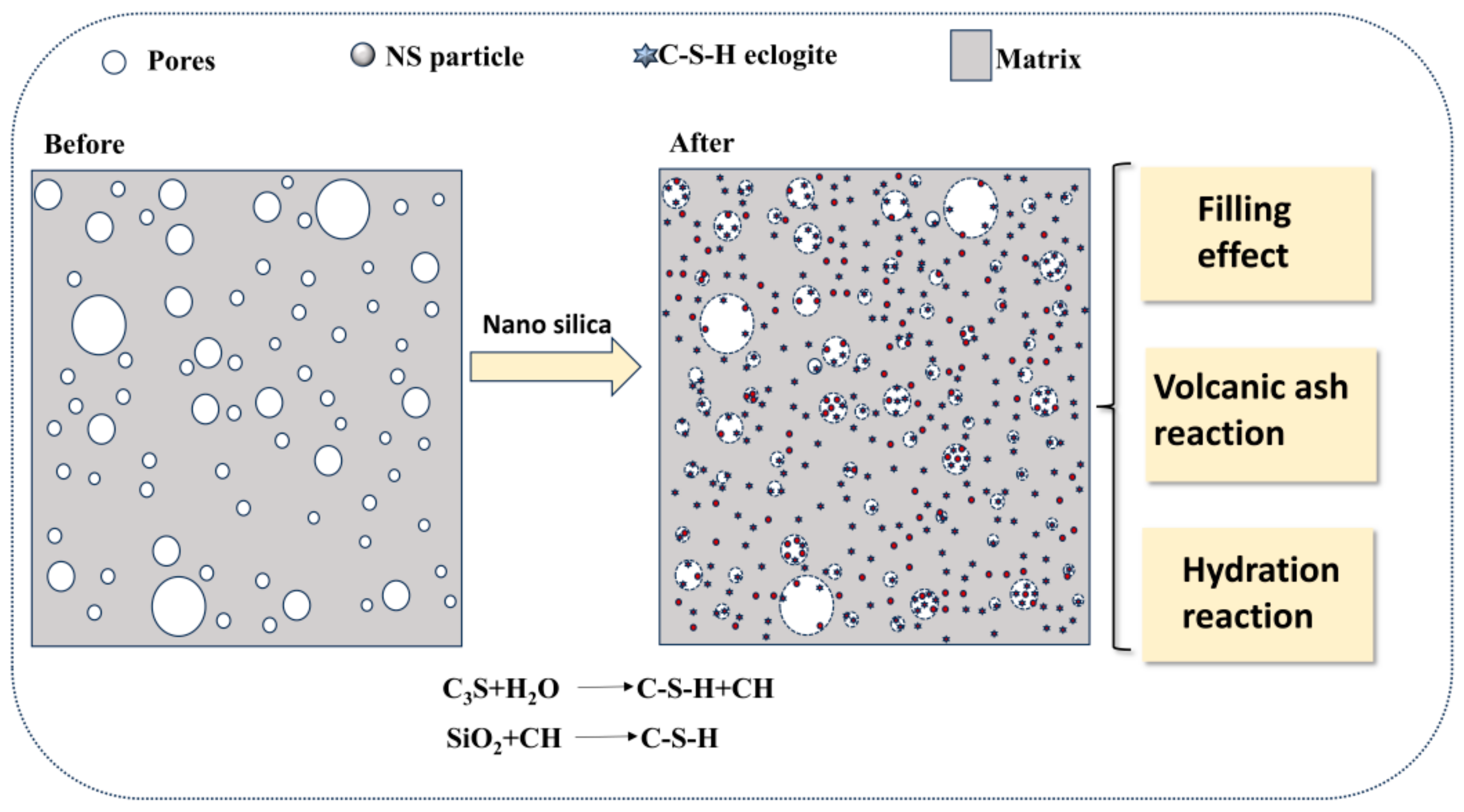
4.1. Mechanism of NS Effect on Pore Structure
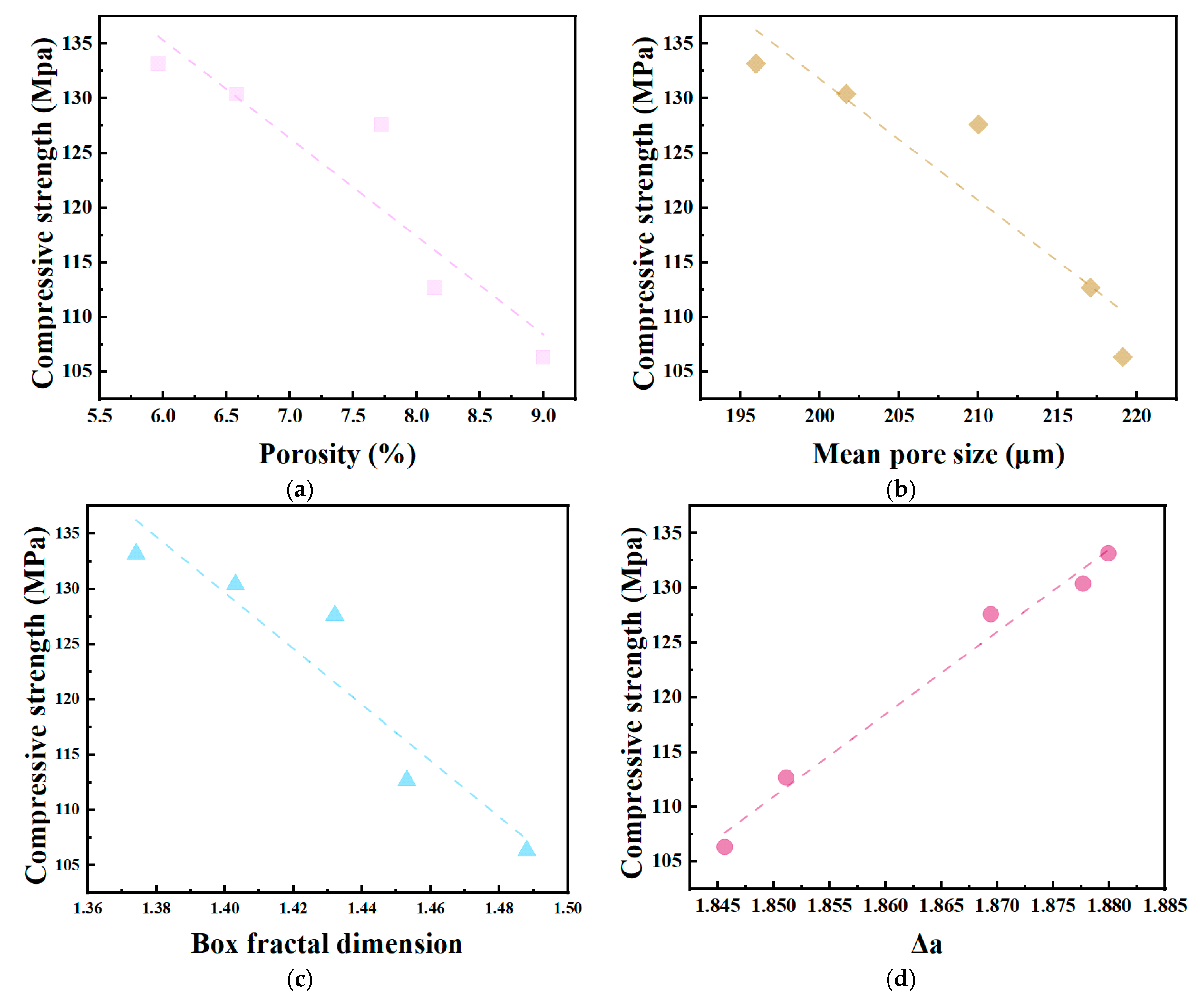
4.2. Correlation Analysis
5. Conclusions
- (1)
- NS played a positive role in improving the microporous structure of UHPC, and this microstructural improvement increased the densification of the microstructure of the UHPC matrix and significantly improved the mechanical properties. Compared with the blank group, the 28d compressive strengths of N1, N2, N3 and N4 were increased by 6.02%, 20.04%, 22.67% and 27.38%.
- (2)
- NS could effectively reduce the porosity and significantly refine the pore size of UHPC, and the total porosity P of N1, N2, N3 and N4 decreased by 9.5%, 14.2%, 20.67% and 24.86%, and the average pore size decreased by 0.93%, 2.79%, 8.8% and 9.9% compared with that of the control OPC. NS has the most obvious effect on the optimization of small pores in the scale of 0~100 μm, while it has a limited effect on the refinement of pores with a pore size of more than 1000 μm.
- (3)
- The fractal dimension and multifractal parameters describe the complementary information of the pore structure of NS-modified UHPC from different perspectives. At the global level, the densification of the UHPC matrix by NS is reflected in the decrease in the counting box dimension, with a D-value of 1.488 for OPC, and D-values of 1.453, 1.432, 1.403, and 1.374 for N1, N2, N3, and N4, respectively. At the local level, the increase in the number of tiny pores leads to the increase in the complexity and heterogeneity of the pore size distribution of the UHPC matrix, which is manifested as the increase in the width of the multifractal spectral spectrum. As an increase in the spectral width of the multifractal spectrum, with ∆a values of 1.846 for OPC and 1.851, 1.864, 1.878 and 1.80 for N1, N2, N3 and N4, respectively.
- (4)
- The pore structure parameters of NS-modified UHPC showed a good fit to the 28d compressive strength, which conformed to a linear functional relationship. p and had regression correlation coefficients of 0.804 and 0.82, respectively, and the fit with D was 0.85, and it had the best fit with ∆a, which was 0.97. F-tests and T-tests indicated that each of the regression equations and the corresponding parameters were statistically significant.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, J.; Meng, W.; Khayat, K.H.; Bao, Y.; Guo, P.; Lyu, Z.; Abu-Obeidah, A.; Nassif, H.; Wang, H. New development of ultra-high-performance concrete (UHPC). Compos. Part B Eng. 2021, 224, 109220. [Google Scholar] [CrossRef]
- Sidodikromo, E.P.; Chen, Z.; Habib, M. Review of the cement-based composite ultra-high-performance concrete (UHPC). Open Civ. Eng. J. 2019, 13, 147–162. [Google Scholar] [CrossRef]
- Wille, K.; Naaman, A.E.; El-Tawil, S.; Parra-Montesinos, G.J. Ultra-high performance concrete and fiber reinforced concrete: Achieving strength and ductility without heat curing. Mater. Struct. 2012, 45, 309–324. [Google Scholar] [CrossRef]
- Aili, A.; Maruyama, I. Review of several experimental methods for characterization of micro-and nano-scale pores in cement-based material. Int. J. Concr. Struct. Mater. 2020, 14, 55. [Google Scholar] [CrossRef]
- Kang, S.H.; Hong, S.G.; Moon, J. The effect of superabsorbent polymer on various scale of pore structure in ultra-high performance concrete. Constr. Build. Mater. 2018, 172, 29–40. [Google Scholar] [CrossRef]
- Jiang, Z.L.; Pan, Y.J.; Lu, J.F.; Wang, Y.-C. Pore structure characterization of cement paste by different experimental methods and its influence on permeability evaluation. Cem. Concr. Res. 2022, 159, 106892. [Google Scholar] [CrossRef]
- Yu, R.; Spiesz, P.; Brouwers, H.J.H. Effect of nano-silica on the hydration and microstructure development of Ultra-High Performance Concrete (UHPC) with a low binder amount. Constr. Build. Mater. 2014, 65, 140–150. [Google Scholar] [CrossRef]
- Luo, Z.; Zhi, T.; Liu, X.; Yin, K.; Pan, H.; Feng, H.; Song, Y.; Su, Y. Effects of different nanomaterials on the early performance of ultra-high performance concrete (UHPC): C–S–H seeds and nano-silica. Cem. Concr. Compos. 2023, 142, 105211. [Google Scholar] [CrossRef]
- Janković, K.; Stanković, S.; Bojović, D.; Stojanović, M.; Antić, L. The influence of nano-silica and barite aggregate on properties of ultra high performance concrete. Constr. Build. Mater. 2016, 126, 147–156. [Google Scholar] [CrossRef]
- Rupasinghe, M.; San Nicolas, R.; Mendis, P.; Sofi, M.; Ngo, T. Investigation of strength and hydration characteristics in nano-silica incorporated cement paste. Cem. Concr. Compos. 2017, 80, 17–30. [Google Scholar] [CrossRef]
- Oh, T.; Chun, B.; Lee, S.K.; Kim, G.W.; Banthia, N.; Yoo, D.Y. Effect of high-volume substituted nanosilica on the hydration and mechanical properties of Ultra-High-Performance Concrete (UHPC). Cem. Concr. Res. 2024, 175, 107379. [Google Scholar] [CrossRef]
- Zeng, Q.; Luo, M.; Pang, X.; Li, L.; Li, K. Surface fractal dimension: An indicator to characterize the microstructure of cement-based porous materials. Appl. Surf. Sci. 2013, 282, 302–307. [Google Scholar] [CrossRef]
- Ghafari, E.; Costa, H.; Júlio, E.; Li, L.; Li, K. The effect of nanosilica addition on flowability, strength and transport properties of ultra high performance concrete. Mater. Des. 2014, 59, 1–9. [Google Scholar] [CrossRef]
- Wu, Z.; Khayat, K.H.; Shi, C.; Tutikian, B.F.; Chen, Q. Mechanisms underlying the strength enhancement of UHPC modified with nano-SiO2 and nano-CaCO3. Cem. Concr. Compos. 2021, 119, 103992. [Google Scholar] [CrossRef]
- Janković, K.; Bojović, D.; Stojanović, M. Influence of nanoparticles on the strength of ultra-high performance concrete. In Nanotechnology in Eco-Efficient Construction; Woodhead Publishing: Sawston, UK, 2019; pp. 13–42. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Oh, T.; Banthia, N. Nanomaterials in ultra-high-performance concrete (UHPC)—A review. Cem. Concr. Compos. 2022, 134, 104730. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, C.; Khayat, K.H.; Wan, S. Effects of different nanomaterials on hardening and performance of ultra-high strength concrete (UHSC). Cem. Concr. Compos. 2016, 70, 24–34. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Cao, F.; Sun, Z.; Shah, S.P. Effects of nano-silica and nano-limestone on flowability and mechanical properties of ultra-high-performance concrete matrix. Constr. Build. Mater. 2015, 95, 366–374. [Google Scholar] [CrossRef]
- Guo, D.; Guo, M.; Zhou, Y.; Zhu, Z. Use of nano-silica to improve the performance of LC3-UHPC: Mechanical behavior and microstructural characteristics. Constr. Build. Mater. 2024, 411, 134280. [Google Scholar] [CrossRef]
- Kim, J.; Choi, S. A fractal-based approach for reconstructing pore structures of GGBFS-blended cement pastes. Constr. Build. Mater. 2020, 265, 120350. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, X.; Yang, H.; Lv, X.; Guo, F.; Shi, Y.; Hanif, A. Investigation and application of fractal theory in cement-based materials: A review. Fractal Fract. 2021, 5, 247. [Google Scholar] [CrossRef]
- Dathe, A.; Tarquis, A.M.; Perrier, E. Multifractal analysis of the pore-and solid-phases in binary two-dimensional images of natural porous structures. Geoderma 2006, 134, 318–326. [Google Scholar] [CrossRef]
- Tang, S.; Huang, J.; Duan, L.; Yu, P.; Chen, E. A review on fractal footprint of cement-based materials. Powder Technol. 2020, 370, 237–250. [Google Scholar] [CrossRef]
- Yang, X.; Wang, F.; Yang, X.; Zhou, Q. Fractal dimension in concrete and implementation for meso-simulation. Constr. Build. Mater. 2017, 143, 464–472. [Google Scholar] [CrossRef]
- Pan, L.; Carrillo, J.; Cao, M.; Sha, G. Multifractal-spectrum shape parameters for characterizing distribution and evolution of multiple cracks in concrete structures. Eng. Fract. Mech. 2022, 264, 108329. [Google Scholar] [CrossRef]
- Tang, S.W.; Cai, R.J.; He, Z.; Cai, X.H.; Shao, H.Y.; Li, Z.J.; Yang, H.M.; Chen, E. Continuous microstructural correlation of slag/superplasticizer cement pastes by heat and impedance methods via fractal analysis. Fractals 2017, 25, 1740003. [Google Scholar] [CrossRef]
- Tang, S.W.; Wang, L.; Cai, R.J.; Cai, X.H.; He, Z.; Chen, E. The evaluation of electrical impedance of three-dimensional fractal networks embedded in a cube. Fractals 2017, 25, 1740005. [Google Scholar] [CrossRef]
- Tang, S.W.; Yu, P.; Wang, L.; Cai, R.J.; Chen, E. The analysis of thermal resistance of three-dimensional fractal networks embedded in a sphere. Fractals 2018, 26, 1850036. [Google Scholar] [CrossRef]
- Martínez, F.S.J.; Martín, M.A.; Caniego, F.J.; Tuller, M.; Guber, A.; Pachepsky, Y.; García-Gutiérrez, C. Multifractal analysis of discretized X-ray CT images for the characterization of soil macropore structures. Geoderma 2010, 156, 32–42. [Google Scholar] [CrossRef]
- Li, W.; Liu, H.; Song, X. Multifractal analysis of Hg pore size distributions of tectonically deformed coals. Int. J. Coal Geol. 2015, 144, 138–152. [Google Scholar] [CrossRef]
- Zarnaghi, V.N.; Fouroghi-Asl, A.; Nourani, V.; Ma, H. On the pore structures of lightweight self-compacting concrete containing silica fume. Constr. Build. Mater. 2018, 193, 557–564. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-Chong, T.; Dangla, P. Surface fractal analysis of pore structure of high-volume fly-ash cement pastes. Appl. Surf. Sci. 2010, 257, 762–768. [Google Scholar] [CrossRef]
- Lü, Q.; Qiu, Q.; Zheng, J.; Wang, J.; Zeng, Q. Fractal dimension of concrete incorporating silica fume and its correlations to pore structure, strength and permeability. Constr. Build. Mater. 2019, 228, 116986. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Wu, Y.; Zhou, Y.; Tang, S. Hydration, shrinkage, pore structure and fractal dimension of silica fume modified low heat Portland cement-based materials. Constr. Build. Mater. 2021, 272, 121952. [Google Scholar] [CrossRef]
- Xie, S.; Cheng, Q.; Ling, Q.; Li, B.; Bao, Z.; Fan, P. Fractal and multifractal analysis of carbonate pore-scale digital images of petroleum reservoirs. Mar. Pet. Geol. 2010, 27, 476–485. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; De Schutter, G.; Ye, G.; Sun, W. Fractal and multifractal analysis on pore structure in cement paste. Constr. Build. Mater. 2014, 69, 253–261. [Google Scholar] [CrossRef]
- Goryainov, P.M.; Ivanyuk, G.Y.; Kalashnikov, A.O. Topography formation as an element of lithospheric self-organization. Russ. Geol. Geophys. 2013, 54, 1071–1082. [Google Scholar] [CrossRef]
- Nikulin, I.I.; Kalashnikov, A.O.; Krylov, I.O.; Mikhailova, J.A.; Groshev, N.Y.; Kadyrov, R.I. Fractal Analysis of the Composition and Structure of Sulfide Disseminated Ores in Picritic Gabbro-Dolerites of the Oktyabrsky Deposit, Norilsk Ore Cluster. Mosc. Univ. Geol. Bull. 2023, 78, 239–253. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Ding, S.; Ashour, A.; Yu, F.; Lv, X.; Han, B. Micro-nano scale pore structure and fractal dimension of ultra-high performance cementitious composites modified with nanofillers. Cem. Concr. Compos. 2023, 141, 105129. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, Q.; Deng, D.; Ye, T.; Fang, L. Measuring the pore structure of cement asphalt mortar by nuclear magnetic resonance. Constr. Build. Mater. 2017, 137, 450–458. [Google Scholar] [CrossRef]
- Valori, A.; McDonald, P.J.; Scrivener, K.L. The morphology of C–S–H: Lessons from 1H nuclear magnetic resonance relaxometry. Cem. Concr. Res. 2013, 49, 65–81. [Google Scholar] [CrossRef]
- Mohan, M.K.; Rahul, A.V.; Van Stappen, J.F.; Cnudde, V.; De Schutter, G.; Van Tittelboom, K. Assessment of pore structure characteristics and tortuosity of 3D printed concrete using mercury intrusion porosimetry and X-ray tomography. Cem. Concr. Compos. 2023, 140, 105104. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, X.; Yang, P.; Wang, J.; Zhou, C. Tracing mercury entrapment in porous cement paste after mercury intrusion test by X-ray computed tomography and implications for pore structure characterization. Mater. Charact. 2019, 151, 203–215. [Google Scholar] [CrossRef]
- Wang, Y.S.; Dai, J.G. X-ray computed tomography for pore-related characterization and simulation of cement mortar matrix. Ndt E Int. 2017, 86, 28–35. [Google Scholar] [CrossRef]
- Wang, G.; Shen, J.; Liu, S.; Jiang, C.; Qin, X. Three-dimensional modeling and analysis of macro-pore structure of coal using combined X-ray CT imaging and fractal theory. Int. J. Rock Mech. Min. Sci. 2019, 123, 104082. [Google Scholar] [CrossRef]
- GB/T 17671-2021; Test Method of Cement Mortar Strength (IOS Method). National Standard of the People's Republic of China: Beijing, China, 2021.
- Mandelbrot, B.B.; Mandelbrot, B.B. The fractal geometry of nature. Am. J. Phys. 1982, 51, 286–287. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Kong, L. Multifractal characteristics of Longmaxi Shale pore structures by N2 adsorption: A model comparison. J. Pet. Sci. Eng. 2018, 168, 330–341. [Google Scholar] [CrossRef]
- Lopes, R.; Betrouni, N. Fractal and multifractal analysis: A review. Med. Image Anal. 2009, 13, 634–649. [Google Scholar] [CrossRef] [PubMed]
- Nili, M.; Ehsani, A. Investigating the effect of the cement paste and transition zone on strength development of concrete containing nanosilica and silica fume. Mater. Des. 2015, 75, 174–183. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, S.; Wang, K.; Al Qunaynah, S.; Wan, S.; Yuan, Z.; Xu, P.; Tang, S. A study on the hydration of calcium aluminate cement pastes containing silica fume using non-contact electrical resistivity measurement. J. Mater. Res. Technol. 2023, 24, 8135–8149. [Google Scholar] [CrossRef]
- Liao, Y.; Yao, J.; Deng, F.; Li, H.; Wang, K.; Tang, S. Hydration behavior and strength development of supersulfated cement prepared by calcined phosphogypsum and slaked lime. J. Build. Eng. 2023, 80, 108075. [Google Scholar] [CrossRef]
- Wang, F.; Zai, Y. Fractal and multifractal characteristics of shale nanopores. Results Phys. 2021, 25, 104277. [Google Scholar] [CrossRef]
- Geng, Z.; Tang, S.; Wang, Y.; He, Z.; Wu, K.; Wang, L. Stress relaxation properties of calcium silicate hydrate: A molecular dynamics study. J. Zhejiang Univ.-Sci. A 2024, 25, 97–115. [Google Scholar] [CrossRef]
- Ju, X.; Jia, Y.; Li, T.; Gao, L.; Gan, M. Morphology and multifractal characteristics of soil pores and their functional implication. Catena 2021, 196, 104822. [Google Scholar] [CrossRef]
- Han, X.; Feng, J.; Wang, B. Relationship between fractal feature and compressive strength of fly ash-cement composite cementitious materials. Cem. Concr. Compos. 2023, 139, 105052. [Google Scholar] [CrossRef]
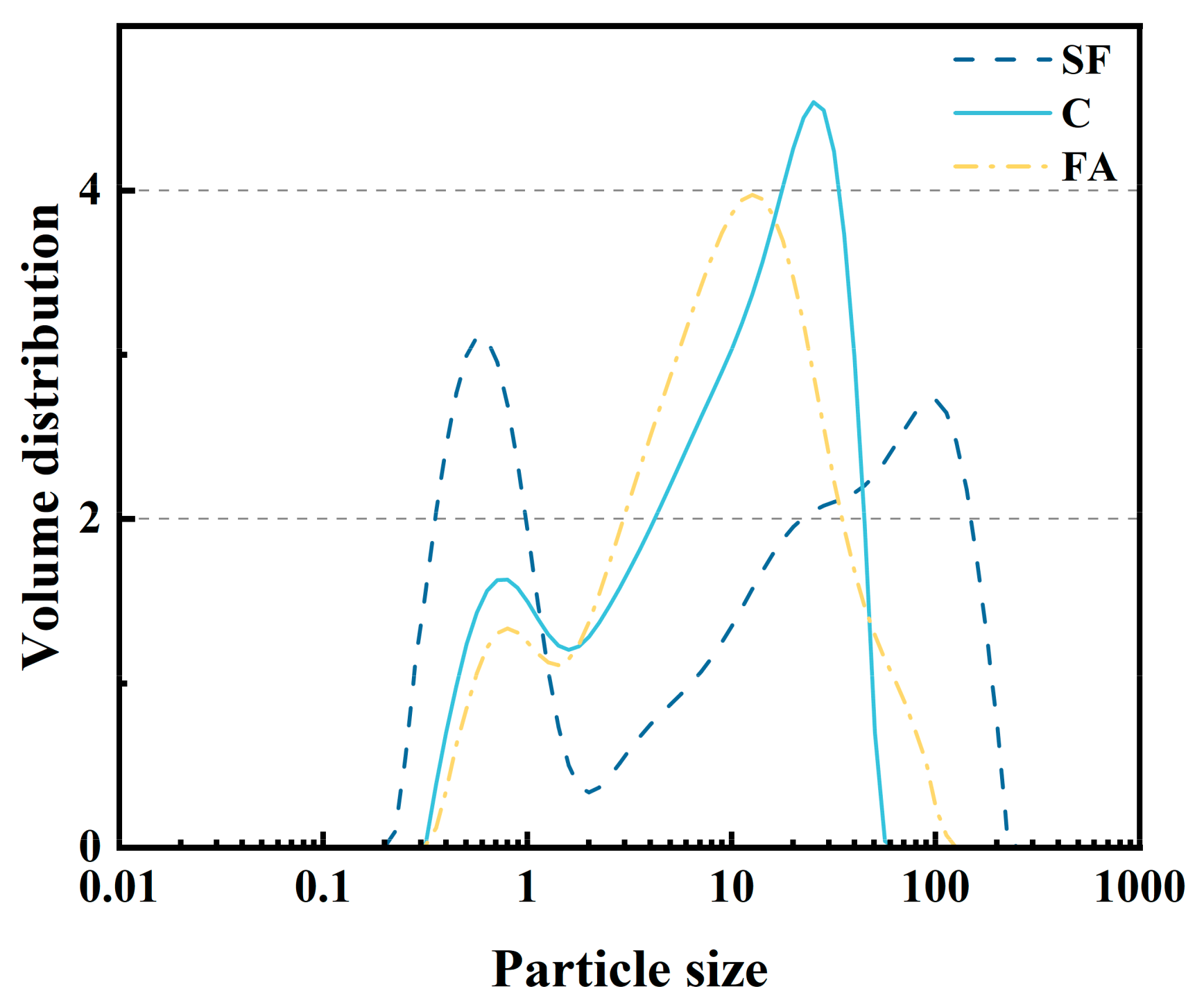
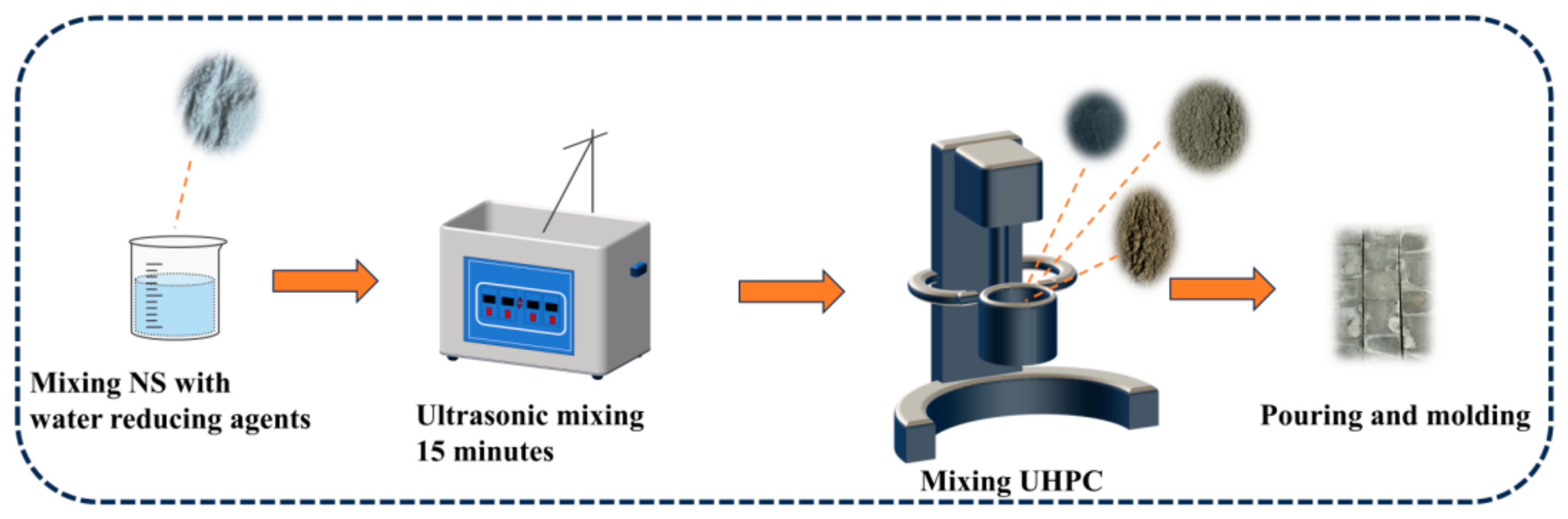



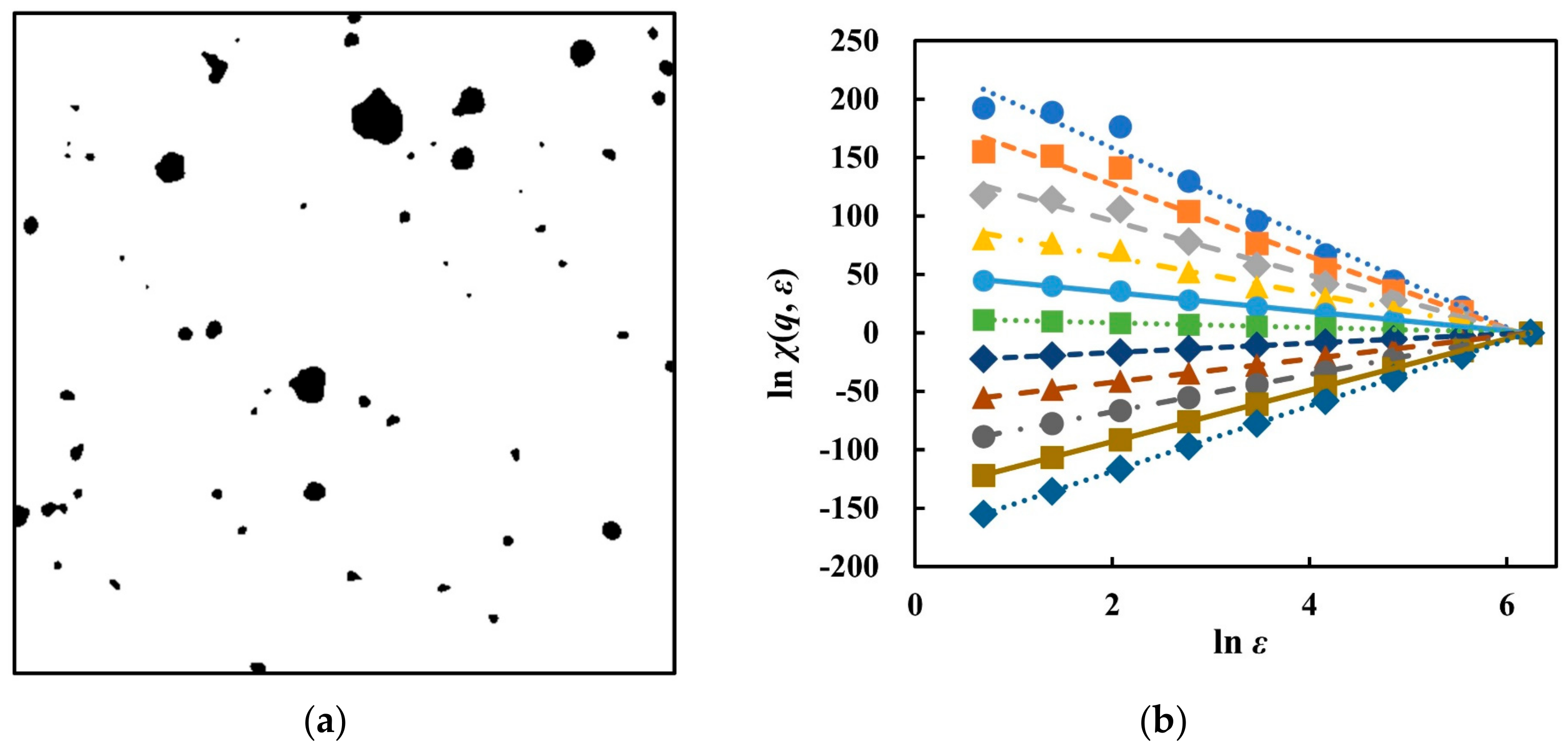
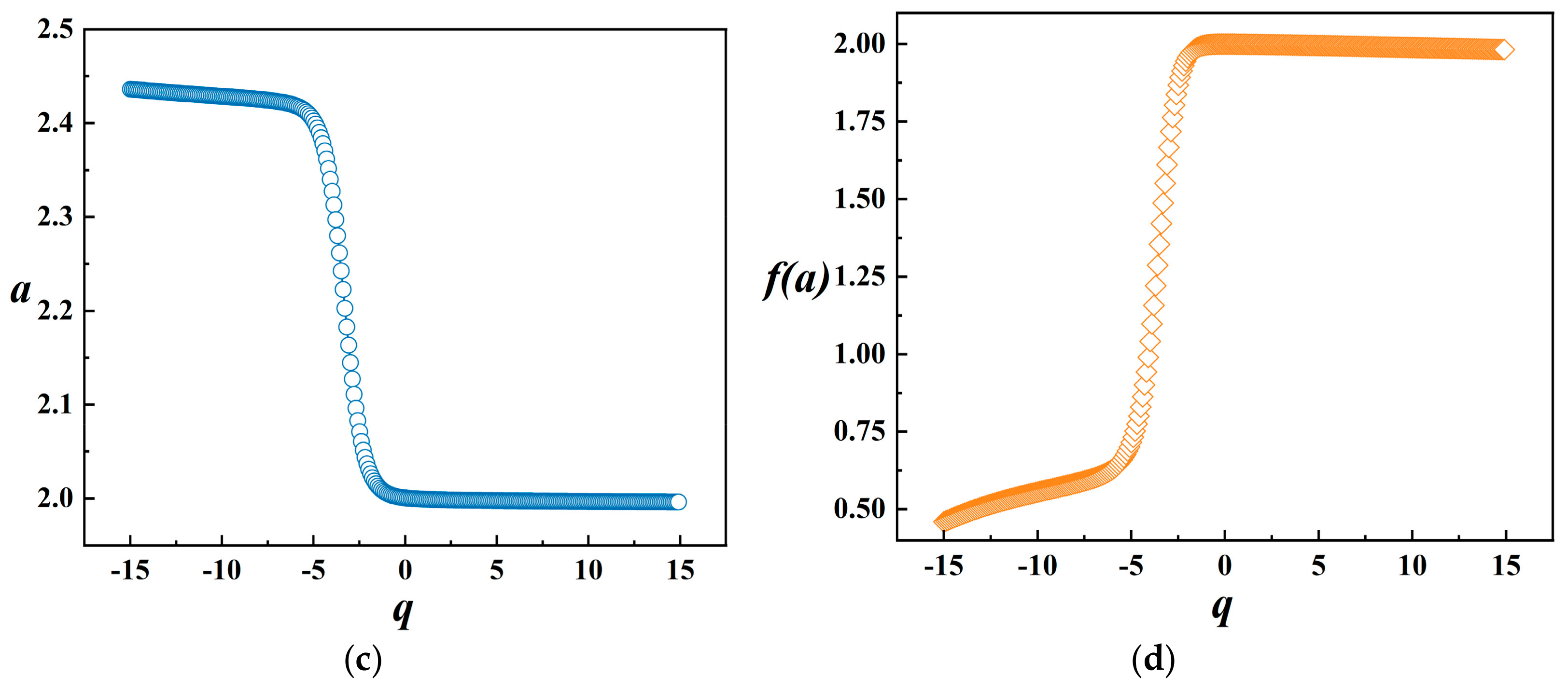

| Chemical Analysis | CaO | Fe2O3 | MgO | SO3 | K2O | SiO2 | Na2O | Al2O3 | TiO2 |
|---|---|---|---|---|---|---|---|---|---|
| C | 66.13 | 2.95 | 3.24 | 3.84 | 0.41 | 17.51 | 0.42 | 4.22 | 1.28 |
| FA | 3.3 | 8.09 | 1.34 | 0.67 | 1.37 | 53 | 0.34 | 24.19 | - |
| SF | 1.82 | 0.24 | 0.87 | 1.65 | 3.07 | 91 | 0.4 | 0.46 | 0.05 |
| No. | C | NS | FA | SF | W | S | Steel Fiber | SP |
|---|---|---|---|---|---|---|---|---|
| OPC | 700 | 0 | 100 | 200 | 180 | 1150 | 156 | 80 |
| N1 | 700 | 10 | 100 | 200 | 180 | 1150 | 156 | 80 |
| N2 | 700 | 20 | 100 | 200 | 180 | 1150 | 156 | 80 |
| N3 | 700 | 30 | 100 | 200 | 180 | 1150 | 156 | 80 |
| N4 | 700 | 40 | 100 | 200 | 180 | 1150 | 156 | 80 |
| No. | Function | F Value | Prob > F |
|---|---|---|---|
| 28d compressive strength vs. Porosity | 17.422275 | 2.25 × 10−2 | |
| 28d compressive strength vs. Mean pore size | 19.19 | 2.20 × 10−2 | |
| 28d compressive strength vs. D | 22.83 | 1.74 × 10−2 | |
| 28d compressive strength vs. ∆a | 190.592455 | 8.23 × 10−4 |
| No. | Parameter | Value | Standard Error | T Value | Prob > |t| | R2 |
|---|---|---|---|---|---|---|
| 28d compressive strength vs. Porosity | A | −8.98 | 2.15 | −4.17 | 0.025 | 0.804 |
| b | 189.198 | 2.34 | 80.85 | 4.17 × 10−6 | ||
| 28d compressive strength vs. Mean pore size | A | −1.118 | 0.25 | −4.38 | 0.022 | 0.82 |
| b | 353.828 | 2.24 | 157.62 | 5.63 × 10−7 | ||
| 28d compressive strength vs. D | A | −253.718 | 51.59 | −4.91 | 0.016 | 0.85 |
| b | 483.93 | 2.03 | 238.08 | 1.63 × 10−7 | ||
| 28d compressive strength vs. ∆a | A | 753.45 | 0.003 | 243,889.8 | 0.0008 | 0.979 |
| b | −1282.94 | 0.005 | −256,324 | 4.58 × 10−10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, D.; Pan, T.; Guo, R.; Wei, Y.; Qi, R.; Fu, C.; Zhang, Z.; Zhu, Y. Fractal and Multifractal Analysis of Microscopic Pore Structure of UHPC Matrix Modified with Nano Silica. Fractal Fract. 2024, 8, 360. https://doi.org/10.3390/fractalfract8060360
Guan D, Pan T, Guo R, Wei Y, Qi R, Fu C, Zhang Z, Zhu Y. Fractal and Multifractal Analysis of Microscopic Pore Structure of UHPC Matrix Modified with Nano Silica. Fractal and Fractional. 2024; 8(6):360. https://doi.org/10.3390/fractalfract8060360
Chicago/Turabian StyleGuan, Dian, Tinghong Pan, Rongxin Guo, Ya Wei, Rongqing Qi, Chaoshu Fu, Ziqi Zhang, and Yukai Zhu. 2024. "Fractal and Multifractal Analysis of Microscopic Pore Structure of UHPC Matrix Modified with Nano Silica" Fractal and Fractional 8, no. 6: 360. https://doi.org/10.3390/fractalfract8060360
APA StyleGuan, D., Pan, T., Guo, R., Wei, Y., Qi, R., Fu, C., Zhang, Z., & Zhu, Y. (2024). Fractal and Multifractal Analysis of Microscopic Pore Structure of UHPC Matrix Modified with Nano Silica. Fractal and Fractional, 8(6), 360. https://doi.org/10.3390/fractalfract8060360









