The Influence of Environmental Temperature on the Passive Oxidation Process in the C/SiC Composite

Abstract

The C/SiC composite plays a crucial role in providing thermal protection for hypersonic vehicles. The ${\mathrm{SiO}}_2$ oxide layer formed via passive oxidation during ablation constitutes a typical porous medium with self-similarity. Given its significant impact on the thermal protection of the material, accurately predicting the variation in the ${\mathrm{SiO}}_2$ oxide layer thickness is of paramount importance. The growth of the oxide layer impedes the diffusion of oxygen within the material. This study considered microstructural parameters of the oxide layer based on high-temperature gas oxidation tests of the C/SiC composite. Fractal theory was utilized to construct a fractal diffusion-reaction kinetics model describing oxygen diffusion within the oxide layer and the evolution of the oxide layer under varying environmental conditions. The finding demonstrated that the existence of the oxide layer significantly influences the passive oxidation of the composite. This study underscored the significance of predicting the impact of environmental parameters on passive oxidation in the practical application of the C/SiC composite and the study result offers a valuable reference for evaluating the thermal resistance of the C/SiC composite.

1. Introduction

In recent years, hypersonic flight in near-space has emerged as a significant research focus. Vehicles in this airspace exhibit characteristics such as a complex lifting body shape, extended aerodynamic heating time and high heat flow. The leading edges of the vehicle’s head and wing rudder, along with other components, confront an extreme environment characterized by ultra-high temperature, strong oxidation and high overload. Therefore, the thermal protection structure and material for hypersonic vehicles represent a crucial technology in aircraft design and manufacturing [1,2]. The C/SiC composite, known for its high specific strength, good thermal stability and excellent antioxidant performance, represents a type of high-temperature thermal protection material with significant development potential in the aerospace field. Research on the oxidation mechanism and the prediction method for the C/SiC material in a high-temperature aerobic environment holds considerable value for engineering application [3,4].

In the study of the oxidation of material, Wagner [5] was the first to theoretically investigate the active and inert oxidation behavior of silicon at high temperature, analyzing the relationship between the oxidation rate of silicon and the partial pressure of oxygen. Deal et al. [6] investigated the kinetics of thermal oxidation of silicon and proposed the well-known parabolic equation for the thickness of the oxide film by considering the reactions taking place at the interface of the oxide layer and the gas diffusion process. Narushima et al. [7] observed that the oxidation behavior of SiC involves passive oxidation and follows a two-step parabolic oxidation kinetics. Sakraker et al. [8] conducted experimental investigations on the passive/active oxidation behavior of C/C-SiC, a thermal protection material for the hypersonic space shuttle, to determine the boundaries between passive and active oxidation in the thermal protection system, occurring when the spacecraft enters the Earth’s atmosphere. In this scenario, active oxidation leads to material loss, while passive oxidation forms a protective film, thus providing a new way of thinking about the study of material oxidation.

The practical application value of composite material has attracted the attention of many scholars. Chen et al. [9] employed chemical equilibrium calculations to analyze the thermodynamic behavior of SiC during the transition between passive and active oxidation state. Material response analysis revealed that surface temperature jumps during the thermal oxidation process of SiC, corresponding to a transition from passive to active oxidation. Zhou et al. [10] developed a novel passive oxidation model for the C/SiC composite, integrating the gas diffusion behavior in the pores with the kinetic relationship of the oxidation reaction. Wang et al. [11] explored the theoretical model and calculation method for oxidative ablation behavior of the C/SiC material based on the oxidation mechanism of the C/SiC composite under varying temperature and pressure conditions. The analysis included the impact of different factors on the passive and active oxidation of the materials. Notably, the above studies did not account for the influence of microstructural parameters of the oxide layer on the diffusion of oxygen in porous media.

Over the years, many scholars have applied the fractal theory to study the complex structure of porous media. Fractal theory investigates structural features that exhibit the same principle of elemental distribution across multiple observation levels. Matter in nature aligns more closely with stochastic fractal matter characterized by a higher complexity [12]. Many natural phenomena described by the fractal model demonstrate statistical self-similarity, rendering them shapeless or amorphous. Examples include coastlines with curved boundaries, pore structures in porous media, clouds, mountains, lightning and more [13,14]. Porous media exhibit a complex and irregular distribution of solid particles and pore channels. In line with the definition of the fractal object, porous media can be conceptualized as a fractal entity, with its solid particles and pore channels representing fractal structures [15,16]. The pores within porous media play a crucial role in fluid flow and transportation. Utilizing fractal characterization for these pores enhances our understanding of the mechanism governing flow and transportation in porous media [17].

In the realm of fractal theory for porous media, Yu and Cai et al. [18,19,20] conducted studies on diverse types of porous media, such as soil, gravel and fibers. Their findings revealed a statistically significant fractal characteristic in the pore channels or internal capillaries of these porous media within a specific range. The researchers formulated a theory to describe porous media with fractal feature, which has been extensively utilized in the domain of heat and mass transfer within porous media. Zheng et al. [21] formulated a fractal model for gas diffusion in porous media based on fractal theory. They conducted an analysis to explore the influence of parameters, including the fractal dimension, on the gas diffusion coefficient. Zhu et al. [22] utilized the image enhancement technique on scanning electron microscopy images of red sandstone. Precise segmentation of SEM images, in conjunction with the box-counting method, can provide crucial fractal parameters for porous media. Wang et al. [23] proposed a fractal reconstruction method for the surface image of ultrahigh-temperature ceramics after repeated thermal shocks, which is of great practical significance for evaluating their thermal resistance performance. Kou et al. [24] proposed an improved pore-solid fractal model to predict the permeability of saturated geotechnical material and the modified model integrated the discrete cavity pore and solid phase of the original model.

Fractal theory had also been applied to the study of gas flow and gas diffusion in porous media. Zheng et al. [25] presented an analytical model for predicting the relative gas diffusivity in porous media containing a y-shaped fractal tree network, establishing the relationship between the gas diffusion coefficient and microstructural parameters. Kou et al. [26] analyzed the optimal structure of tree branching networks for both laminar and turbulent flow in smooth and rough pipes, explaining the application of many natural tree branching network systems in the design of efficient transportation systems. Miao et al. [27] proposed a new permeability model for tree branching networks based on their fractal characteristics, systematically investigating the influence of microstructural parameters on the effective permeability of the networks. Subsequently, Zheng et al. [28] established a fractal model for gas diffusion in porous nanofibers with rough surfaces, considering pore size distribution and rough surfaces according to the fractal scaling law. They also investigated the impact of microstructural parameters of porous fiber material on gas diffusion. Therefore, we can also extend the study of gas diffusion in porous media to the modeling of composite oxidation.

During the occurrence of passive oxidation in the C/SiC composite, factors such as the formation of the oxide layer, consumption of composite material and alteration in the overall material thickness are crucial considerations. This paper introduced a passive oxidation model developed from the experimental results on the heating oxidation of the C/SiC composite and the theory of fractal gas diffusion in porous media. The passive oxidation model considers gas diffusion within the oxide layer relative to its microstructure, taking into account varying environmental temperatures during heating. The objective of this model was to predict the oxidation of the C/SiC composite and evaluate its ablation resistance.

2. Oxidation Behavior of the C/SiC Composite

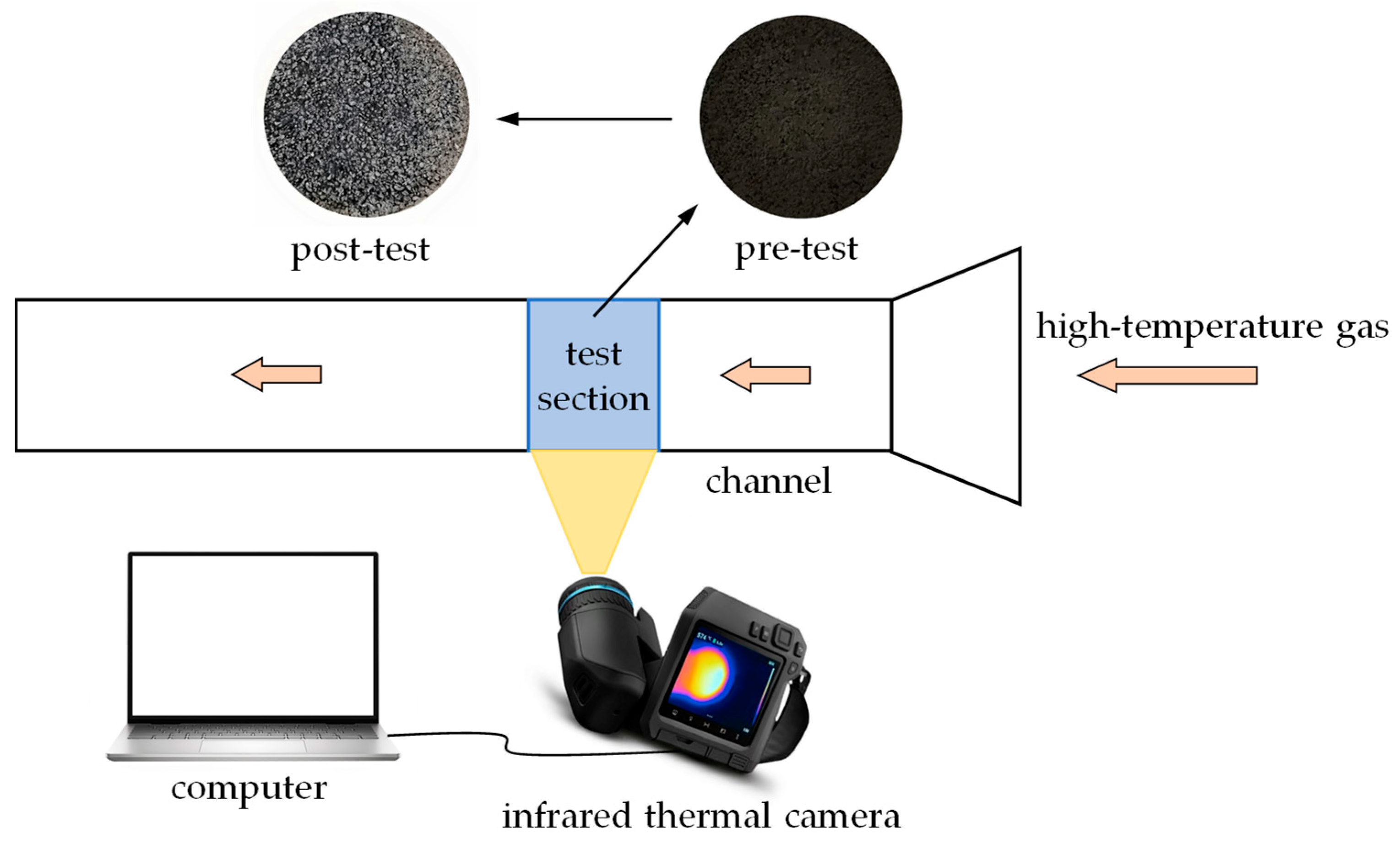
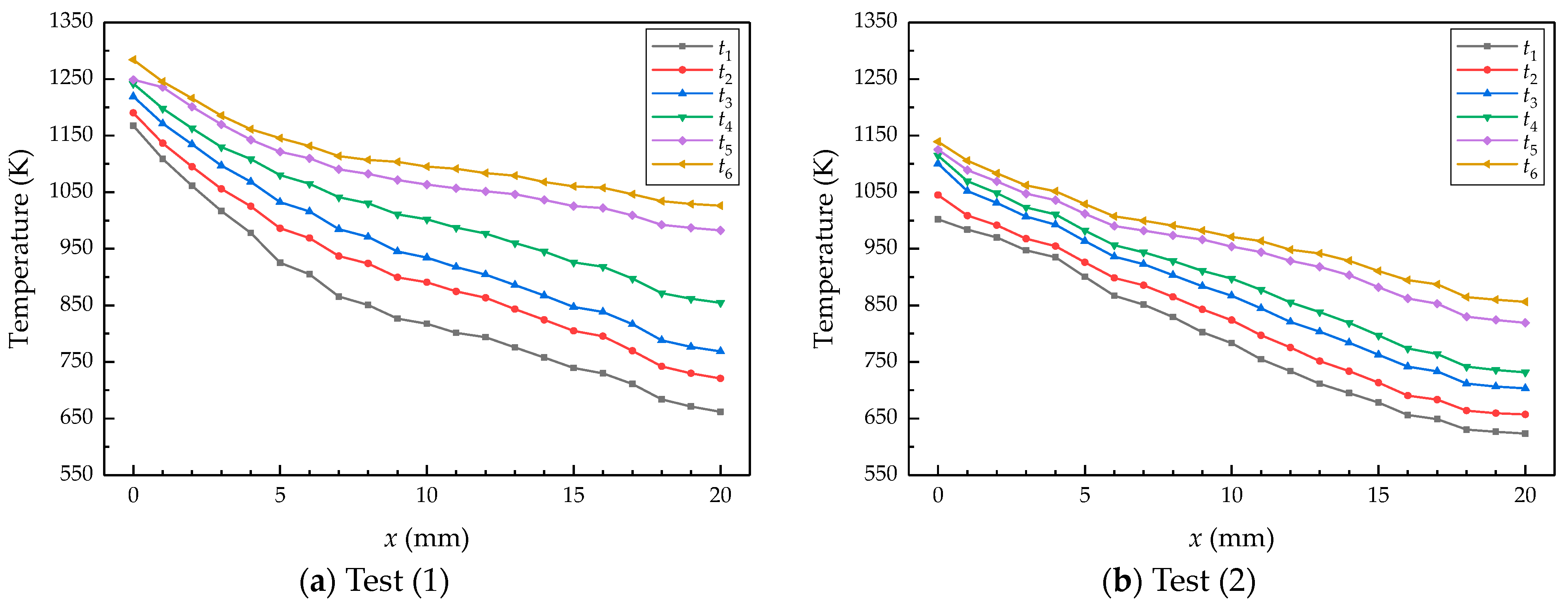
2.1. Heating Oxidation Experiment

The cylindrical C/SiC composite with a diameter of 31.5 mm and a thickness of 6.5 mm was chosen for this experiment to investigate heating oxidation. As depicted in Figure 1, the composite material was positioned in the test section and we heated it by introducing high-temperature gas into the pipe. Furthermore, we directed the infrared thermal camera towards the test section and connected it to a computer to record the temperature distribution on the surface of the composite material. The experimental result revealed the production of a small amount of white substance on the surface of the composite material. Throughout the experiment, the white substance progressively accumulated, acting as a barrier that hindered direct contact between the incoming oxygen and the material. This hindrance prevented the material from undergoing further oxidation, thereby realizing the oxidation resistance of the composite material.

To investigate the influence of incoming gas temperature on the oxidation of the composite, two tests were conducted: one at an incoming gas temperature of 1300 K and the other at 1180 K, each lasting two for hours. The infrared thermal camera can generate a temperature map of the scene by capturing invisible infrared energy emitted by the object. Various colors on the thermal image depict different temperatures of the measured object, allowing for observation of the temperature distribution of the target [29,30]. Figure 2 displays the temperature distribution on the composite surface in the clamping device for test (1) and test (2) captured via the infrared camera at various times during the early stages of the experiment, respectively. The figures illustrate a brief temperature increase in the C/SiC composite during the experiment attributed to the heating of the high-temperature gas. The temperature decreased gradually from the windward front to the rear of the material. Moreover, the material experienced a higher temperature rise with an increase in the incoming gas temperature.

Temperature distribution at various material locations was analyzed along the sampling lines on the thermal image captured via the infrared thermal camera, where the x-axis starts at the edge of the material and the positive direction is the direction of the sampling line from upstream to downstream on the thermal image. Figure 3 illustrates the temperature variation at diverse locations during the initial warming of the composite in both tests, with distinct curves representing various time points ($t_1<\dots <t_6$). Owing to the heating effect of the high-temperature gas, the temperature of the C/SiC composite rose rapidly. The warming of the material decreased gradually from the region closest to the incoming gas towards the material interior. The comparison of the results from the two tests suggests that a higher incoming temperature corresponded to a greater temperature rise in the material.

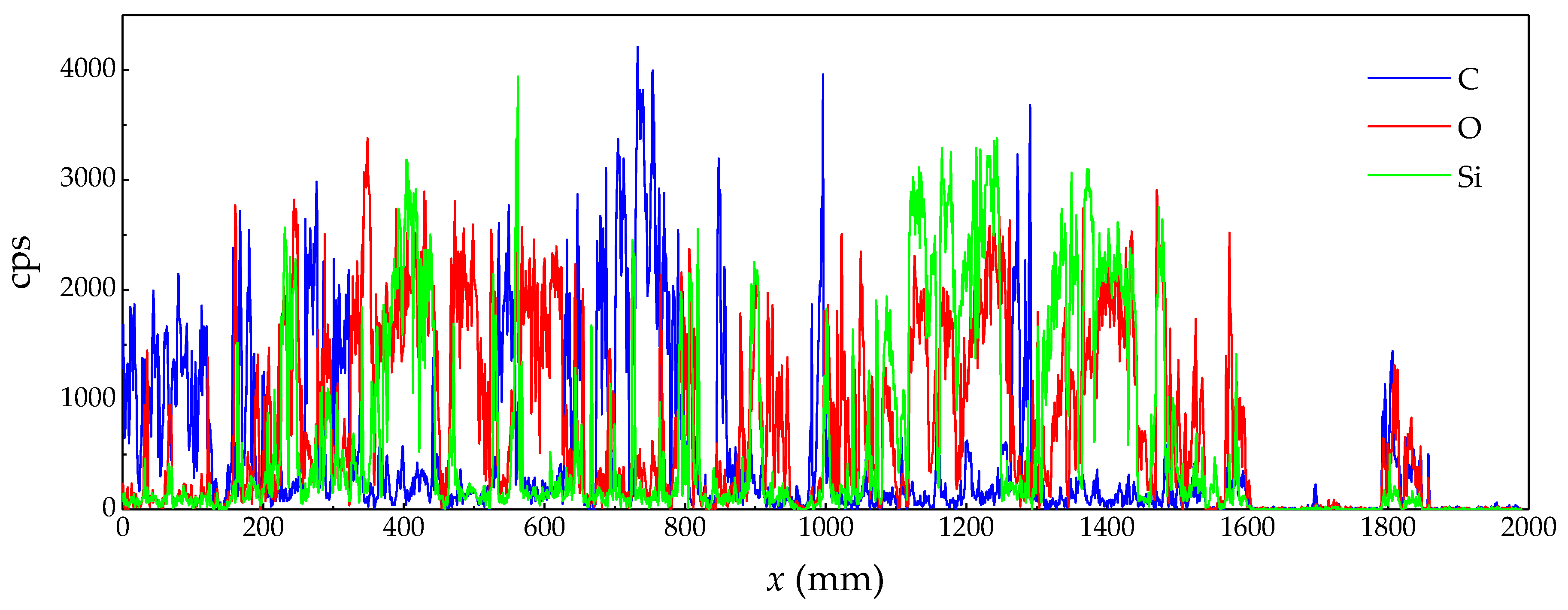
2.2. Analysis of Experimental Product

The scanning electron microscope (SEM) is a modern analytical device with images featuring a large depth of field. This characteristic aids in creating a three-dimensional representation of the sample’s surface structure, allowing us to utilize SEM for the characterization and analysis of porous media surface morphology [31,32]. We took samples from the surface of the oxidized composite and scanned the samples using a SEM model TESCAN MIRA LMS. SEM micrographs, as depicted in Figure 4, reveal the formation of porous media on the surface of the C/SiC composite, exhibiting varying pore sizes. Upon comparing different locations of the oxidized composite, it was observed that porous media resulting from oxidation was more pronounced in the upstream gas location than in the downstream gas location. This suggested that a higher temperature corresponded to an accelerated material oxidation rate, leading to increased formation of porous media in a high-temperature environment.

Energy dispersive X-ray spectroscopy (EDX) analysis is a commonly employed technique for measuring chemical elements in fine particles. It determines the elements present in the sample by analyzing the characteristic X-ray wavelengths of different elements [33,34,35]. Various locations on the surface of the C/SiC composite post-oxidation in high-temperature gas underwent EDX analysis using a detector manufactured by Oxford Instrument. As illustrated in Figure 5, the horizontal axis represents the X-ray energy and the vertical axis denotes the signal intensity. The EDX analysis graph revealed the presence of oxygen element on the surface of the composite material after exposure to high-temperature gas, confirming the oxidation of the composite material in the high-temperature environment, with oxide formation evident on the material surface. Additionally, by comparing the EDX analysis plots at different locations on the composite, it was observed that the percentage of oxygen element in the oxidized material was higher upstream of the gas flow than downstream. This suggested that the oxidation rate of the composite increased with the rise in temperature.

3. Physical Model

3.1. Fractal Theory

Accumulated evidence supports the notion that the majority of random and disordered porous media display distinct fractal feature, classifying them as fractal porous media. In line with fractal geometry theory, Yu [19] employed the fractal scaling law to elucidate the relationship between the cumulative number of pores N and the pore size for pore area greater than or equal to a, which is

$$N(A_d\ge a)={\left(\frac{a_{\max }}{a}\right)}^{\frac{D_f}{2}},$$

(1)

where $A_d$ represents the area scale, a is the pore area and $a_{\max }$ is the maximum pore area. Additionally, $D_f$ denotes the pore area fractal dimension, which is $0<D_f<2$ in two dimensions and $0<D_f<3$ in three dimensions.

One can hypothesize that porous media comprise a series of curved capillaries with variable cross-sectional areas. Yu [19] proposed a fractal model for these curved capillaries, establishing the relationship between the radius and length of the capillary as

$$L_t(\lambda )={\lambda }^{1-D_t}{L}_0^{D_t},$$

(2)

where $D_t$ is the tortuosity fractal dimension, $\lambda$ is the diameter of the capillary, $L_t\left(\lambda \right)$ stands for the length of the capillary and $L_0$ represents the characteristic length in the direction of the pressure gradient.

The cross-sectional SEM images of the oxide layer underwent processing with an image enhancement technique [22]. The pore area fractal dimension $D_f$ and tortuosity fractal dimension $D_t$ of the oxide layer, as depicted in Figure 6, were determined using the box-counting method and fitting a straight line.

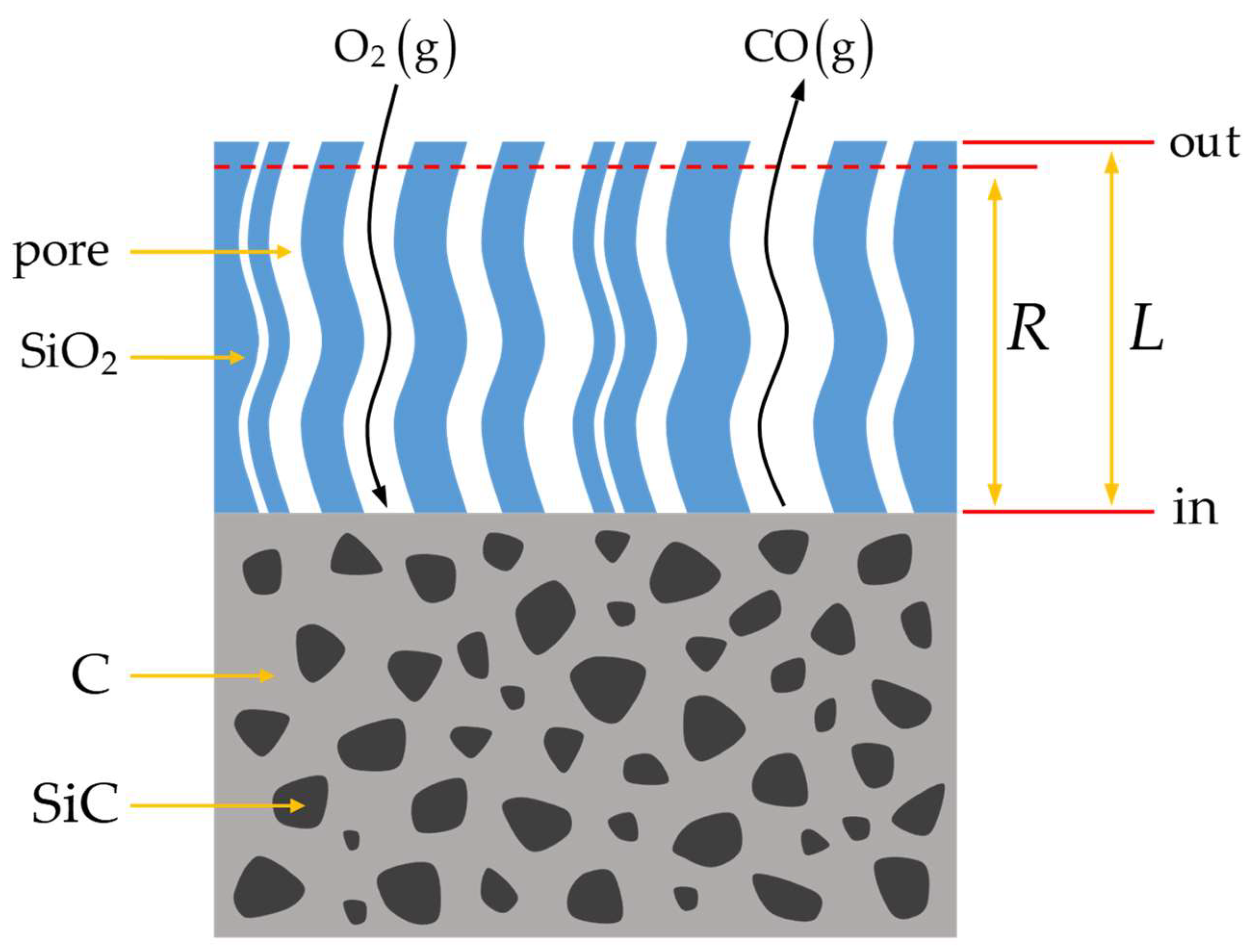
3.2. Oxidation Model

Figure 7 and Figure 8 illustrate the elemental characterization of the C/SiC composite following oxidation in high-temperature gas, achieved via EDX scanning along a straight line, where the horizontal axis of Figure 8 corresponds to the distribution along the yellow line in Figure 7 and the vertical axis indicates the signal intensity. The presence of oxygen element on the surface of the C/SiC composite after exposure to high-temperature gas is evident in the figures, signifying the formation of oxide.

The oxidative ablation characteristic of the C/SiC composite depended on several factors including surface temperature, partial pressure of oxygen and other relevant parameters. Under specific temperature condition, the oxidation mechanism on the surface of the C/SiC material was governed by the partial pressure of incoming oxygen. Moreover, the oxidation mechanism on the surface of the material underwent a gradual transition from active oxidation to passive oxidation as the partial pressure of oxygen shifted from low to high. As indicated by previous research finding [36], the material tested in this paper was in a state of passive oxidation at various locations.

The subsequent fractal diffusion-reaction kinetics model was formulated based on the passive oxidation mechanism of the C/SiC composite. Oxygen primarily reached the bottom layer through gaseous diffusion across pores of varied sizes and curved capillaries within the solid oxide layer. At the interface between the oxide and primary layer, oxygen underwent oxidation with C and SiC, producing ${\mathrm{SiO}}_2$, resulting in the formation of the complex porous oxide layer. Subsequently, the CO generated from the oxidation reaction escaped outward via counter-diffusion through pores of different sizes and curved capillaries. The passive oxidation reaction equation for the C/SiC composite can be represented as

$${\mathrm{C}}_{\alpha }{\left(\mathrm{SiC}\right)}_{1-\alpha }\left(\mathrm{s}\right)+\left(1.5-\alpha \right){\mathrm{O}}_2\left(\mathrm{g}\right)\to \left(1-\alpha \right){\mathrm{SiO}}_2\left(\mathrm{s}\right)+\mathrm{CO}\left(\mathrm{g}\right),$$

(3)

where $\alpha$ represents the mole fraction of C in the C/SiC composite.

Utilizing the fractal diffusion-reaction kinetics model, the passive oxidation model for the C/SiC composite was formulated and is illustrated in Figure 9.

To simplify the modeling process, the following assumptions were made:

• The oxidation reaction was at a steady state, where the rate of oxygen consumption equaled the rate of oxygen diffusion flow;
• The oxidation recession rate of both C and SiC within the C/SiC composite was assumed to be identical;
• Capillaries with distinct pores were disconnected and the pore size within each individual capillary was considered uniform;
• The inlets and outlets of all orifices were positioned on the same plane.

In the process of passive oxidation of the C/SiC composite, a self-similar porous oxide layer develops on the composite surface. Gas diffusion in porous media is influenced by two diffusion mechanisms: bulk diffusion and Knudsen diffusion [21]. The dominance of either bulk or Knudsen diffusion is primarily determined by the pore size or Knudsen number [37]. The Knudsen number is mathematically represented as

$$Kn=\frac{2l}{\lambda },$$

(4)

where l is the mean free path of the gas molecule and $l=k_{B}T/\sqrt{2}\pi p{d}^2$, where $k_B$ denotes the Boltzmann constant, T signifies the temperature, p represents the pressure and d is the diameter of the gas molecule.

Elaborating on the intricate structure and configuration of capillary tubes in relation to curved capillary tortuosity results in $\tau ={\left(L_0,/,\lambda \right)}^{D_t-1}$. When both diffusion modes jointly govern the gas diffusion process within porous media, the adjusted gas diffusion coefficient for gas in a single curved orifice is [21]

$$D_{\mathrm{K}-\mathrm{b}}=\frac{2k_B^{1.5}{T}^{1.5}{\lambda }^{2D_t-2}}{3{\pi }^{1.5}{d}^{2}p{m}^{0.5}{L}_0^{2D_t-2}}\left(1-e^{-\lambda /l}\right),$$

(5)

where m represents the molecular mass of the gas.

Considering a collection of fractal capillary ensembles and based on the principle of fractal geometry and the meandering capillary model, the effective diffusion coefficient of the gas within porous media is determined through integration across the complete spectrum of capillary sizes [21], which can be formulated as

$$D_{eff}=\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}}{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{L}_0^{3D_t-3}{A}_t}{{\displaystyle \int }}_{{\lambda }_{min}}^{{\lambda }_{max}}{\lambda }^{3D_t-D_f-2}\left(1-e^{-\lambda /l}\right)d\lambda ,$$

(6)

where ${\lambda }_{\max }$ is the maximum pore diameter, ${\lambda }_{\min }$ is the minimum pore diameter and $A_t$ is the total cross-sectional area of porous media, expressed as

$$A_t=\frac{\pi D_f{\lambda }_{max}^2}{4\phi \left(2-D_f\right)}\left[1-{\left(\frac{{\lambda }_{\min }}{{\lambda }_{\max }}\right)}^{2-D_f}\right].$$

(7)

where $\phi$ is the porosity of the ${\mathrm{SiO}}_2$ oxide layer.

Oxygen primarily traverses the solid oxide layer via gas diffusion within its pores. The equation describing the molar flow rate of oxygen diffusion per unit area in porous media is expressed as [21]

$$q_{{\mathrm{O}}_2}=D_{eff}\frac{\mathrm{d}{C}_{{\mathrm{O}}_2}}{\mathrm{d}y},$$

(8)

where $C_{{\mathrm{O}}_2}$ denotes the molar concentration of oxygen at a specific height within the pore and y is the height in the direction perpendicular to the mode.

Taking into account the influence of the oxide layer thickness on the gas diffusion coefficient and substituting Equation (6) into Equation (8), the oxygen diffusion flow rate can be derived by integrating along the normal height of the oxide layer as follows

$$q_{{\mathrm{O}}_2}=\frac{\left(3D_t-2\right)k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta }{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t{L}^{3D_t-2}}\left(C_{{\mathrm{O}}_2,\mathrm{o}}-C_{{\mathrm{O}}_2,\mathrm{i}}\right),$$

(9)

$$\beta ={{\displaystyle \int }}_{{\lambda }_{min}}^{{\lambda }_{max}}{\lambda }^{3D_t-D_f-2}\left(1-e^{-\lambda /l}\right)d\lambda ,$$

(10)

where $L$ denotes the thickness of the oxide layer, $C_{{\mathrm{O}}_2,\mathrm{o}}$ is the environmental oxygen concentration and $C_{{\mathrm{O}}_2,\mathrm{i}}$ is the oxygen concentration at the interface between the oxide layer and the original composite.

The oxidation reaction of the C/SiC composite material is represented by the first-order relation [6], given the assumption that the rate of oxygen consumption during the oxidation reaction equals the rate of oxygen diffusion flow, the rate of oxygen flow during the oxidation reaction can be expressed as: $q_{{\mathrm{O}}_2}=k_{{\mathrm{O}}_2}{C}_{{\mathrm{O}}_2,\mathrm{i}}$, where $k_{{\mathrm{O}}_2}$ is the reaction rate constant for the oxidation reaction, determined by the reaction kinetics model. Therefore, the oxygen flow rate per unit area within porous media during the oxidation reaction can be determined as

$$q_{{\mathrm{O}}_2}=\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta C_{{\mathrm{O}}_2,\mathrm{o}}}{\frac{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t{L}^{3D_t-2}}{\left(3D_t-2\right)}+\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta }{k_{{\mathrm{O}}_2}}}.$$

(11)

It was evident that the oxidation process of the C/SiC composite was primarily governed by the combined influence of the gas diffusion characteristic and reaction kinetics within porous media.

Following the linear-parabolic thickness model proposed by Deal and Grove [6], denoted as $x_0^2+A{x}_0=B\left(t+{\tau }_0\right)$, where $x_0$ is the thickness of the oxide layer, a function of time t. ${\tau }_0$ corresponds to the offset of the time coordinate, correcting for the presence of the initial oxide layer. They defined B/A as the linear rate and B as the parabolic rate. The literature [10] provides the two corresponding rate constants for the oxidation of the C/SiC composite as

$$\frac{B}{A}=5.8087\times {10}^{6}exp\left(-\frac{195800}{RT}\right),$$

(12)

$$\left\{\begin{array}{l}B=524.19exp\left(-\frac{119244}{RT}\right),\hspace{1em}\hspace{1em}\hspace{1em} T\le 1673\mathrm{K},\\ B=1.505\times {10}^{6}exp\left(-\frac{230000}{RT}\right),\hspace{1em} T>1673\mathrm{K}.\end{array}\right.$$

(13)

The reaction rate of oxygen in the C/SiC composite can be represented as [10]

$$k_{{\mathrm{O}}_2}=2D_{eff}\frac{B/A}{B}.$$

(14)

Consequently, the oxygen flow rate can be formulated as

$$q_{{\mathrm{O}}_2}=\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta C_{{\mathrm{O}}_2,\mathrm{o}}}{\frac{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t{L}^{3D_t-2}}{\left(3D_t-2\right)}+\frac{3{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t{L}^{3D_t-3}B}{\left(B/A\right)}}.$$

(15)

Assuming that the oxygen consumption rate and the oxygen diffusion flow rate were equal during the oxidation reaction of the C/SiC composite. From Equation (3), the relationship between the molar amount of oxygen consumption and the molar amount of ${\mathrm{SiO}}_2$ generation in the oxidation process is $\left(1.5-\alpha \right)/q_{{\mathrm{O}}_2}=\left(1-\alpha \right)/q_{{\mathrm{SiO}}_2}$. From the conservation of mass, the mass of ${\mathrm{SiO}}_2$ generation per unit area per unit time can be obtained as $m_{{\mathrm{SiO}}_2}=\left(1-\alpha \right)q_{{\mathrm{O}}_2}{M}_{{\mathrm{SiO}}_2}/\left(1.5-\alpha \right)$. Considering that the oxide layer is a porous medium, we can derive the equation for the growth rate of the ${\mathrm{SiO}}_2$ thickness as follows

$$\frac{\mathrm{d}L}{\mathrm{d}t}=\frac{1}{1-\phi }\frac{1-\alpha }{1.5-\alpha }\frac{M_{{\mathrm{SiO}}_2}}{{\rho }_{{\mathrm{SiO}}_2}}{q}_{{\mathrm{O}}_2},$$

(16)

where t represents the oxidation time, $M_{{\mathrm{SiO}}_2}$ is the molar mass of ${\mathrm{SiO}}_2$ and ${\rho }_{{\mathrm{SiO}}_2}$ is the density of ${\mathrm{SiO}}_2$.

As oxygen diffuses into the interior of the oxide layer, the C/SiC composite undergoes gradual consumption through oxidation. From Equation (3), the relationship between the molar amount of oxygen consumption and the molar amount of composite consumption is $\left(1.5-\alpha \right)/q_{{\mathrm{O}}_2}=1/q_{\mathrm{C}/\mathrm{SiC}}$. Therefore, the mass of composite consumption per unit area per unit time can be obtained as $m_{\mathrm{C}/\mathrm{SiC}}=q_{{\mathrm{O}}_2}\left[0.5\alpha M_{\mathrm{C}}+1.5\left(1-\alpha \right)M_{\mathrm{SiC}}\right]/\left(1.5-\alpha \right)$ and the receding rate of the original composite can be formulated as

$$\frac{\mathrm{d}R}{\mathrm{d}t}=-\frac{1}{1.5-\alpha }\left[0.5\alpha \frac{M_{\mathrm{C}}}{{\rho }_{\mathrm{C}}}+1.5\left(1-\alpha \right)\frac{M_{\mathrm{SiC}}}{{\rho }_{\mathrm{SiC}}}\right]q_{{\mathrm{O}}_2},$$

(17)

where $R$ is the recession of the composite, $M_{\mathrm{C}}$ and ${\rho }_{\mathrm{C}}$ are the molar mass and density of C, while $M_{\mathrm{SiC}}$ and ${\rho }_{\mathrm{SiC}}$ are the molar mass and density of SiC, respectively.

The surface of the C/SiC composite recedes due to the gradual reduction in the oxidation reaction, while it grows due to the generation of the oxide layer. Therefore, the overall change in the thickness of the composite during passive oxidation is regarded as

$$\Delta L=L+R.$$

(18)

3.3. Simplification of the Oxidation Model

For the ease of analyzing the physical significance of the fractal diffusion-reaction kinetics model and examining the factors influencing passive oxidation, the oxygen flow rate within porous media can also be expressed as

$$q_{{\mathrm{O}}_2}=\frac{C_{{\mathrm{O}}_2,\mathrm{o}}{D}_{eff}}{\frac{L}{\left(3D_t-2\right)}+\frac{D_{eff}}{k_{{\mathrm{O}}_2}}}.$$

(19)

Thus, the rate equation describing the growth of the oxide layer thickness can be formulated as

$$\frac{\mathrm{d}L}{\mathrm{d}t}=\frac{{\eta }_1}{1-\phi }\frac{C_{{\mathrm{O}}_2,\mathrm{o}}{D}_{eff}}{\frac{L}{\left(3D_t-2\right)}+\frac{D_{eff}}{k_{{\mathrm{O}}_2}}},$$

(20)

$${\eta }_1=\frac{1-\alpha }{1.5-\alpha }\frac{M_{{\mathrm{SiO}}_2}}{{\rho }_{{\mathrm{SiO}}_2}}.$$

(21)

The equation revealed that the growth rate of ${\mathrm{SiO}}_2$ is influenced by both the gas diffusion and oxidation reaction processes. In the context of passive oxidation for the C/SiC composite, the fractal diffusion-reaction kinetics model in this paper considered the variation of the effective diffusion coefficient of the gas within the oxide layer as its thickness increased, aiming to enhance the accuracy of the model.

When $0\le L\ll D_{eff}/k_{{\mathrm{O}}_2}$, at this point $L\to 0$, then:

$$\frac{\mathrm{d}L}{\mathrm{d}t}=\frac{{\eta }_1{C}_{{\mathrm{O}}_2,\mathrm{o}}}{1-\phi }{k}_{{\mathrm{O}}_2}.$$

(22)

According to the equation, the growth rate of the ${\mathrm{SiO}}_2$ oxide layer thickness is governed by the kinetic parameters of the oxidation reaction.

If neither $L\ll D_{eff}/k_{{\mathrm{O}}_2}$ nor $L\gg D_{eff}/k_{{\mathrm{O}}_2}$ is present, then there is

$$\frac{\mathrm{d}L}{\mathrm{d}t}=\frac{{\eta }_1{C}_{{\mathrm{O}}_2,\mathrm{o}}}{1-\phi }\frac{D_{eff}}{\frac{L}{\left(3D_t-2\right)}+\frac{D_{eff}}{k_{{\mathrm{O}}_2}}}.$$

(23)

In this scenario, the growth rate of the ${\mathrm{SiO}}_2$ oxide layer thickness was determined by the gas diffusion coefficient, the oxidation kinetic characterization parameters and the current thickness of ${\mathrm{SiO}}_2$.

When $L\gg D_{eff}/k_{{\mathrm{O}}_2}$, then

$$\frac{\mathrm{d}L}{\mathrm{d}t}=\frac{\left(3D_t-2\right){\eta }_1{C}_{{\mathrm{O}}_2,\mathrm{o}}}{1-\phi }\frac{D_{eff}}{L}.$$

(24)

At this point, the growth rate of the oxide layer thickness is influenced by both the current thickness of the oxide layer and the gas diffusion coefficient within porous media.

As the oxide layer continues to grow, when $L\gg D_{eff}/k_{{\mathrm{O}}_2}$ and $L\gg {\eta }_1{D}_{eff}$, it exhibits $\mathrm{d}L/\mathrm{d}t\to 0$, indicating that as the thickness of the oxide layer increases, its growth rate decreases and gradually approaches zero. At this point, the oxide layer is approximately in a steady state, putting the material surface in a non-ablative state. The oxidation reaction forms a protective antioxidant film that shields the material surface from damage under high-temperature conditions.

In calculating the growth rate of the oxide layer thickness, consider the oxidation kinetic parameters only when dealing with a very thin oxide layer. For simplicity, we choose the case of $L\gg D_{eff}/k_{{\mathrm{O}}_2}$ to numerically analyze the specific situation of the oxide layer thickness change. Therefore, simplifying Equation (19) as

$$q_{{\mathrm{O}}_2}=\frac{\left(3D_t-2\right)C_{{\mathrm{O}}_2,\mathrm{o}}{D}_{eff}}{L}.$$

(25)

Substituting Equation (25) into Equations (16) and (17) respectively, we achieve

$$\frac{\mathrm{d}L}{\mathrm{d}t}=\frac{\left(3D_t-2\right){\eta }_1}{1-\phi }\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta C_{{\mathrm{O}}_2,\mathrm{o}}}{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t{L}^{3D_t-2}},$$

(26)

$$\frac{\mathrm{d}R}{\mathrm{d}t}=-\left(3D_t-2\right){\eta }_2\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta C_{{\mathrm{O}}_2,\mathrm{o}}}{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t{L}^{3D_t-2}},$$

(27)

$${\eta }_2=\frac{1}{1.5-\alpha }\left[0.5\alpha \frac{M_{\mathrm{C}}}{{\rho }_{\mathrm{C}}}+1.5\left(1-\alpha \right)\frac{M_{\mathrm{SiC}}}{{\rho }_{\mathrm{SiC}}}\right].$$

(28)

Integrating Equation (26) yields the equation describing the variation of $L$ with time

$$L={\left[\frac{\left(3D_t-1\right)\left(3D_t-2\right){\eta }_1}{1-\phi }\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta C_{{\mathrm{O}}_2,\mathrm{o}}}{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t}\cdot t\right]}^{\frac{1}{3D_t-1}}.$$

(29)

Substituting Equation (29) into Equation (27), the integral is given by

$$R=-{\eta }_2{\left(\frac{{\eta }_1}{1-\phi }\right)}^{\frac{2-3D_t}{3D_t-1}}{\left[\left(3D_t-1\right)\left(3D_t-2\right)\frac{k_B^{1.5}{T}^{1.5}{D}_f{\lambda }_{max}^{D_f}\beta C_{{\mathrm{O}}_2,\mathrm{o}}}{6{\pi }^{0.5}{d}^{2}p{m}^{0.5}{A}_t}\cdot t\right]}^{\frac{1}{3D_t-1}}.$$

(30)

As indicated by Equations (29) and (30), in porous media, the growth of the oxide layer thickness and the consumption of the composite material are affected by the structural parameters of the porous oxide layer on the material surface, along with factors like environmental oxygen concentration, environmental temperature, oxidization time and material density.

4. Validation and Application of the Model

4.1. Validation of the Oxidation Model

Based on the passive oxidation process of the C/SiC composite, we established a fractal diffusion-reaction kinetics model to investigate the diffusion of gases in porous media and the oxidation reaction of the composite. Subsequently, we compared the thickness of the oxide layer predicted by the passive oxidation model proposed in this paper after two hours of heating with the experimental results for various locations of the composite as shown in Figure 10, where the x-axis starts at the edge of the material and the positive direction is the direction of the sampling line from upstream to downstream on the thermal image of Figure 2.

Figure 11 illustrates the predicted and experimental results of oxide layer thickness at various locations of the composite after two hours of heating and oxidation. Owing to the uneven surface of the material and variations in pore sizes within the oxide film, the experimental results exhibit an uneven distribution of the oxide layer thickness. The two points connected by a dotted line in the figure indicate the maximum and minimum values of the experimental results. As depicted in the figure, the calculated results showed that as the distance from the windward front point of the material increases, the growth in oxide layer thickness decreases. Although the trend in the variation of the calculated thickness was small, the calculated results at a higher temperature fell between the maximum and minimum values of the experimental results, suggesting that the model predictions at higher temperature aligned with the experimental results. Further away from the windward front point of the material, the experimental results showed smaller values compared to the predicted results due to insufficient heating temperature, preventing full oxidation of the composite material. Therefore, the model proposed in this paper is effective at predicting the growth of the oxide layer in the C/SiC composite during passive oxidation at higher temperature.

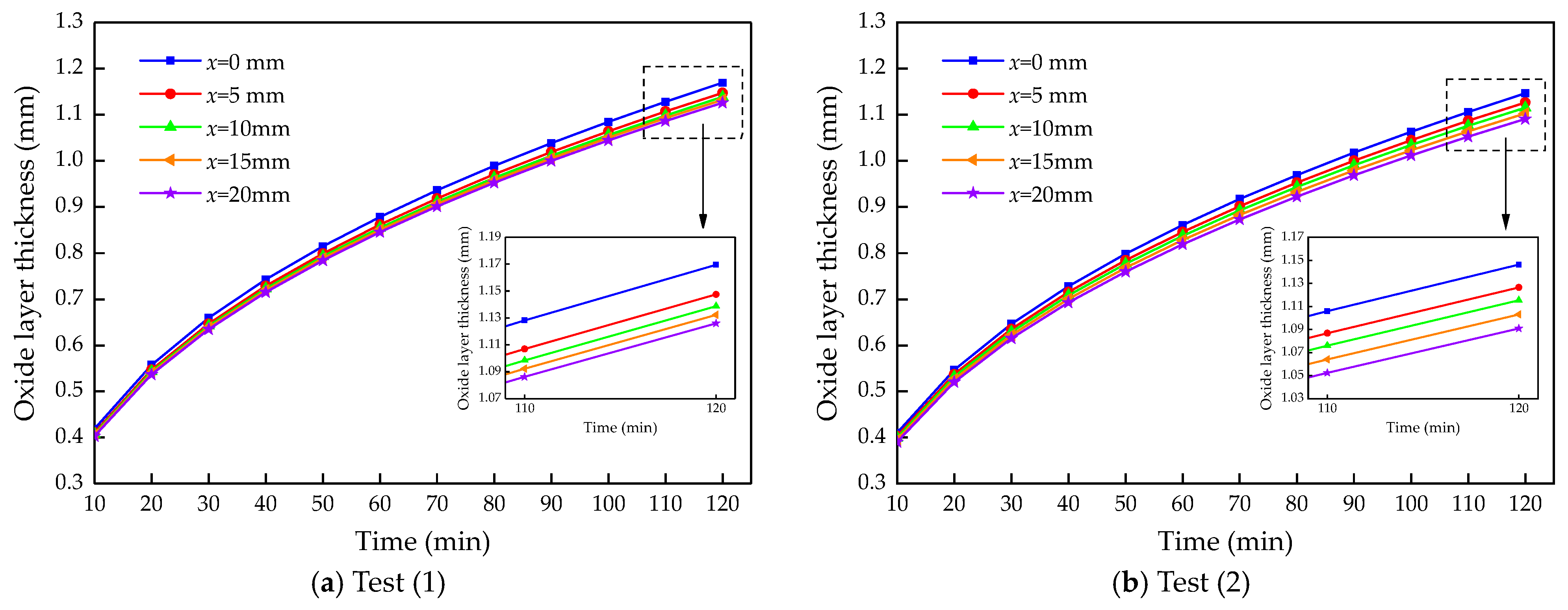
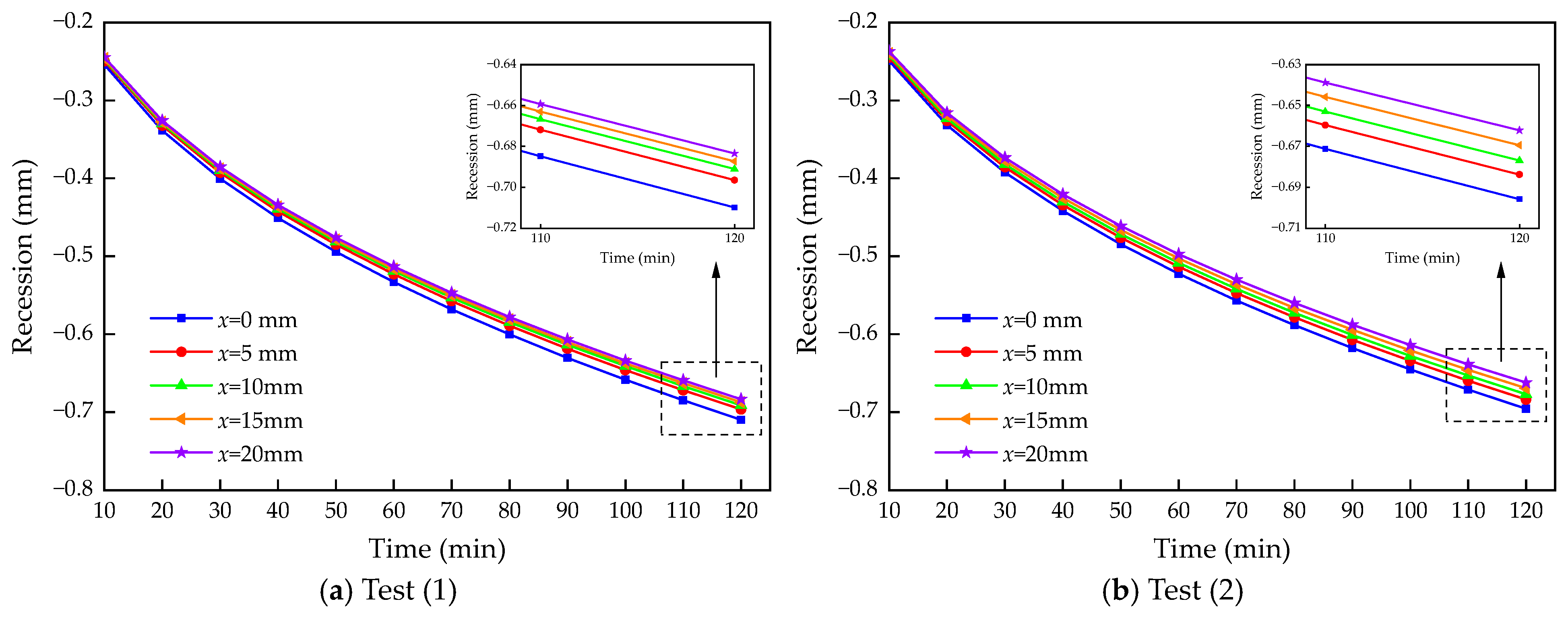
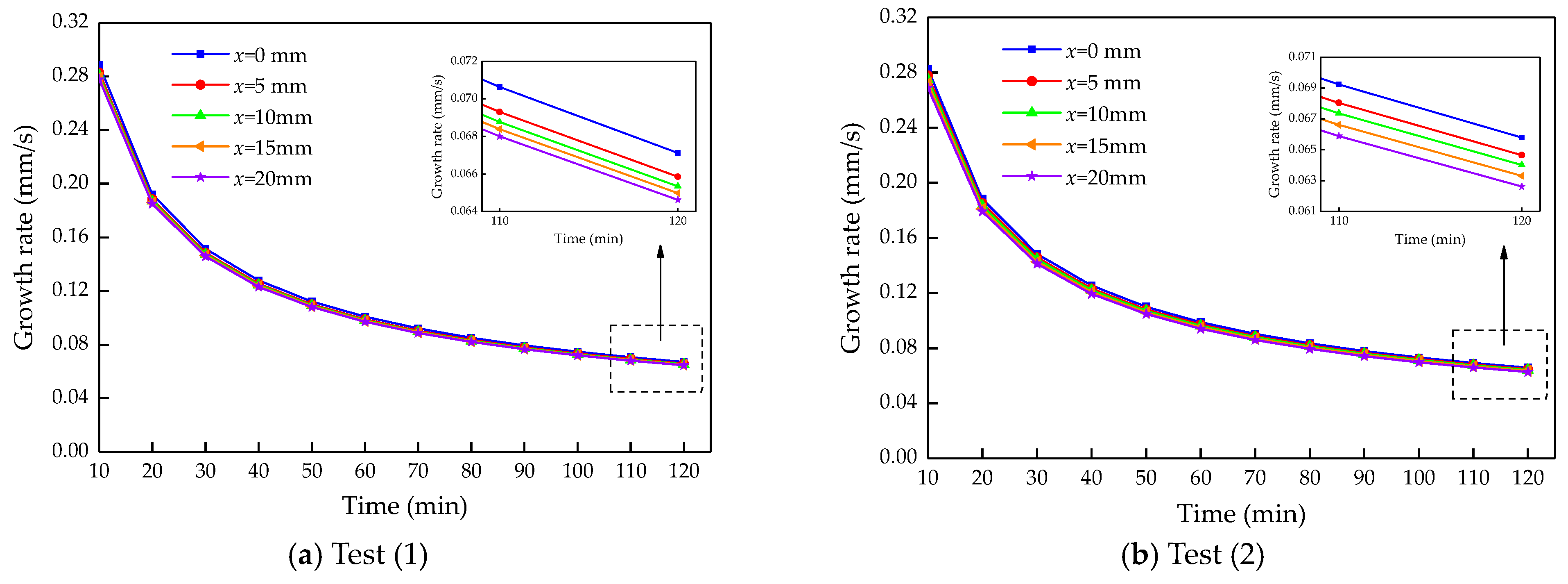
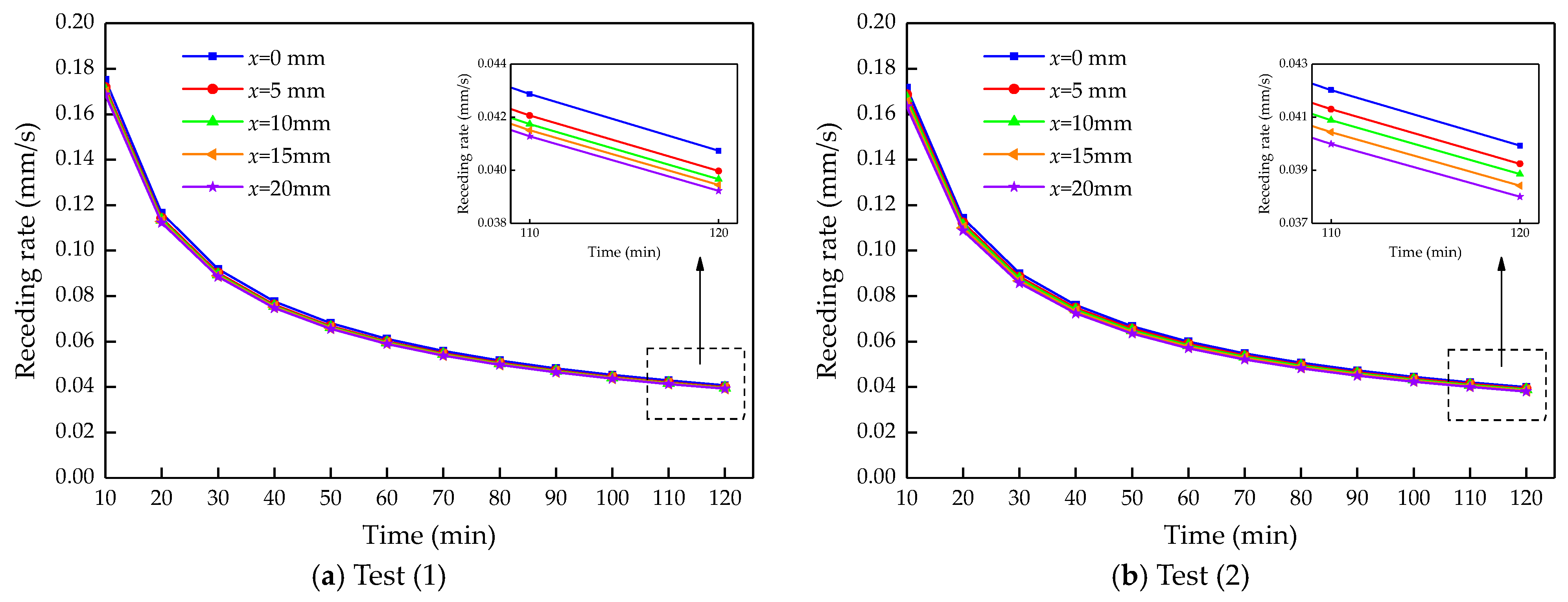
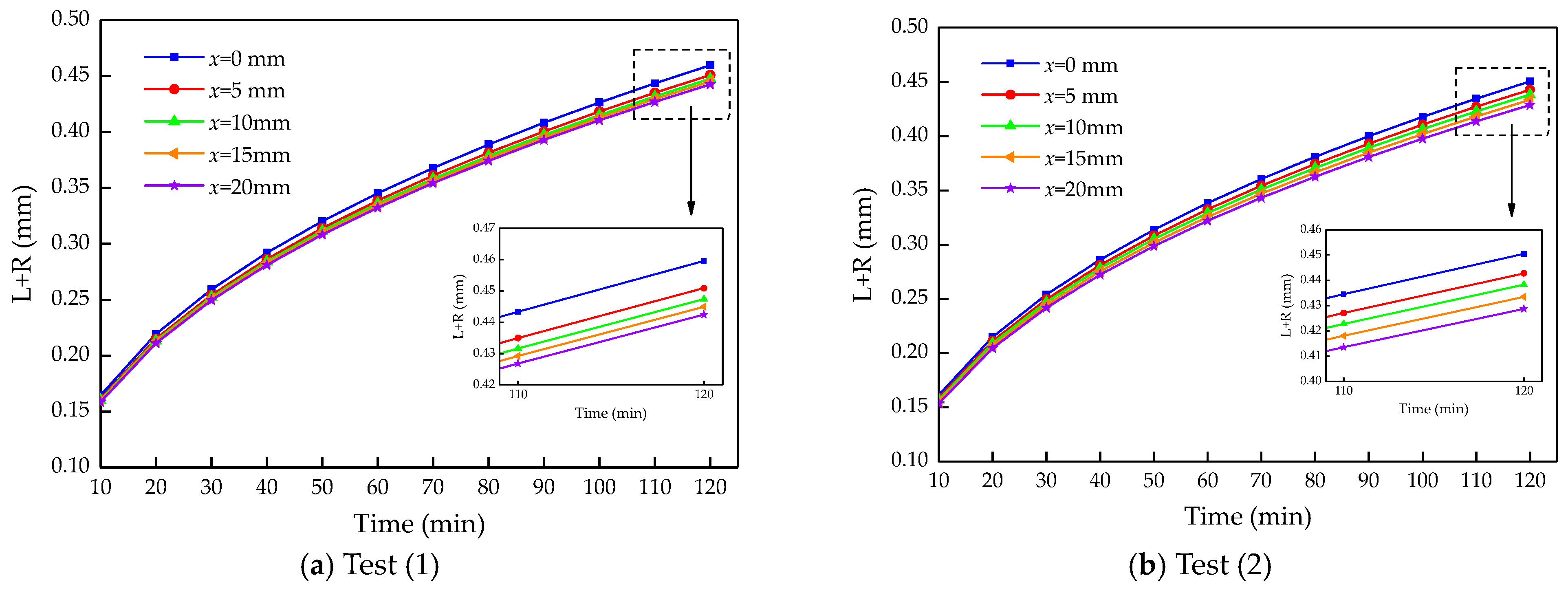
4.2. Calculation Results and Analysis

Experimental findings indicated that passive oxidation took place in the C/SiC composite after exposure to high-temperature gas heating, leading to the consumption of raw material and the formation of an oxide layer. Hence, predicting the impact of environmental parameters on passive oxidation is crucial and can also serve as a theoretical foundation for the application of the C/SiC composite. According to the passive oxidation model proposed in this study for the C/SiC composite, when the oxidation time was sufficiently long, the change in oxide layer thickness was predominantly governed by the existing thickness of the oxide layer and the gas diffusion coefficient within porous media. In the subsequent section, the oxidation from two tests with different incoming temperatures, each lasting more than 10 min, was analyzed. The goal was to predict the long-term oxidation of the C/SiC composite employing the passive oxidation model.

Figure 12 illustrates the time-dependent predicted growth of the oxide layer thickness at various locations of the C/SiC composite in two experiments. The figure indicates that the oxide layer thickness increased over time, with a diminishing growth as the distance from the windward front point of the material increased. This suggested that, with the same incoming flow temperature, the highest oxidation occurred at the upstream windward front point of the composite, with decreasing oxidation downstream. At the same material location, a higher incoming temperature resulted in a greater increase in oxide layer thickness, suggesting that elevated environmental temperature enhanced the oxidation process in the material.

Figure 13 demonstrates the time-dependent predicted recession of the original material at various locations of the C/SiC composite in two experiments. The figure shows that the original composite material underwent recession over time, with a diminishing amount of recession as the distance from the windward front point of the material increased. This implied that, with the same incoming flow temperature, the highest degree of oxidation occurred at the upstream windward front point of the composite, with a gradual decrease in oxidation downstream. At the same material location, a higher incoming temperature resulted in a greater recession of the original composite, suggesting that higher environmental temperature accelerated the consumption of the original material.

Figure 14 depicts the time-dependent predicted growth rate of the oxide layer thickness at various locations of the C/SiC composite in the two experiments. The figure indicates that the growth rate of oxide layer thickness decreased over time and gradually approached zero, suggesting that the increase in oxide layer thickness impeded gas diffusion in the porous oxide layer, leading to a reduction in the oxygen diffusion to the interface of the original material where the oxidation reaction occurred. Consequently, as the oxidation reaction advanced, the oxide layer gradually reached the stable state, signifying excellent ablation resistance of the composite material.

Figure 15 illustrates the time-dependent predicted receding rate of the original material at various locations of the C/SiC composite in two experiments. The figure indicates that the receding rate of the original composite material decreased over time and gradually approached zero. This suggested that as the oxidation reaction advanced, the passive oxidation rate of the material gradually diminished. Consequently, the original composite material moved closer to a stable state, allowing the antioxidant film formed by the oxidation reaction to protect the shape of the vehicle from damage at high temperature.

Throughout the passive oxidation of the C/SiC composite, the growth of the oxide layer and the recession of the original material altered the overall thickness of the C/SiC composite, impacting the aerodynamic characteristic of the aircraft. Figure 16 depicts the predicted overall thickness change of the C/SiC composite versus time in two experiments. The results revealed that the overall thickness of the material increased progressively with the oxidation reaction and the farther from the windward front point of the material, the smaller the incremental growth in overall thickness. This implied that, with the same incoming flow temperature, the overall thickness increased the most at the upstream windward front point of the composite, indicating the highest degree of material oxidation. At the same material location, a higher incoming temperature resulted in a greater increase in the overall thickness, suggesting that higher environmental temperature led to a more substantial overall change in the material.

5. Conclusions

In this study, we performed heating oxidation experiments on the C/SiC composite. Subsequently, the experimental material underwent characterization using scanning electron microscopy and energy dispersive X-ray spectroscopy. The result confirmed that, at high temperature, the composite underwent passive oxidation, resulting in the formation of the porous solid oxide.

Building on the oxidation mechanism of the C/SiC composite and fractal diffusion model, we developed a passive oxidation model for the composite. The passive oxidation model can effectively predict the growth of the oxide layer in the C/SiC composite during passive oxidation at higher temperature. Additionally, it accounts for the impact of the oxidation process on the consumption of the composite material, thereby enhancing the accuracy of predicting the overall thickness change in the C/SiC composite. The model presented in this paper enhances the theoretical foundation for the practical application of the C/SiC composite.

The result indicated that, under a similar incoming temperature, the oxidation degree of the C/SiC composite was highest at the upstream windward front point. Moreover, the oxidation degree gradually decreased from upstream to downstream, emphasizing the need to enhance thermal protection upstream of the vehicle. For the same material location, the recession of the composite increased progressively with the rise in incoming temperature. The reduction in composite material loss prevented damage to the vehicle surface and minimized the impact on vehicle stability and durability.

The growth of the oxide layer obstructed the diffusion of gases through the porous structure, leading to a decrease in the receding rate of the composite over time. With the progression of the oxidation reaction, the material steadily approached a stable state, affirming the excellent ablation resistance of the composite material.