An Efficient Numerical Scheme for Fractional Order Mathematical Model of Cytosolic Calcium Ion in Astrocytes
Abstract
1. Introduction
2. Preliminaries
2.1. Fractional Calculus
2.1.1. Laguerre Polynomial
2.1.2. Laguerre Operational Matrix for Fractional Differentiation
2.1.3. Jacobi Polynomial
2.2. Operational Matrix for JACOBI Polynomials
Function Approximation
3. Thrombin Receptor Activation Mechanism Computational Model
4. Outline of Technique
5. Computational Process by LCM
6. Analysis of the Computational Scheme
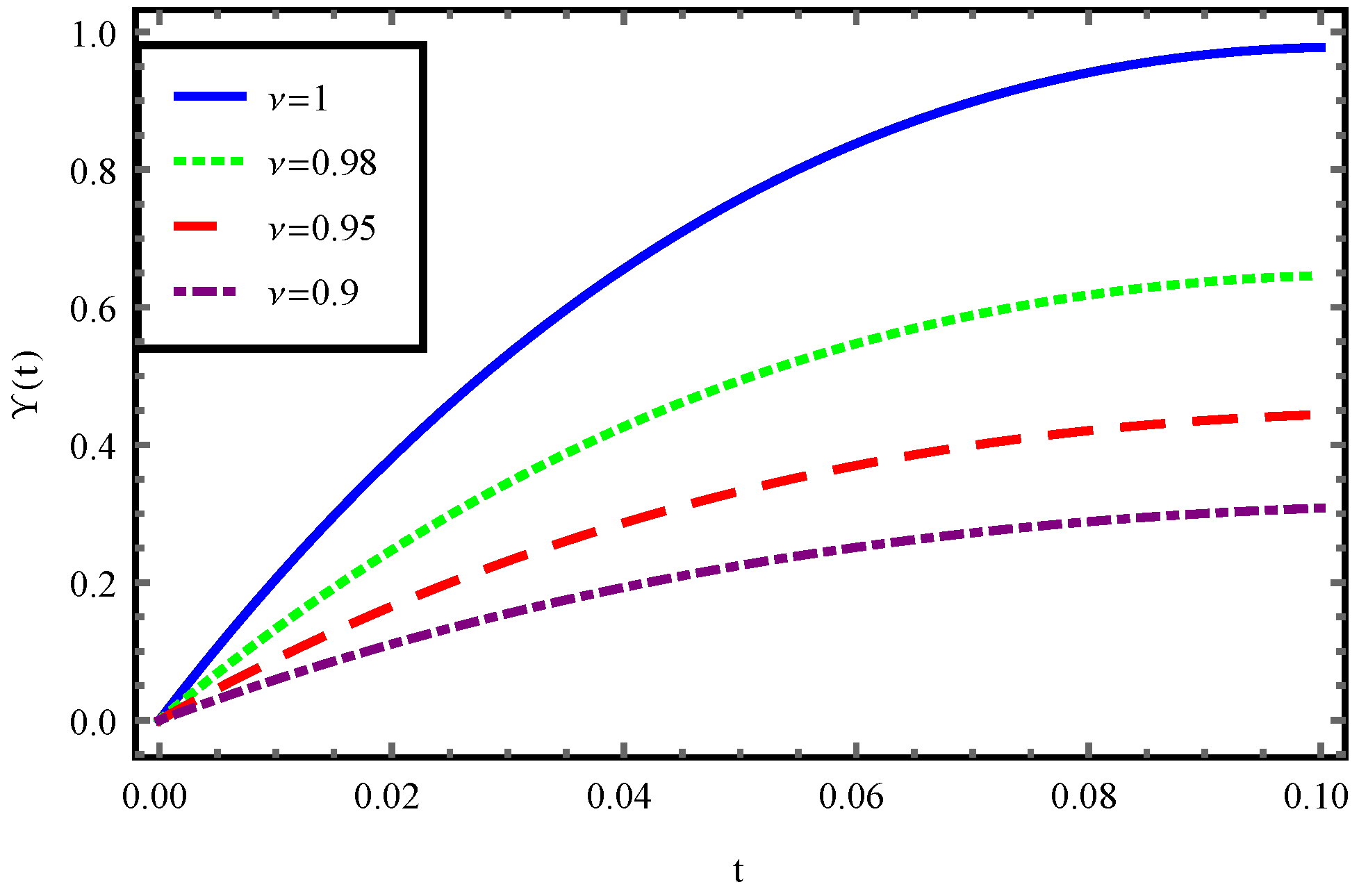
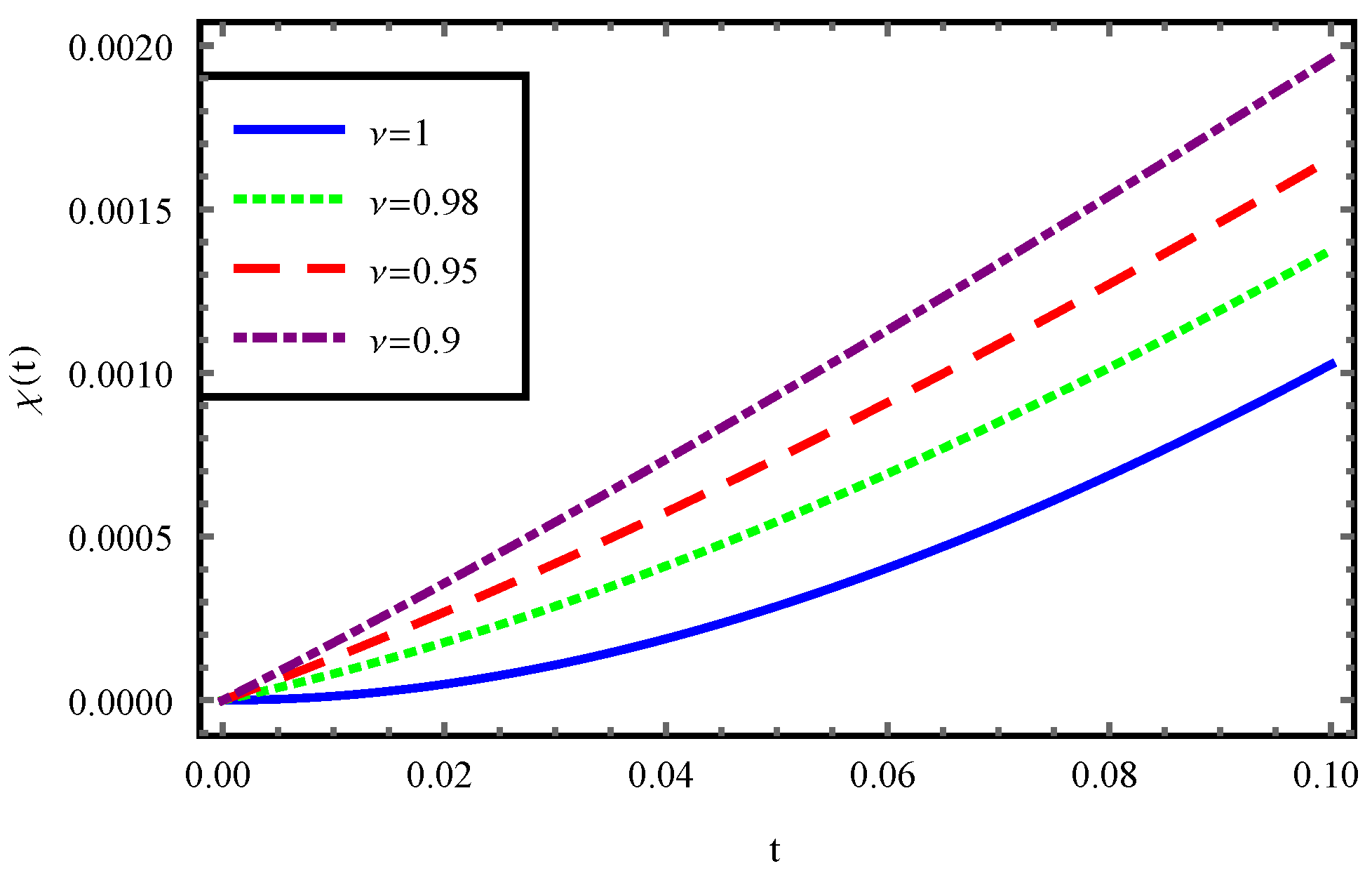
7. Numerical Results and Discussions
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Berridge, M.J. Inositol trisphosphate and diacylglycerol: Two interacting second messengers. Annu. Rev. Biochem. 1987, 56, 159–193. [Google Scholar] [CrossRef]
- Carafoli, E. Intracellular calcium homeostasis. Annu. Rev. Biochem. 1987, 56, 395–433. [Google Scholar] [CrossRef]
- Wiesner, T.F.; Berk, B.C.; Nerem, R.M. A mathematical model of cytosolic calcium dynamics in human umbilical vein endothelial cells. Am. J. Physiol.-Cell Physiol. 1996, 270, C1556–C1569. [Google Scholar] [CrossRef]
- Kim, Y.V.; Di Cello, F.; Hillaire, C.S.; Kim, K.S. Differential Ca2+ signaling by thrombin and protease-activated receptor-1-activating peptide in human brain microvascular endothelial cells. Am. J. Physiol.-Cell Physiol. 2004, 286, C31–C42. [Google Scholar] [CrossRef]
- Lenoci, L.; Duvernay, M.; Satchell, S.; DiBenedetto, E.; Hamm, H.E. Mathematical model of PAR1-mediated activation of human platelets. Mol. BioSyst. 2011, 7, 1129–1137. [Google Scholar] [CrossRef]
- Vu, T.K.H.; Hung, D.T.; Wheaton, V.I.; Coughlin, S.R. Molecular cloning of a functional thrombin receptor reveals a novel proteolytic mechanism of receptor activation. Cell 1991, 64, 1057–1068. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Atangana, A.; Alkahtani, B.S.T. Analysis of the Keller–Segel model with a fractional derivative without singular kernel. Entropy 2015, 17, 4439–4453. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Purohit, S.D.; Swroop, R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math. Model. Nat. Phenom. 2019, 14, 304. [Google Scholar] [CrossRef]
- Djordjević, V.D.; Jarić, J.; Fabry, B.; Fredberg, J.J.; Stamenović, D. Fractional derivatives embody essential features of cell rheological behavior. Ann. Biomed. Eng. 2003, 31, 692–699. [Google Scholar] [CrossRef]
- Agarwal, R.I.T.U.; Jain, S.O.N.A.L.; Agarwal, R.P. Mathematical modeling and analysis of dynamics of cytosolic calcium ion in astrocytes using fractional calculus. J. Fract. Calc. Appl. 2018, 9, 1–12. [Google Scholar]
- Kumar, D.; Singh, J.; Baleanu, D. Numerical computation of a fractional model of differential-difference equation. J. Comput. Nonlinear Dyn. 2016, 11, 061004. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Abbasbandy, S.; Rashidi, M.M. Analytical solution of fractional Navier–Stokes equation by using modified Laplace decomposition method. Ain Shams Eng. J. 2014, 5, 569–574. [Google Scholar] [CrossRef]
- Agarwal, R.; Yadav, M.P.; Agarwal, R.P.; Goyal, R. Analytic solution of fractional advection dispersion equation with decay for contaminant transport in porous media. Mat. Vesn. 2019, 71, 5–15. [Google Scholar]
- Khader, M.M. On the numerical solutions for the fractional diffusion equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2535–2542. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Kumar, D.; Nama, H.; Baleanu, D. Numerical and computational analysis of fractional order mathematical models for chemical kinetics and carbon dioxide absorbed into phenyl glycidyl ether. Results Phys. 2023, 53, 107003. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations, Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon-les-Bains, Switzerland, 1993; Volume 1. [Google Scholar]
- Bhrawy, A.H.; Tharwat, M.M.; Alghamdi, M.A. A new operational matrix of fractional integration for shifted Jacobi polynomials. Bull. Malays. Math. Sci. Soc. 2014, 37, 983–995. [Google Scholar]
- Pandey, P.; Kumar, S.; Jafari, H.; Das, S. An operational matrix for solving time-fractional order Cahn-Hilliard equation. Therm. Sci. 2019, 23, S2045–S2052. [Google Scholar] [CrossRef]
- Abdelkawy, M.A.; Taha, T.M. An operational matrix of fractional derivatives of Laguerre polynomials. Walailak J. Sci. Technol. (WJST) 2014, 11, 1041–1055. [Google Scholar]
- Doha, E.H.; Bhrawy, A.H.; Baleanu, D.; Ezz-Eldien, S.S. The operational matrix formulation of the Jacobi tau approximation for space fractional diffusion equation. Adv. Differ. Equ. 2014, 2014, 231. [Google Scholar] [CrossRef]
- Ahmadian, A.; Suleiman, M.; Salahshour, S.; Baleanu, D. A Jacobi operational matrix for solving a fuzzy linear fractional differential equation. Adv. Differ. Equ. 2013, 2013, 104. [Google Scholar] [CrossRef]
- Agarwal, R.; Purohit, S.D.; Kritika. A mathematical fractional model with nonsingular kernel for thrombin receptor activation in calcium signalling. Math. Methods Appl. Sci. 2019, 42, 7160–7171. [Google Scholar] [CrossRef]
- Rivlin, T.J. An Introduction to the Approximation of Functions; Courier Corporation: Chelmsford, MA, USA, 1981. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications; John Wiley and Sons, Inc.: New York, NY, USA, 1978. [Google Scholar]
- Behroozifar, M.; Sazmand, A. An approximate solution based on Jacobi polynomials for time-fractional convection–diffusion equation. Appl. Math. Comput. 2017, 296, 1–17. [Google Scholar] [CrossRef]
- Ezz-Eldien, S.S.; El-Kalaawy, A.A. Numerical simulation and convergence analysis of fractional optimization problems with right-sided Caputo fractional derivative. J. Comput. Nonlinear Dyn. 2018, 13, 011010. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M. Numerical investigation of the fractional-order Liénard and Duffing equations arising in oscillating circuit theory. Front. Phys. 2020, 8, 120. [Google Scholar] [CrossRef]
- Ezz-Eldien, S.S. New quadrature approach based on operational matrix for solving a class of fractional variational problems. J. Comput. Phys. 2016, 317, 362–381. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, D.; Nama, H.; Singh, J.; Kumar, J. An Efficient Numerical Scheme for Fractional Order Mathematical Model of Cytosolic Calcium Ion in Astrocytes. Fractal Fract. 2024, 8, 184. https://doi.org/10.3390/fractalfract8040184
Kumar D, Nama H, Singh J, Kumar J. An Efficient Numerical Scheme for Fractional Order Mathematical Model of Cytosolic Calcium Ion in Astrocytes. Fractal and Fractional. 2024; 8(4):184. https://doi.org/10.3390/fractalfract8040184
Chicago/Turabian StyleKumar, Devendra, Hunney Nama, Jagdev Singh, and Jitendra Kumar. 2024. "An Efficient Numerical Scheme for Fractional Order Mathematical Model of Cytosolic Calcium Ion in Astrocytes" Fractal and Fractional 8, no. 4: 184. https://doi.org/10.3390/fractalfract8040184
APA StyleKumar, D., Nama, H., Singh, J., & Kumar, J. (2024). An Efficient Numerical Scheme for Fractional Order Mathematical Model of Cytosolic Calcium Ion in Astrocytes. Fractal and Fractional, 8(4), 184. https://doi.org/10.3390/fractalfract8040184







