Abstract
In the context of fractal space, this study presents a higher-order nonlinear local fractional Bratu-type equation and thoroughly examines this generalized nonlinear equation. Additional analysis and identification of particular special situations of the generalized local fractional Bratu equation is performed. Finally, the Adomian decomposition method is utilized to derive that solution for the generalized Bratu equation of local fractional type. This study contributes to a deeper understanding of these equations and provides a practical computational approach to their solutions.
1. Introduction
The utilization of fractional derivatives represents a pivotal mathematical instrument for the development of sophisticated mathematical and physical models within the intriguing realm of fractal space [1,2,3]. Yang’s pioneering introduction of the local fractional derivative, as documented in his seminal works [4,5,6,7], has since captivated the attention of a multitude of researchers. In the realm of applied mathematics and mathematical analysis, the fractal derivative, also known as the Hausdorff derivative, serves as a non-Newtonian extension of the derivative specifically designed for measuring fractals within the framework of fractal geometry. Fractal derivatives have been developed to explore anomalous diffusion, addressing situations where conventional methods overlook the fractal characteristics of the medium. In this context, a fractal measure “t” is scaled by . Notably, this derivative is considered local, distinguishing it from the more commonly employed fractional derivative. Fractal calculus is structured as a generalization of standard calculus. This derivative has found extensive application in various scientific disciplines, notably in the fields of physics and engineering. Its influence spans critical domains such as nanoengineering, dynamic systems, and microelectronics. The main aspiration of fractional calculus is to extend differentiation and integration to fractional order, a concept that has been around since the 17th century due to the groundbreaking work of Leibnitz, Euler, Lagrange, Abel, Liouville, and many others [8,9,10]. A growing area of mathematics called fractional calculus (FC) has diverse applications in all connected sectors of science and problems of engineering. Some of the findings were published in books or related review articles. To learn more about local fractional calculus, see [11]. Incorporating fractal calculus into differential equations presents a robust paradigm for modeling intricate systems featuring self-replicating patterns. Within the domain of porous media, a fractional diffusion equation adeptly characterizes the non-local substance transport in materials exhibiting fractal structures. Likewise, a fractional population growth equation captures the dynamics of species expansion in environments marked by fractal patterns. Rooted in fractal calculus, these equations contribute to a nuanced understanding of phenomena in domains like heat conduction, electrical circuits, and wave propagation. This approach proves versatile and insightful, offering a comprehensive means of modeling the complex behaviors inherent in systems displaying fractal characteristics [12,13,14,15,16,17,18,19].
In the past few years, fractional differential equations have been extensively utilized in physics and engineering. Over the past few decades, fractional differential equations have found widespread application in engineering and science. Ordinary differential equations (ODEs) and fractional-order partial differential equations (PDEs) are commonly encountered in various disciplines, including fluid dynamics, biology, and physics. Numerous fields, such as electrical, mechanical, chemical, biological, and economics, particularly in ground transportation, signal image processing, and control theory, involve the use of these equations. Considerable effort has been invested in developing reliable and consistent numerical and analytical methodologies for solving these fractional equations over the last decade or more. For fractional differential equations, the methods of Adomian decomposition and variational iteration stand out among the rest. These methods distinguish themselves by providing approximations for the issues under consideration without relying on linearization or discretization.
Nonlinear differential equations, such as the Bratu-type equation, find application in various fields of science and engineering. Bratu’s problem has been utilized in addressing various challenges, including the Chandrashekhar model, the fuel ignition model, the thermal response model, and the framework for the electrospun nanofiber fabrication process. It is employed in chemical kinetics to simulate complex reaction kinetics, in combustion theory to comprehend flame propagation, and in heat transfer to examine temperature distributions in materials. Furthermore, it plays a role in mathematical biology, material science, nuclear physics, electrochemistry, and environmental science, enabling the modeling of complex processes such as population dynamics, diffusion in materials, neutron transport in reactors, electrochemical reactions, and pollutant spread. Beyond specific applications, the Bratu-type equation serves as a fundamental mathematical model, providing insights into nonlinear differential equations and their properties. This makes it a versatile and indispensable tool in scientific research and analysis. The “Nonlinear Local Fractional Bratu-Type Equation” is a mathematically intricate and captivating equation residing within the domain of fractional calculus differential equations. This equation presents a specialized variant of the Bratu equation, well known for its relevance in studying combustion processes and reaction–diffusion phenomena. Within the “Nonlinear Local Fractional Bratu-Type Equation,” the incorporation of fractional calculus introduces a unique and labyrinthine facet to the problem. Fractional calculus extends conventional notions of differentiation and integration to noninteger orders, enabling the portrayal of intricate physical processes characterized by memory and anomalous diffusion. Consequently, this equation holds particular significance across a spectrum of scientific and engineering disciplines, including physics, chemistry, biology, and materials science.
The equation typically appears as a differential equation containing a nonlinear term, a fractional derivative, and boundary conditions determined by the specific contextual problem. The solution to this equation provides valuable insights into the behavior of systems governed by fractional diffusion and nonlinear reactions, revealing the intricate interplay between these two phenomena. Ongoing research endeavors focused on the “Non-linear Bratu Equation of Local Fractional Type” captivate mathematicians, physicists, and engineers alike as they grapple with challenges in the realm of non-standard calculus, nonlinear dynamics, and complex systems. A deep understanding of the solutions and attributes of this equation has the potential to advance our understanding of diverse real-world processes, potentially leading to practical applications across domains such as combustion theory, chemical kinetics, and biological modeling.
The Bratu-type equation holds significant utility in the fields of science and engineering. Recognizing its importance, we shift our focus to investigating a generalized local fractional Bratu-type equation [20,21]. In this extension, we employ the Mittag-Leffler function to define a generalized local fractional Bratu-type equation. The inclusion of the Mittag-Leffler function enhances the flexibility of modeling, allowing the customization of equations matching specific behaviors observed in the system under study. This adaptability is crucial to accurately representing the nuances of real-world phenomena. Incorporating the Mittag-Leffler function into the generalization of an equation serves as a valuable approach to enriching the model and addressing the intricacies inherent in fractional calculus. It proves to be a robust tool for characterizing systems with features such as long memory, anomalous diffusion, and other nonlocal or non-Markovian behaviors. Moreover, our approach extends to the n-dimensional generalization of the fractional Bratu-type equation, and the derived model can be easily streamlined to the classical Bratu-type equation by assigning specific values.
In this equation, ℘ is a constant and is the Mittag-Leffler function with real parameter . In addition, and are known and unknown functions.
We also introduce another form of the generalized local fractional Bratu-type equation:
where ℘ is constant. In this equation, is the exponential function.
If , then Equation (1), reduces in to
If , then Equation (2), reduces in to
Establishing the existence and uniqueness of the generalized non-linear local fractional Bratu-type equation formulated is straightforward with the application of the Lipschitz condition. In addition, to address a combustion challenge within a numerical framework, a specific approach is employed. Numerous techniques have been explored to approximate the analytical solution of a nonlinear differential equation. These include the homotopy perturbation method [14,22], the variational iteration method [15,23], the reduced differential transform method [24], the homotopy analysis method [25,26], and the -homotopy analysis transform method [27,28], among others.
In this research work, we utilize the Adomian decomposition method—a powerful tool for solving linear or nonlinear differential equations to derive the results of the generalized Bratu-type equation. The Adomian decomposition method is a powerful technique that provides efficient algorithms for approximate analytical solutions and numerical simulations for real-world applications in engineering and applied sciences. This approach is an excellent technique for solving generalized nonlinear fractional differential equations, even though the outcome is expressed in terms of an infinite series. Variational formulation of the local fractional Bratu-type equation is established by the semi-inverse method and its approximate analytical solution is obtained by the Adomian decomposition method.
In addressing the motivation behind this work, it becomes apparent that conventional derivative definitions prove insufficient when tackling space co-ordinate within a fractal environment. To adequately capture this phenomenon, the utilization of Yang’s local fractional derivative becomes crucial. This research employs the Adomian decomposition method, recognized as a potent technique for solving both linear and nonlinear differential equations [29], serving as the cornerstone for deriving our findings.
The paper is structured into six sections. Section 1 provides an introduction, while Section 2 covers the Preliminaries. Section 3 presents the Adomian decomposition method (ADM), Section 4 addresses the solution of the generalized local fractional Bratu equation, and Section 5 delves into specific cases, including the numerical solution of the model using the Adomian decomposition method. Concluding remarks are presented in Section 6. The references are discussed at the end of the paper.
2. Preliminaries
In this segment, we introduce essential definitions and foundational principles of the Adomian decomposition method in the contexts of local fractional and calculus of fractional domains.
2.1. Local Fractal Derivative
The local fractional derivative of function with an order of at the specific point is provided in accordance with [4,5,6,7]
which, for all satisfies condition where
2.2. Local Fractal Integral
If in fractal space has order , then the local fractal integral of is defined in the interval as follows:
where , = max and , is a division of .
2.3. Properties of Local Fractional Derivatives
We present the following properties associated with local fractional derivatives (see [30,31]):
We let ; then,
- (i)
- (ii)
- (iii)
The higher-order local fractional order can be expressed as
2.4. Mittag-Leffler Function
The Swedish mathematician Gosta Mittag-Leffler explored and introduced a function defined as in the expression of power series in 1903 (see [4,8]):
where .
3. Adomian Decomposition Method (ADM)
We have the well-known ADM approach, which is quite useful for solving linear or non-linear differential equations [32,33]:
where N is a nonlinear operator and is an unknown function. The equation defined in (8) is known as a non-linear system. Now, to find the approximate solutions for Equation (8), first, we consider the solution of (8) is unique with the form
It is evident that finding the solution to (9) becomes notably challenging when the given system involves nonlinear terms. To address this challenge, the Adomian decomposition method (ADM) emerges as a pivotal tool. In this approach, the nonlinear term is decomposed as follows:
where is known as Adomian polynomials with coefficients , , , , …, , hence
Now, to obtain the values of , we set
and
where
Now, putting the value of in (13), from (8), we obtain
Now, to obtain the value of , we define the following relations:
For more details on the method, see [32,33,34,35].
4. Solution of Generalized Local Fractional Bratu Equation
Theorem 1.
Consider the following generalized Bratu-type equation:
where is known as Yang’s fractional derivative of a local type, with
Proof.
We have the Adomian decomposition method, which is quite useful in solving nonlinear ordinary or partial differential equations. To solve the differential equation defined in the statement of Theorem 1, first, we consider
and its inverse integral is
The operator form of Equation (16), with Adomian polynomials, is
Upon using the inverse operator, we obtain the following recurrence relation:
hence, putting , in Equation (21), we obtain
where
And for , Equation (21) offers
with
In the same manner, for , Equation (21) provides us with
where and so on.
Then, we can easily find the solution of Equation (16) as
□
Theorem 2.
Derive the solution of another form of the generalized local fractional Bratu-type equation:
where is known as Yang’s fractional derivative of local type, and
Proof.
Utilizing the Adomian decomposition method, a valuable technique for solving nonlinear ordinary or partial differential equations, we address the solution of the differential equation specified in Theorem 1. Initially, we examine
and its inverse integral is
The operator form of the above equations with Adomian polynomials is
Upon using the inverse operator, we obtain the following recurrence relation:
hence, for , we obtain from (31)
where
And for , Equation (31) offers
with
5. Particular Cases
Now, we discuss some particular cases of the proposed generalized local fractional Bratu-type equations. In the above-defined Theorems 1 and 2, by putting some specific values of different constants, it is reduced into well-known differential equations.
- Special Case (i):
If we put in the defined (16) of Theorem 1, we obtain
with
By using the above-defined procedure, we obtain the following results:
Now, using the method defined in the above section, we obtain the following terms:
in the same manner,
or
Upon solving, we obtain
and using the same approach, we obtain
and the remaining terms can be acquired using a similar methodology.
Now, by putting the above-obtained coefficients in the following equation, we obtain the required solution,
or
Through our investigation, we establish the efficacy of the Adomian decomposition method in solving non-linear differential equations. The results obtained for the generalized local fractional Bratu-type equation offer enhanced clarity and validation of the method’s capabilities.
To examine the spatial behavior, we depict Figure 1, illustrating the variations of the dependent variable concerning the independent variable for Case (i) at various values of and These results are derived with and The findings reveal a noticeable influence of on the behavior of Additionally, it is observed that the value of the space coordinate initially rises and subsequently decreases over a defined time interval.
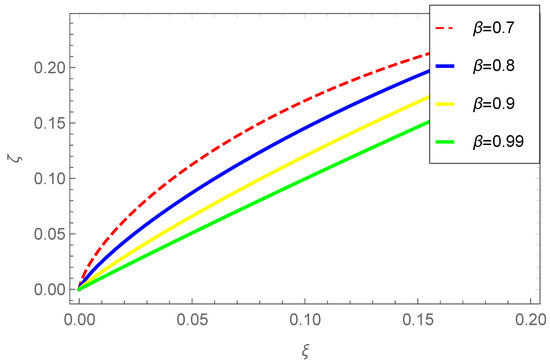
Figure 1.
Change in of Case (i) with respect to for different values of .
- Special Case (ii):
We obtain
and using the same approach, we obtain
and other terms can be obtained by the same approach.
Now, by putting the above-obtained coefficients in the following equation, we obtain the required solution,
or
In our examination, it was demonstrated that the Adomian decomposition method proves highly effective in solving non-linear differential equations. The results obtained for the generalized local fractional Bratu-type equation align with those presented by Yao et al. [21], underscoring the precision and reliability of the method.
To examine the spatial behavior, we depict Figure 2, illustrating the variations of the dependent variable concerning the independent variable for Case (ii) at various values of and These results are derived with and The findings reveal a noticeable influence of on the behavior of Additionally, it is observed that the value of space coordinate initially rises and subsequently decreases over a defined time interval.
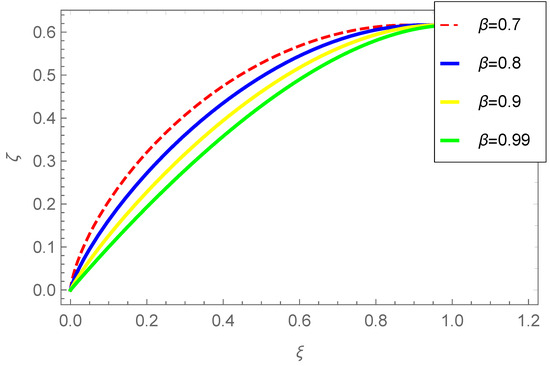
Figure 2.
Change in of Case (ii) with respect to for different values of .
6. Conclusions
In this paper, we introduce the generalized local fractional Bratu-type equation, extending the discussion to encompass the n-dimensional case. We also use the Mittag-Leffler function in this generalization. A more efficient analytical approach is presented for the analysis of the generalized local fractional Bratu-type equation, utilizing the Yang local fractional derivative. Our investigation involves the formulation of two theorems pertaining to the higher-order generalized local fractional Bratu equation, followed by an exploration of its solution using the Adomian decomposition method. Furthermore, we present specific results that underscore the method’s effectiveness in approximating analytical solutions for this equation. The incorporation of a more generalized function enhances the utility of the study compared to the original nongeneralized equation.
Author Contributions
G.A. led the study, formal analysis, funding acquisition, and data creation. R.S.D. wrote the manuscript, conceptualized the research, methodology, validation, interpreted the results, and organized the required literature conducting all numerical calculations. B.S.T.A. conducted the investigation, provided resources, software, and supervised the work. G.L.S. wrote the manuscript, visualization, and formatted the final document. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23066).
Data Availability Statement
The data used are publicly available.
Acknowledgments
We would like to express our sincere thanks to the editor and reviewers for their valuable comments and suggestions. The authors thank the Dean of Scientific Research at Imam Mohammad Ibn Saud Islamic University for their support.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| time co-ordinate | |
| space co-ordinate | |
| constant | |
| ℘ | constant |
References
- Miao, T.; Yu, B.; Duan, Y.; Fang, Q. A Fractal Analysis of Permeability for Fractured Rocks. Int. J. Heat Mass Transf. 2015, 81, 75–80. [Google Scholar] [CrossRef]
- Althobaiti, S.; Dubey, R.S.; Prasad, J.G. Solution of local fractional generalized fokker-planck equation using local fractional Mohand adomian decomposition method. Fractals 2022, 30, 2240028. [Google Scholar] [CrossRef]
- Li, L.; Yu, B. Fractal Analysis of the Effective Thermal Conductivity of Biological Media Embedded with Randomly Distributed Vascular Trees. Int. J. Heat Mass Transf. 2013, 67, 74–80. [Google Scholar] [CrossRef]
- Yang, X.J. Fractional Functional Analysis and Its Applications; Asian Academic: Hong Kong, China, 2011. [Google Scholar]
- Yang, X.J. Local Fractional Calculus and Its Applications; World Science Publisher: New York, NY, USA, 2012. [Google Scholar]
- Jafari, H.; Goswami, P.; Dubey, R.S.; Prasad, J.G. Solution of the local fractional generalized KDV equation using homotopy analysis method. Fractals 2021, 29, 2140014. [Google Scholar] [CrossRef]
- Wang, K.L. Exact travelling wave solution for the local fractional Camassa-Holm-Kadomtsev-Petviashvili equation. Alex. Eng. J. 2023, 63, 371–376. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Vol. 11 of Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; vol. 198 of Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Jafari, H.; Goswami, P.; Dubey, R.S.; Sharma, S.; Chaudhary, A. Fractional SIZR model of Zombie infection. Int. J. Math. Comput. Eng. 2023, 1, 91–104. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies, 204; Elsevier Science B.V.: Amsterdam, The Netherlands, 2006; p. xvi+523. [Google Scholar]
- Barbosa, R.S.; Tenreiro Machado, J.; Ferreira, I.M. PID controller tuning using fractional calculus concepts. Fract. Calc. Appl. Anal. 2004, 7, 119–134. [Google Scholar]
- Duarte, F.B.; Tenreiro Machado, J. Chaotic phenomena and fractional order dynamics in the trajectory control of redundant manipulators. Nonlinear Dyn. 2002, 29, 315–342. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.M. An Asymptotic Perturbation Solution for a Linear Oscillator of Free Damped Vibrations in Fractal Medium Described by Local Fractional Derivatives. Commun. Nonlinear Sci. Numer. Simul. 2015, 29, 499–504. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Khan, Y.; Mohyud-Din, S.T. Local Fractional Variational Iteration Method for Diffusion and Wave Equation on Cantor Sets. Rom. J. Phys. 2014, 59, 36–48. [Google Scholar]
- Yang, X.J.; Tenreiro Machado, J.A.; Baleanu, D.; Cattani, C. On exact traveling-wave solutions for local fractional Korteweg-de Vries equation. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 110–118. [Google Scholar] [CrossRef] [PubMed]
- Kolwankar, K.M.; Gangal, A.D. Local fractional Fokker-Planck equation. Phys. Rev. Lett. 1998, 80, 214–217. [Google Scholar] [CrossRef]
- Jafari, H.; Jassim, H.K.; Tchier, F.; Baleanu, D. On the approximate solutions of local fractional differential equations with local fractional operators. Entropy 2016, 18, 150. [Google Scholar] [CrossRef]
- Zhang, Y.; Baleanu, D.; Yang, X.J. New solutions of the transport equations in porous media within local fractional derivative. Proc. Rom. Acad. Ser. A 2016, 17, 230–236. [Google Scholar]
- Wazwaz, A.M. Adomain Decomposition Method for a Reliable Treatment of the Bratu-type equations. Appl. Math. Comput. 2019, 166, 652–663. [Google Scholar]
- Yao, S.; Li, W.; Wang, K. Analytical solution for non-linear local fractional Bratu-type equation in a fractal space. Therm. Sci. 2020, 24, 3941–3947. [Google Scholar] [CrossRef]
- Wang, K.L. New perspective to the fractal Konopelchenko–Dubrovsky equations with M-truncated fractional derivative. Int. J. Geom. Methods Mod. Phys. 2023, 20, 2350072. [Google Scholar] [CrossRef]
- Yang, Y.J.; Hua, L.Q. Variational Iteration Transform Method for Fractional Differential Equations with Local Fractional Derivative. Abstr. Appl. Anal. 2014, 2014, 760957. [Google Scholar] [CrossRef]
- Wei, C.F.; Wang, K.L. Fractal soliton solutions for the fractal-fractional shallow water wave equation arising in ocean engineering. Alex. Eng. J. 2023, 65, 859–865. [Google Scholar] [CrossRef]
- Wang, K.L. A novel perspective to the local fractional Zakharov–Kuznetsov-modified equal width dynamical model on Cantor sets. Math. Methods Appl. Sci. 2023, 46, 622–630. [Google Scholar] [CrossRef]
- Kumar, S. A New Fractional Modeling Arising in Engineering Sciences and Its Analytical Approximate Solution. Alex. Eng. J. 2013, 52, 813–819. [Google Scholar] [CrossRef]
- Malyk, I.V.; Gorbatenko, M.; Chaudhary, A.; Sharma, S.; Dubey, R.S. Numerical Solution of Nonlinear Fractional Diffusion Equation in Framework of the Yang–Abdel–Cattani Derivative Operator. Fractal Fract. 2021, 5, 64. [Google Scholar] [CrossRef]
- Shah, N.A.; Hamed, Y.S.; Abualnaja, K.M.; Chung, J.D.; Shah, R.; Khan, A. A Comparative Analysis of Fractional Order Kaup–Kupershmidt Equation within Different Operators. Symmetry 2022, 14, 986. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, K.L. Variational Principles for Fractal Whitham-Broer-Kaup Equations in Shallow Water. Fractals 2020, 29, 2150028. [Google Scholar] [CrossRef]
- Yang, X.J. Fractal Vector Analysis: A Local Fractional Calculus Point of View; Academic Press: New York, NY, USA, 2021. [Google Scholar]
- Yang, X.J.; Tenreiro Machado, J.A. A New Fractal Nonlinear Burgers’ Equation Arising in the Acoustic Signals Propagation. Math. Methods Appl. Sci. 2019, 42, 7539–7544. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A Hybrid Computational Approach for Klein-Gordon Equations on Cantor Sets. Nonlinear Dyn. 2017, 87, 511–517. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A Reliable Modification of Adomian Decomposition Method. Appl. Math. Comput. 1999, 102, 77–86. [Google Scholar] [CrossRef]
- Adomian, G. A Review of the Decomposition Method in Applied Mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Wang, K.L.; Yao, S.W.; Liu, Y.P.; Zhang, L.N. A Fractal Variational Principle for the Telegraph Equation with Fractal Derivatives. Fractals 2020, 28, 2050058. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).