A Novel Hybrid Crossover Dynamics of Monkeypox Disease Mathematical Model with Time Delay: Numerical Treatments
Abstract
1. Introduction
2. Fundamental Definitions
3. The Hyprid Picewise Fractional-Variable Order for a Fractional Stochastic Monkeypox Disease Model with Time Delay
4. Theoretical Analysis of the Model
4.1. Positivity
4.2. The Equilibrium Points
5. Numerical Methods for Crossover Models
5.1. Algorithm to Solve (12)–(14)
- Step 1. Let if start with the initial condition
- Step 3. If start with the end point in step 2 and use it as an initial condition for the system (13).
- Step 5. If start with the end point in step 4 and use it as an initial condition for the system (10).
- Step 7. Output the current values as solutions if the values of the variables in this iteration and the last iteration are negligibly close. Return to Step 2 if values are not close.
5.2. Stability of CPC-NAB5SM
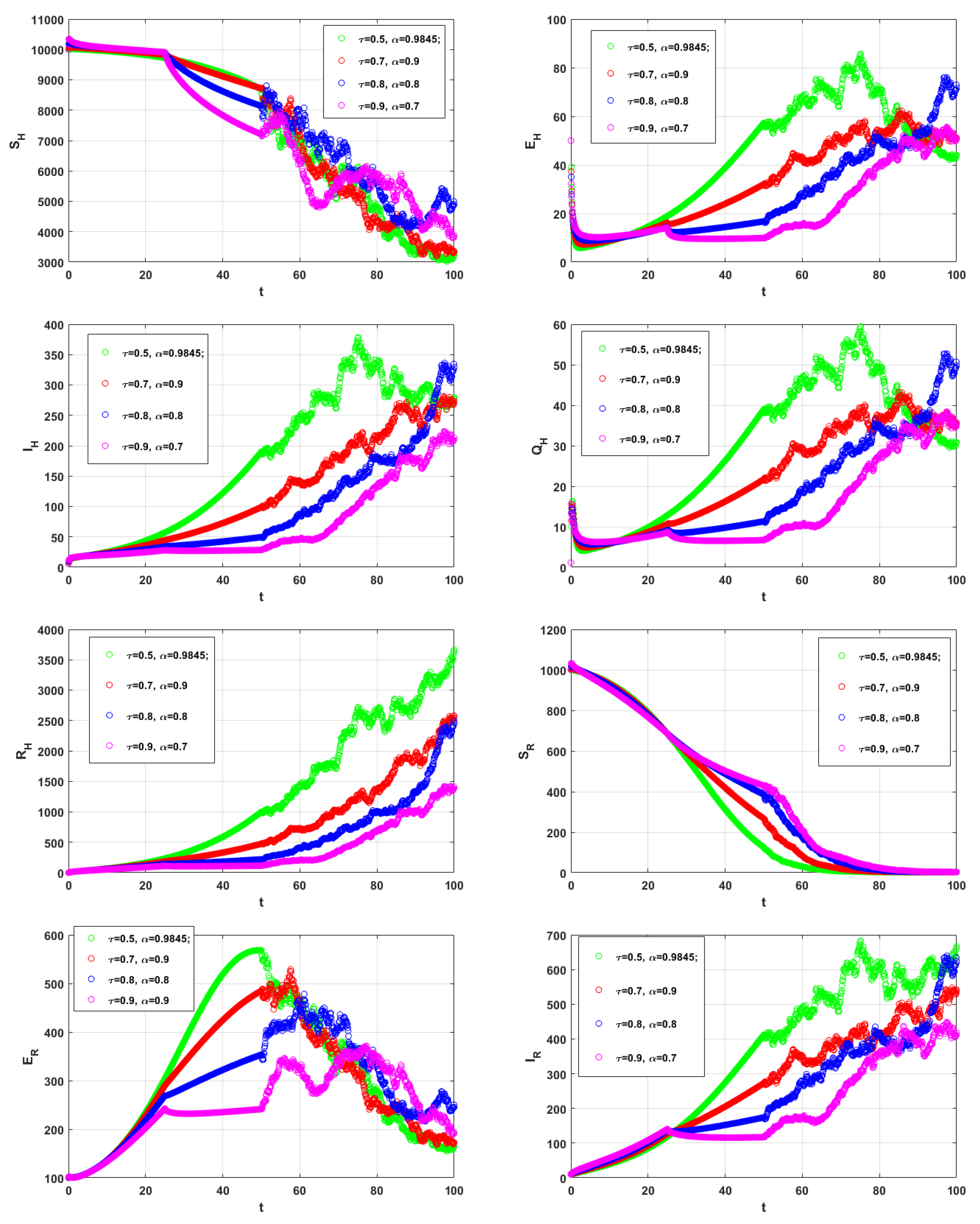
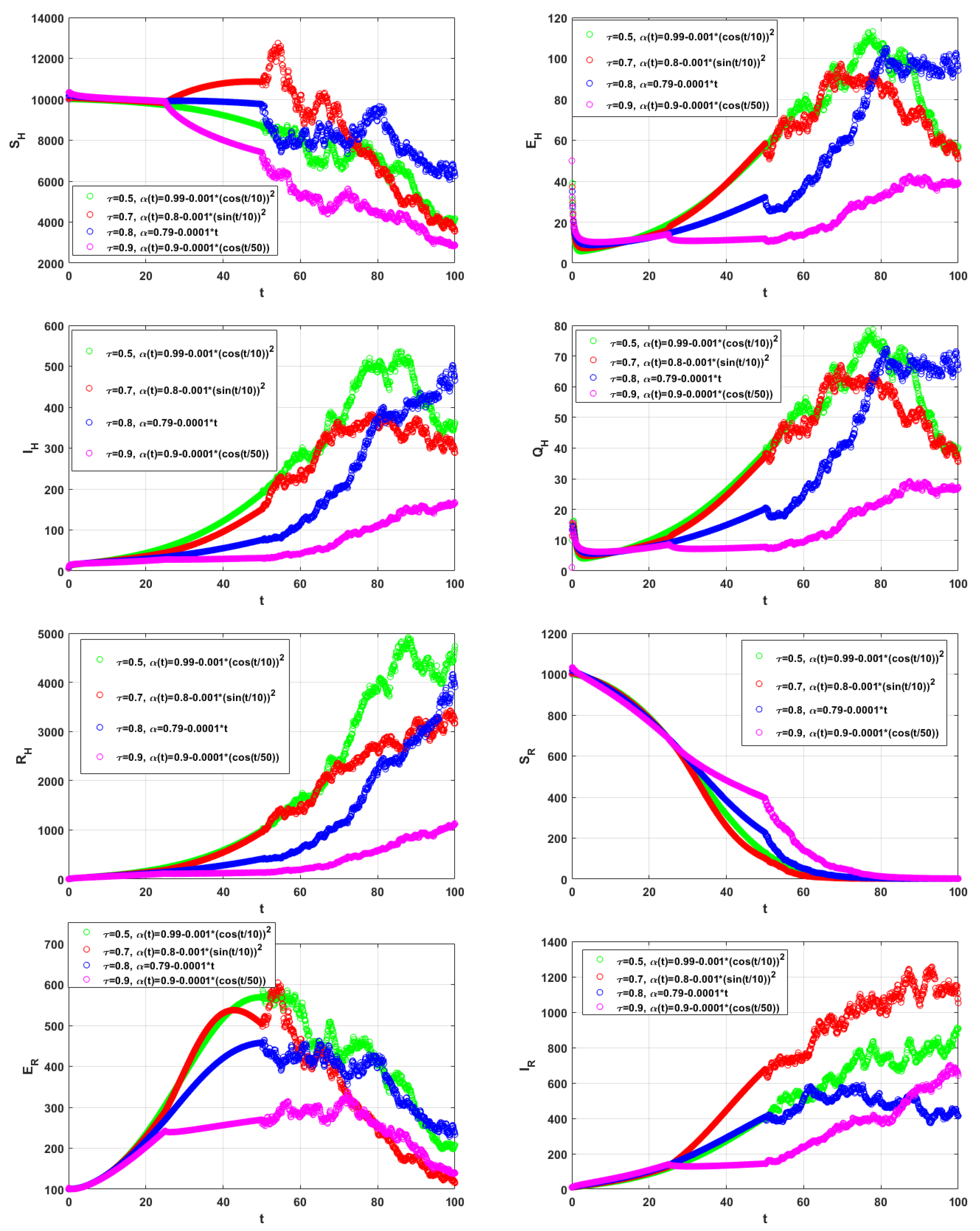
6. Numerical Simulations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Özköse, F.; Yılmaz, S.; Yavuz, M.; Öztürk, İ.; Şenel, M.T.; Bağcı, B.Ş.; Doğan, M.; Önal, Ö. A Fractional Modeling of Tumor-Immune System Interaction Related to Lung Cancer with Real Data. Eur. Phys. J. Plus. 2022, 137, 40. [Google Scholar] [CrossRef]
- Peter, O.J.; Kumar, S.; Kumari, N.; Oguntolu, F.A.; Oshinubi, K.; Musa, R. Transmission dynamics of Monkeypox virus: A mathematical modelling approach. Model. Earth Syst. Environ. 2022, 8, 3423–3434. [Google Scholar] [CrossRef] [PubMed]
- Breman, J.G. Monkeypox: An emerging infection for humans. Emerg. Infect. 2000, 4, 45–67. [Google Scholar]
- Riopelle, J.C.; Munster, V.J.; Port, J.R. Atypical and unique transmission of monkeypox virus during the 2022 outbreak: An overview of the current state of knowledge. Viruses 2022, 14, 2012. [Google Scholar] [CrossRef]
- Kumar, N.; Acharya, A.; Gendelman, H.E.; Byrareddy, S.N. The 2022 outbreak and the pathobiology of the monkeypox virus. J. Autoimmun. 2022, 131, 102855. [Google Scholar] [CrossRef]
- Usman, S.; Adamu, I.I. Modeling the transmission dynamics of the monkeypox virus infection with treatment and vaccination interventions. J. Appl. Math. Phys. 2017, 5, 2335. [Google Scholar] [CrossRef]
- Khan, A.; Sabbar, Y.; Din, A. Stochastic modeling of the Monkeypox epidemic with cross-infection hypothesis in a highly disturbed environment. Math. Biosci. Eng. 2022, 19, 13560–13581. [Google Scholar] [CrossRef] [PubMed]
- Grant, R.; Nguyen, L.B.L.; Breban, R. Modelling human-to-human transmission of monkeypox. Bull. World Health Organ. 2020, 98, 638. [Google Scholar] [CrossRef]
- Bankuru, S.V.; Kossol, S.; Hou, W.; Mahmoudi, P.; Rycht, J.; Taylor, D. A game-theoretic model of Monkeypox to assess vaccination strategies. PeerJ 2020, 8, e9272. [Google Scholar] [CrossRef]
- Syam, M.I.; Al-Refai, M. Fractional differential equations with Atangana-Baleanu fractional derivative: Analysis and applications. Chaos Solitons Fractals 2019, 2, 100013. [Google Scholar] [CrossRef]
- Sweilam, N.H.; L-Mekhlafi, S.M.A.; Baleanu, D. A hybrid stochastic fractional order Coronavirus (2019-nCov) mathematical model. Chaos Solitons Fractals 2021, 145, 110762. [Google Scholar] [CrossRef]
- Agarwal, P.; Baleanu, D.; Chen, Y.-Q.; Momani, S.; Machado, J.A.T. Fractional Calculus; Springer: Singapore, 2019. [Google Scholar]
- Salahshour, S.; Ahmadian, A.; Senu, N.; Baleanu, D.; Agarwal, P. On analytical solutions of the fractional differential equation with uncertainty: Application to the Basset problem. Entropy 2015, 17, 885–902. [Google Scholar] [CrossRef]
- Baleanu, D.; Fernandez, A.; Akgül, A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020, 8, 360. [Google Scholar] [CrossRef]
- Li, B.; Zhang, T.; Zhang, C. Investigation of financial bubble mathematical model under fractal-fractional Caputo derivative. Fractals 2023, 31, 2350050-31. [Google Scholar] [CrossRef]
- Li, B.; Eskandari, Z. Dynamical analysis of a discrete-time SIR epidemic model. J. Frankl. Inst. 2023, 360, 7989–8007. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T.; Ali, A. Mathematical analysis of the Cauchy type dynamical system under piecewise equations with Caputo fractional derivative. Chaos Solitons Fractals 2022, 161, 112356. [Google Scholar] [CrossRef]
- Shah, K.; Abdeljawad, T.; Alrabaiah, H. On coupled system of drug therapy via piecewise equations. Fractals 2022, 30, 2240206. [Google Scholar] [CrossRef]
- Shah, K.; Naz, H.; Abdeljawad, T.; Abdalla, B. Study of fractional order dynamical system of viral infection disease under piecewise derivative. CMES 2023, 136, 921–941. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. New concept in calculus: Piecewise differential and integral operators. Chaos Solitons Fractals 2021, 145, 110638. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. Modeling third waves of COVID-19 spread with piecewise differential and integral operators: Turkey, spain and czechia. Results Phys. 2021, 29, 104694. [Google Scholar] [CrossRef]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Hassan, S.M.; Alsenaideh, N.R.; Radwan, A.E. Numerical treatments for some stochastic-deterministic chaotic systems. Results Phys. 2022, 38, 105628. [Google Scholar] [CrossRef]
- Atangana, A.; Araz, S.İ. Deterministic-Stochastic modeling: A new direction in modeling real world problems with crossover effect. Math. Biosci. Eng. 2022, 19, 3526–3563. [Google Scholar] [PubMed]
- Atangana, A.; Koca, I. Modeling the spread of Tuberculosis with piecewise differential operators. Comput. Model. Eng. Sci. 2022, 131, 787–814. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Z. Analysis of COVID-19 epidemic transmission trend based on a time 190 delayed dynamic model. Commun. Pure Appl. Anal. 2021, 22, 1–18. [Google Scholar] [CrossRef]
- Devipriya, R.; Dhamodharavadhani, S.; Selvi, S. SEIR Model for COVID-19 epidemic using delay differential equation. J. Physics 2021, 1767, 012005. [Google Scholar] [CrossRef]
- Kiselev, I.N.; Akberdin, I.R.; Kolpakov, F.A. A Delay Differential Equation Approach to Model the COVID-19 Pandemic. medRxiv 2021. [Google Scholar] [CrossRef]
- Ebraheem, H.K.; Alkhateeb, N.; Badran, H.; Sultan, E. Delayed dynamics of SIR model for 205 COVID-19. OPen J. Model. Simulation 2021, 9, 146–158. [Google Scholar] [CrossRef]
- Rihan, F.A.; Alsakaji, H.J.; Rajivganthi, C. Stochastic SIRC epidemic model with time-delay for COVID-19. Adv. Differ. Equations 2020, 502, 2020. [Google Scholar] [CrossRef]
- Nastasi, G.; Perrone, C.; Taffara, S.; Vitanza, G. A time-delayed deterministic model for the spread of COVID-19 with calibration on a real dataset. Mathematics 2022, 10, 661. [Google Scholar] [CrossRef]
- Khan, A.; Ikram, R.; Din, A.; Humphries, U.W.; Akgul, A. Stochastic COVID-19 SEIQ epidemic model with time-delay. Results Phys. 2021, 30, 104775. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Sweilam, N.H.; Al-Mekhlafi, S.M.; Ajami, T.M. Optimal control of hybrid variable-order fractional coronavirus (2019-nCov) mathematical model; numerical treatments. Ecol. Complexity 2022, 49, 100983. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Rosales-García, J.J.; Bernal-Alvarado, J.J.; Córdova-Fraga, T.; Guzmán-Cabrera, R. Fractional mechanical oscillators. RevisaMex Fis. 2012, 58, 348–352. [Google Scholar]
- Ullah, M.Z.; Baleanu, D. A new fractional SICA model and numerical method for the transmission of HIV/AIDS. Math Meth. Appl. Sci. 2021, 44, 8648–8659. [Google Scholar] [CrossRef]
- Mickens, R. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Scherer, R.; Kalla, S.; Tang, Y.; Huang, J. The Grünwald-Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Y.; Nualart, D. Modified Euler approximation scheme for stochastic differential equations driven by fractional Brownian motions. arXiv 2013, arXiv:1306.1458vl. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sweilam, N.H.; Al-Mekhlafi, S.M.; Hassan, S.M.; Alsenaideh, N.R.; Radwan, A.E. A Novel Hybrid Crossover Dynamics of Monkeypox Disease Mathematical Model with Time Delay: Numerical Treatments. Fractal Fract. 2024, 8, 185. https://doi.org/10.3390/fractalfract8040185
Sweilam NH, Al-Mekhlafi SM, Hassan SM, Alsenaideh NR, Radwan AE. A Novel Hybrid Crossover Dynamics of Monkeypox Disease Mathematical Model with Time Delay: Numerical Treatments. Fractal and Fractional. 2024; 8(4):185. https://doi.org/10.3390/fractalfract8040185
Chicago/Turabian StyleSweilam, Nasser H., Seham M. Al-Mekhlafi, Saleh M. Hassan, Nehaya R. Alsenaideh, and Abdelaziz E. Radwan. 2024. "A Novel Hybrid Crossover Dynamics of Monkeypox Disease Mathematical Model with Time Delay: Numerical Treatments" Fractal and Fractional 8, no. 4: 185. https://doi.org/10.3390/fractalfract8040185
APA StyleSweilam, N. H., Al-Mekhlafi, S. M., Hassan, S. M., Alsenaideh, N. R., & Radwan, A. E. (2024). A Novel Hybrid Crossover Dynamics of Monkeypox Disease Mathematical Model with Time Delay: Numerical Treatments. Fractal and Fractional, 8(4), 185. https://doi.org/10.3390/fractalfract8040185